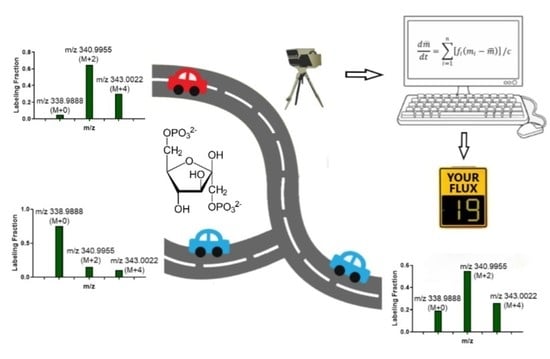
Metabolic Flux Analysis—Linking Isotope Labeling and Metabolic Fluxes
Abstract
:1. Introduction
2. Example on Upper Glycolysis
3. Generalization of the Labeling Balance Equations
4. Basic Assumptions in MFA
5. Predicting Labeling Patterns and Solving Metabolic Fluxes
6. Evaluation of MFA Result and Tracer Selection
7. Kinetic Flux Profiling and Isotopically Non-Stationary MFA
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
Code Availability
References
- Boyle, J. Lehninger Principles of Biochemistry (4th ed.): Nelson, D., and Cox, M. Biochem. Mol. Biol. Educ. 2005, 33, 74–75. [Google Scholar] [CrossRef]
- Caspi, R.; Altman, T.; Billington, R.; Dreher, K.; Foerster, H.; Fulcher, C.A.; Holland, T.A.; Keseler, I.M.; Kothari, A.; Kubo, A.; et al. The MetaCyc database of metabolic pathways and enzymes and the BioCyc collection of Pathway/Genome Databases. Nucleic Acids Res. 2014, D1, D459–D471. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fiehn, O. The link between genotypes and phenotypes. Plant Mol. Biol. 2002, 48, 155–171. [Google Scholar] [CrossRef] [PubMed]
- Beckonert, O.; Keun, H.C.; Ebbels, T.M.D.; Bundy, J.; Holmes, E.; Lindon, J.C.; Nicholson, J.K. Metabolic profiling, metabolomic and metabonomic procedures for NMR spectroscopy of urine, plasma, serum and tissue extracts. Nat. Protoc. 2007, 2, 2692–2703. [Google Scholar] [CrossRef]
- Hollywood, K.; Brison, D.R.; Goodacre, R. Metabolomics: Current technologies and future trends. Proteomics 2006, 6, 4716–4723. [Google Scholar] [CrossRef]
- Nicholson, J.K.; Lindon, J.C. Systems biology: Metabonomics. Nature 2008, 455, 1054–1056. [Google Scholar] [CrossRef]
- Holmes, E.; Antti, H. Chemometric contributions to the evolution of metabonomics: Mathematical solutions to characterising and interpreting complex biological NMR spectra. Analyst 2002, 127, 1549–1557. [Google Scholar] [CrossRef]
- Hoult, D.I.; Busby, S.J.W.; Gadian, D.G.; Radda, G.K.; Richards, R.E.; Seeley, P.J. Observation of tissue metabolites using nuclear magnetic resonance. Nature 1974, 252, 285–287. [Google Scholar] [CrossRef] [PubMed]
- Griffiths, W.J.; Wang, Y. Mass spectrometry: From proteomics to metabolomics and lipidomics. Chem. Soc. Rev. 2009, 38, 1882–1896. [Google Scholar] [CrossRef] [PubMed]
- Gomez-Casati, D.F.; Zanor, M.I.; Busi, M.V. Metabolomics in plants and humans: Applications in the prevention and diagnosis of diseases. Biomed Res. Int. 2013, 2013. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Swanson, M.G.; Zektzer, A.S.; Tabatabai, Z.L.; Simko, J.; Jarso, S.; Keshari, K.R.; Schmitt, L.; Carroll, P.R.; Shinohara, K.; Vigneron, D.B.; et al. Quantitative analysis of prostate metabolites using 1H HR-MAS spectroscopy. Magn. Reson. Med. 2006, 55, 1257–1264. [Google Scholar] [CrossRef] [PubMed]
- Kline, E.E.; Treat, E.G.; Averna, T.A.; Davis, M.S.; Smith, A.Y.; Sillerud, L.O. Citrate Concentrations in Human Seminal Fluid and Expressed Prostatic Fluid Determined via 1H Nuclear Magnetic Resonance Spectroscopy Outperform Prostate Specific Antigen in Prostate Cancer Detection. J. Urol. 2006, 176, 2274–2279. [Google Scholar] [CrossRef]
- Sauer, U. Metabolic networks in motion: 13C-based flux analysis. Mol. Syst. Biol. 2006, 2, 62. [Google Scholar] [CrossRef] [Green Version]
- Jang, C.; Chen, L.; Rabinowitz, J.D. Metabolomics and Isotope Tracing. Cell 2018, 173, 822–837. [Google Scholar] [CrossRef] [PubMed]
- Jeremy, J.Y.; Ballard, S.A.; Naylor, A.M.; Miller, M.A.W.; Angelini, G.D. Effects of sildenafil, a type-5 cGMP phosphodiesterase inhibitor, and papaverine on cyclic GMP and cyclic AMP levels in the rabbit corpus cavernosum in vitro. Br. J. Urol. 1997, 79, 958–963. [Google Scholar] [CrossRef]
- Wiechert, W. 13C metabolic flux analysis. Metab. Eng. 2001, 3, 195–206. [Google Scholar] [CrossRef] [PubMed]
- Antoniewicz, M.R. Methods and advances in metabolic flux analysis: A mini-review. J. Ind. Microbiol. Biotechnol. 2015, 42, 317–325. [Google Scholar] [CrossRef]
- Dai, Z.; Locasale, J.W. Understanding metabolism with flux analysis: From theory to application. Metab. Eng. 2017, 43, 94–102. [Google Scholar] [CrossRef] [PubMed]
- Zamboni, N. 13C metabolic flux analysis in complex systems. Curr. Opin. Biotechnol. 2011, 22, 103–108. [Google Scholar] [CrossRef]
- Cascante, M.; Selivanov, V.; Ramos-Montoya, A. Application of tracer-based metabolomics and flux analysis in targeted cancer drug design. Methods Pharmacol. Toxicol. 2012, 299–320. [Google Scholar] [CrossRef]
- Antoniewicz, M.R. A guide to 13C metabolic flux analysis for the cancer biologist. Exp. Mol. Med. 2018, 50, 1–13. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Boghigian, B.A.; Seth, G.; Kiss, R.; Pfeifer, B.A. Metabolic flux analysis and pharmaceutical production. Metab. Eng. 2010, 12, 81–95. [Google Scholar] [CrossRef]
- Warburg, O.; Posener, K.; Negelein, E. The metabolism of cancer cells. Biochem. Z 1924, 152, 319–344. [Google Scholar]
- Vander Heiden, M.G.; Cantley, L.C.; Thompson, C.B. Understanding the Warburg effect: The metabolic requirements of cell proliferation. Science 2009, 324, 1029–1033. [Google Scholar] [CrossRef] [Green Version]
- Faubert, B.; Li, K.Y.; Cai, L.; Hensley, C.T.; Kim, J.; Zacharias, L.G.; Yang, C.; Do, Q.N.; Doucette, S.; Burguete, D.; et al. Lactate Metabolism in Human Lung Tumors. Cell 2017, 171, 358–371. [Google Scholar] [CrossRef] [Green Version]
- Hui, S.; Ghergurovich, J.M.; Morscher, R.J.; Jang, C.; Teng, X.; Lu, W.; Esparza, L.A.; Reya, T.; Zhan, L.; Yanxiang Guo, J.; et al. Glucose feeds the TCA cycle via circulating lactate. Nature 2017, 551, 115–118. [Google Scholar] [CrossRef] [Green Version]
- Van Gulik, W.M.; Antoniewicz, M.R.; deLaat, W.T.A.M.; Vinke, J.L.; Heijnen, J.J. Energetics of growth and penicillin production in a high-producing strain of Penicillium chrysogenum. Biotechnol. Bioeng. 2001, 72, 185–193. [Google Scholar] [CrossRef]
- Orman, M.A.; Berthiaume, F.; Androulakis, I.P.; Ierapetritou, M.G. Advanced stoichiometric analysis of metabolic networks of mammalian systems. Crit. Rev. Biomed. Eng. 2011, 39, 511–534. [Google Scholar] [CrossRef]
- Carinhas, N.; Bernal, V.; Teixeira, A.P.; Carrondo, M.J.; Alves, P.M.; Oliveira, R. Hybrid metabolic flux analysis: Combining stoichiometric and statistical constraints to model the formation of complex recombinant products. BMC Syst. Biol. 2011, 5, 34. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Feist, A.M.; Palsson, B.O. The biomass objective function. Curr. Opin. Microbiol. 2010, 13, 344–349. [Google Scholar] [CrossRef] [Green Version]
- Orth, J.D.; Thiele, I.; Palsson, B.O. What is flux balance analysis? Nat. Biotechnol. 2010, 28, 245–248. [Google Scholar] [CrossRef]
- Ranganathan, S.; Suthers, P.F.; Maranas, C.D. OptForce: An optimization procedure for identifying all genetic manipulations leading to targeted overproductions. PLoS Comput. Biol. 2010, 6, e1000744. [Google Scholar] [CrossRef]
- Raghunathan, A.; Shin, S.; Daefler, S. Systems approach to investigating host-pathogen interactions in infections with the biothreat agent Francisella. Constraints-based model of Francisella tularensis. BMC Syst. Biol. 2010, 4, 118. [Google Scholar] [CrossRef] [Green Version]
- Harcombe, W.R.; Delaney, N.F.; Leiby, N.; Klitgord, N.; Marx, C.J. The ability of flux balance analysis to predict evolution of central metabolism scales with the initial distance to the optimum. PLoS Comput. Biol. 2013, 9, e1003091. [Google Scholar] [CrossRef] [Green Version]
- Bonarius, H.P.J.; Timmerarends, B.; De Gooijer, C.D.; Tramper, J. Metabolite-balancing techniques vs. 13C tracer experiments to determine metabolic fluxes in hybridoma cells. Biotechnol. Bioeng. 1998, 58, 258–262. [Google Scholar] [CrossRef]
- Schmidt, K.; Marx, A.; De Graaf, A.A.; Wiechert, W.; Sahm, H.; Nielsen, J.; Villadsen, J. 13C tracer experiments and metabolite balancing for metabolic flux analysis: Comparing two approaches. Biotechnol. Bioeng. 1998, 58, 254–257. [Google Scholar] [CrossRef]
- Çalik, P.; Akbay, A. Mass flux balance-based model and metabolic flux analysis for collagen synthesis in the fibrogenesis process of human liver. Med. Hypotheses 2000, 55, 5–14. [Google Scholar] [CrossRef]
- Reisz, J.A.; D’Alessandro, A. Measurement of metabolic fluxes using stable isotope tracers in whole animals and human patients. Curr. Opin. Clin. Nutr. Metab. Care 2017, 20, 366. [Google Scholar] [CrossRef]
- Weitzel, M.; Nöh, K.; Dalman, T.; Niedenführ, S.; Stute, B.; Wiechert, W. 13CFLUX2—High-performance software suite for 13C-metabolic flux analysis. Bioinformatics 2013, 29, 143–145. [Google Scholar] [CrossRef]
- Beste, D.J.V.; Nöh, K.; Niedenführ, S.; Mendum, T.A.; Hawkins, N.D.; Ward, J.L.; Beale, M.H.; Wiechert, W.; McFadden, J. 13C-flux spectral analysis of host-pathogen metabolism reveals a mixed diet for intracellular mycobacterium tuberculosis. Chem. Biol. 2013, 20, 1012–1021. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, Z.; Bommareddy, R.R.; Frank, D.; Rappert, S.; Zeng, A.P. Deregulation of feedback inhibition of phosphoenolpyruvate carboxylase for improved lysine production in Corynebacterium glutamicum. Appl. Environ. Microbiol. 2014, 4, 1388–1393. [Google Scholar] [CrossRef] [Green Version]
- Liu, L.; Shah, S.; Fan, J.; Park, J.O.; Wellen, K.E.; Rabinowitz, J.D. Malic enzyme tracers reveal hypoxia-induced switch in adipocyte NADPH pathway usage. Nat. Chem. Biol. 2016, 12, 345–352. [Google Scholar] [CrossRef] [Green Version]
- Zamboni, N.; Fischer, E.; Sauer, U. FiatFlux—A software for metabolic flux analysis from 13C-glucose experiments. BMC Bioinform. 2005, 6, 209. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, Q.; Zhang, Y.; Yang, C.; Xiong, H.; Lin, Y.; Yao, J.; Li, H.; Xie, L.; Zhao, W.; Yao, Y.; et al. Acetylation of metabolic enzymes coordinates carbon source utilization and metabolic flux. Science 2010, 5968, 1004–1007. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Del Castillo, T.; Ramos, J.L.; Rodríguez-Herva, J.J.; Fuhrer, T.; Sauer, U.; Duque, E. Convergent peripheral pathways catalyze initial glucose catabolism in Pseudomonas putida: Genomic and flux analysis. J. Bacteriol. 2007, 189, 5142–5152. [Google Scholar] [CrossRef] [Green Version]
- Fong, S.S.; Nanchen, A.; Palsson, B.O.; Sauer, U. Latent pathway activation and increased pathway capacity enable Escherichia coli adaptation to loss of key metabolic enzymes. J. Biol. Chem. 2006, 281, 8024–8033. [Google Scholar] [CrossRef] [Green Version]
- Young, J.D. INCA: A computational platform for isotopically non-stationary metabolic flux analysis. Bioinformatics 2014, 30, 1333–1335. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lewis, C.A.; Parker, S.J.; Fiske, B.P.; McCloskey, D.; Gui, D.Y.; Green, C.R.; Vokes, N.I.; Feist, A.M.; Vander Heiden, M.G.; Metallo, C.M. Tracing Compartmentalized NADPH Metabolism in the Cytosol and Mitochondria of Mammalian Cells. Mol. Cell 2014, 55, 253–263. [Google Scholar] [CrossRef] [Green Version]
- Jiang, L.; Shestov, A.A.; Swain, P.; Yang, C.; Parker, S.J.; Wang, Q.A.; Terada, L.S.; Adams, N.D.; McCabe, M.T.; Pietrak, B.; et al. Reductive carboxylation supports redox homeostasis during anchorage-independent growth. Nature 2016, 532, 255–258. [Google Scholar] [CrossRef]
- Vacanti, N.M.; Divakaruni, A.S.; Green, C.R.; Parker, S.J.; Henry, R.R.; Ciaraldi, T.P.; Murphy, A.N.; Metallo, C.M. Regulation of substrate utilization by the mitochondrial pyruvate carrier. Mol. Cell 2014, 56, 425–435. [Google Scholar] [CrossRef] [Green Version]
- Green, C.R.; Wallace, M.; Divakaruni, A.S.; Phillips, S.A.; Murphy, A.N.; Ciaraldi, T.P.; Metallo, C.M. Branched-chain amino acid catabolism fuels adipocyte differentiation and lipogenesis. Nat. Chem. Biol. 2016, 12, 15–21. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yoo, H.; Antoniewicz, M.R.; Stephanopoulos, G.; Kelleher, J.K. Quantifying reductive carboxylation flux of glutamine to lipid in a brown adipocyte cell line. J. Biol. Chem. 2008, 283, 20621–20627. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Metallo, C.M.; Gameiro, P.A.; Bell, E.L.; Mattaini, K.R.; Yang, J.; Hiller, K.; Jewell, C.M.; Johnson, Z.R.; Irvine, D.J.; Guarente, L.; et al. Reductive glutamine metabolism by IDH1 mediates lipogenesis under hypoxia. Nature 2012, 481, 380–384. [Google Scholar] [CrossRef] [Green Version]
- Noguchi, Y.; Young, J.D.; Aleman, J.O.; Hansen, M.E.; Kelleher, J.K.; Stephanopoulos, G. Effect of anaplerotic fluxes and amino acid availability on hepatic lipoapoptosis. J. Biol. Chem. 2009, 48, 33425–33436. [Google Scholar] [CrossRef] [Green Version]
- Sriram, G.; Fulton, D.B.; Iyer, V.V.; Peterson, J.M.; Zhou, R.; Westgate, M.E.; Spalding, M.H.; Shanks, J.V. Quantification of compartmented metabolic fluxes in developing soybean embryos by employing biosynthetically directed fractional 13C labeling, two-dimensional [13C, 1H] nuclear magnetic resonance, and comprehensive isotopomer balancing. Plant Physiol. 2004, 136, 3043–3057. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Murarka, A.; Clomburg, J.M.; Moran, S.; Shanks, J.V.; Gonzalez, R. Metabolic analysis of wild-type Escherichia coli and a Pyruvate Dehydrogenase Complex (PDHC)-deficient derivative reveals the role of PDHC in the fermentative metabolism of glucose. J. Biol. Chem. 2010, 285, 31548–31558. [Google Scholar] [CrossRef] [Green Version]
- Fu, Y.; Yoon, J.M.; Jarboe, L.; Shanks, J.V. Metabolic flux analysis of Escherichia coli MG1655 under octanoic acid (C8) stress. Appl. Microbiol. Biotechnol. 2015, 99, 4397–4408. [Google Scholar] [CrossRef]
- Iyer, V.V.; Sriram, G.; Fulton, D.B.; Zhou, R.; Westgate, M.E.; Shanks, J.V. Metabolic flux maps comparing the effect of temperature on protein and oil biosynthesis in developing soybean cotyledons. Plant Cell Environ. 2008, 31, 506–517. [Google Scholar] [CrossRef]
- Quek, L.E.; Wittmann, C.; Nielsen, L.K.; Krömer, J.O. OpenFLUX: Efficient modelling software for 13C-based metabolic flux analysis. Microb. Cell Fact. 2009, 8, 25. [Google Scholar] [CrossRef] [Green Version]
- Nocon, J.; Steiger, M.G.; Pfeffer, M.; Sohn, S.B.; Kim, T.Y.; Maurer, M.; Rußmayer, H.; Pflügl, S.; Ask, M.; Haberhauer-Troyer, C.; et al. Model based engineering of Pichia pastoris central metabolism enhances recombinant protein production. Metab. Eng. 2014, 24, 129–138. [Google Scholar] [CrossRef]
- Bommareddy, R.R.; Chen, Z.; Rappert, S.; Zeng, A.P. A de novo NADPH generation pathway for improving lysine production of Corynebacterium glutamicum by rational design of the coenzyme specificity of glyceraldehyde 3-phosphate dehydrogenase. Metab. Eng. 2014, 25, 30–37. [Google Scholar] [CrossRef]
- Buschke, N.; Becker, J.; Schäfer, R.; Kiefer, P.; Biedendieck, R.; Wittmann, C. Systems metabolic engineering of xylose-utilizing Corynebacterium glutamicum for production of 1,5-diaminopentane. Biotechnol. J. 2013, 8, 557–570. [Google Scholar] [CrossRef]
- Kajihata, S.; Furusawa, C.; Matsuda, F.; Shimizu, H. OpenMebius: An Open Source Software for Isotopically Nonstationary 13C-Based Metabolic Flux Analysis. Biomed Res. Int. 2014, 2014, 627014. [Google Scholar] [CrossRef] [Green Version]
- Miyazawa, H.; Yamaguchi, Y.; Sugiura, Y.; Honda, K.; Kondo, K.; Matsuda, F.; Yamamoto, T.; Suematsu, M.; Miura, M. Rewiring of embryonic glucose metabolism via suppression of PFK-1 and aldolase during mouse chorioallantoic branching. Development 2017, 144, 63–73. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wada, K.; Toya, Y.; Banno, S.; Yoshikawa, K.; Matsuda, F.; Shimizu, H. 13C-metabolic flux analysis for mevalonate-producing strain of Escherichia coli. J. Biosci. Bioeng. 2017, 123, 177–182. [Google Scholar] [CrossRef]
- Antoniewicz, M.R.; Kelleher, J.K.; Stephanopoulos, G. Elementary metabolite units (EMU): A novel framework for modeling isotopic distributions. Metab. Eng. 2007, 9, 68–86. [Google Scholar] [CrossRef] [Green Version]
- Wiechert, W.; Möllney, M.; Isermann, N.; Wurzel, M.; De Graaf, A.A. Bidirectional reaction steps in metabolic networks: III. Explicit solution and analysis of isotopomer labeling systems. Biotechnol. Bioeng. 1999, 66, 69–85. [Google Scholar] [CrossRef]
- Simmons, E.M.; Hartwig, J.F. On the interpretation of deuterium kinetic isotope effects in C-H bond functionalizations by transition-metal complexes. Angew. Chemie. Int. Ed. 2012, 51, 3066–3072. [Google Scholar] [CrossRef] [PubMed]
- Liuni, P.; Olkhov-Mitsel, E.; Orellana, A.; Wilson, D.J. Measuring kinetic isotope effects in enzyme reactions using time-resolved electrospray mass spectrometry. Anal. Chem. 2013, 85, 3758–3764. [Google Scholar] [CrossRef]
- Tea, I.; Tcherkez, G. Natural Isotope Abundance in Metabolites: Techniques and Kinetic Isotope Effect Measurement in Plant, Animal, and Human Tissues. In Methods in Enzymology; Acacdemic Press: Cambridge, MA, USA, 2017. [Google Scholar]
- Roth, J.P.; Klinman, J.P. Kinetic Isotope Effects. In Encyclopedia of Biological Chemistry, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2013; ISBN 9780123786319. [Google Scholar]
- Westheimer, F.H. The magnitude of the primary kinetic isotope effect for compounds of hydrogen and deuterium. Chem. Rev. 1961, 61, 265–273. [Google Scholar] [CrossRef]
- Fan, J.; Ye, J.; Kamphorst, J.J.; Shlomi, T.; Thompson, C.B.; Rabinowitz, J.D. Quantitative flux analysis reveals folate-dependent NADPH production. Nature 2014, 510, 298–302. [Google Scholar] [CrossRef] [Green Version]
- Williams, T.C.R.; Sweetlove, L.J.; George Ratcliffe, R. Capturing metabolite channeling in metabolic flux phenotypes. Plant Physiol. 2011, 157, 981–984. [Google Scholar] [CrossRef] [Green Version]
- Spivey, H.O.; Ovádi, J. Substrate channeling. Methods A Companion Methods Enzymol. 1999, 19, 306–321. [Google Scholar] [CrossRef] [PubMed]
- Miles, E.W.; Rhee, S.; Davies, D.R. The molecular basis of substrate channeling. J. Biol. Chem. 1999, 274, 12193–12196. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.H.P. Substrate channeling and enzyme complexes for biotechnological applications. Biotechnol. Adv. 2011, 29, 715–725. [Google Scholar] [CrossRef]
- Wahrheit, J.; Nicolae, A.; Heinzle, E. Eukaryotic metabolism: Measuring compartment fluxes. Biotechnol. J. 2011, 6, 1071–1085. [Google Scholar] [CrossRef] [PubMed]
- Allen, D.K.; Shachar-Hill, Y.; Ohlrogge, J.B. Compartment-specific labeling information in 13C metabolic flux analysis of plants. Phytochemistry 2007, 68, 2197–2210. [Google Scholar] [CrossRef]
- Toledano, M.B.; Delaunay-Moisan, A.; Outten, C.E.; Igbaria, A. Functions and cellular compartmentation of the thioredoxin and glutathione pathways in yeast. Antioxid. Redox Signal. 2013, 18, 1699–1711. [Google Scholar] [CrossRef] [Green Version]
- Antoniewicz, M.R.; Kelleher, J.K.; Stephanopoulos, G. Determination of confidence intervals of metabolic fluxes estimated from stable isotope measurements. Metab. Eng. 2006, 8, 324–337. [Google Scholar] [CrossRef]
- Metallo, C.M.; Walther, J.L.; Stephanopoulos, G. Evaluation of 13C isotopic tracers for metabolic flux analysis in mammalian cells. J. Biotechnol. 2009, 144, 167–174. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Crown, S.B.; Long, C.P.; Antoniewicz, M.R. Optimal tracers for parallel labeling experiments and 13C metabolic flux analysis: A new precision and synergy scoring system. Metab. Eng. 2016, 38, 10–18. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nargund, S.; Sriram, G. Designer labels for plant metabolism: Statistical design of isotope labeling experiments for improved quantification of flux in complex plant metabolic networks. Mol. Biosyst. 2013, 9, 99–112. [Google Scholar] [CrossRef] [PubMed]
- Crown, S.B.; Ahn, W.S.; Antoniewicz, M.R. Rational design of 13C-labeling experiments for metabolic flux analysis in mammalian cells. BMC Syst. Biol. 2012, 6, 43. [Google Scholar] [CrossRef] [Green Version]
- Millard, P.; Sokol, S.; Letisse, F.; Portais, J.C. IsoDesign: A software for optimizing the design of 13C-metabolic flux analysis experiments. Biotechnol. Bioeng. 2014, 111, 202–208. [Google Scholar] [CrossRef]
- Isermann, N.; Wiechert, W. Metabolic isotopomer labeling systems. Part II: Structural flux identifiability analysis. Math. Biosci. 2003, 183, 175–214. [Google Scholar] [CrossRef]
- Kadirkamanathan, V.; Yang, J.; Billings, S.A.; Wright, P.C. Markov Chain Monte Carlo Algorithm based metabolic flux distribution analysis on Corynebacterium glutamicum. Bioinformatics 2006, 22, 2681–2687. [Google Scholar] [CrossRef]
- Yang, J.; Wongsa, S.; Kadirkamanathan, V.; Billings, S.A.; Wright, P.C. Metabolic flux distribution analysis by13C-tracer experiments using the Markov chain-Monte Carlo method. Biochem. Soc. Trans. 2005, 33, 1421–1422. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Buescher, J.M.; Antoniewicz, M.R.; Boros, L.G.; Burgess, S.C.; Brunengraber, H.; Clish, C.B.; DeBerardinis, R.J.; Feron, O.; Frezza, C.; Ghesquiere, B.; et al. A roadmap for interpreting 13C metabolite labeling patterns from cells. Curr. Opin. Biotechnol. 2015, 34, 189–201. [Google Scholar] [CrossRef]
- Ma, F.; Jazmin, L.J.; Young, J.D.; Allen, D.K. Isotopically nonstationary 13C flux analysis of changes in Arabidopsis thaliana leaf metabolism due to high light acclimation. Proc. Natl. Acad. Sci. USA 2014, 111, 16967–16972. [Google Scholar] [CrossRef] [Green Version]
- Yuan, J.; Bennett, B.D.; Rabinowitz, J.D. Kinetic flux profiling for quantitation of cellular metabolic fluxes. Nat. Protoc. 2008, 3, 1328. [Google Scholar] [CrossRef] [Green Version]
- Noack, S.; Nöh, K.; Moch, M.; Oldiges, M.; Wiechert, W. Stationary versus non-stationary 13C-MFA: A comparison using a consistent dataset. J. Biotechnol. 2011, 154, 179–190. [Google Scholar] [CrossRef]
- Nöh, K.; Wiechert, W. Experimental design principles for isotopically instationary 13C labeling experiments. Biotechnol. Bioeng. 2006, 94, 234–251. [Google Scholar] [CrossRef]
- Nöh, K.; Grönke, K.; Luo, B.; Takors, R.; Oldiges, M.; Wiechert, W. Metabolic flux analysis at ultra short time scale: Isotopically non-stationary 13C labeling experiments. J. Biotechnol. 2007, 129, 249–267. [Google Scholar] [CrossRef]





| Name | Data Source | Main Features | Number of Citations | Reference and Most Cited Applications |
|---|---|---|---|---|
| 13CFLUX2 | MS and NMR | Compatible to multi-platform | 107 | [39,40,41,42] |
| FiatFlux | GC-MS | 13C Glucose tracer, flux ratio | 160 | [43,44,45,46] |
| INCA | MS and NMR | Isotopically non-stationary MFA | 147 | [47,48,49,50,51] |
| METRAN | MS | Intuitive graphical user interface, confidence interval calculation | 183 | [52,53,54] |
| NMR2Flux+ | NMR | NMR data, plant network | 124 | [55,56,57,58] |
| OpenFLUX | MS | Steady-state 13C MFA, experimental design | 154 | [59,60,61,62] |
| OpenMebius | MS | Isotopically non-stationary MFA | 47 | [63,64,65] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Wondisford, F.E.; Song, C.; Zhang, T.; Su, X. Metabolic Flux Analysis—Linking Isotope Labeling and Metabolic Fluxes. Metabolites 2020, 10, 447. https://doi.org/10.3390/metabo10110447
Wang Y, Wondisford FE, Song C, Zhang T, Su X. Metabolic Flux Analysis—Linking Isotope Labeling and Metabolic Fluxes. Metabolites. 2020; 10(11):447. https://doi.org/10.3390/metabo10110447
Chicago/Turabian StyleWang, Yujue, Fredric E. Wondisford, Chi Song, Teng Zhang, and Xiaoyang Su. 2020. "Metabolic Flux Analysis—Linking Isotope Labeling and Metabolic Fluxes" Metabolites 10, no. 11: 447. https://doi.org/10.3390/metabo10110447
APA StyleWang, Y., Wondisford, F. E., Song, C., Zhang, T., & Su, X. (2020). Metabolic Flux Analysis—Linking Isotope Labeling and Metabolic Fluxes. Metabolites, 10(11), 447. https://doi.org/10.3390/metabo10110447