Numerical and Experimental Investigation of the Design of a Piezoelectric De-Icing System for Small Rotorcraft Part 3/3: Numerical Model and Experimental Validation of Vibration-Based De-Icing of a Flat Plate Structure

Abstract

The objective of this research project is divided in four parts: (1) to design a piezoelectric actuator-based de-icing system integrated to a flat plate experimental setup and develop a numerical model of the system with experimental validation, (2) use the experimental setup to investigate actuator activation with frequency sweeps and transient vibration analysis, (3) add an ice layer to the numerical model and predict numerically stresses at ice breaking with experimental validation, and (4) bring the concept to a blade structure for wind tunnel testing. This paper presents the third part of the investigation in which an ice layer is added to the numerical model. Five accelerometers are installed on the flat plate to measure acceleration. Validation of the vibration amplitude predicted by the model is performed experimentally and the stresses calculated by the numerical model at cracking and delamination of the ice layer are determined. A stress limit criteria is then defined from those values for both normal stress at cracking and shear stress at delamination. As a proof of concept, the numerical model is then used to find resonant modes susceptible to generating cracking or delamination of the ice layer within the voltage limit of the piezoelectric actuators. The model also predicts a voltage range within which the ice breaking occurs. The experimental setup is used to validate positively the prediction of the numerical model.

1. Introduction

This paper describes the results of the third part of a research project investigating the use of piezoelectric actuators in a low-energy de-icing system that could be implemented on small rotorcraft. With all the problematics that rotorcraft encounter during inflight icing events, like decrease in lift and increase in drag, torque, vibration and imbalance, the industry is in active research to find a low-energy solution. Different approaches using piezoelectric actuators have been explored in the past. First investigated by Ramanathan [1] and later by Palacios [2], resonating piezoelectric elements were used to generate ultrasonic surface waves to produce shear stress at the ice interface. Venna and al. [3] used piezoelectric actuators located directly below the iced zones of a NACA 0012 leading edge to generate both local shear strains and normal impulse forces to de-ice—however with limited success. In the first part of this project, an experimental setup of a piezoelectric actuators based de-icing system integrated to a flat plate structure was designed. A numerical model of that setup was developed and validated experimentally. In the second part, the test setup was used to investigate transient vibration during frequency sweeps and determine optimal excitation for de-icing. It was also used to validate the results of transient vibration analysis with de-icing tests in cold room.

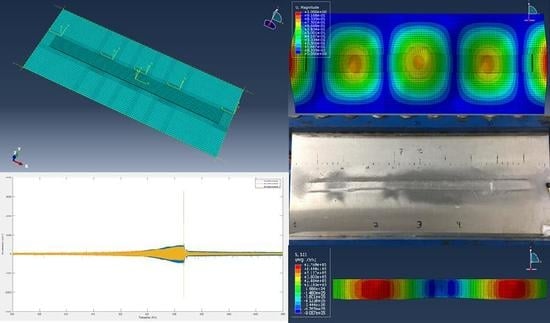
As part of third phase of this study, an ice layer was added to the flat plate structure and investigated numerically and experimentally. Stresses involved in different ice breaking scenarios were studied. The tensile and compressive strength of atmospheric ice are important parameters with regard to predicting and modeling de-icing phenomenon. Ambient environmental conditions during accretion and substrate structural parameters have a significant impact on the properties of atmospheric ice. As opposed to freezer ice formed by a water volume exposed to below freezing temperature, atmospheric ice is formed by small water droplets impinging on a structure under representative atmospheric icing conditions. Several parameters influence ice strength, such as accretion temperature, wind speed, liquid water content, median volumetric diameter, strain rate, porosity, etc. Petrovic [4] published a review of the mechanical properties of ice and snow. In his review, Petrovic stated that tensile strength for atmospheric icing in the literature typically range from 0.70 to 3.10 MPa, with an average value of 1.43 MPa between −20 °C and −10 °C [5]. For compressive strength, the values range from 5 to 25 MPa. The main variables that impact ice strength raised by the literature includes temperature, strain rate, tested volume and grain size. Studies indicate that both the tensile and compressive strength of ice increase with decreasing temperature. Compressive strength dependence to temperature is related to the ice dislocation and grain boundary sliding phenomena and varies by a factor of 4 from −40 °C to 0 °C. Tensile strength shows less dependence on temperature, with a factor of 1.3 over the temperature range as provided in literature [5], which can be explained by the localization of stress-accommodating mechanisms at the tips of tensile flaws. The other important parameters for de-icing is the adhesion strength of the ice to the structure. Guérin [6] has shown in his study of the adhesion of ice on different substrates that the main parameters influencing the properties of ice accretion are the material conduction and the surface roughness. Two types of rupture can be observed: cohesive, which happen in the ice itself, and adhesive, which happens at the ice/substrate interface. The literature review showed that tensile efforts tend to create cohesive break, leaving a small layer of ice on the substrate. Shearing, on the other hand, will generally lead to an adhesive break with a complete removal of ice from the surface. Jellinek [7] reported two different experiments on adhesive strength: shear and tensile. For the shear experiments, the adhesive strength increased linearly and rapidly with decreased in temperature. Pure adhesive breaks were obtained down to −13 °C. Below this temperature, breaks suddenly changed to cohesive, which were almost temperature independent. In the tensile experiments, adhesive strength in tension was at minimum 15 times greater than the one under shear experiments. Jellinek explained this phenomenon by the presence of a liquid-like layer at the interface which hold the ice and substrate together by surface tension forces, adding to the overall adhesion strength [7]. The adherence due to a pressure difference across a curved liquid-like layer-air interface does not have to be overcome in shearing. Hardesty presented the different values found in literature for adhesion strength on a steel plate in function of temperature [8]. At −8 °C, which represents the temperature of the cold room in this study, adhesion varies from 0.20 to 0.90 MPa between studies, with the vast majority of the values between 0.30 and 0.60 MPa. This is a common variation between studies involving ice parameters that is mainly caused by different testing methods and substrate conditions. Very few researches have investigated numerically vibration based de-icing while including ice layers in the numerical model. Budinger [9,10] provided a computational method to estimate voltages and currents to generate first ice cracks or delamination in a piezoelectric de-icing system. The method was based on modal analysis and validated through experiments. They obtained cracking due to tensile stress within the ice, which lead to small delamination zones which followed cracking propagation. They only obtained delamination without cracking, due to shear stress, at high frequencies above around 40 kHz. Furthermore, they separated resonant modes into flexural and extensional modes, where extensional modes were found at higher frequencies. Only cracking of the ice layer was successful with flexural mode on a flat plate, without delaminating it from the plate. There is more power consumption at higher frequencies, making the need for investigating delamination at lower frequencies paramount for low power de-icing. Tian et al. [11] developed a shear stress model with ANSYS to analyze the distribution of the shear stress at the ice/substrate interface. They showed from the shear stress distribution that the delamination starts from the edges of the ice layer. The model developed was a simplified 2D model and no direct experimental validation was done. They still validated the conclusions obtained for shear stress distribution by delaminating small zones of frozen purified water poured at positions of high shear stress on the plate in a freezer. They located those high shear stress zones by observing the resulting distribution of power sprinkled on the plate and not with measuring devices. A validation of the model without ice accumulation was done for the frequency values of the resonant modes, but not for the vibration amplitudes. While they obtained good accordance between the model and the experiments for most of the modes investigated, some discrepancies were found for some resonant modes which were explained by the 2D simplification as well as the inaccuracy of some model parameters. Harvey [12], followed by Villeneuve et al. [13], demonstrated a proof of concept for de-icing with piezoelectric actuator patches exciting structural resonant frequencies (modes of vibration). Total or partial de-icing was successfully achieved for a flat plate, a thinned Bell 206 main rotor blade and a Bell 206 tail rotor blade sections. Numerical simulations were used to predict the resonant frequencies and the mode shapes to optimally position and drive the actuators. However, the damping was not accounted for in these studies [13], and only frequency analyses were used to determine the optimal position of the actuators. Moreover the ice was not modeled numerically and no stresses analysis was performed.

In this new study, an ice layer added on the surface of the structure was considered in the numerical model. Frequency analysis and direct steady-state dynamic analysis were performed with the numerical model and validated experimentally with the test setup. Numerical prediction of the stress calculated by the model were studied for the different ice breaking cases obtained experimentally and were used to predict ice breaking for different modes. The principal objective of this study was to characterize and validate an experimental set-up aiming at the de-icing of a structure using piezoelectric actuators to excite the natural modes of vibration of the structure. For completeness and to better highlight the objective and the outcome of this study it is important to reemphasize the preamble of the first article of the series of three describing the results and the methods used for this work [14]: “Numerous challenges have been observed and addressed while implementing, numerically validating and characterizing this set-up. The numerical modal analysis implemented in this study faced some challenges related to the number and the dimensions of the required piezoelectric actuators. While it was evident that the success of the method was depending on the capability of the actuators to sustain and transfer the required power of excitation at a structural natural resonant frequency of interest, the dimensions of the actuator relative to the wavelength of vibration, their positioning and their number, as well as the phasing of excitation were expected to affect the integrity of some of the high frequency modes and consequently the ability to fully excite the targeted modes.” The numerical analysis served to validate the experimental observations and to define the parameters of the set-up to obtain the de-icing of a flat structure. The aim of this study was also to determine to what extent the large dimensions of the piezoelectric actuators would affect the integrity of the mode shapes, the efficiency of the set-up with regard to the numerically expected versus experimentally achieved amplitudes of deformation resulting in the required stresses generating the ice layer breaking. As was already stated in [14], this comprehensive analysis comprises the evaluation of the numerical and experimental errors due to the sometime inefficient mode of excitation. This study allowed the full understanding of the expected performance of the set-up, shape of the modes of interest resulting in ice layer breaking and delamination as well as the optimal range of the amplitude voltage of excitation.

2. Materials and Methods

Numerical investigations performed in the first phase of this research project [14] have allowed to develop an experimental test setup with piezoelectric actuators generating forced vibration on the plate. The experimental test setup was built in the laboratory and a numerical model of that setup was elaborated and validated. The numerical model and experimental setup were used to investigate vibration based de-icing. An ice layer was added in the numerical model and accumulated on the test setup in a cold room for experimental validation. The model was used to calculate the stresses required to break the ice layer. These stresses were used to determine stress limit criteria. Finally, the numerical model was used to predict ice breaking of the ice layer.

2.1. Numerical Model with Ice Layer

An ice layer was added to the steel plate in the numerical model developed during the first phase of the project [14]. In this numerical model, five actuator patches were positioned at both extremities of the plate, at its center and at positions of the anti-nodes of mode 4, at 16 cm from the free edges. The actuators were all installed in their width direction with their centerline centered with the plate’s width (Figure 1a). The actuators were modeled as 3D extruded deformable solid and connected to the flat plate using a Tie Constraint. PIC255 material was defined in the software with the parameters provided by the manufacturer. The actuators were meshed with standard linear C3D8E 8-node piezoelectric brick, which allowed coupling between mechanical and electrical properties by including displacement and electrical potential degrees of freedom. Electrical boundary condition were applied to the top and bottom face of each actuator to generate the deformation of the patches. On the bottom face, the electrical potential was set constant to zero and on the top face the potential was set to the value of the voltages applied during the different experiment testing. This simulated the two electrodes on the top and bottom of the actuator patch.

The ice layer added in the numerical model on the top surface of the flat plate, as presented on Figure 1b, was a 2 mm thick 450 mm × 35 mm solid homogenous 3D deformable extruded part. The part was connected to the plate with a Tie constraint at 25 mm from the free edges and with its center in the width direction corresponding to the centerline of the plate in the width direction (Figure 1b). Ice material properties obtained from the literature [15,16] corresponding to the conditions of accumulation in the cold room, were implemented in the numerical model. Those properties are presented along the properties of the steel material of the flat plate in

Table 1. Ice and steel material properties.

Properties	Steel	Ice
Density (kg/m³)	8000	897
Young modulus (GPa)	193	9
Poisson’s Ratio	0.27	0.31

. The ice volume was meshed with C3D8R 8-node linear brick elements. This configuration represented the ice accumulation obtained experimentally, which aims to mimic an ice layer accreted on the leading edge of a blade. During in-flight icing on wing or blade structures, a layer of ice accumulates at the leading edge as opposed to on the entire surface of the structure. This explains the selection of an ice layer accumulation instead of an ice surface covering the whole plate.

2.2. Experimental Testing with Ice Accumulation

2.2.1. Ice Accumulation

The flat plate setup was installed in a cold chamber that can maintain temperatures down to −30 °C. The chamber is equipped with a hydraulic spraying system consisting of a pressurized refrigerator connected to a Spraying systems 650017 nozzle. The water pressure in the system was kept at 80 psi to generate droplet of 115 µm of Median Volumetric Diameter. The nozzle was installed on a translation track over the flat plate setup and was moved along this track at constant speed to evenly distribute water droplets over the length of the plate (Figure 2a). Once the nozzle has made its movement back and forth along the track, the spraying was stopped for 10 s before a new spraying run was performed.

An ice layer was accumulated on the plate before each tests at an air ambient temperature of −8 °C. This temperature allowed for a glaze ice to be generated without liquid water flowing off the ice layer. An aluminum cover with a rectangular slit in the middle was installed on the flat plate setup before each ice accumulation (Figure 2b). This allowed the accumulation of a 35 mm wide and 450 mm long ice layer, which was a good representation of ice accumulated on the leading edge portion of a complete profile. The accumulation was completed in one hour at a precipitation of 2 mm/h, resulting in a 2 mm thick ice layer. An example of an accumulated ice layer is presented in Figure 2c.

2.2.2. Experimental Setup

The setup designed during the first phase of the project [14] consists of a 304 stainless steel flat plate, with a thickness of 1.6 mm thick and five piezoelectric actuators bonded on the back face of the plate. The plate was mounted between two massive steel 44 blocks with a thickness of 50.8 mm (2′’) replicating the Clamped boundary conditions applied on the longest edges of the plate in the numerical model. The vibrating surface of the plate was 500 mm (L) × 200 mm (W) (Figure 3b). Five Physik Instrumente (PI) P-876.A15 actuator patches were installed on the back surface of the plate. The patches, which are 61 mm in length by 35 mm wide with a thickness of 0.8 mm, were installed at the positions defined in the previous phase (Figure 1a and Figure 3a).

To drive and monitor the piezoelectric actuator system, an Agilient 33500B waveform generator was used to generate and provide the electrical signal to the actuators. The signal was amplified using an Amp-line AL-1000-HF-A amplifier, with a low voltage (less than 10 V) input and high voltage (50 to 1000 V) output to generate the required levels of vibration. Since the operational voltage of the actuators is −250 to 1000 V, an Amp-line AL-100DC power source was used to offset the voltage to allow testing close to the limit of the actuators. By offsetting the voltage to values around 400 or 500 V, an alternative voltage of 1000 to 1250 Vpp could be applied without compromising the integrity of the actuators. The voltage applied to the actuators was measured with a Fluke 105B oscilloscope. To monitor and record the signals from the accelerometers a high sample rate National Instrument PCIe-6346 data acquisition card is used.

2.2.3. Data Acquisition

Accelerometers were used to measure the vibrations of the flat plate under piezoelectric actuator excitation following the ice accumulation. Miniature single axis piezoelectric accelerometers PCB Piezotronics model 352C22 were selected for the broad frequency range, dynamic range, small size and low weight. Five accelerometers were installed on the flat plate for experimental validation of the numerical model with ice layer accumulation (Figure 3b,c). A first accelerometer (accelerometer 1) was positioned at the edge on the top surface of the plate. Four additional accelerometers were installed underneath the plate to protect them from the ice accumulation. The positions of the accelerometers relative to the right edge of the plate are presented in

Table 2. Accelerometer positions.

Accelerometer (#)	Distance from Right Edge (cm)
1	0
2	0
3	12
4	25
5	30

. As a quality check measure, accelerometer 2 was installed underneath accelerometer 1. At this position, the signals of the two accelerometers are expected to be equal but in opposition of phase. Due to the system’s limitations, only the signal from three accelerometers can be recorded at the same time. The accelerometers were used to measure the frequency response functions of the plate and determine the natural frequencies to be used in the steady-state excitation. The accelerometer frequency response functions were also used to perform the numerical model validation of the set-up with an ice layer accumulation.

3. Results

In this section, the results of frequency sweep tests, performed at very low sweep rates, around the resonant frequency modes of interest, presented in

Table 3. Frequencies and type of ice breaking obtained in previous phase of the study [17].

Frequency (Hz)	Type of Ice Breaking
194	Delamination
431	Crack
1111 to 1215	Delamination
1281	Crack

, to capture the acceleration levels of the plate when cracking or delamination of the ice occurs, are presented. These frequencies and the type of breaking were obtained during de-icing tests in the previous phase of this project [17]. The acceleration measured was used to validate the accelerations predicted by the numerical model when an ice layer was added to the plate. Sweeps at very low sweep rates were used instead of a steady-state regime for two reasons. First, the sweeping allowed the measurement of frequency response functions and structural damping calculation of the ice covered plate using the half power method, as it was performed for the case of the plate without ice in the first phase of the project [14]. The second reason is that in steady-state mode, cracking and delamination occurs instantly when the actuators are activated. This transitory behaviour, is most of the time missed (partially or totally) from being recorded due to the triggering strategy set up in the data acquisition system. In the second phase of the project [17], it was shown that at very low sweep rates, acceleration amplitude at structural natural frequency tends towards the acceleration amplitude obtained using steady-state excitation and for this reason those results will be used to validate the direct-solution steady-state dynamic analysis validation.

The ice layer on the flat plate modifies the bending stiffness of the structure as well as its damping. Damping loss factor in the numerical model was adjusted to reflect the reality of the flat plate covered with the ice layer. A Matlab code was developed to analyze the experimental data and calculate the Fast Fourier Transform (FFT) to calculate the damping loss factor using the half power method. The damping loss factor, experimentally determined using the half power method, was ultimately used in the numerical model.

3.1. Cracking of the Ice Layer

Two structural modes have been identified during the previous tests where cracking of the ice occurred. For each of those modes, ice accumulation was performed on the flat plate and frequency sweep tests at very low sweep rate were completed. Those sweeps were repeated and the voltage of excitation was increased at each step until cracking of the ice occurred. The first structural mode was identified around 430 Hz (Table 3). The steady-state acceleration amplitudes at 136 Vpp with all piezoelectric actuators activated in phase was compared to the acceleration amplitudes obtained during a frequency sweep performed at a rate of 5 Hz/s. The acceleration amplitudes obtained during the frequency sweep, ranged from 96.5% to 98% of the amplitudes measured in a steady-state excitation, which confirmed that a sweep rate of 5 Hz/s was adequate for the mode deployment.

Ice was accumulated on the plate and a resonant mode was identified at 400 Hz. Frequency sweeping tests were performed from 375 Hz to 425 Hz in 10 s, for a sweep rate of 5 Hz/s, at a low excitation voltage of 136 Vpp with accelerometers 1, 2 and 5 followed by a second sweep with accelerometers 1, 3 and 4. Figure 4 presents the acceleration measured during those sweeps. Accelerometer 1 is in phase with accelerometer 3, while accelerometers 2, 4 and 5 are in counter-phase. Accelerometers 1 and 2 measurements were similar and in opposition of phase as expected from their positions. A structural damping of 0.9% was determined using the half power method for the data acquired during the frequency sweeps.

It was observed that two structural modes were predicted numerically in the vicinity of the mode identified experimentally at 400 Hz: the modes 5 and 6, at 350 Hz and 460 Hz, respectively (Figure 5). Mode 6 has no anti-node at the center resulting in a very small amplitude corresponding to the accelerometer 4 location, which was not the case for the experimentally measured amplitude. The phasing of the accelerometers, as well as relative amplitudes, matched exactly the modal deformation of mode 5. Accelerometers 3 and 4, both at anti-nodes, measured an equal but out of phase amplitude, while accelerometer 5 measured accelerations in phase with accelerometer 4 but of a lower amplitude. It was concluded that the resonant mode obtained experimentally is mode 5. A more detailed investigation of phasing and relative magnitude of displacements and accelerations were presented in Reference [14] as one of the outcomes of the first part of this project.

The frequency sweep from 375 to 425 Hz in 10 s was repeated at higher voltages until cracking occurred with signal from accelerometers 1, 3 and 4 recorded by the data acquisition system. During the frequency sweep with an amplitude of excitation of 300 Vpp, a crack was observed in the ice layer at 10 cm from the free edge of the plate (Figure 6a), which was in accordance with the anti-node at 11 cm in the mode shape predicted by the numerical model. A peak amplitude of 610 m/s² was measured with accelerometer 1 and 450 m/s² with accelerometers 3 and 4. The Direct-solution steady-state dynamic analysis predicted 425 m/s² at the edge of the plate and 325 m/s² at the anti-nodes. To determine the repeatability of the observed results, the test was repeated three additional times. Each time, the same process was observed to accumulate the ice, identify the structural natural frequency and determine the damping loss factor. Results for the four test repetitions are presented in

Table 4. Results of test repetitions for mode 5.

Repetition (#)	Frequency (Hz)	Damping (%)	Vpp (V)	Acc. at Edge (m/s2)		Acc. at Anti-Nodes (m/s2)
				Exp.	Num.	Exp.	Num.
1	400	0.9	300	610	425	450	325
2	425	1.3	370	460	375	340	300
3	400	1.0	300	510	390	380	300
4	390	0.9	360	660	500	520	390
5 *	400	1.0	216	850	1050	675	800

* Performed with optimal phasing of actuators.

. Cracks appeared at 370 Vpp, 300 Vpp and 360 Vpp, respectively, for each repetition and each time between 10 and 11 cm from the edge of the plate (Figure 6b). Figure 7 shows the experimental accelerations for repetition 2, while Figure 8 shows the accelerations predicted by the numerical model for repetition 2.

One last repetition is done for mode 5 with the same piezoelectric actuator activation. For this test the frequency is found at very low voltage, below 60 Vpp, and the sweep test is performed directly at 370 Vpp, the highest voltage obtained during previous repetitions. This test is done to validate that no damaging or weakening of the ice occurred during the sweeps at lower voltages for the other repetitions before cracking was obtained. Since the frequency sweep is performed only once at 370 Vpp, it ensures that only this sweep is responsible for cracking of the ice and confirms the results obtained with previous repetitions and validity of the method. The frequency is found around 400 Hz and the sweep is performed directly at 370 Vpp from 375 to 425 Hz in 10 s. A crack is obtained at 12 cm from the edge of the plate, as for the other repetitions, which confirms that there is no effect of weakening or damaging of the ice during sweeps preceding sweep where cracking occurs and that the method and results obtained can be used to determine acceleration at cracking.

In the first phase of the project [14], the optimal activation of the piezoelectric actuators in function of the mode shape was investigated. By using the conclusions obtained, it can be observed from Figure 5 that activating all the actuators in phase is not the optimal activation. Piezoelectric actuators 2 and 4 should be activated out of phase from the three other actuators. An additional test with the optimal activation is done. After the ice layer is accumulated on the flat plate, the resonant frequency is found at 400 Hz. A sweep from 375 Hz to 425 Hz in 10 s is selected, but with piezoelectric actuators 2 and 4 out of phase from the other actuators. Damping is measured once again with sweeps at very low voltage and a value of 1.0% is obtained. A crack is obtained during the sweep at 216 Vpp at 11 cm from the edge, as for the previous tests. The acceleration measured for accelerometer 1 is 850 m/s², for accelerometer 3 and 4 is 675 m/s². After setting the voltage and damping in the numerical model, predictions for the accelerations are of 1050 m/s² at the edge, and 800 m/s² at anti-node positions.

The second mode where cracking was obtained was identified at approximately 1281 Hz (Table 3). The same process utilized for mode 5 was repeated at this frequency. Following the ice accumulation on the flat plate, the resonant frequency was observed to have shifted at 1325 Hz. Frequency sweep tests were performed from 1300 to 1350 Hz in 10 s for a sweep rate of 5 Hz/s at low voltage (136 Vpp), first recording signals from accelerometers 1, 2 and 5 and a second time recording signals from accelerometers 1, 3 and 4. Measured phase and amplitude of the acceleration showed that acceleration of accelerometers 2, 4 and 5 were all in phase, while accelerometer 3 was out of phase with accelerometers 2, 4 and 5. Amplitude of accelerometer 5 was significantly lower than the other accelerometers. As for mode 5, this information allowed to confirm that mode 23 was excited (see [14] for a detailed study of phasing and relative magnitude vibration response of the structure). The frequency of this structural mode was predicted numerically at 1338 Hz (Figure 9).

The same frequency sweep was performed at higher voltages while recording signals from accelerometer 1, 3 and 4 and cracking of the ice was observed at 360 Vpp. Ice layer crack was observed between 11 and 12 cm from the free edge of the plate which corresponded to the position of accelerometer 3 and the center of an anti-node on mode 23. The repeatability of the results was performed following a similar method to mode 5. The test with all piezoelectric actuators in phase was repeated twice, with the same procedure as the first test. The results are presented in

Table 5. Results of test repetitions for mode 23.

Repetition (#)	Frequency (Hz)	Damping (%)	Vpp (V)	Acc. at Edge (m/s2)		Acc. at Accelerometer 3 (m/s2)		Acc. at Center (m/s2)
				Exp.	Num.	Exp.	Num.	Exp.	Num.
1	1325	1.1	360	2100	1700	2600	1550	1700	1300
2	1320	1.2	400	1900	1700	2400	1550	1900	1300
3	1335	1.3	380	1300	1500	2100	1375	1450	1150
4 *	1330	1.5	240	2300	2350	2800	2250	2200	1800

* Performed with optimal phasing of actuators.

. The ice layer cracks appeared at 400 Vpp and 380 Vpp, respectively, and both times at 12 cm from the free edge of the plate. As for mode 5, a last repetition was done to validate that no damaging or weakening of the ice is responsible for cracking at the voltage obtained previously. The natural frequency of interest was identified at 1325 Hz and a sweep from 1300 to 1350 Hz in 10 s was performed directly at 400 Vpp which corresponded to the highest voltage obtained in the previous tests for this mode and activation. Two cracks were obtained during this sweep, confirming the result obtained with mode 5.

Phasing used for the sweeps was not ideal for the deployment of this mode. Piezoelectric actuators 2 and 4 should be activated out of phase as compared to the three other actuators (see Figure 9). A new ice layer was accumulated on the flat plate and a resonant frequency of interest was identified at 1330 Hz. The frequency sweep was performed from 1305 Hz to 1355 Hz in 10 s, but with piezoelectric actuators 2 and 4 out of phase as compared to the other actuators. Sweep tests were performed with increased voltage and a crack was obtained at 240 Vpp between 11 and 12 cm from the free edge of the plate. The acceleration measured and predicted by the numerical model are presented in Table 5.

3.2. Delamination of the Ice Layer

Two modes where delamination of the ice occurred have been identified (Table 3). The same experimental steps used for the modes responsible for ice layer cracking were performed for the numerical model validation of those modes. The first mode identified at 192 Hz was excited using a frequency sweep from 187 Hz to 197 Hz in 10 s, for a sweep rate of 1 Hz/s. Experimental testing have shown that for this mode, 5 Hz/s is too high and 1 Hz/s was required to reach at least 95% of the steady-state measured acceleration peak value. The structural mode excited at this frequency was identified as mode 1 (Figure 10a) and the results are presented in

Table 6. Results obtained for delamination tests.

Mode (#)	Frequency (Hz)	Damping (%)	Vpp (V)	Acc. at Edge (m/s2)		Acc. at Accelerometer 3 (m/s2)		Acc. at Center (m/s2)
				Exp.	Num.	Exp.	Num.	Exp.	Num.
1	192	2.2	560	725	675	400	460	425	440
17	1138	1.3	192	2100	1750	825	1125	725	1025
18	1160	1.6	216	2200	1825	1000	950	-	-
20	1195	1.9	240	1800	2000	600	600	1800	2000

. The delamination obtained is presented in Figure 10b where a white air-filled zone could be observed under the ice layer. This delamination was similar to delamination observed in another part of this research study [17], which include examination and images of delamination cases.

The second mode identified was observed between 1111 and 1215 Hz. For this mode, it was difficult to clearly identify the frequency where delamination happened in the previous phase [17] realised during this project and it appeared to be a phenomena developing over a frequency range instead than at a single frequency. Five modes were predicted within this frequency range by the numerical frequency analysis, and three of those modes, mode 17 at 1158 Hz (Figure 11a) mode 18 at 1164 Hz (Figure 11b) and mode 20 at 1198 Hz (Figure 11c) were susceptible of creating delamination. Those modes were very close in frequency, within 40 Hz, which explains why delamination is obtained over a series of frequencies in this range. Following the ice layer accretion, the five actuators activated in phase within this frequency range resulted in excitation of mode 17, which was expected since activating all the actuators in phase was assumed to be the optimal activation scenario for this mode and explains why this mode is predominant. The testing procedure presented previously was conducted for mode 17 and subsequently repeated for mode 18 and mode 20 but with the respective optimal actuator activation scenario for each case, actuator 1 and 2 out of phase with 4 and 5 for mode 18 and actuator 1 and 5 out of phase with actuator 2, 3 and 4 for mode 20. Delamination of the ice layer was obtained for all three modes, and the results are presented in Table 6.

4. Discussion

4.1. Experimental Test Repeatability

The repeatability of the experimental results was studied by repeating the ice accumulation and frequency sweep tests for two structural modes of interest. For the first mode, mode 5, the test was repeated four times. The resonant frequency of interest measured during these tests was 404 ± 21 Hz and voltage at cracking was 333 ± 38 Vpp. The amplitude of the measured acceleration was 558 ± 103 m/s² for accelerometer 1 and 423 ± 98 m/s² for accelerometer 3 and 4. The measured structural damping loss factor was 1.0% ± 0.3%.

For mode 23, the test was repeated three times. The measured resonant frequency of interest was 1327 ± 8 Hz, while the voltage at cracking was 380 ± 20 Vpp. The measured acceleration amplitudes were 1767 ± 467 m/s² for accelerometer 1, 2367 ± 267 m/s² for accelerometer 3 and 1683 ± 233 m/s² for accelerometer 4. The measured damping loss factor was 1.2% ± 0.1%.

The resulting percentages of variation for the measured natural frequency of the mode, damping loss factor, acceleration amplitude are presented in

Table 7. Percentage of variation for test repetitions for mode 5 and 23.

Mode	Frequency	Damping	Vpp	Acc. at Edge	Acc. at Accelerometer 3	Acc. at Center
5	5%	26%	11%	18%	23%	23%
23	<1%	8%	5%	26%	11%	14%

. The results show that the variation of those parameters can be considered within ± 26%. Damping variation, which is at ± 26% for mode 5, reflects the variation in the ice accumulation for each test. This shows that a significant part of the variation can be attributed to the repeatability of the ice accumulation on the plate.

4.2. Accuracy of the Numerical Model (Numerical Model Validation)

The numerical model predicts the resonant frequency and shape for each mode with the frequency analysis, and predicts the acceleration, displacement, stress, strain, etc., with the direct-solution steady-state dynamic analysis.

Table 8. Comparison of experimental and numerical frequencies for the resonant modes.

Mode (#).	Experimental Frequency (Hz)	Numerical Frequency (Hz)	Discrepancy (%)
1	192	203	6
5	404	350	13
17	1138	1158	2
18	1160	1164	<1
20	1195	1198	<1
23	1327	1338	<1

presents the comparison between the predicted frequencies and the frequencies obtained during the experimental testing. The model is able to accurately predict the resonant frequencies of each of the modes investigated, with a difference of 13% or less. As the frequency increases above 1000 Hz, the model has an accuracy of 98% or higher for all of the modes investigated.

Table 9. Difference of the numerical model prediction with experimental results for modes with cracking of the ice.

Mode (#)	Difference at Edge of Plate (%)	Difference at Accelerometer 3 (%)	Difference at Center (%)
5 (1)	−29	−28	−28
5 (2)	−18	−12	−12
5 (3)	−24	−21	−21
5 (4)	−24	−25	−25
5 (p *)	+24	+19	+19
23 (1)	−19	−40	−24
23 (2)	−11	−35	−32
23 (3)	+15	−35	−21
23 (p *)	+2	−20	−18

* Performed with optimal phasing of actuators.

and

Table 10. Difference of the numerical model prediction with experimental results for modes with delamination of the ice.

Mode (#)	Difference at Edge of Plate (%)	Difference at Accelerometer 3 (%)	Difference at Center (%)
1	−7	+15	+4
17	−17	+36	+41
18	−17	−5	-
20	+11	0	+11

present the difference of the acceleration amplitudes predicted by the direct-solution steady-state dynamic analysis with regard to the accelerations measured experimentally. The damping loss factor used in the numerical model was obtained using the half power method for frequency sweep excitation at 136 Vpp for all resonant modes. The damping coefficient associated to each mode was assumed to be constant irrespective of the voltage range of excitation within the voltage ranges of interest. This was confirmed through testing at different voltages of excitation for mode 1 and 5 and no significant difference in the damping coefficient was observed for each mode irrespective of the voltage range of excitation. Furthermore, since for most cases, the voltage of excitation at each modal frequency of interest resulting in ice breaking was very close to the voltage used to measure the damping coefficient, this assumption was considered acceptable for the numerical simulations. Table 9 shows the comparison for modes where cracking was obtained for all test repetitions, identified by their repetition number in brackets, as well as the tests with the optimal phasing, identified by a “(p)” in the table. * performed with optimal phasing of actuators.

Table 10 presents the comparison for modes where delamination of the ice layer was obtained. The average difference is 20%, while the maximum difference obtained is 41%. The error of the numerical model can be defined at ±41%. This value is considered acceptable considering the test repeatability of ±26%. This difference can also be explained by different factors. First, the ice layer is modeled as a perfect rectangular prism while the ice layer accumulated on the plate had rounded edges and was not perfectly rectangular. The thickness of the layer varied to a certain extent along its length, which is not reflected in the numerical model. The density and elastic modulus of the ice were not measured but taken from literature values. The data was recorded with accelerometers, while still small, could have been slightly intrusive. Furthermore, in some cases, the anti-nodes of the resonant modes obtained experimentally could be offset by a very small distance compared to the position predicted by the numerical model due to a little asymmetry and position of the ice layer accumulated. The model’s accuracy is deemed acceptable for the model’s purpose, which is to predict if and at which voltage and phasing a piezoelectric system can crack and delaminate an ice layer from a structure as well as to assist in the design of an optimal system.

4.3. Numerical Model Stress Predictions

The numerical model was used to define the stress obtained in the ice layer at cracking and delamination. For modes where cracking occurred, the vibration of the plate created bending in the ice layer at the anti-nodes position, which was responsible for the stress generation. From beam theory, it can be concluded that the crack generation was caused by tensile stress normal to the crack. The normal stress S11, normal to the crack direction, was investigated for the two modes where cracking was obtained.

For mode 5, four test repetitions with all actuators in phase were conducted for the model validation, as well as a fifth test with the optimal phasing of the actuators. The normal stress S11 calculated by the numerical model for each case was investigated. Figure 12 presents the S11 stress in the ice layer for the first test performed with all actuators in phase for mode 5. The figure confirms that the maximum stress was obtained at anti-nodes positions where cracks were obtained during the experimental tests (see Figure 12). It can also be observed that, as predicted by beam theory, maximum stress was generated at the top of the ice layer.

Table 11. Normal stress S11 and adjusted normal stress S11 calculated by the numerical model for all repetitions performed experimentally for mode 5.

Repetition	1	2	3	4	5 (o.p. *)	Average
Normal stress S11 (MPa)	0.78	0.71	0.73	0.93	1.90	1.01
Adjusted Normal stress S11 (MPa)	1.08	0.80	0.92	1.24	1.60	1.13

* Performed with optimal phasing of actuators.

presents the maximum normal stress obtained at anti-nodes, where cracking occurred, for all the repetitions. The average normal stress predicted by the numerical model was 1.01 MPa. The results were very close, within 20%, for the four tests with the same phasing. The stress obtained with the optimal phasing was about twice as large as the results obtained during the other four tests. This great difference can be attributed to the fact that the vibration amplitude of the four repetitions was under evaluated by the numerical model while it was over evaluated for the test with the optimal phasing. The normal stress for ice cracking can be adjusted by simply increasing or decreasing the value predicted by the model for the error difference with the experimental results. After adjustment, the stress at cracking varies from an average of 1.01 to 1.13 MPa, and a range of 0.71–1.90 MPa to a range of 0.8–1.60 MPa.

A similar numerical investigation was conducted with the four tests performed experimentally for the mode 23. As expected, the maximum stress was calculated at the anti-node positions where cracking occurred. The average stress was 0.63 MPa, with a stress range from 0.51 MPa to 0.87 MPa. If the normal stress is adjusted as done for mode 5, the average stress increases to 0.93 MPa, with stresses ranging from 0.82 MPa to 1.08 MPa (

Table 12. Normal stress S11 and adjusted normal stress S11 calculated by the numerical model for all repetitions performed experimentally for mode 23.

Repetition	1	2	3	4 (o.p. *)	Average
Normal stress S11 (MPa)	0.51	0.61	0.54	0.87	0.63
Adjusted Normal stress S11 (MPa)	0.86	0.94	0.82	1.08	0.93

* Performed with optimal phasing of actuators.

).

Once the error in the vibration magnitude for the numerical model is taken into account, adjusted averages of 1.13 MPa and 0.93 MPa are obtained for the two modes (mode 5 and 23), which are within 20% difference, meaning that the two modes predict a similar stress for ice failure. When including all tests performed for the two modes, an average of 1.04 MPa is obtained, which is in accordance with literature values [4]. The stress predicted by the numerical model responsible for ice cracking ranges from 0.80 MPa to 1.60 MPa. With the stochastic nature of the ice, as well as difference in the ice structure, ice formation and ice shape from test to test due to test variation, this value compares favorably with the range of 0.70 to 3.10 MPa obtained in the literature [4]. When the numerical model is used to predict ice cracking, the accuracy of the model needs to be taken into account in the stress range. When the 41% error of the numerical model is applied, the stress range at which the numerical model should create cracking is 0.47 MPa to 2.26 MPa.

In a previous study [12], it was shown that two different delamination scenarios can be obtained during de-icing tests, an adhesive break and a cohesive break at the interface. At higher temperatures, the break is adhesive and a delamination occurs between the ice layer and the steel plate. At lower temperatures, the break starts to become cohesive and the break occurs in the ice layer itself instead of at the interface. The results obtained in this testing has shown adhesive breaks, which is in agreement with the results obtained at similar temperatures during the previous phases. Moreover, Guerin has demonstrated that at −8 °C, ice shows adhesive delamination [6]. For the stresses responsible for adhesive delamination of the ice layer, the beam theory for composite beams in flexion predicts that the strain created in the plate during flexion will create shearing at the bottom of the ice layer. Since the ice layer has a much lower young modulus, the difference in strain of the two materials is responsible for shear stresses at the interface.

The anti-nodes generated by the vibration of the plate create flexion in both the length (x-direction) and width (y direction), which creates shearing stresses in those two directions. Figure 13a,b show the distribution of stress S13 and S23 in the ice layer for mode 17. Stress in both directions are maximal at the bottom of the ice layer and around the edges of the ice layer. Stress S13 is higher on the edge corresponding to the width of the ice layer while S23 is higher along its length.

Table 13. Stress S13, S23 and S33 for delamination modes.

Mode	1	17	18	20	Average
Shear stress S13 (MPa)	0.09	0.12	0.12	0.11	0.11
Adjusted shear stress S13 (MPa)	0.10	0.14	0.14	0.10	0.12
Shear stress S23 (MPa)	0.60	0.38	0.33	0.37	0.42
Adjusted shear stress S23 (MPa)	0.65	0.46	0.40	0.33	0.46
Normal stress S33 (MPa)	0.84	0.58	0.53	0.56	0.63
Adjusted normal stress S33 (MPa)	0.90	0.70	0.64	0.50	0.69

shows that S23 is significantly higher, about four times, than S13, with an average of 0.42 MPa compared to 0.11 MPa. The values range from 0.09 to 0.12 MPa for S13 and from 0.33 to 0.60 MPa for S23. When the values are adjusted to take into account the inaccuracy of the model for each mode, S13 ranges from 0.10 to 0.14 MPa with an average of 0.12 MPa and from 0.33 to 0.65 MPa with an average of 0.46 MPa for S23. The shear stress distribution followed the same pattern for all modes investigated. As presented in Figure 13 for mode 17, shearing was concentrated around the edges at the bottom of the ice layer. The shear stress tended towards zero at the middle of the ice layer and increased rapidly close to the edges. It could be concluded that delamination of the ice was initiated at the edges and propagated towards the center as the layer delaminated. This conclusion was in agreement with the shear model developed and finite element results obtained by Tian and al. [11]. In their study, the 2D shear model along the length of an ice patch on a plate in vibration developed showed the same type of distribution. They concluded that the maximum shear stress was found to be concentrated on the edges of the ice and that as a result, the delamination starts off from edges of the ice. The maximum shear stress emerges on the new edges until the shedding off of the entire ice patch or layer.

Numerical prediction of the stresses at the bottom layer of the ice shows that the stresses in other direction are negligible, except for S33. S33 is a normal stress caused by the up and down movement of the plate pushing and pulling the ice layer. S33 is larger than the shear stresses with values ranging from 0.53 to 0.84 MPa and an average of 0.63 MPa (Table 13). When adjusted with the numerical error for each mode, values for S33 ranges from 0.50 to 0.90 MPa with an average of 0.69 MPa. Figure 13c) shows that S33 follows a similar distribution on the ice surface than S23.

S23 and S13 are two stresses which act on the adhesion by shearing the ice layer at the interface. S23 is significantly higher than S13 and acts on a different edge of the ice layer. This means that S23 is considered the principal stress in shearing and S13 is considered negligible. The adjusted average value of S23 (0.46 MPa) is in the range of values found in the literature. Hardesty [8], from his literature study, established that the adhesion strength on steel due to shearing at −8 °C ranges from 0.20 to 0.90 MPa, with the large majority of the results being between 0.30 and 0.60 MPa. A shear stress of 0.61 MPa was obtained with Centrifuge Adhesion Tests performed at the laboratory on steel beams [18]. The numerical model predicts a shearing of 0.33 to 0.65 MPa at ice delamination, which is again in the range obtained in the literature. When including the 41% error of the numerical model, the range of shear stress within which the numerical model predicts ice delamination becomes 0.20 to 0.92 MPa.

S33 is a tensile/compressive stress that acts on the adhesion in the normal direction. The model predicts adjusted stresses of 0.50 to 0.90 MPa, and when including the 41% error, this becomes 0.30 to 1.27 MPa. With an adjusted average of 0.69 MPa, this stress is 1.5 times higher than S23. This stress could be responsible for a tensile adhesive break of the ice, instead of an adhesive break due to shearing stress S23. No literature values for tensile adhesive break on steel were found, making comparison with other results impossible. However, Jellinek [7] has determined that the adhesive breaks for tensile tests were at minimum 15 times larger than for shearing tests, which is 10 times more than the 1.5 times for S33 obtained numerically. This, and the fact that S23 falls within the values found in literature, indicates that S23 is responsible for the delamination of the ice layer. More investigation could be done to validate Jellinek’s results on steel. A summary of the minimum and maximum stress limits calculated by the numerical model, with and without the numerical error taken into account is presented in

Table 14. Summary of the stress limit criteria calculated by the numerical model with and without numerical error.

Stress	Average	Min.	Max.	Min. with 41% Numerical Error	Max. with 41% Numerical Error
S13	1.04	0.80	1.60	0.47	2.26
S23	0.46	0.33	0.65	0.20	0.92
S33	0.69	0.50	0.90	0.30	1.27

.

4.4. Prediction of Ice Breaking with the Numerical Model

The numerical model has been validated experimentally and the stresses at breaking predicted by the numerical model have been analysed and validated with the literature. As a proof of concept, the numerical model was used to find modes where ice breaking occurs and predict voltages at which it will occur. This was performed both to predict cracking and delamination of the ice layer. The frequency analysis was used to identify modes where cracking of the ice is susceptible to occur. Two modes were targeted, e.g., mode 27 at 1577 Hz and mode 35 at 1940 Hz (Figure 14). Those modes are selected due to their mode shapes similar to shape of mode 23 where cracking was successful. For delamination of the ice layer, the results from the frequency analysis allow us to target two modes from their mode shapes, Mode 2 (208 Hz) and 3 (229 Hz). Those modes, as shown in Figure 15, are similar to modes 18 and 20 for which delamination was proven possible. The frequencies of those modes are very close to mode 1, which is similar in shape to mode 17, showing the same pattern between modes 1, 2 and 3 and modes 17, 18 and 20.

Ice accumulation was repeated on the flat plate and the resonant mode at 1600 Hz was selected. The damping loss factor calculated from the measured frequency response function was 1.1%. With this value, the numerical model predicts a voltage of 190 Vpp to obtain 0.8 MPa and 380 Vpp to obtain 1.6 MPa in stress S11 in the ice layer. Those values define the stress limit range defined previously where cracking occurred. By taking into account the error of the numerical model, this means that the numerical model predicts cracking of the ice between 112 Vpp and 535 Vpp (0.47 MPa to 2.26 MPa, Section 4.3). The sweep test was performed at higher voltages and a crack was formed during the sweep at 335 Vpp. The stress calculated with the numerical model for this voltage was 1.4 MPa. Comparison of accelerations measured by the accelerometers with numerical prediction shows an error of 15% for the numerical model, meaning that the adjusted value for stress S11 is 1.64 MPa.

This test method was repeated with optimal phasing for mode 27, as well as for mode 35 with all actuators activated in phase and with optimal phasing. It was also repeated for mode 2 and 3 with optimal phasing. The maximum discrepancy of the numerical model obtained during those tests is 38%, with an average error of 17%. Those results are within the discrepancy established previously for the model of 41% with an average of 20%. Results for mode with cracking of the ice are presented in

Table 15. Stress S11 and voltage prediction by the numerical model compared to experimental results for cracking modes.

Mode (opt. phas.)	Damping (%)	Vpp (V)	Voltage Vpp Predicted for S11 (V)				Stress S11 at Cracking (MPa)
			= 0.80 MPa	= 1.60 MPa	= 0.47 MPa.	= 2.26 MPa.	Num.	Adj.
27	1.1	335	190	380	112	535	1.40	1.64
27 (p)	1.0	170	120	240	70	340	1.15	1.32
35	1.0	265	442	884	265	1245	0.47	0.76
35 (p)	1.4	200	310	620	183	875	0.52	0.71

, while for the mode with delamination of the ice layer is presented in

Table 16. Stress S23 and voltage prediction by the numerical model compared to experimental results for delamination modes.

Mode (#)	Damping (%)	Vpp (V)	Voltage Vpp Predicted for S23 (V)				Stress S23 at Delamination (MPa)
			= 0.33 MPa	= 0.65 MPa	= 0.20 MPa.	= 0.92 MPa.	Num.	Adj.
2	0.7	216	105	207	62	292	0.68	0.66
3	0.8	250	115	226	68	320	0.72	0.65

for stress S23 and

Table 17. Stress S33 and voltage prediction by the numerical model compared to experimental results for delamination modes.

Mode (#)	Damping (%)	Vpp (V)	Voltage Vpp Predicted for S33 (V)				Stress S33 at Delamination (MPa)
			= 0.50 MPa	= 0.90 MPa	= 0.30 MPa.	= 1.27 MPa.	Num.	Adj.
2	0.7	216	108	195	64	275	1.00	0.97
3	0.8	250	108	194	64	274	1.15	1.03

for stress S33. The tables present the voltage predicted to obtain the stress limit criteria established at Section 4.3, as well as the stresses when the 41% maximum numerical error is taken into account (Table 14). It also presents the stress calculated by the model at ice breaking as well as the stress adjusted with the numerical error obtained for each mode.

All results obtained experimentally fall within the voltage range predicted by the numerical model. The stress calculated at cracking, when adjusted for the numerical error of each mode, ranges from 0.71 MPa to 1.64 MPa with an average of 1.11 MPa. The average stress was similar to the values obtained with the previous mode tested of 1.04 MPa, with only a 6% difference. The stress range where cracking occurs, once adjusted with the numerical error, was defined between 0.80 and 1.60 MPa. The range of 0.71 MPa to 1.64 MPa obtained with the four tests is slightly outside this range. This means that, even if the numerical model accurately predicted the voltage range within which cracking occurred, the range of stress S11 must be slightly widened to 0.70 MPa to 1.65 MPa. The stress obtained at delamination when adjusted is 0.66 and 0.65 MPa for S23 and 0.97 MPa and 1.03 MPa for S33. For S23, the stress for mode 2 is very slightly out of the range of 0.33 to 0.65 MPa predicted previously for delamination of the ice, while for mode 3 the value is on the upper limit of the range. For S33, the values are both higher than the range predicted of up to 15% for mode 3, but this is explained by the fact that it is unlikely that this stress is the limiting stress.

The numerical model has been able to predict the voltage range within which cracking and delamination occurs, but some of the adjusted stress results obtained during those tests fall outside the range criteria established. For cracking tests, the range of 0.80 MPa to 1.60 MPa needs to be slightly modified to 0.70 to 1.65 MPa. For shearing stress S23, one mode is within the range and the other one is 0.01 MPa above. The range is modified accordingly to 0.33 to 0.66 MPa. Even with those small increases in range for those stresses, the resulting ranges are still well inside the limit found in the literature and still confirms the viability of the method and the ability of the numerical model to be used to predict ice breaking and to assist in the design of a piezoelectric system. For S33, the change in range is a little bit more significant, from 0.5 to 1.03 MPa, but it is unlikely that it is a limiting stress.

5. Conclusions

A numerical model of a piezoelectric actuator de-icing system integrated to a flat plate structure was developed in the first phase of this research project [14]. An ice layer was added to this model and frequency analysis and direct steady-state dynamic analysis were performed to predict the structural natural frequencies, vibration amplitudes and stresses generated in the ice layer. Experimental validation was performed with a test setup in a cold room. The test variation was established at 26% and the average numerical error of the model was 20% with a maximum error of 41%. Two types of ice breaking were obtained during the experimental testing: cracking within the ice layer and delamination of the ice layer from the flat plate structure. The numerical model predicted an average of 1.04 MPa in normal stress in the ice layer for cracking which is in accordance with the literature. For delamination of the ice layer, numerical model calculated two significant stresses at the bottom of the ice layer, a shearing stress S23 and a normal stress S33. The average shearing stress value predicted by the model was 0.46 MPa, which is right within the literature range for adhesion of ice on steel and also for shear stress obtained in other studies at the laboratory. The average value obtained for normal stress S33 was 0.69 MPa, which is larger than S23. However, even if no value was found in literature for adhesion of ice on steel in tension, a paper established that in tensile experiments, adhesive strength of ice in tension is at minimum 15 times greater than in shearing experiments. This was explained by the presence of a liquid-like layer at the interface which hold the ice and substrate together by surface tension forces. This indicates that S23 is the limiting stress, but more experimentation could be performed on the subject. The stress distribution of the different stresses for delamination cases where concentrated on the edges of the bottom layer of the ice accumulation. Negligible stresses were obtained at the center of the ice layer and concentrated rapidly close to the edges. This result was in accordance with a shear model developed in the literature that showed the same distribution pattern and concluded that shear stress is concentrated on the edges of the ice and delamination starts off from edges and maximum shear stress emerges on the new edges until complete delamination. Stress limit criteria were determined from the prediction of the model for all the modes tested and the numerical model was used, as a proof of concept, to find modes susceptible to generate ice breaking within the voltage limit of the piezoelectric actuators and to predict the voltage range within which breaking should occur. Four modes were found and tested, revealing that the numerical model was successful in predicting ice breaking and voltage range.