Arnold’s Piecewise Linear Filtrations, Analogues of Stanley–Reisner Rings and Simplicial Newton Polyhedra

Abstract

In 1974, the author proved that the codimension of the ideal $(g_1,g_2,\dots ,g_d)$ generated in the group algebra $\mathbb{K}\left[{\mathbb{Z}}^d\right]$ over a field $\mathbb{K}$ of characteristic 0 by generic Laurent polynomials having the same Newton polytope $\mathsf{\Gamma }$ is equal to $d!\times Volume\left(\mathsf{\Gamma }\right)$. Assuming that Newtons polytope is simplicial and super-convenient (that is, containing some neighborhood of the origin), the author strengthens the 1974 result by explicitly specifying the set ${\mathbb{B}}^{sh}$ of monomials of cardinality $d!\times Volume\left(\mathsf{\Gamma }\right)$, whose equivalence classes form a basis of the quotient algebra $\mathbb{K}\left[{\mathbb{Z}}^d\right]/(g_1,g_2,\dots ,g_d)$. The set ${\mathbb{B}}^{sh}$ is constructed inductively from any shelling $sh$ of the polytope $\mathsf{\Gamma }$. Using the ${\mathbb{B}}^{sh}$ structure, we prove that the associated graded $\mathbb{K}$ -algebra $g{r}^{\mathsf{\Gamma }}\left(\mathbb{K}\left[{\mathbb{Z}}^d\right]\right)$ constructed from the Arnold–Newton filtration of $\mathbb{K}$ -algebra $\mathbb{K}\left[{\mathbb{Z}}^d\right]$ has the Cohen–Macaulay property. This proof is a generalization of B. Kind and P. Kleinschmitt’s 1979 proof that Stanley–Reisner rings of simplicial complexes admitting shelling are Cohen–Macaulay. Finally, we prove that for generic Laurent polynomials $(f_1,f_2,\dots ,f_d)$ with the same Newton polytope $\mathsf{\Gamma }$, the set ${\mathbb{B}}^{sh}$ defines a monomial basis of the quotient algebra $\mathbb{K}\left[{\mathbb{Z}}^d\right]/(g_1,g_2,\dots ,g_d)$.

1. Introduction

1.1. Prehistory

Using the Newton polytope $\mathsf{\Gamma }$ of the Taylor series of an analytic function, V.I. Arnold constructed in 1974 a filtration in the ring of germs of analytic functions [1]. He called this filtration piecewise linear filtration. Today, this filtration and similar filtrations in $\mathbb{K}$-algebras of polynomials, Laurent polynomials and formal series over the field $\mathbb{K}$ are called Newton filtrations. The study of the associated graded rings constructed by the Newton-Arnold filtration in the rings of polynomials and formal series was performed by the author in [2,3,4]. The central result of the study was the establishment of the Cohen–Macaulay property of these rings. This property was proved by homological methods, using a nontrivial result obtained by M. Hochster in 1972 that semigroup $\mathbb{K}$-algebras of conic semigroups in ${\mathbb{Z}}^d$ possess the Cohen–Macaulay property [5]. My proof of the Cohen–Macaulay property of the associated graded ring was rather general and complex. In this proof, the associated graded ring arising from the Newton filtration was considered as a result of gluing some graded rings according to the combinatorial scheme determined by the polyhedral complex of faces of the Newton polytope. Similar schemes for proving the Cohen–Macaulay property of complex rings by reduction to simpler rings are discussed in M. Hochster’s article [6]. The simpler rings in my proof were semigroup rings of conical semigroups in ${\mathbb{Z}}^d$. Their Cohen–Macaulayness is a non-trivial fact, proved by M. Hochster in 1972. Furthermore, the Cohen–Macaulayness of the result of gluing such rings according to the combinatorial scheme defined by a polyhedral complex is proved in my article under the assumption that the polyhedral complex has the homology of a sphere or a disk and does not use the fact that the complex can be realized as the boundary of a convex polytope.

Today, I am aware that my 1975 proof applies to simplicial triangulations of homological spheres and allows us to prove the Cohen–Macaulay property of Stanley–Reisner rings of such simplicial triangulations. Another justification for the usefulness of my proof is that it allows us to re-prove the result of M. Hochster on the Cohen–Macaulay property of semigroup rings of conic semigroups. A sketch of the proof of M. Hochster’s theorem by constructing Newton polytopes for elements of semigroup rings of conic semigroups is given in Section 5.12 in [4] and retold in [7].

1.2. Fulfilling the Wishes of V.I. Arnold Dated 1975

My proof of the Cohen–Macaulay property of the associated graded rings was far from the issues that were addressed in V. Arnold’s seminar at Moscow State University in the 1970s. V. Arnold considered this proof to be complicated and, in contrast to the consequences I derived from it, not intuitively clear.

In terms of intuitively clear results, highly appreciated by V.I. Arnold, there were explicit formulas expressing in terms of the volumes of Newton polytopes a number of topological characteristics of generic polynomials and germs of analytic functions: the multiplicity of a singular point of an analytic function, the Euler characteristic of a level surface of a polynomial, and the number of solutions of a polynomial system of d equations with d unknowns in the case when all equations have the same Newton polytope. The simplest and most famous of these results is an explicit formula for the number of solutions of a generic polynomial system of equations with a given Newton polytope. By the well-known theorem of commutative algebra, in the case when the field $\mathbb{K}$ is algebraically closed, this number of solutions, taking into account the multiplicities, is equal to the codimension of the ideal generated in the $\mathbb{K}$-algebra of Laurent polynomials $\mathbb{K}\left[{\mathbb{Z}}^d\right]$ by equations of the system $g_1=g_2=\dots =g_d=0$. For generic polynomials, this codimension is finite and equal to the number of elements of the monomial basis of the quotient algebra $\mathbb{K}\left[{\mathbb{Z}}^d\right]/(g_1,g_2,\dots ,g_d)$. (Here and below, a monomial basis of a quotient algebra is known as the set of monomials of the original algebra whose equivalence classes generate a quotient algebra over $\mathbb{K}$.) Important information about an ideal of finite codimension is provided not only by the number of elements of the monomial basis of the quotient algebra, but also by the arrangement of the elements of this basis with respect to the Newton polytope. The examples of calculating monomial bases for the simplest non-trivial Newton polytopes, given in the work [8], inspired the author to continue, almost half a century later, research dated 1974, for one important special case. It turned out that the monomial basis for generic simplicial Newton polytopes can be specified explicitly. This fact allows to prove the Cohen–Macaulay property of $\mathbb{A}\left(\mathsf{\Gamma }\right)$ by constructive manipulations with monomials in the spirit of V. Arnold’s “crossword solution” technique, Example 9.6 in [1], and in the spirit of the reasoning of the article by B. Kind and P. Kleinschmitt in 1979 on the Cohen–Macaulay property of Stanley–Reisner rings of simplicial complexes admitting shelling [9]. The results of the last article are retold in R. Stanley’s online publications [10].

Having explicitly indicated the basis of the quotient algebra of Laurent polynomials in d variables modulo the ideal generated by d generic polynomials with a given Newton polytope, I, with many years’ delay, succeed in fulfilling V. Arnold’s wish to improve the clarity of the algebraic proof of the theorem on the number of solutions of a system of generic polynomial equations with a given Newton polytope.

At the same time, I was able to improve the formulation of the theorem by constructing, for the super-convenient Newton polytope $\mathsf{\Gamma }$ and its shelling $sh$, the so-called Shelling Extension ${\mathsf{\Gamma }}^{sh}$ of the Newton polytope $\mathsf{\Gamma }$, see Section 2.5 below. The Shelling Extension is non-closed and, generally speaking, a non-convex polytope. The semi-open polytope ${\mathsf{\Gamma }}^{sh}$ is composed of disjoint semi-open parallelepipeds. The volume of each of these parallelepipeds is equal to the number of integral points it contains. Therefore, the cardinality of the set ${\mathbb{B}}^{sh}\in {\mathsf{\Gamma }}^{sh}$ is equal to the volume of ${\mathsf{\Gamma }}^{sh}$, which in turn is equal to $d!\times Volume\left(\mathsf{\Gamma }\right)$. The elements of the set ${\mathbb{B}}^{sh}$, in the general case, define a monomial basis of the quotient algebra $\mathbb{K}\left[{\mathbb{Z}}^d\right]/(g_1,g_2,\dots ,g_d)$. The closure of a Shelling Extension does not depend on the choice of a shelling, and is a polytope homeomorphic to a disk, generally speaking, nonconvex, the boundary of which is composed of flat $(d-1)$-dimensional parallelepipeds.

The volume of this particular polytope ${\mathsf{\Gamma }}^{\mathit{sh}}$ is equal to the number of solutions of a generic polynomial system of equations with a given Newton polytope.

1.3. Associated Graded Rings of Newton Filtered Rings and Stanley–Reisner Face Rings

Working on this paper, I managed to find the idea of the manipulations necessary for proving the Cohen–Macaulay property of associated graded rings in the theory of simplicial complexes. If the polytope $\mathsf{\Gamma }$ is simplicial, then the associated graded ring $\mathbb{A}\left(\mathsf{\Gamma }\right)$ constructed from the Newton–Arnold filtration defined by the super-convenient polytope $\mathsf{\Gamma }$ in the space of Laurent polynomials in several variables over the field $\mathbb{K}$ can be considered as an analogue of the so-called face ring of the simplicial complex of the boundary of the polytope $\mathsf{\Gamma }$. Face rings were introduced in 1974 by R. Stanley and G. Reisner [11] to study the combinatorial properties of simplicial complexes. For the complex of faces of the super-convenient (having the origin of coordinates by an interior point) simplicial Newton polytope $\mathsf{\Gamma }$, the Stanley–Reisner ring can be identified with the subring in the associated graded ring $\mathbb{A}\left(\mathsf{\Gamma }\right)$ generated by the monomials corresponding to the vertices of $\mathsf{\Gamma }$. In the simplest cases, the Stanley–Reisner subring can coincide with the entire ring $\mathbb{A}\left(\mathsf{\Gamma }\right)$. Just as Stanley–Reisner rings are related to f-polynomials and h-polynomials of simplicial complexes, rings of the form $\mathbb{A}\left(\mathsf{\Gamma }\right)$ are related to the Ehrhart polynomial of convex integral polyhedra, but we will not touch on this issue.

I managed to spy on monomial manipulations useful for working with associated graded rings in the 1979 paper by B. Kind and P. Kleinschmitt on the Cohen–Macaulay property of Stanley–Reisner rings of shellable simplicial complexes [9]. The reasoning of B. Kind and P. Kleinschmitt about simplicial complexes admitting shelling can be applied to associated graded rings defined by simplicial Newton polytopes, since H. Bruggesser and P. Mani proved in 1971 that the complex of faces of any convex polytope admits shelling [12]. The results of this original work have been re-exposed in many publications, for example, in [13]. The definition of the shelling of a simplicial convex polytope will be given below in Section 2.1.

1.4. Directions for Further Work

1.4.1. Direct Generalizations of the Results of This Paper to the Case of Conventional Polynomials and Formal Series

Monomial bases similar to that constructed in this article, with minor changes in construction and proof, can be constructed for conventional polynomials and formal series. Furthermore, in this case, an explicit indication of the basis is more informative, since the origin in ${\mathbb{K}}^d$ is fixed by the very proposition of the problem. The author plans to publish these generalizations in the near future.

1.4.2. Approximation of a Non-Simplicial Newton Polytope by a Simplicial One

An arbitrary convex polytope with integer vertices in the space ${\mathbb{R}}^d$ can be approximated by simplicial polytopes with rational vertices. This fact allows us to reduce the question about the number of solutions of a system of equations with an non-simpicial Newton polytope to the question about the number of solutions to a system of equations with a simplicial Newton polytope and thus apply the results of this article to obtain another proof of the formula for the number of solutions of a polynomial system of equations with a given arbitrary (not only simplicial) Newton polytope.

The author plans to include a rigorous justification of this reasoning in a publication devoted to polynomials and formal series with Newtonian simplicial polytopes.

1.4.3. Explicit Construction of a Monomial Basis for Factor Algebra of Laurent Polynomials Modulo Ideal Generated by Generic Polynomials with the Same Non-Simplicial Newton Polytope

The shelling-dependent basis construction can be generalized to the super-convenient Newton polytope $\mathsf{\Gamma }$, which is not simplicial. This is possible because the boundary of an arbitrary convex polytope can be split into simplices so that the resulting simplicial complex admits shelling $sh$. Repeating the constructions of this article, starting with a fixed shelling of the simplicial subdivision $\mathsf{\Gamma }$, we obtain an semi-open polytope ${\mathsf{\Gamma }}^{sh}$, whose integer points define some set of monomials B of cardinality $d!\times Volume\left(\mathsf{\Gamma }\right)$. There are reasons to believe that for generic polynomials this set of monomials will be a basis for the quotient algebra $\mathbb{K}\left[{\mathbb{Z}}^d\right]/(g_1,g_2,\dots ,g_d)$. In the simplest examples, this hypothesis could be verified using computer algebra systems.

The author does not plan to tackle this problem on his own or together with his students and staff in the near future.

1.4.4. Development of a Module for Computer Algebra Systems That Generates the Basis Built in This Article, Having Received as Input a Simplicial Super-Convenient Polytope and Its Shelling

The author does not plan to tackle this problem on his own or together with his students and staff in the near future.

1.4.5. Preparation of Student Workshops on Acquaintance with Computer Systems of Convex Geometry and Commutative Algebra Based on the Material of This Article

Checking the main result of this article in two-dimensional and three-dimensional cases, in view of the clarity of the geometric and algebraic objects appearing in the main theorem, can form the basis of a student workshop on acquaintance with modern computer systems of convex geometry and commutative algebra. The author plans to start developing similar workshops in the 2022–2023 academic year.

1.4.6. An Interesting Unsolved Problem of Explicitly Constructing a Monomial Basis for the Jacobian Ideal of a Formal Series in d Variables with a Given Simplicial Newton Polytope

In this section, I adhere to the notation of paper [4] and denote the Newton polytope of the formal series g in d variables by ${\mathsf{\Gamma }}_{-}\left(g\right)$. For the Laurent polynomial g with Newton polytope $\mathsf{\Gamma }$, the Jacobian ideal J generated by ordinary partial derivatives

$$J\left(g\right)=\left(\frac{\partial g}{\partial x_1},\frac{\partial g}{\partial x_2},\dots ,\frac{\partial g}{\partial x_d}\right)$$

coincides with the ideal $J_{tor}$ generated by tweaked partial derivatives

$$J_{tor}\left(g\right)=x_1\frac{\partial g}{\partial x_1},x_2\frac{\partial g}{\partial x_2},\dots ,x_d\frac{\partial g}{\partial x_d}$$

which we will call “toric” derivatives. Therefore, for a generic Laurent polynomial, the codimensions of these two ideals coincide and are equal to $d!\times Volume\left(\mathsf{\Gamma }\right(g\left)\right)$. The monomial bases of the corresponding rings also coincide. For a tuple of formal series or polynomial g in d variables, the Jacobian ideal is obviously different from the ideal generated by the toric derivatives. Moreover, for a tuple of convenient (in the sense of [4]) formal series g, the toric derivatives have the same Newton polytope ${\mathsf{\Gamma }}_{-}\left(g\right)$ as the original series g, and therefore, for generic tuple of series g the codimension of the ideal $J_{tor}\left(g\right)$ is given by a formula similar in structure to the formula for the codimension of the Jacobi ideal of the Laurent polynomial

$$codi{m}_{\mathbb{K}}\left(J_{log}\left(g\right)\right)=d!\times Volume\left({\mathsf{\Gamma }}_{-}\left(g\right)\right)$$

Moreover, the codimension of conventional Jacobian ideal $J\left(g\right)$ for generic tuple of series g is given by some more complicated formula, the so-called formula for the Newton number $\nu \left({\mathsf{\Gamma }}_{-}\right)$. This formula includes both the volume $V_d$ of the polytope ${\mathsf{\Gamma }}_{-}$ itself, and an alternating sum of the volumes of intersections of this polytope with all possible coordinate subspaces of the same dimension

$$codi{m}_{\mathbb{K}}\left(J\left(g\right)\right)=\nu \left({\mathsf{\Gamma }}_{-}\right)=d!\times V_d\left({\mathsf{\Gamma }}_{-}\right)-(d-1)!\times V_{d-1}\left({\mathsf{\Gamma }}_{-}\right)+\dots +{(-1)}^{d-1}\times V_1+{(-1)}^d$$

V. Arnold was worried about some complexity and unintuitiveness of this formula and he proposed a problem that would stimulate the study of the internal structure of this formula. Namely, V. Arnold proposed to prove by purely combinatorial reasoning the nondecreasity of Newtons number under the extension of a polytope by combinatorial reasoning. In the published list of problems by V. Arnold [14], this problem dates back to 1982 and is formulated as follows:

Consider a Newton polytope $\Delta \in {\mathbb{R}}^n$ and the number

$$\mu (\Delta )=n!V-\Sigma (n-1)!V_i+\Sigma (n-2)!V_{ij}-\cdots ,$$

where V is the volume under Δ, $V_i$ is the volume under Δ on the hyperplane $x_i=0$, $V_{ij}$ is the volume under Δ on the hyperplane $x_i=x_j=0$, and so on.

Then,$\mu (\Delta )$grows (non strictly monotonically) as Δ grows (whenever Δ remains coconvex and integer). There is no elementary proof even for $n=2$.

Particular solutions to this Arnold problem for three variables were found in [15]. In 2020, Moscow student F. Selyanin announced a solution to V. Arnold’s problem in arbitrary dimension [16]. The solution is based on the representation of Newtons number as a sum of positive terms. Since the Newton number is equal to the number of elements of the monomial basis of the factor algebra of the Laurent polynomial algebra modulo Jacobian ideal of the generic Laurent polynomial, the idea arises to construct this monomial basis explicitly and to prove the monotonicity of the Newton number under the extension of the polytope, checking that the sets of basis monomials themselves grow monotonically, and not just the cardinalities of these sets. With this approach, the representation of the cardinality of a set in the form of a sum of positive terms, proposed by F. Selyanin, may hypothetically turn out to be a consequence of some reasonable partition of the set of monomials of the basis into disjoint subsets. Therefore, it is possible that constructions from the cited work of F. Selyanin could help in guessing the structure of the monomial basis. According to F. Selyanin’s private communication, the published announcement [16] contains inaccuracies and F. Selyanin plans to prepare a corrected proof in the near future.

1.5. Definitions and Notations That Do Not Use Newtons Polytope Shelling

All objects, designations, definitions and conventions introduced in this and the following sections marked with • will remain in effect until the end of the article and will not be redefined:

• $d\ge 2$—the dimension of the Newton polytope and the ambient vector space;
• $\mathbb{K}$—field of characteristic 0;
• In this article, only rings endowed with the structure of a $\mathbb{K}$-algebras will be considered, so we will consider the terms $\mathbb{K}$-algebra, algebra, ring as synonyms;
• ${\mathbb{R}}^d$—the vector space over $\mathbb{R}$ of d-tuples of the form $(y_1,y_2,\dots ,y_d)$, equipped with coordinate-wise operations of addition and multiplication by a real number, equipped with the usual topology. We fix coordinates $y_1,y_2,\dots ,y_d$ on this space and call them y-coordinates. It will be convenient for us, depending on the context, to call the elements of the vector space ${\mathbb{R}}^d$points or vectors. We will call a point $p\in {\mathbb{R}}^d$ integer if all of its y-coordinates are integers;
• $Volume$—nonnegative volume (measure) in ${\mathbb{R}}^d$, normalized by the condition: volume of a unit cube in y-coordinates is equal to 1;
• Let X and Y be two sets in ${\mathbb{R}}^d$. We call the set defined by the formula

  $$X\oplus Y=\bigcup _{x\in X,y\in Y}(x+y)$$
  the Minkowski sum of sets X and Y, The Minkowski sum of a finite number of sets is defined in a similar way.
  If Y is a one-point set $\left\{y\right\}$ consisting of one element y, then, to simplify the notation, we will write instead of $X\oplus \left\{y\right\}$ just $X\oplus y$;
• We will consider various subsemigroups of the group ${\mathbb{Z}}^d$, both with a neutral element and without it. An example of a subsemigroup without a neutral element is the set of d-tuples of integers in which the first $r>0$ components are positive and the rest are non-negative;
• Let $G\subset {\mathbb{Z}}^d$ be a subsemigroup of ${\mathbb{Z}}^d$. We denote by $\mathbb{K}\left[G\right]$ the semigroup algebra of functions on G with values in $\mathbb{K}$ that take nonzero values only at a finite number of points. Multiplication in this algebra is the convolution of functions. In particular, we will denote by $\mathbb{K}\left[{\mathbb{Z}}^d\right]$ the group algebra of the group ${\mathbb{Z}}^d$ over the field $\mathbb{K}$. It is convenient to speak of this algebra as the algebra of Laurent polynomials in variables $x_1,x_2,\dots ,x_d$ over the field $\mathbb{K}$ with operations of addition and multiplication of polynomials;
• facet—any highest-dimensional face on the boundary of any convex polytope. The facets of a d-dimensional polytope have dimension $d-1$ and are closed sets in ${\mathbb{R}}^d$;
• A convex polytope is called integer if all its vertices have integer y-coordinates and it is called simplicial if all its facets are simplices;
• A polytope in ${\mathbb{R}}^d$ is called super-convenient if it is convex and contains some neighborhood of the origin. A super-convenient polytope has dimension d, and its boundary is covered with facets of dimension $d-1$. It is obvious that each ray emanating from the origin intersects the boundary of the super-convenient polytope at exactly one point. The super-convenience property of a polytope is not preserved under translations;
• Let $\mathsf{\Gamma }$ be a super-convenient simplicial polytope in ${\mathbb{R}}^d$ with integer vertices. This polytope will be fixed until the end of this article. $\partial \mathsf{\Gamma }$ denotes the boundary of the polytope $\mathsf{\Gamma }$.
  Let
• N be a number of facets of $\mathsf{\Gamma }$;
• L be a number of vertices of $\mathsf{\Gamma }$;
• As a rule, in this article, we will denote:
  - By $\Delta$ a facet, involved in a current reasoning;
  - By ${\Delta }_1,{\Delta }_2,\dots ,{\Delta }_N$ facets of the shelling, defined in Section 2.1;
  - By v, $v_1,\dots v_d$ vertices participating in a current reasoning.
• For any facet $\Delta$ of a superconvenient polytope $\mathsf{\Gamma }$, the vertex-vectors $v_1,\dots v_d$ of this facet are linearly independent. Denote by $Cone(\Delta )$ the rational simplicial cone with generators $v_1,\dots v_d$, that is, the set of all possible linear combinations of the vectors $v_1,v_2,\dots ,v_d$ with non-negative real coefficients. It follows from the superconvenience of the polytope that each cone $Cone(\Delta )$ is proper, that is, it does not contain any one-dimensional vector subspace ${\mathbb{R}}^d$;
• On each simplicial cone $Cone(\Delta )$, where $\Delta$ is a facet of $\mathsf{\Gamma }$, we introduce a coordinate system for working with objects belonging to this cone. Since the facet’s vertex-vectors $v_1,v_2,\dots ,v_d$ form a basis in ${\mathbb{R}}^d$, there exist linear functions $c_1,c_2,\dots ,c_d$ on $R^d$ satisfying the conditions $c_i\left(v_j\right)={\delta }_{ij}$ (the Kronecker delta). These functions will be called c-coordinates on the cone $Cone(\Delta )$. For a point $p\in Cone(\Delta )$, we put $C\left(p\right)=(c_1\left(p\right),c_2\left(p\right),\dots ,c_d\left(p\right))$;
• Let us call the set of all possible linear combinations of vertices $v_1,v_2,\dots ,v_d$ with non-negative integer coefficients the vertex semigroup $V(\Delta )$ of an facet $\Delta$. This set coincides with the set of points of the cone $Cone(\Delta )$ with non-negative integer c-coordinates, so this semigroup is isomorphic to the free commutative additive semigroup of rows of length d composed of non-negative integers;
• Let us call the set of points of the cone $Cone(\Delta )$ with integer y-coordinates the complete semigroup $A(\Delta )$ of an facet $\Delta$. Since the generators of the vertex semigroup $V(\Delta )$ have integer y-coordinates, all elements of the vertex semigroup have integer y-coordinates, that is, $V(\Delta )\subseteq A(\Delta )$;
• We say that a point $p+g\in Cone(\Delta )$ is a shift of a point $p\in Cone(\Delta )$ by an element $g\in V(\Delta )$. Obviously, for $g_1\ne g_2$ the shifts of any point $p\in Cone(\Delta )$ by $g_1$ and $g_2$ do not coincide. The orbit of a point $p\in Cone(\Delta )$ under the action of the vertex semigroup $V(\Delta )$ is the set of all shifts of this point: ${\bigcup }_{g\in V}(p+r)$. The complete semigroup $A(\Delta )$ is invariant under shifts by elements of the vertex semigroup, i.e., the orbit of any point $p\in A(\Delta )$ under the action of the vertex semigroup lies in $A(\Delta )$;
• The number of points in a finite set X will be denoted by $\#X$.

1.6. $\mathbb{K}$-Algebra of Laurent Polynomials

We call the monomial in formal variables $x_1,x_2,\dots ,x_d$ an expression of the form $x^n=x_1^{n_1}{x}_2^{n_2}\dots x_d^{n_d}$, where $n\in {\mathbb{Z}}^d$. We will say that $x^n$ corresponds to a point $n\in {\mathbb{Z}}^d$. The exponent of the monomial $x^n=x_1^{n_1}{x}_2^{n_2}\dots x_d^{n_d}$ is the row vector $(n_1,n_2,\dots ,n_d)\in {\mathbb{Z}}^d$. We will denote this vector by $Log\left(x^n\right)$. Obviously, the monomial $m=x^n$ satisfies the identity $m=x^{Log\left(m\right)}$. A monomial with zero exponent will be called unit monomial. A non-null Laurent polynomial is a formal finite linear combination of monomials with non-null coefficients from the field $\mathbb{K}$. The null Laurent polynomial is an empty linear combination of monomials and we denote this polynomial by the same symbol as the zero element of the field $\mathbb{K}$. Each Laurent polynomial defines a function on the group ${\mathbb{Z}}^d$ with values in $\mathbb{K}$, which takes a nonzero value on a finite set of points. The multiplication of Laurent polynomials corresponds to the convolution of the corresponding functions on the group ${\mathbb{Z}}^d$. Thus, Laurent polynomials with coefficients in the field $\mathbb{K}$ can be considered as a group K-algebra $\mathbb{K}\left[{\mathbb{Z}}^d\right]$ of finite functions on the group ${\mathbb{Z}}^d$. In addition to the group ${\mathbb{Z}}^d$, we will consider different subsemigroups in ${\mathbb{Z}}^d$. If the semigroup $P\subset {\mathbb{Z}}^d$ contains the point 0, then this point is a neutral element in the semigroup P and the polynomial $1\times x^0$ is a neutral element of the multiplication operation in the semigroup algebra $\mathbb{K}\left[P\right]$. If the subsemigroup $P\subset {\mathbb{Z}}^d$ does not contain the point 0, that is, it does not have a neutral element, then the multiplication operation in the $\mathbb{K}$-algebra $\mathbb{K}\left[P\right]$ will not have a neutral element. The terms monomial and exponent will also be applied to semigroup $\mathbb{K}$-algebras of the form $\mathbb{K}\left[P\right]$, where $P\subset {\mathbb{Z}}^d$.

The support of a non-zero Laurent polynomial is the set of exponents of its monomials. When the Laurent polynomial is given as a linear combination of some set of monomials, the support will be a subset of monomials included in such a sum with a nonzero coefficient:

$$supp\left(\sum _{n\in {\mathbb{Z}}^d}{\lambda }_n{x}^n\right)=\{n\in {\mathbb{Z}}^d:{\lambda }_n\ne 0\}$$

The support of the null element of the Laurent polynomial ring is undefined.

1.7. Algorithm for Constructing a Monomial Basis of the Factor Algebra $\mathbb{K}\left[{\mathbb{Z}}^d\right]/(g_1,g_2,\dots ,g_d)$

For simplicity, in this article, we restrict ourselves to constructing a basis for such integer simplicial polytopes that contain some neighborhood of the origin (we call such polytopes super-convenient). The set of monomials of a basis is constructed as a union of disjoint groups of monomials, each of which corresponds to one facet of a polytope. We construct not one single basis, but a whole family of bases, each of which is constructed from the so-called shelling of a convex polytope $\mathsf{\Gamma }$. The shelling of a simplicial polytope $\mathsf{\Gamma }$ is the ordering of facets of the polytope

$$sh=({\Delta }_1,{\Delta }_2,\dots ,{\Delta }_N)$$

(1)

satisfying some conditions. These conditions imply, in particular, a topological property of sequence (1) namely, for $i\in [1,N-1]$ the union of the first i facets of the shelling is homeomorphic to the disc.

Shelling Extension ${\mathsf{\Gamma }}^{sh}$ of Super-Convenient Newton Polytope $\mathsf{\Gamma }$

For each facet $\Delta \in \partial \mathsf{\Gamma }$ of the super-convenient Newton polytope $\mathsf{\Gamma }$ let us construct d segments connecting the origin with the vertices of the facet and drop one of the two endpoints from each segment. Taking the Minkowski sum of the resulting d half-intervals, we obtain a set of points that is a half-open parallelepiped in the sense of the definition (5) of the Section 2.4 below.

For each facet, such a parallelepiped can be constructed in $2^d$ ways. We would like to choose one of these ways for each face so that the constructed N half-open parallelepipeds would not intersect pairwise. The existence of shelling $sh$ of any convex polytope, proved in 1971 by Bruggerser and Mani [13], allows us to prove that such a choice of parallelepipeds can indeed be made and, moreover, in many ways using the shellings of the polytope $\mathsf{\Gamma }$. For any shelling $sh$ of a super-convinient simplicial polytope $\mathsf{\Gamma }$, the semi-open parallelepipeds of facets can be inductively chosen so that they do not intersect, and their union, which we denote by ${\mathsf{\Gamma }}^{sh}$, covered the interior of $\mathsf{\Gamma }$. The polytope ${\mathsf{\Gamma }}^{sh}$ is not closed and, as a rule, is not convex. The volume of the constructed non-closed d-dimensional polytope ${\mathsf{\Gamma }}^{sh}$ is obviously equal to the volume of the Newton polytope $\mathsf{\Gamma }$ multiplied by $d!$. We will prove below that the number of integer points in any integer half-open parallelepiped is equal to its volume (this result is known, see, for example, [17]). Hence, the number of integer points in ${\mathsf{\Gamma }}^{sh}$ is equal to its volume, so

$$d!\times Volume\left(\mathsf{\Gamma }\right)=Volume\left({\mathsf{\Gamma }}^{sh}\right)=\#({\mathsf{\Gamma }}^{sh}\cap {\mathbb{Z}}^d)$$

(2)

Now, we can state the main result of this paper.

Main result.

Fix a super-convenient simplicial Newton polytope Γ and a shelling $sh$ of this polytope. Then, for the generic Laurent polynomials $g_1,g_2,\dots ,g_d$ whose supports belong to the set Γ, as a monomial basis of the quotient algebra $\mathbb{K}\left[{\mathbb{Z}}^d\right]/(g_1,g_2,\dots ,g_d)$ we can take the set ${\mathbb{B}}^{sh}$ of all monomials whose exponents belong to the union of all semi-open parallelepipeds that make up ${\mathsf{\Gamma }}^{sh}$.

Thus, we obtain a new formulation and a new proof of Kushnirenko’s theorem on the number of solutions of an generic unmixed system of Laurent polynomials with the simplicial Newtons polytope.

Note that there is quite a lot of arbitrariness in our construction of the basis. First, the basis depends on the choice of shelling, and a convex polytope has many shellings. Secondly, when all generators of the ideal $(g_1,g_2,\dots ,g_d)$ are multiplied by a monomial, the ideal does not change, but the polytope $\mathsf{\Gamma }$ is shifted in ${\mathbb{R}}^d$ by an integer vector. Therefore, any integer point inside the polytope can be chosen as the origin of coordinates, after which our constructions will give a different Newton filtration and a different basis at the output, since our construction “selects” monomials into the basis, minimizing their Newtonian degrees, which depend on the choice of the origin.

However, the second ambiguity disappears when passing from Laurent polynomials to ordinary polynomials or germs of complex analytic functions or formal power series.

2. Shelling of Super-Convinient Simplicial Polytope and Objects Defined by That Shelling

2.1. Definition of a Shelling

The paper [12] published in 1971 defines the shelling of a convex polytope and proves that shelling exists for any convex polytope. Shelling is a linear ordering of all the facets of a polytope that satisfies certain conditions. Any polytope has many shellings. It is known, in particular, that the initial and final facets of shelling can be chosen arbitrarily. We need the definition of shelling only for convex simplicial polyhedra.

Definition 1.

Theshellingof a simplicial polytope Γ is an ordering (numbering) of all facets ${\Delta }_1,{\Delta }_2,\dots ,{\Delta }_N$ of Γ that satisfies the following condition:

For any $i\ge 2$ the intersection of facet ${\Delta }_i$ with the union of facets ${\Delta }_1\cup {\Delta }_2,\dots \cup {\Delta }_{i-1}$ is the union of some nonzero number r of subfacets of codimension one of facet ${\Delta }_i$.

Until the end of this article, we fix a convex simplicial super-convenient d-dimensional Newton polytope $\mathsf{\Gamma }$ and fix its shelling $sh$:

$$sh=({\Delta }_1,{\Delta }_2,\dots ,{\Delta }_N)$$

(3)

Below, ${\Delta }_1,{\Delta }_2,\dots ,{\Delta }_N$ will always denote the elements of this fixed shelling. We will call ${\Delta }_1$ the initial facet of the shelling, and the remaining facets will be called the typical facets of the shelling.

In this article, we re-prove one known combinatorial result (Section 3.5, the Dehn–Sommerville property of the Poincaré series constructed from Newton’s grading). To prove it, we need (a) the “reversibility” of any shelling of a convex simplicial polytope, and (b) the proposition about the “complementarity” of intersections of any facet of a Newton polytope with the preceding facets of the direct and inverted shellings.

Proposition 1.

Let

$$sh=({\Delta }_1,{\Delta }_2,\dots ,{\Delta }_N)$$

(4)

be a shelling of convex simlicial polytope Γ and

$$\overline{sh}=({\Delta }_N,\dots ,{\Delta }_2,{\Delta }_1)$$

(5)

be the inverted ordering. Then, $\overline{sh}$ is also a shelling of Γ.

The proof of this proposition can be found in Lemma 8.10 in [18]. Let us call shellings $sh$ and $\overline{sh}$ mutually inverse.

Proposition 2.

Let (4) and (5) be two mutually inverse shellings.

Then, for $1<i<N$, each codimension one face $\delta \subset {\Delta }_i$ belongs to exactly one of the intersections

$${\Delta }_i\cap ({\Delta }_1\cup {\Delta }_2,\dots ,\cup {\Delta }_{i-1})$$

(6)

or

$${\Delta }_i\cap ({\Delta }_N\cup {\Delta }_{N-1},\dots ,\cup {\Delta }_{i+1})$$

(7)

Proof. 

For $i\in [2,N-1]$, the set of facets of $\mathsf{\Gamma }$ other than ${\Delta }_i$ is split into two non-empty sequences:

-

Elements of $sh$ preceding the ${\Delta }_i$ facet:

$$({\Delta }_1,{\Delta }_2,\dots ,{\Delta }_{i-1})$$

(8)

-

Elements of $\overline{sh}$ preceding the ${\Delta }_i$ facet:

$$({\Delta }_N,{\Delta }_{N-1},\dots ,{\Delta }_{i+1})$$

(9)

Each face of dimension $d-2$ of any convex d-dimensional polytope belongs to exactly two facets of this polytope. Therefore, any $(d-2)$-dimensional face $\delta \subset {\Delta }_i\subset \partial \mathsf{\Gamma }$ belongs to the boundary of exactly one facet of the polytope other than ${\Delta }_i$. This second facet is a member of sequence (8) or a member of sequence (9). In the first case, the face $\delta$ belongs to the intersection (6), in the second case, the face $\delta$ belongs to the intersection (7).

□

2.2. Shelling Defines a Covering and Partitioning of the Boundary of a Convex Simplicial Polytope

The shelling construction of a simplicial polytope actually refers not to the polytope itself, but to the structure of the simplicial complex on its boundary, which arises from the simplicial triangulation of the boundary of the polytope. As a subset of the topological vector space ${\mathbb{R}}^d$, the boundary $\partial \mathsf{\Gamma }$ of the polytope $\mathsf{\Gamma }$ is covered by closed convex facets:

$$\partial \mathsf{\Gamma }={\Delta }_1\cup {\Delta }_2\cup \dots \cup {\Delta }_N$$

(10)

Any shelling $sh$ defines an ascending sequence of closed sets obtained by the union of the initial piece of the sequence $sh$: $⌀=S_0\subset S_1\subset S_2\subset \dots \subset S_N=\partial \mathsf{\Gamma }$; every subset except the last is homeomorphic to a $(d-1)$-disk and the latter is homeomorphic to a $(d-1)$-dimensional sphere. This sequence is built in the following way:

$$\begin{array}{cc}\hfill & S_1={\Delta }_1\hfill \\ & S_2={\Delta }_1\cup {\Delta }_2\hfill \\ & S_3={\Delta }_1\cup {\Delta }_2\cup {\Delta }_3\hfill \\ & \dots \dots \dots \hfill \\ & S_N=({\Delta }_1\cup {\Delta }_2\cup \dots \cup {\Delta }_N)\hfill \end{array}$$

(11)

Closed triangulated sets $S_1,S_2,\dots ,S_N$ will be called subcomplexes. For $i=1,2,\dots ,N$ the set $S_i\backslash S_{i-1}$ is called $sh$-facet and is denotes by ${\Delta }_i^{sh}$. The set ${\Delta }_1^{sh}$ is called the initial $sh$-facet. This $sh$-facet coinsides to the facet ${\Delta }_1$ and is a closed subset of ${\mathbb{R}}^d$. The remaining $sh$-facets, i.e., ${\Delta }_i^{sh}$ for $i\ge 2$, will be called regular. A regular $sh$-facet ${\Delta }_i^{sh}$ is a proper subset of facet ${\Delta }_i$ and, according to the definition of shelling, is obtained by removing from facet ${\Delta }_i$ a non-zero number r of codimension one faces. Any of the regular $sh$-facets ${\Delta }_i^{sh}$ is not closed in ${\mathbb{R}}^d$ and is the difference of two closed sets. Namely, any regular $sh$-facet is the difference between a convex $d-1$-dimensional set ${\Delta }_i$ and some non-empty closed $(d-2)$-dimensional set lying on the relative boundary of ${\Delta }_i$. It is easy to see, and we will check it below, that any $sh$-facet is convex. It follows from the definition that $sh$-facets are pairwise disjoint and that the sets ${\Delta }_1^{sh},{\Delta }_2^{sh},\dots ,{\Delta }_i^{sh}$ form a partition of $S_i$. Therefore, for $i\ge 2$, the subcomplex $S_i$ is the disjoint union of the subcomplex $S_{i-1}$ and $sh$-facet ${\Delta }_i^{sh}$.

$$\begin{array}{cc}\hfill S_1& ={\Delta }_1^{sh}\hfill \\ \hfill S_2& =S_1\cup {\Delta }_2^{sh}={\Delta }_1^{sh}\cup {\Delta }_2^{sh}\hfill \\ \hfill S_3& =S_2\cup {\Delta }_3^{sh}={\Delta }_1^{sh}\cup {\Delta }_2^{sh}\cup {\Delta }_3^{sh}\hfill \\ \hfill \dots & \dots \dots \hfill \\ \hfill S_i& =S_{i-1}\cup {\Delta }_i^{sh}=({\Delta }_1^{sh}\cup {\Delta }_2^{sh}\cup \dots \cup {\Delta }_i^{sh})\hfill \\ \hfill \dots & \dots \dots \hfill \\ \hfill S_N& =S_{N-1}\cup {\Delta }_N^{sh}=({\Delta }_1^{sh}\cup {\Delta }_2^{sh}\cup \dots \cup {\Delta }_N^{sh})\hfill \end{array}$$

(12)

The right-hand sides of the Formula (12) give the partitions of the $S_1,S_2,\dots ,S_N$ into $sh$-facets. In particular, the boundary of the polytope is split into $sh$-facets:

$$\partial \mathsf{\Gamma }=({\Delta }_1^{sh}\cup {\Delta }_2^{sh}\cup \dots \cup {\Delta }_N^{sh})$$

(13)

The boundary of any convex polytope $\mathsf{\Gamma }$ is homeomorphic to a $(d-1)$-dimensional sphere. It is easy to deduce from the definition of the shelling of a simplicial polytope that for any $i<N$ the subcomplex $S_i=({\Delta }_1^{sh}\cup {\Delta }_2^{sh}\cup \dots \cup {\Delta }_i^{sh})$ is polyhedral hypersurface homeomorphic to a closed $d-1$-dimensional disk (see [12]).

2.3. Covers and Partitions of the Sets ${\mathbb{R}}^d$ and ${\mathbb{Z}}^d$ Defined by the Shelling $sh$ of a Super-Convinient Simplicial Newtons Polytope $\mathsf{\Gamma }$

In Section 1.5, for each facet $\Delta \subset \partial \mathsf{\Gamma }$, the following objects were constructed

• $Cone(\Delta )$ is the union of all closed rays starting from the origin and passing through some point on $\Delta$. The set $Cone(\Delta )$ is closed in $R^d$ and, due to the convexity of the face $\Delta$, is a commutative semigroup with respect to the addition operation with a neutral element $0\in {\mathbb{R}}^d$;
• $A(\Delta )$ is a semigroup with neutral element 0, consisting of all integer points of the cone $Cone(\Delta )$. This semigroup is called the complete semigroup of $\Delta )$. The semigroup $\mathbb{K}$-algebra $\mathbb{K}\left[A\right(\Delta \left)\right]$ is called the complete algebra of the face $\Delta )$;
• $V(\Delta )$ is a subsemigroup with a neutral element in $A(\Delta )$ generated by all vertices $v_1,v_2,\dots ,v_d$ of facet $\Delta$. The semigroup $V(\Delta )$ is freely generated by elements $v_1,v_2,\dots ,v_d$. We call this semigroup vertex semigroup of facet $\Delta$. The $\mathbb{K}$-algebra $\mathbb{K}\left[V\right(\Delta \left)\right]$ will be called the vertex algebra of facet $\Delta$. This $\mathbb{K}$-algebra is isomorphic to the algebra of polynomials in d independent variables. Since the semigroup $V(\Delta )$ is a subsemigroup of $A(\Delta )$, for any facet $\Delta$, the algebra $K\left[A\right(\Delta \left)\right]$ is a module over the vertex algebra $K\left[V\right(Delta\left)\right]$. We verify below that this module is both finitely generated and freely generated.

In view of the superconvenience of the polytope $\mathsf{\Gamma }$, the commutative groups ${\mathbb{R}}^d$ and ${\mathbb{Z}}^d$ can be covered by semigroups with a neutral element

$$\begin{array}{cc}\hfill {\mathbb{R}}^d& =Cone\left({\Delta }_1\right)\cup Cone\left({\Delta }_2\right)\cup \dots \cup Cone\left({\Delta }_N\right)\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill {\mathbb{Z}}^d& =A\left({\Delta }_1\right)\cup A\left({\Delta }_2\right)\cup \dots \cup A\left({\Delta }_N\right)\hfill \end{array}$$

(15)

Now, using the properties of shelling (3), we construct partitions of the commutative groups ${\mathbb{R}}^d$ and ${\mathbb{Z}}^d$ into subsemigroups. In each partition, one semigroup will have a neutral element, and the rest will be semigroups without a neutral element.

Let us define $Cs{h}_1=Cone\left({\Delta }_1\right)$ and $As{h}_1=A\left({\Delta }_1\right)$. For $i>1$, define the subset $Cs{h}_i\subset Cone\left({\Delta }_i\right)$ and the subset $As{h}_i\subset A\left({\Delta }_i\right)$ by the equalities

$$\begin{array}{cc}\hfill Cs{h}_i& =Cone\left({\Delta }_i\right)\backslash (Cone\left({\Delta }_1\right)\cup Cone\left({\Delta }_2\right)\cup \dots \cup Cone\left({\Delta }_{i-1}\right))\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill As{h}_i& =A\left({\Delta }_i\right)\backslash (A\left({\Delta }_1\right)\cup A\left({\Delta }_2\right)\cup \dots \cup A\left({\Delta }_{i-1}\right))\hfill \end{array}$$

(17)

The sets $Cs{h}_1$ and $As{h}_1$ are obviously semigroups with the respect to the addition operation with a neutral element $0\in {\mathbb{Z}}^d\subset {\mathbb{R}}^d$. For $i>1$, neither the set $Cs{h}_i$, nor the set $As{h}_i$ contains the origin. Below, we check that sets $Cs{h}_2,Cs{h}_3,\dots ,Cs{h}_n$ and $As{h}_2,As{h}_3,\dots ,As{h}_n$ are semigroups without a neutral element. This implies that for $i>1$, the semigroup algebra $\mathbb{K}\left[As{h}_i\right]$ is defined. The multiplicative operation in this algebra has no neutral element. It is easy to see that for $i\in [1,N]$, $a\in As{h}_i$, and $g\in V\left({\Delta }_i\right)$, the sum $a+g$ belongs to $As{h}_i$, so the semigroup algebra $\mathbb{K}\left[As{h}_i\right]$ is a module over the algebra $\mathbb{K}\left[V\left({\Delta }_i\right)\right]$. We will check below that this module is both finitely generated and freely generated.

For $i\in [1,N]$, the sets $Cs{h}_i$ will be called $sh$-cones and the sets $As{h}_i$ will be called $sh$-semigroups. From the definitions (16) and (17), we obtain the following:

Proposition 3.

${\mathbb{R}}^d$ admits a partition into $sh$-cones and ${\mathbb{Z}}^d$ admits a partition into $sh$-semigroups:

$$\begin{array}{cc}\hfill {\mathbb{R}}^d& =Cs{h}_1\cup Cs{h}_2\cup \dots \cup Cs{h}_N\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill {\mathbb{Z}}^d& =As{h}_1\cup As{h}_2\cup \dots \cup As{h}_N\hfill \end{array}$$

(19)

Obviously, for any $i\in [1,N]$, the set $As{h}_i$ is nothing but a subset of integer points of the set $Cs{h}_i$:

$$As{h}_i={\mathbb{Z}}^d\cap Cs{h}_i$$

(20)

2.4. Semi-Open Parallelepipeds and Sets of Their Integer Points as Fundamental Domains for Action of Vertex Semigroups on $sh$-Cones and $sh$-Semigroups

Two coordinate systems on a cone $\mathit{Cone}(\Delta )$. Characterization of the semigroups $\mathit{A}(\Delta )$ and $\mathit{V}(\Delta )$. On the whole space ${\mathbb{R}}^d$, there is a global coordinate system $y_1,\dots ,y_d$. We call these coordinates y-coordinates. Recall that in the Section 1.5, for each facet $\Delta$, we introduced an additional coordinate system in ${\mathbb{R}}^d$ to work with objects belonging to the cone $Cone(\Delta )$. We called these additional coordinates c-coordinates.

Proposition 4.

The following obvious propositions are true:

-

$Cone(\Delta )$ is a closed orthant of points with non-negative c-coordinates;

-

Δ is the set of points for which the sum of all c-coordinates is equal to 1 and all c-coordinates are non-negative;

-

A cone with vertex at the origin and base equal to facet Δ is the set of points whose sum of all c-coordinates is less than or equal to 1 and all c-coordinates are non-negative;

-

For any vertex v of the facet Δ, one of the c-coordinates is 1, and the other c-coordinates are 0.

The evidence is clear.

Definition 2.

A face of the cone $Cone(\Delta )$ is a subset of the cone on which a fixed set of r c-coordinates vanishes. A face is called proper if $1\le r$.

In the Section 6, we need the following obvious proposition.

Proposition 5.

Let F be some proper face of the cone $Cone(\Delta )$ and $a,b$ be two points of the cone. If $a+b\in F$, then $a\in F$ and $b\in F$.

Proof. 

Without loss of generality, we can assume that the face F is given by equating to zero the first $r\ge 1$ c-coordinates

$$F=\{x\in Cone(\Delta ):c_1\left(x\right)=c_2\left(x\right)=\dots =c_r\left(x\right)\}$$

Since each of these coordinates $c_i$ is linear and takes non-negative values on the cone $Cone(\Delta )$, $c_i(a+b)=c_i\left(a\right)+c_i\left(b\right)=0$ implies $c_i\left(a\right)=0$ and $c_i\left(b\right)=0$, i.e., $c_1\left(a\right)=c_2\left(a\right)=\dots =c_r\left(a\right)=0$ $c_1\left(b\right)=c_2\left(b\right)=\dots =c_r\left(b\right)=0$. □

Since the polytope $\mathsf{\Gamma }$ is assumed to be integer, the y-coordinates of any of its vertices, and, in particular, of any vertex of the facet $\Delta$, are integers. That is why:

-

The full semigroup $A(\Delta )$ is nothing else than the set of points of the cone $Cone(\Delta )$ with integer y-coordinates;

-

The vertex semigroup $V(\Delta )$ is nothing else than the set of points of the cone $Cone(\Delta )$ with non-negative integer c-coordinates. Since the generators of vertex semigroups $V(\Delta )$ have integer y-coordinates, all elements of the vertex semigroup have integer y-coordinates, that is, $V(\Delta )\subseteq A(\Delta )$.

Definition 3.

We say that a subsemigroup $V(\Delta )$ of the semigroup $Cone(\Delta )$actson a set $X\subseteq Cone(\Delta )$ if for any point $x\in X$ and any element $g\in V(\Delta )$, the sum $x+g$ belongs to X. The sum $x+g$, where $x\in Cone(\Delta )$ and $g\in V(\Delta )$, is called a shift of point x by vector g. Suppose $X_0\subseteq Cone(\Delta )$ and $\left\{g\right\}$ is a one-point set composed of $g\in V(\Delta )$. The Minkovsky sum $X_0\oplus \left\{g\right\}$ is called the shift of set $X_0$ by vector g. Suppose the semigroup $V(\Delta )$ acts on some set $X\subseteq Cone(\Delta )$. The set $X_0\subseteq X$ is called a fundamental domain for this action if any element $x\in X$ is uniquely represented as a shift of some point $x_0\in X_0$ by some element $g_0\in V(\Delta )$. In other words, if the shifts of the set $X_0$ by all possible elements of $V(\Delta )$ form a partition of the set X:

$$X=\bigcup _{g\in V(\Delta )}(X_0\oplus g)$$

Suppose $p\in Cone(\Delta )$. The set ${\bigcup }_{g\in V}(p+g)$ is called the orbit of point p under the action of semigroup $V(\Delta )$. The orbit of the point $p\in Cone(\Delta )$ can be written using the Minkowski sum as $\left\{p\right\}\oplus V(\Delta )$.

Remark 1.

This definition will be applied below in two situations. First, this definition will apply to d-dimensional set $X=Cone\left({\Delta }_1\right)$ and to 0-dimensional set $A\left({\Delta }_1\right)$. Secondly, this definition will apply to the set $Cs{h}_i$ and its subset $As{h}_i$ for $i>1$. Note that in all situations under consideration, the shifts of any point $p\in Cone(\Delta )$ by different vectors $g_1,g_2\in V(\Delta )$ do not coincide, therefore, for any point $p\in Cone(\Delta ))$, the mapping $V(\Delta )\to Cone(\Delta )$ given by the formula $g\mapsto (p+g)$ is an injection.

Below, we will need two standard functions $\mathbb{R}\to \mathbb{Z}$ to round a real number x:

$$\begin{array}{cc}\hfill floor\left(x\right)& =max\{n\in \mathbb{Z}:n\le x\}\hfill \\ \hfill ceil\left(x\right)& =min\{n\in \mathbb{Z}:n\ge x\}\hfill \end{array}$$

(21)

2.4.1. Fundamental Domains for Actions of the Vertex Semigroup on the Sets $Cone\left({\Delta }_1\right)$ and $A\left({\Delta }_1\right)$

Let $\Delta$ be some facet of the polytope $\mathsf{\Gamma }$, for example, the initial facet ${\Delta }_1$ of the shelling $sh$. Obviously, the semigroup $V(\Delta )$ acts on the set $Cone(\Delta )$ and also acts on $A(\Delta )$. In other words, adding a vector with non-negative c-coordinates does not lead outside the cone $Cone(\Delta )$ or outside the semigroup $A(\Delta )$ consisting of points of the cone $Cone(\Delta )$ with integer y-coordinates.

Consider an arbitrary point $p\in Cone(\Delta )$. Denote by $C\left(p\right)$ the vector of c-coordinates of this point. Denote by $floor\left(p\right)$ the vector with the following c-coordinates

$$floor\left(c_1\left(p\right)\right),floor\left(c_2\left(p\right)\right),\dots floor\left(c_d\left(p\right)\right)$$

All coordinates of the vector $floor\left(p\right)$ are non-negative integers. Let us expand the vector $C\left(p\right)$ into the sum of two terms:

$$C\left(p\right)=\left(C\right(p)-floor(p\left)\right)+floor\left(p\right)$$

(22)

The second term of this sum belongs to the semigroup $V(\Delta )$, and each c-coordinate of the first term belongs to the interval $[0,1)$. This means that any point $p\in Cone(\Delta )$ can be represented as the sum of a point with zero integer parts of c-coordinates and a point with non-negative integer c-coordinates. It is quite obvious that such a representation is unique. Thus, we have proven the following assertion.

Proposition 6.

The fundamental domain for the action of the vertex semigroup $V(\Delta )$ on the cone $Cone(\Delta )$ is the bounded subset of the cone $Cone(\Delta )$ defined by the double inequalities:

$$\mathsf{\Pi }(\Delta )=\{p\in Cone(\Delta ):\left\{\begin{array}{cc}\hfill & 0\le c_1\left(p\right)<1\hfill \\ & 0\le c_2\left(p\right)<1\hfill \\ & \dots \hfill \\ & 0\le c_d\left(p\right)<1\hfill \end{array}\right\}$$

(23)

Geometrically, the Proposition 6 means that the entire cone $Cone(\Delta )$ is “tiled” by non-intersecting shifts of the integer semi-open parallelepiped $\mathsf{\Pi }(\Delta )$ by the vectors of the vertex semigroup $V(\Delta )$:

$$Cone(\Delta )=\bigcup _{v\in V(\Delta )}\mathsf{\Pi }(\Delta )\oplus v$$

(24)

The above assertion and its proof are well known, see, for example, [17]. The set $\mathsf{\Pi }(\Delta )$ is called fundamental half-open parallelepiped.

Below, a formally more general definition of integer half-open parallelepiped will be given. The closure of the fundamental semi-open parallelepiped of facet $\Delta$ is called the facet parallelepiped and is denoted by $\overline{\mathsf{\Pi }}(\Delta )$.

Let $B(\Delta )$ be $\mathsf{\Pi }(\Delta )\cap Z^d$. A proposition similar to the Proposition 6 is true for the $B(\Delta )$. From the Formula (23), it follows that the set $B(\Delta )$ is given by the double inequalities:

$$B(\Delta )=\{n\in A(\Delta ):\left\{\begin{array}{cc}\hfill & 0\le c_1\left(n\right)<1\hfill \\ & 0\le c_2\left(n\right)<1\hfill \\ & \dots \hfill \\ & 0\le c_d\left(n\right)<1\hfill \end{array}\right\}$$

(25)

Definition 4.

The set $B(\Delta )$ is called the basis of the semigroup $A(\Delta )$. This set is finite.

Proposition 7.

The basic $B(\Delta )$ is the fundamental domain for the action of the vertex semigroup $V(\Delta )$ on the semigroup $A(\Delta )$, i.e.,

$$A(\Delta )=\bigcup _{v\in V(\Delta )}B(\Delta )\oplus v$$

(26)

Proof. 

Let p be an arbitrary point in $A(\Delta )$. According to the Formula (22), the point p is the sum of two terms, the first of which belongs to $B(\Delta )$, the second has integer c-coordinates, that is, it belongs to $V(\Delta )$. It is easy to see that this representation is unique. □

The fact that the set $B(\Delta )$ is a fundamental domain can be reformulated as follows.

Proposition 8.

The shifts of the set $V(\Delta )$ by elements of the set $B(\Delta )$ are pairwise disjoint and their union gives $A(\Delta )$:

$$A(\Delta )=\bigcup _{b\in B(\Delta )}V(\Delta )\oplus b$$

(27)

The Proposition 8 can be reformulated in terms of finitely generated modules.

Proposition 9.

The algebra $\mathbb{K}\left[A\right(\Delta \left)\right]$ is freely generated by the monomials corresponding to the points of the set $B(\Delta )$ as a module over the algebra $\mathbb{K}\left[V\right(\Delta \left)\right]$.

Proof. 

Let $b\in B(\Delta )$. By ${\mathcal{M}}_b$, denote submodule over $\mathbb{K}\left[V\right(\Delta \left)\right]$ consisting of finite linear combinations over $\mathbb{K}$ of monomials of the form $x^b{x}^v$, where $v\in V(\Delta )$. The submodule ${\mathcal{M}}_b$ is freely generated by the element $x^b$. According to Formula (27), the additive group of the $\mathbb{K}$-algebra $\mathbb{K}\left[A\right(\Delta \left)\right]$ is the direct sum of all such submodules:

$$\mathbb{K}\left[A(\Delta )\right]=\underset{b\in B(\Delta )}{⨁}{\mathcal{M}}_b$$

□

Recall that we denote the number of points in a finite set B by $\#B$.

Proposition 10.

The number of integer points in the fundamental semi-open parallelepiped $\mathsf{\Pi }(\Delta )$ is equal to its volume, i.e.,

$$\#B(\Delta )=Volume\left(\mathsf{\Pi }\right(\Delta \left)\right)$$

(28)

Equality (28) is well known, see for example [17]. However, for completeness, we present an outline of the geometrical proof.

Outline of the proof.

By $k\mathsf{\Pi }(\Delta )$, denote a semi-open parallelepiped $\mathsf{\Pi }(\Delta )$ dilated in a natural number k times with respect to the origin. This dilated semi-open parallelepiped $k\mathsf{\Pi }(\Delta )$ is given by the double inequalities

$$k\mathsf{\Pi }(\Delta )=\{p\in Cone(\Delta ):\left\{\begin{array}{cc}\hfill & 0\le c_1\left(p\right)<k\hfill \\ & 0\le c_2\left(p\right)<k\hfill \\ & \dots \hfill \\ & 0\le c_d\left(p\right)<k\hfill \end{array}\right\}$$

(29)

$k\mathsf{\Pi }(\Delta )$ can be obtained by the union of disjoint shifts of the original semi-open parallelepiped by elements of the set X, consisting of $k^d$ integer vectors, each c-coordinate of which is a non-negative integer less than k. Similarly, the set of integer points in $k\mathsf{\Pi }(\Delta )$ can be obtained as the union of disjoint shifts of the basis $B(\Delta )$ by the same set X of integer vectors, therefore,

$$Volume\left(k\mathsf{\Pi }(\Delta )\right)=Volume\left(\mathsf{\Pi }(\Delta )\right)\times k^d$$

and

$$\#(k\mathsf{\Pi }(\Delta )\cap A(\Delta ))=\#B(\Delta )\times k^d$$

(30)

For $k\to \infty$, the number of integer points in a dilated half-open parallelepiped will be equal to its volume, up to some correction term. This correction term has an order of growth $O\left(k^{d-1}\right)$, therefore,

$$\#(k\mathsf{\Pi }(\Delta )\cap A(\Delta ))=Volume\left(\mathsf{\Pi }(\Delta )\right)\times k^d+O\left(k^{d-1}\right)$$

(31)

From (30) and (31), we obtain

$$\#B(\Delta )\times k^d=Volume\left(\mathsf{\Pi }(\Delta )\right)\times k^d+O\left(k^{d-1}\right)$$

or, after dividing by $k^d$

$$\#B(\Delta )=Volume\left(\mathsf{\Pi }(\Delta )\right)+O\left(k^{d-1}\right)/k^d$$

Letting k tend to infinity, we obtain the equality (28). □

The fundamental integer semi-open parallelepiped $\mathsf{\Pi }(\Delta )$ is a special case of an arbitrary integer semi-open parallelepiped, which we will now define using Minkowski sums.

Definition 5.

Let a and b be two distinct points with integer coordinates in ${\mathbb{R}}^d$. The set of points in ${\mathbb{R}}^d$ of the form $a+(b-a)t$, where t runs over the half-interval $[0,1)$ on the real line is called an integer half-interval and is denoted by $[a,b)$ or, equivalently, by $(b,a]$. We also denote by $[a,b]$ the closure of $[a,b)\subset {\mathbb{R}}^d$.

The Minkowski sum of d integer half-intervals of the form

$$\mathsf{\Pi }=[a_1,a_1+v_1)\oplus [a_2,a_2+v_2)\oplus \dots \oplus [a_d,a_d+v_d)$$

(32)

where the vectors $v_1,v_2,\dots ,v_d$ are linearly independent is called the integer semi-open parallelepiped.

The Minkowski sum of d integer half-intervals of the form

$$[0,v_1)\oplus [0,v_2)\oplus \dots \oplus [0,v_d)$$

(33)

in which the vectors $v_1,v_2,\dots ,v_d$ are linearly independent is called a fundamental integer semi-open parallelepiped.

It is easy to check that the Formulas (33) and (23) define the same set. Below, we verify that any integer semi-open parallelepiped can be obtained from the fundamental parallelepiped by parallel translation to some vector with integer coordinates. Therefore, it is easy to deduce a more general proposition from the Proposition 10.

Proposition 11.

The cardinality of the set of integer points of any integer semi-open parallelepiped is equal to its volume.

Proof. 

Let us check that any integer semi-open parallelepiped can be obtained from the fundamental parallelepiped by parallel transfer to some vector with integer coordinates. Let

$$\mathsf{\Pi }=[a_1,a_1+v_1)\oplus [a_2,a_2+v_2)\oplus \dots \oplus [a_d,a_d+v_d)$$

be a Minkowski sum of integer semi-open intervals, where the vectors $v_1,v_2,\dots ,v_d$ are linearly independent. Then, an integer semi-open parallelepiped $\mathsf{\Pi }$ is obtained by parallel translation onto the vector $a_1+a_2+\dots +a_d$ of the fundamental semi-open parallelepiped

$$[0,v_1)\oplus [0,v_2)\oplus \dots \oplus [0,v_d).$$

(34)

Parallel transfer of an integer semi-open parallelepiped $\mathsf{\Pi }$ by an integer vector does not change the volume $\mathsf{\Pi }$ and the number of integer points in it, and as a result of the transfer, we obtain a fundamental semi-parallelepiped whose volume is equal to the number of integer points according to the Proposition 10.□

2.4.2. Fundamental Domains for Actions of the Vertex Semigroup of Any Facet on the $sh$-Cone and the $sh$-Semigroup of This Facet

Proposition 12.

Let ${\Delta }_i$ be a facet of Γ. Then, the fundamental domain for action of the vertex semigroup $V\left({\Delta }_i\right)$ on the $sh$-cone $Cs{h}_i$ exists and is an integer semi-open parallelepiped.

We will give two proofs of this assertion—a coordinate proof and a proof in terms of Minkowski sums.

Coordinate proof.

Let ${\Delta }_i$ be a facet of $\mathsf{\Gamma }$. By the definition of shelling, $sh$-facet ${\Delta }_i^{sh}$ is obtained from facet ${\Delta }_i$ by removing r subfacets of codimension one. On each subfacet of codimension 1, one of the c-coordinates on the cone $Cone\left({\Delta }_i\right)$ is equal to zero, and the complement to such a subfacet is given by the condition that this c-coordinate is positive. Therefore, the complement to all r subfacets to be removed is given by the condition that r of such c-coordinates are simultaneously positive. The boundary case $r=d$ is not excluded. Without loss of generality, we may assume that the first r c-coordinates are positive on $sh$-facet ${\Delta }_i^{sh}$. Hence, the cone $Cs{h}_i$ is defined in the closed cone $Cone\left({\Delta }_i\right)$ by the inequalities $0<c_1\left(p\right),0<c_2\left(p\right),\dots ,0<c_r\left(p\right)$, and the $sh$-cone $Cs{h}_i$ is given by a system of $r>0$ strict and $(d-r)\ge 0$ non-strict inequalities

$$Cs{h}_i=\{p\in {\mathbb{R}}^d:\left\{\begin{array}{cc}\hfill & 0<c_1\left(p\right)\hfill \\ & 0<c_2\left(p\right)\hfill \\ & \dots \hfill \\ & 0<c_r\left(p\right)\hfill \\ & 0\le c_{r+1}\left(p\right)\hfill \\ & 0\le c_{r+2}\left(p\right)\hfill \\ & \dots \hfill \\ & 0\le c_d\left(p\right)\hfill \end{array}\right\}$$

(35)

From this description, it follows that:

-

The set of points of the $sh$-cone $Cs{h}_i$ is closed with respect to the addition operation, which means that its subset $As{h}_i$ of points with integer y-coordinates is also closed with respect to addition;

-

Adding any vector with non-negative c-coordinates to a point satisfying the inequalities (35) does not violate these inequalities, so the semigroup $V\left({\Delta }_i\right)$ acts on the $sh$-cone $Cs{h}_i$. Finally, shifting an integer point in $Cs{h}_i$ by a vector with non-negative integer y-coordinates from the set $V\left({\Delta }_i\right)$ gives a point $Cs{h}_i$ with integer coordinates, so $V\left({\Delta }_i\right)$ acts on $As{h}_i$.

□

The Proposition 12 can now be detailed as follows.

Proposition 13.

(a) A subset of the cone $Cone\left({\Delta }_i\right)$ defined by double inequalities:

$${\mathsf{\Pi }}_i=\{p\in Cone\left({\Delta }_i\right):\left\{\begin{array}{cc}\hfill & 0<c_1\left(p\right)\le 1\hfill \\ & 0<c_2\left(p\right)\le 1\hfill \\ & \dots \hfill \\ & 0<c_r\left(p\right)\le 1\hfill \\ & 0\le c_{r+1}\left(p\right)<1\hfill \\ & 0\le c_{r+2}\left(p\right)<1\hfill \\ & \dots \hfill \\ & 0\le c_d\left(p\right)<1\hfill \end{array}\right\}$$

(36)

is a fundamental domain for the action of the semigroup $V\left({\Delta }_i\right)$ on the $sh$-cone $Cs{h}_i$; (b) The set ${\mathsf{\Pi }}_i$ is an integral semi-open parallelepiped.

Proof. 

Let us prove (a). Let $p\in Cs{h}_i$, i.e., p satisfies the inequalities (35). We use the functions defined by the Formula (21) and denote by $ceil\_floor\left(p\right)$ the point with the following c-coordinates

$$ceil\left(c_1\left(p\right)\right)-1,\dots ceil\left(c_r\left(p\right)\right)-1,floor\left(c_{r+1}\left(p\right)\right),\dots floor\left(c_d\left(p\right)\right)$$

Let us expand the vector of c-coordinates of the point p into the sum of two terms:

$$C\left(p\right)=\left(C\right(p)-ceil\_floor(p\left)\right)+ceil\_floor\left(p\right)$$

(37)

Let us prove that the second term of this sum is the vector of c-coordinates of some element of the vertex semigroup $V\left({\Delta }_i\right)$. To do this, it suffices to check the non-negativity of all components of this vector, taking into account that $p\in Cs{h}_i$. The non-negativity of the last $d-r$ components follows from the definition of the function $floor$. The non-negativity of the first r components follows from the fact that (a) for the point $p\in Cs{h}_i$ the coordinates $c_1\left(p\right),\dots ,c_r\left(p\right)$ are positive; (b) the value of the $ceil$ function in the Formula (21) for any positive argument is not less than 1 and remains non-negative after subtracting one. It is also easy to see that the first term of the Formula (37) satisfies the inequalities (36), that is, it is a vector of c-coordinates of some point ${\mathsf{\Pi }}_i$. Thus, we have proven that any point $p\in C_i$ is obtained by shifting some point $b\in {\mathsf{\Pi }}_i$ by an element g of the vertex semigroup $V\left({\Delta }_i\right)$.

Let us not be too lazy to check that the representation $p=b+g$ is unique. Indeed, if $p=b_1+g_1=b_2+g_2$, then the difference $b_1-b_2$ equal to $g_2-g_1$ has integer c-coordinates. From the Formula (36) it follows that the difference of any two points in ${\mathsf{\Pi }}_i$ has c-coordinates, by absolute value less than 1. Therefore, being an integer vector, this difference must be equal to zero. In other words, shifts of the set ${\mathsf{\Pi }}_i$ by all possible elements of the vertex semigroup $V\left({\Delta }_i\right)$ form a partition of the $sh$-cone $Cs{h}_i$.

Proposition (b) follows from the fact that the set given by double inequalities (36) can be represented as the Minkowski sum of integer half-intervals

$$\begin{array}{c}\hfill (0,v_1]\oplus (0,v_2]\oplus \dots \oplus (0,v_r]\oplus [0,v_{r+1})\oplus [0,v_{r+2})\oplus \dots \oplus [0,v_d)=\\ \hfill {}_1,v_1+(-v_1))\oplus \dots \oplus [v_r,v_r+(-v_r))\oplus [0,v_{r+1})\oplus [0,v_{r+2})\oplus \dots \oplus [0,v_d)\end{array}$$

where the vectors $-v_1,\dots ,-v_r,v_{r+1},\dots ,v_d$ are linearly independent. The coordinate proof of the Proposition 12 is complete. □

Outline of an alternative proof of the Proposition 13.

For each vertex v of the superconvenient polytope $\mathsf{\Gamma }$, consider a closed ray emanating from the origin and passing through v and an open ray obtained by removing the origin from the closed ray. It is easy to see that each closed cone $Cone\left({\Delta }_i\right)$ can be described as the Minkowski sum of d closed rays emanating from the origin and passing through the vertices of facet ${\Delta }_i$. Similarly, each $sh$-cone $Cs{h}_i$ obtained by removing r faces from the cone $Cone\left({\Delta }_i\right)$ can be described as the Minkowski sum of r open rays and $d-r$ closed rays. As above, the boundary cases $r=d$ and $r=0$ are not excluded either. The terms of these Minkowski sums are referred to as the boundary rays of cone $Cs{h}_i$. Divide each boundary ray of the cone $Cs{h}_i$ into a countable number of non-intersecting and sequentially adjoining integer half-intervals (in the sense of Definition 5), enumerate these intervals from zero to infinity, and represent $Cs{h}_i$ as the Minkowski sum of d terms, each of which is the union of a countable number of non-intersecting integer half-intervals:

$$\begin{array}{c}\hfill Cs{h}_i=\\ \hfill \left(\right(0,v_1]& \cup (v_1,2v_1]\cup (2v_1,3v_1]\dots )\oplus \hfill \\ \hfill \left(\right(0,v_2]& \cup (v_2,2v_2]\cup (2v_2,3v_2]\dots )\oplus \hfill \\ & \dots \dots \dots \hfill \\ \hfill \left(\right(0,v_r]& \cup (v_r,2v_r]\cup (2v_r,3v_r]\dots )\oplus \hfill \\ \hfill \left(\right[0,v_{r+1})& \cup [v_{r+1},2v_{r+1})\cup [2v_{r+1},3v_{r+1})\dots )\oplus \hfill \\ & \dots \dots \dots \hfill \\ \hfill \left(\right[0,v_d)& \cup [v_d,2v_{r+1})\cup [2v_d,3v_d)\dots )\hfill \end{array}$$

(38)

After expanding the brackets, we obtain the union of a countable number of elementary Minkowski sums, each of which is the sum of d integer half-intervals. The first elementary sum is obtained from the first column of the Formula (38) and looks as follows:

$$(0,v_1]\oplus (0,v_2]\oplus \dots \oplus (0,v_r]\oplus [0,v_{r+1})\oplus [0,v_{r+2})\oplus \dots \oplus [0,v_d)$$

(39)

The remaining elementary Minkowski sums, obtained by expanding brackets in the Formula (38), are obtained from the first sum (39) by shifts by the sum of vectors of vertices of facet ${\Delta }_i$ with non-negative coefficients that are not equal to zero at the same time. In other words, each remaining sum is obtained by shifting the first sum by nonzero elements of the vertex semigroup $V\left({\Delta }_i\right)$. □

Proposition 14.

(i) Finite subset $Bs{h}_i$ of set $As{h}_i$ defined by double inequalities:

$$Bs{h}_i=\{n\in As{h}_i:\left\{\begin{array}{cc}\hfill & 0<c_1\left(n\right)\le 1\hfill \\ & 0<c_2\left(n\right)\le 1\hfill \\ & \dots \hfill \\ & 0<c_r\left(n\right)\le 1\hfill \\ & 0\le c_{r+1}\left(n\right)<1\hfill \\ & 0\le c_{r+2}\left(n\right)<1\hfill \\ & \dots \hfill \\ & 0\le c_d\left(n\right)<1\hfill \end{array}\right\}$$

(40)

is the fundamental domain for of the action of the vertex semigroup $V\left({\Delta }_i\right)$ on the $sh$-semigroup $As{h}_i$;

(ii) 

$Bs{h}_i={\mathsf{\Pi }}_i\cap {\mathbb{Z}}^d$;

(iii) 

The number of integer points in a semi-open parallelepiped ${\mathsf{\Pi }}_i$ is equal to its volume:

$$\#Bs{h}_i=Volume\left({\mathsf{\Pi }}_i\right)$$

(41)

Proof. 

(i) It follows from Proposition 12 that an arbitrary point $p\in As{h}_i$ is uniquely represented as a sum $p=b+g$, where $b\in Cs{h}_i$ and $g\in V\left({\Delta }_i\right)$. Both the point p and the second summand have integer y-coordinates. This means that the first term b of this sum also has integer y-coordinates, that is, it belongs to $As{h}_i$ and satisfies the inequalities (40). This means that we have uniquely represented an arbitrary point p as a shift of the point $b\in Bs{h}_i$ by the vector $g\in V\left({\Delta }_i\right)$. Thus, we have proven that

$$As{h}_i=\bigcup _{g\in V(\Delta )}(Bs{h}_i\oplus g)$$

(42)

(ii)

follows from the Formulas (35) and (40);

(iii)

follows from the Proposition 11.

□

Definition 6.

The set $Bs{h}_i$ given by the double inequalities (40) is called the basis of the $sh$-semigroup $As{h}_i$. Basis $Bs{h}_1$ is the same as basis $B\left({\Delta }_1\right)$ previously defined by Formula (25).

The fact that the set $Bs{h}_i$ is the fundamental domain for the action of the semigroup $V\left({\Delta }_i\right)$ on the set $As{h}_i$ can obviously be reformulated as follows.

Proposition 15.

(i) The orbits of the points of the set $Bs{h}_i$ under the action of the semigroup $V\left(\mathsf{\Gamma }\right)$, are pairwise disjoint; (ii) The union of these orbits is equal to $As{h}_i$, i.e.:

$$As{h}_i=\bigcup _{b\in Bs{h}_i}V\left({\Delta }_i\right)\oplus b$$

(43)

We now reformulate the Proposition 15 in algebraic terms, considering the $\mathbb{K}$-algebra $\mathbb{K}\left[As{h}_i\right]$ as a module over the algebra $\mathbb{K}\left[V\left({\Delta }_i\right)\right]$. Note that for $i>1$, the subsemigroup $As{h}_i$ does not have a neutral element, and therefore, the multiplicative operation in the $\mathbb{K}$-algebra $\mathbb{K}\left[As{h}_i\right]$ will not have a neutral element. However, in this article, we need to multiply elements of the $\mathbb{K}$-algebra $\mathbb{K}\left[As{h}_i\right]$ only by elements of the $\mathbb{K}$-algebra $\mathbb{K}\left[V\left({\Delta }_i\right)\right]$, so we will consider $\mathbb{K}\left[As{h}_i\right]$ as a module over $\mathbb{K}\left[V\left({\Delta }_i\right)\right]$.

Proposition 16.

As a module over the algebra $\mathbb{K}\left[V\left({\Delta }_i\right)\right]$, the algebra $\mathbb{K}\left[As{h}_i\right]$ is freely generated by the monomials corresponding to the points of the finite set $Bs{h}_i$.

The proof can be performed in the same way as the proof of the Proposition 9 assertion with reference to the Proposition 14 assertion instead of the Proposition 8 assertion.

Proposition 17.

(a) Only one of the sets $Bs{h}_1,Bs{h}_2,\dots ,Bs{h}_N$, namely the set $Bs{h}_1$, contains the origin;

(b) 

For any point p of any of the sets $Bs{h}_1,Bs{h}_2,\dots ,Bs{h}_N$ the sum of the c-coordinates of the point p does not exceed d;

(c) 

Only one of the sets $Bs{h}_1,Bs{h}_2,\dots ,Bs{h}_N$, namely, the set $Bs{h}_N$, contains a point whose sum of c-coordinates equals d and such a point is unique;

(d) 

Newtonian degree of any point of the set

$${\mathbb{B}}^{sh}=Bs{h}_1\cup Bs{h}_2\cup \dots \cup Bs{h}_N$$

does not exceed $dM$, this set contains exactly one element of Newtonian degree 0 and exactly one element of maximum Newtonian degree $dM$.

Proof. 

(a) and (b) obviously follow from the specification of $Bs{h}_i$ by double inequalities (40). (c) follows from the definition of $Bs{h}_i$ and the fact that only the last facet of the shelling $sh=({\Delta }_1,{\Delta }_2,\dots ,{\Delta }_N)$ intersects the union of the previous facet over all its codimension one subfaces.

(d) follows from (a)–(c) and the fact that the Newtonian degree of any vertex of $\mathsf{\Gamma }$ is equal to M. Indeed, the Newtonian degree of any point p of a closed cone of any facet, is expressed in terms of the c-coordinates of a point on this cone by the formula

$$\phi \left(p\right)=M\times (c_1\left(p\right)+c_2\left(p\right)+\dots +c_N\left(p\right))\le dM$$

so $\phi \left(p\right)\le dM$ for any $p\in {\mathbb{B}}^{sh}$ □

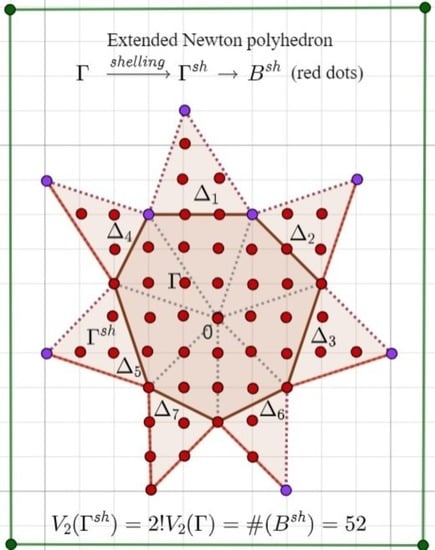
2.5. Shelling Extensions of the Super-Convenient Newton Polytope

Let $\Delta$ be a facet with vertices $v_1,v_2,\dots ,v_d$. By $Pyramid(\Delta )$, denote the union of all closed segments starting at the origin and ending at some point of facet $\Delta$. It is obvious that

$$d!\times Volume\left(Pyramid(\Delta )\right)=Volume\left(\overline{\mathsf{\Pi }}(\Delta )\right)=abs\left(det(v_1,v_2,\dots ,v_d)\right)$$

Obviously, $\mathsf{\Gamma }={\bigcup }_{i=1}^{N}Pyramid\left({\Delta }_i\right)$. That is why

$$d!\times Volume\left(\mathsf{\Gamma }\right)=\sum _{i=1}^{N}d!\times Volume\left(Pyramid\left({\Delta }_i\right)\right)=\sum _{i=1}^{N}Volume\left(\overline{\mathsf{\Pi }}\left({\Delta }_i\right)\right)$$

(44)

Since for any i$Volume(\overline{{\mathsf{\Pi }}_i}\backslash {\mathsf{\Pi }}_i)=0$ the right-hand side of identity (44) can be replaced by the volume of the disjoint union of semi-open parallelepipeds,

$$d!\times Volume\left(\mathsf{\Gamma }\right)=Volume\left(\bigcup _{i=1}^N{\mathsf{\Pi }}_i\right)$$

(45)

This disjoint union is constructed from a super-convenient Newton simplicial polytope and any of its shellings. This object deserves separate consideration.

Definition 7.

Let $sh$ be a shelling of a convex super-convenient simplicial Newton polytope Γ. The disjunct union ${\bigcup }_{i=1}^N\mathsf{\Pi }\left({\Delta }_i^{sh}\right)$ is calledshelling extension of $\mathsf{\Gamma }$and is denoted by ${\mathsf{\Gamma }}^{sh}$:

$${\mathsf{\Gamma }}^{sh}=\bigcup _{i=1}^N\mathsf{\Pi }\left({\Delta }_i^{sh}\right)$$

(46)

The union of bases of all $sh$-semigroups ${\bigcup }_{i=1}^{N}Bs{h}_i$ is called the basis of shelling extension ${\mathsf{\Gamma }}^{sh}$ and is denoted by ${\mathbb{B}}^{sh}$:

$${\mathbb{B}}^{sh}=\bigcup _{i=1}^{N}Bs{h}_i$$

(47)

Definition 8.

Let $P\in {\mathbb{R}}^d$ a convex polytope. By $\mu \left(P\right)$, denote the product $d!\times Volume\left(P\right)$.

Proposition 18.

The shelling extension ${\mathsf{\Gamma }}^{sh}$ of the super-convenient simplicial integral Newton polytope Γ has the following properties

(i) 

$interior\left(\mathsf{\Gamma }\right)\subset {\mathsf{\Gamma }}^{sh}$

(ii) 

${\mathbb{B}}^{sh}={\mathbb{Z}}^d\cap {\mathsf{\Gamma }}^{sh}$

(iii) 

The number of integer points in any shelling extension of the polytope Γ does not depend on the shelling $sh$ and is equal to $\mu \left(\mathsf{\Gamma }\right)$, i.e.,

$$\#(Z^d\cap {\mathsf{\Gamma }}^{sh})=Volume\left({\mathsf{\Gamma }}^{sh}\right)=d!\times Volume\left(\mathsf{\Gamma }\right)=\mu \left(\mathsf{\Gamma }\right)$$

(48)

Proof. 

(i) follows from (18) and (36), (ii) follows from (41) and (44).

Let us prove (iii). From Statesments 8 and 18, it follows that

$$\begin{array}{cc}\hfill \#{\mathbb{B}}^{sh}& =(\#Bs{h}_1+\#Bs{h}_2+\dots +\#Bs{h}_N)\hfill \\ & =(Volume\left({\mathsf{\Pi }}_1\right)+Volume\left({\mathsf{\Pi }}_1\right)+\dots +Volume\left({\mathsf{\Pi }}_1\right))\hfill \\ & =d!\times Volume\left(\mathsf{\Gamma }\right)\hfill \\ & =\mu \left(\mathsf{\Gamma }\right)\hfill \end{array}$$

(49)

□

3. Combinatorial Problem Whose Solution Leads to Construction of Monomial Basises for Quotient Algebras $\mathbb{K}\left[{\mathbb{Z}}^{\mathit{d}}\right]/({\mathit{g}}_{\mathit{1}},{\mathit{g}}_{\mathit{2}},\dots ,{\mathit{g}}_{\mathit{d}})$

This section informally presents a new approach to solving the combinatorial problem of counting the number of integer points on the boundary of a super-convenient integer polytope $\mathsf{\Gamma }$ and any rational dilations of this boundary with respect to the origin. This problem is close to the problems of studying Erhart’s polynomials and h-vectors of simplicial complexes. A similar problem was studied in the work of the author [4] and in the works [19,20,21].

3.1. Newtonian Degree

Let us fix a super-convenient convex integer polytope $\mathsf{\Gamma }\in {\mathbb{R}}^d$, not necessarily simplicial. Following V.I. Arnold, we define the so-called Newtonian (“piecewise linear”) degree of any point in ${\mathbb{R}}^d$[1]. This “degree” is a real-valued function $\phi :{\mathbb{R}}^d\to \mathbb{R}$ with the following properties

(i) $\phi$ takes non-negative values;

(ii) $\phi$ is a linearly homogeneous function on $Cone(\Delta )$ for any facet $\Delta$ of $\mathsf{\Gamma }$;

(iii) $\phi$ takes a non-negative integer value at any point in ${\mathbb{Z}}^d$;

(iv) $\phi$ takes some positive integer value M on the boundary of $\mathsf{\Gamma }$.

The existence of such a function can be proved using the well-known properties of convex polyhedra.

The number $\phi \left(n\right)$, where $n=(n_1,n_2,\dots ,n_d)\in {\mathbb{Z}}^d$, is called the Newtonian degree of the monomial $x^n=x_1^{n_1}{x}_2^{n_2}\dots x_d^{n_d}$.

Defining a Convex Super-Convenient Polytope by a Non-Negative Piecewise Linear Function

Let $\mathsf{\Gamma }\subset {\mathbb{R}}^d$ be a compact convex d-dimensional polytope with N facets. It is known, see for example Theorem 1.1 in [18], that $\mathsf{\Gamma }$ can be defined as the intersection of N half-spaces, the boundary of each of which intersects with the polytope in one of the facets ${\Delta }_i$. If the polytope $\mathsf{\Gamma }$ is known to be superconvenient, then each of these half-spaces can be defined on ${\mathbb{R}}^d$ by the inequality ${\phi }_i\left(x\right)\le 1$, where ${\phi }_i$ is a linear function, such that

(i)

${\phi }_i\left(x\right)\le 1$ for any $x\in \mathsf{\Gamma }$;

(ii)

${\phi }_i\left(x\right)=1\iff x\in {\Delta }_i$.

Define a piecewise linear function $\phi :{\mathbb{R}}^d\to \mathbb{R}$ by the formula

$$\phi \left(x\right)=\underset{i=1}{\overset{N}{max}}{\phi }_i\left(x\right)$$

(50)

It is obvious that

(i)

$\phi \left(x\right)\ge 0$ for any $p\in {\mathbb{R}}^d$;

(ii)

$\phi \left(x\right)=0\Rightarrow x=0$;

(iii)

$\phi \left(x\right)\le 1\iff x\in \mathsf{\Gamma }$;

(iv)

$\phi \left(x\right)=1\iff x\in \partial \mathsf{\Gamma }$.

Neither the simpliciality, nor the integrality of the polytope was used in the definition of this function $\phi$. Recall that we denote by $Cone(\Delta )$ the union of all closed rays starting from the origin and passing through some point of facet $\Delta \subset \mathsf{\Gamma }$.

Proposition 19.

The function φ has the following properties:

(a) 

$\forall x\in R^d\forall \lambda \ge 0\phi \left(\lambda x\right)=\lambda \phi \left(x\right)$;

(b) 

$x\in Cone\left({\Delta }_i\right)$, where ${\Delta }_i$ is some facet of Γ if and only if $\phi \left(x\right)={\phi }_i\left(x\right)$;

(c) 

For any $s\ge 2$ and any $x_1,x_2,\dots ,x_s\in {\mathbb{R}}^d$

$$\phi (x_1+x_2+\dots +x_s)\le \phi \left(x_1\right)+\phi \left(x_2\right)+\dots +\phi \left(x_s\right);$$

(d) 

(c) becomes an equality if and only if there exists a facet ${\Delta }_i$ such that any of points $x_1,x_2,\dots ,x_s$ belongs to $Cone\left({\Delta }_i\right)$;

(e) 

For any $i\in [1,N]$, any $s\ge 2$, and any $x_1,x_2,\dots ,x_s\in Cone\left({\Delta }_i\right)$

$$\phi (x_1+x_2+\dots +x_s)=\phi \left(x_1\right)+\phi \left(x_2\right)+\dots +\phi \left(x_s\right).$$

The proof is left to the reader.

Since the polytope $\mathsf{\Gamma }$ is integral, it follows that the coefficients of all linear functions ${\phi }_1,{\phi }_2,\dots ,{\phi }_N$ are rational numbers. Therefore, there exists a natural number M such that, after multiplying the function $\phi$ by M, we obtain a new function, which we denote by the same letter $\phi$, which takes at integer points ${\mathbb{R}}^d$ only integer values, and on the boundary of the polytope $\mathsf{\Gamma }$ takes the value M. This function is called Newtonian degree associated with a super-convinient polytope Γ.

3.2. Newtonian Generating Functions of Various Subsets of ${\mathbb{Z}}^d$

The Newtonian degree associated with the super-convenient polytope $\mathsf{\Gamma }$ defines a mapping of the countable set ${\mathbb{Z}}^d$ into the set of non-negative integers $\mathbb{N}$. The inverse image of each point under this mapping is finite. Therefore, for any subset $Y\subset {\mathbb{Z}}^d$, the following formal sum is well defined:

$$H_{\mathsf{\Gamma }}(Y,t)=\sum _{n\in Y}{t}^{\phi \left(n\right)}=\sum _{i\in \mathbb{N}}{c}_i{t}^i.$$

(51)

This sum is called Newtonian generating function of the set Y associated with the super-convenient polytope $\mathsf{\Gamma }$.

Proposition 20.

(a) If the set $Y\subset {\mathbb{Z}}^d$ is finite, then its Newtonian generating function is a polynomial and the cardinality of Y is equal to the value of this polynomial at point 1:

$$\#Y=H_{\mathsf{\Gamma }}(Y,1)=\sum _{n\in Y}{1}^{\phi \left(n\right)}=\sum _{n\in Y}1$$

(52)

(b) 

If the set $Y\subset {\mathbb{Z}}^d$ is the union of a finite or countable number of pairwise disjoint subsets

$$Y=Y_1\cup Y_2\cup \dots$$

then

$$H_{\mathsf{\Gamma }}(Y,t)=H_{\mathsf{\Gamma }}(Y_1,t)+H_{\mathsf{\Gamma }}(Y_2,t)+\dots$$

(53)

The proofs are evident.

Below, we will consider the Newtonian generating functions of various subsets of ${\mathbb{Z}}^d$ introduced in Section 2.3 and Section 2.4.

Definition 9.

For $i\in [1,N]$, denote by $q_i\left(t\right)$ the Newtonian generating function of the finite set $Bs{h}_i$ defined by the Formula (40). Denote by $Q\left(t\right)$ the Newtonian generating function of a finite set

$${\mathbb{B}}^{sh}=Bs{h}_1\cup Bs{h}_2\cup \dots \cup Bs{h}_N$$

Obviously, the polynomial $Q\left(t\right)=q_1\left(t\right)+q_2\left(t\right)+\dots +q_N\left(t\right)$ and the polynomials $q_i\left(t\right)$ for $i\in [1,N]$ have non-negative integers coefficients. It follows from the definition of the generating function of a finite set that $\#Bs{h}_i=q_i\left(1\right)$ and $\#{\mathbb{B}}^{sh}=Q\left(1\right)$. From the Formulas (41) and (49), it follows that

$$\begin{array}{cc}\hfill q_i\left(1\right)& =\#Bs{h}_i=Volume\left({\mathsf{\Pi }}_i\right)\hfill \end{array}$$

(54)

$$\begin{array}{cc}\hfill Q\left(1\right)& =\#{\mathbb{B}}^{sh}=\mu \left(\mathsf{\Gamma }\right)\hfill \end{array}$$

(55)

The Proposition 17 implies that the polynomial $Q\left(t\right)$ has the form $Q\left(t\right)=1+\dots +t^{dM}$, in particular, $deg\left(Q\right)=dM$.

Proposition 21.

Let $sh$ be a shelling of a super-convenient simplicial polytope Γ, ${\Delta }_i$ be an element of $sh$. Then,

(a) 

$$H_{\mathsf{\Gamma }}(V\left({\Delta }_i\right),t)=\frac{1}{{(1-t^M)}^d}$$

(56)

(b) 

$$H_{\mathsf{\Gamma }}(As{h}_i,t)=H_{\mathsf{\Gamma }}(V\left({\Delta }_i\right),t)\times H_{\mathsf{\Gamma }}(Bs{h}_i,t)=\frac{q_i\left(t\right)}{{(1-t^M)}^d}$$

(57)

(c) 

$$H_{\mathsf{\Gamma }}({\mathbb{Z}}^d,t)=\frac{Q\left(t\right)}{{(1-t^M)}^d},\mathrm{where}Q\left(t\right)=q_1\left(t\right)+q_2\left(t\right)+\dots +q_N\left(t\right)$$

(58)

(d) 

$$deg\left(Q\right(t\left)\right)=dM,Q\left(1\right)=\mu \left(\mathsf{\Gamma }\right)$$

(59)

Proof of assertion (a) will be given below in Section 3.3. Proofs of assertions (b)–(c) will be given below in Section 3.4. Proof of assertion (d) follows from the Formulas (41) and (49) and the Proposition 17.

The series $H_{\mathsf{\Gamma }}({\mathbb{Z}}^d,t)$ provides combinatorial information about the location of the polytope $\mathsf{\Gamma }$ with respect to the set ${\mathbb{Z}}^d\subset {\mathbb{R}}^d$. For example, the coefficient of $t^M$ in the series $H_{\mathsf{\Gamma }}({\mathbb{Z}}^d,t)$ is equal to the number of integer points on the boundary of $\mathsf{\Gamma }$, and the coefficient of $t^{kM}$ is equal to the number integer points on the boundary of the polytope $\mathsf{\Gamma }$, dilated k times with respect to origin. In my works [2,4] dating back to 1974–1975, I combinatorially proved a fairly simple fact that the series $H_{\mathsf{\Gamma }}({\mathbb{Z}}^d,t)$ has the form $\frac{Q\left(t\right)}{{(1-t^M)}^d}$, where $Q\left(t\right)$ is a polynomial whose sum of coefficients is equal to $\mu \left(\mathsf{\Gamma }\right)=d!\times Volume\left(\mathsf{\Gamma }\right)$. A more complicated fact of the non-negativity of the coefficients of this polynomial was not stated in [4], although it can be deduced from the algebraic reasoning given in this article. It turns out that for a super-convinient simplicial Newton polytope $\mathsf{\Gamma }$, the non-negativity and integrality of the coefficients of the numerator $Q\left(t\right)$ of the Newtonian generating function can be proved combinatorially using the shelling of $\mathsf{\Gamma }$. In the process of solving the problem of explicitly describing the Newtonian generating function $H_{\mathsf{\Gamma }}({\mathbb{Z}}^d,t)$ using shelling, we explicitly construct the set of integer points ${\mathbb{B}}^{sh}\subset {\mathbb{Z}}^d$. Later, we will prove that the set of monomials $\{x^n:n\in {\mathbb{B}}^{sh}\}$ forms a monomial basis of the quotient algebra $\mathbb{K}\left[{\mathbb{Z}}^d\right]/(g_1,g_2,\dots ,g_d)$ for generic Laurent polynomials having the same Newton polytope $\mathsf{\Gamma }$.

Using shelling, we also prove the following refinement of Proposition 21.

Proposition 22.

Let $H_{\mathsf{\Gamma }}({\mathbb{Z}}^d,t)=\frac{Q\left(t\right)}{{(1-t^M)}^d}$ be the Newtonian generating function of simplicial super-convinient polytope Γ. Then, the numerator $Q\left(t\right)$ is a palindromic polynomial of degree $dM$, i.e.,

$$Q\left(t\right)=t^{dM}Q(1/t)$$

(60)

The proof will be given below in Section 3.5.

This proposition can be considered as an analogue of the Dehn–Sommerville property of the h-vector of a simplicial convex polytope [22].

The Proposition 22 is not new, for example, it is stated in Proposition 2.6 in [21]. However, the published proofs available to the author, see, for example, [19], are based on other approaches and differ from the author’s proof based on the existence and invertibility of shellings of convex simplicial polyhedra.

The requirement that the polytope be simplicial in Proposition 22 can be removed, since the boundary of any convex polytope $\mathsf{\Gamma }$ can always be cut up into simplices, that is, $\partial \mathsf{\Gamma }$ can be subdivided into a simplicial complex. Moreover, the subdivision can be chosen so that the resulting simplicial complex admits shelling.

3.3. Graded Vector Spaces and Their Poincaré Series

We will use the Newtonian generating functions defined by (51) for various subsets of $Z^d$ in the study of graded $\mathbb{K}$-algebras associated with these subsets. These combinatorially defined generating functions turn out to be the Poincaré series of various graded algebraic objects.

The standard Definitions 10 and 11 are borrowed from Wikipedia. For brevity, we use the term Poincaré series instead of Hilbert–Poincaré series.

Definition 10.

Let $\mathbb{N}$ be the set of non-negative integers. An $\mathbb{N}$-graded vector space is a vector space X over a fild $\mathbb{K}$ together with a decomposition into a direct sum of the form

$$X=\underset{n\in N}{⨁}{X}_n$$

where each $X_n$ is a vector space over $\mathbb{K}$. For a given n the elements of $X_n$ are then called homogeneous elements of degree n.

According to the definition of a direct sum, any element of the space X is the sum of a finite number of homogeneous elements. In what follows, we will consider only $\mathbb{N}$-gradings. Therefore, we will use the term graded without explicitly specifying $\mathbb{N}$.

Definition 11.

Given a $\mathbb{N}$ -graded vector space that is finite-dimensional for every $n\in \mathbb{N}$, its Poincaré series is the formal power series

$$\sum _{n\in \mathbb{N}}{dim}_{\mathbb{K}}\left(X_n\right)t^n.$$

(61)

Often, this series can be folded into a rational function of t. Assume that a homogeneous basis is given in the space X. We say that each element of this basis of degree i, contributes term $1·t^i$ to the Poincaré series $H(X,t)$. Then, the sum of the contributions of all elements of the basis will give the Poincaré series of the vector space X. Assume that a homogeneous basis is represented as a disjoint union of several sets. Then, we can count the contributions to the Poincaré series of each of these sets, and the sum of these contributions gives the Poincaré series of X.

Note. 

A particular case of this proposition is the additivity property expressed by the Formula (53).

Example 1.

Denote by X the algebra $\mathbb{K}[x,x^{-1}]$. Let us introduce a gradation on X by setting $X_0=\mathbb{K}$ and $X_i=\mathrm{linear}\mathrm{span}\mathrm{of}\mathrm{two}\mathrm{vectors}{x}^i\mathrm{and}{x}^{-i}$ for $i>0$. Then, the contribution to the Poincaré series from monomials of non-negative degree will be equal to $1+t+t^2+t^3+\dots =\frac{1}{1-t}$ and the contribution from monomials of negative degree will be equal to $t+t^2+t^3+\dots =\frac{t}{1-t}$. These two sets of basis monomials are a partition of the set of basis vectors and the Poincaré series of the entire algebra can be represented as the sum of two rational functions

$$\frac{1}{1-t}+\frac{t}{1-t}=\frac{1+t}{1-t}=1+2t+2t^2+3t^3+\dots$$

Example 2.

Denote by X the algebra $X=\mathbb{K}[x_1,x_2]$. Each polynomial in the variables $x_1,x_2$ can be represented as a linear combination of monomials $x_1^{n_1}{x}_2^{n_2}$. The degree of such a monomial is $n_1+n_2$. Let us expand brackets in a formal product:

$$(1+x_1+x_1^2+x_1^3+\dots )(1+x_2+x_2^2+x_2^3+\dots )$$

Each monomial in $x_1,x_2$ appears in the resulting expression exactly once. To count the number of monomials of degree d, replace in the product $x_1$ and $x_2$ by t, then expand brackets and reduce the similar terms. The coefficient at $t^d$ in the expanded product will be equal to the number of monomials in X of power d. That is why,

$$H(X,t)=(1+t+t^2+t^3+\dots )(1+t+t^2+t^3+\dots )=\frac{1}{{(1-t)}^2}$$

In the general case of polynomial algebras in d variables, where $deg\left(x^n\right)=n_1+n_2+\dots +n_d$ we obtain

$$H(\mathbb{K}[x_1,x_2,\dots ,x_d],t)=\frac{1}{{(1-t)}^d}$$

(62)

In the case when $deg\left(x^n\right)=M{n}_1+M{n}_2+\dots +M{n}_d$, the Poincaré series becomes

$$H(\mathbb{K}[x_1,x_2,\dots ,x_d],t)=\frac{1}{{(1-t^M)}^d}$$

(63)

Proof of the Proposition 21 (a).

A graded semigroup $\mathbb{K}$-algebra $\mathbb{K}\left[V\right(\Delta \left)\right]$ of any facet $\Delta$ is freely generated by d monomials $x^{v_1},x^{v_2},\dots ,x^{v_N}$, where $v_1,v_2,\dots ,v_d$ are facet vertices. Since the Newtonian degree of each vertex of the polytope is M, the Formula (63) applies. □

Example 3.

Let $\mathsf{\Gamma }\subset {\mathbb{R}}^d$ be a super-convenient simplicial integer polytope, X be the vector space $\mathbb{K}\left[{\mathbb{Z}}^d\right]$. Section 3.1 shows that Γ determines the Newtonian degree $\phi \left(n\right)$ for any monomial $x^n\in X$. Denote by $X_i$ the span of all monomials of Newtonian degree i. Thus, a $\mathbb{N}$-grading is constructed in the vector space of Laurent polynomials. The Poincaré series of this graded vector space, calculated by the general definition (61), is identical to the Newtonian generating function of the set ${\mathbb{Z}}^d$, defined by the Formula (51).

It will be shown below that the constructed Newtonian grading of the vector space of Laurent polynomials defines an exhaustive increasing filtration in the ring ($\mathbb{K}$-algebra) of Laurent polynomials and a grading in the associated graded ring constructed for this filtration.

3.4. Calculation of the Newtonian Generating Function $H_{\mathsf{\Gamma }}({\mathbb{Z}}^d,t)$ by Two-Stage Partitioning of the Group ${\mathbb{Z}}^d$ into Disjoint Subsets

3.4.1. Stage 1. Partitioning the Group ${\mathbb{Z}}^d$ into $sh$-Semigroups

This step, carried out in Section 2.3, allows us to reduce the problem of calculating the Newtonian generating function of the entire set ${\mathbb{Z}}^d$ to the problem of calculating the generating functions of $sh$-semigroups. The solution of the problem of calculating the Newtonian generating functions of $sh$-semigroups is facilitated by the fact that on the closed cone of any facet, the Newtonian degree is additive.

According to Proposition 3 of Section 2.3, the group ${\mathbb{Z}}^d$ splits into $sh$-semigroups. For the convenience of the reader, we reproduce the Formula (19) of this partition:

$${\mathbb{Z}}^d=As{h}_1\cup As{h}_2\cup \dots \cup As{h}_N$$

From this formula, according to Proposition 20(b), we obtain

$$H_{\mathsf{\Gamma }}({\mathbb{Z}}^d,t)=H_{\mathsf{\Gamma }}(As{h}_1,t)+H_{\mathsf{\Gamma }}(As{h}_2,t)+\dots +H_{\mathsf{\Gamma }}(As{h}_N,t)$$

(64)

In the second stage, to find the summands $H_{\mathsf{\Gamma }}(As{h}_i,t)$ of this sum (64), we must subdivide each countable set $As{h}_i$ of integer points of the $sh$-cone $Cs{h}_i$ into a finite number non-intersecting orbits starting at points of the finite set $Bs{h}_i\subset As{h}_i$.

3.4.2. Stage 2. Partitioning the Set of Integer Points of the $sh$-Cone into Orbits of the Action of the Semigroup of Vertices

Proof of Proposition 21   (b).

To calculate the Newtonian generating function $H_{\mathsf{\Gamma }}(As{h}_i,t)$ of the set of integer points $As{h}_i\subset Cs{h}_i$, note that, according to the Proposition 21 (a), the Newtonian generating function of the semigroup of facet ${\Delta }_i$ vertices is equal to $\frac{1}{{(1-t^M)}^d}$. In Proposition 14, the following fact it proven. There exists a a finite set of integer points $Bs{h}_i\subset As{h}_i$ such that the set $As{h}_i$ of integer points of the $sh$-cone $Cs{h}_i$ is tiled by the orbits of the points of this finite set under action of semigroup $V\left({\Delta }_i\right)$. We denoted by $q_i\left(t\right)$ the Newtonian generating function of this set and proved that $q\left(1\right)=Volume\left(\mathsf{\Pi }\right)$. Note that both the vertex semigroup $V\left({\Delta }_i\right)$ and the set $As{h}_i$ belong to the closed cone $Cone\left({\Delta }_i\right)$, and the Newtonian degree on this cone is additive, so for any $b\in As{h}_i$ and any $g\in V\left({\Delta }_i\right)$

$$\phi (b+g)=\phi \left(b\right)+\phi \left(g\right)$$

Therefore, the contribution to the Poincaré series of the orbit of any integer point $b\in Bs{h}_i$ under the action of the vertex semigroup $V\left({\Delta }_i\right)$ is equal to

$$\sum _{g\in V\left({\Delta }_i\right)}{t}^{\phi (b+g)}=t^{\phi \left(b\right)}\times \sum _{g\in V\left({\Delta }_i\right))}{t}^{\phi \left(g\right)}=t^{\phi \left(b\right)}{H}_{\mathsf{\Gamma }}(V\left({\Delta }_i\right),t)=\frac{t^{\phi \left(b\right)})}{{(1-t^M)}^d}$$

Since the orbits of all points of the finite set $Bs{h}_i$ form a partition of the $sh$semigroup $As{h}_i$, we obtain

$$H_{\mathsf{\Gamma }}(As{h}_i,t)=\frac{1}{{(1-t^M)}^d}\sum _{b\in Bs{h}_i}{t}^{\phi \left(b\right)}=\frac{q_i\left(t\right)}{{(1-t^M)}^d},\mathrm{where}{q}_i\left(t\right)=H_{\mathsf{\Gamma }}(Bs{h}_i,t)$$

(65)

□

Proof of the Proposition 21 (c).

From the Formulas (65) and (64), we obtain

$$H_{\mathsf{\Gamma }}({\mathbb{Z}}^d,t)=\frac{q_1\left(t\right)+q_2\left(t\right)+\dots +q_N\left(t\right)}{{(1-t^M)}^d}=\frac{Q\left(t\right)}{{(1-t^M)}^d}$$

(66)

□

3.5. The Dehn–Sommerville Property of the Newtonian Generating Function

Draft proof of the Proposition 22. 

Let $\mathsf{\Gamma }$ be a simplicial super-convinient polytope $\mathsf{\Gamma }$, sh be a shelling of $\mathsf{\Gamma }$ and $\overline{sh}$ be the reverse shelling defined by the Proposition 1.

In Section 2.3, using the shelling $sh$, we inductively constructed the following objects

-

Cones $Cs{h}_1,Cs{h}_2,\dots ,Cs{h}_N$;

-

Fundamental domains ${\mathsf{\Pi }}_1,{\mathsf{\Pi }}_2,\dots ,{\mathsf{\Pi }}_N$;

-

Finite sets of integer points $Bs{h}_1,Bs{h}_2,\dots ,Bs{h}_N$; and

-

Polynomials $q_1,q_2,\dots ,q_N$.

Let us construct with reverse shelling $\overline{sh}$ similar objects:

-

Cones $\overline{Cs{h}_N},\overline{Cs{h}_{N-1}},\dots ,\overline{Cs{h}_1}$;

-

Fundamental domains $\overline{{\mathsf{\Pi }}_N},\overline{{\mathsf{\Pi }}_{N-1}},\dots ,\overline{{\mathsf{\Pi }}_1}$;

-

Finite sets of integer points $\overline{Bs{h}_N},\overline{Bs{h}_{N-1}},\dots ,\overline{Bs{h}_1}$; and

-

Polynomials $\overline{q_N},\overline{q_{N-1}},\dots ,\overline{q_1}$.

To prove the identity (60), we compare the sets ${\mathsf{\Pi }}_i$ and $\overline{{\mathsf{\Pi }}_i}$. From the definition of shelling and the Proposition 2 of Section 2, it is easy to deduce that the integer semi-open parallelepipeds ${\mathsf{\Pi }}_i$ and $\overline{{\mathsf{\Pi }}_i}$ are in some sense complementary. Namely, if

$${\mathsf{\Pi }}_i=(0,v_1]\oplus (0,v_2]\oplus \dots \oplus (0,v_r]\oplus [0,v_{r+1})\oplus \dots \oplus [0,v_d)$$

then

$$\overline{{\mathsf{\Pi }}_i}=[0,v_1)\oplus [0,v_2)\oplus \dots \oplus [0,v_r)\oplus (0,v_{r+1}]\oplus \dots \oplus (0,v_d]$$

Denote by ${\mathsf{\Pi }}_i$ the closed set

$$[0,v_1]\oplus [0,v_2]\oplus \dots \oplus [0,v_r]\oplus [0,v_{r+1}]\oplus \dots \oplus [0,v_d]$$

The closures of the semi-open parallelepipeds ${\mathsf{\Pi }}_i$ and $\overline{{\mathsf{\Pi }}_i}$ coincide with ${\mathsf{\Pi }}_i$. Denote by v the sum of vertices of facet ${\Delta }_i$. Thus,

$$v=v_1+v_2+\dots +v_d.$$

It is easy to see that the closed parallelepiped ${\mathsf{\Pi }}_i$ is centrally symmetric with respect to the point $v/2$. The central symmetry $\sigma :{\mathsf{\Pi }}_i\to {\mathsf{\Pi }}_i$ can be given by $\sigma \left(b\right)=v-b$. This symmetry is the inversion of the set ${\mathsf{\Pi }}_i$, which maps the set ${\mathbb{Z}}^d\cap {\mathsf{\Pi }}_i$ into itself. This inversion defines a bijective correspondence between the semi-open parallelepipeds ${\mathsf{\Pi }}_i$ and $\overline{{\mathsf{\Pi }}_i}$, as well as between the sets of their integer points $Bs{h}_i$ and $\overline{Bs{h}_i}$.

In view of the additivity of the Newtonian degree on the cone $Cone\left({\Delta }_i\right)$, the equality $\phi \left(\sigma \right(b\left)\right)=dM-\phi \left(b\right)$ holds for any point $b\in {\mathsf{\Pi }}_i$. Let us check that

$$\overline{q_i}\left(t\right)=t^{dM}q(1/t)$$

(67)

Indeed,

$$\overline{q_i}\left(t\right)=\sum _{\overline{b}\in \overline{Bs{h}_i}}{t}^{\phi \left(\overline{b}\right)}=\sum _{b\in Bs{h}_i}{t}^{\phi \left(\sigma \right(b\left)\right)}=\sum _{b\in Bs{h}_i}{t}^{dM-\phi \left(b\right)}=t^{dM}\sum _{b\in Bs{h}_i}{(1/t)}^{\phi \left(b\right)}=t^{dM}{q}_i(1/t)$$

The Newtonian generating function $H_{\mathsf{\Gamma }}({\mathbb{Z}}^d,t)$ defined by the Formula (66) does not depend on the choice of shelling. The numerator of the Newtonian generating function $H_{\mathsf{\Gamma }}({\mathbb{Z}}^d,t)$ can be calculated by the formula

$$Q\left(t\right)={(1-t^M)}^d{H}_{\mathsf{\Gamma }}\left(t\right)$$

and also does not depend on shelling. We calculate this numerator in two ways.

When calculated using shelling $sh$, the numerator $Q\left(t\right)$ of the Newtonian generating function turns out to be equal to the sum

$$q_1\left(t\right)+q_2\left(t\right)+\dots +q_N\left(t\right)$$

Furthermore, when calculating using shelling $\overline{sh}$, the numerator $Q\left(t\right)$ of the Newtonian generating function turns out to be equal to the sum

$$\overline{q_1}\left(t\right)+\overline{q_2}\left(t\right)+\dots +\overline{q_N}\left(t\right)$$

Therefore, using (67), we obtain the desired identity

$$\begin{array}{cc}\hfill Q\left(t\right)=& q_1\left(t\right)+q_2\left(t\right)+\dots +q_N\left(t\right)\hfill \\ \hfill =& \overline{q_1}\left(t\right)+\overline{q_2}\left(t\right)+\dots +\overline{q_N}\left(t\right)\hfill \\ \hfill =& t^{dM}(q_1(1/t)+q_2(1/t)+\dots +q_N(1/t))\hfill \\ \hfill =& t^{dM}Q(1/t)\hfill \end{array}$$

□

4. Standard Information about Filtered and Graded Objects and Their Poincaré Series

In this section, we recall well-known definitions and propositions related to filtered and graded objects and finitely generated graded algebras. In our paper, we consider only finitely generated $\mathbb{K}$-algebras over a field $\mathbb{K}$ of characteristic 0, graded by non-negative integers.

Definition 12.

Let X be a finitely generated graded $\mathbb{K}$-algebra and $H(X,t)$ be its Poincaré series. The multiplicity of the pole $t=1$ of the Poincaré series $H(X,t)$ is called the dimension of X.

Comment. It follows from Formula (62) that the dimension of the $\mathbb{K}$-algebra of polynomials in d variables, graded to be formula $deg\left(x^n\right)=n_1+n_2+\dots +n_d$, is equal to d.

In the book [23] one can find proofs of the following two theorems

Theorem 1.

Let X be a finitely generated graded $\mathbb{K}$-algebra. Then, $H(X,t)$ is either a rational function with a single pole at the point $t=1$ or a polynomial.

Proposition 23.

The dimension of a finitely generated graded $\mathbb{K}$-algebra introduced in the Definition 12 coincides with the dimension of Krull.

4.1. Elementwise Comparison of Poincaré Series of Graded Algebras

We reproduce the reasoning from online publication by R. Stanley, 2017 [10].

Let $A\left(t\right)=a_0+a_{1}t+a_2{t}^2+a_3{t}^3+\dots$ and $B\left(t\right)=b_0+b_{1}t+b_2{t}^2+b_3{t}^3+\dots$ be two formal series with real coefficients. We say that $A\left(t\right)\le B\left(t\right)$ if $a_0\le b_0$ and $a_1\le b_1$ and $a_2\le b_2$ and $a_3\le b_3,$ etc. If the series $C\left(t\right)$ has non-negative coefficients and $c_0\ne 0$, then $A\left(t\right)\le B\left(t\right)$ implies $A\left(t\right)C\left(t\right)\le B\left(t\right)C\left(t\right)$, and $A\left(t\right)C\left(t\right)=B\left(t\right)C\left(t\right)$ if and only if $A\left(t\right)=B\left(t\right)$. If $A\left(t\right)$ and $B\left(t\right)$ simultaneously satisfy the inequalities $A\left(t\right)\le B\left(t\right)$ and $B\left(t\right)\le A\left(t\right)$, then $A\left(t\right)=B\left(t\right)$. If R is a graded algebra and $g\in R$ is a homogeneous element of degree M that is not a zero divisor, then

$$H(R,t)=\frac{H(R/(g),t)}{1-t^M}$$

For an arbitrary homogeneous element $g\in R$ of positive degree M, we have the relation

$$H(R,t)\le \frac{H(R/(g),t)}{1-t^M}$$

(68)

where equality is attained if and only if g is not a zero divisor in R.

Let $g_1,g_2,\dots ,g_r$ be a sequence of elements of a graded $\mathbb{K}$-algebra R of positive degrees $M_1,M_2,\dots ,M_r$. Iterating the inequality (68), we get

$$H(R,t)\le \frac{H(R/(g_1,g_2,\dots ,g_r),t)}{(1-t^{M_1})(1-t^{M_2})\dots (1-t^{M_r})}$$

(69)

where equality is achieved if and only if the element $g_1$ is not a zero divisor in R, the element $g_2$ is not a zero divisor in $R/\left(g_1\right)$, the element $g_3$ is not a zero divisor in $R/(g_1,g_2)$, …, the element $g_r$ is not a zero divisor in $R/(g_1,g_2,\dots ,g_{r-1})$.

4.2. Graded Cohen–Macaulay Rings

In this section, we list a number of known facts. To describe the conditions on the sequence of ring elements under which the inequality (69) becomes an equality, the following definition introduces a special term.

Definition 13.

A sequence of elements $g_1,g_2,\dots g_r$ of a commutative ring R is called regular if

(i) 

the ideal generated by all elements of the sequence does not coincide with R;

(ii) 

the element $g_1$ is not a zero divisor in R, the element $g_2$ is not a zero divisor in the quotient algebra $R/\left(g_1\right)R$, the element $g_3$ is not a zero divisor in the quotient algebra $R/(g_1,g_2)R$,…, and, finally, the element $g_r$ is not a zero divisor in the quotient algebra $R/(g_1,g_2,\dots ,g_{r-1})R$.

Definition 14.

A finitely generated graded ring R (a $\mathbb{K}$-algebra) of dimension d is called a Cohen–Macaulay ring if there exists a regular sequence consisting of d homogeneous elements R of positive degree.

The next two theorems describe the properties of graded Cohen–Macaulay rings. Proofs can be found in [24].

Theorem 2.

If a sequence $g_1,g_2,\dots ,g_d$ of homogeneous elements of positive powers of a d-dimensional graded Cohen–Macaulay ring R generates an ideal of finite codimension, then this sequence is regular.

The regularity of a sequence in graded Cohen–Macaulay rings can be checked in several ways.

Theorem 3.

Let R be a finitely generated graded Cohen–Macaulay $\mathbb{K}$-algebra of dimension d; $g_1,g_2,\dots ,g_d$ be a sequence of homogeneous elements R of positive powers $M_1,M_2,\dots ,M_d$; I be an ideal in R generated by elements of this sequence; $\mathbb{K}[g_1,g_2,\dots ,g_d]$ be a subgebra in R generated by the elements of the sequence.

(a) 

The following conditions are equivalent:

(i) 

$codi{m}_K\left(I\right)$is finite;

(ii) 

Sequence $g_1,g_2,\dots ,g_d$ is regular;

(iii) 

The $\mathbb{K}$-algebra R is a free module with a finite number of homogeneous generators over its subalgebra $\mathbb{K}[g_1,g_2,\dots ,g_d]$;

(iv) 

The Poincaré series of the $\mathbb{K}$-algebra $R/I$, is given by the formula

$$H(R,t)=\frac{H(R/I,t)}{(1-t^{M_1})(1-t^{M_2})\dots (1-t^{M_d})}$$

(b) 

If the conditions of part a) are satisfied, then:

-

The formal series H(R/I,t) is actually a polynomial with non-negative coefficients;

-

The sum of the coefficients of this polynomial is equal to the codimension of the ideal I, and is also equal to the number of generators of the free module defined in (iii);

-

Any homogeneous basis of the quotient algebra $R/I$ can be taken as the set of generators of the free module from (iii);

-

The cosets of any minimal set of generators from (iii) form a basis of the vector space $R/I$.

5. Newton Filtration on Algebra of Laurent Polynomial and Associated Graded Algebra

5.1. Newton’s Filtration on $\mathbb{K}\left[{\mathbb{Z}}^d\right]$

Filtrations constructed from the Newton polytope of the germ of an analytic function were introduced by V.I. Arnold at work [1] and were extensively used in [2,4].

5.1.1. Newtoninian Degrees of Monomials

In Section 3.1, we defined the Newtonian degree $\phi \left(n\right)$ of any point $n\in {\mathbb{Z}}^d$ with respect to the super-convenient integer polytope $\mathsf{\Gamma }$. For $x^n\in \mathbb{K}\left[{\mathbb{Z}}^d\right]$, the integer $\phi \left(n\right)$ is called Newtonian degree of the monomial $x^n$. Since the polytope $\mathsf{\Gamma }$ is assumed to be super-convenient, i.e., the origin is an interior point of $\mathsf{\Gamma }$, for any monomial $x^n$ its Newtonian degree is non-negative and equals zero if and only if the monomial is equal to $x^0$. V. Arnold in [1] used the term piecewise linear degree. We now define the Newtonian degree $\phi$ for any nonzero elements of the $\mathbb{K}$-algebra $\mathbb{K}\left[{\mathbb{Z}}^d\right]$. For a linear combination of monomials with nonzero coefficients $S={\sum }_i{\lambda }_i{m}_i$, we set $\phi \left(S\right)=\underset{i}{max}\phi \left(Log\left(m_i\right)\right)$. We set the Newtonian degree of the zero element of the $\mathbb{K}$-algebra equal to $-\infty$.

5.1.2. Definition of Newton’s Filtration

For brevity, denote by A the $\mathbb{K}$-algebra of Laurent polynomials $\mathbb{K}\left[{\mathbb{Z}}^d\right]$. Denote by “·” the operation of multiplication in A. For $i\in \mathbb{N}$ we put $A_i=\{f\in A:\phi \left(f\right)\le i\}$. The vector spaces $A_i$ are finite-dimensional and grow with the growth of i: $\mathbb{K}=A_0\subset A_1\subset A_2\subset \dots$ and their union is equal to the algebra A. The Proposition 19 of the Section 3.1 implies that the Newtonian degree is subadditive. Therefore, the vector spaces in the algebra A defined above with respect to the operation of multiplication “·” satisfy the condition $A_i·A_j\subseteq A_{i+j}$.

Thus, in the terminology of the book [25], these vector spaces define in the $\mathbb{K}$-algebra of Laurent polynomials A an integer increasing exhaustive filtration, which V. Arnold in his 1974 paper [1] called the Newton’s filtration. This filtered ring should be denoted by $A\left(\mathsf{\Gamma }\right)$, but for brevity, we will simply denote it by A.

5.2. Associated Graded Ring $\mathbb{A}\left(\mathsf{\Gamma }\right)$ of the Arnold–Newton Filtered Ring $A\left(\mathsf{\Gamma }\right)$ of Laurent Polynomials

Denote by $\mathbb{A}\left(\mathsf{\Gamma }\right)$, for brevity simply by $\mathbb{A}$, the associated graded ring of the Newton-filtered ring A. Recall that we use the terms $\mathbb{K}$-algebra, algebra, and ring as synonyms. First, we introduce into $\mathbb{A}$ the structure of a vector space over $\mathbb{K}$. In accordance with the definition of an associated graded ring [25], we set ${\mathbb{A}}_0=A_0=\mathbb{K}$; for a natural number i, we define the vector space ${\mathbb{A}}_i$ as the quotient space $A_i/A_{i-1}$ and finally put $\mathbb{A}={⨁}_{i\ge 0}{\mathbb{A}}_i$. Associating with each monomial $x^n$ of Newtonian degree $\phi \left(n\right)$ its equivalence class $x^n+A_{\phi \left(n\right)-1}$, we obtain a set that is a basis of the vector space $\mathbb{A}$. The elements of this basis will also be called monomials, i.e., by abuse of notations, we will not distinguish between monomials in A and their equivalence classes in $\mathbb{A}$, that is, we will denote monomials in the filtered and graded algebras in the same way.

Denote by “·” the multiplication operation in the filtered algebra A and denote by “∘” the multiplication operation in the associated graded algebra $\mathbb{A}$. We describe clearly the operation of multiplication “∘” in the associated graded ring $\mathbb{A}$, showing how the product of the equivalence classes of two or more monomials is calculated.

5.2.1. Monomials Multiplication Rule in the Associated Graded Ring $\mathbb{A}$

Let $x^{n_1}$ and $x^{n_2}$ be two monomials in the filtered algebra A of Newtonian degrees $d_1=\phi \left(n_1\right)$ and $d_2=\phi \left(n_2\right)$, respectively. Their equivalence classes in $A_{d_1}/A_{d_1-1}$ and $A_{d_1}/A_{d_1-1}$ are $x^{n_1}+A_{d_1-1}$ and $x^{n_2}+A_{d_2-1}$ respectively. According to the standard definition of an associated graded ring, we obtain

$$(x^{n_1}+A_{d_1-1})\circ (x^{n_2}+A_{d_2-1})=x^{n_1}·x^{n_2}+A_{d_1+d_2-1}\in A_{d_1+d_2}/A_{d_1+d_2-1}$$

(70)

The Formula (70) is generalized to the case of the product of several monomials

$$\begin{array}{cc}\hfill & (x^{n_1}+A_{d_1-1})\circ (x^{n_2}+A_{d_2-1})\circ \dots \circ (x^{n_s}+A_{d_s-1})=\hfill \\ \hfill & x^{n_1}·x^{n_2}·\dots ·x^{n_s}+A_{d_1+d_2+\dots +d_s-1}\in A_{d_1+d_2+\dots +d_s}/A_{d_1+d_2+\dots +d_s-1}\hfill \end{array}$$

(71)

Definition 15.

(i) Let $n_1$ and $n_2$ be two integer points of the set ${\mathbb{Z}}^d\subset {\mathbb{R}}^d$. Let us call them homoconical if there exists at least one facet $\Delta \subset \partial \mathsf{\Gamma }$ such that $n_1\in Cone(\Delta )$ and $n_2\in Cone(\Delta )$. According to Proposition 19 in Section 3.1, two points $n_1$ and $n_2$ are homoconical if and only if

$$\phi (n_1+n_2)=\phi \left(n_1\right)+\phi \left(n_2\right)$$

Two points $n_1$ and $n_2$ are called heteroconical if there is no facet Δ such that $n_1\in Cone(\Delta )$ and $n_2\in Cone(\Delta )$. According to Proposition 19, two points $n_1$ and $n_2$ are heteroconical if and only if

$$\phi (n_1+n_2)<\phi \left(n_1\right)+\phi \left(n_2\right)$$

(ii) The homoconicality/heteroconicality of several, say $s>2$, integer points of the set ${\mathbb{Z}}^d$ is defined similarly.

Points $n_1,n_2,\dots ,n_s$ are called homoconical if there exists at least one facet $\Delta \subset \partial \mathsf{\Gamma }$ such that $n_1\in Cone(\Delta )$, $n_2\in Cone(\Delta )$, …, and $n_s\in Cone(\Delta )$

According to Proposition 19, points $n_1$, $n_2$, …, and $n_s$ are homoconical if and only if

$$\phi (n_1+n_2+\dots +n_s)=\phi \left(n_1\right)+\phi \left(n_2\right)+\dots +\phi \left(n_s\right)$$

Points $n_1,n_2,\dots ,n_s$ are called heteroconical if there is no facet $\Delta \subset \partial \mathsf{\Gamma }$ such that $n_1\in Cone(\Delta )$, $n_2\in Cone(\Delta )$, …, and $n_s\in Cone(\Delta )$

According to Proposition 19 points $n_1$, $n_2$, …, and $n_s$ are heteroconical if and only if

$$\phi (n_1+n_2+\dots +n_s)<\phi \left(n_1\right)+\phi \left(n_2\right)+\dots +\phi \left(n_s\right)$$

Proposition 24.

(i) The product of monomials $x^{n_1}$ and $x^{n_2}$ in the associated graded algebra $\mathbb{A}$ is given by the rule

$$x^{n_1}\circ x^{n_2}=\left\{\begin{array}{cc}\hfill x^{(n_1+n_2)}& :\mathit{if}\mathit{points}{n}_1,n_2\mathit{are}\mathit{homoconical}\hfill \\ \hfill 0& :\mathit{otherwise}\hfill \end{array}\right.$$

(72)

(ii) 

A similar rule is valid for the product of an arbitrary number of monomials:

$$x^{n_1}\circ x^{n_2}\circ \dots \circ x^{n_s}=\left\{\begin{array}{cc}\hfill x^{(n_1+n_2+\dots +n_s)}& :\mathit{if}\mathit{points}{n}_1,n_2,\dots ,n_s\mathit{are}\mathit{homoconical}\hfill \\ \hfill 0& :\mathit{otherwise}\hfill \end{array}\right.$$

(73)

Proof. 

$\left(i\right)$ By Formula (70),

$$(x^{n_1}+A_{d_1-1})\circ (x^{n_2}+A_{d_2-1})=x^{n_1}·x^{n_2}+A_{d_1+d_2-1}$$

If points $n_1,n_2$ are heteroconical, then

$$\phi (n_1+n_2)\le \phi \left(n_1\right)+\phi \left(n_2\right)-1=d_1+d_2-1$$

i.e., $x^{n_1}·x^{n_2}\in A_{d_1+d_2-1}$ and

$$x^{n_1}·x^{n_2}+A_{d_1+d_2-1}=A_{d_1+d_2-1}=0\in A_{d_1+d_2}/A_{d_1+d_2-1}$$

If the points $n_1,n_2$ are homoconical, then

$$\phi (n_1+n_2)=\phi \left(n_1\right)+\phi \left(n_2\right)=d_1+d_2,$$

i.e., $x^{n_1}·x^{n_2}\in A_{d_1+d_2}$

$$x^{n_1}·x^{n_2}+A_{d_1+d_2-1}=x^{(n_1+n_2)}+A_{d_1+d_2-1}\ne 0$$

$\left(ii\right)$ is proved similar to $\left(i\right)$ using (71) instead of (70). □

The above constructions of the Newton filtration and the graded ring repeated the arguments of [4] and did not use the simplicial property of the polytope $\mathsf{\Gamma }$. Below, we start using this simpliciality.

5.2.2. The Subring of Vertices of the Graded Ring $\mathbb{A}\left(\mathsf{\Gamma }\right)$ of the Super-Convenient Convex Integer Simplicial Polytope $\mathsf{\Gamma }$

Consider in the algebra $\mathbb{A}$ the vector space generated by the monomial $x^0$ and the monomials corresponding to the vertices of the polytope $\mathsf{\Gamma }$. An element of this vector space is a finite linear combination of monomials in $\mathbb{A}$ corresponding to points of the following set in ${\mathbb{Z}}^d$:

$$V\left(\mathsf{\Gamma }\right)=\bigcup _{i=1}^{N}V\left({\Delta }_i\right)$$

(74)

The elements of the set $V\left(\mathsf{\Gamma }\right)$, generally speaking, do not form a semigroup; when adding points from different cones, we can go beyond the limits of the set $V\left(\mathsf{\Gamma }\right)$. However, the monomials corresponding to any two points of the set $V\left(\mathsf{\Gamma }\right)$ can be multiplied inside $\mathbb{A}$ without leaving the set $V\left(\mathsf{\Gamma }\right)\cup 0$. Indeed, if the points are homoconical, the product is a nonzero monomial in $\mathbb{K}\left[V\right(\mathsf{\Gamma }\left)\right]$; if the points are heteroconical, the product will be zero. The resulting ring is called the subring of vertices of the super-convenient simplicial polytope $\mathsf{\Gamma }$.

Remark 2.

In contrast to the structure of the ring $\mathbb{A}\left(\mathsf{\Gamma }\right)$, the structure of the vertex subring is determined only by the combinatorial structure of the complex of faces of the simplicial polytope Γ and, generally speaking, does not depend on the embedding of the vertices of the polytope in the set ${\mathbb{Z}}^d$. In this paper, however, we are interested in the vertex ring not in itself, but as a subring of the ring $\mathbb{A}\left(\mathsf{\Gamma }\right)$, which defines a module structure over $\mathbb{K}\left[V\right(\mathsf{\Gamma }\left)\right]$ on it. The structure of this module depends not only on the combinatorial structure of the polytope Γ, but also on how the vertices of this integral convex polytope are embedded in the set ${\mathbb{Z}}^d\subset {\mathbb{R}}^d$.

5.3. The Vertex Ring Is Nothing Else Than the Stanley–Reisner Ring of the Simplicial Complex of Facets of the Convex Integer Simplicial Polytope $\mathsf{\Gamma }$

Definition 16.

Denote by $v_1,v_2,\dots ,v_L$ vertices of Γ. Associate with each vertex $v_i$ of the simplicial polytope Γ an independent variable $V_i$. A product of distinct independent variables is said to be simplicial if the vertices corresponding to these variables are vertices of some simplex on the boundary of the polytope Γ. Denote by I the ideal generated in $\mathbb{K}[V_1,V_2,\dots ,V_L]$ by those products of unknowns that are not simplicial. The ideal I is called the the Stanley–Reisner ideal of the polytope Γ, and the quotient by this ideal is called the ring of faces or Stanley–Reisner ring (see [11]).

Proposition 25.

Let $\pi :\mathbb{K}[V_1,V_2,\dots ,V_L]\to \mathbb{K}\left[V\left(\mathsf{\Gamma }\right)\right]$, the map defined on the generators of the ring $\mathbb{K}[V_1,V_2,\dots ,V_L]$ by the formulas $\pi \left(V_i\right)=x^{v_i}$, $i=1,2,\dots ,L$. Then $ker\left(\pi \right)=I$. In other words, the subring of the graded ring $\mathbb{A}$ generated by the monomials corresponding to the vertices (zero-dimensional faces) of the polytope Γ is isomorphic to the Stanley–Reisner ring of the simplicial complex of faces of the polytope Γ.

Proof. 

First, check that $I\subseteq ker\left(\pi \right)$. Let P be a generator of the ideal I, that is, some non-simplicial product of independent variables $V_1{V}_2\dots V_s$. The element $\pi \left(P\right)$ of the ring $\mathbb{K}\left[V\right(\mathsf{\Gamma }\left)\right]$ is a product of monomials

$$x^{v_1}\circ x^{v_2}\circ \dots \circ x^{v_s}$$

Since the product P is non-simplicial, the vertices $v_1,v_2,\dots ,v_s$ do not belong to any one face of the polytope $\mathsf{\Gamma }$, and by the Formula (73), the product vanishes.

Let us now prove the inclusion $ker\left(\pi \right)\subseteq I$. First, we prove that any monomial $p\in ker\left(\pi \right)$ belongs to the ideal I. Let p be an arbitrary monomial. Let us write out the product of all variables that are included in the monomial p to a positive power. Two cases are possible.

If a nonsimplicial product is obtained, then the monomial p turns out to be a multiple of this nonsimplicial product of independent variables, that is, $p\in I$.

If a simplicial product is obtained, then the monomial p includes only independent variables corresponding to the vertices of some face ${\Delta }_i$ of the polytope $\mathsf{\Gamma }$, and the image of p turns out to be a monomial in $\mathbb{K}\left[V\left({\Delta }_i\right)\right]$, which, according to the definition of $\mathbb{K}\left[V\right(\mathsf{\Gamma }\left)\right]$, uniquely determines some basis vector of the vector space $\mathbb{K}\left[V\right(\mathsf{\Gamma }\left)\right]$ and, therefore, $\pi \left(p\right)\ne 0$.

Finally, let the sum of different monomials with nonzero coefficients $f={\lambda }_1{p}_1+{\lambda }_2{p}_2+\dots +{\lambda }_s{p}_s$ belong to the kernel $\pi$. Such a sum cannot contain any monomial $p_i$ for which $\pi \left(p_i\right)\ne 0$ since the images of such monomials in $\mathbb{K}\left[V\right(\mathsf{\Gamma }\left)\right]$ are linearly independent and any linear combination with nonzero coefficients images of such monomials is not equal to zero. Thus, from $\pi \left(f\right)=0$, it follows that each monomial $p_i$ contained in f also belongs to $ker\left(\pi \right)$, hence, by what was proved earlier, it belongs to I, and hence, the linear combination f of such monomials belongs to I. □

Remark 3.

Let us assume for a moment that we decide to perform calculations in the ring $\mathbb{A}$ using some kind of computer system. Description of the ring $\mathbb{A}$ in the classical form, in the form of free generators and relations, would require the introduction of a large number of variables, which grows with the number of vertices Γ. Our description of the additive structure of the ring $\mathbb{A}$ requires the introduction of only d variables. One has to pay for this by increasing the complexity of the monomial multiplication algorithm, the execution of which now requires not only the addition of vectors of exponents of monomials, but also the calculation of the homoconicality predicate on the set of pairs of monomials.

6. “Shelling” of the Set ${\mathbb{Z}}^{\mathit{d}}$ and “Shelling” of the Rings $\mathbb{A}\left(\mathsf{\Gamma }\right)$

Given the shelling of the polytope $\mathsf{\Gamma }$, that is, the sequence facets that satisfies certain conditions, we constructed two other sequences of objects in Section 2.3:

-

A sequence of subsemigroups $As{h}_1,As{h}_2,\dots ,As{h}_N$ of the group ${\mathbb{Z}}^d$ belonging to the cones $Cone\left({\Delta }_1\right),Cone\left({\Delta }_2\right),\dots ,Cone\left({\Delta }_N\right)$;

-

A sequence of finite sets $Bs{h}_1,Bs{h}_2,\dots ,Bs{h}_N$ of the group ${\mathbb{Z}}^d$ belonging to the semigroups $As{h}_1,As{h}_2,\dots ,As{h}_N$.

These sequences were constructed in such a way that for any $i\in [1,N]$ the following conditions are satisfied:

-

$As{h}_i\in A\left({\Delta }_i\right)$

-

$As{h}_1\cup As{h}_2\cup \dots \cup As{h}_i=A\left({\Delta }_1\right)\cup A\left({\Delta }_2\right)\cup \dots \cup A\left({\Delta }_i\right)$

, in particular, $As{h}_1\cup As{h}_2,\cup \dots ,\cup As{h}_N={\mathbb{Z}}^d$;

-

for $i>1$$As{h}_i\cap (As{h}_1\cup As{h}_2,\cup \dots ,\cup As{h}_{i-1})=⌀$;

-

The subsemigroup $As{h}_i$ is invariant under the action of the vertex semigroup $V\left({\Delta }_i\right)$ on the semigroup $\mathsf{\Gamma }$;

-

For any i, $Bs{h}_i\subset As{h}_i$ and for $i>1$, $Bs{h}_i\cap (Bs{h}_1\cup Bs{h}_2,\cup \dots ,\cup Bs{h}_{i-1})=⌀$;

-

The set $Bs{h}_i$ is the fundamental domain for action of the vertex semigroup $V\left({\Delta }_i\right)$ on the subsemigroup $As{h}_i$, that is, shifts of the finite set $Bs{h}_i$ by all possible elements of the vertex semigroup $V\left({\Delta }_i\right)$ form a partition of the set $As{h}_i$;

-

The cardinality of $Bs{h}_i$ is equal to the volume of the parallelepiped ${\mathsf{\Pi }}_i$ defined in the Section 2.4.2.

6.1. “Shelling” of the Ring $\mathbb{A}\left(\mathsf{\Gamma }\right)$

Let us now construct an analogue of the “shelling” for the ring $\mathbb{A}\left(\mathsf{\Gamma }\right)$: an increasing sequence of graded $\mathbb{K}$-algebras $R_1,R_2,\dots ,R_N$, ending with the $\mathbb{K}$-algebra $\mathbb{A}\left(\mathsf{\Gamma }\right)$. This construction is similar to the construction of the article [9], re-stated in the online publication by R. Stanley [10].

While the objects $As{h}_i$ and $Bs{h}_i$ are located inside the cone of one facet ${\Delta }_i$, i.e., “associated“ with one facet, the $\mathbb{K}$-algebra $R_i$ will be “associated” with the union of facets ${\Delta }_1\cup {\Delta }_2\cup \dots \cup {\Delta }_i$. First, we define $R_1,R_2,\dots ,R_N$ as vector spaces over the field $\mathbb{K}$.

Definition 17.

For each $i\in [1,N]$, construct the vector space $R_i$ over $\mathbb{K}$, taking as a basis the monomials whose exponents belong to the union of the semigroups

$$E_i=(As{h}_1\cup As{h}_2\cup \dots \cup As{h}_i)\subset (Cone\left({\Delta }_1\right)\cup Cone\left({\Delta }_2\right)\cup \dots \cup Cone\left({\Delta }_i\right))$$

Since

$$E_1\subset E_2\subset \dots \subset E_N={\mathbb{Z}}^d$$

then for $1\le j<i$ the basis of each vector space $R_j$ is contained in the basis of the next vector space $R_{j+1}$ and, therefore, it can be considered that

$$R_1\subset R_2\subset \dots \subset R_N=\mathbb{A}\left(\mathsf{\Gamma }\right)$$

The vector space $R_N=\mathbb{A}\left(\mathsf{\Gamma }\right)$ has the structure of a $\mathbb{K}$-algebra. We introduce the structure of a $\mathbb{K}$-algebra on vector spaces $R_i$ for $1\le i<N$. Using the analogue of the Definition 15 and the analogue of the rule (70) for multiplying monomials in $\mathbb{A}\left(\mathsf{\Gamma }\right)$, we define the rule for multiplying basis vectors in $R_j$, that is, the rule for multiplying monomials of the form $x^n$, where the exponent $n=Log\left(x^n\right)$ belongs to the union of the sets $E_i=As{h}_1\cup As{h}_2\cup \dots \cup As{h}_i$. The unit monomial $x^0$, which has a zero exponent, also belongs to such monomials. The operation of multiplying monomials with exponents from the set $E_i$ is denoted by “${\circ }_i$”. The result of this operation will be a monomial (basis vector) in $R_i$ or $0\in R_i$. Further, we extend this operation to the entire vector space $R_i$. As a first step, we extend the operation “${\circ }_i$” allowing us to use as its arguments not only monomials, but also 0 of the vector space $R_i$ (different from the unit monomial $x^0\in E_i$). Namely, for any monomial $x^n$, we put

$$x^n{\circ }_{i}0=0{\circ }_i{x}^n=0{\circ }_{i}0=0\in R_i$$

Definition 18.

(i) Let $n_1$ and $n_2$ be two integer points in $E_i=As{h}_1\cup As{h}_2\cup \dots \cup As{h}_i$. Let us call them$\mathbf{i}-$homoconical if there is at least one number $j\in [1,i]$ such that $n_1\in Cone\left({\Delta }_j\right)$ and $n_2\in Cone\left({\Delta }_j\right)$. Points $n_1$ and $n_2$ will be called $\mathbf{i}-$ heteroconical if they are not $\mathbf{i}-$ homoconical;

(ii) 

Similarly, we define $\mathbf{i}-$ homoconicality and $\mathbf{i}-$ heteroconicality for several points in $E_i=As{h}_1\cup As{h}_2\cup \dots \cup As{h}_i$:

integer points $n_1,n_2,\dots ,n_s$ in $E_i=As{h}_1\cup As{h}_2\cup \dots \cup As{h}_i$ will be called $\mathbf{i}-$ homoconical if there is at least one number $j\in [1,i]$ such that $n_1\in Cone\left({\Delta }_j\right),n_2\in Cone\left({\Delta }_j\right)$, …$n_s\in Cone\left({\Delta }_j\right)$. Points $n_1,n_2,\dots ,n_s$ will be called $\mathbf{i}-$ heteroconical if they are not $\mathbf{i}-$ homoconical ;

(iii) 

Define the operation “${\circ }_i$” with a rule similar to the rule (72):

$$x^{n_1}{\circ }_i{x}^{n_2}=\left\{\begin{array}{cc}\hfill x^{(n_1+n_2)}& :\mathit{if}\mathit{points}{n}_1,n_2\mathit{are}\mathbf{i}-\mathit{homoconical}\hfill \\ \hfill 0& :\mathit{otherwise}\hfill \end{array}\right.$$

(75)

(iv) 

Let us extend the operation “${\circ }_i$”, allowing us to use as its arguments not only monomials of the form $x^n,\mathrm{where}n\in E_i$, but also $0\in R^i$ and assuming in this case, the result of the operation is equal to $0\in R^i$.

Example 4.

Let Γ be Newton polygon having vertices $v_1=(1,0),v_2=(-1,-1),v_3=(0,1)$. Then, the facets of Γ are segments ${\Delta }_1=[v_1,v_2],{\Delta }_2=[v_2,v_3],{\Delta }_3=[v_3,v_1]$. Set for Γ the shelling $sh=({\Delta }_1,{\Delta }_2,{\Delta }_3)$. Then,

the cone $Cone\left({\Delta }_1\right)$ contains the points $v_1$ and $v_2$

the cone $Cone\left({\Delta }_2\right)$ contains the points $v_2$ and $v_3$

the cone $Cone\left({\Delta }_3\right)$ contains the points $v_1$ and $v_3$

Both vector spaces $R_2$ and $R_3$ are three-dimensional and contain basis vectors $v_1,v_2,v_3$. In this way, the monomials $x^{v_1}$ and $x^{v_3}$ belong to both $R_2$ and $R_3$, but the products of these monomials in $R_2$ and $R_3$ differ:

$$\begin{array}{cc}& x^{v_1}{\circ }_2{x}^{v_3}=0\hfill \\ & x^{v_1}{\circ }_3{x}^{v_3}=x^{v_1+v_3}\ne 0\hfill \end{array}$$

Let us prove the associativity of the operation “${\circ }_i$” on the discrete set of basis vectors of the vector space $R_i$ extended by the point 0 and continue this operation to the entire vector space $R_i$.

Proposition 26.

(i) The operation “${\circ }_i$” is an associative operation on a discrete set consisting of 0 and the basis vectors of the vector space $R_i$;

(ii) 

Extension by linearity of this operation on the entire vector space $R_i$ defines $\mathbb{K}$-algebra structure on $R_i$;

(iii) 

The product of an arbitrary number of monomials in the $\mathbb{K}$-algebra $R_i$ is calculated according to the rule

$$x^{n_1}{\circ }_i{x}^{n_2}{\circ }_i\dots {\circ }_i{x}^{n_s}=\left\{\begin{array}{cc}\hfill x^{(n_1+n_2+\dots +n_s)}& :\mathrm{if}\mathrm{points}{n}_1,n_2,\dots ,n_s\mathrm{are}\mathbf{i}-\mathit{homoconical}\hfill \\ \hfill 0& :\mathrm{otherwise}\hfill \end{array}\right.$$

(76)

Proof. 

(i) Let $x^a$, $x^b$ and $x^c$ be three monomials in $R_i$. We must prove that

$$\left(x^a{\circ }_i{x}^b\right){\circ }_i{x}^c=x^a{\circ }_i\left(x^b{\circ }_i{x}^c\right)$$

(77)

If at least one monomial is $x^0=1$, then the equality (77) is obvious. Therefore, we can assume that the points $a,b\mathrm{and}c$ are non-zero. It suffices to prove that the three points $a,b\mathrm{and}c$ are homoconical. Indeed, in this case, the equality (77) follows from the associativity of the addition operation in ${\mathbb{R}}^d$

$$\left(x^a{\circ }_i{x}^b\right){\circ }_i{x}^c=x^{(a+b)}{\circ }_i{x}^c=x^{(a+b)+c}=x^{a+b+c}$$

$$x^a{\circ }_i\left(x^b{\circ }_i{x}^c\right)=x^a{\circ }_i{x}^{(b+c)}=x^{a+(b+c)}=x^{a+b+c}$$

□

Case 1. Let us pretend that

$$\left(x^a{\circ }_i{x}^b\right){\circ }_i{x}^c\ne 0$$

(78)

Let us prove that the points $a,b\mathrm{and}c$ are homoconical. The first factor in the product (78) is non-zero, because the product is non-zero. Thus, from definition “${\circ }_i$” we can conclude that

$$\left(x^a{\circ }_i{x}^b\right)=x^{a+b}\mathrm{which}\mathrm{means}{x}^{(a+b)}{\circ }_i{x}^c\ne 0$$

Therefore, two points $(a+b)$ and c are $\mathbf{i}-$homoconical, i.e., among the cones

$$Cone\left({\Delta }_1\right),Cone\left({\Delta }_2\right),\dots ,Cone\left({\Delta }_i\right),$$

there is a cone $Cone$ such that $(a+b)\in Cone$ and $c\in Cone$. Since $\left(x^a{\circ }_i{x}^b\right)\ne 0$, the points a and b are homoconical, that is, there exists a cone $Con{e}_j$, where $1\le j\le i$ such that $a\in Con{e}_j$, $b\in Con{e}_j$ and $(a+b)\in Con{e}_j$. Thus, $(a+b)\in Cone\cap Con{e}_j$. If $Con{e}_j$ coincides with $Cone$, then all three points belong to $Cone$ and homoconicality is proved. However, if $Con{e}_j\ne Cone$, then the point $(a+b)$ belongs to the intersection of the cones $F=Con{e}_j\cap Cone$. This intersection F is a proper face of the cone $Cone$ according to the properties of the faces of the convex superconvenient simplicial polytope $\mathsf{\Gamma }$. According to Proposition 5 in Section 2.4, $(a+b)\in F$ implies that $a\in F\subset Cone$ and $b\in F\subset Cone$. Therefore, all three exponents $a,b,c$ belong to the same cone $Cone$. Thus, for case 1, Formula (77) is proved.

Case 2. Assume that

$$\left(x^a{\circ }_i{x}^b\right){\circ }_i{x}^c=0$$

Prove that

$$x^a{\circ }_i\left(x^b{\circ }_i{x}^c\right)=0$$

Assume the opposite

$$x^a{\circ }_i\left(x^b{\circ }_i{x}^c\right)\ne 0$$

(79)

Repeating the arguments of case 1, we find that the three exponents $a,b,c$ belong to the same cone $Cone$, and hence,

$$\left(x^a{\circ }_i{x}^b\right){\circ }_i{x}^c=x^{(a+b)}{\circ }_i{x}^c=x^{(a+b)+c}=x^{a+b+c}\ne 0$$

which contradicts the original assumption (79).

The proofs of (ii) and (iii) are left to the reader.

6.2. Ring’s $\mathbb{A}$ “Shelling” Properties

For $i\in [1,N]$ denote by $I_i$ the vector subspace of $R_i$ spanned by monomials $x^n$, where $n\in As{h}_i$ Then the bases in the three vector spaces $R_i$, $R_{i-1}$ and $I_i$ will be formed by monomials corresponding to the points of the three sets $E_i=(As{h}_1\cup As{h}_2\cup \dots \cup As{h}_{i-1})\cup As{h}_i$, $E_{i-1}=(As{h}_1\cup As{h}_2\cup \dots \cup As{h}_{i-1})$, and $As{h}_i$ respectively. For $1<i\le N$, the basis of the vector space $R_{i-1}$ is a subset of the basis of the space $R_i$, therefore, the coordinate-wise embedding $h_i:R_{i-1}\to R_i$ and the coordinate-wise projection ${\pi }_i:R_i\to R_{i-1}$ vector spaces. It is obvious that $R_i$ is a direct sum of $h_i\left(R_{i-1}\right)\oplus I_i$ and, as a vector space, $R_{i-1}$ is isomorphic to the factor space $R_i/I_i$.

The Newtonian degree assigns a gradation to $R_i$. By specifying in the Definition 18 the multiplication of the elements of $R_i$, we have introduced the structure of a graded $\mathbb{K}$-algebra on $R_i$. The graded algebra $R_i$ for $i=N$ coincides with the associated graded ring $\mathbb{A}\left(\mathsf{\Gamma }\right)$.

In the proposition and proof of the following assertion, the number $i>1$ will be fixed and, to simplify the formulas, $h_i,{\pi }_i$ will be denoted as h and $\pi$, respectively.

Proposition 27.

(a) The $\mathbb{K}$-algebra $R_i$ is finitely generated by the monomials corresponding to the vertices of the faces ${\Delta }_1,{\Delta }_2,\dots ,{\Delta }_i$ and by the monomials corresponding to the elements of the sets $Bs{h}_1,Bs{h}_2,\dots ,Bs{h}_i$; (b) The vector space $I_i$ is a subalgebra of $R_i$; (c) The subalgebra $I_i$ is an ideal in $R_i$; (d) For $i>1$, for any monomials $x^p$ and $x^q$ from $R_{i-1}$, the following identity holds:

$$h\left(x^p{\circ }_{i-1}{x}^q\right)=h\left(x^p\right){\circ }_{i}h\left(x^q\right)+r,\mathit{where}r\in I_i$$

(80)

(e) The quotient algebra $R_i/I_i$ is isomorphic to $R_{i-1}$.

Proof. 

(a) follows from the Proposition 14; (b),(c) obviously follow from Proposition 26, which defines the operation of multiplication in $R_i$.

Prove (d). Let $p,q$ be two points in $(As{h}_1\cup As{h}_2\cup \dots \cup As{h}_{i-1})$. Consider monomials $x^p$ and $x^q$ in $R_{i-1}$. We must find correcting term $r\in I_i$ that ensures that the identity (80) holds. The points $p,q$ satisfy one of three mutually exclusive conditions.

(1)

Points $p,q$ simultaneously belong to one of the cones

$Cone\left({\Delta }_1\right),Cone\left({\Delta }_2\right),\dots ,Cone\left({\Delta }_{i-1}\right)$. In this case, according to the Definition 18,

$h\left(x^p{\circ }_{i-1}{x}^q\right)=h\left(x^p\right){\circ }_{i}h\left(x^q\right)$ and equality (80) holds for $r=0$.

(2)

The points $p,q$ do not simultaneously lie in any of the cones

$Cone\left({\Delta }_1\right),Cone\left({\Delta }_2\right),\dots ,Cone\left({\Delta }_i\right)$. In this case, according to Definition 18,

$x^p{\circ }_{i-1}{x}^q=0$ and $h\left(x^p\right){\circ }_{i}h\left(x^q\right)=0$ and again equality (80) holds for $r=0$. It remains to analyze the last case.

(3)

The points $p,q$ do not simultaneously lie in any of the cones

$Cone\left({\Delta }_1\right),Cone\left({\Delta }_2\right),\dots ,Cone\left({\Delta }_{i-1}\right)$, i.e., $x^p{\circ }_{i-1}{x}^q=0$, but both lie in the cone $Cone\left({\Delta }_i\right)$, that is, $h\left(x^p\right){\circ }_{i}h\left(x^q\right)\ne 0$. Let us prove that in this case $(p+q)\in As{h}_i$, and hence $h\left(x^p\right){\circ }_{i}h\left(x^q\right)=x^{(p+q)}\in I_i$ and the equality (80) holds for $r=x^{(p+q)}$.

Indeed, let $\delta \in {\Delta }_i$ be one of the subfacets of codimension 1 of facet ${\Delta }_i$ such that $\delta \subset ({\Delta }_1\cup {\Delta }_2\cup \dots \cup {\Delta }_{i-1})$. Let c be a local coordinate function on the cone $Cone\left({\Delta }_i\right)$ that vanishes on the face $\delta$. The points p and q cannot simultaneously lie in the cone of $\delta$, since in this case, they would simultaneously lie in one of the cones $Cone\left({\Delta }_1\right),Cone\left({\Delta }_2\right),\dots ,Cone\left({\Delta }_{i-1}\right)$, which would contradict the original assumption of case 3). This means that one of the numbers $c\left(p\right)$ and $c\left(q\right)$ is positive, and hence, the number $c(p+q)=c\left(p\right)+c\left(q\right)$ is also positive. This reasoning is applicable to any subfacet of dimension one of facets ${\Delta }_i$ that can be represented as intersection of facet ${\Delta }_i$ with one of the faces ${\Delta }_1,{\Delta }_2,\dots ,{\Delta }_{i-1}$. According to the definition of the set $As{h}_i$, this means that $p+q\in As{h}_i$, which completes the proof of the Equality (80).

Let us prove (e). Since $ker\left(\pi \right)=I_i$, it suffices to prove that $\pi :R_i\to R_{i-1}$ is a ring homomorphism. Since $R_i$ is a direct sum $h\left(R_{i-1}\right)\oplus I_i$, any two monomials $A,B$ in $R_i$ can be represented as $A=h\left(a\right)+u,B=h\left(b\right)+v$, where the monomials $a,b$ belong to $R_{i-1}$ and $u,v$ belong to $I_i$. That is why

$$\pi (A\circ B)=\pi \left(h\left(a\right){\circ }_{i}h\left(b\right)\right)+\pi (h\left(a\right){\circ }_{i}v+h\left(b\right){\circ }_{i}u+u{\circ }_{i}v)=\pi \left(h\left(a\right){\circ }_{i}h\left(b\right)\right)$$

According to the Equality (80),

$$\pi \left(h\left(a\right){\circ }_{i}h\left(b\right)\right)=\pi \left(h\left(a{\circ }_{i-1}b\right)\right)-r)=a{\circ }_{i-1}b=\pi \left(A\right){\circ }_{i-1}\pi \left(B\right),\mathrm{where}r\in I_i.$$

We have proven that $\pi \left(A{\circ }_{i}B\right)=\pi \left(A\right){\circ }_{i-1}\pi \left(B\right)$, that is, we have proven that $\pi$ is a ring homomorphism. □

7. Cohen–Macaulayness of Algebra $\mathbb{A}\left(\mathsf{\Gamma }\right)$

In this section, we construct a regular sequence of d homogeneous elements of the ring $\mathbb{A}\left(\mathsf{\Gamma }\right)$, representable as linear combinations of monomials corresponding to the vertices of $\mathsf{\Gamma }$, and present a monomial basis for the quotient algebra of the ring $\mathbb{A}\left(\mathsf{\Gamma }\right)$ by the ideal generated by the elements of this sequence. This basis consists of equivalence classes of monomials whose exponents belong to the set ${\mathbb{B}}^{sh}=Bs{h}_1\cup Bs{h}_2\cup \dots \cup Bs{h}_N$ constructed in Section 2.5. The cardinality of this monomial basis, according to 18 (ii), is equal to $\mu \left(\mathsf{\Gamma }\right)=d!\times Volume\left(\mathsf{\Gamma }\right)$.

7.1. Non-Degeneracy of Sequence Homogeneous Elements $f_1,f_2,f_3,\dots ,f_d$ of the Ring $\mathbb{A}\left(\mathsf{\Gamma }\right)$ Having Supports in $\mathsf{\Gamma }$. “Shelling” of Such a Sequence

Denote the vertices of the polytope $\mathsf{\Gamma }$ by $w_1,w_2,\dots ,w_L$ and consider the sequence $f_1,f_2,f_3,\dots ,f_d$ of elements of the ring $\mathbb{A}\left(\mathsf{\Gamma }\right)$ given by the formulas:

$$\left\{\begin{array}{cc}\hfill f_1=& c_{11}{x}^{w_1}+c_{12}{x}^{w_2}+c_{13}{x}^{w_3}+\dots +c_{1L}{x}^{w_L}\hfill \\ \hfill f_2=& c_{21}{x}^{w_1}+c_{22}{x}^{w_2}+c_{23}{x}^{w_3}+\dots +c_{2L}{x}^{w_L}\hfill \\ \hfill f_3=& c_{31}{x}^{w_1}+c_{32}{x}^{w_2}+c_{33}{x}^{w_3}+\dots +c_{2L}{x}^{w_L}\hfill \\ \hfill \dots \\ \hfill f_d=& c_{d1}{x}^{w_1}+c_{d2}{x}^{w_2}+c_{d3}{x}^{w_2}+\dots +c_{dL}{x}^{w_L}\hfill \end{array}\right.$$

(81)

The coefficients of these elements form a $d\times L$ matrix C over $\mathbb{K}$. Each vertex of $\mathsf{\Gamma }$ corresponds to a column of the matrix C, and each facet corresponds to $d\times d$ minor.

Definition 19.

We call a sequence $f_1,f_2,f_3,\dots ,f_d$ nondegenerate if all $d\times d$ minors of the matrix C corresponding to the facets of Γ are nonzero.

The existence of non-degenerate sequences can be easily deduced from the infinity of the field $\mathbb{K}$. Using the assumption that the characteristic of the field $\mathbb{K}$ is zero, it is easy to present one non-degenerate sequence explicitly.

Example of a non-degenerate sequence.

Let us start with the sum of monomials of all vertices Γ

$$f=x^{w_1}+x^{w_2}+x^{w_3}+\dots +x^{w_L}$$

and take the sequence of “toric” partial derivatives f:

$$f_1=x_1\partial f/\partial x_1,f_2=x_2\partial f/\partial x_2,\dots ,f_d=x_d\partial f/\partial x_d$$

(82)

It is easy to see that the sequence (82) is non-degenerate. Indeed, for such a sequence, the matrix C will consist of the column vectors of the coordinates of the vertices of the polytope Γ. Therefore, the minor corresponding to a facet of Γ is equal to the determinant of the $d\times d$-matrix composed of facet’s vertices. Moreover, due to the super-convenience of the Γ polytope, this determinant does not vanish for any facet of Γ.

For $i\in [1,N]$, we construct “constraints”$f_1^{\left(i\right)},f_2^{\left(i\right)},f_3^{\left(i\right)},\dots ,f_d^{\left(i\right)}$ of elements $f_1,f_2,\dots ,f_d$ onto the $\mathbb{K}$-algebra $R_i$. To obtain a set of functions $f_1^{\left(i\right)},f_2^{\left(i\right)},\dots ,f_d^{\left(i\right)}$ from the set of functions $f_1,f_2,\dots ,f_d$, you need in each line of (81) leave only the terms with monomials corresponding to the vertices of $\mathsf{\Gamma }$ lying in the union of facets ${\Delta }_1\cup {\Delta }_2\cup \dots \cup {\Delta }_i$. Denote by $C^{\left(i\right)}$ the matrix corresponding to the sequence $f_1^{\left(i\right)},f_2^{\left(i\right)},\dots ,f_d^{\left(i\right)}$. In the sequence $f_1^{\left(i\right)},f_2^{\left(i\right)},f_3^{\left(i\right)},\dots ,f_d^{\left(i\right)}$ elements of the ring $R_i$ all minors of the matrix $C^{\left(i\right)}$ corresponding to facets ${\Delta }_1,{\Delta }_2,\dots ,{\Delta }_i$ will be non-zero.

Proposition 28.

Suppose $i\in [1,N]$ and $w_1,w_2,\dots ,w_d$ are vertices of the facet ${\Delta }_i$. Then: (a) There exist linear combinations

${\theta }_1^{\left(i\right)},{\theta }_2^{\left(i\right)},\dots ,{\theta }_d^{\left(i\right)}$ of elements $f_1^{\left(i\right)},f_2^{\left(i\right)},f_3^{\left(i\right)},\dots ,f_d^{\left(i\right)}$ such that each monomial $x_j^w$, where $j\in [1,d]$ occurs with nonzero coefficient only into the combination ${\theta }_j^{\left(i\right)}$;

(b) 

Subalgebras $\mathbb{K}[f_1^{\left(i\right)},f_2^{\left(i\right)},\dots ,f_d^{\left(i\right)}]$ and $\mathbb{K}[{\theta }_1^{\left(i\right)},{\theta }_2^{\left(i\right)},\dots ,{\theta }_d^{\left(i\right)}]$ of $R_i$ are identical.

The proof follows from the non-degeneracy of the sequence $f_1,f_2,f_3,\dots ,f_d$. When using Proposition 28, we will assume that the monomial $x_j^w$ is included in ${\theta }_j^{\left(i\right)}$ with coefficient 1.

Remark 4.

Elements $f_1,f_2,f_3,\dots ,f_d$, $f_1^{\left(i\right)},f_2^{\left(i\right)},f_3^{\left(i\right)},\dots ,f_d^{\left(i\right)}$ and their linear combinations will sometimes be called functions.

7.2. Formulation of the Main Technical Result of This Article

Let us now formulate the main technical result of this article, related to the graded algebra $\mathbb{A}\left(\mathsf{\Gamma }\right)$.

Theorem 4.

Let $f_1,f_2,\dots ,f_d$ be a sequence of functions in $\mathbb{A}\left(\mathsf{\Gamma }\right)$ that is non-degenerate in the sense of Definition 19. For $i\in [1,N]$, let us denote

$$X_i=\mathbb{K}[f_1^{\left(i\right)},f_2^{\left(i\right)},\dots ,f_d^{\left(i\right)}]\subset R_i$$

Then,

(A) 

For any $i\in [1,N]$, the equivalence classes of monomials with exponents running through the set $Bs{h}_1\cup Bs{h}_2\cup \dots \cup Bs{h}_i$ generate $R_i$ as a module over $X_i$;

(B) 

The sequence $f_1,f_2,\dots ,f_d$ is regular and hence, $\mathbb{A}\left(\mathsf{\Gamma }\right)$ is a Cohen–Macaulay ring;

(C) 

The equivalence classes of monomials with exponents running through the set

$${\mathbb{B}}^{sh}=(Bs{h}_1\cup Bs{h}_2\cup \dots \cup Bs{h}_N)$$

form a basis of $\mathbb{A}\left(\mathsf{\Gamma }\right)/(f_1,f_2,\dots ,f_d)$, hence, the codimension of the ideal I is equal to $\mu \left(\mathsf{\Gamma }\right)=d!\times Volume\left(\mathsf{\Gamma }\right)$.

Assertion (A) will be proved below by induction on i. This proof is the central argument of this article. It generalizes the proof given in [9] and rewritten in [10].

We will now deduce conclusions (B) and (C) of Theorem 4 from conclusion (A) of this theorem. To do this, we use the well-known method of element-by-element comparison of Poincaré series, described, for example, in [10]. We will formalize this reasoning in the form of Proposition 29. The assumption of this Proposition is the conclusion (A) of Theorem 4, and conclusions (1), (2) and (3) of this Proposition imply conclusions (B) and (C) of Theorem 4.

7.3. Derivation of Conclusions (B) and (C) of Theorem 4 from Conclusion (A) of This Theorem

Proposition 29.

Let $f_1,f_2,\dots ,f_d$ be a sequence of homogeneous elements of degree M in the ring $\mathbb{A}\left(\mathsf{\Gamma }\right)$. Denote by I and X the ideal and subalgebra generated by these functions. If monomials with exponents running through the set ${\mathbb{B}}^{sh}=(Bs{h}_1\cup Bs{h}_2\cup \dots \cup Bs{h}_N)$ generate $\mathbb{A}\left(\mathsf{\Gamma }\right)$ as a module over X, then:

(1) 

The equivalence classes of these monomials form a basis of the quotient algebra $\mathbb{A}\left(\mathsf{\Gamma }\right)/I$ and the codimension of I is equal to $d!\times Volume\left(\mathsf{\Gamma }\right)$;

(2) 

These monomials freely generate $\mathbb{A}\left(\mathsf{\Gamma }\right)$ as a module over X;

(3) 

The sequence $f_1,f_2,\dots ,f_d$ of elements of algebra $\mathbb{A}\left(\mathsf{\Gamma }\right)$ is regular.

Proof. 

Let us denote $\mu \left(\mathsf{\Gamma }\right)$ by $\mu$ for brevity. The cardinality of the set ${\mathbb{B}}^{sh}=(Bs{h}_1\cup Bs{h}_2\cup \dots \cup Bs{h}_N)$ is equal to $\mu$. Let $m_1,m_2,\dots ,m_{\mu }$ be the set of monomials in $\mathbb{A}\left(\mathsf{\Gamma }\right)$ corresponding to points in the set ${\mathbb{B}}^{sh}$. Denote by ${\mathbb{B}}_{\mathbb{K}}^{sh}$ the finite-dimensional vector space generated by these monomials, endowed with a Newtonian grading. Denote by $Q\left(t\right)$ Poincaré series $H({\mathbb{B}}_{\mathbb{K}}^{sh},t)$ of this graded vector space. Let us prove that the equivalence classes of monomials $m_1,m_2,\dots ,m_{\mu }$ generate the quotient algebra $\mathbb{A}\left(\mathsf{\Gamma }\right)/I$ over the field $\mathbb{K}$. Since it is given that the monomials corresponding to the elements of this set generate $\mathbb{A}\left(\mathsf{\Gamma }\right)$ as a module over the subalgebra X, an arbitrary element $G\in \mathbb{A}\left(\mathsf{\Gamma }\right)$ can be represented as

$$G=\sum _{i=1}^{\mu }{S}_i(f_1,f_2,\dots ,f_d)m_i,\mathrm{where}{S}_i\in \mathbb{K}[x_1,x_2,\dots ,x_d]$$

(83)

By $s_i\in \mathbb{K}$, denote the constant term of the polynomial $S_i$ and rewrite (83) as

$$G=\sum _{i=1}^{\mu }{s}_i{m}_i+\sum _{i=1}^{\mu }(S_i(f_1,f_2,\dots ,f_d)-s_i)m_i$$

(84)

Since each difference $S_i(f_1,f_2,\dots ,f_d)-s_i$ belongs to the ideal I, the second sum in (84) belongs to the ideal I. Hence, the equivalence classes of monomials $m_1,m_2,\dots ,m_{\mu }$ generate the quotient algebra $\mathbb{A}\left(\mathsf{\Gamma }\right)/I$. Therefore, the following element-by-element inequality between Poincaré series holds

$$Q\left(t\right)\ge H(\mathbb{A}\left(\mathsf{\Gamma }\right)/(f_1,f_2,f_3,\dots ,f_d),t)$$

(85)

According to the Formula (69) of Section 4.1, the successive factorization of $\mathbb{A}\left(\mathsf{\Gamma }\right)$ over the elements of $f_1,f_2,\dots ,f_d$ yields the inequality

$$H(\mathbb{A}\left(\mathsf{\Gamma }\right),t)\le \frac{H(\mathbb{A}\left(\mathsf{\Gamma }\right)/(f_1,f_2,\dots ,f_d),t)}{{(1-t^M)}^d}$$

(86)

According to Formula (66) and Proposition 20, the Poincaré series of the $\mathbb{K}$-algebra $\mathbb{A}\left(\mathsf{\Gamma }\right)$ is equal to

$$H(\mathbb{A}\left(\mathsf{\Gamma }\right),t)=\frac{Q\left(t\right)}{{(1-t^M)}^d}$$

(87)

where $Q\left(t\right)$ is the Poincaré series of the finite-dimensional vector space ${\mathbb{B}}_K^{sh}$ generated by monomials whose exponents belong to the set ${\mathbb{B}}^{sh}=(Bs{h}_{1}cupBs{h}_2\dots \cup Bs{h}_N$). Substituting (87) into LHS of (86), we obtain

$$\frac{Q\left(t\right)}{{(1-t^M)}^d}\le \frac{H(\mathbb{A}\left(\mathsf{\Gamma }\right)/(f_1,f_2,\dots ,f_d),t)}{{(1-t^M)}^d}$$

(88)

Multiplying the element-wise inequality (85) by a series with non-negative coefficients $\frac{1}{{(1-t^M)}^d}$ and a positive constant term, we obtain

$$\frac{Q\left(t\right)}{{(1-t^M)}^d}\ge \frac{H(\mathbb{A}\left(\mathsf{\Gamma }\right)/(f_1,f_2,\dots ,f_d),t)}{{(1-t^M)}^d}$$

(89)

From (88) and (89), it follows that

$$\frac{Q\left(t\right)}{{(1-t^M)}^d}=\frac{H(\mathbb{A}\left(\mathsf{\Gamma }\right)/(f_1,f_2,\dots ,f_d)}{{(1-t^M)}^d}$$

(90)

hence

$$Q\left(t\right)=H(\mathbb{A}\left(\mathsf{\Gamma }\right)/(f_1,f_2,\dots ,f_d),t)$$

(91)

hence, the set of monomials of the form $x^b$, where $b\in {\mathbb{B}}^{sh}=(Bs{h}_1\cup Bs{h}_2\cup \dots \cup Bs{h}_N$) form a basis of the quotient algebra $\mathbb{A}\left(\mathsf{\Gamma }\right)/(f_1,f_2,\dots ,f_d)$, which proves 29 (1). By Theorem 3 Proposition 29 (1) implies 29 (2) and 29 (3). □

7.4. Proof of Theorem 4 (A)

Definition 20.

A monomial $m\in R_i$ is called representable in $R_i$ if m belongs to an $X_i$-submodule generated in $R_i$ by monomials with exponents running through ${\mathbb{B}}^{sh}=(Bs{h}_1\cup Bs{h}_2\cup \dots \cup Bs{h}_i$).

To prove the assertion (A) of Theorem 4, it suffices to establish that any monomial in $R_i$ is representable. We start by proving two auxiliary assertions.

Proposition 30.

Let v be a vertex of some of facets ${\Delta }_1,{\Delta }_2,\dots ,{\Delta }_i$. Then, for any $b\in Bs{h}_i$, the product $x^v{\circ }_i{x}^b$ is representable in $R_i$.

Proof of Proposition 30 in the case when $\mathit{v}\notin {\Delta }_{\mathit{i}}$.

For $i>1$, the points of the set $Bs{h}_i$ by construction do not belong to

$$Cone\left({\Delta }_1\right)\cup Cone\left({\Delta }_2\right)\cup \dots \cup Cone\left({\Delta }_{i-1}\right)$$

Therefore, if the vertex v does not belong to the face ${\Delta }_i$, then the points v and b cannot be homoconical and, by the definition of the operation of multiplication in $R_i$, the product $x^v{\circ }_i{x}^b$ is equal to 0. □

Proof of the statement 30 in the case when $\mathit{v}\in {\Delta }_{\mathit{i}}$.

If the vertex v belongs to the face ${\Delta }_i$, then according to Proposition 28, there exists a linear combination $\theta$ of functions $f_1^{\left(i\right)},f_2^{\left(i\right)},f_3^{\left(i\right)},\dots ,f_d^{\left(i\right)}$ which has the form

$$\theta =x^v+\sum _{w\notin {\Delta }_i}{f}_w{x}^w$$

(92)

Multiply the equality (92) in $R_i$ by $x^b$, where $bis\in Bs{h}_i$. According to the previous case, for each $w\notin {\Delta }_i$, the product $f_w\left(x^w{\circ }_i{x}^b\right)$ is equal to 0 and we obtain $\theta {\circ }_i{x}^b=x^v{\circ }_i{x}^b$, which means that the product $x^v{\circ }_i{x}^b$ is representable since $\theta \in X_i$. □

Proposition 31.

Let $v_1,v_2,\dots ,v_l$ be a sequence (possibly with repetitions) of vertices of facet ${\Delta }_i$ and $b\in Bs{h}_i$. Then, for $l\ge 1$, the product

$$x^{v_1}{\circ }_i{x}^{v_2}{\circ }_i\dots {\circ }_i{x}^{v_l}{\circ }_i{x}^b$$

(93)

is representable in $R_i$.

Proof. 

According to Proposition 28(i) for each vertex $v\in {\Delta }_i$ there exist a linear combination $\theta$ of functions $f_1^{\left(i\right)},f_2^{\left(i\right)},f_3^{\left(i\right)},\dots ,f_d^{\left(i\right)}$ such that

$$\theta =x^v+r,\mathrm{where}r=\sum _{w\notin {\Delta }_i}{f}_w{x}^w$$

(94)

Let us construct such a representation for each vertex of the product (93)

$$\begin{array}{cc}\hfill & {\theta }_1=x_1^v+r_1\hfill \\ \hfill & {\theta }_2=x_2^v+r_2\hfill \\ \hfill & \dots \hfill \\ \hfill & {\theta }_l=x_l^v+r_l\hfill \end{array}$$

Let us prove by induction a somewhat more precise assertion

$$(x^{v_1}{x}^{v_2}\dots x^{v_l})x^b=({\theta }_1{\theta }_2\dots {\theta }_l)x^b$$

(95)

□

Base case in the proof of the Formula (95). The case $l=1$, that is, the representability of the product $x^{v_1}{x}^b$ as a product $\theta x^b$, is analyzed in the proof of the Statement 30.

Induction step $(\mathit{l}-\mathit{1})\to \mathit{l}$ in the proof of the Formula (95). By the inductive hypothesis,

$$(x^{v_1}{x}^{v_2}\dots x^{v_{l-1}})x^b=({\theta }_1{\theta }_2\dots {\theta }_{l-1})x^b$$

Hence,

$$\begin{array}{c}\hfill (x^{v_1}{x}^{v_2}\dots x^{v_{l-1}})x^{v_l}{x}^b=\\ \hfill x^{v_l}(x^{v_1}{x}^{v_2}\dots x^{v_{l-1}})x^b=\\ \hfill x^{v_l}({\theta }_1{\theta }_2\dots {\theta }_{l-1})x^b=\\ \hfill ({\theta }_1{\theta }_2\dots {\theta }_{l-1})x^{v_l}{x}^b=\\ \hfill ({\theta }_1{\theta }_2\dots {\theta }_l)x^b\end{array}$$

Proposition 32.

Any element $x^a,\mathrm{where}a\in As{h}_i$ is representable.

Proof. 

According to Proposition 16, the element $x^a$ can be represented as $x^a=x^v{x}^b$, where $v\in V\left({\Delta }_i\right)$ and $b\in Bs{h}_i$. It remains to apply Proposition 31. □

Proof of Theorem 4(A)

(Induction on i

Base case. For $i=1$, $R_1=A\left({\Delta }_1\right)$, $Bs{h}_1=B\left({\Delta }_1\right)$, $X_1=V\left({\Delta }_1\right)$ and the monomials of $B\left({\Delta }_1\right)$ generate $A({\Delta }_1$) as a $V\left({\Delta }_1\right)$-module according to 9.

Induction step $(i-1)\to i$ when the set of vertices does not increase. Let us use the notation of Section 6.1. In this notation, the representation as a linear combination of monomials for the functions $f_1^{\left(i\right)},f_2^{\left(i\right)},f_3^{\left(i\right)},\dots ,f_d^{\left(i\right)}$ is the same as representation for functions $h_i\left(f_1^{(i-1)}\right),h_i\left(f_2^{(i-1)}\right),h_i\left(f_3^{(i-1)}\right),\dots ,h_i(f_d^{(i-1)}$). Let us represent $R_i$ as $h_i\left(R_{i-1}\right)\oplus I_i$. We must show that each element of $R_i$ is representable. The basic elements of $I_i$ are of the form $x^a$, where $ais\in As{h}_i$. Such elements are representable according to Statement 32. Find a representation for any element $h_i\left(e\right)\in h_i\left(R_{i-1}\right)$. By the induction hypothesis, any element of $e\in R_{i-1}$ can be represented as a sum of products of the form $f_b{x}^b$, where $f_b\in X_{i-1},b\in Bs{h}_1\cup Bs{h}_2\cup \dots \cup Bs{h}_{i-1}$. From the equality (80) and the fact that $I_i$ is an ideal, it follows that for any elements p and q of $R_{i-1}$, the following equality holds

$$h\left(p{\circ }_{i-1}q\right)=h\left(p\right){\circ }_{i}h\left(q\right)+r,\mathrm{where}r\in I_i$$

From this, it is easily deduced that for any polynomial P in several variables and any elements $a_1,a_2,\dots ,a_j$ of the ring $R_{i-1}$ the relation

$$h_i(P(a_1,a_2,\dots ,a_j)=P(h_i\left(a_1\right),h_i\left(a_2\right),\dots ,h_i\left(a_j\right))+r,\mathrm{where}r\in I_i$$

holds. Applying this relation to each product $f_b{x}^b$, we obtain that the element $h\left(e\right)$ belongs to $I_i$ and, therefore, is representable according to the Statement 32.

Induction step $(i-1)\to i$ in the case when the set of vertices increases by one. In this case, the new facet ${\Delta }_i$ contains $d-1$ old vertex and one new vertex, say w. Monomials in $R_i$ can be divided into old monomials belonging to $h_i\left(R_{i-1}\right)$ and new monomials corresponding to $As{h}_i$ points. The new monomials are representable according to the Statement 31. For old monomials, the result of multiplication in $R_i$ coincides with multiplication in $R_{i-1}$, more precisely, in contrast to the previous case, the embedding of $\mathbb{K}$-vector spaces $h_i:R_{i-1}\to R_i$ is a ring homomorphism. The only thing left to prove is the fact that the old monomials representable in $R_{i-1}$ remain representable in $R_i$ despite the change in functions. Each new function $f_1^{\left(i\right)},f_2^{\left(i\right)},f_3^{\left(i\right)},\dots ,f_d^{\left(i\right)}$ is obtained from the corresponding old function by adding the monomial w with some coefficient. Let us label the old and new functions as ${\theta }_1^{\prime },{\theta }_2^{\prime },\dots ,{\theta }_d^{\prime }$ and ${\theta }_1,{\theta }_2,\dots ,{\theta }_d$, respectively. Then, for some constants ${\lambda }_1,{\lambda }_2,\dots ,{\lambda }_d$

$$\begin{array}{cc}\hfill & {\theta }_1^{\prime }={\theta }_1-{\lambda }_1{x}^w\hfill \\ \hfill & {\theta }_2^{\prime }={\theta }_2-{\lambda }_2{x}^w\hfill \\ \hfill & \dots \hfill \\ \hfill & {\theta }_d^{\prime }={\theta }_d-{\lambda }_d{x}^w\hfill \end{array}$$

(96)

By the induction hypothesis, each monomial $m\in R_{i-1}$ can be represented as

$$m=\sum _{b\in Bsh1\cup Bs{h}_2\cup \dots \cup Bs{h}_{i-1}}{P}_b({\theta }_1^{\prime },{\theta }_2^{\prime },\dots ,{\theta }_d^{\prime })x^b$$

(97)

It suffices to prove the representability of each term of the sum (97). We choose one term of the sum, make the substitution (96), and expand the result of the substitution in powers of $x^w$:

$$\begin{array}{cc}\hfill & P_b({\theta }_1-{\lambda }_1{x}^w,{\theta }_2-{\lambda }_2{x}^w,\dots ,{\theta }_d-{\lambda }_d{x}^w)x^b=\hfill \\ \hfill & S_0({\theta }_1,{\theta }_2,\dots ,{\theta }_d)x^b+\hfill \\ \hfill & S_1({\theta }_1,{\theta }_2,\dots ,{\theta }_d)x^w{x}^b+\hfill \\ \hfill & S_2({\theta }_1,{\theta }_2,\dots ,{\theta }_d){\left(x^w\right)}^2{x}^b+\hfill \\ \hfill & S_2({\theta }_1,{\theta }_2,\dots ,{\theta }_d){\left(x^w\right)}^3{x}^b+\hfill \\ \hfill & \dots \hfill \end{array}$$

(98)

The member with $S_0$ is representable by definition. To prove the representability of the remaining terms, it suffices to prove the representability of the products

$$x^w{x}^b,{\left(x^w\right)}^2{x}^b,{\left(x^w\right)}^3{x}^b,\dots$$

Note that the new vertex w does not belong to the cones $Cone\left({\Delta }_1\right),Cone\left({\Delta }_2\right),\dots Cone\left({\Delta }_{i-1}\right)$. Hence, if $b\notin Cone\left({\Delta }_i\right)$, then the products $x^w{x}^b,{\left(x^w\right)}^2{x}^b,\dots$ are equal to zero by the definition of multiplication in $R_i$.

If $b\in Cone\left({\Delta }_i\right)$, then these products belong to the new cone $Cone\left({\Delta }_i\right)$, but do not belong to the intersection of this cone with the old cones $Cone\left({\Delta }_1\right),Cone\left({\Delta }_2\right),\dots Cone\left({\Delta }_{i-1}\right)$. This means that these products belong to $As{h}_i$ and are therefore representable according to Proposition 32. The proof of conclusion (A) of Theorem 4 is complete. □

8. Main Theorem

The proofs in this section are of a routine nature and largely repeat the arguments both given and omitted in my 1976 paper [4], published in French. These proofs were never published in Russian or English.

The proofs below use the regularity of the sequence of elements of the algebra $\mathbb{A}$ given by explicit Formula (82) and the corollaries following from it by Theorem 3.

Let us formulate the main theorem without omitting details.

8.1. Verbose Formulation of the Main Theorem

Theorem 5. (Main Theorem).

We fix the following objects:

• Super-convenient convex integer simplicial polytope $\mathsf{\Gamma }\subset {\mathbb{R}}^d$;
• The number $\mu \left(\mathsf{\Gamma }\right)=d!\times Volume\left(\mathsf{\Gamma }\right)$ defined by this polytope;
• Field $\mathbb{K}$ of characteristic 0;
• An exhaustive increasing Newton $\mathbb{N}$-filtration of $\mathbb{K}$-algebra $\mathbb{K}\left[{\mathbb{Z}}^d\right]$; this $\mathbb{K}$-algebra will be denoted for brevity by A:

  $$A=\bigcup _{0\le i}{A}_i\mathrm{where}\mathbb{K}=A_0\subset A_1\subset A_2\subset \dots$$
• Natural number M defined by the condition that the monomials corresponding to the vertices of Γ belong to $A_M\backslash A_{M-1}$;
• An exhaustive increasing $\mathbb{N}$-filtration of free A-module $A^d$ formed by tuples of d elements of the algebra A, defined by the relations

  $${\left(A^d\right)}_0={\left(A^d\right)}_1=\dots ={\left(A^d\right)}_{M-1}=0;\mathrm{for}k\ge M{\left(A^d\right)}_k={\left(A_{k-M}\right)}^d$$
• The $\mathbb{N}$-graded algebra $gr\left(\mathbb{K}\left[{\mathbb{Z}}^d\right]\right)$ associated with the Newton filtration, denoted for brevity by $\mathbb{A}$;
• $\mathbb{N}$-grading of the free module ${\mathbb{A}}^d$ formed by tuples of d elements of the algebra $\mathbb{A}$, defined by the relations

  $${\left({\mathbb{A}}^d\right)}_0={\left({\mathbb{A}}^d\right)}_1=\dots ={\left({\mathbb{A}}^d\right)}_{M-1}=0;\mathrm{for}k\ge M{\left({\mathbb{A}}^d\right)}_k={\left({\mathbb{A}}_{k-M}\right)}^d$$
• Definition of the Newtonian degree of an element $g\in A$, well defined since Newtons filtering is exhaustive:

  $$\begin{array}{cc}\hfill \mathit{for}\mathit{non}-\mathit{null}\mathit{element}deg\left(g\right)& =min\{n:g\in A_n\}\hfill \\ \hfill \mathit{for}\mathit{element}\mathit{zero}deg\left(0\right)& =-\infty \hfill \end{array}$$
• Definition of leading_term (aka boundary_term) of a nonzero element $v\in A$ of the filtered algebra, this leading_term is denoted by $\widehat{v}$, belongs to ${\mathbb{A}}_k$, where $k=deg\left(v\right)$, and is defined by the formula

  $$\widehat{v}=v+A_{k-1}\in A_k/A_{k-1}={\mathbb{A}}_k,$$
• Shelling $sh$ of polytope Γ;
• Finite set constructed from the super-convenient simplicial polytope Γ and its shelling $sh$

  $${\mathbb{B}}^{sh}=\{b_1,b_2,\dots ,b_{\mu \left(\mathsf{\Gamma }\right)}\}\subset {\mathbb{Z}}^d,$$
  containing all points of Newtonian degree less M and not containing points of Newtonian degree higher than $dM$;
• The set of monomials in the filtered algebra $\mathbb{K}\left[{\mathbb{Z}}^d\right]$ consisting of the elements

  $$m_1=x^{b_1}=x^0,m_2=x^{b_2},\dots ,m_{\mu }=x^{b_{\mu }},$$
• The set of monomials in the graded algebra $\mathbb{A}$, consisting of the elements

  $${\widehat{m}}_1,{\widehat{m}}_2,\dots ,{\widehat{m}}_{\mu },$$
• Finite-dimensional vector space $W\subset A^d$ of d-tuples of Laurent polynomials whose supports belong to the polytope Γ;
• Finite-dimensional vector space $\mathbb{W}\subset {\mathbb{A}}^d$ of d-tuples of Laurent polynomials whose supports belong to the boundary $\partial \mathsf{\Gamma }$ of the polytope Γ;
• Linear mappingLeading_term:$W\to \mathbb{W}$ (aka Boundary_term) of finite-dimensional vector spaces, which deletes from each component of the tuple of Laurent polynomials the monomials corresponding to the interior points of the polytope Γ, leaving only the terms of the Newtonian degree M corresponding to monomials with exponents lying on the boundary of the polytope Γ.

Then:

(main.a) There exists a Zariski-open non-empty subset $\mathcal{N}{\mathcal{S}}_{codim}\subset \mathbb{W}$ such that for any tuple of polynomials $[G_1,G_2,\dots ,G_d]\in \mathcal{N}{\mathcal{S}}_{codim}$ the ideal $(G_1,G_2,\dots ,G_d)\subset \mathbb{A}$ has finite codimension $\mu \left(\mathsf{\Gamma }\right)$ and moreover any element of $\mathbb{A}$ of degree greater than $dM$ belongs to the ideal $(G_1,G_2,\dots ,G_d)$;

(main.b) For any tuple of polynomials $[g_1,g_2,\dots ,g_d]\in W$ such that $\mathit{Leading}\_\mathit{terms}\left([g_1,g_2,\dots ,g_d]\right)\in \mathcal{N}{\mathcal{S}}_{codim}$, where $\mathcal{N}{\mathcal{S}}_{codim}$ is defined in (main.a), it is true that the codimension of ideal $(g_1,g_2,\dots ,g_d)\subset \mathbb{K}\left[Z^d\right]$ is finite and equals to $\mu \left(\mathsf{\Gamma }\right)$;

(main.c) There exists a Zariski open non-empty subset $\mathcal{N}{\mathcal{S}}_{basis}\subset \mathbb{W}$ such that for any tuple $[G_1,G_2,\dots ,G_d]\in \mathcal{N}{\mathcal{S}}_{basis}$ equivalence classes of monomials ${\widehat{m}}_1,{\widehat{m}}_2,\dots ,{\widehat{m}}_{\mu }$ form a basis over K of the factor algebra

$$\mathbb{K}\left[{\mathbb{Z}}^d\right]/(G_1,G_2,\dots ,G_d)$$

(main.d) For any tuple of polynomials $[g_1,g_2,\dots ,g_d]\in W\subset \mathbb{K}\left[Z^d\right]$ such that $\mathit{Leading}\_\mathit{terms}\left([g_1,g_2,\dots ,g_d]\right)\in \mathcal{N}{\mathcal{S}}_{basic}$, where $\mathcal{N}{\mathcal{S}}_{basic}$ is defined in (main.c), it is true that the ideal $(g_1,g_2,\dots ,g_d)$ has the codimension equal to $\mu \left(\mathsf{\Gamma }\right)$ and the equivalence classes of monomials $m_1,m_2,\dots ,m_{\mu }$ form a basis over $\mathbb{K}$ of the quotient algebra

$$\mathbb{K}\left[{\mathbb{Z}}^d\right]/(g_1,g_2,\dots ,g_d)$$

Remark 5.

The abbreviation $\mathcal{N}\mathcal{S}$ should be understood as N on S ingular.

Statements (main.b) and (main.d) can be reformulated and abbreviated using the term generic.

Theorem 6.

Let $\mathsf{\Gamma }\subset {\mathbb{R}}^d$ be a convex super-convenient integer simplicial polytope and $\mathbb{K}$ be a field of characteristic 0. Then:

(b’) For generic Laurent polynomials $g_1,g_2,\dots ,g_d$ whose supports belong to the polytope Γ, the codimension of the ideal $(g_1,g_2,\dots ,g_d)$, generated by these polynomials in the $\mathbb{K}$-algebra $\mathbb{K}\left[{\mathbb{Z}}^d\right]$ is equal to $d!\times Volume\left(\mathsf{\Gamma }\right)$;

(d’) For each shelling of a convex, super-convenient integer simplicial polytope Γ, a set of monomials $m_1,m_2,\dots ,m_{\mu }$ can be explicitly constructed, where $\mu =d!\times Volume\left(\mathsf{\Gamma }\right)$, such that for generic Laurent polynomials $g_1,g_2,\dots ,g_d$ whose supports belong to the polytope Γ, ideal $(g_1,g_2,\dots ,g_d)\subset \mathbb{K}\left[Z^d\right]$ has a finite codimension equal to $\mu \left(\mathsf{\Gamma }\right)$ and the equivalence classes of monomials $m_1,m_2,\dots ,m_{\mu }$ form a basis of the quotient algebra $\mathbb{K}\left[{\mathbb{Z}}^d\right]/(g_1,g_2,\dots ,g_d).$

8.1.1. Proof of Conclusion (Main.a)

Let us prove the conclusion (main.a) of Theorem 5. The homogeneous ideal $(G_1,G_2,\dots ,G_d)$ is the image of the mapping ${\mathbb{A}}^d\stackrel{d_1}{\to }\mathbb{A}$ given by the formula

$$d_1(H_1,H_2,\dots ,H_d)=(H_1{G}_1+H_2{G}_2+\dots +H_d{G}_d)$$

This mapping of infinite-dimensional vector spaces reduces to the family of mappings of finite-dimensional vector spaces

$${\left({\mathbb{A}}_{n-M}\right)}^d\stackrel{d_{1,n}}{\to }{\mathbb{A}}_n,\mathrm{where}n\ge M$$

In bases defined by monomials, each finite-dimensional mapping $d_{1,n}$ is given by its matrix, the coefficients of which depend linearly on the coefficients of Laurent polynomials $G_1,G_2,\dots ,G_d$ of Newtonian degree M; these coefficients form a finite-dimensional vector space, which we previously denoted by $\mathbb{W}$. The homogeneous component ${\mathbb{A}}_n$ of the algebra $\mathbb{A}$ belongs to the ideal if and only if the matrix of $d_1\left(n\right)$ has the maximum possible rank equal to $di{m}_{\mathbb{K}}\left({\mathbb{A}}_n\right)$. Therefore, the homogeneous ideal $(G_1,G_2,\dots ,G_d)$ has finite codimension if and only if for all $n\ge M$, except for a finite number, the matrix of $d_{1,n}$ has the highest possible rank.

Formula (82) explicitly defines a non-degenerate sequence, which is regular by the Theorem 4. According to (59) and (91), the Poincare series of the factor algebra generated by this regular sequence is a polynomial of degree $dM$. Thus, there is at least one point in the space $\mathbb{W}$ for which all subspaces ${\mathbb{A}}_n$, where $n>dM$ lie in the ideal $(G_1,G_2,\dots ,G_d)$. Therefore, all corresponding matrices have the maximum rank. Let us fix a number $n\in (dM,2dM]$. Let us denote by ${\mathcal{S}}_n\subset \mathbb{W}$ the set of such elements of the vector space $\mathbb{W}$ that ${\mathbb{A}}_n$ does not belongs to the ideal $(G_1,G_2,\dots ,G_d)$.

Elements of the matrix of linear mapping

$${\left({\mathbb{A}}_{n-M}\right)}^d\stackrel{d_1}{\to }{\mathbb{A}}_n$$

are polynomials in the coefficients of the polynomials $G_1,G_2,\dots ,G_d$. According to the well-known theorem of linear algebra, for the rank of a rectangular matrix to be nonmaximal, it is necessary and sufficient that all minors of this matrix of maximum dimension vanish. That is, it is necessary and sufficient to fulfill a finite number of algebraic conditions on the coefficients of the matrix. Applying this statement to the matrix of the mapping

$${\left({\mathbb{A}}_{n-M}\right)}^d\stackrel{d_1}{\to }{\mathbb{A}}_n$$

we obtain that ${\mathcal{S}}_n$ is a Zariski closed subset of $\mathbb{W}$. The complement to this subset is non-empty because it contains a point (82). Let us put

$$\begin{array}{cc}\hfill {\mathcal{S}}_{codim}& =\bigcup _{dM<n\le 2dM}{\mathcal{S}}_n\hfill \\ \hfill \mathcal{N}{\mathcal{S}}_{codim}& =\mathbb{W}\backslash {\mathcal{S}}_{codim}\hfill \end{array}$$

(99)

The Zariski open set $\mathcal{N}{\mathcal{S}}_{codim}$ is non-empty because it contains the point (82). Let us now prove that any tuple of polynomials from the set $\mathcal{N}{\mathcal{S}}_{codim}$ generate ideals of finite codimension. To do this, it suffices to prove that if $[G_1,G_2,\dots ,G_d]\in \mathcal{N}{\mathcal{S}}_{codim}$, then the ideal $(G_1,G_2,\dots ,G_d)$ contains all Newtonian monomials greater than $2dM$. To prove this, it suffices to prove that any such monomial is divisible by some monomial whose Newtonian degree lies in the range $(dM,2dM]$. By definition of $\mathcal{N}{\mathcal{S}}_{codim}$, any such monomial belongs to the ideal.

Proposition 33.

Any monomial in $\mathbb{A}$ of a Newtonian degree greater than $2dM$ is divisible by some monomial whose Newtonian degree lies in the range $(dM,2dM]$.

Proof. 

According to Proposition 16, any monomial $m\in \mathbb{A}$ can be represented as $m=b{w}_1{w}_2\dots w_k$, where the degree of the monomial b lies in the range $[0,dM]$, and all other monomials are of degree M. Since the degree of the monomial m is greater than $2dM$, the product $b{w}_1{w}_2\dots w_k$ does not reduce to the monomial b. Splitting off from the right end of this product groups of d monomials of degree M, i.e., successively decreasing the degree of the product by $dM$, we sooner or later obtain a product $b{w}_1{w}_2\dots w_l$ whose degree lies in the half-interval $(dM,2dM]$ of length $dM$, i.e., we obtain the decomposition

$$m=(b{w}_1{w}_2\dots w_l)(w_{l+1}\dots w_k)$$

in which the degree of the first factor lies in the required range $(dM,2dM]$.

The proof of Proposition 33 is complete. □

We can now complete the proof of assertions (main.a). Consider a tuple $[G_1,G_2,\dots ,G_d]\in \mathcal{N}{\mathcal{S}}_{codim}$. We have just proven that the ideal $(G_1,G_2,\dots ,G_d)$ contains all monomials of degree greater than $2dM$. That is, the codimension of an ideal generated by the sequence $(G_1,G_2,\dots ,G_d)$ of d elements in a finitely generated graded algebra $\mathbb{A}$ of dimension d is finite. We have found in the algebra $\mathbb{A}$ one regular sequence, namely, (82). By Theorem 4, we have thus proven that $\mathbb{A}$ is a Cohen–Macaulay algebra. Therefore, according to Theorem 3, the sequence $G_1,G_2,\dots ,G_d$ is regular and therefore

$$H(\mathbb{A}/(G_1,G_2,\dots ,G_d),t)=H(\mathbb{A},t){(1-t^M)}^d=Q\left(t\right),$$

(100)

According to (59), $deg\left(Q\right)=dM,Q\left(1\right)=\mu \left(\mathsf{\Gamma }\right)$. This implies that for any d-tuple $[F_1,F_2,\dots ,F_d]\in \mathcal{N}{\mathcal{S}}_{codim}$ the codimension of the ideal $(F_1,F_2,\dots ,F_d)$ is equal to $\mu \left(\mathsf{\Gamma }\right)$ and all monomials of the algebra $\mathbb{A}$ of degree greater than $dM$ belong to the ideal.

The proof of the assertion (main.a) is complete.

8.1.2. Outline of the Proof of (Main.b)

Consider a tuple of polynomials $[g_1,g_2,\dots ,g_d]\in W$ such that $\mathit{Leading}\_\mathit{terms}\left([g_1,g_2,\dots ,g_d]\right)\in \mathcal{N}{\mathcal{S}}_{codim}$. Denote by $[G_1,G_2,\dots ,G_d]$ the tuple Leading_term($[g_1,g_2,\dots ,g_d]$). Then, according to (main.a), the codimension of $(G_1,G_2,\dots ,G_d)$ is finite and equals $\mu \left(\mathsf{\Gamma }\right)$. For brevity, let us denote this codimension by $\mu$. The factor algebra $\mathbb{A}/(G_1,G_2,\dots ,G_d)$ has dimension $\mu$ over K and hence has a basis of $\mu$ elements, say $[E_1,E_2,\dots ,E_{\mu }]$. It is easy to see that as elements of the basis, one can choose the equivalence classes of homogeneous elements of the algebra $\mathbb{A}$. Every non-zero homogeneous element of $\mathbb{A}$ is the leading_term of some non-zero element of A. Therefore, in the filtered algebra A of Laurent polynomials, elements $(e_1,e_2,\dots ,e_{\mu })$ can be found such that $[E_1,E_2,\dots ,E_{\mu }]=[{\widehat{e}}_1,{\widehat{e}}_2,\dots ,{\widehat{e}}_{\mu }]$. Assertion (main.b) will be proven if we manage to set two properties of these elements $e_1,e_2,\dots ,e_{\mu }$.

Proposition 34.

The equivalence classes of elements $e_1,e_2,\dots ,e_{\mu }$ span the quotient algebra $A/(g_1,g_2,\dots ,g_d)$ over $\mathbb{K}$.

Proposition 35.

The equivalence classes of elements $e_1,e_2,\dots ,e_{\mu }$ are linearly independent in the quotient algebra $A/(g_1,g_2,\dots ,g_d)$.

Let us reformulate the Statement 34 in more convenient notation.

Proposition 36.

(Assumption.) Assume that the codimension of the ideal $({\widehat{g}}_1,{\widehat{g}}_2,\dots ,{\widehat{g}}_d)\subset \mathbb{A}$ is finite and the equivalence classes of elements ${\widehat{e}}_1,{\widehat{e}}_2,\dots ,{\widehat{e}}_{\mu }$ form a basis of the quotient algebra $\mathbb{A}/({\widehat{g}}_1,{\widehat{g}}_2,\dots ,{\widehat{g}}_d)$.

(Conclusion.) Then, the codimension of the ideal $(g_1,g_2,\dots ,g_d)\subset A$ is finite and the equivalence classes of elements $e_1,e_2,\dots ,e_{\mu }$ span quotient algebra $A/(g_1,g_2,\dots ,g_d)$.

Proof. 

It suffices to prove that an arbitrary element $e\in A$ can be represented as

$$e=\sum _{1\le i\le d}{h}_i{g}_i+\sum _{1\le j\le \mu }{\lambda }_j{e}_j,\mathrm{where}{h}_i\in A,{\lambda }_j\in \mathbb{K}$$

(101)

Element 0 is obviously representable. The union of zero and all nonzero elements of zero degree forms in the algebra A a one-dimensional vector space spanned by the identity monomial. The leading term of this monomial necessarily enters the monomial basis of any quotient algebra by the ideal generated by the elements of positive degrees. Therefore, we can assume that if Assumption is true, then we can choose the unit monomial as $e_1$. Thus, any element of the algebra A of degree zero is representable in the required form (101).

For an arbitrary element $e\in A$ of a positive Newtonian degree, there exists $k\le deg\left(e\right)$ such that the element e can be represented approximately, up to some correction term $r_k\in A_k$, in the form

$$e=\sum _{1\le i\le d}{h}_i{g}_i+\sum _{1\le j\le \mu }{\lambda }_j{e}_j+r_k,\mathrm{where}{r}_k\in A_k,h_i\in A,{\lambda }_j\in \mathbb{K}$$

(102)

Indeed, there exists a trivial representation of the form (102) in which k is equal to Newtonian degree of the element e, the element e is taken as the correction term $r_k$, and the remaining terms are chosen to be zero.

Among the non-empty set of possible representations of the element e of the form (102), we choose some representation with the minimum Newtonian degree of the correction term $r_k$. Let us prove that this minimal Newtonian degree is equal to $-\infty$. Thus, we prove that there exists an exact representation of the monomial e of the form (101). Thus, to prove the existence of an exact representation of an element e of the form (101), it is sufficient for any representation of an element e of the form (102) with a non-zero correction term $r_k$ to construct a more accurate representation with a smaller Newtonian degree of the correction term. □

Proof of the possibility of lowering the Newtonian degree of the correction term in the representation (102).

Consider the term $r_k\in A_k$ of the representation (102) and its leading_term ${\widehat{r}}_k\in {\mathbb{A}}_k$. According to the Assumption, the element ${\widehat{r}}_k$, like any element of the $\mathbb{A}$ algebra, is represented as:

$${\widehat{r}}_k=\sum _{1\le i\le d}{\widehat{p}}_i{\widehat{g}}_i+\sum _{1\le j\le \mu }{\beta }_j{\widehat{e}}_j,\mathrm{where}{p}_i\in A_k,{\widehat{p}}_i=p_i+A_{k-1}\in {\mathbb{A}}_k,{\beta }_j\in \mathbb{K}$$

(103)

For $k>0$, it follows from (103) that

$$r_k=\sum _{1\le i\le d}{p}_i{g}_i+\sum _{1\le j\le \mu }{\beta }_j{e}_j+r_{k-1},\mathrm{where}{r}_{k-1}\in A_{k-1},p_i\in A_k,{\beta }_j\in \mathbb{K}$$

(104)

Substituting the found expression for the correction term $r_k$ into (102), we obtain a new approximate representation of the element e with a correction term $r_{k-1}$ whose Newtonian degree has decreased

$$\begin{array}{cc}\hfill e& =\sum _{1\le i\le d}{h}_i{g}_i+\sum _{1\le j\le \mu }{\lambda }_j{e}_j+\sum _{1\le i\le d}{p}_i{g}_i+\sum _{1\le j\le \mu }{\beta }_j{e}_j+r_{k-1}\hfill \\ & =\sum _{1\le i\le d}(h_i+p_i)g_i+\sum _{1\le j\le \mu }({\lambda }_i+{\beta }_j)e_j+r_{k-1},\hfill \\ & \mathrm{where}{r}_i\in A_{k-1},h_i+p_i\in A,{\lambda }_i+{\beta }_j\in \mathbb{K}\hfill \end{array}$$

(105)

For $k=0$, the correction term $r_0$ is proportional to $e_1$ and changing the term ${\lambda }_1{e}_1$ turns the approximate representation (102) into an exact representation (101). Proposition 36 is proven. This also proves Proposition 34. □

To prove the assertion (main.b), it remains to prove the assertion 35. This proof is the most difficult step in the proof of the assertion (main.b). At this point, we need two tools:

-

A sufficient condition for the strictness of mapping filtered modules, formulated in Proposition 38 below;

-

A known theorem on the vanishing of the homology of dimension 1 of the Koszul complex of a regular sequence of homogeneous elements of positive degrees of a finitely generated graded algebra over a field of characteristic 0, see, for example, Theorem 06 in [26]

Proof 

(Proof of Proposition 35). We need to prove that if some linear combination

$$z=\sum _{1\le j\le \mu }{\lambda }_j{e}_j,\mathrm{where}{\lambda }_j\in \mathbb{K}$$

(106)

belongs to the ideal $(g_1,g_2,\dots ,g_d)$, i.e., z is represented as

$$z=\sum _{1\le i\le d}{h}_i{g}_i,\mathrm{where}{h}_i\in A$$

(107)

then this combination z is trivial, that is:

$${\lambda }_1={\lambda }_2=\dots {\lambda }_{\mu }=0$$

(108)

Let us prove the Formula (108) by contradiction. If at least one coefficient in the linear combination (106) is nonzero, then the leading term $\widehat{z}$ of the element z is some non-trivial linear combination of representatives of the basis vectors of the quotient algebra $\mathbb{A}/({\widehat{g}}_1,{\widehat{g}}_2,\dots ,{\widehat{g}}_{\mu })$. Due to its nontriviality, this linear combination of basis vectors is nonzero. This means that the element z is also different from zero and therefore has a finite Newtonian degree k. We calculate the leading term $\widehat{z}$ of the element z of the Newtonian degree k in two ways, using the representation of z by the Formula (106) or by the Formula (107).

First way. From the Formula (106), it follows that $\widehat{z}$ is a non-trivial linear combination of those elements ${\widehat{e}}_j$, for which the Newtonian degree of $e_j$ equals k:

$$\widehat{z}=\sum _{deg\left(e_j\right)=k}{\lambda }_j{\widehat{e}}_j,\mathrm{where}{\lambda }_j\in \mathbb{K}$$

(109)

Second way. Let us start with representation (107). By itself, it does not give us anything, since the multipliers $h_1,h_2,\dots ,h_d$ of arbitrarily high Newtonian degrees can participate in it. However, we use the very fact of the existence of such a representation. Below, we prove that the existence of some representation (107) of the element z of the Newtonian degree k implies the existence of such a representation that each of the elements $h_1,h_2,\dots ,h_d$ belongs to $A_{k-M}$:

$$z=\sum _{1\le i\le d}{h}_i{g}_i,\mathrm{where}{h}_i\in A_{k-M}$$

(110)

Therefore, calculating the leading term $\widehat{z}$ from the Formula (110) yields

$$\widehat{z}=\sum _{1\le i\le d}{h}_i{\widehat{g}}_i,\mathrm{where}{h}_i\in {\mathbb{A}}_{k-M}$$

(111)

Comparing the representations (109) and (111) of the element $\widehat{z}\in \mathbb{A}$, we obtain that a non-trivial linear combination of representatives of the basis vectors of the quotient algebra $\mathbb{A}/({\widehat{g}}_1,{\widehat{g}}_2,\dots ,{\widehat{g}}_{\mu })$ belongs to the ideal $({\widehat{g}}_1,{\widehat{g}}_2,\dots ,{\widehat{g}}_{\mu })$. That is, from the negation of the equality (108), we deduced the existence of a non-trivial linear relation between the basis vectors of the factor algebra. The resulting contradiction proves the equality (108). □

Proof of the existence of representation (110)

We will consider $A^d$ and A as filtered modules over the Newton filtered $\mathbb{K}$-algebra A. The ideal $(g_1,g_2,\dots ,g_d)$ can be considered as the image of the mapping

$$A^d\stackrel{{\partial }_1}{\to }A$$

(112)

of filtered modules, where ${\partial }_1$ is given by the formula

$${\partial }_1(h_1,h_2,\dots ,h_d)=(h_1{g}_1+h_2{g}_2+\dots +h_d{g}_d)$$

The existence of a representation (110) in terms of mappings of filtered modules would follow from the relation

$${\partial }_1\left(A^d\right)\cup A_k={\partial }_1\left({\left(A^d\right)}_k\right)\mathrm{for}\mathrm{any}k\in \mathbb{N}$$

(113)

if we could prove it. In terms of mappings of filtered modules, the fulfillment of the relation (113) is called the strictness of the mapping ${\partial }_1$. Therefore, to complete the proof of the existence of representation (110), it remains to prove the strictness of the mapping ${\partial }_1$, i.e., to prove (113). This proof uses the known sufficient condition of strictness (see Proposition 38 below). The proof of existence of representation (110) completes the proof of Proposition 35, which in turn completes the proof of the assertion (main.b). □

Proof of the relation (113).

Definition 21. 

The mapping of $\mathbb{N}$-filtered modules

$$\mathcal{Y}\stackrel{{\partial }_1}{\to }\mathcal{Z}$$

is called strict if

$${\partial }_1\left(\mathcal{Y}\right)\cap {\mathcal{Z}}_k={\partial }_1\left({\mathcal{Y}}_k\right)\mathrm{for}\mathrm{any}k\in \mathbb{N}$$

(114)

Proposition 37.

Let $\mathcal{Y}\stackrel{{\partial }_1}{\to }\mathcal{Z}$ be a strict mapping of filtered modules. Then,

$$gr(\mathcal{Z}/{\partial }_1\left(\mathcal{Y}\right))=gr\left(\mathcal{Z}\right)/gr\left({\partial }_1\right)\left(gr\left(\mathcal{Y}\right)\right)$$

The proof follows from the definitions of associated graded objects constructed from filtered objects. □

Proposition 38.

Sufficient condition for strictness of mapping of filtered modules.Let

$$\mathcal{X}\stackrel{{\partial }_2}{\to }\mathcal{Y}\stackrel{{\partial }_1}{\to }\mathcal{Z}$$

be a complex of filtered modules, i.e., each of two mappings ${\partial }_2$ and ${\partial }_1$ preserve the filtering and the composition of these mappings is zero. Let us denote

$$gr\left(\mathcal{X}\right)=X,gr\left(\mathcal{Y}\right)=Y,gr\left(\mathcal{Z}\right)=Z,gr\left({\partial }_2\right)=d_2,gr\left({\partial }_1\right)=d_1$$

Suppose that $\mathcal{Y}={\bigcup }_{k\in \mathbb{N}}{\mathcal{Y}}_k$ and the sequence

$$X\stackrel{d_2}{\to }Y\stackrel{d_1}{\to }Z$$

(115)

is exact at Y. Then, the mapping ${\partial }_1$ is a strict mapping of filtered modules.

An example of applying Proposition 38 to Koszul complexes. Let us consider $A^d$ and A as filtered modules over the Newton filtered $\mathbb{K}$-algebra A. Let us consider two tuples $[g_1,g_2,\dots ,g_d]\in A^d$ and $[G_1,G_2,\dots ,G_d]\in {\mathbb{A}}^d$ such that

$$[G_1,G_2,\dots ,G_d]=\mathrm{Leading}\_\mathrm{term}\left([g_1,g_2,\dots ,g_d]\right)$$

The ideal $(g_1,g_2,\dots ,g_d)\subset A$ can be considered as the image of the mapping

$$A^d\stackrel{{\partial }_1}{\to }A$$

(116)

of filtered modules, where ${\partial }_1$ is given by the formula

$${\partial }_1(h_1,h_2,\dots ,h_d)=(h_1{g}_1+h_2{g}_2+\dots +h_d{g}_d)$$

The sequence of module mappings (116) can be extended to the right by the natural projection of the algebra onto the quotient algebra

$$A^d\stackrel{{\partial }_1}{\to }A\stackrel{}{\to }A/(g_1,g_2,\dots ,g_d)$$

(117)

The sequence (117) can be continued to the left as a fragment of the Koszul complex of the sequence $g_1,g_2,\dots ,g_d$ of elements of the algebra A

$$A^{\left(\genfrac{}{}{0pt}{}{d}{2}\right)}\stackrel{{\partial }_2}{\to }{A}^d\stackrel{{\partial }_1}{\to }A\stackrel{}{\to }A/(g_1,g_2,\dots ,g_d)$$

(118)

Let us move now from filtered objects to graded objects. It is clear that the associated graded modules for the filtered modules $A^{\left(\genfrac{}{}{0pt}{}{d}{2}\right)}$, $A^d$, and A are the modules ${\mathbb{A}}^{\left(\genfrac{}{}{0pt}{}{d}{2}\right)}$, ${\mathbb{A}}^d$, and $\mathbb{A}$. The sequence (118) of filtered objects corresponds to the sequence of graded objects that is a fragment of the Koszul complex of of the sequence $G_1,G_2,\dots ,G_d$ of elements of the algebra $\mathbb{A}$

$${\mathbb{A}}^{\left(\genfrac{}{}{0pt}{}{d}{2}\right)}\stackrel{d_2}{\to }{\mathbb{A}}^d\stackrel{d_1}{\to }\mathbb{A}\stackrel{}{\to }\mathbb{A}/(G_1,G_2,\dots ,G_d)$$

(119)

Proposition 38 will be applied to the first three members of the sequence (118), which will play the role of $\mathcal{X}$, $\mathcal{Y}$, and $\mathcal{Z}$ and to the first three members of the sequence (119), which will play the role of X, Y, and Z. A meaningful fact that allows us to apply Proposition 38 is the regularity of the sequence $(G_1,G_2,\dots ,G_d)$. This regularity is provided by assertion (main.a).

Proof of Proposition 38.

We have to prove the relation (114). Consider a nonzero element $z\in \partial \left(\mathcal{Y}\right)\cap {\mathcal{Z}}_k$. Since $\mathcal{Y}={\bigcup }_{k\in \mathbb{N}}{\mathcal{Y}}_k$, there are an index $l\ge k$ and an element $y\in {\mathcal{Y}}_l$ such that ${\partial }_{1}y=z\in {\mathcal{Z}}_k$. Let us put

$$k_1=min\{n\in \mathbb{N}:n\ge k,z\in {\partial }_1\left({\mathcal{Y}}_n\right)\}.$$

The set described by curly brackets is non-empty because it contains the number l, so the number $k_1$ is well defined. Let us prove that $k_1=k$. Assume that $k_1>k$. This means that there exists $y_1\in {\mathcal{Y}}_{k_1}$ such that ${\partial }_1{y}_1=z$. Therefore,

$${\partial }_1(y_1+{\mathcal{Y}}_{k_1-1})\subseteq z+{\mathcal{Z}}_{k_1-1}\subseteq {\mathcal{Z}}_{k_1}$$

Since the sequence (115) is exact, there exists an element $x\in {\mathcal{X}}_{k_1}$ such that

$${\partial }_2(x+{\mathcal{X}}_{k_1-1})\subseteq y_1+{\mathcal{Y}}_{k_1-1}$$

This implies that $y_1-{\partial }_{2}x\in {\mathcal{Y}}_{k_1-1}$ and

$${\partial }_1(y_1-{\partial }_{2}x)={\partial }_1{y}_1=z$$

That is, we have represented z as the image of a point from the set ${\mathcal{Y}}_{k_1-1}$, which contradicts the definition of $k_1$. □

Completing the proof of the assertion (main.b)

Let us fix a tuple $[G_1,G_2,\dots ,G_d]\in \mathcal{N}{\mathcal{S}}_{codim}\subset \mathbb{W}$. Let $[g_1,g_2,\dots ,g_d]$ be a tuple in W such that

$$[{\widehat{g}}_1,{\widehat{g}}_2,\dots ,{\widehat{g}}_d]=[G_1,G_2,\dots ,G_d]\in \mathbb{W}$$

According to assertion (main.a), the sequence ${\widehat{g}}_1,{\widehat{g}}_2,\dots ,{\widehat{g}}_d$ generates in $\mathbb{A}$ an ideal of finite codimension equal to $\mu \left(\mathsf{\Gamma }\right)$. Therefore, according to Theorem 3, the sequence ${\widehat{g}}_1,{\widehat{g}}_2,\dots ,{\widehat{g}}_d$ is regular. It is known, see, for example, Theorem 06 in [26], that for a regular sequence ${\widehat{g}}_1,{\widehat{g}}_2,\dots ,{\widehat{g}}_d$ of homogeneous elements of a graded algebra the Koszul complex is acyclic in positive dimensions, in particular, it is acyclic in dimension 1. Therefore, the sequence

$${\mathbb{A}}^{\left(\genfrac{}{}{0pt}{}{d}{2}\right)}\stackrel{d_2}{\to }{\mathbb{A}}^d\stackrel{d_1}{\to }\mathbb{A}\stackrel{}{\to }\mathbb{A}/(G_1,G_2,\dots ,G_d)$$

is exact at ${\mathbb{A}}^d$. According to Proposition 38 it follows that mapping ${\partial }_1$ (118) is strict. According to Proposition 37, this implies that the dimension of the factor algebra $A/(g_1,g_2,\dots ,g_d)$ is equal to $\mu \left(\mathsf{\Gamma }\right)$. The proof of the assertion (main.b) is complete. □

8.1.3. Proof of Assertion (Main.c)

Proposition 18(ii) implies that the set ${\mathsf{\Gamma }}^{sh}$ contains interior($\mathsf{\Gamma }$) so the finite set ${\mathbb{B}}^{sh}$ contains all integer points of ${\mathbb{Z}}^d$ of Newtonian degree less than M. Assumptions of Theorems 5 describe a finite set of monomials

$$\{m_1,m_2,\dots ,m_{\mu }\}\subset A$$

Consider the leading terms of these monomials $\{{\widehat{m}}_1,{\widehat{m}}_2,\dots ,{\widehat{m}}_{\mu }\}$ Their equivalence classes form a basis of the factor algebra $\mathbb{A}/(f_1,f_2,\dots ,f_d)$ for at least one tuple of Laurent polynomials, namely, for the tuple (82). Denote by $\mathcal{M}$ the set of monomials

$$\{{\widehat{m}}_1,{\widehat{m}}_2,\dots ,{\widehat{m}}_{\mu }\}$$

This set contains all the monomials of the Newtonian degre less than M, does not contain any of the monomials of the Newtonian degre greater than $dM$, and contains some monomials of the Newtonian degree in range $[M,dM]$. For $n\in [M,dM]$, denote by $Bspac{e}_n\subset {\mathbb{A}}_n$ vector space spanned by all monomials of Newtonian degree n and by $p_n:{\mathbb{A}}_n\mapsto {\mathbb{A}}_n/Bspac{e}_n$ the quotient map. Further reasoning will be similar to the proof of assertion (main.a).

The homogeneous ideal $(G_1,G_2,\dots ,G_d)$ is the image of the mapping ${\mathbb{A}}^d\stackrel{d_1}{\to }\mathbb{A}$ given by the formula

$$d_1(H_1,H_2,\dots ,H_d)=(H_1{G}_1+H_2{G}_2+\dots +H_d{G}_d)$$

This mapping of infinite-dimensional vector spaces reduces to the family of mappings of finite-dimensional vector spaces

$${\left({\mathbb{A}}_{n-M}\right)}^d\stackrel{d_{1,n}}{\to }{\mathbb{A}}_n,\mathrm{where}n\ge M$$

Let us construct for each $n\in [M,DM]$ the composition of mappings

$${\left({\mathbb{A}}_{n-M}\right)}^d\stackrel{d_{1,n}}{\to }{\mathbb{A}}_n\stackrel{p_n}{\to }{\mathbb{A}}_n/Bspac{e}_n,\mathrm{where}n\in [M,dM]$$

Denote $compositio{n}_n=d_{1,n}\circ p_n$. Each composition is a linear mapping of finite-dimensional vector spaces. In bases defined by monomials, each composition $compositio{n}_n$ is given by its matrix, the coefficients of which depend linearly on the coefficients of Laurent polynomials in the tuple $[G_1,G_2,\dots ,G_d]\in \mathbb{W}$. Any homogeneous component ${\mathbb{A}}_n\subset \mathbb{A}$ is spanned by basis monomials’ modulo the image of $d_{1,n}$ if and only if the rectangular matrix of $compositio{n}_n$ has the maximum possible rank. There is at least one tuple for which the matrices of all compositions $compositio{n}_n$, where $n\in [M,dM]$, have the highest possible rank.

According to the well-known theorem of linear algebra, for the rank of a rectangular matrix to be nonmaximal, it is necessary and sufficient that all minors of this matrix of maximum dimension vanish. That is, it is necessary and sufficient to fulfill a finite number of algebraic conditions on the coefficients of the matrix.

When proving (main.a), we have constructed in the vector space $\mathbb{W}$ a finite number of Zariski closed sets ${\mathcal{S}}_j$, where $j\in (dM,2dM]$. We denote the complement to these subsets in $\mathbb{W}$ by $\mathcal{N}{\mathcal{S}}_{codim}$. To prove assertion (main.c), we additionally define in $\mathbb{W}$ Zariski-closed sets ${\mathcal{S}}_n$, where $n\in [M,dM]$. Let us define each of these sets ${\mathcal{S}}_n$ by the condition that the matrix of mapping $compositio{n}_n$ has nonmaximal rank. As shown above, each ${\mathcal{S}}_n$ is a Zarisky closed subset of $\mathbb{W}$ whose complement is non-empty. Next, we set

$$\begin{array}{cc}\hfill {\mathcal{S}}_{basis}& ={\mathcal{S}}_{codim}\cup \left(\bigcup _{M\le n\le 2dM}{\mathcal{S}}_n\right)\hfill \\ \hfill \mathcal{N}{\mathcal{S}}_{basis}& =\mathbb{W}\backslash {\mathcal{S}}_{basis}\hfill \end{array}$$

(120)

Consider a tuple $G=[G_1,G_2,\dots ,G_d]\in \mathcal{N}{\mathcal{S}}_{basis}$. Let us prove that the quotient algebra $\mathbb{A}/(G_1,G_2,\dots ,G_d)$ is generated by the equivalence classes of monomials belonging to the set $\mathcal{M}$. The tuple F does not belong to ${\mathcal{S}}_{codim}$. Therefore, according to (main.a), the codimension of the ideal $(F_1,F_2,\dots ,F_d)$ is equal to $\mu \left(\mathsf{\Gamma }\right)$ and all elements of the algebra $\mathbb{A}$ whose degree is greater than $dM$ belong to the ideal. In other words, the quotient algebra $\mathbb{A}/(F_1,F_2,\dots ,F_d)$ is generated by the equivalence classes of homogeneous elements of the algebra $\mathbb{A}$ degree $n\le dM$. Let us prove that each homogeneous element of the factor algebra of degree $n\le dM$ is a linear combination of representatives of monomials of the set $\mathcal{M}$. For any $n<M$ the homogeneous component ${\mathbb{A}}_n\subset \mathbb{A}$ is generated by monomials from the set $\mathcal{M}$. It is given that the tuple F does not belong to the set ${\mathcal{S}}_n$. Therefore, by definition of ${\mathcal{S}}_n$, any homogeneous component ${\mathbb{A}}_n\subset \mathbb{A}$ is spanned by basis monomials modulo the image of $d_{1,n}$. Thus, we have proved that if a tuple F belongs to the non-empty Zarisky open set $\mathcal{N}{\mathcal{S}}_{basis}$ it follows that any homogeneous element of the quotient algebra $\mathbb{A}/(F_1,F_2,\dots ,F_d)$ of Newtonian degree $n\le dM$ expands in the basis $\mathcal{M}$.

Now, consider homogeneous elements of degree $n>dM$. Since, by construction, $\mathcal{N}{\mathcal{S}}_{basis}\subset \mathcal{N}{\mathcal{S}}_{codim}$, it follows from (main.a) that all homogeneous elements of the factor algebra degree above $dM$ vanish, and hence any element of the factor algebra decomposes in the equivalence classes of the monomials of the set $\mathcal{M}$. Since the cardinality of this set is equal to the dimension of the quotient algebra, the equivalence classes of monomials of the set $\mathcal{M}$ form a basis for the quotient algebra $\mathbb{A}/(F_1,F_2,\dots ,F_d)$. The proof of assertion (main.c) is complete.

8.1.4. Proof of Assertion (Main.d)

Consider a tuple $[g_1,g_2,\dots ,g_d]\in W$ such that the tuple of their leading terms $[{\widehat{g}}_1,{\widehat{g}}_2,\dots ,{\widehat{g}}_d]$ belongs to the set $\mathcal{N}{\mathcal{S}}_{basis}$. According to (main.c), the equivalence classes of monomials ${\widehat{m}}_1,{\widehat{m}}_2,\dots ,{\widehat{m}}_{\mu }$ form a basis over K of the factor algebra

$$\mathbb{K}\left[{\mathbb{Z}}^d\right]/({\widehat{g}}_1,{\widehat{g}}_2,\dots ,{\widehat{g}}_d)$$

Let us apply Proposition 36 taking as ${\widehat{e}}_1,{\widehat{e}}_2,\dots ,{\widehat{e}}_{\mu }$ the monomials ${\widehat{m}}_1,{\widehat{m}}_2,\dots ,{\widehat{m}}_{\mu }$. We obtain that the ideal $(g_1,g_2,\dots ,g_d)\subset \mathbb{K}\left[Z^d\right]$ has a finite codimension equal to $\mu \left(\mathsf{\Gamma }\right)$ and the equivalence classes of monomials $m_1,m_2,\dots ,m_{\mu }$ form a basis of the quotient algebra

$$\mathbb{K}\left[{\mathbb{Z}}^d\right]/(g_1,g_2,\dots ,g_d)$$

The proof of assertion (main.d) is complete.