Robust Parametric Identification for ARMAX Models with Non-Gaussian and Coloured Noise: A Survey

Abstract

In this paper the Cramer-Rao information bound for ARMAX (Auto-Regression-Moving-Average-Models-with-Exogenuos-inputs) under non-Gaussian noise is derived. It is shown that the direct application of the Least Squares Method (LSM) leads to incorrect (shifted) parameter estimates. This inconsistency can be corrected by the implementation of the parallel usage of the MLMW (Maximum Likelihood Method with Whitening) procedure, applied to all measurable variables of the model, and a nonlinear residual transformation using the information on the distribution density of a non-Gaussian noise, participating in Moving Average structure. The design of the corresponding parameter-estimator, realizing the suggested MLMW-procedure is discussed in details. It is shown that this method is asymptotically optimal, that is, reaches this information bound. If the noise distribution belongs to some given class, then the Huber approach (min-max version of MLM) may be effectively applied. A numerical example illustrates the suggested approach.

1. Introduction

1.1. Road Map of This Survey

The topic of parameter identification in a large class of linear models with external noise acting on-line and perturbing the dynamics of an investigated system is addressed in this overview. The considered models are classified as ARMAX (auto-regression-moving average with exogenous inputs) and are commonly expressed in discrete-time format by recurrent linear stochastic difference equations. The class of distribution functions is supposed to be known a priori but not its exact analytical expression: such models contain “uncertainties” in their descriptions, which are associated with unknown parameters and probabilistic characteristics of external noise (perturbations): only a class of distribution functions is supposed to be known a priori but not its exact analytical expression. As a result, any identification technique that may be used in such a circumstance should be robust (resilient) with respect to existing uncertainty. The focus of this work is on a critical examination of robust parametric identification techniques, highlighting a gap in the current literature in which the vast majority of publications adopt the traditional assumption that external stochastic perturbations are independent and Gaussian (have a “normal distribution”). Only a few papers deal with a different non-standard assumption about the available stochastic characteristics of external noisy disturbances. Here, we expose readers to the underlying difficulties (mathematical and computational) and discuss a few distinct ways that have shown to be successful in the absence of available probabilistic data.

The structure of the paper is as follows:

−

Review of publications:

• It contains the descriptions of the important survey published in the 1970’s–1990’s (Åström, Becky, Ljung and Gunnarson, Billings among others).
• Nongaussian noises have been studied by Huber, Tsypkin and Polyak.

−

Problem formulation and model description:

• The ARMAX model with correlated non-Gaussian noise, generated by a stable and non-minimal phase filter, is introduced.

−

Some classes ${\mathcal{P}}_{3be}$ of noise p.d.f.:

• In a rigorous mathematical manner several classes of random stationary sequences with different p.d.f. as an input of a forming filter are considered (all symmetric distributions non-singular in origin, all symmetric distributions with a bounded variance, all symmetric “approximately normal” distributions and “approximately uniform” distributions).

−

Main assumptions:

• These concern the martingale difference property with conditional bounder second moment for stochastic sequences in the input of the forming filter, stability and minimal-phase property for this filter, independent of this sequence with other measurable inputs).

−

Regression representation format:

• The extended regression form of the considered model is introduced.

−

Main contribution of the paper:

• The exact presentation of the main contribution of the paper.

−

Why LSM does not work for the identification of ARMAX models with correlated noise:

• A simple example exhibiting the lack of workability of this technique in the case of dynamic (autoregression) models is described in detail for a reader who is not actively involved in the least-squares method.

−

Some other identification techniques:

• Identification of non-stationary parameters and the Bayesian method, matrix forgetting factor and its adaptive version are reviewed.

−

Regular observations and information inequality for observations with coloured noise:

• the Cramér–Rao bound (CRB) and the Fisher information, characterising the maximal possible rate of estimation under the given information resource, are presented.

−

Robust version of the maximum likelihood method with whitening (MLMW procedure):

• This approach is demonstrated to reach the CRB bound, indicating that it is asymptotically the best among all identification procedures.

−

Recurrent identification procedures with nonlinear residual transformations: static (regression) and dynamic (autoregression) models:

• Within a specified noise p.d.f. class, it is proven that such a strategy with particular selection of nonlinear residual transformation is resilient (robust) optimum in achieving min–max error variance in CRB inequality.

−

Instrumental variables ethod (IVM):

• IV or total least-squares estimators is the method which also recommends to estimate parameters in the presence of coloured noises with a finite correlation.

−

Joint parametric identification of ARMAX model and the forming filter:

• The “generalised residual sequence” is introduced, which is shown to be asymptotically closed to the independent sequence acting in the input of the forming filter, which helps to resolve the identification problem in an extended parametric space.
• Numerical example.
• Discussion and conclusions.

−

Appendix A and abbreviations:

• This part offers proofs of some of the article’s claims that appear to be significant from the authors’ perspective, as well as a list of acronyms used throughout the work.

1.2. Review of the System Identification Literature

A mathematical model is a simplified mathematical structure connected to a component of reality and produced for a specific purpose of system analysis [1]. Differential equations, state space models and transfer functions are all examples of mathematical models of dynamic systems that are useful in a variety of fields [2]. System identification, which can be applied to nearly any system and give models that explain the system behaviour, is an alternative to modelling.

1.3. Classical Surveys on Identification

The least-squares method (LSM), as well as some of its variants, have been extensively researched in the past, according to the survey given by Åström [3]. The least squares, maximum likelihood, instrumental variables and tally principle are examples of these variety. Several approaches for the identification of dynamic systems using computer techniques, such as spectral analysis, certain gradient methods, quasi-linearization and stochastic approximations, were provided by Becky [4]. In the case of a time-varying situation, Ljung and Gunnarson investigated several methods for developing identification algorithms that could take into account the time-varying dynamics of systems as well as signals [5]. Some mean square expressions were examined in this study. In [6] by Billings, several methods for the nonlinear case were described; these algorithms were based on the functional expansion of Wiener and Volterra, block-oriented and bi-linear systems, structure detection and some catastrophe theory. System identification is a vast field of study, with a variety of methods based on the models to be estimated: linear, nonlinear, continuous, discrete, time-varying and so on. Ljung’s survey [7] demonstrates that, despite the wide range of techniques, the field can be defined by a few key principles, such as data information, validation and model complexity and offers some basic principles and results, as well as a method for solving real-world problems. As it is mentioned by Ljung in [8], system identification is a well established research area, whose paradigms are most of the time based on classical statistical methods. Some recent techniques are based on kernel regularisation methods. The paper presented by Ljung presents some of the main ideas and results of kernel-based regularisation methods for system identification.

1.4. Identification under Correlated Noise Perturbations

In the measurements and modelling of dynamic systems [9], the unpredictability inherent in physical processes always creates inaccuracy. Stochastic processes make it possible to model these random events and create more realistic models [10]. It is commonly assumed that only white noise is presented in stochastic systems, however, there are also cases where the noise is correlated or “coloured”. Coloured noise is prevalent in linear and pseudo-linear regression identification models, where one of the challenges is the presence of unknown inner variables and immeasurable noise components [11]. The stochastic gradient algorithm proved to be a useful technique for those cases. In situations where there are a lot of noisy sources, noise suppression is crucial. In many practical circumstances, coloured noise may be converted to white noise [12] by passing it through an invertible time-invariant linear (“whitening”) filter. The existence of coloured noise typically leads to robust identification theory, which was first proposed by P. Huber [13] and Ya. Z. Tsypkin-B. Polyak [14] over fifty years ago. In [15], the basic principles of robust identification were presented, as well as the identification methods for auto regression with exogenous input (ARX) models. The suggested approach used a whitening procedure and a variant of the maximum likelihood method in parallel to conduct asymptotically the estimation of unknown parameters. The need of system identification has grown in some areas, such as robotics, due to the increasing interest in showing movement accuracy in the industry. The application of system identification in DC servomotors is widely used in robotics; in [16], a study on identifying two model structures, ARX and ARMAX, of the system to test and compare their performance on validation criterion is presented.

1.5. Identification of ARMAX and NARMAX Models

For many years, the parameter estimation for autoregressive moving average exogenous input (ARMAX) models has been investigated [17,18]. The importance of parameter-bounding methods in the identification process is highlighted in [19] and stands for such models. These methods offer a radical alternative to compute parameter point estimates and covariances. They require constraints in an effectively deterministic model formulation instead of p.d.f. or mean and covariance for the noise and previous parameter estimations.

In the context of parameter-bounding identification, this study offers a preliminary assessment of certain typical tasks, such as experiment design, testing for outliers, tolerance prediction and worst-case control design. In [20], the parametrisation of ARMAX models was also discussed. The results reported in this work were aimed at developing a technique for modelling and fitting multivariable time-series data based on spatial approach and parametrisation, with tolerance for missing or incomplete data.

ARMAX models are widely used in industrial modelling nowadays [21,22,23]. For example, functional time series are the realisation of a stochastic process where each observation is a continuous function defined on a finite interval. These processes are commonly used in electricity markets and are gaining more importance as more market data become available and markets head toward continuous time-marginal pricing approaches. In [24], the authors propose a new functional forecasting method that attempts to generalise the standard seasonal ARMAX time-series model to the $L_2$ Hilbert space; the proposed approach is tested by forecasting the daily price profile of the Spanish and German electricity markets, and it is compared with other functional reference models. A physic-based ARMAX model of room temperature in office buildings was presented in [25], where thermodynamic equations are used to determine the structure and order of the model. In this study, extensive measurements over 109 days are used to develop and validate the model. This model can be used to predict the variations of the room temperature accurately in short-term, and long-term periods and has shown to be suitable for real-time fault detection and control applications.

Traditional stochastic information gradient methods for ARMAX identification have a lower computational cost, but its convergence speed is still low, in [26], a two-step algorithm based on gradient acceleration strategies is proposed to deal with this problem. When in the ARMAX process, the noises presented are additive; it is possible to introduce additional information to the estimation problem using nuisances variables to model the output noises (see [27]). Then, a regularised estimator suppresses the adverse effects of the noises and provides minimum variance estimates.

In [18], a technique for concurrently picking the order and identifying the parameters of an ARMAX model was explored, and it was also assessed by computational experiments. The technique presented in that work was based on reformulating the issue for a standard state space, then implementing a bank of Kalman filters, identifying the true model and utilizing multi-model partitioning theory to solve it. In the study presented by Correa and Poznyak in 2001 (see [28]), the problem of simultaneous robust state and parameter estimation for some class of MIMO non-linear systems under mixed uncertainties (unmodeled dynamics as well as observation noises) is presented. A switching gain robust “observer-identifier” is introduced to obtain the estimation. This is achieved by applying an observer to the so-called nominal extended system, obtained from the original system without any uncertainties and considering the parameters as additional constant states. As it was shown in general the extended systems, these can lose the global observability property, supposed to be valid for the original non-extended system, and a special procedure is needed to provide a good estimation process in this situation [29]. The suggested adaptive observer has the Luenberger-type observer structure with switching matrix gain that guarantees a good enough upper bound for the identification error performance index [30]. The Van der Monde generalised transformation is introduced to derive this bound which turns out to be “tight” (it is equal to zero in the absence of both noises and unmodeled dynamics). One approach for dealing with coloured noises is to utilise parameter estimate algorithms based on Kalman filters. The Kalman filter is frequently used for control and estimate (see [31]), and this technique may be thought of as Hammerstein–Wiener ARMAX models. An extended Kalman filter, or the unscented Kalman filter, can be implemented to extend this approach to the nonlinear situation. For the nonlinear autoregressive moving average with exogenous inputs (NARMAX) models, Kalman filters are a commonly used identification method. The off-line observer/Kalman filter presented in [32] was implemented as an identification method, since it has shown a good initial guess of the NARMAX model to reduce the on-line system identification process time, this method showed to be effective in the case of system faults and input failures. In the case of Hammerstein nonlinear systems with coloured noises, a maximum likelihood-based stochastic gradient algorithm was implemented in [33], where the unknown noises were replaced in the information vector by their estimates and through these, one can obtain the parameters. For multivariable Hammerstein controlled autoregressive moving average systems, an interactive maximum likelihood estimation method was implemented in [34]. In that paper, the logarithmic likelihood function over multiple parameter vectors is maximised; the proposed method overcomes the limit on an autoregressive model form with one parameter vector.

In this survey, we present a compendium of some of the existing literature regarding identification in ARMAX models and some of the techniques used in these type of models. We also obtain the Cramer–Rao information bound for ARMAX models with non-Gaussian noises and show that the maximum likelihood method with whitening procedure (MLMW) reaches this low bound, or in other words, is asymptotically optimal.

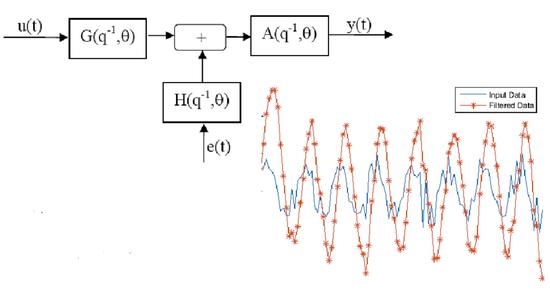
2. Problem Formulation

2.1. Robust Parametric Identification Model Description

Consider the following ARMAX (autoregression moving average exogenous input) model given by

$$y_n=\sum _{l=1}^L{a}_l{y}_{n-l}+\sum _{k=0}^K{b}_k{w}_{n-k}+{\eta }_n,n\ge 0,$$

(1)

where

• $\left\{y_n\right\}\in R^1$ is scalar sequence of available on-line state variables.
• $\left\{w_n\right\}$ is a measurable input sequence (deterministic or, in general, stochastic).
• $\left\{{\eta }_n\right\}\in R^1$ is a noise sequence (not available during the process) generated by the exogenous system

  $${\eta }_n+\sum _{s=1}^{K_2}{d}_{2,s}{\eta }_{n-s}={\xi }_n+\sum _{s=1}^{K_1}{d}_{1,s}{\xi }_{n-s},$$

  (2)

  which can be symbolically represented as the forming filter

  $${\eta }_n=H\left(q^{-1}\right){\xi }_n$$

  (3)

  with the transition function

  $$\left.\begin{array}{c}H\left(q^{-1}\right)=H_1\left(q^{-1}\right)/H_2\left(q^{-1}\right),\\ H_1\left(q^{-1}\right)=1+{\displaystyle \sum _{s=1}^{K_1}}{d}_{2,s}{q}^{-s},H_2\left(q^{-1}\right)=1+{\displaystyle \sum _{s=1}^{K_2}}{d}_{2,s}{q}^{-s}\\ q^{-1}\mathrm{is}\mathrm{the}\text{one-step}\mathrm{delay}\mathrm{operator}\mathrm{acting}\mathrm{as}{y}_{k-1}=q^{-1}{y}_k,\end{array}\right\}$$

  (4)
• $\left\{{\xi }_n\right\}$ as an independent zero mean stationary sequence with the probability density function (p.d.f.) $p_{\xi }\left(x\right)$ which may be unknown but belonging to some given class ${\mathcal{P}}_{\xi }$ of p.d.f., that is,

  $$p_{\xi }\left(x\right)\in {\mathcal{P}}_{\xi }.$$

2.2. Some Classes ${\mathcal{P}}_{\xi }$ of p.d.f.

All possible classes ${\mathcal{P}}_{\xi }$ of p.d.f., considered in practical applications, are related with a priori information on stationary generating sequence $\left\{{\xi }_n\right\}$. Here we present some of them which look natural from practical point of views.

• Class ${\mathcal{P}}_{\xi }^1$ (of all symmetric distributions non singular in the point $x=0$):

  $${\mathcal{P}}_{\xi }^1=\left\{p_{\xi }:p_{\xi }\left(0\right)\ge {\displaystyle \frac{1}{2a}}>0\right\}.$$

  (5)
  We deal with this class if there is not any a priori information on a noise distribution $p_{\xi }$.
• Class ${\mathcal{P}}_{\xi }^2$ (of all symmetric distributions with a bounded variance):

  $${\mathcal{P}}_{\xi }^2=\left\{p_{\xi }:\underset{\mathbb{R}}{\int }{x}^2{p}_{\xi }\left(x\right)ds\le {\sigma }^2<\infty \right\}.$$

  (6)
• Class ${\mathcal{P}}_{\xi }^3$ (of all symmetric “approximately normal” distributions):

  $${\mathcal{P}}_{\xi }^3=\left\{p_{\xi }:p_{\xi }\left(x\right)=\left(1-\alpha \right)p_{\mathcal{N}\left(0,{\sigma }^2\right)}\left(x\right)+\alpha q\left(x\right)\right\},$$

  (7)

  where $p_{\mathcal{N}\left(0,\sigma \right)}\left(x\right)$ is the centred Gaussian distribution density with the variance defined by ${\sigma }^2$ and $q\left(x\right)$ is another distribution density. The parameter $\alpha \in \left[0,1\right]$ characterises the level of the effect of a “dirty” distribution $q\left(x\right)$ to the basic Gaussian distribution $p_{\mathcal{N}\left(0,{\sigma }^2\right)}\left(x\right)$.
• Class ${\mathcal{P}}_{\xi }^4$ (of all symmetric “approximately uniform” distributions):

  $${\mathcal{P}}_{\xi }^4=\left\{p_{\xi }:p_{\xi }\left(x\right)=\left(1-\alpha \right)p_{U\left(0,a\right)}\left(x\right)+\alpha q\left(x\right)\right\}$$

  (8)

  where

  $$\begin{array}{c}{p}_{U\left(0,a\right)}\left(x\right):={\displaystyle \frac{1}{2a}}\chi \left(\left|x\right|\le a\right)\\ \chi \left(\left|x\right|\le a\right)=\left\{\begin{array}{ccc}1& \mathrm{if}& \left|x\right|\le a\\ 0& \mathrm{if}& \left|x\right|>a\end{array}\right.\end{array}$$

  is the centred uniform distribution and $q\left(x\right)$ is one process with a different distribution density. The parameter $\alpha \in \left[0,1\right]$ characterises the level of the effect of a “dirty” distribution $q\left(x\right)$ to the basic one $p_{U\left(0,a\right)}\left(x\right)$.

2.3. Main Assumptions

• All random variables $\left\{w_n,{\xi }_n\right\}$ are defined on the probability space $\left(\mathsf{\Omega },\mathcal{F},P\right)$ with the $\sigma$-algebras flow ${\mathcal{F}}_n\subseteq {\mathcal{F}}_{n+1}$

  $${\mathcal{F}}_{n-1}=\sigma \left(y_{-l},\dots ,y_{-1},\dots ,y_{n-1};w_0,\dots ,w_n;{\eta }_{-K_2,\dots ,}{\eta }_{n-1};{\xi }_{-K_1,\dots ,}{\xi }_{n-1}\right).$$

  (9)
• For all n

  $$\mathrm{E}\left\{{\xi }_n\mid {\mathcal{F}}_{n-1}\right\}\stackrel{a.s.}{=}0,\mathrm{E}\left\{{\xi }_n^2\mid {\mathcal{F}}_{n-1}\right\}\stackrel{a.s.}{=}{\sigma }_{\xi }^2<\infty .$$

  (10)
• The measurable input sequence ${\left\{w_n\right\}}_{n\ge 0}$ is of bounded power:

  $$\mathrm{E}\left\{w_n^2\mid {\mathcal{F}}_{n-1}\right\}\stackrel{a.s.}{=}{\sigma }_{w,n}^2<\infty ,$$

  (11)

  and is independent of $\left\{{\xi }_n\right\},$ i.e.,

  $$\mathrm{E}\left\{w_n{\xi }_n\mid {\mathcal{F}}_{n-1}\right\}\stackrel{a.s.}{=}{w}_n\mathrm{E}\left\{{\xi }_n\mid {\mathcal{F}}_{n-1}\right\}\stackrel{a.s.}{=}0.$$

  (12)
• It is assumed that the forming filter is stable and “minimal-phase”, that is, both polynomials $H_1\left(q^{-1}\right)$ and $H_2\left(q^{-1}\right)$ are Hurwitz, i.e., have all roots inside of the unite circle in the complex plain.
• The ARMAX plant (1) is stable: the polynomial

  $$A\left(q^{-1}\right)=1-\sum _{l=1}^L{a}_l{q}^{-l}$$

  (13)

  is Hurwitz.

Remark 1.

As it follows from the assumptions above, the noise sequence admits to be non-Gaussian and correlated (coloured).

2.4. Regression Format Representation

The system (1) can be represented in the, regression format as

$$y_n=z_n^{\top }c+{\eta }_n,$$

(14)

where the extended vector

$$c={\left(a_1,\dots ,a_L;b_0,\dots ,b_K\right)}^{⊺}\in R^{L+K+1},$$

(15)

represents the collection of unknown parameters to be estimated, and the vector

$$z_n={\left(y_{n-1},\dots ,y_{n-L};w_n,\dots ,w_{n-K}\right)}^{⊺}\in R^{L+K+1},$$

(16)

is referred to as the generalised regression measurable (available on-line) input.

2.5. Robust Parametric Identification Problem Formulation

Problem 1.

We need to estimate the vector c of unknown parameters based on available data $\left\{z_n\right\}$ and a priory knowledge of the p.d.f. class ${\mathcal{P}}_{\xi }$ of the stationary noise sequence $\left\{{\xi }_n\right\}$ in the input of the forming filter. Two possible cases may be considered:

−

the parameters $\left(d_{1,s},d_{2,s}\right)$ of the forming filter $H\left(q^{-1}\right)$ are known.

−

The parameters $\left(d_{1,s},d_{2,s}\right)$ of the forming filter $H\left(q^{-1}\right)$ are also unknown.

2.6. Main Contribution of the Paper

• The Cramer–Rao information bound for ARMAX (autoregression moving average models with exogenous inputs) under non-Gaussian noises is derived.
• It is shown that the direct implementation of the least-squares method (LSM) leads to an incorrect (shifted) parameter estimation.
• This inconsistency can be corrected by the implementation of the parallel use of the MLMW (maximum likelihood method with whitening) procedure, applied to all measurable variables of the model, and a nonlinear residual transformation using the information on the distribution density of a non-Gaussian noise, participating in moving average structure.
• The design of the corresponding parameter estimator, realising the suggested MLMW procedure, containing a parallel on-line “whitening” process as well as a nonlinear residual transformation, is presented in detail.
• It is shown that the MLMW procedure attains the obtained information bound, and hence, is asymptotically optimal.

3. Why LSM Does Not Work for the Identification of ARMAX Models with Correlated Noise

The problem of LSM estimation and identification in ARMAX models has been widely studied in the past. The estimation of the noise-induced bias was presented, for example, in [35], where a unique structure of the ARMAX model was proposed, utilising extra outputs delay. Let us show in this section that for dynamic models (in particular for ARMA-models) the least-squares method (LSM) does not work properly, this means, it leads to biased estimates!

Consider the simplest stable ARMA model with the 1-step correlated noise given by

$$\left.\begin{array}{l}{y}_{n+1}=a{y}_n+{\xi }_n+d{\xi }_{n-1},y_0\in \mathbb{R}\mathrm{is}\mathrm{given},\\ \left|a\right|<1,d\in \mathbb{R},\mathrm{E}\left\{{\xi }_n\right\}=0,\mathrm{E}\left\{{\xi }_n^2\right\}={\sigma }^2>0\end{array}\right\}$$

(17)

where $\left\{{\xi }_n\right\}$ is a sequence of independent random variables. Then, the LSM estimate, realising

$$a_n=arg\underset{a\in \mathbb{R}}{min}\sum _{t=1}^n{\left(y_{t+1}-a{y}_t\right)}^2,$$

is

$$a_n=\left[\sum _{t=1}^n{y}_t{y}_{t+1}\right]{\left[\sum _{t=1}^n{y}_t^2\right]}^{-1}$$

(18)

and under by the strong version of large number law (LNL) [36] it becomes

$$\begin{array}{c}{a}_n\stackrel{a.s.}{=}{\displaystyle \frac{{\displaystyle \frac{1}{n}}{\displaystyle \sum _{t=1}^n}\mathrm{E}\left\{y_t{y}_{t+1}\right\}}{{\displaystyle \frac{1}{n}}{\displaystyle \sum _{t=1}^n}\mathrm{E}\left\{y_t^2\right\}}}+o_{\omega }\left(1\right),\\ o_{\omega }\left(1\right)\underset{n\to \infty }{\to }0\left(\mathrm{with}\mathrm{Prob}.1\right)\end{array}$$

or, equivalently,

$$\begin{array}{c}{a}_n\stackrel{a.s.}{=}{\displaystyle \frac{{\displaystyle \frac{1}{n}}{\displaystyle \sum _{t=1}^n}\mathrm{E}\left\{y_t\left(a{y}_t+{\xi }_t+d{\xi }_{t-1}\right)\right\}}{{\displaystyle \frac{1}{n}}{\displaystyle \sum _{t=1}^n}\mathrm{E}\left\{y_t^2\right\}}}+o_{\omega }\left(1\right)=\\ a{\displaystyle \frac{{\displaystyle \frac{1}{n}}{\displaystyle \sum _{t=1}^n}\mathrm{E}\left\{y_t\left({\xi }_t+d{\xi }_{t-1}\right)\right\}}{{\displaystyle \frac{1}{n}}{\displaystyle \sum _{t=1}^n}\mathrm{E}\left\{y_t^2\right\}}}+o_{\omega }\left(1\right)=a+d{\displaystyle \frac{{\displaystyle \frac{1}{n}}{\displaystyle \sum _{t=1}^n}\mathrm{E}\left\{y_t{\xi }_{t-1}\right\}}{{\displaystyle \frac{1}{n}}{\displaystyle \sum _{t=1}^n}\mathrm{E}\left\{y_t^2\right\}}}+o_{\omega }\left(1\right).\end{array}$$

So, the corresponding identification error comes to be as

$$a_n-a\stackrel{a.s.}{=}d{\displaystyle \frac{{\displaystyle \frac{1}{n}}{\displaystyle \sum _{t=1}^n}\mathsf{E}\left\{y_t{\xi }_{t-1}\right\}}{{\displaystyle \frac{1}{n}}{\displaystyle \sum _{t=1}^n}\mathsf{E}\left\{y_t^2\right\}}}+o_{\omega }\left(1\right)$$

For stable models with $\left|a\right|<1$ there exist limits

$$\underset{n\to \infty }{lim}\mathrm{E}\left\{y_n{\xi }_{n-1}\right\}\mathrm{and}\underset{n\to \infty }{lim}\mathrm{E}\left\{y_n^2\right\}$$

and hence, by the Kronecker lemma

$$a_n-a\stackrel{a.s.}{=}d{\displaystyle \frac{{\displaystyle \underset{n\to \infty }{lim}}\mathrm{E}\left\{y_n{\xi }_{n-1}\right\}}{{\displaystyle \underset{n\to \infty }{lim}}\mathrm{E}\left\{y_n^2\right\}}}+o_{\omega }\left(1\right)$$

(19)

Let us calculate these limits. From (17), it follows

$$\mathsf{E}\left\{y_{n+1}{\xi }_n\right\}=a\mathrm{E}\left\{y_n{\xi }_n\right\}+\mathrm{E}\left\{{\xi }_n^2\right\}+d\mathrm{E}\left\{{\xi }_{n-1}{\xi }_n\right\}={\sigma }^2$$

(20)

$$\begin{array}{c}\mathrm{E}\left\{y_{n+1}^2\right\}=a^2\mathrm{E}\left\{y_n^2\right\}+\mathrm{E}\left\{{\xi }_n^2\right\}+d^2\mathrm{E}\left\{{\xi }_{n-1}^2\right\}+\\ 2a\mathrm{E}\left\{y_n{\xi }_n\right\}+2ad\mathrm{E}\left\{y_n{\xi }_{n-1}\right\}+2d\mathrm{E}\left\{{\xi }_{n-1}{\xi }_n\right\}=\\ a^2\mathsf{E}\left\{y_n^2\right\}+\left(1+d^2\right){\sigma }^2+2ad\mathrm{E}\left\{y_n{\xi }_{n-1}\right\}=\\ a^2\mathrm{E}\left\{y_n^2\right\}+\left(1+d^2\right){\sigma }^2+2ad{\sigma }^2\end{array}$$

(21)

Since, for the stable linear recursion

$$z_{n+1}=\overline{a}{z}_n+c,\left|\overline{a}\right|<1$$

we have

$$\begin{array}{c}{z}_{n+1}=\overline{a}{z}_n+c=\overline{a}\left(\overline{a}{z}_{n-1}+c\right)+c=\\ {\overline{a}}^2{z}_{n-1}+c+\overline{a}c=\cdots ={\overline{a}}^n{z}_1+c+\overline{a}c+{\overline{a}}^{2}c+\cdots +{\overline{a}}^{n}c=\\ {\overline{a}}^n{z}_1+c\left({\displaystyle \frac{1-{\overline{a}}^{n+1}}{1-\overline{a}}}\right)\underset{n\to \infty }{\to }{\displaystyle \frac{c}{1-\overline{a}}}.\end{array}$$

Then, for (21), we get

$$\begin{array}{c}\mathrm{E}\left\{y_n^2\right\}\to {\displaystyle \frac{\left(1+d^2\right)+2ad}{1-a^2}}{\sigma }^2=\\ {\displaystyle \frac{\left(1-a^2\right)+\left(a^2+2ad+d^2\right)}{1-a^2}}{\sigma }^2=\left[1+{\displaystyle \frac{{\left(a+d\right)}^2}{1-a^2}}\right]{\sigma }^2\end{array}$$

(22)

Substitute the obtained limits (20) and (22) into (19) leads to

$$\begin{array}{c}{a}_n-a\stackrel{a.s.}{=}d{\displaystyle \frac{{\sigma }^2}{\left[1+{\displaystyle \frac{{\left(a+d\right)}^2}{1-a^2}}\right]{\sigma }^2}}+o_{\omega }\left(1\right)=\\ d{\displaystyle \frac{1}{1+{\displaystyle \frac{{\left(a+d\right)}^2}{1-a^2}}}}+o_{\omega }\left(1\right)\stackrel{a.s.}{\underset{n\to \infty }{\to }}d{\displaystyle \frac{1}{1+{\displaystyle \frac{{\left(a+d\right)}^2}{1-a^2}}}}.\end{array}$$

The derivative calculation of the limit value with respect to d then gives

$${\left(d{\displaystyle \frac{1}{1+{\displaystyle \frac{{\left(a+d\right)}^2}{1-a^2}}}}\right)}^{\prime }=\left(a^2-1\right)\frac{d^2-1}{{\left(d^2+2ad+1\right)}^2}$$

So, the extremal points are $d=\pm 1,$ and hence,

$${\left(d{\displaystyle \frac{1}{1+\frac{{\left(a+d\right)}^2}{1-a^2}}}\right)}_{d=1}={\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{2}}a,{\left(d{\displaystyle \frac{1}{1+\frac{{\left(a+d\right)}^2}{1-a^2}}}\right)}_{d=-1}=-\frac{1}{2}a-\frac{1}{2}$$

These relations imply the following conclusion: the maximum bias of the LSM estimate is

$$\underset{d}{max}\underset{n\to \infty }{lim}\left|a_n-a\right|=\frac{1}{2}max\left\{\left|1-a\right|;\left|1+a\right|\right\}$$

The illustrative graphic ($x:=d$, $y:=\left|a_n-a\right|$ for $a=0.5$) is shown in Figure 1.

Conclusion: Be careful! The LS method does not work for identification of parameters of dynamic models with correlated noises!

As a result, certain unique approaches, distinct from LSM, must be developed.

4. Some Other Identification Techniques

Identification of Non-Stationary Parameters and Bayesian Method

Some other parameter estimation/identification methods have been proposed for more complex situations. In [37], a combination of recursive version of the IV method with the matrix forgetting factor was presented for identification of time-varying parameters for ARMAX models, showing that the identification error in average has a bound dependent on the rate of the parameter variation, as well as on the variance of the noise. The version of IV method with adaptive matrix forgetting factor was studied in [38]. In some cases equation-error and output-error approaches have been used to deal with the problem where all the observed variables are corrupted by noise. The parameter bounding by the bounded equation error and the bounded errors in variables based on these approaches was studied in [39]. Bayesian parameter estimation and prediction of lineal-in-parameters models under the presence of coloured noise is addressed in [40], and it is based on a model called ARMAX. This model is a finite mixture of ARMAX elements with a common ARX part. This ARX part described a fixed deterministic input–output relationship: this model is estimated using a recursive quasi-Bayes algorithm that relies on a classical Bayesian solution without restriction on the MA component. The proposed model provides flexibility with respect to varying characteristics of the model noise. The measurement errors that affect data entries make the estimation problem more complicated. A solution to this problem was proposed in [41] by enhancing the ARMAX models by including some additive error terms on the output, and then developing a moving horizon estimator for the extended ARMAX model. The proposed method then models the measurement errors as nuisance variables and these are estimated simultaneously with the states, and the identifiability was achieved by regularising the LS cost with the ${\ell }_2$ norm of the nuisance variables, leading to an optimisation problem with an analytical solution. The nuisance variables have been recently used to model the output noise, as well as the potentially existing outliers (see [27]). These outliers are regularised with the ${\ell }_2$ norm for the estimation, and the regularised estimator suppresses the influence of the output noise and provides a minimum-variance estimate.

For the continuous-time case, the LSM with forgetting factor has been implemented for estimating constant and time-varying parameters ([42,43,44]). The proposed algorithms in [45] showed a good performance, but the bias, as in the discrete-time case, affects the estimation. The estimation algorithm was implemented for additive and multiplicative noises (see [46]), and in both scenarios, LSM is affected by the noise level, showing that is not the best method for stochastic systems, either in discrete or continuous time. To deal with the bias problem, a method combining the equivalent control with LSM was proposed, these two algorithms working in parallel reduce the bias in the estimation even in the presence of coloured noises (see [47]).

5. Regular Observations and Information Inequality for Observations with Coloured Noise

In estimation theory and statistics [48,49], the Cramér–Rao bound (CRB) expresses a lower bound on the variance of unbiased estimators $c_n$ of a deterministic (fixed, though unknown) parameter c, stating that the variance of any such estimator is at least as high as the inverse of the Fisher information (FIM) ${\mathbb{I}}_F^{-1}\left(c,n\right)$. Namely, for every unbiased estimator $c_n$ (n is the number of available regular observations), an inequality of the type

$${\mathrm{Var}}_c\left(c_n\right)\ge {\mathbb{I}}_F^{-1}\left(c,n\right)$$

(23)

for every c in the parameter space C, it is called an information inequality, which plays a very important role in parameter estimation. The early works of Cramér (1946) [50] and Rao (1945) [51] introduced the Cramer–Rao inequality for regular density functions. Later, Vincze (1979) [52] and Khatri (1980) (see [53]) introduced information inequalities by imposing the regularity assumptions on a priori distribution rather than on the model. An unbiased estimator which achieves this lower bound is usually said to be (fully) efficient. This is a solution that achieves the lowest possible mean squared error among all unbiased methods, and therefore is the minimum variance unbiased (MVU) estimator. However, in some cases, there are no unbiased techniques that achieve this bound. This may occur either if for any unbiased estimator there exists another estimator with a strictly smaller variance, or if an MVU estimator exists but its variance is strictly greater than the inverse of the Fisher information. The Cramér–Rao bound (37) can also be used to bound the variance of biased estimators of given bias. In some cases, a biased approach can result in both a variance and a mean squared error that are below the unbiased Cramér–Rao lower bound.

Recall some important definitions.

5.1. Main Definitions and the Cramer–Rao Information Inequality

In a general case, the observable output sequence ${\mathbf{y}}_n:=\left\{y_1,y_2,\dots ,y_n\right\}$ may be of a vector type $\left(y_t\in {\mathbb{R}}^L\right)$ containing the information on the parameter $c\in {\mathbb{R}}^N$. The function $p\left({\mathbf{y}}_n\mid c\right),$ $c\in C\subseteq {\mathbb{R}}^N$ is called the joint density of the distribution of the vector ${\mathbf{y}}_n$. Any Borel function $c_n=c_n\left({\mathbf{y}}_n\right)\in {\mathbb{R}}^N$ can be considered as an estimate of the parameter c.

Definition 1.

The vector-function

$$\begin{array}{c}{m}_n\left(c\right)=\mathrm{E}\left\{c_n\right\}=\underset{Y_n}{\int }{c}_n\left({\mathbf{y}}_n\right)p\left({\mathbf{y}}_n\mid c\right)d{\mathbf{y}}_n\in {\mathbb{R}}^N,\\ Y_n=\left\{{\mathbf{y}}_n\mid p\left({\mathbf{y}}_n\mid c\right)>0,c\in C\right\},\end{array}$$

is referred to as the averaged value of the estimate $c_n$, based on available observations ${\mathbf{y}}_n$;

−

If $m_n\left(c\right)=c,$ then the estimate $c_n$ is called unbiased and asymptotically unbiased if ${lim}_{n\to \infty }{m}_n\left(c\right)=c$.

−

The observations ${\mathbf{y}}_n$ are referred to be as regular on the class C of parameters if

$$\underset{c\in C}{sup}\mathrm{E}\left\{{∥lnp\left({\mathbf{y}}_n\mid c\right)∥}^2\right\}=\underset{c\in C}{sup}\underset{Y_n}{\int }{∥lnp\left({\mathbf{y}}_n\mid c\right)∥}^{2}p\left({\mathbf{y}}_n\mid c\right)d{\mathbf{y}}_n<\infty ,$$

(24)

and for any $c\in C$

$$\begin{array}{c}{\mathbb{I}}_F\left(c,n\right)=\mathrm{E}\left\{{\nabla }_{c}lnp\left({\mathbf{y}}_n\mid c\right){\nabla }_c^{⊺}lnp\left({\mathbf{y}}_n\mid c\right)\right\}=\\ \underset{Y_n}{\int }\left[{\nabla }_{c}lnp\left({\mathbf{y}}_n\mid c\right){\nabla }_c^{⊺}lnp\left({\mathbf{y}}_n\mid c\right)\right]p\left({\mathbf{y}}_n\mid c\right)d{\mathbf{y}}_n>0.\end{array}$$

(25)

−

The matrix ${\mathbb{I}}_F\left(c,n\right)$ is called the Fisher information matrix for the set of available observations ${\mathbf{y}}_n$.

As it was mentioned in [54], when the Fisher information takes into account the stochastic complexity and the associated universal processes are derived for a class of parametric processes. The main condition required is that the maximum likelihood estimates satisfy the central limit theorems.

In some cases, the Fisher information matrix (FIM) is required to be non-singular (25) to guarantee the observability of the system (see [55]). The algebraic properties of FIM for stationary processes have been widely studied, for example there is a survey paper written by André Klein where this study is presented [56]. The FIM is necessary for the Cramer–Rao inequality; it is a basic tool for estimation theory in mathematical statistics, and in stationary processes is related to the solution of Stein equations. A procedure to compute the theoretical periodic autocovariance function in terms of the parameters of the periodic model for periodic autoregressive moving average models was presented in [57], where the necessary and sufficient condition for non-singular FIM of a periodic ARMA model was calculated. So, the Fisher information matrix for the Gaussian case in ARMAX processes has been previously studied. In [58], an algorithm composed by Chandrasekhar recursion equations at a vector-matrix level was proposed, where the recursions consist of derivatives based on appropriate differential rules that are applied to a state space model for a vector process. The recursions obtained were given in terms of expectations of derivatives of innovations.

Theorem 1.

Cramer–Rao information inequality. For any set $Y_n$ of regular observations, and for any estimate $c_n$ with differentiable averaged value function $m_n\left(c\right)$ the following inequality holds

$$\begin{array}{c}\mathrm{E}\left\{\left(c_n-c\right){\left(c_n-c\right)}^{⊺}\right\}\ge \\ \left[m_n\left(c\right)-c\right]{\left[m_n\left(c\right)-c\right]}^{⊺}+\nabla m_n\left(c\right){\mathbb{I}}_F^{-1}\left(c,n\right){\nabla }^{⊺}{m}_n\left(c\right).\end{array}$$

(26)

Corollary 1.

For unbiased estimates satisfying $m_n\left(c\right)=c,$ $\nabla m_n\left(c\right)=I_{n\times n},$ the Cramer–Rao inequality becomes

$$\mathrm{E}\left\{\left(c_n-c\right){\left(c_n-c\right)}^{⊺}\right\}\ge {\mathbb{I}}_F^{-1}\left(c,n\right).$$

(27)

This inequality is widely used in discrete-time systems for various purposes. The posterior Cramer–Rao bound on the mean square error in tracking the bearing, bearing rate and power level of a narrowband source is developed in [59]. Their formulation used a lineal process model with additive noise and a general nonlinear measurement model, where the measurements are the sensor array data. This bound can be applied to multidimensional nonlinear and possibly non-Gaussian systems. In [60], the case of a singular conditional distribution of the one-step-ahead state vector given the present state was considered. The bound was evaluated for recursive estimation of slowly varying parameters of AR processes, tracking a slowly varying single cisoid in noise and tracking the parameters of a sinusoidal frequency with a sinusoidal phase modulation. A variation of the Cramer–Rao inequality is the Cramer–Rao–Frechet inequality, which has been applied for discrete-time nonlinear filtering. In [61], this inequality was reviewed and extended to track fitting, where it is shown that the inequality does not cause the limitations of the resolution of the track fits with a certain number of observations, and that the inequality remains valid even in irregular models supporting the similar improvement of resolution for realistic models.

5.2. Fisher Information Matrix Calculation

Using the Bayes formula

$$\begin{array}{c}p\left({\mathbf{y}}_n\mid c\right)=p\left(y_n\mid {\mathbf{y}}_{n-1};c\right)p\left({\mathbf{y}}_{n-1}\mid c\right)=\\ \cdots =\left[{\displaystyle \prod _{k=1}^n}p\left(y_k\mid {\mathbf{y}}_{k-1};c\right)\right]p\left(y_0\mid c\right),\end{array}$$

for the likelihood function $L_n\left({\mathbf{y}}_n\mid c\right)=-lnp\left({\mathbf{y}}_n\mid c\right)$ we have the following representation:

$$L_n\left({\mathbf{y}}_n\mid c\right)=-lnp\left({\mathbf{y}}_n\mid c\right)=-{\displaystyle \sum _{k=1}^n}lnp\left(y_k\mid {\mathbf{y}}_{k-1};c\right)-lnp\left(y_0\mid c\right).$$

(28)

Define also

$$\begin{array}{c}{u}_t\left(c\right)={\nabla }_c{L}_t\left({\mathbf{y}}_t\mid c\right)-{\nabla }_c{L}_{t-1}\left({\mathbf{y}}_{t-1}\mid c\right)=\\ -{\displaystyle \frac{{\nabla }_{c}p\left(y_t\mid {\mathbf{y}}_{t-1};c\right)}{p\left(y_t\mid {\mathbf{y}}_{t-1};c\right)}}=-{\nabla }_{c}lnp\left(y_t\mid {\mathbf{y}}_{t-1};c\right),\end{array}$$

which is a martingale difference, since $\mathrm{E}\left\{u_t\left(c\right)\mid {\mathcal{F}}_{t-1}\right\}\stackrel{a.s.}{=}0,$ and satisfies the property

$${\nabla }_c{u}_t\left(c\right)=-{\displaystyle \frac{{\nabla }_c^{2}p\left(y_t\mid {\mathbf{y}}_{t-1};c\right)}{p\left(y_t\mid {\mathbf{y}}_{t-1};c\right)}}+{\displaystyle \frac{{\nabla }_{c}p\left(y_t\mid {\mathbf{y}}_{t-1};c\right){\nabla }_c^{⊺}p\left(y_t\mid {\mathbf{y}}_{t-1};c\right)}{p^2\left(y_t\mid {\mathbf{y}}_{t-1};c\right)}}.$$

(29)

For regular unbiased observations, the Fisher information matrix ${\mathbb{I}}_F\left(c,n\right)$ can be calculated as

$$\left.\begin{array}{c}{\mathbb{I}}_F\left(c,n\right)={\displaystyle \sum _{k=1}^n}\mathrm{E}\left\{u_k{u}_k^{⊺}\right\}={\displaystyle \sum _{k=1}^n}\mathrm{E}\left\{{\nabla }_c{u}_k\left(c\right)\right\}=\\ \mathrm{E}\left\{{\displaystyle \sum _{k=1}^n}{\displaystyle \frac{{\nabla }_{c}p\left(y_k\mid {\mathbf{y}}_{k-1};c\right){\nabla }_c^{⊺}p\left(y_k\mid {\mathbf{y}}_{k-1};c\right)}{p^2\left(y_k\mid {\mathbf{y}}_{k-1};c\right)}}\right\}=\\ \mathrm{E}\left\{{\displaystyle \sum _{k=1}^n}{\nabla }_{c}lnp\left(y_k\mid {\mathbf{y}}_{k-1};c\right){\nabla }_c^{⊺}lnp\left(y_k\mid {\mathbf{y}}_{k-1};c\right)\right\}.\end{array}\right\}$$

(30)

5.3. Asymptotic Cramer–Rao Inequality

Multiplying both sides of (27) by n we get

$$n\mathrm{E}\left\{\left(c_n-c\right){\left(c_n-c\right)}^{⊺}\right\}\ge {\left(\frac{1}{n}{\mathbb{I}}_F\left(c,n\right)\right)}^{-1}.$$

Taking $n\to \infty$ we get

$$\underset{n\to \infty }{lim\; inf}n\mathrm{E}\left\{\left(c_n-c\right){\left(c_n-c\right)}^{⊺}\right\}\ge {\mathbb{I}}_F^{-1}\left(c\right),$$

(31)

where

$${\mathbb{I}}_F\left(c\right):=\underset{n\to \infty }{lim\; sup}{\displaystyle \frac{1}{n}}{\mathbb{I}}_F\left(c,n\right)=\underset{n\to \infty }{lim\; sup}\mathrm{E}\left\{{\displaystyle \frac{1}{n}}{\displaystyle \sum _{k=1}^n}{u}_k\left(c\right)u_k^{⊺}\left(c\right)\right\}>0.$$

Remark 2.

In view of (29) it follows

$${\mathbb{I}}_F\left(c\right)=\underset{n\to \infty }{lim\; sup}{\displaystyle \frac{1}{n}}\mathrm{E}\left\{{\nabla }_c^2{L}_n\left({\mathbf{y}}_t\mid c\right)\right\}.$$

(32)

5.4. Whitening Process for Stable and Minimal-Phase Forming Filters

Although additive Gaussian white noise is widely used, in many research areas the present noises are non-Gaussian. In some cases, detectors are used to whiten the data and then the estimation/identification is performed (see for example [62]). In the presence of non-white noises, one of the most common methods to deal with this perturbation is a whitening filter. A transfer function of an estimated noise can be used to filter the input–output data of the system and presents a filtering-based recursive analogue of the LSM algorithm for the ARMAX model. In [63], it is shown that through data filtering one can obtain two identification models, the first one including the parameter of the system model and the second including the parameter of the noise model; this can lead to a more accurate parameter estimation. A whitening filter can be applied in coloured Gaussian noises when there is a residual white noise component present. The existence of a realisable whitening filter is demonstrated in [64].

The model (14) can be symbolically represented as

$$y_n=z_n^{⊺}c+{\eta }_n=z_n^{⊺}c+{\displaystyle \frac{H_1\left(q\right)}{H_2\left(q\right)}}{\xi }_n.$$

(33)

In view of the Assumption 4, the polynomials $H_1\left(q\right)$ and $H_2\left(q\right)$ are stable and, hence, we are able to apply the inverse operator ${\displaystyle \frac{H_2\left(q\right)}{H_1\left(q\right)}}$ to both sides of the model (33), obtaining

$$\begin{array}{c}{\tilde{y}}_n={\displaystyle \frac{H_2\left(q\right)}{H_1\left(q\right)}}{y}_n,{\tilde{y}}_{-s}:=0,s=0,1,\dots ,K_1,\\ {\tilde{z}}_n={\displaystyle \frac{H_2\left(q\right)}{H_1\left(q\right)}}{z}_n,{\tilde{z}}_{-s}:=0,s=0,1,\dots ,K_1,\\ {\tilde{\xi }}_n:={\displaystyle \frac{H_2\left(q\right)}{H_1\left(q\right)}}{\displaystyle \frac{H_1\left(q\right)}{H_2\left(q\right)}}{\xi }_n\stackrel{a.s.}{=}{\xi }_n+O_{\omega }\left({\lambda }^n\right),\left|\lambda \right|<1,\end{array}$$

(34)

where $\lambda$ is one of the eigenvalues of the polynomials $H_1\left(q\right)$ and $H_2\left(q\right)$ which is most close to the unitary circle. The function $O_{\omega }\left({\lambda }^n\right)$ is a random process, defined on $\left(\mathsf{\Omega },\mathcal{F},P\right)$ and such that

$$0\stackrel{a.s.}{<}\underset{n}{lim\; inf}{O}_{\omega }\left({\lambda }^n\right)/{\lambda }^n\le \underset{n}{lim\; sup}{O}_{\omega }\left({\lambda }^n\right)/{\lambda }^n\le \mathrm{const}\left(\omega \right)\stackrel{a.s.}{<}\infty .$$

So, finally, after the “whitening process” (inverse operator) application we get

$${\tilde{y}}_n={\tilde{z}}_n^{⊺}c+{\tilde{\xi }}_n.$$

(35)

Remark 3.

This means that on-line application of the “whitening process” to the initial model (33) permits considering the corresponding transformed model (34) which deals with “quasi” white noise ${\tilde{\xi }}_n$ exponentially quickly, tending to the exact white noise ${\xi }_n$, fulfilling

$$∥{\tilde{\xi }}_n-{\xi }_n∥=O_{\omega }\left({\lambda }^n\right)\stackrel{a.s.}{\to }0$$

when $n\to \infty$. This permits to represent (35) as

$${\tilde{y}}_n={\tilde{z}}_n^{⊺}c+{\xi }_n+O_{\omega }\left({\lambda }^n\right).$$

(36)

5.5. Cramer–Rao Inequality for ARMAX Models with a Generating Noise from the Class ${\mathcal{P}}_{\xi }$ of p.d.f.

Theorem 2.

The Cramer–Rao inequality (see [15]) in the form (31) is

$$\left.\begin{array}{c}\underset{n\to \infty }{lim\; inf}n\mathrm{E}\left\{\left(c_n-c\right){\left(c_n-c\right)}^{⊺}\right\}\ge {\displaystyle \underset{p_{\xi }\in {\mathcal{P}}_{\xi }}{sup}}{\mathbb{I}}_F^{-1}\left(c\right)=\\ {\displaystyle \underset{p_{\xi }\in {\mathcal{P}}_{\xi }}{sup}}{\left(I_{F,\xi }\left(p_{\xi }\right)\mathcal{R}\left(p_{\xi }\right)\right)}^{-1}\end{array}\right\}$$

(37)

where

$$\left.\begin{array}{c}\mathcal{R}\left(p_{\xi }\right):={\displaystyle \underset{n\to \infty }{lim\; sup}}{\displaystyle \frac{1}{n}}{\displaystyle \sum _{k=1}^n}\mathrm{E}\left\{{\tilde{z}}_k{\tilde{z}}_k^{⊺}\right\},\\ I_{F,\xi }\left(p_{\xi }\right)=\mathrm{E}\left\{{\left({\displaystyle \frac{\partial }{\partial \xi }}ln{p}_{\xi }\left(\xi \left(\omega \right)\right)\right)}^2\right\}=\underset{x\in {\mathbb{R}}^1}{\int }{\displaystyle \frac{{\left(\frac{\partial }{\partial x}{p}_{\xi }\left(x\right)\right)}^2}{p_{\xi }\left(x\right)}}dx.\end{array}\right\}$$

(38)

Remark 4.

In the regression case $\left(a_l=0,l=1,\dots ,L\right)$ the matrix $\mathcal{R}$ (38) does not depend on $p_{\xi }.$

Conclusion. According to the information inequality (37), the “best” (asymptotically optimum or efficient) estimate $c_n^{*}$ of the parameter $c\in C$ is the one that achieves equality in the (37). The inequality given by (37) implies that after n regular observations ${\mathbf{y}}_n$ the covariance matrix of the estimation error $\left(c_n-c\right)$, which defines the quality of the estimation process, can not be less than the corresponding Fisher information matrix (25). In other words, the Fisher information matrix (25) will define the maximal possible quality of the identification process, which can not be improved by any other identification algorithm.

6. Robust Version of Maximum Likelihood Method with Whitening: MLMW Procedure

For parameter estimation and system modelling, the maximum likelihood technique is critical. The maximum of the likelihood function in Gaussian case is equivalent to minimising the least-squares cost function [65]. In this paper, a recursive maximum likelihood least-squares identification algorithm for systems with autoregressive moving average noises was derived. The maximum likelihood has been widely implemented under Gaussian perturbations, for example in [66], the Gaussian likelihood function was studied when data are generated by a high-order continuous-time ARMAX mode, and these data are observed as stocks and flows at different frequencies. The maximum likelihood method can be modified using the stochastic gradient; this modification was presented in [67], where this modification was proposed for ARMAX models. In this case, the modified algorithm can estimate unknown parameters and the unknown noise simultaneously, with less computational cost and better accuracy. Non-asymptotic deviations bounds for least-squared estimation in Gaussian AR processes have been recently studied (see [68]). The study relies on martingale concentration inequalities and tail bound for ${\chi }^2$-distributed variables; in the end, they provided a concentration bound for the sample covariance matrix of the process output.

6.1. Whitening Method and Its Application

The whitening method is commonly used to prevent the bias problem [69]. A modified version of direct whitening method, which is called MDWM, was proposed as an ARMA model parameter estimation technique in [70]. The proposed direct whitening method (DWM) provides the parameter estimates which make the prediction errors uncorrelated, in some cases this algorithms might fall at local minima and give parameter estimates. To deal with this problem, an MDWM which chooses the consistent estimates among a large number of DWM estimates can be implemented. Pre-whitening can be performed with first order differentiation of signals and/or the implementation of an inverse filter based on linear prediction, as it is shown in [71], where the whitening was the previous step in a cross-correlation method for identifying aircraft noise, showing that whitening can be successfully developed for real-time operation in the detection of correlation peaks. An iterative procedure for minimising and whitening the residual of the ARMAX model was presented in [72], since usually when the system is identified from input–output data in the time domain, it is assumed that the data is enough and the ARX model order is large enough. The results show that in the residual whitening method we can use an ARMAX model that includes the noise dynamics, instead of an ARX model, and the properties of the residual sequence, such as the orthogonal conditions, can convert to the optimal properties of the Kalman filter. The influence function is an analysis tool in robust statistics we used to formulate a recursive solution for ARMAX processes filtering in [73], in particular for a t-distribution noise. The filter was formulated as a maximum likelihood problem, where an influence function approximation was used to obtain a recursive solution to reduce computational load and facilitate the implementation.

Whitening techniques have also been implemented for noise cancellation, in [74] is the base for an approach to adaptive white noise cancellation based on adaptive control principles. In this case, the goal was to create a physical noise-reduced environment at the vicinity of noisy machinery for a stochastic machine noise. Another method implemented for filtering is signal smoothing when the data are generated (or represented) by an autoregressive moving average with exogenous inputs (ARMAX) model. In the case presented in [75], the original ARMAX recurrence relation is used and combined with a constrained LS optimisation to filter the system as well as the measurement noise components and estimate the desired signal in the form of a block-wise matrix formulation.

Whitening processes are a very useful pre-processing technique to deal with the presence of non-white noises, and the improve the estimation results regardless of the estimation algorithm used [76]. In [77], a residual whitening method enforces the properties of the Kalman filter for a finite set of data. This technique has been implemented in ARMAX models for the identification of inductor motor systems. The importance of the study and development of estimation/identification algorithms for ARMAX models with coloured noises relies on the importance of this model in various areas of study and its many applications. The identification of the ARMAX models allows the implementation of control techniques, such as the predictive control presented in [78], which is applied for the control of a pneumatic actuator based on an ARX model built by a neural network. There, the control showed a quick response and an accurate tracking. The estimation has been implemented for electromechanical modes and mode shapes for multiple synchrophasors (see [79]). Their approach was based on identifying the transfer function of the state space model of a linearised power system through the estimation of a multichannel ARMAX mode, and it was simulated using data from a reduced-order model of the Western Electricity Coordinating Council (WECC) system. The ARMAX model has been used to model an outlet temperature of the first-stage cyclone pre-heater in the cement firing system (see [80]). In that case, a Butterworth low-pas filter and normalized processing are used to process a cement firing system data, and the input variables modelled are selected by the Pearson correlation analysis. The parameters of the model were identified using a recursive maximum likelihood algorithm, and the results validated with a residual analysis method.

Econometrics is an area where the estimation/identification of ARMAX models (the integral version of the ARMAX model) has great importance (see [66,81,82]). The integration of macroeconomic indicators in the accuracy of throughput time-series forecasting model can be addressed using ARMAX models, as it is shown in [83]. There, the dynamic factors are extracted from external macroeconomic indicators influencing the observed throughput, and then a family of ARMAX models is generated based on derived factors. This model can be used to produce future forecasts. Some variations of the ARMAX model, such as the autoregressive moving average explanatory input model of the Koyck kind (KARMAX) are also used in econometrics. Another interesting application in econometrics is presented in [84], where it is shown how the recent deregulation of the electricity industry and reliance on competitive wholesale markets has generated significant volatility in wholesale electricity prices. Due to the importance of short-term price forecasts, an estimation and evaluation of the forecasting performance of four ARMAX–GARCH models for five MISO pricing hubs (Cinergy, First Energy, Illinois, Michigan and Minnesota) using hourly data from 1 June 2006 to 6 October 2007 is given. In this study, the importance of the patterns of the electricity price volatility is shown, as well as the volatility dynamics regulated by the states.

In [85], an identification algorithm is presented, where the debt management in indebted poor countries is studied, using data from the World Bank database from 1970 to 2018 based on the maximum likelihood method, and then comparing the results with prediction error and the instrumental variable methods.

6.2. Recurrent Robust Identification Procedures with Whitening and a Nonlinear Residual Transformation

Consider the following class of recurrent identification procedures [15] which may be applied to the transformed model (36):

$$\left.\begin{array}{c}{c}_n=c_{n-1}+{\mathsf{\Gamma }}_n{\tilde{z}}_n\phi \left({\tilde{y}}_n-{\tilde{z}}_n^{⊺}{c}_{n-1}\right)\\ c_0—\mathrm{any}\mathrm{given}\mathrm{value}\\ {\mathsf{\Gamma }}_n={\left({\displaystyle \sum _{t=0}^n}{\tilde{z}}_t{\tilde{z}}_t^{⊺}\right)}^{-1},n\ge n_0:=\left\{{\displaystyle \underset{k}{min}}{\displaystyle \sum _{t=0}^n}{\tilde{z}}_t{\tilde{z}}_t^{⊺}\right\}>0.\end{array}\right\}$$

(39)

Remark 5.

Notice that ${\mathsf{\Gamma }}_n$ in (39) can be calculated recursively (as in the least-square method)

$${\mathsf{\Gamma }}_n={\mathsf{\Gamma }}_{n-1}-{\displaystyle \frac{{\mathsf{\Gamma }}_{n-1}{\tilde{z}}_n{\tilde{z}}_n^{⊺}{\mathsf{\Gamma }}_{n-1}}{1+{\tilde{z}}_n^{⊺}{\mathsf{\Gamma }}_{n-1}{\tilde{z}}_n}},n\ge n_0,$$

(40)

and possesses (in the accepted assumptions) the following property

$$\begin{array}{c}{\mathsf{\Gamma }}_n\stackrel{a.s.}{\simeq }{\displaystyle \frac{1}{n}}{\mathcal{R}}^{-1}\\ \mathcal{R}={\displaystyle \underset{n\to \infty }{lim}}{\displaystyle \frac{1}{n}}{\displaystyle \sum _{k=1}^n}\mathrm{E}\left\{{\tilde{z}}_k^{⊺}{\tilde{z}}_k\right\}>0.\end{array}$$

(41)

Theorem 3

([15]). If

1. 

${\xi }_n$ is i.i.d. sequence with

$$\mathrm{E}\left\{{\xi }_n\right\}=0,\mathrm{E}\left\{{\xi }_n^2\right\}={\sigma }^2>0,\mathrm{E}\left\{{\xi }_n^4\right\}=\mathrm{E}\left\{{\xi }_1^4\right\}<\infty .$$

2. 

The nonlinear transformation $\phi :\mathbb{R}\to \mathbb{R}$ satisfies the conditions

$$x\psi \left(x\right)\ge \delta x^2,\delta >0,\psi \left(0\right)=0,S\left(x\right)\le k_0+k_1{x}^2,$$

with

$$\psi \left(x\right)=\mathrm{E}\left\{\phi \left(x+{\xi }_n\right)\right\},S\left(x\right):=\mathrm{E}\left\{{\phi }^2\left(x+{\xi }_n\right)\right\},$$

then

$${\Delta }_n=c_n-c\underset{n\to \infty }{\stackrel{a.s.}{\to }}0.$$

(42)

Following to Lemma 13.7 in [36] and defining a new process ${\{{\tilde{\Delta }}_n\}}_{n\ge 0}$ as

$${\tilde{\Delta }}_n=\left[1-{\displaystyle \frac{{\psi }^{\prime }\left(0\right)}{n}}\right]{\tilde{\Delta }}_{n-1}+{\displaystyle \frac{1}{n}}{\mathcal{R}}^{-1}{\tilde{z}}_n\left(o_{\omega }\left(1\right)+{\zeta }_n\right),{\tilde{\Delta }}_0={\Delta }_0,$$

(43)

we may formulate the following auxiliary result.

Theorem 4

(on $\sqrt{n}$-equivalency). Under the assumptions of Theorem 3, the process (42) is $\sqrt{n}$-equivalent to the process (43), that is,

$$\sqrt{n}\left({\Delta }_n-{\tilde{\Delta }}_n\right)\underset{n\to \infty }{\stackrel{a.s.}{\to }}0.$$

(44)

The property of the asymptotic normality of the process ${\left\{\sqrt{n}{\Delta }_n\right\}}_{n\ge 0}$ helps us to estimate the exact rate of convergence (not only the order of convergence, but also its constant) of the identification procedure (39).

Theorem 5

(on asymptotic normality). Suppose that the conditions of Theorem 3 are fulfilled and, additionally,

$$\psi \left(0\right)=0,S\left(0\right)>0,{\psi }^{\prime }\left(0\right)>1/2.$$

(45)

Then, the process ${\left\{\sqrt{n}{\Delta }_n\right\}}_{n\ge 0}$ is asymptotically normal

$$\sqrt{n}{\Delta }_n\underset{n\to \infty }{\stackrel{d}{\to }}\mathcal{N}\left(0,V\right),$$

(46)

with the covariation matrix V, equal to

$$V={\displaystyle \frac{S\left(0\right)}{2{\psi }^{\prime }\left(0\right)-1}}{\mathcal{R}}^{-1}.$$

(47)

It results directly from Theorem 13.6 in [36].

Remark 6.

The matrix V defines the rate of the convergence of the procedure (39), that is

$${\Delta }_n\underset{n\to \infty }{\stackrel{d}{\to }}\mathcal{N}\left(0,n^{-1}V\right).$$

As it follows from (47), V depends on a real noise density distribution $p_{\xi }$ (since $S\left(0\right)$, ${\psi }^{\prime }\left(0\right)$ and $\mathcal{R}$ may be dependent on $p_{\xi })$ and on a nonlinear function $\phi$ (through $S\left(0\right)$ and ${\psi }^{\prime }\left(0\right)$). That’s why, to emphasise this dependence, we use the notation

$$V=V\left(p_{\xi },\phi \right).$$

Following [13,14], let us introduce the main definition of this section.

Definition 2.

The pair of functions given by $\left(p_{\xi }^{*},{\phi }^{**}\right)$ define the estimating procedure (54) with the nonlinear residual transformation ${\phi }^{*},$ which is robust with respect to a distribution $p_{\xi }$, belonging to a class ${\mathcal{P}}_{\xi }$, if for any admissible φ, satisfying the assumptions of Theorem 5, and any generating noise distribution $p_{\xi }\in {\mathcal{P}}_{\xi }$ the following “saddle-point” inequalities hold:

$$V\left(p_{\xi },{\phi }^{**}\right)\le V\left(p_{\xi }^{*},{\phi }^{**}\right)\le V\left(\phi ,p_{\xi }^{*}\right).$$

(48)

Here, both inequalities should be treated in a “matrix sense”, that is,

$$A=A^{⊺}\le B=B^{⊺}ifB-A\ge 0.$$

In other words:

−

The distribution $p_{\xi }^{*}$ is the “worst” within the class ${\mathcal{P}}_{\xi }$.

−

The nonlinear transformation ${\phi }^{**}$ is “the best one” oriented on the “worst” noise with the distribution $p_{\xi }^{*}$.

This can be expressed mathematically as follows:

$$\left.\begin{array}{c}{\phi }^{**}=arg{\displaystyle \underset{\phi }{inf}}{\displaystyle \underset{p_{\xi }\in {\mathcal{P}}_{\xi }}{sup}}V\left(p_{\xi },\phi \right),\\ p_{\xi }^{*}=arg{\displaystyle \underset{p_{\xi }\in {\mathcal{P}}_{\xi }}{sup}}{\displaystyle \underset{\phi }{inf}}V\left(p_{\xi },\phi \right),\end{array}\right\}$$

(49)

so that

$$\underset{\phi }{inf}\underset{p_{\xi }\in {\mathcal{P}}_{\xi }}{sup}V\left(p_{\xi },\phi \right)=\underset{p_{\xi }\in {\mathcal{P}}_{\xi }}{sup}\underset{\phi }{inf}V\left(p_{\xi },\phi \right):=V^{*}.$$

(50)

According to (37), for any fixed $p_{\xi }\in {\mathcal{P}}_{\xi }$

$$\underset{\phi }{inf}V\left(p_{\xi },\phi \right)=\underset{\phi }{inf}\left({\displaystyle \frac{S\left(0\right)}{2{\psi }^{\prime }\left(0\right)-1}}{\mathcal{R}}^{-1}\right)\ge \underset{p_{\xi }\in {\mathcal{P}}_{\xi }}{sup}{\left[I_{F,\xi }\left(p_{\xi }\right)\mathcal{R}\left(p_{\xi }\right)\right]}^{-1}$$

(51)

Lemma 1

([15]). The low bound in (51) coincides with the Cramer–Rao bound (37) and is achieved when the nonlinear function in (39) is

$${\phi }^{**}\left(v\right)=-I_{F,\xi }^{-1}\left(p_{\xi }^{*}\right){\displaystyle \frac{d}{dv}}ln{p}_{\xi }^{*}\left(v\right)$$

(52)

with

$$p_{\xi }^{*}=arg\underset{p_{\xi }\in {\mathcal{P}}_{\xi }}{sup}{\left[I_{F,\xi }\left(p_{\xi }\right)\mathcal{R}\left(p_{\xi }\right)\right]}^{-1}$$

(53)

In other words, this lemma states that the nonlinear residual transformation ${\phi }^{**}$ (52) is robust with respect to distributions $p_{\xi }\in {\mathcal{P}}_{\xi }$.

So, the asymptotically optimal recurrent robust identification procedure (39) for coloured noise perturbations in (33) is

$$\left.\begin{array}{c}{c}_n=c_{n-1}-{\mathsf{\Gamma }}_n{\tilde{z}}_n{I}_{F,\xi }^{-1}\left(p_{\xi }^{*}\right){\displaystyle \frac{d}{dv}}ln{p}_{\xi }^{*}\left(v\right){\mid }_{v={\tilde{y}}_n-{\tilde{z}}_n^{⊺}{c}_{n-1}}\\ {\mathsf{\Gamma }}_n={\mathsf{\Gamma }}_{n-1}-{\displaystyle \frac{{\mathsf{\Gamma }}_{n-1}{\tilde{z}}_n{\tilde{z}}_n^{⊺}{\mathsf{\Gamma }}_{n-1}}{1+{\tilde{z}}_n^{⊺}{\mathsf{\Gamma }}_{n-1}{\tilde{z}}_n}},n\ge n_0,\end{array}\right\}$$

(54)

which in fact is the maximum likelihood recurrent procedure with the worst p.d.f. $p_{\xi }^{*}\left(v\right)$ on the given class ${\mathcal{P}}_{\xi }.$

Remark 7.

Notice that for the class of ARMAX models with coloured noises and regular observations, there does not exist any other algorithm providing, asymptotically, a rate of convergence better than the suggested procedure (54).

As we can see, whitening is a pre-processing step in the estimation process which can be applied simultaneously with the identification procedure (54). In [86], this step was implemented in the blind source separation process, where a robust whitening is based on the eigenvalue decomposition of a positive definite linear combination of correlation matrices.

This problem can be addressed analysing the noise power spectra density. This has been implemented by identifying the noise power spectral density of interferometric detectors using parametric techniques (see [87]). This is an adaptive technique used to identify and to whiten data provided my the interferometric detectors. The least-squares lattice filter proved to be the best among the analysed filters. One of the applications for this technique was presented in [88] where it was implemented for gravitational data wave analysis. There, it is shown how it is possible to estimate the noise power spectral density of gravitational wave detectors using parametric techniques, and it also shows how is it possible to whiten the noise data before they pass the detection algorithms.

6.3. Particular Cases for Static (Regression) Models

Recall that for regression models $\left(a_l=0,l=1,\dots ,L\right)$ the matrix $\mathcal{R}$ does not depend on p.d.f. $p_{\xi },$ and the relation (53) becomes

$$p_{\xi }^{*}\left(v\right)=arg\underset{p_{\xi }\in {\mathcal{P}}_{\xi }}{sup}{\left[I_{F,\xi }\left(p_{\xi }\right)\right]}^{-1}=arg\underset{p_{\xi }\in {\mathcal{P}}_{\xi }}{inf}{I}_{F,\xi }\left(p_{\xi }\right).$$

Lemma 2.

In the class ${\mathcal{P}}_{\xi }^1:=\left\{p_{\xi }:p_{\xi }\left(0\right)\ge {\displaystyle \frac{1}{2a}}>0\right\}$ (5) the worth distribution density $p_{\xi }^{*}\left(x\right)$ is the Laplace p.d.f. given by

$$p_{\xi }^{*}\left(x\right)=arg\underset{p_{\xi }\in {\mathcal{P}}_{\xi }^1}{inf}{I}_{F,\xi }\left(p_{\xi }\right)={\displaystyle \frac{1}{2a}}exp\left\{-{\displaystyle \frac{\left|x\right|}{a}}\right\}.$$

(55)

See Figure 2.

Corollary 2.

The robust on ${\mathcal{P}}_{\xi }^1$ version of the procedure (54) contains

$${\phi }^{**}\left(x\right)=-I_{F,\xi }^{-1}\left(p_{\xi }^{*}\right){\displaystyle \frac{d}{dv}}ln{p}_{\xi }^{*}\left(v\right)=a\mathrm{sign}\left(x\right)$$

(56)

Lemma 3.

In the class ${\mathcal{P}}_{\xi }^2:=$ $\left\{p_{\xi }:\underset{\mathbb{R}}{\int }{x}^2{p}_{\xi }\left(x\right)ds\le {\sigma }^2<\infty \right\}$ (6), the worth distribution density $p_{\xi }^{*}\left(x\right)$ is the Laplace p.d.f. given by

$$p_{\xi }^{*}\left(x\right)=arg\underset{p_{\xi }\in {\mathcal{P}}_2}{inf}{I}_F\left(p_{\xi }\right)={\displaystyle \frac{1}{\sqrt{2\pi }\sigma }}exp\left\{-{\displaystyle \frac{x^2}{2{\sigma }^2}}\right\},$$

(57)

that is, the worth on ${\mathcal{P}}_{\xi }^2$ distribution density is the Gaussian p.d.f. (57).

Corollary 3.

The robust on ${\mathcal{P}}_{\xi }^2$ version of the procedure (54) contains

$${\phi }^{*}\left(x\right)=-I_F^{-1}\left(p_{\xi }^{*}\right){\displaystyle \frac{d}{dv}}ln{p}_{\xi }^{*}\left(v\right)=x$$

(58)

which means that the standard LSM algorithm with linear residual transformation is robust within the class ${\mathcal{P}}_2$.

Lemma 4.

In the class ${\mathcal{P}}_{\xi }^3:=\left\{p_{\xi }:p_{\xi }\left(x\right)=\left(1-\alpha \right)p_{\mathcal{N}\left(0,{\sigma }^2\right)}\left(x\right)+\alpha q\left(x\right)\right\}$ (7) (of all symmetric “approximately normal” p.d.f.), the worth distribution density $p_{\xi }^{*}\left(x\right)$ is Gaussian p.d.f. within some zone Δ and the Laplace p.d.f. out of this zone:

$$\begin{array}{c}{p}_{\xi }^{*}\left(x\right)=arg{\displaystyle \underset{p_{\xi }\in {\mathcal{P}}_{\xi }^3}{inf}}{I}_{F,\xi }\left(p_{\xi }\right)=\\ \left\{\begin{array}{c}\frac{1-\alpha }{\sqrt{2\pi }\sigma }exp\left\{-\frac{x^2}{2{\sigma }^2}\right\}for\left|x\right|\le \Delta \\ \frac{1-\alpha }{\sqrt{2\pi }\sigma }exp\left\{-\frac{\Delta \left|x\right|}{{\sigma }^2}+\frac{{\Delta }^2}{2{\sigma }^2}\right\}for\left|x\right|>\Delta \end{array}\right..\end{array}$$

(59)

The parameter $\alpha \in \left[0,1\right]$ characterises the level of the effect of a “dirty” distribution $q\left(x\right)$ to the basic one $p_{\mathcal{N}\left(0,\sigma \right)}\left(x\right)$, and Δ is a solution of the transcendent equation

$${\displaystyle \frac{1}{1-\alpha }}=\underset{-\Delta }{\overset{\Delta }{\int }}{p}_{\mathcal{N}\left(0,\sigma \right)}\left(x\right)dx+2p_{\mathcal{N}\left(0,\sigma \right)}\left(\Delta \right)\frac{{\sigma }^2}{\Delta }$$

(60)

that is, the worth on ${\mathcal{P}}_{\xi }^3$ distribution density is the Gaussian one for $\left|x\right|\le \Delta$ and the Laplace type for $\left|x\right|>\Delta$, (see Figure 3).

Corollary 4.

The robust on ${\mathcal{P}}_{\xi }^3$ version of the procedure (54) contains

$${\phi }^{**}\left(x\right)=-I_F^{-1}\left(p_{\xi }^{*}\right){\displaystyle \frac{d}{dv}}ln{p}_{\xi }^{*}\left(v\right)=\left\{\begin{array}{c}xfor\left|x\right|\le \Delta \\ \Delta \mathrm{sign}\left(x\right)for\left|x\right|>\Delta \end{array}\right.$$

(61)

Lemma 5.

In the class

$$\begin{array}{c}{\mathcal{P}}_{\xi }^4=\left\{p_{\xi }:p_{\xi }\left(x\right)=\left(1-\alpha \right)p_{U\left(0,a\right)}\left(x\right)+\alpha q\left(x\right)\right\},\\ p_{U\left(0,a\right)}\left(x\right):=\frac{1}{2a}\chi \left(\left|x\right|\le a\right)\end{array}$$

(7) (of all symmetric “approximately uniform” distributions) the worth distribution density $p_{\xi }^{*}\left(x\right)$ is

$$\begin{array}{c}{p}_{\xi }^{*}\left(x\right)=arg{\displaystyle \underset{p_{\xi }\in {\mathcal{P}}_{\xi }^4}{inf}}{I}_{F,\xi }\left(p_{\xi }\right)=\\ \left\{\begin{array}{c}\frac{1-\alpha }{2a}for\left|x\right|\le a\\ \frac{1-\alpha }{2a}exp\left\{-\left(1-\alpha \right)\frac{\left|x\right|-a}{\alpha a}\right\}for\left|x\right|>a>0\end{array}\right.,\end{array}$$

(62)

that is, the worth on ${\mathcal{P}}_{\xi }^4$ distribution density is the uniform p.d.f. for $\left|x\right|\le a$ and the Laplace type for $\left|x\right|>a$.

Corollary 5.

The robust on ${\mathcal{P}}_{\xi }^4$ version of the procedure (54) contains

$${\phi }^{**}\left(x\right)=-I_F^{-1}\left(p_{\xi }^{*}\right){\displaystyle \frac{d}{dv}}ln{p}_{\xi }^{*}\left(v\right)=\left\{\begin{array}{c}0for\left|x\right|\le a\\ {\displaystyle \frac{1-\alpha }{\alpha a}}\mathrm{sign}\left(x\right)for\left|x\right|>a\end{array}\right.$$

(63)

See Figure 4.

6.4. Robust Identification of Dynamic ARX Models

In the case of dynamic autoregression models (ARX model) where the generalised inputs are dependent on the state of the system, the matrix $\mathcal{R}$ depends on $p_{\xi }$, too, and therefore, we deal with the complete problem, namely, we need to calculate

$$\underset{p_{\xi }\in \mathcal{P}}{sup}{\left[I_{F,}\left(p_{\xi }\right)\mathcal{R}\left(p_{\xi }\right)\right]}^{-1}$$

(64)

For the ARX model (65) (for simplicity we put here $b_k=0,$ $\left(k=0,\dots ,K\right)$, so $c_l=a_l$ $\left(l=1,\dots ,L\right)$) the relation (36) becomes

$$\left.\begin{array}{c}{\tilde{y}}_n=a^{⊺}{\tilde{v}}_n+{\xi }_n+O_{\omega }\left({\lambda }^n\right)\\ a^{⊺}=\left(a_1,\dots ,a_L\right),{\tilde{v}}_n^{⊺}=\left(y_{n-1},\dots ,y_{n-L}\right)\end{array}\right\}$$

(65)

Here we have

$${\displaystyle \frac{1}{n}}\sum _{t=0}^n\mathrm{E}\left\{{\tilde{v}}_t{\tilde{v}}_t^{⊺}\right\}\to \mathcal{R}\left(p_{\xi }\right)$$

where $\mathcal{R}\left(p_{\xi }\right)$ satisfies

$$\mathcal{R}\left(p_{\xi }\right)=A\mathcal{R}\left(p_{\xi }\right)A^{⊺}+{\sigma }^2{\Xi }_0$$

(66)

with

$$A=∥\begin{array}{ccccc}{a}_0& a_1& \cdots & \cdots & a_{L_a}\\ 1& 0& \cdots & \cdots & 0\\ 0& 1& 0& \cdots & 0\\ 0& \cdots & \ddots & 0& 0\\ 0& \cdots & 0& 1& 0\end{array}∥,{\Xi }_0:=∥\begin{array}{ccccc}1& 0& \cdots & \cdots & 0\\ 0& 0& \cdots & \cdots & 0\\ 0& 0& 0& \cdots & 0\\ 0& \cdots & \ddots & 0& 0\\ 0& \cdots & 0& 0& 0\end{array}∥$$

Obviously, $\mathcal{R}\left(p_{\xi }\right)$ can be represented as $\mathcal{R}\left(p_{\xi }\right)={\sigma }^2{\mathcal{R}}_0\left(p_{\xi }\right)$, where ${\mathcal{R}}_0$ is the solution of

$${\mathcal{R}}_0\left(p_{\xi }\right)=A{\mathcal{R}}_0\left(p_{\xi }\right)A^{⊺}+{\Xi }_0.$$

(67)

In this case, the problem (64) is reduced to

$$\underset{p_{\xi }\in {\mathcal{P}}_{\xi }}{sup}{\left[{\sigma }^2\left(p_{\xi }\right)I_F\left(p_{\xi }\right)\right]}^{-1}$$

or equivalently, to

$$\underset{p_{\xi }\in {\mathcal{P}}_{\xi }}{inf}\left[{\sigma }^2\left(p_{\xi }\right)I_F\left(p_{\xi }\right)\right]$$

(68)

Consider now some classes ${\mathcal{P}}_{\xi }$ of a priory informative generating noise distributions and solutions of the problem (68) within these classes.

(1)

Class ${\mathcal{P}}_{\xi }^{ARX-1}$ (containing among others the Gaussian distribution $p_{\mathcal{N}\left(0,{\sigma }_0^2\right)}\left(x\right)$).

Lemma 6.

For the class ${\mathcal{P}}_{\xi }^{ARX-1}$

$$p_{\xi }^{*}\left(x\right)=arg\underset{p_{\xi }\in {\mathcal{P}}_1^{AR}}{inf}\left[{\sigma }^2\left(p_{\xi }\right)I_F\left(p_{\xi }\right)\right]=p_{\mathcal{N}\left(0,{\sigma }_0^2\right)}\left(x\right)$$

(69)

that is, the worth on ${\mathcal{P}}_{\xi }^{ARX-1}$ p.d.f. is exactly that the Gaussian distribution $p_{\mathcal{N}\left(0,{\sigma }_0^2\right)}\left(x\right)$.

Proof. 

Taking in (A1)

$$f\left(x\right)=x,\phi \left(x\right)=p_{\xi }^{\prime }\left(x\right)/p_{\xi }\left(x\right)$$

we get

$${\sigma }^2{I}_F\left(p_{\xi }\right)\ge {\left(\underset{\mathbb{R}}{\int }{xp}_{\xi }^{\prime }\left(x\right)dx\right)}^2={\left(\underset{\mathbb{R}}{\int }{p}_{\xi }\left(x\right)dx\right)}^2=1$$

such that the equality is attained when $p_{\xi }^{\prime }\left(x\right)/p_{\xi }\left(x\right)=\lambda x$, which leads to

$$p_{\xi }\left(x\right)={\displaystyle \frac{1}{\sqrt{2\pi /\lambda }}}exp\left\{-{\displaystyle \frac{\lambda x^2}{2}}\right\}$$

But since $I_F\left(p_{\mathcal{N}\left(0,{\sigma }_0^2\right)}\right)={\sigma }_0^{-2}$ from the inequality above we get

$${\sigma }^2\left(p_{\xi }\right)I_F\left(p_{\xi }\right)\ge 1={\sigma }_0^2{I}_F\left(p_{\mathcal{N}\left(0,{\sigma }_0^2\right)}\right)$$

which means that $p_{\xi }^{*}\left(x\right)=p_{\mathcal{N}\left(0,{\sigma }_0^2\right)}\left(x\right)$. □

Corollary 6.

The robust on ${\mathcal{P}}_{\xi }^{ARX-1}$ version of the procedure (54) contains

$${\phi }^{**}\left(x\right)=-I_F^{-1}\left(p_{\xi }^{*}\right){\displaystyle \frac{d}{dv}}ln{p}_{\xi }^{*}\left(v\right)=x.$$

(2)

Class ${\mathcal{P}}_{\xi }^{ARX-2}$ (containing all centred distributions with a variance not less than a given value):

$${\mathcal{P}}_{\xi }^{ARX-2}=\left\{p_{\xi }:\underset{\mathbb{R}}{\int }{x}^2{p}_{\xi }\left(x\right)dx\ge {\sigma }_0^2\right\}$$

(70)

Lemma 7.

For the class ${\mathcal{P}}_{\xi }^{ARX-2}$

$$p_{\xi }^{*}\left(x\right)=arg\underset{p_{\xi }\in {\mathcal{P}}_{\xi }^{ARX-2}}{inf}{I}_F\left(p_{\xi }\right)$$

(71)

that is, the worth on ${\mathcal{P}}_{\xi }^{ARX-2}$ distribution density $p_{\xi }^{*}\left(x\right)$ coincides with the worth p.d.f. on the classes ${\mathcal{P}}_{\xi }^i$ $\left(i=1,\dots ,4\right)$ characterising distribution uncertainties (if additional information is available) for static regression models provided that

$${\sigma }^2\left(p_{\xi }^{*}\left(x\right)\right)={\sigma }_0^2$$

(72)

Proof. 

It follows directly from the inequality ${\sigma }^2\left(p_{\xi }\right)I_F\left(p_{\xi }\right)\ge {\sigma }_0^2{I}_F\left(p_{\xi }\right)$. □

Remark 8.

Notice that all of the preceding analysis is based on the assumption that the transfer function (4) of the forming filter (3) is known a priory, allowing the parallel whitening process (34) to be applied and the information Cramer–Rao bound (37) to be reached, resulting in the asymptotically effective (the “best” ones) procedure, which is robust on given p.d.f. classes ${\mathcal{P}}_{\xi }$ of generating noises.

Below, we look at a considerably more challenging scenario where the forming filter (3) is unknown a prior. In this situation, nobody can definitely achieve the information Cramer–Rao bound (37) and build an asymptotically successful parametric estimate technique in this circumstance. However, the problem can be handled utilising alternative techniques of identification.

7. Instrumental Variables Method for ARMAX Model with Finite Noise Correlation

7.1. About IVM

Instrumental variables (IV) or total least-squares estimators is the method which also recommends to estimate parameters in the presence of white or coloured noises [89,90,91]. Even if the accuracy of the estimator for errors-in-variables models cannot be handled with a conventional analysis, the results produced by any of these estimators in practice demonstrate that their response can be well theoretically anticipated. The instrumental variables algorithms have been implemented for multivariable model forms, such as ARMAX models, dynamic adjustments with autoregressive errors and multivariable transfer functions (see [92]), where the IV algorithm provides asymptotically efficient estimation results and a low variance. The IV method can be adapted to work with the maximum likelihood method [93]. An analysis of the refined instrumental variable-approximate maximum likelihood (IVAML) method was presented. The proposed technique proved to be asymptotically efficient and to approach minimum variance estimation of the model parameters, even with a low sample size and low signal noise rations. An unified refined instrumental variable (RIV) approach was proposed in [94] for the estimation of discrete and continuous-time transfer functions. The estimator was based on the formulation of a pseudo-linear regression involving an optimal prefiltering process derived from a Box–Jenkins transfer function model. This method showed a reliable solution to the maximum likelihood optimisation equations, and the estimates are optimal in the maximum likelihood sense. The optimal refined instrumental variables for Box–Jenkins models has been studied on various occasions, for example in [95]. There, in contrast to the most common forms of the algorithm used in ARMAX models, a modification that facilitates the representation of the more general noise component of the Box–Jenkins model was proposed, and that could also be used as an adaptive filter and as a state variable feedback control. For the nonlinear case, the instrumental variable method has been used in particular for nonlinear Hammerstein models. The nonlinear recursive instrumental variables method has been used to deal with these models due to its simplicity in practical applications (see [96]). The recursive IV method also proves to be superior to the recursive LSM in terms of accuracy and convergence under the presence of coloured noises, and this is valid either for discrete or continuous-time [97].

Consider now the system (1) in the regression format

$$\left.\begin{array}{c}{y}_n=z_n^{\top }c+{\eta }_n,\\ c={\left(a_1,\dots ,a_L;b_0,\dots ,b_K\right)}^{⊺}\in R^{L+K+1},\\ z_n={\left(y_{n-1},\dots ,y_{n-L};w_n,\dots ,w_{n-K}\right)}^{⊺}\in R^{L+K+1}\end{array}\right\}$$

(73)

where the exogenous noise input ${\eta }_n$ has a finite correlation, that is, the transfer matrix of the forming filter has only the nominator:

$$H\left(q^{-1}\right)=H_1\left(q^{-1}\right)=1+\sum _{s=1}^{K_1}{d}_{2,s}{q}^{-s},H_2\left(q^{-1}\right)=1$$

(74)

It is acknowledged that the parameters $d_{2,s}$ $\left(s=1,\dots ,K_1\right)$ may be unknown a priory.

7.2. Instrumental Variables and the System of Normal Equations

Let $v_n$ $\in R^{L+K+1}$ be an auxiliary vector variable (an instrumental variable) depending on information available up to time n. Considering the moments $t=1,\dots ,n$ and multiplying both sides of (73) by $v_t$ we get the so-called system of “normal equations”:

$$\left.\begin{array}{c}{v}_1{y}_1=v_1{z}_1^{\top }c+v_1{\eta }_1,\\ v_2{y}_2=v_2{z}_2^{\top }c+v_2{\eta }_2,\\ ⋮\\ v_n{y}_n=v_n{z}_n^{\top }c+v_n{\eta }_n\end{array}\right\}$$

(75)

Summing these relations, after multiplying by $n^{-1}$, we obtain

$$n^{-1}\sum _{t=1}^n{v}_t{y}_t=\left(n^{-1}\sum _{t=1}^n{v}_t{z}_t^{\top }\right)c+n^{-1}\sum _{t=1}^n{v}_t{\eta }_t$$

(76)

Define the instrumental variable estimate $c_n^{IV}$ of the vector c as a vector which in each time n satisfies the relation

$$\sum _{t=1}^n{v}_t{y}_t=\left(\sum _{t=1}^n{v}_t{z}_t^{\top }\right)c_n^{IV}.$$

(77)

If the matrix $\left({\displaystyle \sum _{t=1}^n}{v}_t{z}_t^{\top }\right)$ is invertible, that is, the matrix ${\mathsf{\Gamma }}_n^{IV}:={\left({\displaystyle \sum _{t=1}^n}{v}_t{z}_t^{\top }\right)}^{-1}$ exists (for all $n\ge n_0$), then $c_n^{IV}$ can be expressed as

$$c_n^{IV}={\mathsf{\Gamma }}_n^{IV}{\displaystyle \sum _{t=1}^n}{v}_t{y}_t,$$

(78)

or in the recurrent form

$$\left.\begin{array}{c}{c}_n^{IV}=c_{n-1}^{IV}+{\mathsf{\Gamma }}_n^{IV}{v}_t\left(y_n-z_n^{\top }{c}_{n-1}^{IV}\right),\\ {\mathsf{\Gamma }}_n^{IV}={\mathsf{\Gamma }}_{n-1}^{IV}-{\displaystyle \frac{{\mathsf{\Gamma }}_{n-1}^{IV}{v}_n{z}_n^{⊺}{\mathsf{\Gamma }}_{n-1}^{IV}}{1+z_n^{⊺}{\mathsf{\Gamma }}_{n-1}^{IV}{v}_n}},z_n^{⊺}{\mathsf{\Gamma }}_{n-1}^{IV}{v}_n\ne -1\end{array}\right\}$$

(79)

Remark 9.

Notice that if $v_n=z_n$ the estimates $c_n^{IV}$ (77)–(79) coincide with LSM estimates.

As it follows from (76) and (77), the estimation error ${\delta }_n=c_n^{IV}-c$ satisfies

$$-n^{-1}\sum _{t=1}^n{v}_t{\eta }_t=\left(n^{-1}\sum _{t=1}^n{v}_t{z}_t^{\top }\right){\delta }_n$$

(80)

Under the main assumptions accepted above, in view of the strong large number law (see Theorem 8.10 in [36]), we have

$$\begin{array}{c}{n}^{-1}{\displaystyle \sum _{t=1}^n}{v}_t{y}_t\stackrel{a.s.}{=}{n}^{-1}{\displaystyle \sum _{t=1}^n}\mathrm{E}\left\{v_t{y}_t\right\}+o_{\omega }\left(1\right),\\ n^{-1}{\displaystyle \sum _{t=1}^n}{v}_t{z}_t\stackrel{a.s.}{=}{n}^{-1}{\displaystyle \sum _{t=1}^n}\mathrm{E}\left\{v_t{z}_t\right\}+o_{\omega }\left(1\right),\\ n^{-1}{\displaystyle \sum _{t=1}^n}{v}_t{\eta }_t\stackrel{a.s.}{=}{n}^{-1}{\displaystyle \sum _{t=1}^n}\mathrm{E}\left\{v_t{\eta }_t\right\}+o_{\omega }\left(1\right)\\ a.s.\mathrm{means}\mathrm{almost}\mathrm{sure}\mathrm{or}\mathrm{with}\mathrm{probability}1.\end{array}$$

and the relation (80) becomes

$$-n^{-1}\sum _{t=1}^n\mathrm{E}\left\{v_t{\eta }_t\right\}\stackrel{a.s.}{=}\left(n^{-1}\sum _{t=1}^n\mathrm{E}\left\{v_t{z}_t\right\}\right){\delta }_n+o_{\omega }\left(1\right)$$

from which one may conclude that if

(1)

$$n^{-1}\sum _{t=1}^n\mathrm{E}\left\{v_t{z}_t\right\}\to {\mathcal{R}}_{IV},det{\mathcal{R}}_{IV}\ne 0;$$

(81)

(2)

$$n^{-1}\sum _{t=1}^n\mathrm{E}\left\{v_t{\eta }_t\right\}\to 0,$$

(82)

then the estimate $c_n^{IV}$ is asymptotically consistent with probability 1, namely, ${\delta }_n\stackrel{a.s.}{\to }0$.

Corollary 7.

Evidently, the condition (82) holds if the instrumental variable $v_t$ and the external noise ${\eta }_t$ are not correlated:

$$\mathrm{E}\left\{v_t{\eta }_t\right\}=0forallt=1,\dots$$

So, in the example (17), instead of the LSM estimate (18) we need to use (see [98]) the IV estimate $c_n^{IV}$ (78) with $v_t=y_{t-k}$ $\left(k\ge 1\right):$

$$a_n=\left[\sum _{t=1}^n{y}_{t-k}{y}_{t+1}\right]{\left[\sum _{t=1}^n{y}_t{y}_{t-k}\right]}^{-1}\stackrel{a.s.}{\to }a$$

In general cases for the model (73) and (74) with a finite correlation ($\mathrm{E}\left\{{\eta }_t{\eta }_{t-k}\right\}=0,$ $k>K_1$) we may use the following IV estimate $c_n^{IV}$ with $v_t=z_{t-k}$ $\left(k\ge K_1\right):$

$$\left.\begin{array}{c}{c}_n^{IV}=c_{n-1}^{IV}+{\mathsf{\Gamma }}_n^{IV}{z}_{t-k}\left(y_n-z_n^{\top }{c}_{n-1}^{IV}\right),\\ {\mathsf{\Gamma }}_n^{IV}={\mathsf{\Gamma }}_{n-1}^{IV}-{\displaystyle \frac{{\mathsf{\Gamma }}_{n-1}^{IV}{z}_{n-k}{z}_n^{⊺}{\mathsf{\Gamma }}_{n-1}^{IV}}{1+z_n^{⊺}{\mathsf{\Gamma }}_{n-1}^{IV}{z}_{n-k}}},z_n^{⊺}{\mathsf{\Gamma }}_{n-1}^{IV}{z}_{n-k}\ne -1.\end{array}\right\}$$

(83)

8. Joint Parametric Identification of ARMAX Model and the Forming Filter

Unfortunately, IVM identification algorithms cannot be applied in the situation when the correlation function of a coloured noise is not finite. Below, we treat exactly this case considering that the transfer function of a finite-dimensional forming filter is completely unknown, including both numerator and denominator parameters in (4). So, here our problem under the consideration is as follows: based on the available data (16) we need to construct an identification procedure, generating some parameter estimates ${\widehat{a}}_{n,i}$ $\left(i=1,\dots ,L\right)$, ${\widehat{b}}_{n,i}$ $\left(i=0,\dots ,K\right)$, ${\widehat{h}}_{n,1i}$ $\left(i=0,\dots ,K_1\right)$ and ${\widehat{h}}_{n,2i}$ $\left(i=1,\dots ,K_2\right)$ which asymptotically convergence with probability 1 (or almost sure) to the real values, namely,

$${\widehat{a}}_{n,i}\stackrel{a.s.}{\to }{a}_i,{\widehat{b}}_{n,i}\stackrel{a.s.}{\to }{b}_i,{\widehat{h}}_{n,1i}\stackrel{a.s.}{\to }{h}_{1,i},{\widehat{h}}_{n,2i}\stackrel{a.s.}{\to }{h}_{2,i}\mathrm{when}n\to \infty .$$

(84)

8.1. An Equivalent ARMAX Representation

Multiplying (1) by $H_2\left(q\right)=1+\underset{i=1}{\stackrel{K_2}{\mathsf{\Sigma }}}{h}_{2,i}{q}^i$ we obtain the corresponding ARMAX (autoregression with moving average noise term model)

$$\begin{array}{c}\left(1+\underset{i=1}{\stackrel{K_2}{\mathsf{\Sigma }}}{h}_{2,i}{q}^i\right)\left(1+{\displaystyle \sum _{i=1}^L}{a}_i{q}^i\right)y_n=\\ \left(1+\underset{i=1}{\stackrel{K_2}{\mathsf{\Sigma }}}{h}_{2,i}{q}^i\right)\left({\displaystyle \sum _{i=0}^K}{b}_i{q}^i\right)u_n+\left(h_{1,0}+\underset{i=1}{\stackrel{K_1}{\mathsf{\Sigma }}}{h}_{1,i}{q}^i\right){\xi }_n\end{array}$$

or, equivalently, in the “open format” (with $m_A:=max\left\{K_2,L\right\}$ and $m_B:=max\left\{K_2,K\right\}$)

$$\left.\begin{array}{c}\left(1+{\displaystyle \underset{i=1}{\sum ^{m_A}}}{q}^i\left[a_i\chi \left(i\le n_A\right)+h_{2,i}\chi \left(i\le n_{D_2}\right)\right.\right.\\ \left.\left.+\left(h_{2,i}\chi \left(i\le n_{D_2}\right){\displaystyle \underset{j=1}{\sum ^{m_A}}}{a}_j\chi \left(j\le n_A\right)q^j\right)\right]\right)y_n=\\ \left(b_0+{\displaystyle \underset{i=1}{\sum ^{M_B}}}{q}^i\left[b_i\chi \left(i\le M_B\right)+h_{2,i}\chi \left(i\le n_{D_2}\right){\displaystyle \underset{j=0}{\sum ^{M_B}}}{b}_j\chi \left(j\le n_B\right)q^j\right]\right)u_n\\ +\left(1+{\displaystyle \underset{i=1}{\sum ^{n_{D_1}}}}{h}_{1,i}{q}^i\right){\xi }_n,\end{array}\right\}$$

(85)

where

$$\chi \left(\mathcal{A}\right)=\left\{\begin{array}{ccc}1& \mathrm{if}& \mathrm{the}\mathrm{event}\mathcal{A}\mathrm{is}\mathrm{valid}\\ 0& \mathrm{if}& \mathrm{not}\end{array}\right..$$

Remark 10.

Notice that since the polynomial $H_2\left(q\right)$ is stable, the reactions ${\left\{y_{\tau }\right\}}_{\tau =\overline{1,n}}$ of both difference Equations (4) and (85) on the same inputs ${\left\{u_{\tau }\right\}}_{\tau =\overline{-2m_B,n}}$ and ${\left\{{\xi }_{\tau }\right\}}_{0=\overline{-K_1,n}}$ are asymptotically closed, namely, the difference between these reactions tends to zero exponentially quickly with probability one. That is why to obtain the desired property (84), designing the identification procedure using the data of the model (4) can be realised based on data but generated by the ARMAX model (85) (see [99]).

The ARMAX model (85) can be represented in the standard regression format (different from (14)) as

$$y_n=x_n^{⊺}c+h_{1,0}{\xi }_n$$

(86)

with

$$\begin{array}{c}{x}_n={\left(-y_{n-1},\cdots ,-y_{n-2m_A};u_n,\cdots ,u_{n-2m_B};{\xi }_{n-1},\cdots ,{\xi }_{n-n_{K_1}}\right)}^{⊺}\in R^N\\ N:=2m_A+2m_B+1+K_1\end{array}$$

(87)

and

$$c={\left({\tilde{a}}_1,\cdots ,{\tilde{a}}_{2m_A},{\tilde{b}}_0,\cdots ,{\tilde{b}}_{2m_B},h_{1,1},\cdots ,h_{1,K_1}\right)}^{⊺}\in R^N,$$

(88)

containing the components

$$\left.\begin{array}{c}{\tilde{a}}_1=a_1+h_{2,1},\\ {\tilde{a}}_i=a_i\chi \left(i\le n_L\right)+h_{2,i}\chi \left(i\le n_{K_2}\right)+\\ {\displaystyle \underset{k=1}{\sum ^{m_A}}}{h}_{2,k}\chi \left(k\le n_{K_2}\right)a_{i-k}\chi \left(i-k\le L\right),{i=2,\dots ,2m}_A,\\ {\tilde{b}}_0=b_0,{\tilde{b}}_i=b_i\chi \left(i\le m_B\right)+\\ {\displaystyle \underset{k=1}{\sum ^{m_B}}}{h}_{2,k}\chi \left(k\le n_{K_2}\right)b_{i-k}\chi \left(i-k\le K\right),{i=1,\dots ,2m}_B.\end{array}\right\}$$

(89)

Remark 11.

Notice that the extended input vector $x_n$ is not completely available since it contains immeasurable components ${\xi }_{n-1},$$\cdots ,$ ${\xi }_{n-n_{K_1}}.$ This property is the main difference with the standard ARMAX model identification problem where the vector $x_n$ does not contain these immeasurable term.

8.2. Auxiliary Residual Sequence

Now, let us define the “generalised residual sequence” given by the recursion relation

$${\epsilon }_n=y_n-{\widehat{x}}_n^{⊺}{c}_{n-1}$$

(90)

where the “extended vector” ${\widehat{x}}_n\in R^{2m_A+2m_B+1+K_1}$ is defined as

$${\widehat{x}}_n={\left(-y_{n-1},\cdots ,-y_{n-2m_A};u_n,\cdots ,u_{n-2m_B};{\epsilon }_{n-1},\cdots ,{\epsilon }_{n-n_{K_1}}\right)}^{⊺}$$

(91)

with ${\epsilon }_{-1}$=⋯=${\epsilon }_{-n_{D_1}}$= 0. Notice that the “extended vector” ${\widehat{x}}_n$ is measurable on-line.

Lemma 8

([99]). For $n\to \infty$

$${\Delta }_n={\epsilon }_n-{\xi }_n=O\left({\left|{\lambda }_{H_1}\right|}^n\right)\stackrel{a.s.}{\to }0,$$

(92)

where ${\lambda }_{H_1}$ is the eigenvalue of the polynomial $H_1$ with minimal module $\left|{\lambda }_{H_1}\right|<1$.

From (A5) we get

$$y_n={\widehat{x}}_n^{⊺}c-\sum _{i=1}^{n_{D_1}}{h}_{1,i}{\Delta }_{n-i}+h_{1,0}{\xi }_n={\widehat{x}}_n^{⊺}c+h_{1,0}{\xi }_n+O\left({\left|{\lambda }_{H_1}\right|}^n\right).$$

(93)

8.3. Identification Procedure

To estimate the extended vector c from the relation (93) let us apply the least-squares method (LSM), defining the current estimate ${\widehat{c}}_n$ as

$${\widehat{c}}_n={\left(\sum _{t=0}^n{\widehat{x}}_t{\widehat{x}}_t^{⊺}\right)}^{-1}\sum _{t=0}^n{\widehat{x}}_t{y}_t,n\ge n_0=\left\{infn:\sum _{t=t}^n{\widehat{x}}_t{\widehat{x}}_t^{⊺}>0\right\}$$

(94)

In the recurrent form, this estimate can be represented as in (39):

$$\left.\begin{array}{c}{\widehat{c}}_n={\widehat{c}}_{n-1}+{\mathsf{\Gamma }}_n{\widehat{x}}_n\phi \left(y_n-{\widehat{x}}_n^{⊺}{\widehat{c}}_{n-1}\right),\\ {\mathsf{\Gamma }}_n={\mathsf{\Gamma }}_{n-1}-{\displaystyle \frac{{\mathsf{\Gamma }}_{n-1}{\widehat{x}}_n{\widehat{x}}_n^{⊺}{\mathsf{\Gamma }}_{n-1}}{1+{\widehat{x}}_n^{⊺}{\mathsf{\Gamma }}_{n-1}{\widehat{x}}_n}},n\ge n_0+1,\\ {\mathsf{\Gamma }}_{n_0}^{-1}:={\displaystyle \sum _{t=t}^{n_0}}{\widehat{x}}_t{\widehat{x}}_t^{⊺}\end{array}\right\}$$

(95)

Notice that taking ${\mathsf{\Gamma }}_{n_0}^{-1}$ as

$${\mathsf{\Gamma }}_{n_0}^{-1}=\rho I_{N\times N}+\sum _{t=t}^{n_0}{\widehat{x}}_t{\widehat{x}}_t^{⊺},0<\rho \ll 1,$$

(96)

we can select $n_0=0,$ and the procedure (95) can be applied from the beginning of the process.

Theorem 6

([100]). If

(1) 

the following “persistent excitation condition” (PEC) holds:

$$\begin{array}{c}{\displaystyle \underset{n}{lim\; inf}}\left({\displaystyle \frac{1}{n}}{\displaystyle \sum _{t=0}^n}{x}_t{x}_t^{⊺}\right)\stackrel{a.s.}{\ge }\nu I_{M\times M}\stackrel{a.s.}{>}0,\\ M:=2m_A+2m_B+1+D_1.\end{array}$$

(2) 

$\left\{{\xi }_n\right\}$ is a martingale difference sequence satisfying (10),

then, the LSM procedure (95) and (96) generates the sequence of the estimates ${\left\{{\widehat{c}}_n\right\}}_{n\ge 0}$, which is asymptotically consistent with probability 1, that is, ${\widehat{c}}_n\underset{n\to \infty }{\stackrel{a.s}{\to }}c$.

8.4. Recuperation of the Model Parameters from the Obtained Current Estimates

8.4.1. Special Case When the Recuperation Process Can Be Realised Directly

When $K=0$ and the gain parameter $b_0\ne 0$ are a priori known, the system of algebraic Equations (89) becomes linear with respect to the unknown parameters $a_i\left(i=0,\dots ,L\right)$ and $h_{2,i}\left(i=0,\dots ,n_{K_2}\right),$ and may be resolved analytically without application of any numerical procedure.

8.4.2. General Case Requiring the Application of Gradient Descent Method (GDM)

In view of (89), we can recuperate the parameters $a_i\left(i=\overline{0,L}\right),$ $b_i$ $\left(i=\overline{0,K}\right)$ and $h_{2,i}$ $\left(i=0,\dots ,n_{K_2}\right)$ for this purpose using the command Fsolve in Matlab or some numerical method such as GDM.

For example, if we consider the case when $K=L=n_{K_2}=m_A=m_B=2$, the component relations from (89) become

$$\begin{array}{c}{\tilde{a}}_1=a_1+h_{2,1},{\tilde{a}}_2=a_2+h_{2,2}+h_{2,1}{a}_1,\\ {\tilde{a}}_3=h_{2,1}{a}_2+h_{2,2}{a}_1,{\tilde{a}}_4=h_{2,2}{a}_2,\end{array}$$

$$\begin{array}{c}{\tilde{b}}_0=b_0,{\tilde{b}}_1=b_1+h_{2,1}{b}_0,\\ {\tilde{b}}_2=b_2+h_{2,1}{b}_1+h_{2,2}{b}_0,\\ {\tilde{b}}_3=h_{2,1}{b}_2+h_{2,2}{b}_1,{\tilde{b}}_4=h_{2,2}{b}_2.\end{array}$$

Since this system is formed by nonlinear equations, and in some particular cases it is actually possible to solve the equations analytically, the gradient descent method (GDM) is implemented to estimate the values from the original system, taking the best average value from the estimated parameters. For this purpose, we define the following objective function:

$$\begin{array}{c}F(a_1,a_2,b_1,h_{21})={(a_1+h_{21}-c_1)}^2+\\ {(a_1{h}_{21}+a_2-c_2)}^2+{(a_2{h}_{21}-c_3)}^2+\\ {(b_1+h_{21}{b}_0-c_5)}^2+{(b_1{h}_{21}-c_6)}^2\to \min \end{array}$$

The original parameter can be recovered using some of the existing optimisation commands in Matlab, suc as Fsolve or optimvar, or some algorithms such as GDM mentioned previously, although some other optimisation techniques could be implemented (see [99]). The performance of Fsolve is good in second or third order systems; in these cases, the command can recover all the original parameters from the nonlinear system. In higher order systems, this method presents problems at recovering the original values, while gradient descent has a good performance with low- and high-order systems. In some cases, such as the example presented before, it is possible to recover the original values by a mathematical simplification. The main condition for a good estimation is that in the objective function one should have at least as many terms as variables to estimate, otherwise it is not possible to recover all the original values.

9. Numerical Example

The algorithms presented in the previous sections are illustrated with a numerical example.

Raised Cosine Distribution

Consider the following system

$$\begin{array}{c}y\left(k\right)=0.85y(k-1)+2u\left(k\right)+\eta \left(k\right),\\ \eta \left(k\right)=-0.3\eta (k-1)+\xi \left(k\right)+0.8\xi (k-1),\end{array}$$

with $\xi$ having the raised cosine distribution

$$p_{\xi }\left(v\right)=\frac{1}{2s}\left[1+cos\left(\frac{v-\mu }{s}\pi \right)\right],\mu >0,s>0,$$

which is a continuously differentiable function supported on the interval $\left[\mu -s,\mu +s\right]$. The system can be rewritten as follows

$$y\left(k\right)=z{\left(k\right)}^{\top }c+\eta \left(k\right),$$

with

$$z\left(k\right)=\left(\begin{array}{c}y(k-1)\\ u\left(k\right)\end{array}\right),c:=\left(\begin{array}{c}0.85\\ 2\end{array}\right).$$

The whitening process is then given by

$$\tilde{y}\left(k\right)=H\left(q^{-1}\right)y\left(k\right),\tilde{z}\left(k\right)=H\left(q^{-1}\right)z\left(k\right),$$

or in the extended form,

$$\begin{array}{c}\tilde{y}\left(k\right)+0.3\tilde{y}(k-1)=y\left(k\right)+0.8y(k-1),\tilde{y}\left(0\right)=y\left(0\right),\\ \tilde{z}\left(k\right)+0.3\tilde{z}(k-1)=z\left(k\right)+0.8z(k-1),\tilde{z}\left(0\right)=z\left(0\right),\end{array}$$

where the “inverse filter” has the transfer function

$$H\left(q^{-1}\right)=\frac{1+0.8q^{-1}}{1+0.3q^{-1}}.$$

The recursive WLSM algorithm with the residual nonlinear transformation is given by

$$\begin{array}{c}{c}_n=c_{n-1}-I_{F,\xi }^{-1}{\mathsf{\Gamma }}_n{\tilde{z}}_n{\displaystyle \frac{p_{\xi }^{\prime }\left(v\right)}{p_{\xi }\left(v\right)}}{\mid }_{v={\tilde{y}}_n-{\tilde{z}}_n^{⊺}{c}_{n-1}}=\\ c_{n-1}+2\pi I_{F,\xi }^{-1}{\mathsf{\Gamma }}_n{\tilde{z}}_n{\displaystyle \frac{sin\left({\displaystyle \frac{v-\mu }{s}}\pi \right)}{1+cos\left({\displaystyle \frac{v-\mu }{s}}\pi \right)}}{\mid }_{v={\tilde{y}}_n-{\tilde{z}}_n^{⊺}{c}_{n-1}}=\\ c_{n-1}+{\displaystyle \frac{s}{\pi }}{\mathsf{\Gamma }}_n{\tilde{z}}_n{\displaystyle \frac{sin\left({\displaystyle \frac{\pi }{s}}\left[{\tilde{y}}_n-{\tilde{z}}_n^{⊺}{c}_{n-1}-\mu \right]\right)}{1+cos\left({\displaystyle \frac{\pi }{s}}\left[{\tilde{y}}_n-{\tilde{z}}_n^{⊺}{c}_{n-1}-\mu \right]\right)}}.\end{array}$$

(97)

Here, we have used that for the raised cosine distribution

$$I_{F,\xi }=2{\displaystyle \frac{{\pi }^2}{s}}.$$

(98)

The initial conditions are $c\left(0\right)=2$, $y\left(0\right)=3$, $\mathsf{\Gamma }\left(0\right)={10}^5$. The Figure 5 and Figure 6 show the estimated parameters a and b using LSM and MLLM+ whitening with a nonlinear residual transformation.

In the Figure 5 and Figure 6, one can see that in the LSM case the noise has a strong influence in the estimation results, while in the MLLM+ whitening, the noise influence is minimised in the estimated parameter, reducing the bias, which is the most common problem in parameter estimation using LSM under the presence of the correlated noises. The performance index of the estimated algorithm is illustrated in Figure 7; here, one can see that the MLLM+ whitening is a better option for parameter estimation in systems with coloured noises.

In this case, the filter structure is known; a numerical example where the filter structure is unknown is presented in [99].

10. Discussion

In this paper, we demonstrated that the traditional LSM algorithm failed to accurately estimate the parameters of ARX (dynamic) models when subjected to a coloured perturbation, and because of this, it is necessary to implement a different estimation strategy. For the identification issue under non-Gaussian and coloured noises, the Cramer–Rao inequality and the related Fisher information limits were explored, when the forming filter (the noise spectral function) is known a priori.

It was shown that a recurrent process, which employs both the whitening technique and the nonlinear residual transformation (operating in parallel), is the asymptotically effective (the “best”) identification algorithm.

The main limitation of the proposed method is that in the case of having a partially unknown filter, the method cannot be implemented. In this case, there are two different identification methods that might be used:

−

Instrumental variables method (IVM) for ARMAX models with a finite noise-correlation.

−

The nonlinear residual transformation method for simultaneous parametric identification of the ARMAX model and the forming filter.

Both techniques are not asymptotically effective, as they do not achieve the Cramer–Rao information limits.

In a future work, we plan to analyse the case in which the filter is partially known, or even unknown, and if it is possible to achieve the information limits that were previously mentioned.

11. Conclusions

In the present work, the limits for the Cramer–Rao inequality and the related Fisher information were explored under coloured noise perturbations, and we demonstrated that the whitening technique and the nonlinear residual transformation working in parallel generate an estimation sequence with the asymptotic convergence rate that proves to be the best identification algorithm for the case studied in this manuscript, reaching the Fisher information bound, which cannot be improved by any other estimation algorithm. The effectiveness of the suggested approach is illustrated by a numerical example with a non-Gaussian noise, having a raised cosine distribution.