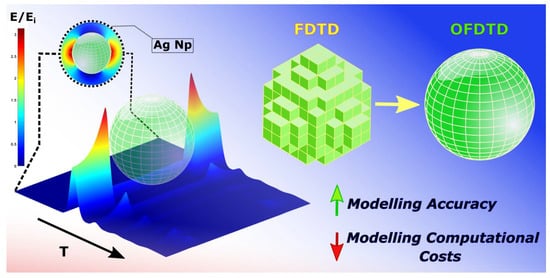
Optimized 3D Finite-Difference-Time-Domain Algorithm to Model the Plasmonic Properties of Metal Nanoparticles with Near-Unity Accuracy
Abstract
:1. Introduction
2. Materials and Methods
2.1. OFDTD Method Development for Plasmonic Effect Modelling
2.2. Description of Samples and Experimental Measurements
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ritchie, R. Plasma losses by fast electrons in thin films. Phys. Rev. 1957, 106, 874. [Google Scholar] [CrossRef]
- Maier, S.A. Plasmonics: Fundamentals and Applications; Springer Science & Business Media: Cham, Switzerland, 2007. [Google Scholar]
- Chicanne, C.; David, T.; Quidant, R.; Weeber, J.-C.; Lacroute, Y.; Bourillot, E.; Dereux, A.; Des Francs, G.C.; Girard, C. Imaging the local density of states of optical corrals. Phys. Rev. Lett. 2002, 88, 097402. [Google Scholar] [CrossRef] [Green Version]
- Rechberger, W.; Hohenau, A.; Leitner, A.; Krenn, J.; Lamprecht, B.; Aussenegg, F. Optical properties of two interacting gold nanoparticles. Opt. Commun. 2003, 220, 137–141. [Google Scholar] [CrossRef]
- Grand, J.; Kostcheev, S.; Bijeon, J.-L.; De La Chapelle, M.L.; Adam, P.-M.; Rumyantseva, A.; Lérondel, G.; Royer, P. Optimization of SERS-active substrates for near-field Raman spectroscopy. Synth. Met. 2003, 139, 621–624. [Google Scholar] [CrossRef]
- Orendorff, C.J.; Sau, T.K.; Murphy, C.J. Shape-Dependent Plasmon-Resonant Gold Nanoparticles. Small 2006, 2, 636–639. [Google Scholar] [CrossRef]
- Ghosh, S.K.; Pal, T. Interparticle coupling effect on the surface plasmon resonance of gold nanoparticles: From theory to applications. Chem. Rev. 2007, 107, 4797–4862. [Google Scholar] [CrossRef]
- Haiss, W.; Thanh, N.T.; Aveyard, J.; Fernig, D.G. Determination of size and concentration of gold nanoparticles from UV− Vis spectra. Anal. Chem. 2007, 79, 4215–4221. [Google Scholar] [CrossRef] [PubMed]
- Efrima, S.; Metiu, H. Classical theory of light scattering by an adsorbed molecule. I. Theory. J. Chem. Phys. 1979, 70, 1602–1613. [Google Scholar] [CrossRef]
- Aravind, P.; Metiu, H. The enhancement of Raman and fluorescent intensity by small surface roughness. Changes in dipole emission. Chem. Phys. Lett. 1980, 74, 301–305. [Google Scholar] [CrossRef]
- Gersten, J.; Nitzan, A. Electromagnetic theory of enhanced Raman scattering by molecules adsorbed on rough surfaces. J. Chem. Phys. 1980, 73, 3023–3037. [Google Scholar] [CrossRef]
- Wang, D.-S.; Chew, H.; Kerker, M. Enhanced Raman scattering at the surface (SERS) of a spherical particle. Appl. Opt. 1980, 19, 2256–2257. [Google Scholar] [CrossRef]
- Mirkin, C.; Ratner, M. Controlled synthesis and quantum-size effect in gold-coated nanoparticles. Annu. Rev. Phys. Chem. 1997, 101, 1593. [Google Scholar]
- Rampi, M.A.; Schueller, O.J.; Whitesides, G.M. Alkanethiol self-assembled monolayers as the dielectric of capacitors with nanoscale thickness. Appl. Phys. Lett. 1998, 72, 1781–1783. [Google Scholar] [CrossRef]
- Scaffardi, L.; Pellegri, N.; De Sanctis, O.; Tocho, J. Sizing gold nanoparticles by optical extinction spectroscopy. Nanotechnology 2004, 16, 158. [Google Scholar] [CrossRef]
- Myroshnychenko, V.; Rodríguez-Fernández, J.; Pastoriza-Santos, I.; Funston, A.M.; Novo, C.; Mulvaney, P.; Liz-Marzán, L.M.; de Abajo, F.J.G. Modelling the optical response of gold nanoparticles. Chem. Soc. Rev. 2008, 37, 1792–1805. [Google Scholar] [CrossRef] [Green Version]
- Alvarez, M.M.; Khoury, J.T.; Schaaff, T.G.; Shafigullin, M.N.; Vezmar, I.; Whetten, R.L. Optical absorption spectra of nanocrystal gold molecules. J. Phys. Chem. B 1997, 101, 3706–3712. [Google Scholar] [CrossRef] [Green Version]
- Lyon, L.A.; Pena, D.J.; Natan, M.J. Surface plasmon resonance of Au colloid-modified Au films: Particle size dependence. J. Phys. Chem. B 1999, 103, 5826–5831. [Google Scholar] [CrossRef]
- Link, S.; El-Sayed, M.A. Spectral Properties and Relaxation Dynamics of Surface Plasmon Electronic Oscillations in Gold and Silver Nanodots and Nanorods; ACS Publications: Washington, DC, USA, 1999. [Google Scholar]
- Collin, R. Field Theory of Guided Waves, 2nd ed.; IEEE: Piscataway, NJ, USA, 1990. [Google Scholar]
- Raether, H. Springer Tracts in Modern Physics; Springer: Berlin/Heidelberg, Germany, 1988; Volume 111. [Google Scholar]
- Barnes, W.L.; Dereux, A.; Ebbesen, T.W. Surface plasmon subwavelength optics. Nature 2003, 424, 824–830. [Google Scholar] [CrossRef]
- Moskovits, M. Surface-enhanced spectroscopy. Rev. Mod. Phys. 1985, 57, 783. [Google Scholar] [CrossRef]
- Metiu, H.; Das, P. The electromagnetic theory of surface enhanced spectroscopy. Annu. Rev. Phys. Chem. 1984, 35, 507–536. [Google Scholar] [CrossRef]
- Ahmed, H.; Doran, J.; McCormack, S. Increased short-circuit current density and external quantum efficiency of silicon and dye sensitised solar cells through plasmonic luminescent down-shifting layers. Sol. Energy 2016, 126, 146–155. [Google Scholar] [CrossRef]
- Ahmed, H.; McCormack, S.; Doran, J. External Quantum Efficiency Improvement with Luminescent Downshifting Layers: Experimental and Modelling. Int. J. Spectrosc. 2016, 2016. [Google Scholar] [CrossRef] [Green Version]
- Ahmed, H.; McCormack, S.; Doran, J. Plasmonic luminescent down shifting layers for the enhancement of CdTe mini-modules performance. Sol. Energy 2017, 141, 242–248. [Google Scholar] [CrossRef]
- Chandra, S.; Doran, J.; McCormack, S.; Kennedy, M.; Chatten, A. Enhanced quantum dot emission for luminescent solar concentrators using plasmonic interaction. Sol. Energy Mater. Sol. Cells 2012, 98, 385–390. [Google Scholar] [CrossRef] [Green Version]
- Purcell, E.M.; Pennypacker, C.R. Scattering and absorption of light by nonspherical dielectric grains. Astrophys. J. 1973, 186, 705–714. [Google Scholar] [CrossRef]
- Inan, U.S.; Marshall, R.A. Numerical Electromagnetics: The FDTD Method; Cambridge University: Cambridge, UK, 2011. [Google Scholar]
- Taflove, A. Computational Electrodynamics: The Finite-Difference Time-Domain Method; Artech House: Boston, MA, USA, 1995. [Google Scholar]
- Hao, F.; Nehl, C.L.; Hafner, J.H.; Nordlander, P. Plasmon resonances of a gold nanostar. Nano Lett. 2007, 7, 729–732. [Google Scholar] [CrossRef]
- Jain, P.K.; Lee, K.S.; El-Sayed, I.H.; El-Sayed, M.A. Calculated absorption and scattering properties of gold nanoparticles of different size, shape, and composition: Applications in biological imaging and biomedicine. J. Phys. Chem. B 2006, 110, 7238. [Google Scholar] [CrossRef] [Green Version]
- Yee, K. Numerical solution of initial boundary value problems involving Maxwell’s equations in isotropic media. IEEE Trans. Antennas Propag. 1966, 14, 302–307. [Google Scholar]
- Vial, A.; Grimault, A.-S.; Macías, D.; Barchiesi, D.; de La Chapelle, M.L. Improved analytical fit of gold dispersion: Application to the modeling of extinction spectra with a finite-difference time-domain method. Phys. Rev. B 2005, 71, 085416. [Google Scholar] [CrossRef]
- Grand, J.; Adam, P.-M.; Grimault, A.-S.; Vial, A.; De La Chapelle, M.L.; Bijeon, J.-L.; Kostcheev, S.; Royer, P. Optical extinction spectroscopy of oblate, prolate and ellipsoid shaped gold nanoparticles: Experiments and theory. Plasmonics 2006, 1, 135–140. [Google Scholar] [CrossRef]
- Linden, S.; Kuhl, J.; Giessen, H. Controlling the interaction between light and gold nanoparticles: Selective suppression of extinction. Phys. Rev. Lett. 2001, 86, 4688. [Google Scholar] [CrossRef] [PubMed]
- Chandra, S. Approach to Plasmonic Luminescent Solar Concentration; Dublin Institute of Technology: Dublin, Ireland, 2013. [Google Scholar]
- Rafiee, M.; Chandra, S.; Ahmed, H.; Barnham, K.; McCormack, S.J. Small and large scale plasmonically enhanced luminescent solar concentrator for photovoltaic applications: Modelling, optimisation and sensitivity analysis. Opt. Express 2021, 29, 15031–15052. [Google Scholar] [CrossRef] [PubMed]
- Sethi, A.; Rafiee, M.; Chandra, S.; Ahmed, H.; McCormack, S. Unified Methodology for Fabrication and Quantification of Gold Nanorods, Gold Core Silver Shell Nanocuboids, and Their Polymer Nanocomposites. Langmuir 2019, 35, 13011–13019. [Google Scholar] [CrossRef]
- Courant, R.; Friedrichs, K.; Lewy, H. On the partial difference equations of mathematical physics. IBM J. 1967, 11, 215–234. [Google Scholar] [CrossRef]
- Atef, E.; Demir, V. The Finite-Difference Time-Domain Method for Electromagnetics with MATLAB Simulations; The Institution of Engineering and Technology: Raleigh, NC, USA, 2016. [Google Scholar]
- Ahmed, H.; Sc, B.; Sc, M. Materials Characterization and Plasmonic Interaction in Enhanced Luminescent Down-Shifting Layers for Photovoltaic Devices; Dublin Institute of Technology: Dublin, Ireland, 2014. [Google Scholar]
- Ledwith, D.M.; Whelan, A.M.; Kelly, J.M. A rapid, straight-forward method for controlling the morphology of stable silver nanoparticles. J. Mater. Chem. 2007, 17, 2459–2464. [Google Scholar] [CrossRef]
- Osinkina, L. Interactions of Molecules in the Vicinity of Gold Nanoparticles; LMU: Munich, Germany, 2014. [Google Scholar]
- Darvill, D.; Centeno, A.; Xie, F. Plasmonic fluorescence enhancement by metal nanostructures: Shaping the future of bionanotechnology. Phys. Chem. Chem. Phys. 2013, 15, 15709–15726. [Google Scholar] [CrossRef]
- Soller, T.; Ringler, M.; Wunderlich, M.; Klar, T.; Feldmann, J.; Josel, H.-P.; Markert, Y.; Nichtl, A.; Kürzinger, K. Radiative and nonradiative rates of phosphors attached to gold nanoparticles. Nano Lett. 2007, 7, 1941–1946. [Google Scholar] [CrossRef]
- Johnson, P.B.; Christy, R.-W. Optical constants of the noble metals. Phys. Rev. B 1972, 6, 4370. [Google Scholar] [CrossRef]
- Rakić, A.D.; Djurišić, A.B.; Elazar, J.M.; Majewski, M.L. Optical properties of metallic films for vertical-cavity optoelectronic devices. Appl. Opt. 1998, 37, 5271–5283. [Google Scholar] [CrossRef]




| Existing FDTD Advantages | Existing FDTD Drawbacks |
|---|---|
|
|
| Type of the Matrix Group | Equal Matrix Group | Alternative Matrix | Required Memory Deduction of Matrix Group (%) | ||
|---|---|---|---|---|---|
| 1 | terms | , , , , | 84% | ||
| 2 | H and D update coefficient m0 terms | , , , , , | 84% | ||
| 3 | H and D update coefficient m1 terms | , , , , , | 84% | ||
| 4 | H update coefficient m2 terms | , , | 67% | ||
| 5 | H update coefficient m3 terms | , , | 67% | ||
| 6 | H and D update coefficient m4 terms | , , , , , | 84% | ||
| 7 | D update coefficient m2 terms | , , | 67% | ||
| 8 | D update coefficient m3 terms | , , | 67% | ||
| 9 | E update coefficient m terms | , , | 67% | ||
| 10 | terms | , , | 67% |
| Low Resolution Condition | High Resolution Condition | |||
|---|---|---|---|---|
| (nm) | 5.56 | 0.877 | ||
| Method | FDTD | OFDTD | FDTD | OFDTD |
| Total Yee Grid size (x × y × z) | 10 × 10 × 330 | 10 × 10 × 330 | Simulation Crashed Due to High Calculations and Memory Requirements | 62 × 62 × 1530 |
| Total Iterations of Main Loop | 1505 | 1505 | 2743 | |
| (nm) (Exp. Reference = 435) | 455 | 455 | 438 (~99% Accuracy) | |
| Discrepancy (nm) | −20 | −20 | +3 | |
| EF Peak (Reference = 10.57) | 2.73 | 2.73 | 10.52 | |
| EF Accuracy (%) | 25.8 | 25.8 | 99.5 | |
| EF Peak Position (nm)(Reference: ±25) | ±30.5 | ±30.5 | ±24.5 | |
| EF Peak Position Discrepancy (nm) | ±5.5 | ±5.5 | ±0.5 | |
| Simulation Time (Hour) | 0.74 | 0.67 | 121.85 | |
| Required Memory (%) | 89 | 42 | 93 | |
| Deduction in Simulation Time in OFDTD (%) | ~ 9.4 | |||
| Deduction in Required Memory in OFDTD (%) | ~ 52.8 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rafiee, M.; Chandra, S.; Ahmed, H.; McCormack, S.J. Optimized 3D Finite-Difference-Time-Domain Algorithm to Model the Plasmonic Properties of Metal Nanoparticles with Near-Unity Accuracy. Chemosensors 2021, 9, 114. https://doi.org/10.3390/chemosensors9050114
Rafiee M, Chandra S, Ahmed H, McCormack SJ. Optimized 3D Finite-Difference-Time-Domain Algorithm to Model the Plasmonic Properties of Metal Nanoparticles with Near-Unity Accuracy. Chemosensors. 2021; 9(5):114. https://doi.org/10.3390/chemosensors9050114
Chicago/Turabian StyleRafiee, Mehran, Subhash Chandra, Hind Ahmed, and Sarah J. McCormack. 2021. "Optimized 3D Finite-Difference-Time-Domain Algorithm to Model the Plasmonic Properties of Metal Nanoparticles with Near-Unity Accuracy" Chemosensors 9, no. 5: 114. https://doi.org/10.3390/chemosensors9050114
APA StyleRafiee, M., Chandra, S., Ahmed, H., & McCormack, S. J. (2021). Optimized 3D Finite-Difference-Time-Domain Algorithm to Model the Plasmonic Properties of Metal Nanoparticles with Near-Unity Accuracy. Chemosensors, 9(5), 114. https://doi.org/10.3390/chemosensors9050114