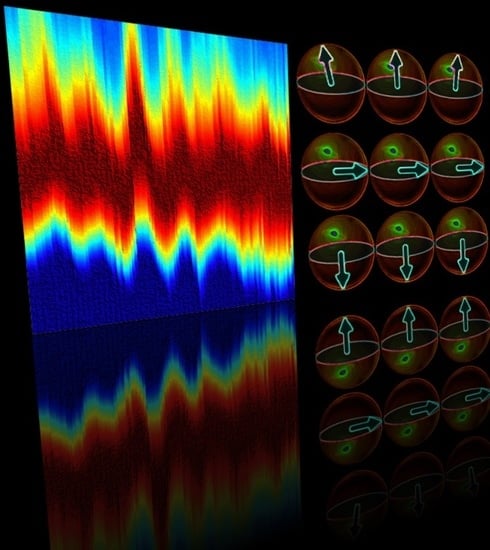
On Macroscopic Quantum Coherence with Synchronized Atoms and Molecules: Superradiance
Abstract
:1. Introduction
2. Superradiance and Synch Phenomenon
3. Macroscopic Quantum Coherence with Synched Atoms
4. Macroscopic Quantum Coherence with Synched Molecules
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| MDPI | Multidisciplinary Digital Publishing Institute |
| DOAJ | Directory of open access journals |
| QAVI | Quantum Analog of Vibration Isolation |
| SR | Superradiance |
| MQC | Macroscopic Quantum Coherence |
| Synch | Synchronization |
| QS | Quantum Synchronization |
References
- Averin, D.V.; Ruggiero, B.; Silvestrini, P. Macroscopic Quantum Coherence and Quantum Computing, 2001st ed.; Springer: Berlin, Germany, 2001. [Google Scholar]
- Cohen-Tannoudji, C.; Dupont-Roc, J.; Grynberg, G. Photons and Atoms, 1st ed.; Wiley-VCH Verlag GmbH: Weinheim, Germany, 1997. [Google Scholar]
- Kurizki, G.; Bertet, P.; Kubo, Y.; Mølmer, K.; Petrosyan, D.; Rabl, P.; Schmiedmayer, J. Quantum technologies with hybrid systems. Proc. Nat. Acad. Sci. USA 2015, 112, 3866. [Google Scholar] [CrossRef]
- Findik, G.; Biliroglu, M.; Seyiitliiyev, D.; Mendes, J.; Barrette, A.; Ardekani, H.; Lei, L.; Dong, Q.; So, F.; Gundogdu, K. High-temperature superfluorescence in methyl ammonium lead iodide. Nat. Photonics 2021, 15, 676. [Google Scholar] [CrossRef]
- Biliroglu, M.; Findik, G.; Mendes, J.; Seyiitliiyev, D.; Lei, L.; Dong, Q.; Mehta, Y.; Temnov, V.V.; So, F.; Gundogdu, K. Room-temperature superfluorescence in hybrid perovskites and its origins. Nat. Photonics 2022, 16, 324. [Google Scholar] [CrossRef]
- Gundogdu, K.; So, F.; Brongersma, M.L.; Biliroglu, M.; Findik, G. Quantum Analog of Vibration Isolation: From Room-Temperature Superfluorescence to High-Temperature Superconductivity. arXiv 2022, arXiv:2204.09807. [Google Scholar]
- Strogatz, S.H. Sync: How Order Emerges from Chaos in the Universe, Nature, and Daily Life, 1st ed.; Hachette: London, UK, 2012. [Google Scholar]
- Domokos, P.; Ritsch, H. Collective Cooling and Self-Organization of Atoms in a Cavity. Phys. Rev. Lett. 2002, 89, 253003. [Google Scholar] [CrossRef]
- Black, A.T.; Chan, H.W.; Vuletic, V. Observation of Collective Friction Forces due to Spatial Self-Organization of Atoms: From Rayleigh to Bragg Scattering. Phys. Rev. Lett. 2003, 91, 203001. [Google Scholar] [CrossRef]
- Asboth, J.; Domokos, P.; Ritsch, H.; Vukics, A. Self-organization of atoms in a cavity field: Threshold, bistability, and scaling laws. Phys. Rev. A 2005, 72, 053417. [Google Scholar] [CrossRef]
- Scully, M.O.; Zubairy, M.S. Quantum Optics; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Benedict, M.G.; Ermolaev, A.M.; Malyshev, V.A.; Sokolov, I.V.; Trifonov, E.D. Super-Radiance Multiatomic Coherent Emission; Institute of Physics Publishing: Bristol, UK; Philadelphia, PA, USA, 1996. [Google Scholar]
- Dicke, R.H. Coherence in Spontaneous Radiation Processes. Phys. Rev. 1954, 93, 99. [Google Scholar] [CrossRef]
- Gross, M.; Haroche, S. Superradiance: An essay on the theory of collective spontaneous emission. Phys. Rep. 1982, 93, 301. [Google Scholar] [CrossRef]
- Kocharovsky, V.V.; Zheleznyakov, V.V.; Kocharovskaya, E.K.; Kocharovsky, V.V. Superradiance: The principles of generation and implementation in lasers, Reviews of Topical Problems. Phys. Uspekhi 2017, 60, 345. [Google Scholar] [CrossRef]
- Cong, K.; Zhang, Q.; Wang, Y.; Noe, G.T., II; Belyanin, A.; Kono, J. Dicke superradiance in solids (Invited Review). J. Opt. Soc. Am. B 2016, 33, C80. [Google Scholar] [CrossRef]
- Wang, T.; Yelin, S.F.; Côté, R.; Eyler, E.E.; Farooqi, S.M.; Gould, P.L.; Koštrun, M.; Tong, D.; Vrinceanu, D. Superradiance in ultracold Rydberg gases. Phys. Rev. A 2007, 75, 033802. [Google Scholar] [CrossRef]
- Das, D.; Lemberger, B.; Yavuz, D.D. Subradiance and superradiance-to-subradiance transition in dilute atomic clouds. Phys. Rev. A 2020, 102, 043708. [Google Scholar] [CrossRef]
- Gold, D.C.; Huft, P.; Young, C.; Safari, A.; Walker, T.G.; Saffman, M.; Yavuz, D.D. Spatial Coherence of Light in Collective Spontaneous Emission. PXR Quantum 2022, 3, 010338. [Google Scholar] [CrossRef]
- Braggio, C.; Chiossi, F.; Carugno, G.; Ortolan, A.; Ruoso, G. Spontaneous formation of a macroscopically extended coherent state. Phys. Rev. Res. 2020, 2, 033059. [Google Scholar] [CrossRef]
- Chiossi, F.; Braggio, C.; Khanbekyan, A.; Carugno, G.; Ortolan, A.; Ruoso, G.; Calabrese, R.; Di Lieto, A.; Tomassetti, L.; Tonelli, M. Cascade superfluorescence in Er:YLF. Phys. Rev. Res. 2021, 3, 013138. [Google Scholar] [CrossRef]
- Meiser, D.; Ye, J.; Carlson, D.R.; Holl, M.J. Prospects for a Millihertz-Linewidth Laser. Phys. Rev. Lett. 2009, 102, 163601. [Google Scholar] [CrossRef]
- Meiser, D.; Holland, M.J. Steady-state superradiance with alkaline-earth-metal atoms. Phys. Rev. A 2010, 81, 033847. [Google Scholar] [CrossRef]
- Norcia, M.A.; Winchester, M.N.; Cline, J.R.; Thompson, J.K. Superradiance on the millihertz linewidth strontium clock transition. Sci. Adv. 2016, 2, e1601231. [Google Scholar] [CrossRef]
- Toth, G.; Apellaniz, I. Quantum metrology from a quantum information science perspective. J. Phys. A Math. Theor. 2014, 47, 424006. [Google Scholar] [CrossRef]
- Yavuz, D.D. Superradiance as a source of collective decoherence in quantum computers. JOSA B 2014, 31, 2665. [Google Scholar] [CrossRef] [Green Version]
- Vrehen, Q.H.F.; Der Weduwe, J.J. Quantum fluctuations in superfluorescence delay times. Phys. Rev. A 1981, 24, 2857. [Google Scholar] [CrossRef]
- Vrehen, Q.H.; Schuurmans, M.F.; Polder, D. Superfluorescence: Macroscopic quantum fluctuations in the time domain. Nature 1980, 70, 285. [Google Scholar] [CrossRef]
- Ariunbold, G.O.; Sautenkov, V.A.; Scully, M.O. Quantum fluctuations of superfluorescence delay observed with ultrashort optical excitations. Phys. Lett. A 2012, 376, 335. [Google Scholar] [CrossRef]
- Ariunbold, G.O.; Sautenkov, V.A.; Scully, M.O. Temporal coherent control of superfluorescent pulses. Opt. Lett. 2012, 37, 2400. [Google Scholar] [CrossRef]
- Thompson, J.; Ballmann, C.W.; Cai, H.; Yi, Z.; Rostovtsev, V.; Sokolov, A.V.; Hemmer, P.; Zheltikov, A.M.; Ariunbold, G.O.; Scully, M.O. Pulsed cooperative backward emissions from non-degenerate atomic transitions in sodium. New J. Phys. 2014, 16, 103017. [Google Scholar] [CrossRef]
- Nasu, M.; Kawamura, K.; Yoshida, T.; Ishihara, J.; Miyajima, K. Influences of quantum fluctuation on superfluorescent spectra observed by single-shot measurement for semiconductor quantum dots. Appl. Phys. Express 2020, 13, 062005. [Google Scholar] [CrossRef]
- Khitrova, G.; Gibbs, H. Collective radiance. Nat. Phys. 2007, 3, 84. [Google Scholar] [CrossRef]
- Scully, M.O.; Svidzinsky, A.A. The Super of Superradiance. Science 2009, 325, 1510. [Google Scholar] [CrossRef]
- Rehler, N.E.; Eberly, J.H. Superradiance. Phys. Rev. A 1971, 3, 1735. [Google Scholar] [CrossRef]
- Ariunbold, G.O.; Yang, W.; Sokolov, A.; Sautenkov, V.A.; Scully, M.O. Superradiance in a Three-Photon Resonant Medium. Phys. Rev. A 2012, 85, 023424. [Google Scholar] [CrossRef] [Green Version]
- Skribanowitz, N.; Herman, I.P.; MacGillivray, J.C.; Feld, M.S. Observation of Dicke Superradiance in Optically Pumped HF Gas. Phys. Rev. Lett. 1973, 30, 309. [Google Scholar] [CrossRef]
- Marek, J. Observation of superradiance in Rb vapour. J. Phys. B 1979, 12, L229. [Google Scholar] [CrossRef]
- Ariunbold, G.O.; Sautenkov, V.A.; Scully, M.O. Ultrafast laser control of backward superfluorescence towards standoff sensing. Appl. Phys. Lett. 2014, 104, 021114. [Google Scholar] [CrossRef]
- Ariunbold, G.O. A Cascade Superradiance Model. arXiv 2022, arXiv:2207.11841. [Google Scholar] [CrossRef]
- Okada, J.; Ikeda, K.; Matsuoka, M. Cooperative cascade emission. Opt. Commun. 1978, 26, 189. [Google Scholar] [CrossRef]
- Ikeda, K.; Okada, J.; Matsuoka, M. Theory of Cooperative Cascade Emission. II. J. Phys. Soc. Jpn. 1980, 48, 1646. [Google Scholar] [CrossRef]
- Brownell, J.H.; Lu, X.; Hartmann, S.R. Yoked Superfluorescence. Phys. Rev. Lett. 1995, 75, 3265. [Google Scholar] [CrossRef]
- Ariunbold, G.O.; Kash, M.M.; Sautenkov, V.A.; Li, H.; Rostovtsev, Y.V.; Welch, G.R.; Scully, M.O. Observation of Picosecond Superfluorescent Pulses in Rubidium Vapor Pumped by 100-Femtosecond Laser Pulses. Phys. Rev. A 2010, 82, 043421. [Google Scholar] [CrossRef]
- Ariunbold, G.O.; Sautenkov, V.A.; Li, H.; Murawski, R.K.; Wang, X.; Zhi, M.; Begzjav, T.; Sokolov, A.V.; Scully, M.O.; Rostovtsev, Y.V. Observations of Ultrafast Superfluorescent Beatings in a Cesium Vapor Excited by Femtosecond Laser Pulses. Phys. Lett. A 2022, 428, 127945. [Google Scholar] [CrossRef]
- Acebrón, J.A.; Bonilla, L.L.; Vicente, C.J.P.; Ritort, F.; Spigler, R. The Kuramoto model: A simple paradigm for synchronization phenomena. Rev. Mod. Phys. 2005, 77, 137. [Google Scholar] [CrossRef] [Green Version]
- Kuramoto, Y. International Symposium on Mathematical Problems in Theoretical Physics; Lecture Notes in Physics; Araki, H., Ed.; Springer: New York, NY, USA, 1975; Volume 39, p. 420. [Google Scholar]
- Akkermans, E.; Gero, A.; Kaiser, A. Photon Localization and Dicke Superradiance in Atomic Gases. Phys. Rev. Lett. 2008, 101, 103602. [Google Scholar] [CrossRef] [PubMed]
- Quiroz-Juarez, M.A.; Chavez-Carlos, J.; Aragon, J.L.; Hirsch, J.G.; Leon-Montiel, R.J. Experimental realization of the classical Dicke model. Phys. Rev. Res. 2020, 2, 033169. [Google Scholar] [CrossRef]
- Wang, H.; Chudnovskiy, A.L.; Gorsky, A.; Kamenev, A. Sachdev-Ye-Kitaev superconductivity: Quantum Kuramoto and generalized Richardson models. Phys. Rev. Res. 2020, 2, 033025. [Google Scholar] [CrossRef]
- Witthaut, D.; Timme, M. Kuramoto dynamics in Hamiltonian systems. Phys. Rev. Res. 2014, 90, 032917. [Google Scholar] [CrossRef]
- Eshaqi-Sani, N.; Manzano, G.; Zambrini, R.; Fazio, R. Synchronization along quantum trajectories. Phys. Rev. Res. 2020, 2, 023101. [Google Scholar] [CrossRef]
- Bergmann, M.; Guehne, O. Entanglement criteria for Dicke states. J. Phys. A Math. Theor. 2013, 46, 385304. [Google Scholar] [CrossRef]
- Tralle, I.; Zieba, P. Induced N2-cooperative phenomenon in an ensemble of the nonlinear coupled oscillators. Phys. Lett. A 2014, 378, 1364. [Google Scholar]
- Alcalde, M.A.; Kullock, R.; Svaiterc, N.F. Virtual processes and super-radiance in spin-boson models. J. Math. Phys. 2009, 50, 013511. [Google Scholar] [CrossRef]
- Morrison, S.; Parkins, A.S. Collective spin systems in dispersive optical cavity QED: Quantum phase transitions and entanglement. Phys. Rev. A 2008, 77, 043810. [Google Scholar] [CrossRef]
- Kirton, P.; Roses, M.M.; Keeling, J.; Dalla Torre, E.G. Introduction to the Dicke Model: From Equilibrium to Nonequilibrium, and Vice Versa. Adv. Quantum Technol. 2019, 2, 1800043. [Google Scholar] [CrossRef]
- Wang, Y.K.; Hioe, F.T. Phase Transition in the Dicke Model of Superradiance. Phys. Rev. A 1973, 7, 831. [Google Scholar] [CrossRef]
- Rzazewski, R.; Wodkiewicz, K.; Zakowicz, W. Phase Transitions, Two-Level Atoms, and the A2 Term. Phys. Rev. Lett. 1975, 35, 432. [Google Scholar] [CrossRef]
- Nataf, P.; Ciuti, C. No-go theorem for superradiant quantum phase transitions in cavity QED and counter-example in circuit QED. Nat. Commun. 2010, 1, 72. [Google Scholar] [CrossRef]
- Agarwal, G.S. Quantum Optics: Quantum Statistical Theories of Spontaneous Emission and Their Relation to Other Approaches; Volume 70 of Springer Tracts in Modern Physics; Springer: Berlin/Heidelberg, Germany, 1974. [Google Scholar]
- Ariunbold, G.O.; Rostovtsev, Y.V.; Sautenkov, V.A.; Scully, M.O. Intensity correlation and anti-correlations in coherently driven atomic vapor. J. Mod. Opt. 2010, 57, 1417. [Google Scholar] [CrossRef]
- Malcuit, M.S.; Maki, J.J.; Simkin, D.J.; Boyd, R.W. Transition from Superfluorescence to Amplified Spontaneous Emission. Phys. Rev. Lett. 1987, 59, 1189. [Google Scholar] [CrossRef]
- Lvovsky, A.I.; Hartmann, S.R.; Moshary, F. Superfluorescence-Stimulated Photon Echoes. Phys. Rev. Lett. 2002, 89, 263602. [Google Scholar] [CrossRef]
- Dogariu, A.; Michael, J.B.; Scully, M.O.; Miles, R.B. High-gain backward lasing in air. Science 2011, 331, 442. [Google Scholar] [CrossRef]
- Traverso, A.J.; Sanchez-Gonzalez, R.; Yuan, L.; Wang, K.; Voronine, D.V.; Zheltikov, A.M.; Rostovtsev, Y.; Sautenkov, V.A.; Sokolov, A.V.; North, S.W.; et al. Coherence brightened laser source for atmospheric remote sensing. Proc. Natl. Acad. Sci. USA 2012, 109, 15185. [Google Scholar] [CrossRef]
- Zhang, R.; Klinger, E.; Bustos, F.P.; Akulshin, A.; Guo, H.; Wickenbrock, A.; Budker, D. Stand-Off Magnetometry with Directional Emission from Sodium Vapors. Phys. Rev. Lett. 2021, 127, 173605. [Google Scholar] [CrossRef]
- Akulshin, A.; Budker, D.; Mclean, R.J. Parametric wave mixing enhanced by velocity-insensitive two-photon excitation in Rb vapor. J. Opt. Soc. Am. B 2017, 34, 1016. [Google Scholar] [CrossRef]
- Akulshin, A.; Rahaman, N.; Suslov, S.A.; Budker, D.; Mclean, R.J. Spiking dynamics of frequency upconverted field generated in continuous-wave excited rubidium vapors. J. Opt. Soc. Am. B 2020, 37, 2430. [Google Scholar] [CrossRef]
- Kitano, K.; Tomida, H.; Takei, D.; Maeda, H. Polarization correlation in the superfluorescent decay process. Opt. Lett. 2021, 46, 5055. [Google Scholar] [CrossRef]
- Yi, Z.; Begzjav, T.; Ariunbold, G.O.; Zheltikov, A.M.; Sokolov, A.V.; Scully, M.O. Multiple Pathway Quantum Beats Spectroscopy. Front. Phys. Sect. Quantum Eng. Technol. 2022; in press. [Google Scholar] [CrossRef]
- Ariunbold, G.; Perina, J.; Gantsog, T. Nonclassical states in cavity with injected atoms. J. Opt. B Quantum Semiclass. Opt. 1999, 1, 219. [Google Scholar] [CrossRef]
- Gombojav, A. Ultrafast Cooperative Phenomena in Coherently Prepared Media: From Superfluorescence to Coherent Raman Scattering and Applications. Ph.D. Thesis, Texas A & M University, College Station, TX, USA, 2011. [Google Scholar]
- Ariunbold, G.O.; Sautenkov, V.A.; Scully, M.O. Switching from a sequential transition to quantum beating in atomic rubidium pumped by a femtosecond laser. J. Opt. Soc. Am. B 2011, 28, 462. [Google Scholar] [CrossRef]
- Zewail, A.H. Femtochemistry: Ultrafast Dynamics of the Chemical Bond, 1st ed.; World Scientific: Singapore, 1994; Volume 1. [Google Scholar]
- Maker, P.D.; Terhune, R.W. Study of optical effects due to an induced polarization of third order in the electric field strength. Phys. Rev. 1965, 137, A801. [Google Scholar] [CrossRef]
- Cheng, J.X.; Xie, X.S. Coherent Raman Scattering Microscopy, 1st ed.; CRC Press: New York, NY, USA, 2013. [Google Scholar]
- Pestov, D.; Murawski, R.K.; Ariunbold, G.O.; Wang, X.; Zhi, M.; Sokolov, A.V.; Sautenkov, V.A.; Rostovtsev, Y.V.; Dogariu, A.; Huang, Y.; et al. Optimizing the Laser-Pulse Configuration for Coherent Raman Spectroscopy. Science 2007, 316, 265. [Google Scholar] [CrossRef]
- Pestov, D.; Wang, X.; Ariunbold, G.O.; Murawski, R.K.; Sautenkov, V.A.; Dogariu, A.; Sokolov, A.V.; Scully, M.O. Single-shot Detection of Bacterial Endospores via Coherent Raman Spectroscopy. Proc. Natl. Acad. Sci. USA 2007, 105, 422. [Google Scholar] [CrossRef]
- Pestov, D.; Ariunbold, G.O.; Wang, X.; Murawski, R.K.; Sautenkov, V.A.; Sokolov, A.V.; Scully, M.O. Coherent versus incoherent Raman scattering: Molecular coherence excitation and measurement. Opt. Lett. 2007, 32, 1725. [Google Scholar] [CrossRef]
- Pestov, P.; Sokolov, A.V.; Scully, M.O.; Murawski, R.; Gombojav, A.; Wang, X.; Sautenkov, V. Hybrid Technique for Coherent Anti-Stokes/Stokes Raman Spectroscopy. U.S. Patent 20100027000, 4 February 2010. [Google Scholar]
- Ariunbold, G.O.; Altangerel, N. Coherent anti-Stokes Raman spectroscopy: Understanding the essentials. Review article. Coherent Opt. Phenom. 2016, 3, 6. [Google Scholar]
- Ariunbold, G.O.; Altangerel, N. Quantitative interpretation of time-resolved coherent anti-Stokes Raman spectroscopy with all Gaussian pulses. J. Raman Spectrosc. 2017, 48, 104. [Google Scholar] [CrossRef]
- Ariunbold, G.O. Asymmetric spectral noise correlations in coherent Stokes and anti-Stokes Raman scatterings. OSA Contin. 2018, 1, 832. [Google Scholar] [CrossRef]
- Ariunbold, G.O.; Semon, B.; Nagpal, S.; Adhikari, P. Coherent Anti-Stokes—Stokes Raman Cross-Correlation Spectroscopy: Asymmetric Frequency Shifts in Hydrogen-Bonded Pyridine-Water Complexes. Appl. Spectrosc. 2019, 73, 1099. [Google Scholar] [CrossRef] [PubMed]
- Ariunbold, G.O.; Nagpal, S.; Semon, B. Quantitative time-resolved buildup in three-color coherent anti-Stokes Raman scattering. Spectrosc. Lett. 2020, 53, 383. [Google Scholar] [CrossRef]
- Ariunbold, G.O.; Semon, B.; Nagpal, S.; Rostovtsev, Y. Ultrafast dephasing in hydrogen-bonded pyridine–water mixtures. Open Phys. 2021, 19, 234. [Google Scholar] [CrossRef]
- Nagpal, S.; Semon, B.; Ariunbold, G.O. Distinguishing Resonant from Non-Resonant Nonlinear Optical Processes Using Intensity—Intensity Correlation Analyses. Appl. Spectrosc. 2021, 75, 1382. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ariunbold, G.O. On Macroscopic Quantum Coherence with Synchronized Atoms and Molecules: Superradiance. Processes 2022, 10, 1885. https://doi.org/10.3390/pr10091885
Ariunbold GO. On Macroscopic Quantum Coherence with Synchronized Atoms and Molecules: Superradiance. Processes. 2022; 10(9):1885. https://doi.org/10.3390/pr10091885
Chicago/Turabian StyleAriunbold, Gombojav O. 2022. "On Macroscopic Quantum Coherence with Synchronized Atoms and Molecules: Superradiance" Processes 10, no. 9: 1885. https://doi.org/10.3390/pr10091885
APA StyleAriunbold, G. O. (2022). On Macroscopic Quantum Coherence with Synchronized Atoms and Molecules: Superradiance. Processes, 10(9), 1885. https://doi.org/10.3390/pr10091885