Identification of Cell Culture Factors Influencing Afucosylation Levels in Monoclonal Antibodies by Partial Least-Squares Regression and Variable Importance Metrics
Abstract
:1. Introduction
2. Theory
2.1. Variable Importance in Projection Scores (VIP-Scores)
2.2. Selectivity Ratio (SR)
2.3. Significance Multivariate Correlation (sMC)
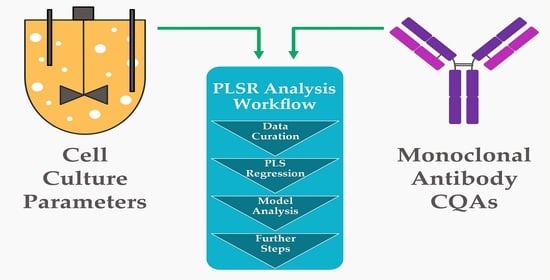
3. Methods
3.1. Dataset Description
3.2. Models and Software
4. Results
4.1. PLSR-Model-Based Workflow
4.2. Application of Workflow: Complex Afucosylation of mAb-δ
4.3. Summary of Models and Influential Parameters
5. Discussion
5.1. Variable Importance Metrics
5.2. Influential Parameters to Afucosylation
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fan, Y.; Jimenez Del Val, I.; Müller, C.; Wagtberg Sen, J.; Rasmussen, S.K.; Kontoravdi, C.; Weilguny, D.; Andersen, M.R. Amino acid and glucose metabolism in fed-batch CHO cell culture affects antibody production and glycosylation. Biotechnol. Bioeng. 2015, 112, 521–535. [Google Scholar] [CrossRef] [Green Version]
- Rish, A.J.; Drennen, J.K.; Anderson, C.A. Metabolic trends of Chinese hamster ovary cells in biopharmaceutical production under batch and fed-batch conditions. Biotechnol. Prog. 2022, 38, e3220. [Google Scholar] [CrossRef]
- Fan, J.; Han, F.; Liu, H. Challenges of big data analysis. Natl. Sci. Rev. 2014, 1, 293–314. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- de Micheaux, P.L.; Liquet, B.; Sutton, M. Pls for big data: A unified parallel algorithm for regularised group pls. Stat. Surv. 2019, 13, 119–149. [Google Scholar] [CrossRef]
- Wold, S.; Sjöström, M.; Eriksson, L. PLS-regression: A basic tool of chemometrics. Chemom. Intell. Lab. Syst. 2001, 58, 109–130. [Google Scholar] [CrossRef]
- Chong, I.-G.; Jun, C.-H. Performance of some variable selection methods when multicollinearity is present. Chemom. Intell. Lab. Syst. 2005, 78, 103–112. [Google Scholar] [CrossRef]
- Rajalahti, T.; Arneberg, R.; Berven, F.S.; Myhr, K.-M.; Ulvik, R.J.; Kvalheim, O.M. Biomarker discovery in mass spectral profiles by means of selectivity ratio plot. Chemom. Intell. Lab. Syst. 2009, 95, 35–48. [Google Scholar] [CrossRef]
- Rajalahti, T.; Arneberg, R.; Kroksveen, A.C.; Berle, M.; Myhr, K.-M.; Kvalheim, O.M. Discriminating variable test and selectivity ratio plot: Quantitative tools for interpretation and variable (biomarker) selection in complex spectral or chromatographic profiles. Anal. Chem. 2009, 81, 2581–2590. [Google Scholar] [CrossRef]
- Tran, T.N.; Afanador, N.L.; Buydens, L.M.; Blanchet, L. Interpretation of variable importance in partial least squares with significance multivariate correlation (sMC). Chemom. Intell. Lab. Syst. 2014, 138, 153–160. [Google Scholar] [CrossRef]
- Kirdar, A.O.; Green, K.D.; Rathore, A.S. Application of multivariate data analysis for identification and successful resolution of a root cause for a bioprocessing application. Biotechnol. Prog. 2008, 24, 720–726. [Google Scholar] [CrossRef]
- Goldrick, S.; Holmes, W.; Bond, N.J.; Lewis, G.; Kuiper, M.; Turner, R.; Farid, S.S. Advanced multivariate data analysis to determine the root cause of trisulfide bond formation in a novel antibody–peptide fusion. Biotechnol. Bioeng. 2017, 114, 2222–2234. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shields, R.L.; Lai, J.; Keck, R.; O’Connell, L.Y.; Hong, K.; Meng, Y.G.; Weikert, S.H.; Presta, L.G. Lack of fucose on human IgG1 N-linked oligosaccharide improves binding to human FcγRIII and antibody-dependent cellular toxicity. J. Biol. Chem. 2002, 277, 26733–26740. [Google Scholar] [CrossRef] [Green Version]
- Shinkawa, T.; Nakamura, K.; Yamane, N.; Shoji-Hosaka, E.; Kanda, Y.; Sakurada, M.; Uchida, K.; Anazawa, H.; Satoh, M.; Yamasaki, M. The absence of fucose but not the presence of galactose or bisecting N-acetylglucosamine of human IgG1 complex-type oligosaccharides shows the critical role of enhancing antibody-dependent cellular cytotoxicity. J. Biol. Chem. 2003, 278, 3466–3473. [Google Scholar] [CrossRef] [Green Version]
- Russolillo, G.; Lauro, C.N. A Proposal for Handling Categorical Predictors in Pls Regression Framework. In Classification and Multivariate Analysis for Complex Data Structures; Springer: Berlin/Heidelberg, Germany, 2011; pp. 343–350. [Google Scholar] [CrossRef]
- Trinchera, L.; Russolillo, G.; Lauro, C.N. Using categorical variables in PLS Path Modeling to build system of composite indicators. Stat. Appl. 2008, 20, 309–330. [Google Scholar]
- Chin, W.W. The partial least squares approach to structural equation modeling. Mod. Methods Bus. Res. 1998, 295, 295–336. [Google Scholar]
- Henseler, J.; Ringle, C.M.; Sinkovics, R.R. The Use of Partial Least Squares Path Modeling in International Marketing. In New Challenges to International Marketing; Emerald Group Publishing Limited: Bradford, UK, 2009. [Google Scholar] [CrossRef] [Green Version]
- Farrésa, M.; Platikanova, Y.; Tsakovskib, L.; Taulera, R. Comparison of the variable importance in prediction (VIP) and of the selectivity ratio (SR) variable selection methods in the analysis of three different data sets. J. Chemom. 2015, 29, 528–536. [Google Scholar] [CrossRef]
- Kvalheim, O.M. Variable importance: Comparison of selectivity ratio and significance multivariate correlation for interpretation of latent-variable regression models. J. Chemom. 2020, 34, e3211. [Google Scholar] [CrossRef] [Green Version]
- Li, W.; Zhu, Z.; Chen, W.; Feng, Y.; Dimitrov, D.S. Crystallizable fragment glycoengineering for therapeutic antibodies development. Front. Immunol. 2017, 8, 1554. [Google Scholar] [CrossRef] [Green Version]
- Miyoshi, E.; Noda, K.; Yamaguchi, Y.; Inoue, S.; Ikeda, Y.; Wang, W.; Ko, J.H.; Uozumi, N.; Li, W.; Taniguchi, N. The α1-6-fucosyltransferase gene and its biological significance. Biochim. Et Biophys. Acta (BBA) Gen. Subj. 1999, 1473, 9–20. [Google Scholar] [CrossRef]
- Goh, J.B.; Ng, S.K. Impact of host cell line choice on glycan profile. Crit. Rev. Biotechnol. 2018, 38, 851–867. [Google Scholar] [CrossRef]
- Thaysen-Andersen, M.; Packer, N.H. Site-specific glycoproteomics confirms that protein structure dictates formation of N-glycan type, core fucosylation and branching. Glycobiology 2012, 22, 1440–1452. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Welch, J.T.; Arden, N.S. Considering “clonality” A regulatory perspective on the importance on the clonal derivation of mammalian cell banks in biopharmaceutical development. Biologicals 2019, 62, 16–21. [Google Scholar] [CrossRef]
- Ko, P.; Misaghi, S.; Hu, Z.; Zhan, D.; Tsukuda, J.; Yim, M.; Sanford, M.; Shaw, D.; Shiratori, M.; Snedecor, B.; et al. Probing the importance of clonality: Single cell subcloning of clonally derived CHO cell Lines yields widely diverse clones differing in growth, productivity, and product quality. Biotechnol. Prog. 2018, 34, 624–634. [Google Scholar] [CrossRef] [PubMed]
- Agarabi, C.D.; Schiel, J.E.; Lute, S.C.; Chavez, B.K.; Boyne II, M.T.; Brorson, K.A.; Khan, M.; Read, E.K. Bioreactor process parameter screening utilizing a Plackett-Burman design for a model monoclonal antibody. J. Pharm. Sci. 2015, 104, 1919–1928. [Google Scholar] [CrossRef] [PubMed]
- Sou, S.N.; Sellick, C.; Lee, K.; Mason, A.; Kyriakopoulos, S.; Polizzi, K.M.; Kontoravdi, C. How does mild hypothermia affect monoclonal antibody glycosylation? Biotechnol. Bioeng. 2015, 112, 1165–1176. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nam, J.H.; Zhang, F.; Ermonval, M.; Linhardt, R.J.; Sharfstein, S.T. The effects of culture conditions on the glycosylation of secreted human placental alkaline phosphatase produced in Chinese hamster ovary cells. Biotechnol. Bioeng. 2008, 100, 1178–1192. [Google Scholar] [CrossRef] [Green Version]
- Saraste, J.; Palade, G.E.; Farquhar, M.G. Temperature-sensitive steps in the transport of secretory proteins through the Golgi complex in exocrine pancreatic cells. Proc. Natl. Acad. Sci. USA 1986, 83, 6425–6429. [Google Scholar] [CrossRef] [Green Version]
- Zalai, D.; Hevér, H.; Lovász, K.; Molnár, D.; Wechselberger, P.; Hofer, A.; Párta, L.; Putics, Á.; Herwig, C. A control strategy to investigate the relationship between specific productivity and high-mannose glycoforms in CHO cells. Appl. Microbiol. Biotechnol. 2016, 100, 7011–7024. [Google Scholar] [CrossRef] [Green Version]
- Nguyen Dang, A.; Mun, M.; Rose, C.M.; Ahyow, P.; Meier, A.; Sandoval, W.; Yuk, I.H. Interaction of cell culture process parameters for modulating mAb afucosylation. Biotechnol. Bioeng. 2019, 116, 831–845. [Google Scholar] [CrossRef]
- Gramer, M.J.; Eckblad, J.J.; Donahue, R.; Brown, J.; Shultz, C.; Vickerman, K.; Priem, P.; van den Bremer, E.T.; Gerritsen, J.; van Berkel, P.H. Modulation of antibody galactosylation through feeding of uridine, manganese chloride, and galactose. Biotechnol. Bioeng. 2011, 108, 1591–1602. [Google Scholar] [CrossRef]
- St Amand, M.M.; Radhakrishnan, D.; Robinson, A.S.; Ogunnaike, B.A. Identification of manipulated variables for a glycosylation control strategy. Biotechnol. Bioeng. 2014, 111, 1957–1970. [Google Scholar] [CrossRef]
- Surve, T.; Gadgil, M. Manganese increases high mannose glycoform on monoclonal antibody expressed in CHO when glucose is absent or limiting: Implications for use of alternate sugars. Biotechnol. Prog. 2015, 31, 460–467. [Google Scholar] [CrossRef] [PubMed]
- Prabhu, A.; Gadgil, M. Nickel and cobalt affect galactosylation of recombinant IgG expressed in CHO cells. Biometals 2019, 32, 11–19. [Google Scholar] [CrossRef] [PubMed]
- Cordero, B.; Gómez, V.; Platero-Prats, A.E.; Revés, M.; Echeverría, J.; Cremades, E.; Barragán, F.; Alvarez, S. Covalent radii revisited. Dalton Trans. 2008, 21, 2832–2838. [Google Scholar] [CrossRef] [PubMed]
- Luo, Y.; Lovelett, R.J.; Price, J.V.; Radhakrishnan, D.; Barnthouse, K.; Hu, P.; Schaefer, E.; Cunningham, J.; Lee, K.H.; Shivappa, R.B. Modeling the effect of amino acids and copper on monoclonal antibody productivity and glycosylation: A modular approach. Biotechnol. J. 2021, 16, 2000261. [Google Scholar] [CrossRef] [PubMed]





| Molecules | Number of Bioreactor Runs | Culture Duration (Days) | Culture Process Parameters | |
|---|---|---|---|---|
| mAb-α | 55 | 14 | Basal Glucose Conc. | pH Setpoint |
| Basal Osmolality | Seeding Density | |||
| Daily Feed % | Temperature Shift Difference | |||
| Feed Glucose Conc. | Temperature Setpoint | |||
| Feed Osmolality | ||||
| Feed pH | ||||
| mAb-β | 80 | 14 | Basal Glucose Conc. | Feed pH |
| Basal Osmolality | pH Setpoint | |||
| Daily Feed % | Seeding Density | |||
| Feed Glucose Conc. | Temperature Setpoint | |||
| Feed Osmolality | ||||
| mAb-γ | 61 | 12 | Additive 1 Bolus Conc. | Feed Glucose Conc. |
| Additive 1 Bolus Day | Feed Glutamate Conc. | |||
| Additive 1 Feed | Feed Glutamine Conc. | |||
| Basal Ammonia | Feed Na+ Conc. | |||
| Basal Glucose Conc. | Feed Glucose Conc. | |||
| Basal Glutamate Conc. | Feed Osmolality | |||
| Basal Glutamine Conc. | Feed pH | |||
| Basal Na+ Conc. | pH Setpoint | |||
| Basal Osmolality | pH Lower Bound | |||
| Daily Feed % | Seeding Density | |||
| Feed Ammonia | ||||
| mAb-δ | 81 | 14 | Additive 2 Conc. | Feed Osmolality |
| Basal Glucose Conc. | Feed pH | |||
| Basal Osmolality | Feed Start Day | |||
| Copper Supp. Conc. | Glucose Setpoint | |||
| Feed Glucose Conc. | Seeding Density | |||
| Total Afucosylation | High Mannose | Complex Afucosylation | ||
|---|---|---|---|---|
| mAb-α | VIP |
|
|
|
| SR |
|
|
| |
| sMC |
|
|
| |
| mAb-β | VIP |
|
|
|
| SR |
|
|
| |
| sMC |
|
|
| |
| mAb-γ | VIP |
|
|
|
| SR |
|
|
| |
| sMC |
|
|
| |
| mAb-δ | VIP |
|
|
|
| SR |
|
|
| |
| sMC |
|
|
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rish, A.J.; Huang, Z.; Siddiquee, K.; Xu, J.; Anderson, C.A.; Borys, M.C.; Khetan, A. Identification of Cell Culture Factors Influencing Afucosylation Levels in Monoclonal Antibodies by Partial Least-Squares Regression and Variable Importance Metrics. Processes 2023, 11, 223. https://doi.org/10.3390/pr11010223
Rish AJ, Huang Z, Siddiquee K, Xu J, Anderson CA, Borys MC, Khetan A. Identification of Cell Culture Factors Influencing Afucosylation Levels in Monoclonal Antibodies by Partial Least-Squares Regression and Variable Importance Metrics. Processes. 2023; 11(1):223. https://doi.org/10.3390/pr11010223
Chicago/Turabian StyleRish, Adam J., Zhuangrong Huang, Khandaker Siddiquee, Jianlin Xu, Carl A. Anderson, Michael C. Borys, and Anurag Khetan. 2023. "Identification of Cell Culture Factors Influencing Afucosylation Levels in Monoclonal Antibodies by Partial Least-Squares Regression and Variable Importance Metrics" Processes 11, no. 1: 223. https://doi.org/10.3390/pr11010223
APA StyleRish, A. J., Huang, Z., Siddiquee, K., Xu, J., Anderson, C. A., Borys, M. C., & Khetan, A. (2023). Identification of Cell Culture Factors Influencing Afucosylation Levels in Monoclonal Antibodies by Partial Least-Squares Regression and Variable Importance Metrics. Processes, 11(1), 223. https://doi.org/10.3390/pr11010223