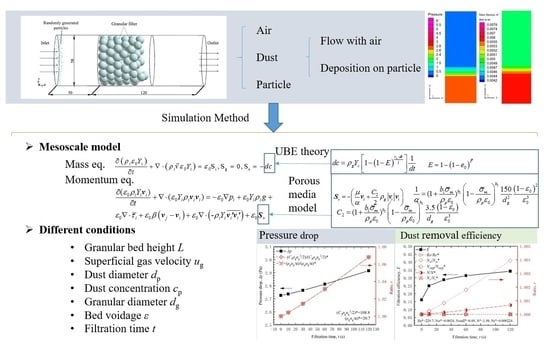
1. Introduction
Large amounts of fine-dust emissions affect air quality and visibility, which also endangers human health. With the development of the economy and the improvement of people’s living standards, people in various countries are becoming more and more concerned about air pollution and have set strict emission standards: the World Health Organization (WHO) air quality guidelines of 2021 [
1] stipulate that the annual average emission concentration of PM2.5 should not be higher than 5 μg/m
3. A granular bed filter (GBF) is a device that uses granular media as a filter layer to purify dust-containing gases. Granules are accumulated inside the GBF, and the dust inside is captured by the granules through inertial collision, diffusion, interception, gravitational settling, and electrostatic forces [
2,
3]. Compared with inertial, cyclone, wet, and electrostatic de-dusting devices, GBF has the advantages of a high dust-removal efficiency (especially <10 μm), high-temperature and high-pressure resistance, simultaneous desulfurization, denitrification, the removal of volatile organic compounds (VOCs) and drying of materials, etc. It is widely used in thermal power, steel, petrochemicals, and other industries [
4,
5].
GBF contains filter media, gas, and dust. The dust can flow with the gas or accumulate on the surface of the filter media by inertial collision and diffusion, making the flow field more complex. At present, a lot of research has been conducted to reveal the flow-field distribution law and to propose macroscopic calculation models for pressure drop and dust-removal efficiency. The pressure-drop model is generally modified based on the Ergun equation by introducing parameters such as the amount of dust deposited on the surface of the filter media. For example, Xiao et al. [
6], Robert et al. [
7], Denis [
8], and Yin et al. [
9] have systematically studied and analyzed the pressure drop in the GBF and found that the pressure drop increases with increasing dust deposition. Moreover, the macroscopic calculation model is established for the pressure drop during dust loading by modifying the traditional Ergun equation and considering the effect of dust deposition. Based on different assumptions, different macroscopic models of dust-removal efficiency have been developed. For example, Iwasaki et al. [
10] and Ruben et al. [
11] assumed that the concentration of dust deposited on the surface of media granules has an exponential distribution, and then a macroscopic model of dust-removal efficiency is proposed. Tardos et al. [
12] and Jung et al. [
13] developed a single-granule dust-removal efficiency model based on the interaction forces between dust, gas, and filter granules, and modified it to obtain a granular dust-removal-efficiency model. Yu et al. [
14] and Bruno et al. [
15] constructed a dust-removal-efficiency model by assuming that the bed consists of a series of unit bed elements (UBE) connected in series. The dust-removal efficiency of each UBE is the same under the initial conditions. The dust-removal-efficiency model constructed by UBE theory includes the Reynolds number, Stokes number, equivalent granular diameter ratio, bed height, and other numbers, and takes into account the influence of different conditions and dust deposition, which is chosen in this study.
The macroscopic calculation models of pressure drop and dust-removal efficiency can reflect the bed performance of GBF. However, most of the fluid flows in real industrial installations are non-plug flows and the calculation results may have large errors. Numerical simulation is a much easier way to obtain detailed information about the flow field inside the bed than experimental studies; this method is also suitable for GBF with different structural parameters. If the macroscopic models can be combined into numerical simulations, the flow-field distribution in the granular bed filter can be obtained more quickly and accurately.
Different simulation methods are used in the modeling of the flow field in GBF, e.g., the Eulerian–Lagrangian two-phase flow (CFD-DEM) method and the Eulerian single-phase flow method. For the CFD-DEM method, filter granules are calculated by the Lagrangian method; gases and dusts can be calculated by the combined models of Eulerian single-phase flow, multi-component transport, and DPM. For example, Chen et al. [
16] and Li et al. [
17] used CFD-DEM to obtain the dust-removal characteristics of a fixed GBF before the formation of filter cake. Wang et al. [
18], Chou et al. [
19], Kloss et al. [
20], and You et al. [
21] used the combined models of an Eulerian single-phase flow and DPM to investigate the flow-field characteristics in a randomly filled GBF and obtain the variation in initial pressure drop and dust-removal efficiency. In addition, the flow-field space can be directly simulated after the volume deletion of filtered granules. For example, Chen et al. [
22], Guan et al. [
23], and Wang et al. [
24] used the DEM method to determine the location of filter granules under random accumulation, and then numerically simulated the fluid space after the removal of filter granules in GBF. The above methods allow us to investigate the interaction forces between dusts, gas, and filter granules. The dust-filtration mechanisms are also analyzed according to the simulation results such as dust collision, gravitational settling, diffusion, and interception. However, large installations contain tens of millions or even hundreds of millions of granules. The interaction forces between the gas, the dust, and the filter granules also increase the computational difficulty and workload.
In contrast, the use of a porous media model can significantly reduce the computational effort of the simulation. For example, Ahmed et al. [
25], Wojciech et al. [
26], Cheng et al. [
27], and Rodrigo et al. [
28] used the porous media model to simulate the flow-field information in the granules and obtained accurate pressure drop data. However, the variation in dust-removal efficiency and flow field with dust deposition in the granules cannot be obtained by a porous media model.
Therefore, this study combines the macroscopic models, i.e., the pressure drop and the dust-removal efficiency equations based on unit bed elements (UBE) theory [
15], into the porous media model and the source term of the conservation equations. A new mesoscale simulation method is then obtained. A three-dimensional full-scale model is developed based on the structural parameters of the axial GBF described in reference [
29]. Grid-dependent tests and model validation are performed. The effects of different operating conditions and physical parameters, e.g., bed height, superficial gas velocity, dust diameter, dust concentration, granular diameter, bed voidage, and filtration time, on the flow field are investigated. The feasibility of this mesoscale simulation method can be further verified when the variation laws of pressure drop and dust-removal efficiency obtained by the simulation results coincide well with the experimental results.
2. Numerical Simulation
2.1. Geometry Model and Mesh
Based on the structural parameters of the axial granular bed filter described in reference [
29], a cylindrical flow field with a diameter of 58 mm and a height of 170 mm is created. A section of the granular bed is in the middle, as shown in
Figure 1. One side of the cylindrical bed is the gas inflow, where the randomly generated dust granules are mixed with air to form a dusty gas. When the dusty gas flows through the granular bed, the dust is removed by the filter granules and the cleaned gas is discharged from the outflow side. The constants in the equations are dependent on the gas, dust, and filter parameters.
The gas is air at room temperature and pressure with a density of 1.205 kg/m3 and a kinetic viscosity of 1.81 × 10−5 Pa·s. The filtered granules and dust are glass spheres and silica with a bulk density of 2500 and 1400 kg/m3, respectively.
Different parameter values are varied in the simulation to examine their effects on the flow field. The parameters examined include bed height L = 20–100 mm, superficial gas velocity ug = 0.15–0.55 m/s, dust concentration cp = 100–100,000 mg/m3, dust diameter dp = 1–10 μm, granular diameter dg = 1–10 mm, bed voidage ε = 0.40–0.55, and filtration time t = 0–120 s. In order to facilitate the analysis, a baseline working condition is chosen: L = 20 mm, ug = 0.345 m/s, cp = 6985 mg/m3, dp = 2.24 μm, dg = 10 mm, ε = 0.49, t = 0 s.
Gambit 2.4.6 software was used to draw the geometry model and mesh. Three fluid calculation areas were set up: left fluid, middle granules, and right fluid. The structured hexahedral mesh was created by combining O-planar partitioning and Cooper’s methods. The maximum distortion of the mesh was less than 0.5, as shown in
Figure 1.
2.2. Mathematical Model
In this study, a distinction is made between the dust flowing with the gas and the dust deposited on the surface of the filter granules, which are assumed to belong to different phases. The Eulerian two-phase flow and porous media models in Fluent 6.3.26 software are used to the simulation studies: the gas and the carried dust are considered as one phase and simulated by the multi-component transport model; the dust deposited on the surface of the filter media is the other phase, and the influence of the filter granules on the flow field is simulated by the porous media model. In addition, the macroscopic model of pressure drop and dust-removal efficiency is combined into the porous media model with the source term of the continuity equations in the form of a user-defined function (UDF). The flow-field information in GBF is then obtained by this mesoscale simulation method. It refers to the fact that the variations in the parameters are calculated from a mesoscopic view (each mesh), rather than a macroscopic view (the whole bed) or a microscopic view (each dust and granules).
2.2.1. Continuity and Momentum Conservation Equations
The Eulerian two-phase flow model is applied in this study. The primary phase is the mixture of air and carried dust granules, which are simulated by a multi-component transport model. The local average continuity Equation (1) and the momentum Equation (2) are used. The mass sources of the gas and dust are zero and -
dc, respectively. The interaction forces and turbulence are calculated by Equation (3) and k-ε RNG models, respectively, which are not described here [
30].
The secondary phase is the dust phase accumulated on the surface of filter granules, which is calculated by using the local average continuity Equation (3). As the dust phase accumulates on the granule surface, the velocity of the dust phase is set to 0 m/s in this study. It is no longer calculated by the momentum conservation equation.
2.2.2. Porous Media Model
The resistance effect of the granular bed on the flow field is realized by the application of a porous media model (4). In the momentum conservation equation, the macroscopic model of pressure drop given in [
15] is used to change the coefficients of the viscous and inertial resistance terms (5 and 6) by means of UDF.
where
ρp is the dust density,
dg is the filter granular diameter, and
ε0 is the initial bed voidage.
is the dust deposition quantity and can be calculated by Equation (7).
b1,
b2, and
b3 are constants, which are fitted by the experimental results of pressure drop (taken as 28.92, 1.254, and 4.2171, 159 [
15], respectively, in this study) as shown in Equations (5) and (6).
2.2.3. Source Term in Continuity Equations
By changing the source term of the continuity equations, the dust is transferred from one phase to another in the granular bed region. The amount of transfer affects the dust-removal efficiency. According to the UBE theory [
15], the conservation and macroscopic equations are connected by Equation (8). In each cell, the gas velocity remains unchanged with the positions. Thus, when “
dt” is sufficiently small, the gas flows a distance of “
vgdt” where
vg is the real gas velocity in each cell. According to the UBE theory, the mass sources of dust “
dc” can be calculated by Equation (8) when the distance of gas flow is “
vgdt”. However, the gas velocity may vary widely in different cells, which allows for the attainment of the flow-field distribution in an axial granular bed filter by this approach. The thickness
l of each layer can be calculated by Equation (9). In addition, the actual bed voidage
ε within the granular bed will, in turn, affect
l.
For the UBE theory, the granular bed is considered as a series of unit beds. According to the work of [
15], the total dust-removal efficiency
E is related to the initial dust-removal efficiency
e0 and can be calculated using Equation (10);
e0 is related to the dust-removal efficiency of the single unit bed
η0, as shown in Equation (11);
is the average relative filtration coefficient, which is an important parameter to characterize the deep-filtration performance. The constants of a
1, a
2, and a
3 are fitted by means of the experimental results of the filtration efficiency (taken as 290,600, 0.1374, and 4.338 [
15], respectively, in this study), as shown in Equation (12).
According to Equations (13)–(19) [
15],
η0 is related to the effective Stokes number
Nsteff, dust diameter
dp, granular diameter
dg, and adhesion probability
γ. The constants are obtained directly from the work in [
15], which summarizes the relevant research.
Nsteff is a modified value of the Stokes number
Nst [
13], which characterizes the ratio of inertial to diffusion forces. The smaller the value, the smaller the inertia of the dust, the easier it is to follow the fluid motion, and the more pronounced the diffusion effect. The dust-removal efficiency tends to decrease. In order to better predict the traction effect on dust of the gas, the Cunningham correction factor
Cs is introduced by taking into account the discontinuous medium effect of dust transition between continuous and free molecular flow. The Reynolds number
Re is the ratio of inertial and viscous forces. In Equation (18),
ρg,
vg, and
μg are the density, the superficial gas velocity, and the viscosity of the dusty gas, respectively;
dg is the diameter of the filter granules. As
Re increases, the inertial effect increases, and the probability of inertial collision between dust and filter granules increases significantly.
2.3. Parameter Settings
The Eulerian two-phase flow, multi-component transport, and porous media models in Fluent 6.3.24 software are used for the simulation study. The inlet and outlet boundary conditions are set as the velocity inlet and pressure outlet, respectively; the wall surface is selected as a no-slip boundary condition. The simulation type is chosen as transient simulation, and the algorithm is chosen as SIMPLE. The time step is chosen as 0.001 s with a maximum iteration step of 20.
In this study, a single-factor variable method, or the one-factor-at-a-time method, is used to investigate the effect of different conditions on the flow field by changing a parameter value in a baseline working condition (
Section 2.1).
2.4. Grid-Dependent Test and Experimental Validation
According to the relevant numerical simulation studies of GBF [
21,
24,
29], the grid sizes of 1, 2, 3, 4, and 5 mm are chosen for study here.
Figure 2a indicates that both the pressure drop and dust-removal efficiency vary less for the grid sizes of 1, 2, 3, 4, and 5 mm. In large installations, large grid sizes such as 5 mm can be chosen for the simulation. As the minimum bed height is 20 mm in this study, a 2 mm grid is used for subsequent calculations to obtain more information in the granular bed.
In order to simplify the computational complexity, some assumptions are made in the simulation, e.g., the bed height remains unchanged with radius and the Sauter mean diameter of the granules and dust are used. According to the experimental conditions [
29], the superficial gas velocity is set as 0.345 m/s in the simulation; the dust diameter and concentration are 2.24 μm and 6985 mg/m
3, respectively; the granular diameter is 10 mm; and the initial bed voidage is 0.49. The simulation results of pressure drop and dust-removal efficiency are in good agreement with the experimental results under different bed heights [
29], for which the relative error is less than ±10.0%, as shown in
Figure 2b. It indicates that the mesoscale simulation method can calculate the flow field in GBF in a simple and accurate way.
3. Results and Discussion
In order to further validate the accuracy of this mesoscale simulation method, the influences of different conditions are also studied by this method. The variation trend in the pressure drop and the dust-removal efficiency obtained in this paper are compared with previous studies. In particular, a single-variable method is adopted to investigate the effects of different conditions, e.g., bed height, superficial gas velocity, dust concentration, dust diameter, granular diameter, bed voidage, and filtration time, on the flow field. A certain parameter value in the baseline working condition is varied with reference to the related studies of GBF.
As shown in
Figure 3 and
Figure 4, the pressure and dust-mass fraction vary less along the radial direction and more along the axial direction. Compared to other parts of the bed, the pressure and dust-mass fraction vary more in the granular bed, and the variation varies with different conditions. In order to quantitatively analyze the effects of different conditions on pressure drop and dust-removal efficiency, the average pressure difference between the gas inlet and outlet sections is defined as the pressure drop of the bed; the reduction ratio of dust concentration between the two sections is defined as the dust-removal efficiency of the bed.
3.1. Flow-Field Distribution under Different Operating Conditions
The operating conditions mainly include the initial granular bed height
L and superficial gas velocity
ug, which will significantly affect the pressure drop and dust-removal efficiency. According to the relevant studies in GBF [
29],
L and
ug change in the range of 20–100 mm and 0.15–0.55 m/s, respectively. In particular, it is better to display and compare the variation in results between the ratios of the results in the working condition and those in the baseline working condition. The results in the baseline working condition are marked as * in
Figure 5,
Figure 6,
Figure 7,
Figure 8,
Figure 9,
Figure 10 and
Figure 11.
3.1.1. Flow-Field Distribution under Different Bed Heights
When the bed height
L increases from 20 mm to 100 mm gradually, the pressure in the granular bed varies less in the axial direction, while the pressure drop increases linearly, as shown in
Figure 2 and
Figure 5a. This is because when
L increases, it does not affect the gas flow cross-sectional area of the granular bed. The gas–solid slip velocity does not change nor does the gas resistance of the granular bed with per unit thickness. Thus, the inertial and viscous resistance terms do not change (
Figure 5a), and the pressure drop is approximately linear with
L. The conditions and methods in the relevant references are summarized in
Appendix A (
Table A1).
The dust-removal efficiency increases from 17.55% to 62.01% gradually with the increase in
L. The dust concentration in the gas phase within the granular bed, near the gas inlet side, changes little with the increase in
L, as shown in
Figure 4 and
Figure 5b. The dust-removal efficiency is related to inertial collision, gravitational sedimentation, and adsorption, etc. As
L increases, the probability of inertial collision between dust and filter granules increases significantly. As indicated by
Figure 5b, when
L grows,
Re remains unchanged, as do the
Nst and effective Stokes number
Nsteff. Meanwhile, the number of granular units
N increases, which effectively improves the dust-removal efficiency.
3.1.2. Different Superficial Gas Velocities
When the superficial gas velocity
ug increases from 0.15 m/s to 0.55 m/s gradually, the pressure inside the granular bed increases in the axial direction. The pressure drop increases with increasing
ug, whose change trend is consistent with the work described in [
21,
22,
24,
29,
31], as shown in
Figure 3 and
Figure 6a. The conditions and methods in the relevant references are summarized in the Appendix (
Table A1). This is due to the fact that as
ug increases, the gas–solid slip velocity increases in the granular bed. The inertial force of the gas grows, as well as the gas resistance of filtered granules in granular bed, which causes the pressure drop to increase. According to Equations (5)–(7) and
Figure 6a, the viscous resistance of the filtered granules to the gas is proportional to
ug, and the inertial resistance is proportional to
ug2. The pressure drop is then approximately proportional to 1–2 times
ug.
With the increase in
ug, the dust-removal efficiency increases; while the increase rate decreases, as shown in
Figure 4 and
Figure 6b. This is due to the fact that the dust-removal efficiency is related to inertial collision, gravitational settling, diffusion, and interception, etc. The superficial gas velocity is generally recommended to be 0–0.55 m/s in GBF [
21,
22,
24,
30]. When
ug grows, the probability of inertial collision between dust and filter granules increases significantly. Moreover, as shown in
Figure 6b,
Re,
Nst, and
Nsteff increase, which effectively improves the dust-removal efficiency.
3.2. Flow-Field Distribution under Different Dust and Filter Granular Parameters
The characteristics of the flow field in a GBF are closely related to the forces between the dust and filter granules. For this reason, the effect of different dust concentrations, particle diameters of dust, granular diameters, and bed voidages on the flow field must be investigated.
3.2.1. Different Dust Concentrations
With the increase in dust concentration
cp, the pressure variation and pressure drop in the granular bed along the axial direction increase gradually, which is consistent with the work in [
32,
33], as shown in
Figure 3 and
Figure 7. The conditions and methods in the relevant references are summarized in the Appendix (
Table A1). As indicated in
Figure 7a, with the increase in
cp, the overall density of dusty gas increases, as well as the inertial and viscous resistance of filter granules to the gas. The pressure drop grows accordingly.
The dust-removal efficiency decreases gradually with increasing
cp, as shown in
Figure 4 and
Figure 7b. As the decrease in gas velocity during dust filtration is not taken into account, the dimensionless numbers of
Re,
Nst, and
Nsteff, which are computed by theoretical methods, vary less. However, during the actual filtration process, the total amount of dusty gas decreases for the decrease in dust and the gas velocity decreases. According to the analysis in
Section 3.1.2, the probability of inertial collision between the dust and filter granules decreases at low
ug, which causes the dust-removal efficiency to decrease.
3.2.2. Different Dust Diameters
When the dust diameter
dp increases from 1 to 10 μm gradually, the pressure variation in the granular bed are basically unchanged along the axial direction as well as the pressure drop, which is consistent with the work in [
21,
22,
24,
29], as shown in
Figure 3 and
Figure 8a. The conditions and methods in the relevant references are summarized in the Appendix (
Table A1). This is because the dust concentration is low, and thus the effect of dust diameter on the pressure drop seems to be small.
With the increase in
dp, the dust-removal efficiency increases gradually, while the increase rate decreases, as shown in
Figure 4 and
Figure 8b. With the increase in
dp, the inertial collision and interception probability of dust and filter granules decrease significantly. As shown in
Figure 8b, when
dp grows,
Nst increases, as well as
Nsteff and the equivalent granular diameter ratio
Nr. The dust-removal efficiency increases afterwards.
3.2.3. Different Granular Diameters
When the granular diameter
dg increases from 1 to 20 mm gradually, the pressure inside the granular bed changes along the axial direction, and the pressure drop of GBF decreases. Moreover, the decrease amplitude of pressure drop becomes smaller and smaller, which is consistent with the references [
24,
29], as shown in
Figure 3 and
Figure 9a. The conditions and methods in relevant references are summarized in the Appendix (
Table A1). With the increase in
dg, the contact area between the gas and filter granules in the granular bed decreases. According to Equation (21), it is inversely proportional to
dg. At this time,
Figure 9a shows that the viscous and inertial resistance of the filter granules to the gas phase decreases, which causes the pressure drop to decrease.
When
dg increases, the dust-removal efficiency decreases gradually, as shown in
Figure 4 and
Figure 9b. When
dg grows, the probability of inertial collision and interception of dust and filter granules decreases significantly. Meanwhile, as indicated by
Figure 9b, the decrease in
Nst,
Nsteff, and
Nr is greater than the increase in
Re, which causes the dust-removal efficiency to decrease.
3.2.4. Different Initial Bed Voidages
When the initial bed voidage
ε0 increases from 0.40 to 0.55 gradually, the pressure drop decreases and the rate of decrease becomes slower and slower, which is consistent with the work in [
34], which can be seen in
Figure 3 and
Figure 10a. The conditions and methods in the relevant references are summarized in the Appendix (
Table A1). With the increase in
ε0, the gaps between filter granules become larger, the contact area between the gas and filter granules in the granular bed decreases (Equation (21)). Thus, the viscous and inertial resistance of the filter granules to gas decreases, as shown in
Figure 10a. According to Equations (4)–(6), as the viscous and inertial resistances are inversely proportional to 1–2 and 2–3 times
ε0, respectively, the pressure drop is approximately inversely proportional to 1–3 times
ε0.
With the increase in
ε0, the dust-removal efficiency decreases gradually, and the decrease rate becomes smaller and smaller, which can be seen in
Figure 4 and
Figure 10b. As
ε0 increases, the contact area between the gas and filter granules decreases. Meanwhile, as
Figure 10b indicates, the probability of inertial collision and interception between the dust and filter granules decreases, as well as
Nsteff, and the dust-removal efficiency decreases.
3.3. Flow-Field Distribution under Different Filtration Times
The spatial distribution of dust deposition varies with filtration time t, which affects the distribution of the flow field in GBF. In this study, the average dust deposition in the granular bed is chosen in the theoretical calculation, which is used to compute the viscous and inertial resistance, Re, and other dimensionless numbers. The effect of t on pressure drop and dust-removal efficiency is then analyzed.
When
t increases from 0 to 120 s gradually, the pressure changes in the axial direction and pressure drop grow in the granular bed, which is consistent with the work in [
21], as shown in
Figure 3 and
Figure 11. The conditions and methods in the relevant references are summarized in the Appendix (
Table A1). This is due to the fact that the amount of dust deposited in the granular bed increases with increases in
t. The actual bed voidage decreases, which causes the viscosity and inertial resistances of the filter granules to the gas phase to increase. The pressure drop increases accordingly.
With the increase in
t, the dust-removal efficiency increases gradually, and the increase rate becomes smaller and smaller, as shown in
Figure 4 and
Figure 11. With the increase in dust deposition, the actual bed voidage of the granular bed decreases. The probability of inertial collision and interception of the dust and filter granules also increases. Moreover,
Nsteff grows, as well as the number of filter unit layers
N and the dust-removal efficiency.