1. Introduction
Incremental Sheet Forming (ISF) is a flexible manufacturing process because complex three-dimensional (3D) parts can be fabricated by using only specific tool path programming on the existing setup without the use of dedicated dies. It is widely used for small batches and customized production. Patented in 1967, the process has attracted the eyes of aerospace, automotive [
1], and biomedical sectors [
2] for manufacturing complex sheet metal components. The process was used by Iseki et al. [
3] for small batch production of non-symmetrical shallow shells using path-controlled spherical rollers. Various shapes were produced using the process of ISF, and a bulging test was used to predict the forming limit of ISF. In ISF, necking is either suppressed or delayed, due to which higher strains can be induced than in conventional stamping, deep drawing, and stretching processes [
4].
Since the establishment of the process, there have been numerous attempts to establish the mechanism of ISF. Several FEA and theoretical analyses have been done to understand the underlying mechanism of the process. Initially, it was understood that the underlying mechanism behind the process is near biaxial stretching, as confirmed by Shim and Park [
5] by FEA modeling. They concluded that Near Biaxial Stretching occurs in the closed loop, and near plane strain occurs along the straight line. They further concluded that the Forming Limit Curve (FLC), which is a plot of major strain vs. minor strain for ISF, is a straight line with a negative slope in the positive direction of minor strain and recommended the straight groove test as a standard test for plotting FLC for ISF [
5]. Kim and Park predicted the same results by performing a series of experiments to produce various shapes [
6].
Sheet thickness in the ISF process can be approximated by the famous sine law
, where
is the wall angle in the formed conical part. Since the thickness in the case of shear spinning is also given by the same sine law, the underlying deformation mechanism, as established by Avitzur and Yang [
7] and demonstrated mathematically by Kim et al. [
8], was initially considered to be pure shear through the thickness of the sheet and plane strain in the plane parallel to the undeformed sheet. Jackson et al. [
9] found the presence of through-thickness shear along tool movement by measuring relative displacement in the sandwich panel. They took two pieces of 3 mm thick copper sheet, engraved their cross-section with square mesh, and brazed them. This method was adopted and suggested by Kalpakcioglu [
10]. After deformation, they measured the mesh configuration and found the presence of through-thickness shear in the tool direction [
11]. The presence of out-of-plane through-thickness stresses can lead to improved formability in the case of ISF, as suggested by Ma and Wang [
12]. They further suggested that the conventional M-K model, which includes in-plane stresses only, needs to be extended and should also consider the through-thickness shear stresses. Allwood and Shoulder [
13] proposed a generalized forming limit diagram (GFLD) that considered the out-of-plane stresses. It is evident that the stress state in ISF is complex, which was studied by Emmens and Boogard [
14], and they presented an overview of the mechanisms responsible for higher strain in the single-point incremental forming (SPIF) process. They suggested that there are various factors responsible for higher strain in the ISF process. The nature of the complex stress state also plays a vital role in the higher strains in ISF [
15]. Eyckens et al. [
16] demonstrated, through finite element modeling, the presence of shear in the direction of tool movement but only a little shear in the perpendicular direction [
8]. In addition to shear in the tool direction, Bending Under Tension (BUT) also plays a role in the enhancement of formability. Sawada et al. [
17] performed a numerical study of stretch forming and ISF and found that bending and unbending happen along the meridional line, and shear happens along the circumferential direction. They also concluded that necking is induced on the part of the sheet which is in contact with the punch and stops after the punch surpasses the necking point. Recently, Li et al. [
18] used the FE model to affirm that the deformation mechanism in ISF is a combination of bending, stretching, and shear.
Even after so many attempts, the underlying deformation mechanism of the process is still not clear due to the evolution of the complex stress state during the process. However, it can be said with affirmation that the stress state appearing during ISF consists of shear, normal, and bending stresses. Understanding of deformation mechanism is pivotal in developing an analytical model for force prediction in the process. Therefore, for developing such a model, all the stress components must be taken into consideration.
For in situ measurement of forces appearing during the ISF process, a dynamometer is fixed on the tool, and it measures the forces appearing during forming. The forces acting in ISF are (a) the axial force (
Fz), acting in the direction along the tool axis, (b) force in the radial direction (
Fr), and (c) force along the tangential direction (
Fθ). The vector diagram of forces appearing during the process is given in
Figure 1. Recently, Kumar et al. [
19] presented a comprehensive review of the state of the arts of forming force and their effects on various forming outputs.
Duflou et al. [
20] presented a model based on regression equations for force prediction during cone forming by SPIF as a function of step size, wall angle, tool diameter, and sheet thickness. Duflou et al. [
21] performed a large set of experiments to form empirical relations for the calculation of force components for five different materials: AA3033, AA5754, DC01, AISI 304, and spring steel 65Cr
2. Saidi et al. [
22] conducted a set of experiments on sheets of AA1050 and 304 steel and validated their results, as predicted by Jeswiet et al. [
23] and Aerens et al. [
21]. Xiao et al. [
24] measured forming forces by an in situ force monitoring system and studied the effect of forming temperature on the forming of an AA7075-T6 sheet. They found that the peak force was reduced to 1300 N from 1900 N when forming temperature was increased from 140 to 200 °C.
In addition to various experimental measuring methodologies, numerous attempts have been made to develop analytical and FEA models, considering various deformation mechanisms based on available literature for the calculation of forces and other parameters like strain, thickness, etc., during the process.
Flores et al. [
25] used the FEA simulation of SPIF and studied the effects of constitutive laws on force prediction. They concluded that the selection of constitutive laws plays a vital role in force prediction, as the results were different for elastoplastic laws with isotropic and kinematic hardening. Henrard et al. [
26] used FEA simulation to predict the forces for 20° and 60° cones using the Lagamine model, first-order brick element model for various simulation parameters, and inverse method for material data fit. They also conducted experiments for the validation of results obtained from FE modeling. Honarpisheh et al. [
27] performed FEM analysis on ABAQUS to predict forces appearing during forming of Al/Cu bimetals and studied the effects of various parameters in ISF.
Iseki [
28] used the equilibrium of the shell element to model bulge height, strain, and load during the process. He also used FEA analysis for validation of the results of the theoretical model. Silva et al. [
29] proposed membrane analysis to consider the friction between the tool and sheet for analysis of the small plastic zone created during forming of symmetrical axis shapes in SPIF. They proposed that friction stress at the contact between tool and sheet can be assumed to be made of a couple of in-plane components, viz. meridional component (
) and circumferential component (
). They considered the thickness, meridional, and circumferential direction as principal directions and gave the following equations for the corresponding stresses:
Further, Chang et al. [
30] used membrane analysis for the analytical modeling of the single-pass and multi-pass incremental sheet forming process (MPISF) and incremental hole flanging process (IHF). Bansal et al. [
31] used the above equations for force calculation for single-stage and multi-stage ISF, modeling the contact area and validating with experiments and the formula given by Duflou et al. [
20]. Similarly, Fang et al. [
32] did analytical modeling of the process and validated it with numerical modeling, and also studied the fracture behavior of the sheet in ISF. Liu et al. [
33] modeled the process in the 3D polar coordinate system and validated it experimentally. They further extended their work [
34] and gave a comprehensive analytical model for the prediction of forming forces in three directions and studied the effect of step depth, tool diameter, and sheet thickness on forming forces occurring in ISF.
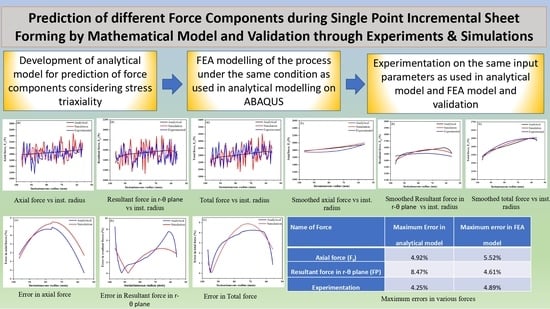
It can be concluded from the literature survey that although attempts have been made to develop a mathematical model of ISF, a comprehensive model for force prediction has not been established yet. Further, most of the models are empirical in nature, and they are used to calculate average forces during the process. Some other models consider only plane stresses in thickness, meridional, and circumferential direction and do not consider shear stresses. Very few works have been done considering all the six stress components to finally arrive at forces. In this current work, a simple mathematical model for the ISF process has been developed in a cylindrical coordinate system considering all the stress components. All force components have been calculated at different forming depths where the tool moves in different radii. The obtained results have been compared with the FEA model developed using the ABAQUS platform. Finally, experiments have been performed on aluminum alloy 6061 on a six-axis industrial robotic arm with the same experimental conditions as used for the analytical and FEA model. Different force components were measured using a dynamometer mounted on the robotic arm. The obtained results for various force components and total force have been compared.
2. Mathematical Model Development
For solving the mathematical equations, the cylindrical 3D coordinate has been chosen as tool motion to give a conical shape that can be easily replicated in this coordinate system. The center of the undeformed sheet has been chosen as the origin of the global coordinate system. The element has been taken in a local 3D polar co-ordinate system which is at a forming depth h and of length
rdθ in the radial direction at an angle
θ in the circumferential direction on the surface of the sheet in contact with the tool in the local polar coordinate system, as shown in
Figure 2a,b. It is worth noting that the three directions—radial (
r-direction), circumferential (
θ-direction), and axial (
z-direction)—may not necessarily be the principal directions. Hence all the six-stress component has been considered.
A few assumptions listed below have been made to develop the model:
In circumferential direction
The major shear component has been assumed to act only along the radial direction only. Hence
has been neglected throughout the model. Further, from membrane analysis, it can be said that
Using the membrane analysis (4) and Equation (1) becomes
Membrane analysis (4) and the assumption 2, Equation (3) becomes
For any incremental sheet forming, the fabrication of 3D shapes is done by making the tool move over the sheet and providing increments to the tool so that it can perform fabrication in different passes. For fabricating a conical wall, the increments are provided in vertical and horizontal directions. In the current work, the increments are provided in radial and the vertically downward direction. These increments are generally small in comparison to r, and if the given assumption holds, then it can be assumed that, on neglecting spring back
, where
is the increment in the vertical direction and
is the increment in radial direction. If these are small, then
Using assumption 3, it can be directly said that normal stress in radial and
z-directions are distributed in the same ratio as that of increments.
Taking differentials on both sides, it can be said that
From (7) and (8), it can be said that
Using Equation (9), Equation (6) further converges to
Taking integrals on both sides of the above relation
From the above analysis, it is evident that for one complete cycle, the stress in the radial direction is constant. This analysis was performed on ABAQUS with the same parameters as used for the analytical model, and considering the element when the instantaneous radius of the undeformed part is 82.5 mm, the RMS value of the S
11 was found to be approximately equal to 140 MPa as shown in
Figure 3.
Since
depends on instantaneous circle radius only, hence
From the equilibrium equation in the
r-direction, we have
Using Equations (18) and (20)
We can directly say this using Equation (17)
In the circumferential direction, using assumption 4, hence the equation in the circumferential direction converges to
From Equations (23) and (25), we have
From Von-Mises criteria, we have
The model is valid for all wall angles; however, for validation purposes, a 45° wall angle has been chosen because of its simplicity.
If we consider the strain to be acting from bending and stretching only [
34], we have from volume conservation
Total bending strain can be given by,
Whereas total tensile strain can be given as,
Total strain can be given by
Taking the simple power law for annealed sheet, we have
. From tensile test we have
K = 205 MPa, and
n = 0.2
From the analytical model developed, it can be said that the stress state appearing during the process is complex, but a few simple conclusions can be summarized:
- (a)
The largest stress component is normal stress on the theta plane along the tool movement direction. Appreciable shear stress appears in the direction perpendicular to the tool motion along the radial and z planes;
- (b)
From the Equation (28), it is clear that
3. Contact Area Model
For contact area estimation, the approach of Bansal et al. [
31] has been implemented. The contact area has been divided into two parts. The area directly below the tool in the region below the top of the undeformed sheet and the area above the undeformed sheet, as shown in
Figure 4a,b. The area above the undeformed sheet leaves contact with the sheet tangentially in the circumferential direction. Let section XX′ be cut, and the top sectioned view is shown in
Figure 4c.
From
Figure 5b, it can be directly said that
The area of portion
AB can be directly estimated by considering the concept of solid angle. The area can be given by
The area of the portion above the top of the undeformed surface can be given by integrating the perimeters of the strips of width
taken at an angle
the length of which will be
rβ where
r =
R sin
As to 0.
Taking the variation of
β to be linear with
, we have
From (39) and (40), we obtain
The total area of contact can be given by
Putting R = 5 mm, , and .
Considering the whole contact area as a rectangle of .
= 6.10
and
b = 3.11 mm, the length of the portion above the top of the undeformed sheet is
.
Different forces acting on the sheet in the contact region can be represented by the force diagram as given in
Figure 1.
Once the relations for various force components were established, the calculation for forces using different developed equations was done on MATLAB for different instantaneous radii. The whole process was modeled on ABAQUS, and average forming forces were evaluated from the FEA model for the same instantaneous radii. The values obtained from the analytical model were compared with FEA and experimental results, as discussed in subsequent sections.
4. Simulation Study
The simulation analysis on the formed cone was carried out on ABAQUS. The finite element model was made on the software, which consisted of a rigid tool with a tool diameter of 10 mm, a deformable aluminum alloy 6061 sheet of thickness 1.05 mm, and a flange to hold the sheet. The geometry of the model used for simulation is given in
Figure 5.
The properties of the material used in the simulation were obtained from the uniaxial tensile test and are given in
Table 1.
For simulation, a true stress-true strain curve up to maximum load was obtained from the tensile test. Since a large strain is obtained in ISF for post-necking values of true stress and true strain, the following method was adopted. The log-log plot of true stress and the true strain was made till necking. Thereafter, a linear relation was assumed between the logarithm of true stress and the logarithm of true strain from necking to fracture. The strain hardening exponent in this region can be evaluated by finding the slope of this linear portion of the plot from necking to fracture. In this way, the true stress-true strain data was obtained and fed in ABAQUS till fracture. The engineering and true stress-strain curve obtained after tensile testing is given in
Figure 6.
The isotropic hardening model was used for analysis as the sheet was annealed. Square meshing was done on the plate and tool with an average mesh size of 6.96 mm.
Loading and Boundary condition:
Penalty contact between the tool and sheet was taken with the coefficient of friction between the tool and the sheet to be 0.2, which was obtained from the wear test. The boundary of the sheet was encastred, and the blank was made rigid and encastred. The tip of the tool was chosen as a reference point and was given corresponding motions as per the conical geometry. The tool path was generated on MATLAB, and the corresponding positions were fed in ABAQUS to obtain the conical shape. The simulation was run, and dynamic analysis was done for stresses, strains, and tool forces arising during the tool motion, the results of which are given in
Figure 7.
As can be seen from
Figure 7a, the Von-Mises stress is maximum in the direct contact region between the undeformed sheet and the tool. The middle region of the cone is strained to the maximum value, as can be seen in
Figure 7b. Further, it can also be seen from
Figure 7c that the middle region of the cone has the minimum thickness showing that this region has undergone the maximum amount of thinning, which also affirms the distribution as seen in
Figure 7b. A path along the central meridional plane was chosen in the cone after deformation and strain occurred along the path, and the thickness of the sheet along the path was plotted, which is shown in
Figure 8a,b.
The simulation analysis was used to find out the forces appearing on the tool during the deformation. The tool force has been assumed to have two components. The axial components of the force Fzz and the resultant of in-plane X and Y components of forces is also equal to the resultant of tangential and radial force components.
As can be seen from
Figure 9, the largest force component arising during the deformation is in the axial direction, as was reported by Duflou et al. [
20] as well. Additionally, it was observed that the largest axial force appearing in the axial direction was found to be 2629.11 N. The mean force was found to be 1512.24 N. The variation of in-plane force, that is, the resultant of the forces appearing in the plane of the undeformed sheet with time, has been shown in
Figure 9b, and the force diagram for the same has been given in
Figure 9c. The largest value corresponding to in-plane forming force was found to be 2172.31 N, and the average force during forming was found to be 1109.3 N. Finally, the variation of total forming force with time has been given in
Figure 9d. The maximum forming force appearing on the tool was found to be 2747.46 N, and the average tool force was found to be 1812 N.