Mathematical Modeling and Parameter Estimation of Intracellular Signaling Pathway: Application to LPS-induced NFκB Activation and TNFα Production in Macrophages
Abstract
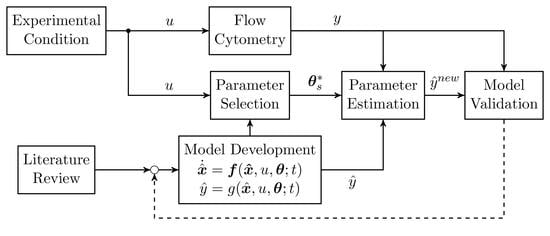
:1. Introduction
2. Material and Methods
2.1. Materials and Cell Culture
2.2. Flow Cytometry Analysis
2.3. Model Development
2.4. Parameter Estimation
3. Results
3.1. Model Validation
3.2. Golgiplug™-Induced ER Stress
3.3. Model Refinement
3.4. Final Model Validation
4. Discussion
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| LPS | lipopolysaccharide |
| NFB | nuclear factor B |
| TNF | tumor necrosis factor |
| IB | inhibitor of B, |
| TLR4 | Toll-like receptor 4 |
| IKK | IB kinase |
| MyD88 | myeloid differentiation primary response 88 |
| TIR | Toll/interleukin-1 receptor |
| TRIF | TIR-domain-containing adaptor-inducing interferon- |
| TRAF6 | TNF receptor-associated factor 6 |
| IKKK | IKK kinase |
| ER | endoplasmic reticulum |
| TNFR | TNF receptor |
| CD14 | cluster of differentiation 14 |
| MFI | mean fluorescence intensity |
| IB | IB transcript |
| eIF2 | eukaryotic initiation factor 2 -subunit |
| C1 | TNFR complex |
References
- Hughey, J.J.; Lee, T.K.; Covert, M.W. Computational modeling of mammalian signaling networks. Wiley Interdisciplin. Rev. Syst. Biol. Med. 2010, 2, 194–209. [Google Scholar] [CrossRef] [PubMed]
- Handly, L.N.; Yao, J.; Wollman, R. Signal transduction at the single-cell level: Approaches to study the dynamic nature of signaling networks. J. Mol. Biol. 2016, 428, 3669–3682. [Google Scholar] [CrossRef] [PubMed]
- Gaudet, S.; Miller-Jensen, K. Redefining signaling pathways with an expanding single-cell toolbox. Trends Biotechnol. 2016, 34, 458–469. [Google Scholar]
- Cohen, A.A.; Geva-Zatorsky, N.; Eden, E.; Frenkel-Morgenstern, M.; Issaeva, I.; Sigal, A.; Milo, R.; Cohen-Saidon, C.; Liron, Y.; Kam, Z.; et al. Dynamic proteomics of individual cancer cells in response to a drug. Science 2008, 322, 1511–1516. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Z.; Taylor, B.; Ourthiague, D.R.; Hoffmann, A. Distinct single-cell signaling characteristics are conferred by the MyD88 and TRIF pathways during TLR4 activation. Sci. Signal. 2015, 8, ra69. [Google Scholar] [CrossRef] [PubMed]
- Hasenauer, J.; Waldherr, S.; Doszczak, M.; Radde, N.; Scheurich, P.; Allgöwer, F. Identification of models of heterogeneous cell populations from population snapshot data. BMC Bioinform. 2011, 12, 125. [Google Scholar] [CrossRef] [PubMed]
- Hasenauer, J.; Waldherr, S.; Doszczak, M.; Scheurich, P.; Radde, N.; Allgöwer, F. Analysis of heterogeneous cell populations: A density-based modeling and identification framework. J. Process Control 2011, 21, 1417–1425. [Google Scholar] [CrossRef]
- Williams, R.A.; Timmis, J.; Qwarnstrom, E.E. Computational models of the NF-κB signalling pathway. Computation 2014, 2, 131–158. [Google Scholar] [CrossRef] [Green Version]
- Gábor, A.; Villaverde, A.F.; Banga, J.R. Parameter identifiability analysis and visualization in large-scale kinetic models of biosystems. BMC Syst. Biol. 2017, 11, 54. [Google Scholar] [CrossRef] [PubMed]
- Kravaris, C.; Hahn, J.; Chu, Y. Advances and selected recent developments in state and parameter estimation. Comput. Chem. Eng. 2013, 51, 111–123. [Google Scholar] [CrossRef]
- Raue, A.; Kreutz, C.; Maiwald, T.; Bachmann, J.; Schilling, M.; Klingmüller, U.; Timmer, J. Structural and practical identifiability analysis of partially observed dynamical models by exploiting the profile likelihood. Bioinformatics 2009, 25, 1923–1929. [Google Scholar] [CrossRef] [PubMed]
- Kravaris, C.; Seinfeld, J.H. Identification of parameters in distributed parameter systems by regularization. SIAM J. Control Optim. 1985, 23, 217–241. [Google Scholar] [CrossRef]
- Xue, Q.; Lu, Y.; Eisele, M.R.; Sulistijo, E.S.; Khan, N.; Fan, R.; Miller-Jensen, K. Analysis of single-cell cytokine secretion reveals a role for paracrine signaling in coordinating macrophage responses to TLR4 stimulation. Sci. Signal. 2015, 8, ra59. [Google Scholar] [CrossRef] [PubMed]
- Tay, S.; Hughey, J.J.; Lee, T.K.; Lipniacki, T.; Quake, S.R.; Covert, M.W. Single-cell NF-κB dynamics reveal digital activation and analogue information processing. Nature 2010, 466, 267. [Google Scholar] [CrossRef] [PubMed]
- Maiti, S.; Dai, W.; Alaniz, R.C.; Hahn, J.; Jayaraman, A. Mathematical modeling of pro- and anti-inflammatory signaling in macrophages. Processes 2015, 3, 1–18. [Google Scholar] [CrossRef]
- Hayden, M.S.; Ghosh, S. NF-κB, the first quarter-century: Remarkable progress and outstanding questions. Genes Dev. 2012, 26, 203–234. [Google Scholar] [CrossRef] [PubMed]
- Chu, Y.; Hahn, J. Parameter set selection via clustering of parameters into pairwise indistinguishable groups of parameters. Ind. Eng. Chem. Res. 2009, 48, 6000–6009. [Google Scholar] [CrossRef]
- Yao, K.Z.; Shaw, B.M.; Kou, B.; McAuley, K.B. Modeling ethylene/butene copolymerization with multi-site catalysts: Parameter estimability and experimental design. Polym. React. Eng. 2003, 3, 563–588. [Google Scholar] [CrossRef]
- Prussin, C. Cytokine flow cytometry: Understanding cytokine biology at the single-cell level. J. Clin. Immunol. 1997, 17, 195. [Google Scholar] [CrossRef] [PubMed]
- Schulz, K.R.; Danna, E.A.; Krutzik, P.O.; Nolan, G.P. Single-cell phospho-protein analysis by flow cytometry. Curr. Protoc. Immunol. 2012, 8–17. [Google Scholar] [CrossRef]
- Caldwell, A.B.; Cheng, Z.; Vargas, J.D.; Birnbaum, H.A.; Hoffmann, A. Network dynamics determine the autocrine and paracrine signaling fucntions of TNF. Genes Dev. 2014, 28, 2120–2133. [Google Scholar] [CrossRef] [PubMed]
- Hoffmann, A.; Levchenko, A.; Scott, M.L.; Baltimore, D. The IκB-NF-κB signaling module: Temporal control and selective gene activation. Science 2002, 298, 1241–1245. [Google Scholar] [CrossRef] [PubMed]
- Werner, S.L.; Kearns, J.D.; Zadorozhnaya, V.; Lynch, C.; O’Dea, E.; Boldin, M.P.; Ma, A.; Baltimore, D.; Hoffmann, A. Encoding NF-κB temporal control in response to TNF: Distinct roles for the negative regulators IκBα and A20. Genes Dev. 2008, 22, 2093–2101. [Google Scholar] [CrossRef] [PubMed]
- Junkin, M.; Kaestli, A.J.; Cheng, Z.; Jordi, C.; Albayrak, C.; Hoffmann, A.; Tay, S. High-content quantification of single-cell immune dynamics. Cell Rep. 2016, 15, 411–422. [Google Scholar] [CrossRef] [PubMed]
- Krikos, A.; Laherty, C.D.; Dixit, V.M. Transcriptional activation of the tumor necrosis factor α-inducible zinc finger protein, a20, is mediated by κB elements. J. Biol. Chem. 1992, 267. [Google Scholar]
- Lee, E.G.; Boone, D.L.; Chai, S.; Libby, S.L.; Chien, M.; Lodolce, J.P.; Ma, A. Failure to regulate TNF-induced NF-κB and cell death responses in A20-deficient mice. Science 2000, 289, 2350–2354. [Google Scholar] [CrossRef] [PubMed]
- Boone, D.L.; Turer, E.E.; Lee, E.G.; Ahmad, R.C.; Wheeler, M.T.; Tsui, C.; Hurley, P.; Chien, M.; Chai, S.; Hitotsumatsu, O.; et al. The ubiquitin-modifying enzyme A20 is required for termination of Toll-like receptor responses. Nat. Immunol. 2004, 5, 1052–1060. [Google Scholar] [CrossRef] [PubMed]
- Chardin, P.; McCormick, F. Brefeldin A: The advantage of being uncompetitive. Cell 1999, 97, 153–155. [Google Scholar] [CrossRef]
- Ward, T.H.; Polishchuk, R.S.; Caplan, S.; Hirschberg, K.; Lippincott-Schwartz, J. Maintenance of Golgi structure and function depends on the integrity of ER export. J. Cell Biol. 2001, 155, 557–570. [Google Scholar] [CrossRef] [PubMed]
- Latz, E.; Visintin, A.; Lien, E.; Fitzgerald, K.A.; Monks, B.G.; Kurt-Jones, E.A.; Golenbock, D.T.; Espevik, T. Lipopolysaccharide rapidly traffics to and from the Golgi apparatus with the Toll-like Receptor 4-MD-2-CD14 complex in a process that Is distinct from the initiation of signal transduction. J. Biol. Chem. 2002, 49, 47834–47843. [Google Scholar] [CrossRef] [PubMed]
- Liaunardy-Jopeace, A.; Bryant, C.E.; Gay, N.J. The COPII adaptor protein TMED7 is required to initiate and mediate the anterograde trafficking of Toll-like receptor 4 to the plasma membrane. Sci. Signal. 2014, 7, ra70. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; Lou, J.; Ouyang, C.; Chen, W.; Liu, Y.; Liu, X.; Cao, X.; Wanga, J.; Lu, L. Ras-related protein Rab10 facilitates TLR4 signaling by promoting replenishment of TLR4 onto the plasma membrane. Proc. Natl. Acad. Sci. USA 2010, 107, 13806–13811. [Google Scholar] [CrossRef] [PubMed]
- Jones, S.J.; Ledgerwood, E.C.; Prins, J.B.; Galbraith, J.; Johnson, D.R.; Pober, J.S.; Bradley, J.R. TNF recruits TRADD to the plasma membrane but not the trans-Golgi Network, the principal subcellular location of TNF-R1. J. Immunol. 1999, 162, 1042–1048. [Google Scholar] [PubMed]
- Neznanov, N.; Kondratova, A.; Chumakov, K.M.; Angres, B.; Zhumabayeva, B.; Agol, V.I.; Gudkov, A.V. Poliovirus protein 3A inhibits tumor necrosis factor (TNF)-induced apoptosis by eliminating the TNF receptor from the cell surface. J. Virol. 2001, 75, 10409–10420. [Google Scholar] [CrossRef] [PubMed]
- Xaus, J.; Comalada, M.; Valledor, A.F.; Lloberas, J.; López-Soriano, F.; Argilés, J.M.; Bogdan, C.; Celada, A. LPS induces apoptosis in macrophages mostly through the autocrine production of TNF-α. Blood 2000, 95, 3823–3831. [Google Scholar] [PubMed]
- Covert, M.W.; Leung, T.H.; Gaston, J.E.; Baltimore, D. Achieving stability of lipopolysaccharide-induced NF-κB activation. Science 2005, 309, 1854–1857. [Google Scholar] [CrossRef] [PubMed]
- Lombardo, E.; Alvarez-Barrientos, A.; Maroto, B.; Boscà, L.; Knaus, U.G. TLR4-mediated survival of macrophages is MyD88 dependent and requires TNF-α autocrine signalling. J. Immunol. 2007, 178, 3731–3739. [Google Scholar] [CrossRef] [PubMed]
- Zanoni, I.; Ostuni, R.; Marek, L.R.; Barresi, S.; Barbalat, R.; Barton, G.M.; Granucci, F.; Kagan, J.C. CD14 controls the LPS-induced endocytosis of Toll-like Receptor 4. Cell 2011, 147, 868–880. [Google Scholar]
- Tan, Y.; Zanoni, I.; Cullen, T.W.; Goodman, A.L.; Kagan, J.C. Mechanisms of Toll-like receptor 4 endocytosis reveal a common immune-evasion strategy used by pathogenic and commensal bacteria. Immunity 2015, 43, 909–922. [Google Scholar] [CrossRef] [PubMed]
- Rajaiah, R.; Perkins, D.J.; Ireland, D.D.C.; Vogel, S.N. CD14 dependence of TLR4 endocytosis and TRIF signaling displays ligand specificity and is dissociable in endotoxin tolerance. Proc. Natl. Acad. Sci. USA 2013, 112, 8391–8396. [Google Scholar] [CrossRef] [PubMed]
- Kagan, J.C.; Su, T.; Horng, T.; Chow, A.; Akira, S.; Medzhitov, R. TRAM couples endocytosis of Toll-like receptor 4 to the induction of interferon-β. Nat. Immunol. 2008, 9, 361–368. [Google Scholar] [CrossRef] [PubMed]
- Chu, Y.; Jayaraman, A.; Hahn, J. Parameter sensitivity analysis of IL-6 signaling pathways. IET Syst. Biol. 2007, 1, 342–352. [Google Scholar] [CrossRef] [PubMed]
- Lin, S.C.; Lo, Y.C.; Wu, H. Helical assembly in the MyD88-IRAK4-IRAK2 complex in TLR/IL-1R signalling. Nature 2010, 465, 885–890. [Google Scholar] [CrossRef] [PubMed]
- Bagnall, J.; Boddington, C.; Boyd, J.; Brignall, R.; Rowe, W.; Jones, N.A.; Schmidt, L.; Spiller, D.G.; White, M.R.; Paszek, P. Quantitative dynamic imaging of immune cell signalling using lentiviral gene transfer. Integr. Biol. 2015, 7, 713–725. [Google Scholar] [CrossRef] [PubMed]
- Moya, C.; Huang, Z.; Cheng, P.; Jayaraman, A.; Hahn, J. Investigation of IL-6 and IL-10 signalling via mathematical modelling. IET Syst. Biol. 2011, 5, 15–26. [Google Scholar] [CrossRef] [PubMed]
- Sung, M.H.; Li, N.; Lao, Q.; Gottschalk, R.A.; Hager, G.L.; Fraser, I.D.C. Switching of the relative dominance between feedback mechanisms in lipopolysaccharide-Induced NF-κB signaling. Sci. Signal. 2014, 7, ra6. [Google Scholar] [CrossRef] [PubMed]
- Tsukamoto, H.; Fukudome, K.; Takao, S.; Tsuneyoshi, N.; Kimoto, M. Lipopolysaccharide-binding protein-mediated Toll-like receptor 4 dimerization enables rapid signal transduction against lipopolysaccharide stimulation on membrane-associated CD14-expressing cells. Int. Immunol. 2010, 22, 271–280. [Google Scholar] [CrossRef] [PubMed]
- Sakai, J.; Cammarota, E.; Wright, J.A.; Cicuta, P.; Gottschalk, R.A.; Li, N.; Fraser, I.D.C.; Bryant, C.E. Lipopolysaccharide-induced NF-κB nuclear translocation is primarily dependent on MyD88, but TNFα expression requires TRIF and MyD88. Sci. Rep. 2017, 7, 1428. [Google Scholar] [CrossRef] [PubMed]
- Shao, R.G.; Shimizu, T.; Pommier, Y. Brefeldin A Is a potent inducer of apoptosis in human cancer cells independently of p53. Exp. Cell Res. 1996, 227, 190–196. [Google Scholar] [CrossRef] [PubMed]
- Moon, J.L.; Kim, S.Y.; Shin, S.W.; Park, J.W. Regulation of brefeldin A-induced ER stress and apoptosis by mitochondrial NADP+-dependent isocitrate dehydrogenase. Biochem. Biophys. Res. Commun. 2012, 417, 760–764. [Google Scholar] [CrossRef] [PubMed]
- Cláudio, N.; Dalet, A.; Gatti, E.; Pierre, P. Mapping the crossroads of immune activation and cellular stress response pathways. EMBO J. 2013, 32, 1214–1224. [Google Scholar] [CrossRef] [PubMed]
- Mellor, H.; Kimball, S.R.; Jefferson, L.S. Brefeldin A inhibits protein synthesis through the phosphorylation of the α-subunit of eukaryotic initiation factor-2. FEBS Lett. 1994, 350, 143–146. [Google Scholar] [CrossRef]
- Tam, A.B.; Mercado, E.L.; Hoffmann, A.; Niwa, M. ER stress activates NF-κB by integrating functions of basal IKK activity, IRE1 and PERK. PLoS ONE 2012, 7, e45078. [Google Scholar] [CrossRef] [PubMed]
- Fishman, P.E.; Curran, P.K. Brefeldin A inhibits protein synthesis in cultured cells. FEBS Lett. 1992, 314, 371–374. [Google Scholar] [CrossRef]
- Ando, Y.; Oku, T.; Tsuji, T. Platelet supernatant suppresses LPS-induced nitric oxide production from macrophages accompanied by inhibition of NF-κB signaling and increased Arginase-1 expression. PLoS ONE 2016. [Google Scholar] [CrossRef] [PubMed]
- Selimkhanov, J.; Taylor, B.; Yao, J.; Pilko, A.; Albeck, J.; Hoffmann, A.; Tsimring, L.; Wollman, R. Accurate information transmission through dynamic biochemical signaling networks. Science 2014, 346, 1370–1373. [Google Scholar] [CrossRef] [PubMed]
- Kellogg, R.A.; Tian, C.; Lipniacki, T.; Quake, S.R.; Tay, S. Digital signaling decouples activation probability and population heterogeneity. eLife 2015, 4, e08931. [Google Scholar] [CrossRef] [PubMed]
- Noman, A.S.M.; Koide, N.; Hassan, F.; I.-E.-Khuda, I.; Dagvadorj, J.; Tumurkhuu, G.; Islam, S.; Naiki, Y.; Yoshida, T.; Yokochi, T. Thalidomide inhibits lipopolysaccharide-induced tumor necrosis factor-a production via down-regulation of MyD88 expression. Innate Immun. 2009, 15, 33–41. [Google Scholar] [CrossRef] [PubMed]
- Gillespie, D.T. Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem. 1977, 82, 2340–2361. [Google Scholar]
- Haseltine, E.L.; Rawlings, J.B. Approximate simulation of coupled fast and slow reactions for stochastic chemical kinetics. J. Chem. Phys. 2002, 117, 6959–6969. [Google Scholar] [CrossRef]
- Cao, Y.; Petzold, L.R. The numerical stability of leaping methods for stochastic simulation of chemically reacting systems. J. Chem. Phys. 2004, 121, 12169–12178. [Google Scholar] [CrossRef] [PubMed]
- Kwon, J.S.I.; Nayhouse, M.; Christofides, P.D.; Orkoulas, G. Modeling and control of protein crystal shape and size in batch crystallization. AIChE J. 2013, 59, 2317–2327. [Google Scholar] [CrossRef]
- Kwon, J.S.; Nayhouse, M.; Christofides, P.D.; Orkoulas, G. Modeling and control of shape distribution of protein crystal aggregates. Chem. Eng. Sci. 2013, 104, 484–497. [Google Scholar] [CrossRef]
- Lipniacki, T.; Paszek, P.; Brasier, A.R.; Luxon, B.A.; Kimmel, M. Stochastic regulation in early immune response. Biophys. J. 2006, 90, 725–742. [Google Scholar] [CrossRef] [PubMed]
- Nelson, D.E.; Ihekwaba, A.E.C.; Elliott, M.; Johnson, J.R.; Gibney, C.A.; Foreman, B.E.G.; Nelson, V.S.; Horton, C.A.; Spiller, D.G.; Edwards, S.W.; et al. Oscillations in TNFα signaling control the dynamics of gene expression. Science 2004, 306, 704–708. [Google Scholar] [CrossRef] [PubMed]
- Wilkinson, D.J. Stochastic modelling for quantitative description of heterogeneous biological systems. Nat. Rev. Genet. 2009, 10, 122. [Google Scholar] [CrossRef] [PubMed]
- Gupta, A.; Rawlings, J.B. Comparison of parameter estimation methods in stochastic chemical kinetic models: Examples in systems biology. AIChE J. 2014, 60, 1253–1268. [Google Scholar] [CrossRef] [PubMed]
- Ashyraliyev, M.; Fomekong-Nanfack, Y.; Kaandorp, J.A.; Blom, J.G. Systems biology: Parameter estimation for biochemicalmodels. FEBS J. 2009, 276, 886–902. [Google Scholar] [CrossRef] [PubMed]
- Kiparissides, A.; Koutinas, M.; Kontoravdi, C.; Mantalaris, A.; Pistikopoulos, E.N. ‘Closing the loop’ in biological systems modeling—from the in silico to the in vitro. Automatica 2011, 47, 1147–1155. [Google Scholar] [CrossRef]
- Lamoreaux, L.; Roederer, M.; Koup, R. Intracellular cytokine optimization and standard operating procedure. Nat. Protoc. 2006, 1, 1507–1516. [Google Scholar] [CrossRef] [PubMed]
- Lee, T.K.; Denny, E.M.; Sanghvi, J.C.; Gaston, J.E.; Maynard, N.D.; Hughey, J.J.; Covert, M.W. A noisy paracrine signal determines the cellular NF-κB response to lipopolysaccharide. Sci. Signal. 2009, 2, ra65. [Google Scholar] [CrossRef] [PubMed]
- Xiu, D.; Karniadakis, G.E. The Wiener-Askey Polynomial Chaos for Stochastic Differential Equations. SIAM J. Sci. Comput. 2006, 24, 619–644. [Google Scholar] [CrossRef]
- Misumi, Y.; Yuko Misumi, K.M.; Takatsuki, A.; Tamura, G.; Ikehara, Y. Novel blockade by brefeldin A of intracellular transport of secretory proteins in cultured rat hepatocytes. J. Biol. Chem. 1986, 261, 1139–11403. [Google Scholar]
- Bueno, C.; Almeida, J.; Alguero, M.; Sánchez, M.; Vaquero, J.; Laso, F.; Miguel, J.S.; Escribano, L.; Orf, A. Flow cytometric analysis of cytokine production by normal human peripheral blood dendritic cells and monocytes: Comparative analysis of different stimuli, secretion-blocking agents and incubation periods. Cytometry Part A 2001, 46, 33–40. [Google Scholar] [CrossRef]
- Gottschalk, R.A.; Martins, A.J.; Angermann, B.R.; Dutta, B.; Ng, C.E.; Uderhardt, S.; Tsang, J.S.; Fraser, I.D.C.; Meier-Schellersheim, M.; Germain, R.N. Distinct NF-κB and MAPK activation thresholds uncouple steady-state microbe sensing from anti-pathogen inflammatory responses. Cell Syst. 2016, 2, 378–390. [Google Scholar] [CrossRef] [PubMed]





| Parameter |
|---|
| TLR4 constitutive generation rate |
| IKKK-mediated IKK activation (IKK → IKKa) |
| IB transcript degradation rate |
| Hill coefficient of IB transcription |
| Hill coefficient of IB transcription |
| Hill coefficient of TNF transcription |
| Parameter | New Value |
|---|---|
| Coefficient for eIF2 phosphorylation () | 1.00 |
| A20-mediated C1 deactivation | 9.04 × 10 M min |
| TLR4 constitutive generation rate | 3.75 × 10 M min |
| IKKK-mediated IKK activation | 4.75 × 10 M min |
| Constitutive inactivation of IKK | 2.85 × 10 |
| IB mRNA degradation rate | 5.83 × 10 |
| Hill coefficient of IB transcription | 4.16 |
| Hill coefficient of IB transcription | 5.00 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, D.; Ding, Y.; Jayaraman, A.; Kwon, J.S. Mathematical Modeling and Parameter Estimation of Intracellular Signaling Pathway: Application to LPS-induced NFκB Activation and TNFα Production in Macrophages. Processes 2018, 6, 21. https://doi.org/10.3390/pr6030021
Lee D, Ding Y, Jayaraman A, Kwon JS. Mathematical Modeling and Parameter Estimation of Intracellular Signaling Pathway: Application to LPS-induced NFκB Activation and TNFα Production in Macrophages. Processes. 2018; 6(3):21. https://doi.org/10.3390/pr6030021
Chicago/Turabian StyleLee, Dongheon, Yufang Ding, Arul Jayaraman, and Joseph S. Kwon. 2018. "Mathematical Modeling and Parameter Estimation of Intracellular Signaling Pathway: Application to LPS-induced NFκB Activation and TNFα Production in Macrophages" Processes 6, no. 3: 21. https://doi.org/10.3390/pr6030021
APA StyleLee, D., Ding, Y., Jayaraman, A., & Kwon, J. S. (2018). Mathematical Modeling and Parameter Estimation of Intracellular Signaling Pathway: Application to LPS-induced NFκB Activation and TNFα Production in Macrophages. Processes, 6(3), 21. https://doi.org/10.3390/pr6030021