Multimode Operating Performance Visualization and Nonoptimal Cause Identification

Abstract

In the traditional performance assessment method, different modes of data are classified mainly by expert knowledge. Thus, human interference is highly probable. The traditional method is also incapable of distinguishing transition data from steady-state data, which reduces the accuracy of the monitor model. To solve these problems, this paper proposes a method of multimode operating performance visualization and nonoptimal cause identification. First, multimode data identification is realized by subtractive clustering algorithm (SCA), which can reduce human influence and eliminate transition data. Then, the multi-space principal component analysis (MsPCA) is used to characterize the independent characteristics of different datasets, which enhances the robustness of the model with respect to the performance of independent variables. Furthermore, a self-organizing map (SOM) is used to train these characteristics and map them into a two-dimensional plane, by which the visualization of the process monitor is realized. For the online assessment, the operating performance of the current process is evaluated according to the projection position of the data on the visual model. Then, the cause of the nonoptimal performance is identified. Finally, the Tennessee Eastman (TE) process is used to verify the effectiveness of the proposed method.

1. Introduction

With the advancement of society, industrial production relies heavily on efficient processes that can generate a variety of products. Changes in production schedules or product types result in multiple operating modes with different characteristics in the production process, including multiple stable production modes and different transition modes. The multimode process has gradually become the dominant production mode of modern industries. To obtain comprehensive economic benefits in the production process, academia and industry have increasingly focused on multimode operating performance monitoring technology [1,2].

At present, scholars have conducted extensive research on the monitoring of process operating performance [3,4,5,6,7]. Data-driven multivariate statistical process detection methods are most commonly and widely used because the mechanism model of the industrial process is highly complex; these methods include principal component analysis (PCA) [8,9,10] and partial least squares (PLS) [11,12,13], which can extract key information from the process. Through these methods, a single feature model of the whole production process can be obtained; however, in the multimode process, different production modes have different features, thus, it is impossible to describe different modal characteristics with one model. Therefore, these methods cannot be directly applied to the multimode process. To achieve the monitoring of multimode process, Ye et al. [14] used the Gaussian mixture model (GMM) to describe data distribution characteristics of multiple stable modes, which puts all the modes together to create a large hybrid model and does not require modal recognition. However, this method does not consider the transition modes of the multimode process and may provide inaccurate results during the monitoring process.

To solve this problem and establish the relationship between multimode processes and economic benefits, obtaining description models of various production modes is necessary. Zhao et al. [15] proposed using the multi-space principal component analysis (MsPCA) algorithm to obtain common information among all production modes, where each mode is divided into a common subspace and an independent subspace. Zhou et al. [16,17,18] proposed the total projection to latent structures (T-PLS) method, which uses the output data of the process to fully decompose the input space. Liu et al. [19,20] divided process data into multiple datasets based on comprehensive economic indicators, each corresponding to a performance grade. They believed that the process characteristic information contained in different performance grades are different, and then used the feature extraction methods, such as PCA or T-PLS, to extract the process features of each grade for performance assessment. In addition, different production modes can be distinguished by time-series analysis [21,22]. Although these methods can solve the impact of the transition modes, the multimode data need to be classified first in application. Therefore, the modal division and recognition of offline modeling data are prerequisites for monitoring the operating performance of multimode processes. The problems with the above methods are as follows: (1) Classification of offline data through expert knowledge, which means that no clear classification standard exists, and different classification results are generated for the same process due to different operator experience. (2) Although the data can be divided into different classes, distinguishing stable-mode data and transition-mode data in different datasets is infeasible, which reduces the accuracy of description models for different production modes. (3) In online monitoring processes, the process operating performances are not displayed through the visual form, which is inconvenient for the operator to observe.

In this study, a multimode operating performance visualization and nonoptimal cause identification method is proposed. First, historical data are clustered according to similarities across the data using subtractive clustering. This approach can automatically divide the data into multiple datasets with different characteristics and set a similarity threshold in the classification process to eliminate the transition-mode data. Then, the method calculates the comprehensive economic indicators of each dataset to determine the performance grade, so that the classification of the data is more general and scientific, which improves the accuracy of models for different stable modes. Thereafter, the common features among the datasets are obtained by MsPCA. Each common feature is removed from each dataset to obtain performance-dependent features, thereby improving the robustness of the established model to performance-independent variables. Then, the obtained features are visualized by a self-organizing map (SOM) neural network [23,24], and the corresponding areas of each performance grade are marked in the visualization, so that the monitoring results of the process operating performances are more concise and intuitive. Proposed by Kohonen et al. [25], SOM is a non-tutor learning network that can project data from high-dimensional space into low-dimensional space, with good classification and visualization effects, and can map data in a two-dimensional (2D) plane. When an online process is monitored, the operating performances of the current process are determined according to the projected position of the online data on the plane. The monitoring model not only evaluates the performance grade of different steady-state processes but also determines whether the process is in a transition mode. For data in nonoptimal performance, the correlation variables with nonoptimal result are identified by calculating the relative contributions of their process variables. Finally, the proposed method is applied to the Tennessee Eastman (TE) process and the effectiveness of the method is verified.

The rest of the paper is organized as follows. In Section 2, the realization process of the visual monitoring model for multimode operating performance is introduced. Subsequently, the method of online process operating performance assessment and the cause identification approach for nonoptimal performance grades are developed in Section 3. In Section 4, a case of TE process is studied to demonstrate the feasibility and efficiency of the proposed method. Finally, conclusions are provided in Section 5.

2. Visual Monitoring Model for Operating Performance of Multimode Process

2.1. Multimode Data Recognition Based on Subtractive Clustering

To obtain a visual monitoring model for multimode operating performance, identifying data of different modes in the collected historical data and obtaining datasets corresponding to each operating mode are necessary. Subtractive clustering algorithm can effectively reflect the data distribution according to the data density principle and can automatically determine the number of clusters and cluster center [26]. Most of the production process is in normal operation; thus, the cluster centers can reflect the data characteristics corresponding to different stable modes in the normal state.

The offline modeling data are assumed to be $X=\left\{x_1,x_2,\dots ,x_M\right\}\in R^{M\times N}$, where $M$ is the number of samples and $N$ is the number of variables. The specific steps for different stable modes of data partition and transition mode data elimination in offline data are as follows:

(1)

For offline data, the data are normalized with the mean and standard deviation. For convenience of description, it is still indicated by $X$.

(2)

Each data point is considered as a potential cluster center, and a measure of the potential of data point $x_i$ is defined as:

$$P_i={\displaystyle \sum _{j=1}^M{e}^{-\alpha {\Vert x_i-x_j\Vert }^2}},i=1,\dots ,M,$$

(1)

where $\alpha =4/r_a^2$ and $r_a$(5 < $r_a$ < 15) is a positive constant, which defines the radius of the neighborhood and affects the number of clusters. Data points outside this radius have minimal influence on the potential. The data point with many neighboring data points have a high potential value. After the potential of every data point has been computed, the data point with the highest potential is selected as the first cluster center.

(3)

Let $x_1^{*}$ be the location of the first cluster center and $P_1^{*}$ be its potential value. Then, the potential of each data point $x_i$ can be updated by the following formula:

$$P_i=P_i-P_1^{*}{e}^{-\beta {\Vert x_i-x_1^{*}\Vert }^2},i=1,\dots ,M,$$

(2)

where $\beta =4/r_b^2$ and $r_b$ is a positive constant, generally defined as $r_b=1.5r_a$ [19]. Then, the data point corresponding to the maximum value in $P_i$ is selected as the second cluster center and iterated through the above formula until the $C$ cluster centers are obtained, so that $P_k^{\ast }<\epsilon P_1^{*}$, $\epsilon$(0 < $\epsilon$ < 0.5) is a small fraction and its size determines the number of cluster centers. As $\epsilon$ increases, the number of cluster centers will decrease.

(4)

After each cluster center is obtained, different datasets are divided by calculating the similarity between each data point and each cluster center. The calculation formula is as follows:

$${\mu }_{i,j}=\mu (x_i,x_j^{*})=e^{-\alpha {\Vert x_i-x_j^{*}\Vert }^2},i=1,\dots ,M,j=1,\dots ,C,$$

(3)

(5)

The larger ${\mu }_{i,j}$ is, the closer the data point is to the cluster center. According to the maximum similarity of each data point corresponding to the cluster center, all data are divided into $C$ datasets, and a similarity threshold $\delta$ (0.5 < $\delta$ < 1) is set. When the maximum similarity corresponding to the data point is less than $\delta$, it is considered to be transition mode data and is removed from the dataset. In this way, only datasets that contain a steady-state process of different operating modes are obtained. In this paper, the values of $r_a$, $\epsilon$, and $\delta$ are determined in Section 4.1.

2.2. Feature Extraction of Multimode Data

A certain similarity exists among different operating-mode data because the multimode process is in normal operation most of the time. In this paper, the MsPCA is used to extract variation information related to performance of different operating modes. Compared with PCA, MsPCA can obtain the common variable relationship among datasets, by removing these common variables, the independent features of each dataset can be obtained; PCA is used to obtain the feature information of single dataset, thus, it is more suitable for the cases when the variation information contained in the process data is already closely related to performance.

The extraction process of the common variable relationship by the MsPCA is divided into two steps [27]. $C$ datasets are assumed, and the $c$th dataset is denoted as $X_c={[x_{c,1},x_{c,2},\dots ,x_{c,M_c}]}^T\in R^{M_i\times N}$, where $M_i$ is the number of samples and $N$ is the number of process variables.

The first step is to calculate the following formula:

$${\displaystyle \sum _{c=1}^C(X_c^T{X}_c){\overline{p}}_g={\overline{\lambda }}_g{\overline{p}}_g},$$

(4)

$${\overline{p}}_c=X_c^T{\overline{\alpha }}^c=\frac{1}{\sqrt{{\overline{\lambda }}_c}}{X}_c^T{X}_c{\overline{p}}_g,$$

(5)

where ${\overline{\lambda }}_c={\overline{p}}_g^T{X}_c^T{X}_c{\overline{p}}_g$. From the above formulas, $A$ sub-basis vectors of a dataset span a new subspace ${\overline{P}}_c=[{\overline{p}}_{c,1},{\overline{p}}_{c,2},\dots ,{\overline{p}}_{c,A}]\in R^{N\times A}$, which is equivalent to picking $A$ representatives out of the $M_c$ observations while keeping the dimension of variables fixed.

In the second step, ${\overline{P}}_c$ is substituted into the formula:

$${\displaystyle \sum _{c=1}^C({\overline{P}}_c^T{({\overline{P}}_c{\overline{P}}_c^T)}^{-1}{\overline{P}}_c)p_g={\lambda }_g{p}_g},$$

(6)

where the obtained feature vector is the common variable correlation subspace $P_g=[p_{g,1},p_{g,2},\dots ,p_{g,A}]\in R^{N\times A}$ among the datasets.

On this basis, further analyzing the amplitude of the data space $X_c$ on the obtained common basis vector $p_{g,a}$ is necessary, as shown in Figure 1.

$X_c$ is projected to the basis vector $p_{g,a},a=1,2,\dots ,A$ and the variation information in that direction is calculated as follows:

$$t_c^a=X_c{p}_{g,a},c=1,2,\dots ,C,$$

(7)

Under the given parameter $\phi (0<\phi <1)$, let ${\eta }_c^a=\Vert t_c^a\Vert /\Vert t_C^a\Vert ,c=1,2,\dots ,C-1$. If the condition $1-\phi <{\eta }_1^a,{\eta }_2^a,\dots ,{\eta }_{C-1}^a<1+\phi$ is satisfied, then its corresponding basis vectors in $P_g$ constitute the basis vector subspace:

$${\stackrel{⌣}{P}}_g=[p_{g,(1)},p_{g,(2)},\dots ,p_{g,(\stackrel{⌣}{A})}]\in R^{R\times \stackrel{⌣}{A}},$$

(8)

The remaining basis vectors in $P_g$ form the basis vector subspace:

$${\tilde{P}}_g=[p_{g,(1)},p_{g,(2)},\dots ,p_{g,(\tilde{A})}]\in R^{R\times \tilde{A}},$$

(9)

where $\stackrel{⌣}{A}=A-\tilde{A}$, and the independent feature vector space corresponding to each dataset is:

$${\stackrel{⌢}{X}}_c^s=X_c{\tilde{P}}_g{\tilde{P}}_g^T+X_c(I-P_g{P}_g^T),c=1,2,\dots ,C,$$

(10)

${\stackrel{⌢}{X}}_c^s$ represents the performance related variations, based on ${\stackrel{⌢}{X}}_c^s$, the traditional PCA is used to remove the noise, and the main information is obtained as follows:

$${\stackrel{⌢}{X}}_c^s=T_c^s{P}_c^{sT}+E_c^s,$$

(11)

where $T_c^s$ is the score matrix and represents the systematic process variations in ${\stackrel{⌢}{X}}_c^s$; $P_c^s$ is the loading matrix and reveals the systematic variation directions specific to performance grade $c$; $E_c^s$ is the residual matrix.

2.3. Visualization of Different Operation Mode Features

The self-organizing map neural network (SOM) can autonomously train and evaluate input patterns, and finally map different types of data to different regions [25]. Compared with traditional classification methods, SOM can be used to visualize data because it could project high-dimensional data into a 2D grid. The topology is shown in Figure 2.

The $i$th sample of input dataset $X$ is assumed as $x_i=\{x_{i1},\dots ,x_{in},\dots ,x_{iN}\}$, where $N$ is the number of process variables. The SOM is an ordered collection of neurons, each having a weight vector $m_j=\{m_{j1},\dots ,m_{jn},\dots ,m_{jN}\}$ associated with the input layer. An SOM with $J$ neurons is considered to train to represent and visualize $X$, because the size of $J$ affects the accuracy and generalization capabilities of SOM, which generally satisfies the following [28]:

$$J=8\sqrt{N},$$

(12)

When training the neural network, the Euclidean distance between $x_i$ and $m_j$ is calculated to obtain the best matching unit (BMU) [29]:

$$b_i=\arg \underset{j}{\min }\Vert x_i-m_j\Vert \forall i\in [1,N],\forall j\in [1,J],$$

(13)

Then, the weight vector of the input and output layers are updated by:

$$m_j(t+1)=m_j(t)+\alpha (t)h_{bj}(t)\Vert x_i(t)-m_j(t)\Vert ,\forall j\in [1,J],$$

(14)

where $\alpha (t)$ is the learning rate factor and $h_{bj}(t)$ is the neighborhood function, which is generally chosen as a Gaussian function. The position of the $j$th neuron is defined on the output layer as $r_j$, and $r_{bi}$ is the position of the winning neuron. Then:

$$h_{bj}(t)=\exp (-\frac{{\Vert r_{bi}-r_j\Vert }^2}{2{\sigma }^2(t)}),$$

(15)

where $\sigma (t)$ is the width of the neighborhood. To achieve convergence, the initial values of $\sigma (t)$ and $\alpha (t)$ are generally large and then decrease over time. When $t\to \infty ,\alpha (t)\to 0$, $\sigma (t)$ approaches 1.

When the number of iterations exceeds a predetermined value, the training phase ends, and the input data are marked on the final output map by searching each input vector for their wining neurons and marking their name on the winning neurons.

2.4. Realization of Visual Monitoring Process for Multimode Operating Performance

To eliminate the human interference generated in multimode data recognition, improve the accuracy of the process operating performance monitoring model, and reduce the influence of the performance-independent variables in the operating performance assessment, visualization of the multimode operating performance monitoring needs to be realized. First, the standardized data are divided by subtractive clustering method to obtain the datasets corresponding to different operating modes. Then, the data of the transition process are eliminated, so that only the data of the steady-mode process are included. Furthermore, the economic performance indicators of each of the obtained datasets are calculated to determine the performance grade corresponding to each dataset. Some of the data features among them are the same because the datasets obtained by the classification are in the normal operating mode of the multimode process. To effectively identify the characteristics among different performance-grade data, the MsPCA algorithm is used to remove common features that are unrelated to performance grades to obtain unique features. Then, through the SOM algorithm, the obtained features are mapped into a 2D grid for classification, and the feature model is visualized. The specific steps are as follows, and the method flow is shown in Figure 3.

(1)

The collected historical data in the normal running state of the production process are normalized to the value of [0, 1].

(2)

Through subtractive clustering, different cluster centers are obtained according to Equations (1) and (2), and then all data are classified according to Equation (3), and the transition process data are eliminated. The economic benefits of the classified datasets are then calculated based on the process knowledge to determine the performance grade of each dataset (e.g., optimal, average, or poor).

(3)

The common variable correlation subspace $P_g$ between each dataset classified in step (2) is extracted by the MsPCA algorithm using Equations (4)–(6). Then, the amplitudes of all datasets on $P_g$ is calculated according to Equation (7), and the sub-vectors that make their amplitudes different from ${\tilde{P}}_g$ are obtained. Finally, the unique feature vectors $T_s^c$ related to the performance grade of each dataset are obtained by Equations (10) and (11).

(4)

The unique feature vectors in step (3) are trained on the SOM. First, the number of neurons is determined by Equation (12), and weights are initialized using $T_c^s$ as the input of SOM. Then, winning neurons are selected according to Equation (13), and weights are updated according to Equations (14) and (15) until $\alpha (t)\to 0$. Finally, the training results are displayed on a 2D grid, and a visual monitoring model is obtained so that the multimode operating performance can be monitored in real time according to the model.

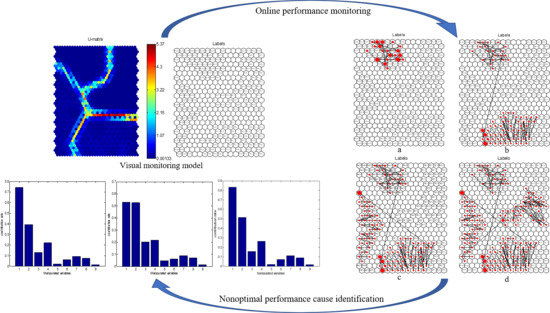
3. Online Process Operating Performance Assessment and Nonoptimal Cause Identification

3.1. Online Process Operating Performance Assessment Method

In visual monitoring, because a single sample cannot fully reflect the development of the process condition and is susceptible to process noise, a sliding time window of width $H$ is introduced as the basic unit of assessment. The online process operating performance assessment and nonoptimal cause identification steps are as follows:

Step 1: A sliding data window $X^{on,k}$ is constructed at time $k$.

Step 2: The $X^{on,k}$ is normalized by using the mean and standard deviation of the datasets corresponding to the respective performance grades, which are obtained when training the visualization model to obtain $X_c^{on,k}={[x_c^{on}(k-H+1),\dots ,x_c^{on}(k)]}^T$.

Step 3: The score vector $T_{on,k}^c$ for $X_{on,k}^c$ is calculated corresponding to each performance grade as follows:

$$T_c^{on,k}={(X_c^{on,k})}^T{P}_c^s,$$

(16)

Step 4: The obtained $T_c^{on,k}$ is projected into a two-dimensional grid of the SOM, and the operating performance of the current process is evaluated according to the performance grade marked by the projected position.

This method not only determines which performance grade the process is in, but also identifies whether the process is in transition mode. When the projection position is in a blank area between the areas where the performance grades are located, the process is in transition mode.

3.2. Nonoptimal Cause Identification Method

When the operating performance of the process is nonoptimal, identifying the nonoptimal causes and finding the key manipulated variables that cause nonoptimal performance are necessary. Only the contribution rate of each manipulated variable when calculating the score vector with respect to the optimal performance needs to be considered because the classification of the process operating performance is determined by the score vector $T_c^{on,k}$ of each dataset. The variable with a large contribution rate is the key variable that causes the process to be nonoptimal. Based on the assumption that the optimal performance grade $c*$ is used as a reference and the score vector in the optimal performance is $T_{c*}^s$, the specific calculation steps of the contribution rate of each manipulated variable are as follows:

Step 1: The mean value of the contribution of each m variable to the score matrix $T_{c*}^s$. is calculated in all modeling data in the optimal performance grade. The formula is as follows:

$${\overline{C}}_l={\displaystyle \sum _{m=1}^{M_{c*}}\left|\right|x_{c*}^l(m)p_{c*}^{s,l}|{|}^2/M_{c*}},$$

(17)

where $l=1,2,\dots ,L$ is the number of manipulated variables; $x_{c*}^l(m)$ is the $l$th manipulated variable of the $m$th sample in $X_{c*}$; $M_{c*}$ represents the number of samples at grade $c*$ and $p_{c*}^{s,l}$ is the row vector corresponding to the $l$th manipulated variable in $P_{c*}^s$.

Step 2: The contribution value of nonoptimal performance data to $T_{c*}^s$ is calculated as follows:

$$Cont{r}_l^{raw}=\left|\right|x^{k,l}{p}_{c*}^{s,l}|{|}^2,$$

(18)

where $x^{k,l}$ represents the measured value of the $l$th manipulated variable at the $k$th time. Finally, the contribution rate of the variable is:

$$Cont{r}_l=\frac{Cont{r}_l^{raw}}{{\overline{C}}_l},$$

(19)

The manipulated variable with a large contribution rate is the causal variable that causes the process to be nonoptimal.

4. Simulation Study of Tennessee Eastman Process

4.1. Process Description and Experimental Setting

The Tennessee Eastman (TE) process, which was proposed by Downs et al. [30], is a simulation system based on real industrial processes. This process is widely used in fields such as fault diagnosis, monitoring, and optimization. In this paper, this simulation system is used to obtain production process data with different performance grades.

The TE process generates two main products from four reactants, including five main units: reactor, condenser, compressor, separator, and stripper. Six different modes of operation are available depending on the mass ratio of the final product as shown in

Table 1. Six operation modes.

Mode	G/H Mass Ratio	Production Rate
1	50/50	7038 kg/h G and 7038 kg/h H
2	10/90	1408 kg/h G and 12,669 kg/h H
3	90/10	10,000 kg/h G and 1111 kg/h H
4	50/50	maximum production rate
5	10/90	maximum production rate
6	90/10	maximum production rate

.

The process has 42 measured variables and 12 manipulated variables. The operating mode of the TE process can be switched by changing the data of the manipulated variable as shown in

Table 2. Manipulated variables for six operating modes.

Manipulated Variables (%)	Mode 1 (50/50)	Mode 2 (10/90)	Mode 3 (90/10)	Mode 4 (50/50)	Mode 5 (10/90)	Mode 6 (90/10)
D Feed	62.935	12.637	89.130	100.000	13.098	100.000
E Feed	53.147	96.216	8.381	86.715	100.000	9.438
A Feed	26.248	30.421	19.114	49.477	32.009	21.543
A+C Feed	60.566	56.092	51.368	96.595	58.155	57.640
Recycle valve	1.000	1.000	77.621	1.000	1.000	71.166
Purge valve	25.770	44.347	9.501	48.742	47.095	10.654
Separate valve	37.266	35.799	29.146	60.960	37.422	32.685
Stripper valve	46.444	42.865	39.425	74.522	44.491	44.251
Steam valve	1.000	1.000	1.000	1.000	1.000	1.000
Reactor coolant	35.992	25.257	35.550	60.794	26.070	40.538
Condenser coolant	12.431	12.907	99.000	35.534	14.115	99.000
Agitator speed	100.000	100.000	100.000	100.000	100.000	100.000

.

According to the simulation model established by Ricker [31,32], 12 manipulated variables are changed to switch the TE process between operating modes 1, 2, and 4. A total of 70 h of simulation is conducted, and 100 samples are taken every hour. Therefore, a total of 7000 samples are obtained, of which 3500 are selected as training samples with a sampling interval of 2. In addition, 1400 samples are selected for testing from the 3500 samples which were not considered for training. Since the samples are from the switch between three operating modes, the number of clusters should be close to three and not less than three. According to experiments, the parameters in the subtractive clustering algorithm are set as $r_a=12$, $\epsilon =0.2$, $\delta =0.6$, and the width of sliding time window is set as $H=30$.

4.2. Multimode Process Data Classification, Recognition, and Visualization Model Establishment

After the training samples are obtained, they are first standardized to obtain standardized data of zero mean unit variance. Then, subtractive clustering is performed. After the transition process data are removed, four sets of steady-state data are obtained. The economic performance index of each dataset is calculated by the economic performance index calculation formula defined in [33]. The benefits are shown in Figure 4.

Figure 4 shows that after the data are classified according to the characteristic of the data themselves, the economic benefits are also divided into four grades, thereby preventing the uncertainty and difference in the classification of data performance grades through human experience. According to the economic indicators corresponding to each dataset, this paper classifies them into four grades: best, good, general, and poor.

After obtaining the data of four different performance grades, the unique features corresponding to each performance grade data are obtained by MsPCA and entered the SOM for training to create a visual model as shown in Figure 5. Figure 5a shows a U matrix diagram in which a brightly colored area indicates a boundary line of data, and a brighter color of the boundary line indicates that the data are more dispersed and the classification effect is better. Figure 5b shows four performance grades (best, good, general, and poor), and the numbers in parentheses indicate the number of training data mapped to the current grid. The figure shows that the boundaries of the four regions are evident and will not easily cause misclassification.

To compare the differences between the data-based classification method and the traditional method of using the operator’s experience classification in the training process of the monitoring model, this study applies the classification method of training data using human experience. First, the economic performance indicators of each data point are calculated, and then, the economic benefits are equally divided into four intervals according to the maximum and minimum of the economic benefits. Thereafter, all the data corresponding to each interval are divided into four levels, and then, each dataset is trained by MsPCA–SOM. The obtained visual monitoring model is presented in Figure 6.

A comparison of Figure 5 and Figure 6 show that the classification effect of the data-based visual monitoring model is evidently better than the visual monitoring model based on the manual operating experience. In Figure 5, the data of the same performance grade are closely distributed, the data of different performance grades have evident boundaries, and each performance grade uniformly divides the 2D plane into four regions. However, in Figure 6, the areas corresponding to the poor and general grades are much larger than those corresponding to the best and good grades, the data distribution in the same performance grade are not close, and the data boundaries of different performance levels are not evident. In addition, when the data are classified by the operator experience, the data of the transition modes are not removed. Therefore, the training model cannot accurately distinguish the stable operating modes and the transition operating modes of the process, which reduces the accuracy of the monitoring model.

To verify the accuracy of the training result of the data-based visual monitoring model, this study uses the test data to project on the trained SOM grid (taking the general and best performance level data as an example) as shown in Figure 7. Figure 7a,b are the projections of the test data of the general grade and the best grade on the SOM training model, respectively, where the larger the area of the red hexagon, the more test data are projected into the grid. The figure shows that the data under these two performance grades are projected in the corresponding areas and the distinction is evident.

4.3. Online Process Performance Assessment and Variable Weight Identification of Nonoptimal Causes

The method proposed in this paper is not only suitable for offline data monitoring but also has a good monitoring effect on online data. The result of the online monitoring of the data by sliding data window is shown in Figure 8. The trajectory changes in Figure 8a–d show the trend of performance grades (general–poor–good–best) of multimode processes, where the data of the transition process are mapped into the blank area without the performance grade label. According to the running trajectory of the above four figures, the online performance grade change shown in Figure 9 can be obtained, which shows the change of the process running state with time. The integers (1: general, 2: poor, 3: good, and 4: best) indicate the performance grade of the stable operating performance, and the decimal indicates that the process is in transition.

Figure 10 shows the case where the process operating performance grade is nonoptimal, which is obtained by calculating the contribution rate of the manipulated variables of each performance grade with respect to the optimal performance grade.

Figure 10a–c show that in each performance grade, the contribution rate of D feed (variable 1) and E feed (variable 2) to the optimal performance grade is greater than those of other variables, and the switching of the TE process mode is mainly achieved by changing the proportion of the feed amount. Therefore, this result is consistent with the actual situation, and the accuracy of the identification of nonoptimal cause is verified, which can be fed back to the control personnel as a reference for the adjustment of the control strategy.

5. Conclusions

This paper proposes a method for visualizing multimode operating performance and identifying nonoptimal causes. This method uses subtractive clustering algorithm (SCA) to divide the historical data of multimode processes into different datasets according to the similarity between the data, which solves the problem of classifying the different production mode data and distinguishing the stable mode data from the transition mode data. Compared with the traditional performance assessment methods in which data are classified by expert knowledge, the proposed method reduces human influence and improves the accuracy and consistency of data classification and makes the feature extraction of different stable-mode processes more accurate by separating steady-state data from transition data. Simultaneously, this method realizes the identification of stable operation modes and transition modes of multimode processes during online assessment. In addition, in this method, SOM is used to solve the problem of visualizing the results of online monitoring, so that the monitoring results are more intuitive and easier to understand and are convenient for the operator to observe. For nonoptimal operating performances, the causes are identified by calculating the contribution rate of the manipulated variables for each performance grade, which provides a reference for improving the production performance. Finally, the effectiveness and accuracy of the proposed method are verified by monitoring the performance grades of various operating modes in the TE process.