Quality Control for Medium Voltage Insulator via a Knowledge-Informed SPSA Based on Historical Gradient Approximations

Abstract

Medium voltage insulators are essential and versatile components in electrical engineering. Quality control of the manufacturing process for the insulators has a significant role in their economic production and reliable operation. As the quality of medium voltage insulator is mainly affected by the process parameters of the automatic pressure gelation process (APG), the optimal process settings are required to achieve a satisfactory quality target. However, traditional process parameters’ optimization methods are often cumbersome and cost-consuming. Moreover, the operational cost of APG for insulator production is relatively high. Therefore, the determination of the optimal settings becomes a significant challenge for the quality control of insulators. To address the above issues, an idea of knowledge-informed optimization was proposed in this study. Based on the above idea, a knowledge-informed simultaneous perturbation stochastic approximation (SPSA) methodology was formulated to reduce the optimization costs, and thus improve the efficiency of quality control. Considering the characteristics of SPSA, the historical gradient approximations generated during the optimization process were utilized to improve the accuracy of gradient estimations and to tune the iteration step size adaptively. Therefore, an implementation of a quality control strategy of knowledge-informed SPSA based on historical gradient approximations (GK-SPSA) was thus constructed. In this paper, the GK-SPSA-based quality control method was applied to the weight control of a kind of post insulators. The experimental simulation results showed that the revised knowledge-informed SPSA was effective and efficient on quality control of medium voltage insulators.

1. Introduction

Medium voltage insulators are widely used in electrical switches, electrical control devices, and other electrical equipment [1,2]. Quality control for the insulators is of great significance for its economical manufacturing and safe, reliable operations. Currently, most of the medium voltage insulators are manufactured by a widely used technology—the epoxy resin automatic pressure gelation technology (APG) [3]. For APG technology, the critical process for quality control is the automatic pressure gelation process. The APG process is a typical batch process, which is of high complexity and nonlinearity [4]. Meanwhile, the insulators have a wide range of types with continually changing customer demands. Therefore, it must meet the needs of flexible manufacturing. All the above factors make it a challenge to implement quality control of medium voltage insulators efficiently. Thus, a severe challenge is put forward for quality control of the production of insulators.

During the manufacturing process of the medium voltage insulators, process parameters have a significant impact on product quality. Once the material recipe and the APG device are determined, the process parameters are the only controllable factors left. In practice, after the design stage, quality control of insulators is mainly achieved via the tuning of process parameters. Traditional quality control methods for batch processes can be categorized into three different types, that is, trial-and-error, design of experiments (DOE), simulation optimization based on product quality models (i.e., model-based optimization, MBO) [5]. Generally speaking, the trial-and-error and the DOE are inefficient, inaccurate, and experience-dependent. However, for the MBO, although it has high efficiency in its optimization stage, the cost for model construction is very high, and the model mismatch always exists. Hence, the application of MBO is costly, time-consuming, and still cannot guarantee the optimality of the optimal process settings. Considering the flexibility required for the flexible manufacturing of the medium voltage insulators, the problem of inefficiency of MBO becomes more severe. Due to the inefficiency of MBO on model construction and the model mismatch, the trial-and-error and the DOE are still widely used in the industrial practice. The reason is that although the trial-and-error and the DOE are inefficient, they still have the advantage of easy implementation. To address the challenges, Kong et al. proposed a systematic model-free optimization (MFO) framework for a type of batch processes with short cycle time and low operational cost [5], and Zhu and Yang et al. [6,7] further extended the framework. In their MFO framework, they suggested using relatively fewer direct experiments to substitute the role of the model in MBO based on the characteristics of batch processes with short cycle time and low operational cost. Hence, the MFO framework can keep the high-efficiency optimization characteristics of MBO and simultaneously avoids high modeling costs. Different methodologies, such as simultaneous perturbation stochastic approximation (SPSA), simplex search method, are integrated to form different realizations of MFO, and thus the efficiency of quality control is improved. However, MFO is formulated and constructed under an implicit hypothesis that the operational cost for a single batch is relatively low, and thus the cost of fewer experiments can be tolerable. Based on the hypothesis, MFO is less sensitive to fewer experiment costs. However, for the APG process, the above hypothesis is invalid anymore. Although the APG process has the same batch-to-batch characteristics as the low-operational-cost batch process, the operational cost and the cycle time for a single batch are relatively higher that they cannot be ignored. Due to the above reason, traditional MFO methodology cannot be extended to the APG process directly.

To reduce the experimental costs of MFO further, Zhao et al. proposed iterative modeling and the trust-region optimization method (IMTO) according to the advantages of both the MFO and the MBO [8]. To improve the efficiency of the traditional MFO, the IMTO method utilizes a series of surrogate models to guide the optimization process, and the surrogate models are constructed based on iterative information generated during the optimization. That method actually tries to incorporate process knowledge generated during the optimization. IMTO is a hybrid strategy, which is no longer pure model-free; it can, to some extent, reduce the experimental cost of the traditional MFO. Lu et al. proposed a model-free quality optimization method based on the natural gradient for the injection molding processes [9]. In their study, the natural gradient was used, and an adaptive stepping strategy based on Riemannian geodesic distance was constructed. Their method had been verified that it could improve the optimization convergence speed of MFO and reduce the costs of quality control. As model-free algorithms are critical for quality control, some researchers focus on the efficiency of the algorithms [10,11]. Hou et al. focused on the development of the data-driven strategy to improve the efficiency of model-free control (MFC) [12,13,14]. The development process of MFC is instructive to the MFO. Xing et al. considered that when a complex optimization problem is to be solved, the knowledge of the problem could be excavated from the optimization process and could be utilized to guide the subsequent optimization process to improve the optimization efficiency. They had proposed a series of knowledge-based algorithms and learning-guided algorithms [15,16]. However, their study focused on global optimization algorithms, which are not suitable for MFO scenarios. To summarize, all the above research from IMTO to Xing’s study, knowledge either generated during the optimization or obtained as a prior are utilized to promote the efficiency of their methods. It provides us a definitive direction for the enhancement of the MFO, which is to mine and use knowledge fully to guide the optimization process.

To address the challenges faced by quality control for a type of batch process with relatively high operational costs, such as the production of the medium voltage insulators, an idea of knowledge-informed optimization, which integrates iteration knowledge generated during the optimization process, is put forward systematically. This optimization strategy is elaborately designed to guide the optimization process based on historical information to improve the efficiency of quality control for batch processes. The characteristics of the traditional SPSA method were analyzed in this paper. Considering the potential drawbacks of the SPSA, a revised SPSA method, knowledge-informed SPSA based on historical gradient approximations (GK-SPSA), was proposed. This method could cope with the stationary iteration step size problem of the SPSA and could be used to compensate for the gradient approximations at each iteration point. Thus, the efficiency of the revised SPSA could be improved.

The remainder of this paper is organized as follows. In Section 2, the quality control problem for the manufacturing of medium voltage insulators was defined and analyzed. In Section 3, the idea of a knowledge-informed optimization strategy was introduced, and a revised SPSA method (GK-SPSA) based on historical gradient approximations was proposed and detailed. In Section 4, the GK-SPSA method was verified on the weight control of a kind of post insulator. At last, conclusions from this research are presented.

2. Quality Control for Medium Voltage Insulators

Once the manufacturing device and materials are predetermined, the quality of the medium voltage insulators would mainly be determined by the APG process parameters. Under this circumstance, quality control for the production of medium voltage insulators could thus be converted to the tuning of APG process parameters.

Considering the uncertainty in the actual manufacturing process, the mathematical relationship between a particular insulator quality index and the corresponding APG process parameters could be generally expressed as below:

$$Q=f\left(x\right)+e,\hspace{1em}x={\left[x_1,\cdots x_n\right]}^T$$

(1)

where $Q$ represents the quality response of the quality index to be controlled, $x$ is an n-dimensional vector for the APG process parameters, and $x_i \left(i=1,\cdots ,n\right)$ is the ith process parameters of $x$, $n$ is the dimension of $x$, $e$ represents the overall process uncertainty, $f\left(x\right)$ is the theoretical function between the quality response and the process parameters. However, due to the high complexity and nonlinearity of the process, the above quality model is mostly difficult or unable to obtain at a reasonable cost.

Correspondingly, quality control of medium voltage insulators could be formulated as:

$$\begin{array}{ll}\underset{x}{\min }& Q_E=\left|E\left(Q\right)-Q_t\right|=\left|f\left(x\right)+E\left(e\right)-Q_t\right|\\ s.t.& R_i^L\le x_i\le R_i^H, i=1,2,\cdots ,n;\\ & x={\left[x_1,\cdots x_n\right]}^T.\end{array}$$

(2)

where $Q_t$ represents the target of the quality index, $E\left(e\right)$ represents the mathematical expectation of the uncertainties, $Q_E$ is the quality error between the mathematical expectation of the actual quality $E\left(Q\right)$ and the quality target, $R_i^L$ and $R_i^H$ represent the lower and upper bounds of $x_i$, respectively. Equation (2) is a constrained nonlinear optimization problem in essence, and the optimization objective is to find the optimal process parameters with a minimal quality error.

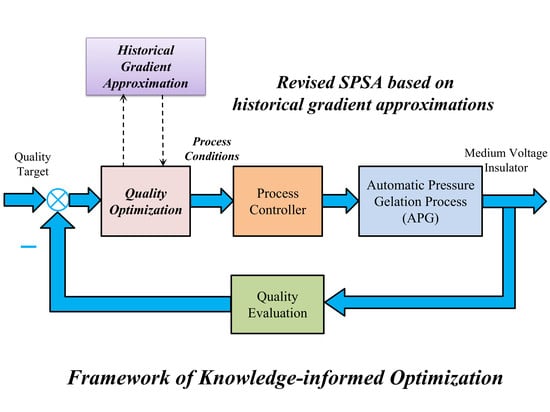
As the quality model of the APG process is usually unavailable, optimum process parameters mostly cannot be obtained via traditional simulation optimization strategy. Since the APG process is a typical batch process with run-to-run repetitive characteristics, to accomplish the quality control for medium voltage insulators, a model-free style optimization methodology is adopted. As a result, a closed-loop and online quality control methodology without a quality model is formulated. The schematics are shown in Figure 1. Under the optimization framework, the role of the quality model is substituted by direct online measurements, and the model-free quality optimization methodology is elaborately designed and implemented. As the optimization process progresses, the quality target of medium voltage insulators could be achieved iteratively. Each iteration consists of four stages, i.e., process parameters tuning, experimentation, quality evaluation, and feedback. For this strategy, each iteration has a specific experimental cost. For a type of batch process with short cycle time and low operational cost, the optimization is not sensitive to the iteration number. Thus, a number of limited iterations for quality control are tolerable.

However, the APG process is different from the kind of batch processes with short cycle time and low operational cost. The experimental cost for a single batch of APG process is relatively high that it is sensitive to the iteration number of quality control. Thus, a critical challenge is presented for the online implementation of quality control for the insulators. To improve the efficiency of quality control, the iteration costs should be minimized, and thus the iteration number of quality optimization should be minimized. The traditional model-free optimization method should be improved further.

3. Knowledge-Informed SPSA Based on Historical Gradient Approximations

This section consists of five subsections: in the first subsection, an idea of integrating process knowledge in the traditional MFO optimization strategy was proposed and discussed, aiming to address the challenge mentioned above. In the second subsection, the traditional SPSA methodology was introduced. In the third subsection, the characteristics of the SPSA were discussed, and a basic idea on knowledge-informed SPSA, with the utilization of historical gradient approximation, was thus proposed. In the fourth subsection, an implementation scheme of the knowledge-informed SPSA based on historical gradient approximation was formulated and analyzed. In the fifth subsection, the efficiency of the revised methodology was demonstrated on a benchmark function.

3.1. Knowledge-Informed Optimization Strategy

For a type of batch process with high operational cost, such as an APG process for the medium voltage insulators, optimization celerity is a central concern of quality control. With the optimization framework, as shown in Figure 1, the quality optimization strategy becomes the key to quality control. The performance of the optimization strategy significantly influences the efficiency of quality control. Generally speaking, the traditional MFO could meet the requirements of quality control on a type of batch processes with short cycle time and low operational cost. However, as the scenario is different for medium voltage insulators, quality control is faced with a great challenge of relatively high experimental cost at each batch. Although MFO already exhibits high efficiency in the previous scenario, it cannot satisfy the requirements on medium voltage insulators.

Whether or not the efficiency of quality control can be improved further under this optimization framework? Considering that in the iterative process of quality control, the optimization process will generate a series of historical iterative process information, which, in fact, contains specific process knowledge. In traditional MFO methods, this kind of information is not fully utilized. Taking the SPSA-based MFO method as an example, the optimization at each iteration only depends on the current iteration point and its corresponding perturbation points. If we could thoroughly investigate the characteristics of the process and monitor the status of quality control progress by using the information of historical iteration points generated during the quality control optimization process, then we could use this kind of knowledge to evaluate and adjust the quality control progress, to reduce the cost for quality control and improve the efficiency of quality control. This strategy, which improves the efficiency of the traditional quality control method and integrates process knowledge information to guide the optimization progress, is called a knowledge-informed quality optimization strategy. From the idea of optimization fused by iterative knowledge during the optimization, this section discusses a kind of SPSA-based knowledge-informed strategy based on historical gradient approximations in-depth and puts forward a feasible implementation mechanism.

3.2. Basic Principles of SPSA Methodology

SPSA is a type of stochastic gradient approximation optimization method [17,18]. For a multi-dimensional optimization problem, it perturbs all elements simultaneously at each iteration point to generate two perturbation points. Then, the gradient at the current iteration point is estimated by using the information of the loss functions of the two perturbation points. Compared with the finite difference stochastic approximation (FDSA) method, the cost of gradient estimation is significantly reduced [19]. Thus, SPSA has higher optimization efficiency. The basic steps of the SPSA are as follows:

• Method initialization: Determine the process parameters to be optimized and their feasible regions, and select the initial point X₁ by experience or according to specific rules. Set appropriate optimization method coefficients $\left\{a,A,c,\alpha ,\gamma \right\}$ and iteration termination conditions.
• Step size calculation: Update the step size $a_k,c_k$ at the current iteration batch, and the iteration step size could be calculated as below:

  $$a_k=\frac{a}{{\left(A+k+1\right)}^{\alpha }}$$

  (3)

  where $a$, $A$, $\alpha$ are coefficients of SPSA, $k$ is the current iteration number, $a_k$ represents the iteration step size of SPSA at kth iteration, which is the kth element of the monotonic decreasing sequence of the iteration step size. According to Equation (3), the iteration step size decreases with the progress of the iterative optimization process.
  The perturbation step size could be calculated as follows:

  $$c_k=\frac{c}{{(k+1)}^{\gamma }}$$

  (4)

  where $c$, $\gamma$ are coefficients of SPSA, $c_k$ represents the perturbation step size of SPSA at kth iteration. It also decreases with the progress of the iterative optimization process.
• Perturbation points generation: Generating an n-dimensional perturbation vector ${\Delta }_k$ by Monte Carlo method, with each of its elements generated randomly by Bernoulli $\pm 1$ distribution. Each component in the vector is independent and satisfies the zero mean principles. Suppose the current iteration point as X_k, then the positive perturbation point is $X_k+c_k{\Delta }_k$, and the negative perturbation point is $X_k-c_k{\Delta }_k$.
• Loss function evaluation: Evaluate the loss functions of the iteration point, the positive perturbation point, and the negative perturbation point at the kth iteration, $L\left(X_k\right)$ and $L\left(X_k\pm c_k{\Delta }_k\right)$.
• Gradient approximation calculation: The gradient approximation could be calculated according to the positive and negative perturbation points and their corresponding loss function values. The formula for the gradient approximation is as below:

  $$G\left(X_k\right)=\frac{L\left(X_k+c_k{\Delta }_k\right)-L\left(X_k-c_k{\Delta }_k\right)}{\left(X_k+c_k{\Delta }_k\right)-\left(X_k-c_k{\Delta }_k\right)}$$

  (5)
• Iteration point updating: Determine the next iteration point by utilization of gradient approximations according to the following formula:

  $$X_{k+1}=X_k-a_{k}G(X_k)$$

  (6)
• Termination conditions judgment: Determine whether the optimization termination criteria are met. Stop the optimization when the quality requirement is satisfied, or a maximum iterations number is achieved.

3.3. Basic Ideas for Knowledge-Informed SPSA Based on Historical Gradient Approximation

Although the traditional SPSA method already has high optimization efficiency, it still has some potential disadvantages. Firstly, as illustrated in Equation (3), the iteration step size of the SPSA method is a monotonic decreasing sequence only related to the number of iterations, which regularly decreases while the optimization progress is carrying forward. Essentially, this adjustment mechanism for the iteration step size is static and solidified, which is beneficial to the convergence of SPSA. As a result, the iteration step size does not have the adaptability to the status of the optimization progress. Thus, the traditional SPSA method lacks adaptive optimization search capability. As an example, at the initial stage of SPSA, even if the search direction is not in the descent direction, a larger iteration step size would be obtained according to the current adjustment mechanism, which might cause oscillation of the optimization progress. However, with the increase in the number of iterations, the iteration step size would decrease continually. At this moment, even if a proper descent direction is found, a fast descent could not be achieved by the SPSA due to the limits of small iteration step size. Therefore, the static adjustment mechanism of the iteration step size limits the optimization efficiency of SPSA. Secondly, SPSA only uses a few information at the current iteration point, which makes SPSA simple and easy to implement. Nevertheless, it also means that the method loses the global perception ability of the optimization process. Thirdly, with the restrictions of the above two factors, SPSA is easy to fall into local minima, which might seriously deteriorate the optimization performance in complex optimization scenarios.

Under the optimization framework of MFO, in order to improve the efficiency of quality control for the medium voltage insulators, a significant challenge brought by the above potential defects should be addressed. How to cope with the challenge mentioned before to improve the efficiency of quality control? Two critical questions are to be answered. The first question is: Whether the fixed step size tuning mechanism of SPSA could be changed to a dynamic tuning mechanism so that the method could have a kind of dynamic adaptive capability? The second question is: Whether the information of historical iteration points could be used to provide a certain extent of perception ability for the optimization progress? The answers to both the above questions are yes. As the historical iteration points carry some knowledge of the optimization process, this kind of knowledge could be integrated to investigate the status of the optimization progress, and thus could be used to guide the proceeding optimization process. According to Equation (6), the iteration step size and the gradient approximation are crucial for the iteration progress of SPSA. Suppose that the historical iteration points information could be effectively integrated to form a revised knowledge-informed method. Then, based on a dynamic adaptation mechanism, the iteration step size could be tuned adaptively; and based on a gradient approximation compensation mechanism, the gradient estimations could be compensated dynamically.

To construct such an improved knowledge-informed optimization method, as described above, the characteristics of the general optimization progress of industrial problems are further considered. Without loss of generality, a typical minimization problem is employed. Figure 2 shows a typical sketch for a 2-dimensional optimization problem. In general, considering the different development trends of the optimization process in a small local neighborhood, the status of the optimization progress could be divided into two typical scenarios: the local rapidly descending scenario and the local stagnation scenario. When the optimization progress lies in the descending zone, the optimization progress should be accelerated by increasing the iteration step size; while when the optimization progress lies in the stagnation zone, the iteration step size might be decreased moderately to accelerate the convergence rate of SPSA.

Considering the framework of the MFO and the idea of a knowledge-informed quality optimization strategy, only knowledge generated during the optimization process would be incorporated. In this paper, the historical gradient approximations as important information during the optimization process were utilized. The key to the knowledge-informed method is how to judge the current status of optimization progress. Suppose that the iterative gradient approximations keep following the same search direction in several successive iterations, it is reasonable to indicate that the optimization progress lies in the descending zone. Thus, the iteration step size might be enlarged according to the consistency of the directions of the adjacent gradients. Conversely, if the gradient approximations keep changing their search directions, it might be indicated that it has already fallen into a stagnation zone. In this case, the iteration step size thus could be cut down correspondingly to accelerate its convergence.

SPSA is a highly efficient method due to its two-measurements gradient approximation principles, which dramatically reduces gradient approximation costs for the stochastic approximation method. However, its efficiency is accomplished at the cost of only obtaining relatively poor gradient approximation at each single iteration point. If the accuracy of the gradient approximations could be further improved under the SPSA framework, it certainly could enhance the efficiency of SPSA. Considering that the iterative gradient approximations generated during the optimization process certainly carry some knowledge, such as the gradient tendency, they might be utilized to compensate for the gradient approximations at each iteration point. In fact, gradient averaging or gradient smoothing technique for optimization algorithm efficiency promotion had already been investigated before [20,21]. However, these methods were not widely used in engineering for they still stay at the algorithm investigation stage and lack of application in engineering practice.

Based on the above ideas, a revised knowledge-informed SPSA strategy, which incorporates the historical gradient approximations to guide the optimization progress, was proposed and formulated. This method utilized historical gradients to determine the status of the current optimization progress and tunes the iteration step size adaptively. Furthermore, the gradient approximations at each iteration point could be compensated moderately by the historical gradients. This methodology was named as knowledge-informed SPSA based on historical gradient approximations (GK-SPSA for short), and it is a typical knowledge-informed optimization strategy. An implementation scheme for GK-SPSA was proposed and illustrated in detail in the following subsection.

3.4. An Implementation Scheme of GK-SPSA

The basic procedure of GK-SPSA was almost the same as that of the traditional SPSA. The difference lies that GK-SPSA tried to effectively utilize the information of the gradient approximations during the optimization process and guided the optimization process via the historical data. Through the usage of information on historical gradient approximations, the gradient approximations compensation could be accomplished, and the iteration step size could be tuned adaptively. An implementation scheme of GK-SPSA was formulated based on the above ideas. The detailed mechanism is illustrated.

The gradient compensation rule was as follows:

$$\widehat{G}(X_k)={\rho }_k\widehat{G}(X_{k-1})+\left(1-{\rho }_k\right)G(X_k),\hspace{1em}\widehat{G}(X_1)=G(X_1)$$

(7)

where $X_k$ is the kth iteration point, $G(X_k)$ is the current simultaneous perturbation gradient approximation (CSPGA) at $X_k$, as shown in Equation (5), $\widehat{G}(X_k)$ is the kth compensated composite gradient approximation (CGA) at the $X_k$, ${\rho }_k$ is the gradient compensation coefficient at the kth iteration point. From Equation (7), the CGA at the $X_k$ is a linear combination of the previous CGA at $X_{k-1}$ and the CSPGA at the $X_k$. Through the above mechanism, the historical gradient approximations were integrated into the SPSA. The CGA was utilized to substitute the original simultaneous perturbation gradient approximations.

Considering that the credibility of CGA increases with the iteration number k according to the characteristics of SPSA, the gradient compensation coefficient could be constructed as follows:

$${\rho }_k={\rho }_F-\frac{\Delta {\rho }_{init}}{k^{\tau }}$$

(8)

where ${\rho }_F$ is an upper limit that a CGA could be approached, which is usually set to 0.5, $\Delta {\rho }_{init}$ is the initial deviation between ${\rho }_F$ and its lower limit, which is usually set to 0.2, and $\tau$ is a coefficient, which counts on the iteration number effects on the credibility of CGA. The coefficient ${\rho }_k$ represents the tendency of the cumulative effect of historical gradient approximations on compensated gradients.

To evaluate the status of the optimization process, an indicator, which is the angle between the CGA and the CSPGA, was adopted. A sketch of the angle could be seen in Figure 3. The smaller the angle was, the better the consistency of the gradient direction between the current iteration point and the previous iteration point was. Thus, if the optimization progress lied in the descending zone, the angle might be relatively small; conversely, if the optimization progress lied in the stagnation zone, the angle might be relatively larger. The cosine value of the angle was set as the status indicator (SI), and it could be calculated as below:

$$\cos \left({\phi }_k\right)=\frac{\widehat{G}(X_k)\cdot G(X_k)}{\left|\widehat{G}(X_k)\right|\left|G(X_k)\right|}$$

(9)

where ${\phi }_k$ is the angle between the CGA and the CSPGA at the current iteration point.

Based on the SI, the status of the optimization progress could be roughly evaluated quantitatively. Considering that the angle lied between 0 and $\pi$, accordingly, the range of SI was [−1, 1]. When the CSPGA was exactly consistent with CGA, the SI approached 1 as the angle approached 0. When the direction of CSPGA was in contrary to the CGA, the SI approached –1 as the angle approached $\pi$.

With the above SI, the iteration step size thus could be tuned according to the estimated status of the current iteration point. The tuning formula for the revised iteration step size was defined as below:

$$d_k=a_k\times \left(\frac{R}{\pi k^{\omega }}\left(\arctan \left(2\pi \left(\cos \left({\phi }_k\right)-\frac{1}{2}\right)\right)\right)+1\right)$$

(10)

where $d_k$ is the revised iteration step size, $R$ is a tuning coefficient for iteration step size ($0<R<2$), $\omega$ is a coefficient that counts on the iteration number effects on $R$. To make the tuning coefficient have nonlinear asymptotic characteristics with the SI, the tangent function trajectory was chosen to construct the distribution trajectory for the adjustment coefficients of the iteration step size. The formula was intentionally designed to tune the iteration step size into a theoretical range of $\left[1-\frac{R}{2}, 1+\frac{R}{2}\right]a_k$ according to the SI. Thus, the GK-SPSA would obtain the capability to tune the iteration step size adaptively based on the estimated status of the optimization progress.

The iteration points updating rule was substituted as follows:

$$X_{k+1}=X_k-d_k\widehat{G}(X_k)$$

(11)

The frameworks of SPSA and GK-SPSA are illustrated in Figure 4. Compared to the SPSA, an additional step was added by GK-SPSA to compensate for the gradient approximation and to tune the iteration step size based on the historical gradient approximation.

3.5. Benchmark Function Test

To illustrate the performance of GK-SPSA vs. SPSA, an optimization test on a benchmark function was conducted. The Rosenbrock function, which is a widely-used benchmark function, with a dimension of 10, was adopted. The initial settings was set at X₀ = [0.0015, 1, 0.4208, 0.4503, 0.3416, 0.3424, 0.9372, 0.5422, 0.867, 0.1635]^T, which was a randomly selected initial point. Figure 5 shows one typical optimization result of a single run with the two methods. It was indicated that GK-SPSA behaved very well relative to the traditional SPSA in this case. It could be concluded that the GK-SPSA was effective and fast that the optimization cost was significantly reduced. Figure 5b shows the trajectories of the iteration step size of GK-SPSA and SPSA. It was clear to see that the GK-SPSA could tune its iteration step size adaptively, in the meantime, not deteriorate the convergence ability of SPSA.

4. Experimental Verification

4.1. Experimental Setups and Simulation Platform Construction

A kind of post insulator was selected as the experimental subject for method verification in this study. As one of the common classes of medium voltage insulators, post insulators are widely used as supports for breakers and capacitor banks in switchgear, and in transformer substation yards as support for bus-bars. The material for the post insulator is epoxy resin. In this study, an epoxy molding compound with the brand of Duresco NU 5680V was selected. As part weight is a critical quality index for the post insulators, it was chosen as the controlled variable. The part weight target should be set according to the product specification requirements. Two different types were supposed to use in the test. The weight target of type A post insulator was set to 635 g, while type B was set to 620 g. According to the process characteristics and its control requirements, the weight bias tolerance for a qualified insulator is 0.5 g. According to the literature review and field investigation, four process parameters, including melt temperature, injection time, packing pressure, and packing time, have the most significant influence on the weight of the post insulators. Thus, these four parameters were chosen as process parameters to be optimized, represented as X = [x₁, x₂, x₃, x₄]^T. The descriptions and the ranges of the parameters are listed in

Table 1. Process Parameters for Weight Control of Post Insulator.

Process Parameters	Process Variables	Range	Units
Melt Temperature	x1	120–255	°C
Injection Time	x2	0.2–0.88	s
Packing Pressure	x3	75–90	MPa
Packing Time	x4	3–10	s

.

With the quality control framework, as shown in Figure 1, when quality control is conducted, a series of iterative experiments would be carried out, and the corresponding part weights under different parameter settings would be measured during the optimization. Considering that the actual experimental costs for a single batch are relatively high, meanwhile, the simulation experiments of the first-principle model of the post insulator based on Moldflow is time-consuming and cumbersome. Therefore, a simulation platform based on a surrogate model was constructed and utilized to reduce the costs for method verification. As the key of the paper mainly focused on the quality control methodology, the utilization of surrogate models with enough accuracy would not affect the validity of the verification for the quality control methods.

To build a surrogate simulation platform for the part weight prediction of the post insulator, several steps should be conducted. Firstly, a 3D model should be constructed according to the actual type specifications and technical parameters of the post insulator. A solid modeling computer-aided design software, Solidworks, was used in this project. The prototype and the 3D model of the post insulator could be seen in Figure 6. Secondly, based on the previous 3D model, a first-principle model for the insulator could be constructed by a plastic injection-molding simulation software, Moldflow. Thirdly, to thoroughly investigate the relationships between the part weight and the process settings, a systematic screening experiment scheme based on Latin hypercube sampling (LHS) was adopted. Thus, a series of experiments were conducted on the Moldflow model, with all the weight predictions and their corresponding process settings be recorded. Fourthly, a surrogate model based on the above experiments data could be constructed to form a simulation platform. Without loss of generality, a widely-used surrogate modeling technique, back-propagation artificial neural network (BP-ANN), was adopted in this study. The construction procedure for the platform could be summarized in Figure 7. Figure 8 shows the weight prediction performance of the simulation platform on the validation samples. By calculation, the platform has a maximum prediction error of 1.5%. It was indicated that the platform exhibited a satisfactory fitting precision; thus, the accuracy of the platform was enough for part weight control verification.

4.2. Results and Discussions

The performance of GK-SPSA methodology on quality control of medium-voltage insulators was evaluated through a series of optimization tests. To fully demonstrate the effectiveness and efficiency of GK-SPSA, different scenarios were constructed and tested. All the tests were conducted on the previously built simulation platform for part weight control of the post insulator. The results are presented and discussed as follows.

4.2.1. Quality Control from Different Initial Points

To verify the efficiency of GK-SPSA, a comparative study for traditional SPSA and GK-SPSA was carried out. Without loss of generality, type A post insulator was utilized for the test. The target of the part weight was set to 635 g with a tolerance of a quality deviation of 0.5 g. To avoid confusion, these two methodologies were conducted with the same method coefficients; that is, they were different only on their specific iteration rules. Thus, the results were credible and reasonable to show their relative performance and characteristics under the same conditions. A screening experiment based on Latin hypercube sampling was conducted to generate enough different initial points. These two methodologies were separately implemented on all the selected different initial points in sequence. The weight control results of the two methods on each round were recorded. Thus, the performance and the relative efficiency for GK-SPSA could be evaluated as objectively as possible.

At the first round, SPSA and GK-SPSA were both conducted on the insulator weight control from a randomly selected initial point X₁ = [137.77, 0.36, 8.79, 83.29]^T with an initial weight of 654.4 g. The dynamic weight control processes are shown in Figure 9. GK-SPSA reached the weight target in 13 iterations, while SPSA in 20 iterations. From Figure 9a, it was apparent that GK-SPSA behaved better than SPSA in this round. Figure 9b shows the different step size trajectories under the two methods. The iteration step size of SPSA was changed over the iteration number in a relatively fixed way. However, based on the historical gradient information, the iteration step size of GK-SPSA changed adaptively according to the quantification on the status of the optimization progress, which made the method more active to approach the weight control target.

To verify the effectiveness of GK-SPSA further, another initial point X₁ = [224.91, 0.82, 6.66, 86.12]^T was selected. The initial weight started at 628.8 g, which was below the weight target. Both the SPSA and GK-SPSA were conducted at the same conditions. Utilizing the two optimization methods, weight control tests of the post insulators were both succeeded. The results could be seen in Figure 10. GK-SPSA quickly reached the target with 16 iterations in this round, while SPSA, with 22 iterations, behaved significantly worse than GK-SPSA. It was indicated that GK-SPSA behaved better in this round. To illustrate the simultaneous perturbation nature of GK-SPSA, the iterative changing trajectories of all the process parameters are presented in Figure 11. All the four parameters, as described in Table 1, were normalized to a range of 0–100% according to their physical bounds. From the figure, it could be seen that all the parameters were perturbed simultaneously. As the optimization process progressed, the parameters converged to the optimal parameter settings iteratively.

Does GK-SPSA always behave better than SPSA? The answer is, of course, not. Due to the stochastic nature of the stochastic approximation (SA) methods, their optimization trajectories always vary at every different run. Sometimes, it could be observed that SPSA might behave better than GK-SPSA. From the screening experiments, the above phenomenon was verified. It was observed that GK-SPSA might behave worse than SPSA in some rounds. Figure 12 shows one of such cases. From the figure, SPSA just used seven iterations to reach the target, while GK-SPSA used 11 iterations. It was apparent that, in this round, GK-SPSA ran slightly slower than SPSA. This phenomenon was natural; thus, it was consistent with the stochastic nature of GK-SPSA with no conflicts.

However, how to evaluate the performance of these two methods? As the efficiency of SA methods could only be evaluated by statistics, the statistical results of the deliberately designed random screening experiments could be effectively incorporated to assess their relative efficiency. A series of 50 experiments with different initial points, which was generated by Latin hypercube sampling, was adopted. The samples by LHS were highly representative of all the feasible regions. The iteration costs for both the two methods on the same starting points were compared. The statistical results were shown in Figure 13. As in all the 50 rounds, GK-SPSA behaved better in 35 rounds; that is to say, it costed fewer iterations with a ratio of 70% in the test. At the same time, in the other 15 rounds, which was 30% of the test, SPSA behaved better. The average iteration number cost by GK-SPSA in all the 50 runs was 17.56, while SPSA was 25.5. It could be easily calculated that the iteration number costs of GK-SPSA were significantly cut down by 31.14% relative to SPSA in this test. The result indicated that GK-SPSA had obvious superiority compared to SPSA in statistics. The key to the performance promotion of GK-SPSA is that the revised knowledge-informed method makes full utilization of the historical gradient approximations to provide more accurate gradient approximations information for the optimization search progress, and thus make the optimization more effective. Moreover, the historical gradient approximations are also used to capture the tendency of the gradients and dynamically adjust the iteration step size accordingly.

4.2.2. Repeatability Test on Quality Control

As GK-SPSA is a stochastic method in nature, to demonstrate its effectiveness, repeatability from the same initial points should be tested. Without loss of generality, a random initial point X₁ = [208.64, 0.31, 3.09, 80.13]^T was selected in this test. Three different runs were conducted with the GK-SPSA under the same conditions. The results for the three runs are shown in Figure 14. As could be seen in the figure, all the optimization runs reached the weight target speedily and efficiently. However, the optimization trajectories were different. The 1st run reached the target in 10 iterations, while the 2nd run used 12 iterations, and the 3rd run costed 15 iterations. Owing to the stochastic nature of GK-SPSA, this phenomenon was reasonable. Nevertheless, the specified weight control could all be achieved satisfactorily by the different optimization runs. It could be concluded that under different optimization batches, although the optimization trajectory was not repeatable, its optimization performance was repeatable.

4.2.3. Quality Target Tracking Test under Type Transition

As a typical batch process, the product specifications of the post insulators might frequently change due to the market demand shifting. The weight control methodology for the post insulators should have the flexibility to cope with type transitions that occur when the market demand shifts. To further demonstrate the effectiveness of GK-SPSA on quality target tracking under type transition, a weight setpoint tracking test was conducted. Type A insulator was manufactured with a setpoint of 635 g. An initial point X₁ = [127.28, 0.37, 5.85, 85.56]^T was selected. The initial weight was 681 g, which deviated a lot from the target. GK-SPSA and SPSA were conducted separately. Both two methods reached the target weight speedily. GK-SPSA used 10 iterations, while SPSA used 12 iterations. At a certain moment, it was supposed that the type B insulator was needed to meet the new market requirement. The target weight of type B was 620 g. At the moment, type transition occurred. To achieve the new target, both GK-SPSA and SPSA were implemented. Weight tracking results could be seen in Figure 15. Utilizing the GK-SPSA, the weight of the insulator reached the new steady-state within 15 iterations. As a comparison, the SPSA costed 28 iterations. It was indicated that GK-SPSA was effective in quality setpoint tracking.

4.2.4. Quality Control under Disturbance

In the industrial environment, the APG process for the production of the insulators is always susceptible to all kinds of disturbances. When the process is affected by any disturbance, the steady-state on the product weight control might be interrupted. The process parameters should be tuned to revert to the target. To test the effectiveness of GK-SPSA on the robustness of quality control to cope with disturbances, a disturbance signal was artificially introduced. Type A insulator was used in the test. The target weight of the insulator was 635 g. However, at one moment, to simulate a change of the material receipt of the epoxy resin, the part weight model was added a weight deviation by 10 g intentionally. Subsequently, the weight of the insulator under the previous process conditions deviated from the target. The weight deviation could be seen in Figure 16. When the disturbance occurred, GK-SPSA was reactivated. It could be seen from Figure 16 that GK-SPSA returned the weight to the target within only eight iterations. It was indicated that the robustness of GK-SPSA to cope with weight disturbance was effective.

5. Conclusions

In this paper, the idea of a knowledge-informed optimization strategy was proposed to address the challenges faced by the quality control of the medium voltage insulators, which provides a possible solution for quality control of a type of batch process with relatively high operational costs. Given the basic idea of maximum utilization of iteration knowledge generated during the optimization process, the strategy tries to guide the search process with suitable knowledge-informed mechanisms. Based on the knowledge-informed idea, an improved insulator quality control method via a knowledge-based SPSA based on historical gradient approximations was proposed and formulated according to the characteristics of SPSA. GK-SPSA was designed to have a more accurate gradient approximation estimates, and it was designed to have the ability to detect the status of the optimization progress and accomplish the iteration step size tuning adaptively. A thorough test of the GK-SPSA-based quality control method was conducted on the weight control of a kind of post insulator. The experimental results showed that, relative to the traditional SPSA, GK-SPSA reduced the costs on the weight control of the post insulators significantly. It could be concluded that GK-SPSA was effective and efficient. The idea and the framework of GK-SPSA could be extended to other similar industrial applications. The theoretical analysis of GK-SPSA might be investigated further in the future.