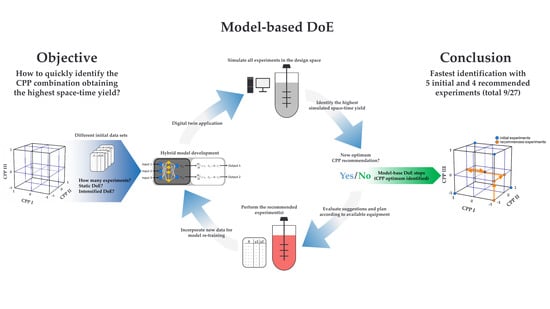
Digital Twin Application for Model-Based DoE to Rapidly Identify Ideal Process Conditions for Space-Time Yield Optimization

Abstract

The fast exploration of a design space and identification of the best process conditions facilitating the highest space-time yield are of great interest for manufacturers. To obtain this information, depending on the design space, a large number of practical experiments must be performed, analyzed, and evaluated. To reduce this experimental effort and increase the process understanding, we evaluated a model-based design of experiments to rapidly identify the optimum process conditions in a design space maximizing space-time yield. From a small initial dataset, hybrid models were implemented and used as digital bioprocess twins, thus obtaining the recommended optimal experiment. In cases where these optimum conditions were not covered by existing data, the experiment was carried out and added to the initial data set, re-training the hybrid model. The procedure was repeated until the model gained certainty about the best process conditions, i.e., no new recommendations. To evaluate this workflow, we utilized different initial data sets and assessed their respective performances. The fastest approach for optimizing the space-time yield in a three-dimensional design space was found with five initial experiments. The digital twin gained certainty after four recommendations, leading to a significantly reduced experimental effort compared to other state-of-the-art approaches. This highlights the benefits of in silico design space exploration for accelerating knowledge-based bioprocess development, and reducing the number of hands-on experiments, time, energy, and raw materials.

1. Introduction

For the production of biopharmaceuticals, it is of high importance to guarantee a specified product quality for patient safety. Raw materials, process deviations, and unrecognized faults may result in altered quality, and finally in batch rejection [1]. Process characterization in the biopharmaceutical industry has long been known and emphasized by the authorities, thus, processes must be closely monitored and well understood to ensure robust and uniform product quality. The most prominent guidance is the process analytical technology (PAT) guide by the US federal drug administration (FDA). Additionally, the quality by design (QbD) initiative [2] greatly emphasizes process understanding during the development of a bioprocess to guarantee a stable and uniform product quality output and fewer rejected batches [3]. To achieve these objectives, the statistical design of experiments (DoE) and advanced online monitoring are highlighted. The herein experimentally investigated design space is built by different combinations of critical process parameters (CPP) and critical material attributes (CMA), which affect the target parameters and the critical quality attributes (CQA) [4]. For such a design space exploration, different DoEs can be applied, e.g., full factorial, fractional factorial, Box–Behnken, Doehlert, and hypercubes, differing in the number of required experiments and the amount of information generated [5]. Besides the increased process understanding, for process optimization of the target molecule, it is still important to quickly find the best CPP combination in the design space, at which the production process will be performed, e.g., biomass, product titer, or space-time yield [6]. Such DoE studies are combined with process modeling to generate added value and further accelerate these tasks [7].

The most common techniques for bioprocess modeling are data-driven (black box) and mechanistic (white box) approaches, each with their own characteristics, advantages, and disadvantages [8]. Since the parameters in data-driven models do not have a physical meaning, no further process knowledge is needed, enabling a fast and easy implementation of these model types. Currently, various regression algorithms are available and commonly used, e.g., partial least squares, random forests, support vector machines, artificial neural networks (ANN) [9], and many more. However, such models are based on correlation and do not mandatorily imply causality, which can lead to inaccurate or even incorrect model predictions and conclusions. Contrarily, mechanistic models are based on theoretical considerations, i.e., the parameters have a physical meaning, and therefore ensure causality. Since these model predictions follow a purely mechanistic trend, temporary process deviations and unknown CPP impacts are not considered, which also interferes with the model performance and accuracy. To exploit the advantages of each individual model structure, a combined approach can be considered, called hybrid modeling (grey box) [10]. Since both models can complement each other in this combined structure, more precise predictions are anticipated. Such a hybrid model can be built in a parallel or serial structure, e.g., first, the data-driven part estimates parameters used in the mechanistic part, which otherwise would have to be assumed. Thereby, it is possible to also incorporate the CPP’s impact into the hybrid model, which significantly strengthens the explanatory power of the model [11]. Additionally, to have assurance about the model performance and the risk of model mispredictions, typically cross-validation is performed to reduce variance, avoid overfitting, and investigate how the model performs when applied to new data [12]. A similar approach with a higher degree of freedom for creating the final model is model averaging from a leave-one-batch-out cross-validation, i.e., several developed models are averaged to improve the model stability and accuracy [13]. Even though this hybrid modeling approach has been the state-of-the-art in other industries for many years, due to the higher complexity of biological processes, it has only gained interest during the last few years [14]. Even though hybrid modeling is increasingly adopted for downstream applications [15,16,17], the response surface modeling of process endpoints is still more commonly applied [18], and the full potential of hybrid process modeling applications in bioprocessing has not yet been realized.

The high added value and the benefits of hybrid modeling for upstream bioprocessing become tangible when considering three major aspects of progressing towards digital biomanufacturing, i.e., delivering an increased process understanding, accelerating bioprocess development, and enabling advanced process control [19]. For all these components, various tools with different levels of complexity can be considered. Herein, soft sensors are frequently used, i.e., advanced online sensor systems such as spectrometry [20] or spectroscopy [21] in combination with a software algorithm to estimate the variables of interest in real-time, without any sampling and analytical time delay [22]. Depending on the used model structure, such soft sensors can be descriptive or predictive. While the descriptive model type can only be used to get estimated values up to the current time point, predictive models can also predict future values with a degree of uncertainty and therefore can additionally be used for process control [23]. Along with process models for the variables of interest, model-based methods for the optimization of process parameters such as the gained process information, the maximum amount of cells, or productivity were also introduced [24]. A highly interesting concept for accelerating bioprocess development and optimization in combination with model-related DoE approaches is a digital bioprocess twin [25,26]. Based on a minimal number of experiments, a hybrid model can be developed and subsequently be applied as a digital bioprocess. This digital twin then enables the simulation of further experiments, i.e., in silico exploration of the design space to shed light on the process behavior, without any additional laboratory experiments. This can be used to investigate the impact of the CPPs on the desired output, and thereby recommend the best CPP combination that maximizes it. A validation experiment at the recommended CPPs can be performed and compared to the simulation [27]. Subsequently, this digital twin model can be re-trained with the new experimental data, improving its performance by gaining a higher understanding of the process, and allowing it to explore a potential new optimum [28]. Once the recommendation of the digital twin converges at the process optimum, no new CPP combination will be proposed. Such model-based DoE and process modeling to find the best CPP combination in a design space saves raw materials and additionally operates more quickly and is cheaper compared to approaches in which experiments are only performed in the laboratory [29].

To accelerate the design space exploration and thereby greatly decrease the time needed to identify the optimum CPP combination for the variables of interest, we present a digital bioprocess twin used for model-based DoE [30]. This digital twin simultaneously delivers additional process understanding, while accelerating bioprocess development and optimization by applying in silico simulations that only perform the recommended experiments. We were particularly interested in determining the minimal number of required experiments for developing an initial digital twin, recommending further experiments to rapidly identify the best CPP combination in the design space. Such an iterative approach towards digitalization leads to a reduced experimental effort and saves various propositions of economic value while tackling current shortcomings for the implementation of such novel and promising tools [31]. Therefore, we present our structured workflow using different initial data sets to reduce experimental effort, evaluate the results, and additionally to investigate the applicability of an intensified DoE (iDoE) [32] for such a model-based DoE, to rapidly find the best CPP combinations in a design space and obtain the highest space-time yield.

2. Materials and Methods

2.1. Experimental Design

The experimental data set was derived from E. coli (HMS174 (DE3)) (Novagen, Germany) fed-batch cultivations at 20 L scale. For the workflow and the evaluation, a design space with three CPPs, each at three levels, was considered: the feed controlled specific growth rate μ (0.10, 0.15, and 0.20 h⁻¹), the cultivation temperature T (30, 34, and 37 °C), and the induction strength I (0.2, 0.5, and 0.9 μmol IPTG g⁻¹ cell dry mass), respectively. The variables of interest to be modeled were the biomass concentration (g L⁻¹) and the space-time yield (g L⁻¹ h⁻¹) of the soluble fraction of the expressed protein, recombinant human superoxide dismutase. The biomass was analytically measured by thermogravimetric analysis [33] once before induction and then hourly, and the soluble product titer was measured every 2 h from the time point of induction to the last sampling at the end of the process by ELISA [34]. The fed-batch phase was carried out for four doubling times, and induction of the cells took place after the first doubling time, i.e., product formation took place for the remaining three doubling times. The values for the online measurements were available every minute and included the pH (controlled by the addition of 12.5% NaOH), off-gas (%), cultivation temperature (°C), inlet air (slpm), dissolved oxygen (%), stirrer speed (rpm), base consumption (L), accumulated feed (L), inducer (kg), and head pressure (bar). More details about the applied exponential feeding strategy for the fed-batch phase, the utilized E. coli strain, the expression vector system, the online monitoring, and the offline measurements have already been presented elsewhere [35,36,37].

To receive meaningful information about the performance of the different digital twins and model-based DoE approaches, the design space was completely characterized. Once by common static cultivations (one CPP combination per experiment, i.e., 27 cultivations to cover all CPP combinations) and by iDoE cultivations (three CPP combinations per experiment, i.e., nine cultivations covering all 27 CPP combinations).

The intra-experimental CPP shifts in the intensified fed-batch fermentations were performed after each theoretical cell doubling post-induction of the cells, with a temporarily increased sampling interval, and executed by adjusting the setpoint value of the feed controlled specific growth rate and cultivation temperature in the process control system. Additionally, the feasibility of these shifts and the exclusion of a potential memory effect on the cells is presented in detail elsewhere [38]. A list of all the performed experiments used for comprehensive comparison is given in Appendix A.1 (

Table A1. CPP combinations of the static experiments for the model-based DoE approach.

CPP Combination	CPP 1 (µ)	CPP 2 (T)	CPP 3 (I)	Maximum Biomass (g L−1)	Maximum Space-Time Yield (g L−1 h−1)
1		30	0.2	33.18	0.0193
2		34	0.2	31.12	0.0726
3		37	0.2	30.31	0.0311
4		30	0.5	29.88	0.0733
5	0.10	34	0.5	23.96	0.0837
6		37	0.5	20.6	0.0621
7		30	0.9	26.07	0.0800
8		34	0.9	20.69	0.0915
9		37	0.9	18.23	0.0432
10		30	0.2	34.28	0.0264
11		34	0.2	32.09	0.0415
12		37	0.2	29.7	0.0430
13		30	0.5	31.74	0.0564
14	0.15	34	0.5	28.66	0.0997
15		37	0.5	24.06	0.0663
16		30	0.9	26.89	0.0564
17		34	0.9	25.17	0.0815
18		37	0.9	21.62	0.0485
19		30	0.2	34.51	0.0157
20		34	0.2	33.68	0.0227
21		37	0.2	32.93	0.0274
22		30	0.5	31.49	0.0418
23	0.20	34	0.5	30.97	0.0783
24		37	0.5	28.85	0.0578
25		30	0.9	29.14	0.0518
26		34	0.9	29.25	0.0818
27		37	0.9	23.98	0.0513

and

Table A2. CPP combinations of the intensified experiments for the model-based DoE approach.

iDoE CPP Combination	CPP 1 (µ)	CPP 2 (T)	CPP 3 (I)	CPP Shift 1	CPP Shift 2
1		37	0.2	37 °C to 34 °C 0.10 h−1 to 0.20 h−1	0.20 h−1 to 0.10 h−1
2	0.10	30	0.5	30 °C to 34 °C	34 °C to 37 °C 0.10 h−1 to 0.20 h−1
3		34	0.9	34 °C to 37 °C	0.10 h−1 to 0.15 h−1
4		37	0.2	37 °C to 30 °C 0.15 h−1 to 0.10 h−1	30 °C to 34 °C 0.10 h−1 to 0.15 h−1
5	0.15	30	0.5	0.15 h−1 to 0.20 h−1	30 °C to 34 °C
6		34	0.5	34 °C to 37 °C	0.15 h−1 to 0.10 h−1
7		30	0.2	30 °C to 37 °C	37 °C to 30 °C 0.20 h−1 to 0.15 h−1
8	0.20	37	0.9	37 °C to 34 °C 0.20 h−1 to 0.15 h−1	34 °C to 30 °C 0.15 h−1 to 0.20 h−1
9		34	0.9	34 °C to 30 °C 0.20 h−1 to 0.15 h−1	0.15 h−1 to 0.10 h−1

). Moreover, for the static cultivations, the maximum experimental values of the variables to be modeled are indicated. For the intensified cultivations, the maximum values were not conclusive, due to the intra-experimental shifts and the resulting multiple characterized CPP combinations, and therefore are not displayed. The two complete DoE and iDoE data sets are presented extensively and available for download as supporting information for an earlier publication [38].

2.2. Data Sets

For the initial hybrid model building and the model-based DoE, different initial data sets were used, and the respective performances for identifying the best CPP combination, obtaining the highest space-time yield were compared. These data sets were assembled out of the presented static and intensified fed-batch fermentations:

• Full factorial DoE: the fully characterized design space, used as a reference (N = 27)
• Fractional factorial DoE: the center point and the eight corners of the design space (N = 9)
• Fractional factorial DoE: the center point and four corners of the design space (N = 5)
• Fractional factorial DoE: the center point and two corners of the design space (N = 3)
• Complete iDoE: all iDoE cultivations, covering the entire design space (N = 9)
• Fractional iDoEs: one iDoE cultivation per induction level (N = 3, three different assemblies)

2.3. Hybrid Model Development

2.3.1. Model Building

For initial model training, the different data sets were considered. To deal with the small initial data sets, avoid loss of information, and provide a more robust basis for the digital twin simulations, for each practically performed experiment, two additional in silico experiments were generated, i.e., each performed experiment was available in triplicate. For these in silico experiments, an appropriate level of analytical error was considered as random noise for the biomass (up to 5%) and the soluble product titer (up to 10%). As model inputs, the cultivation temperature (°C), the accumulated feed (L), and the accumulated inducer (kg) were chosen to estimate the two response variables: the biomass (g L⁻¹) and the space-time yield (g L⁻¹ h⁻¹). Prior to model building, the input variables were standardized using the z-score. To predict the response variables, a serial hybrid model structure was implemented. The data-driven model, an ANN, embedded in the hybrid model, and applying a Levenberg–Marquardt regularization algorithm, was chosen to estimate the specific growth rate μ and the soluble product formation rate v_p/x as propagated predictions for the mechanistic part. The ANN consisted of three layers. The nodes of the hidden layer used hyperbolic tangent transfer functions, while the output layer used linear transfer functions. The values derived from the ANN were subsequently used in the mechanistic model, as shown in Equations (1) and (2), where X is the biomass concentration (g L⁻¹), P is the soluble product titer (g L⁻¹), I_y/n is the inducer switch (zero for no induction or one for induction), and D is the dilution rate (h⁻¹). Herein, D is used as the comprehensive term to describe the ratio between the flow of all volume additions into the reactor (L h⁻¹), i.e., substrate feed, inductor feed and base, and the overall reactor volume (L), which comprises the initial volume and all the added volumes. Consequently, in Equation (3), the space-time yield (STY) was calculated with the soluble product titer (g L⁻¹) divided by the current utilization time of the bioreactor (h). This Bioreactor Utilization Time comprised the duration of the sterilization in place, inoculum, batch, harvest, cleaning, and the respective feed time.

$$\frac{\mathrm{d}X}{\mathrm{dt}}=\mu ·X-\mathrm{D}·X$$

(1)

$$\frac{\mathrm{dP}}{\mathrm{dt}}=v_{p/x}·X·{\mathrm{I}}_{y/n}-\mathrm{D}·\mathrm{P}$$

(2)

$$STY=\frac{\mathrm{P}}{Bioreactor Utilization Time}$$

(3)

2.3.2. Model Validation

For validation of the model performance, leave-one-batch-out cross-validation was performed, i.e., the initial model was built on all but one experiment, and the parameters were optimized by applying them to the experiment left out. Once no further improvement was observed, the model training stopped. To find the optimal setting to fit the experimental data, the number of neurons and hidden layers were varied. While the number of neurons was individually adapted for each data set, a single hidden layer delivered the best performance in all cases with respect to the normalized root mean square error (NRMSE) in Equation (4), where y is the analytical value, ŷ is the estimated counterpart for each sampling point (t), ȳ is the mean of the analytical values, and N the total number of observations.

$$\mathrm{NRMSE} [\%]=\frac{\sqrt{\frac{1}{\mathrm{N}}·{\displaystyle \sum }{(y_{\left(\mathrm{t}\right)}-{\hat{y}}_{\left(\mathrm{t}\right)})}^2} }{\overline{y}}·100$$

(4)

2.3.3. Model Averaging

To assess the risk of model misprediction, averaging of the individual models was performed. This averaging of the estimations from multiple models represents a robust way to deal with model uncertainties. This approach allows selecting a single model from each of the cross-validations. Depending on the initial data set, the averaged hybrid models consisted of three to five individual models. To validate this averaged model performance and its uncertainty, the NRMSE was taken into account, along with its standard deviation (SD) (Equation (5)) and the prediction interval (PI) (Equation (6)), where ŷ_average is the estimation of the averaged model, ŷ_model is the estimation of the respective model, i the index of these models, and n is the number of observations for each time point.

$${\mathrm{SD}}_{\left(\mathrm{t}\right)}=\sqrt{\frac{1}{n-1}·{\displaystyle \sum }{({\hat{y}}_{\mathrm{average}\left(\mathrm{t}\right)}-{\hat{y}}_{\mathrm{model}{\left(i\right)}_{\left(\mathrm{t}\right)}})}^2}$$

(5)

$${\mathrm{PI}}_{\left(\mathrm{t}\right)}={\hat{y}}_{\mathrm{average}}\pm {\mathrm{SD}}_{\left(\mathrm{t}\right)}$$

(6)

Subsequently, the final averaged hybrid models were transferred to a digital twin environment.

2.4. Digital Twin Application

The developed hybrid models were implemented as digital twins to simulate all experiments in the given design space. Therefore, the accumulated feed, the inducer, and the inducer switch were simulated according to the feeding strategy and process time of the individual constant CPP levels, according to the desired design space boundaries. Once the simulations were performed by the digital twin, a lookup table could be used to individually evaluate the digital twin simulations. This lookup table provides the options for investigating the simulations, i.e., find the minimum or maximum values for the response variables and their respective associated CPP combination along with the process time duration. For this case study, the lookup table was used to find the optima (maximum value) for the space-time yield in all simulated experiments, i.e., recommending the CPPs to obtain this simulated value. To validate the derived recommendation of the digital twin, a laboratory experiment with the respective settings was performed. The new experiment was then added to the previous data set and the hybrid model was re-trained including the new setup and its findings. This model-based DoE for optimizing the space-time yield was repeated until the digital twin identified the best CPP combination and no new CPP combination was recommended. The entire workflow of the model-based DoE is presented in Figure 1. This workflow was carried out for all of the different initial data sets presented before, to evaluate the possible minimum number of required experiments for each case.

The hybrid model development, digital twin simulation, and model-based DoE were accomplished in the Novasign GmbH (Vienna, Austria) hybrid modeling toolbox.

3. Results

3.1. Analytical Space-Time Yield Maxima in the Design Space

To confirm the simulated values and correctness of the CPP recommendation by the digital twin, the space-time yield of each CPP combination was investigated. The analytical maximum space-time yield of each cultivation is presented as a response surface in Figure 2. For simpler visualization, the results are separated into the three levels of induction strength.

The graphical investigation of the analytical space-time yield of each CPP combination in Figure 2 reveals the local and global optima in the design space. While at induction level I = 0.2, the local maximum was found at 0.0726 g L⁻¹ h⁻¹ (µ = 0.10 h⁻¹ and T = 34 °C), and the induction level I = 0.5 contained the global maximum at the center point (µ = 0.15 h⁻¹, T = 34 °C, and I = 0.5) with 0.0997 g L⁻¹ h⁻¹. The local maximum at induction level I = 0.9 resulted in 0.0915 g L⁻¹ h⁻¹ (µ = 0.10 h⁻¹ and T = 34 °C). This visualization demonstrates that a cultivation temperature of 34 °C seems to be highly favorable for product formation, along with a trend towards slower specific growth rates.

3.2. Initial Training Data for the Model-Based DoE

The objective for this model-based DoE for parameter optimization was to quickly identify the best CPP combination for the highest space-time yield in the design space. To determine the minimum number of required experiments to develop meaningful hybrid models, and applied as digital twins recommending the next experiments, different initial data sets were utilized (Section 2.2 Data sets). These comprised either static or intensified cultivations, as presented in Figure 3.

As presented in Figure 2 and Table A1, the best CPP combination in the design space to maximize the space-time yield was obtained at the center point. However, there was also a local maximum with a high space-time yield at the highest induction level, which is assumed to be challenging not to become trapped in. For the design space investigation and determination of this CPP combination, different approaches can be consulted, as presented in Figure 3. First, experiments at each CPP combination were performed, characterizing the entire space without comprehensive process modeling (Figure 3A). Using this approach, the optimum in the design space was found, but this was paired with a high experimental effort and therefore time and costs. This experimental effort can be reduced by selecting a fractional factorial design and process modeling, i.e., only certain CPP combinations are performed. For this comparison, three fractional factorial designs were performed with the center point and the corners of the design space, either using nine (Figure 3B), five (Figure 3C), or only three initial experiments to build the hybrid model (Figure 3D). Since the iDoE concept proved to be suitable for accelerating the process characterization, this approach was additionally considered. Therefore, a complete set of iDoE experiments (Figure 3E) and three fractional iDoE approaches (Figure 3F–H) were used. The initial experiments of these last seven approaches were used in combination with process modeling to find the optimal CPP combination for obtaining the highest space-time yield as fast as possible, and using the workflow presented in Figure 1.

3.3. Digital Twin Simulations of the Model-Based DoE

Out of all the presented initial data sets for the model-based DoE parameter optimization, the fractional factorial DoE with five initial static cultivations performed best, i.e., the fewest total experiments were needed by the digital twin to identify the CPP optimum for the space-time yield. A graphical presentation of this model-based DoE is presented in Figure 4. The step-by-step progression of the recommended experiments in the design space along with the simulated values compared to the analytical values for each re-trained digital twin are shown.

The model-based DoE quickly recommended the best CPP combination to obtain the highest space-time yield (Figure 4A). The correct induction level was already found after implementing the gained process knowledge from the first recommended experiment and the correct cultivation temperature after the second re-training of the digital twin. Even though the specific growth rate was the most difficult to properly assert, after two additional cultivations the optimum in the design space was found, identifying the center point CPPs as the optimum process conditions, which were already present in the initial training data. This resulted in nine performed experiments instead of twenty-seven, highlighting the advantages of knowledge-based bioprocess development. However, with this small initial data set, the simulated biomass of the first recommended experiment (Figure 4B) almost matched the analytical results, and the space-time yield was highly overestimated. Likewise, high overestimations were observed for the second (Figure 4C) and the third recommendation (Figure 4D). By adding these new recommended experiments to the initial data set, the resulting retrained hybrid model iteratively gained knowledge about the process for the next recommendation. Already, after only these three re-trainings, the fourth simulation almost converged on the analytical values (Figure 4E). The digital twin gained precision and certainty at the fifth and final recommendation (Figure 4F). Since this recommended experiment had already been performed, the model-based DoE stopped, i.e., the best CPP combination was identified, and the biomass and space-time yield of the process were accurately simulated.

With five initial static experiments, the digital twin simulated the biomass concentration with an appropriate accuracy from the beginning, but highly overestimated the experimental values of the space-time yield. By consecutively adding the four recommended experiments, and extending the initial data set, precise simulations were obtained. This fast convergence of the simulated space-time yield on the analytical values, along with the SD, is displayed in

Table 1. Progression of the model-based DoE until the optimum was found using five initial experiments.

Digital Twin Conversion	CPP I (µ)	CPP II (T)	CPP III (I)	Analytical Maximum (g L−1 h−1)	Simulated Maximum (g L−1 h−1)
1st recommendation	0.10	30	0.2	0.0185 (±0.0006)	0.1605 (±0.0185)
2nd recommendation	0.10	30	0.5	0.0696 (±0.0029)	0.1220 (±0.0058)
3rd recommendation	0.10	34	0.5	0.0820 (±0.0018)	0.1303 (±0.0040)
4th recommendation	0.20	34	0.5	0.0755 (±0.0032)	0.0848 (±0.0079)
5th recommendation	0.15	34	0.5	0.0976 (±0.0026)	0.0955 (±0.0186)

.

As seen in Table 1, the obtained recommendations of the digital twin, at which CPP combination the next experiment should be performed, converged at the best CPP combination in the design space after five recommended experiments, i.e., no new recommendation was derived. Moreover, a steep learning curve of the hybrid model was observed when the new experiments were added for re-training the digital twin. While the simulated space-time yield of the first recommended experiment, derived from the information gained from the initial five experiments, resulted in an 8.68-fold deviation compared to the analytical value, this factor quickly decreased after including the respective validation experiments in the training data and subsequent re-training of the hybrid model. For example, the simulation of the second recommendation already displayed a decreased deviation of only 1.75-fold compared to the analytical value, while the third simulation was down to a 1.59-fold deviation. The fourth simulation only displayed a deviation from the analytical value by 1.12-fold, and the final simulation of the fifth recommendation was highly precise, displaying a simulated maximum of 0.98-fold the analytical value. This demonstrates that with only five initial experiments to start the model-based DoE, the hybrid model promptly gained process knowledge and its digital twin was able to provide the best CPP combination to obtain the highest space-time yield.

A complete quantitative and qualitative performance comparison of all the presented approaches (Figure 3) is given in

Table 2. Performance summary of the model-based DoE approaches. Capital letters in brackets represent the DoE conditions from Figure 3.

Initial Data Set	Initial Experiments	Recommended Experiments	Total Experiments	Optimum Found
full factorial DoE (A)	27	0	27	yes
fractional factorial DoE (B)	9	2	11	yes
fractional factorial DoE (C)	5	4	9	yes
fractional factorial DoE (D)	3	7	10	yes
complete iDoE (E)	9	2	11	no
fractional iDoEs (F–H)	3	1–4	4–7	no

. Herein, the three different fractional iDoE approaches are summarized.

Table 2 presents the quantitative effort and qualitative performance of each initial data set. With respect to the total required time for each presented approach, only the duration of the practical experiments (including pre- and post-processing) was taken into account for the evaluation, since using our setup, an entire experiment takes approximately one working week. However, the computational time for the hybrid model training and subsequent re-training can be neglected, since it ranges between half an hour and three hours, and depending highly on the performance of the utilized computer. While the number of required experiments remains unchanged, the needed experimental time can further be reduced by the utilization of multiple bioreactors or parallel bioreactor systems.

Since in the full factorial DoE all experiments are performed, comprehensive process modeling is redundant to find the best CPP combination for the highest space-time yield in the design space. By using this approach, the optimum was found, but paired with the highest experimental effort. For the other initial data sets, model-based DoE was applied to reduce the required number of experiments. For the fractional factorial DoEs, the number of recommended experiments increased until the optimum was found when decreasing the number of initial experiments. Herein, the fastest approach was the fractional factorial DoE with five initial experiments and four validation experiments required, i.e., only 9/27 experiments had to be performed. Moreover, in all cases, the optimum was identified. However, in this case study, the utilization of initial iDoE cultivations for model-based DoE did not lead to the identification of the best CPP combination in the design space. Regardless of selecting the entire iDoE data set or varying fractional iDoEs, the model-based DoE ended up at different locations in the design space than the optimum CPP combination. Herein, the final recommendations by the digital twin were all located at µ = 0.10, I = 0.9 and either 30 °C or 34 °C, indicating a model bias towards slow specific growth rates and temperatures, apart from 37 °C, where a high value or local maximum of the space-time yield is located. A more detailed progression of the recommended experiments in the design space for each of the other six model-based DoEs is shown in Appendix A.2, Figure A1 (excluding the full factorial DoE).

4. Discussion

The prominent emerging concept of model-based DoE for parameter optimization is an interesting, and yet not completely explored, topic. To accelerate this identification of optimum process conditions is of great interest for manufacturers, to reduce bioprocess development timelines. Typically, by performing all experiments in a design space, these optimum process conditions can be found, but with high experimental effort. Herein, we challenged this approach by investigating the minimum requirements for such a model-based DoE workflow (Figure 1) to rapidly and properly discover the best CPP combinations in a design space (Figure 2), utilizing varying numbers of initial experiments (Figure 3). We demonstrated with our case study that the fastest approach to identifying the best process conditions for the highest space-time yield was an initial fractional factorial DoE with five static cultivations and four consecutively performed recommendations from the digital twin (Figure 4 and Table 1). In case scientists are limited to certain time slots for further experiments, the best x-recommendations from the digital twin can be used in the next campaign to obtain the maximum learning, according to the experimental possibilities. Interestingly, all model-based DoEs using initial iDoE cultivations failed to find the global maximum in the design space (Table 2), and recommending an incorrect optimal CPP combination after a few iterations (Figure A1). It has already been demonstrated that iDoE is favorable for accelerating process characterization. Here, a trade-off between decreased experimental effort and reduced process information can be accepted. This consideration must be handled with care when iDoE is used for process optimization, i.e., an increased model uncertainty due to decreased process information may result in divergent optima, as was the case herein. To the best of our knowledge, this iDoE concept has not been well investigated and little literature is available as a reference for microbial, and even less for mammalian, systems. Additionally, several degrees of freedom are introduced by iDoE, e.g., the number and duration of the intra-experimental CPP shifts, as well as how these should be performed. Therefore, before reliably applying iDoE for such model-based DoE approaches, more research should be performed on this subject.

Furthermore, the identification of optimum process conditions for the response to be optimized in design spaces with a higher dimensionality, as in our case study (>3 CPPs), could lead to new challenges, e.g., the occurrence of various local optima, which complicate the accurate identification of the global optimum. The robustness and applicability of digital twins to also perform reliably when confronted with this higher complexity must be further investigated. Moreover, our findings demonstrate that bioprocess modeling is not an all-in-one solution, eliminating all current limitations and obstacles; showing that it is important to consider many potentially influencing factors [39].

For instance, it is advisable for the initially used data set to introduce every CPP level to the hybrid model training, i.e., the minimal fractional factorial DoE with three initial cultivations in our case study. Otherwise, the hybrid model will be biased towards the included CPP levels in the training data and potentially would not recommend the missing setting, since the ability to correctly determine these causal relationships is lost. This bias towards CPP levels should be considered when initially investigating a design space, for which no prior process knowledge about process behavior and the responses is available, i.e., the CPPs and the appropriate levels should be well-considered and not too far apart. Hereby, the accidental generation of independent data sets, becoming missing and getting trapped in local optima, can be avoided at the start. Since this case study mainly focused on the practical application of digital twins, more detailed theoretical analysis should be performed in future studies. However, it might be desirable to re-define the CPP levels and look for new, more beneficial settings in the design space, e.g., with smaller intervals of the cultivation temperatures simulated by the digital twin. However, if a digital twin recommends an experiment next to the identified optimum CPP combination, but with a 0.5 °C decreased cultivation temperature and an increased space-time yield by 0.3%, the execution of this cultivation should be critically questioned. Additionally, for some CPPs, such simulated intervals are not always practically feasible, e.g., steps of 0.5 °C for the cultivation temperature, which might be adjustable but difficult to precisely control. This exemplary scenario demonstrates that such approaches must still be guided by human knowledge, rather than completely trusting an algorithm.

Herein, it has been demonstrated that such digital solutions enable a new knowledge-based perspective on bioprocess development and optimization, and to get more out of the available data. Even though several of these advantages have already been recognized and discussed, much more research will be required to fully implement and exploit the potential of digitalization in the biopharmaceutical industry [40]. For instance, an up-and-coming area for future application of model-based DoE, hybrid modeling, and digital twins is found in simulating new CPP combinations out of the design space, i.e., extrapolation where appropriate. However, this again poses new challenges, such as how to validate this new setting outside the design space, e.g., an additional smaller design space with the new CPP combination as the center point could potentially be performed. Besides the validation issue, the stability of the digital twin and the underlying hybrid model structure must also be ensured. Additionally, if the mechanistic relationships are known and understood, such digital twins could be used as a basis to initially simulate new bioprocesses with similar product properties without prior experiments, e.g., product size and cytotoxicity supporting platform approaches.

5. Conclusions

In silico design space exploration using a digital bioprocess twin increases the process understanding for QbD; the impact of the CPPs on the variables of interest can rapidly be investigated. The presented workflow enabled us to quickly find process optima in a design space despite using only a small initial experimental setup. Moreover, this approach to decreasing the number of required practical experiments for process optimization becomes even more advantageous for larger design spaces. Even though, herein the dimensionality and complexity increase, which will lead to new challenges, model-based DoE has the potential to significantly lower the experimental effort; saving money, time, raw materials, and other propositions of economic value for later stages.