Synthesis Target Structures for Alkaline Earth Oxide Clusters

Abstract

Knowing the possible structures of individual clusters in nanostructured materials is an important first step in their design. With previous structure prediction data for BaO nanoclusters as a basis, data mining techniques were used to investigate candidate structures for magnesium oxide, calcium oxide and strontium oxide clusters. The lowest-energy structures and analysis of some of their structural properties are presented here. Clusters that are predicted to be ideal targets for synthesis, based on being both the only thermally accessible minimum for their size, and a size that is thermally accessible with respect to neighbouring sizes, include global minima for: sizes $n=9,15,16,18$ and 24 for (MgO)${}_n$; sizes $n=8,9,12,16,18$ and 24 for (CaO)${}_n$; the greatest number of sizes of (SrO)${}_n$ clusters ($n=8,9,10,12,13,15,16,18$ and 24); and for (BaO)${}_n$ sizes of $n=8,10$ and 16.

1. Introduction

Structure determination of materials plays an important role in materials design because the properties of materials are inherently linked to their atomic and electronic structure. Nanoclusters in particular are of special interest as they offer a means of creating a large variety of structurally different materials without any change in stoichiometry, enabling the fine-tuning of properties for common materials such as metal oxides. However, size-selective fabrication and experimental structure determination of nanoclusters is a complex, expensive and time-intensive endeavour. Therefore, it is advantageous to first use computational structure prediction techniques that can then help guide experiments, for example, by highlighting what size clusters would make promising targets for fabrication.

Unfortunately, even relatively efficient algorithms for structure prediction of clusters require exploration of large regions of conformational space; in our previous paper [1], we chose to use an evolutionary algorithm (EA) [2] in combination with a set of classical interatomic potentials (IPs) followed by refinement of results with density functional theory (DFT), for (BaO)${}_n$ clusters with $n\le 18$ and $n=24$. For each cluster size, the top 20 structures were uploaded into the freely available HIVE online database [3] of published atomic structures of nanoclusters. One of the aims of the HIVE database is to help the scientific community search, discover and disseminate the structures and properties of nanoclusters. Using the assumption that the potential energy surfaces (PES) of barium oxide clusters resemble those of clusters of the other alkaline earth oxides and that only the ranking of local minima (LM) changes instead of new low-energy structural motifs appearing, the aim is to reuse the LM structures gained from the EA runs for BaO. This should allow for a very efficient way of finding minima, and ideally the global minima (GM), for magnesium oxide, calcium oxide and strontium oxide clusters of the same sizes. Similar data-mining techniques have previously been employed for both bulk crystal structures [4,5] and by us for other inorganic nanoclusters [6]. For a more general review of how databases can assist with the prediction of chemical compounds, we refer the reader to Ref. [6].

In order to give these results further context in relation to experiments, we will compare with previous mass spectrometry results for (MgO)${}_n^{+}$ and (CaO)${}_n^{+}$ [7,8,9], and will be able to evaluate whether the general trends in structural motifs found here agree with experiments. Comparison with previous computational results for magnesium oxide and calcium oxide clusters [10,11,12,13,14,15,16,17,18,19], as well as a comparison of theory with infrared data [20,21], will also be discussed below. A comparison with results for alkali halides is also offered.

2. Methods

2.1. Data Mining and Interatomic Potentials

In this investigation, our initial set of configurations are based upon the atomic structures previously reported for (BaO)${}_n$ [1]. These structures were themselves generated using an EA [2] to search for all low-lying local minima on the energy landscape, defined by IPs originally fitted to reproduce the structure and properties of bulk BaO [22] for each composition (value of n). The lower energy minima structures were then further optimised using DFT. Further details of the method used to predict and the analysis of the DFT optimised structures for (BaO)${}_n$ can be found in Ref. [1]. The top 20 IP-ranked structures were then used to data mine structures and rankings for magnesium oxide, calcium oxide and strontium oxide equivalent structures.

It is important that the (BaO)${}_n$ configurations are appropriately rescaled before standard local optimisation routines are employed. Otherwise, there is a greater chance that the connectivity of a configuration may change during the relaxation and, for example, several data-mined (BaO)${}_n$ LM will generate just one (MgO)${}_n$ LM. This process is automated in the data mining module implemented in our in-house code, the Knowledge-Led Master Code (KLMC) [23]. XYZ files of (BaO)${}_n$ clusters are used as input into KLMC, which then rescaled each geometry based on relative atomic radii, generated input files for and then initiated DFT calculations as implemented within an external code, and, once the DFT calculations were completed, KLMC extracted key data from the DFT outputs including determination of rankings of LM based on DFT energies.

Unless an exhaustive search is conducted, there is always an uncertainty to whether the lowest energy structures have been found. As the energy landscape, as well as the number of LM, increases rapidly with the number of atoms ($2n$), it becomes impractical to perform exhaustive searches and the certainty that the tentative GM is the true GM will typically decrease with increasing n. In our approach, the true GM for a particular composition may not be found if we are not careful with our choice of configurations that we data-mine from. Apart from changes in bond lengths and bond angles, we have initially assumed that the alkaline earth oxides can adopt the same set of LM configurations and that we have previously found the lowest energy LM for (BaO)${}_n$. The ranking, from lowest to highest energy, of the LM for each compound is not, however, expected to be the same, and may also change when the energy is calculated using DFT rather than IPs. Thus, in our quest to find the lowest three DFT-ranked LM for each composition, we data-mined from the best twenty barium oxide IP-ranked LM. As a check that using only the top twenty was sufficient, we expanded our data mined set to 58 different initial configurations for one of the largest sized systems, $n=17$, which for barium oxide also had a large density of LM near its GM. Furthermore, as the largest disparity is expected to be found when comparing (MgO)${}_n$ and (BaO)${}_n$ clusters (since they have the largest ratio of cationic radii), we also checked that the GM and LM previously reported for (MgO)${}_n$ [11,12,13,14,15,16,17,20,21,24,25] were not missing from our results. Four of these previous studies [12,16,17,21] used genetic algorithms to predict their tentative GM. Success in both our checks provided greater certainty that our approach has found the GM for (XO)${}_n$, where X = Mg, Ca, Sr, Ba and $n=$ 4–18 and 24.

2.2. Predicted Structures—Density Functional Theory

All energy calculations and local optimisations, as well as dipole determinations where they were of particular interest, were performed using the FHI-aims [26] electronic structure code. The choice of functional may change the resulting ranking of LM; in our study, we have chosen the PBEsol GGA functional [27,28,29], which is used frequently for inorganic materials. It was employed in combination with a tight basis set including first-tier basis functions for metals and first- and second-tier functions for oxygen; these tiers are defined within the FHI-aims software and result in the accuracy of the total energy of these species to be within 10 meV/atom [26].

3. Results and Discussion

PBEsol GM of (MgO)${}_n$, (CaO)${}_n$ and (SrO)${}_n$ nanoclusters are presented below. They are compared to the PBEsol (BaO)${}_n$ structures we reported in our previous paper [1].

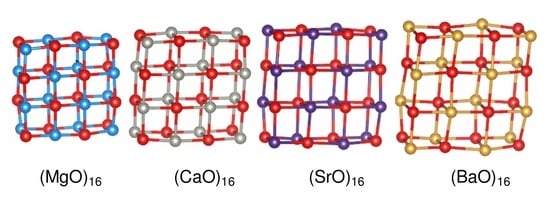
3.1. Structures of (MO)${}_n$ Clusters ($n\le 18$ and 24)

Table 1. Lowest energy local minima (LM) for (MO)${}_n$, $n=4$ to 12. The first, second, third and fourth character in the labels indicate the rank found for when M = Mg, Ca, Sr, and Ba, respectively, where A implies the global minimum, B the 2nd lowest LM, C the 3rd and X implies that the LM is outside of the top three. For each LM, only one representative configuration is shown for all compounds, with colour representations Mg, Ca, Sr, Ba and . A stick is shown if an oxygen anion is within the first coordination shell of a cation (typically less than 2.5 Å  for Mg and 2.85 Å  for Ba).

n	Structures/Labels
$\mathbf{4}$
	AAAA
(MgO)${}_n$ $E_{\mathrm{rel}}$ / meV/MgO	0.0
(CaO)${}_n$ $E_{\mathrm{rel}}$ / meV/CaO	0.0
(SrO)${}_n$ $E_{\mathrm{rel}}$ / meV/SrO	0.0
BaO $E_{\mathrm{rel}}$ / meV/BaO	0.0
$\mathbf{5}$
	AAXX	BCBX	CBAC	XXCB	XXXA
(MgO)${}_n$ $E_{\mathrm{rel}}$ / meV/MgO	0.0	121.3	132.9	N/A	N/A
(CaO)${}_n$ $E_{\mathrm{rel}}$ / meV/CaO	0.0	19.4	2.1	N/A	N/A
(SrO)${}_n$ $E_{\mathrm{rel}}$ / meV/SrO	N/A	11.5	0.0	13	N/A
(BaO)${}_n$ $E_{\mathrm{rel}}$ / meV/BaO	N/A	N/A	10.4	2.1	0.0
$\mathbf{6}$
	ABBB	BAAA	CCXX	XXCX	XXXC
(MgO)${}_n$$E_{\mathrm{rel}}$ / meV/MgO	0.0	44.5	400.5	N/A	527.4
(CaO)${}_n$$E_{\mathrm{rel}}$ / meV/CaO	62.9	0.0	338.8	N/A	443.7
(SrO)${}_n$$E_{\mathrm{rel}}$ / meV/SrO	58.1	0.0	N/A	410.2	N/A
(BaO)${}_n$$E_{\mathrm{rel}}$ / meV/BaO	22.4	0.0	N/A	N/A	111.1
$\mathbf{7}$
	AAAB	BXXX	CXXX	XBCC	XCXX	XXBA
(MgO)${}_n$$E_{\mathrm{rel}}$ / meV/MgO	0.0	72.1	73.6	161.0	N/A	N/A
(CaO)${}_n$$E_{\mathrm{rel}}$ / meV/CaO	0.0	N/A	147.5	48.7	51.1	N/A
(SrO)${}_n$$E_{\mathrm{rel}}$ / meV/SrO	0.0	N/A	149.8	25.0	N/A	9.2
(BaO)${}_n$$E_{\mathrm{rel}}$ / meV/BaO	1.1	N/A	117.3	16.1	N/A	N/A
$\mathbf{8}$
	AXXC	BAAA	CXXX	XBBB	XCCX
(MgO)${}_n$$E_{\mathrm{rel}}$ / meV/MgO	0.0	6.0	60.2	N/A	313.1
(CaO)${}_n$$E_{\mathrm{rel}}$ / meV/CaO	113.7	0.0	216.8	71.2	78.1
(SrO)${}_n$$E_{\mathrm{rel}}$ / meV/SrO	111.7	0.0	221.2	64.9	72.9
(BaO)${}_n$$E_{\mathrm{rel}}$ / meV/BaO	73.5	0.0	169.9	35.5	206.1
$\mathbf{9}$
	ABBX	BCXX	CXXX	XAAA	XXCB	XXXC
(MgO)${}_n$$E_{\mathrm{rel}}$ / meV/MgO	0.0	91.4	241.5	N/A	342.2	303.5
(CaO)${}_n$$E_{\mathrm{rel}}$ / meV/CaO	49.3	161.3	259.2	0.0	430.5	284.4
(SrO)${}_n$$E_{\mathrm{rel}}$ / meV/SrO	47.7	N/A	223.8	0.0	127.0	137.3
(BaO)${}_n$$E_{\mathrm{rel}}$ / meV/BaO	22.4	54.9	128.1	0.0	8.5	18.4
$\mathbf{10}$
	AAAA	BBXX	CXXX	XCBB	XXCX	XXXC
(MgO)${}_n$$E_{\mathrm{rel}}$ / meV/MgO	0.0	18.8	34.5	90.8	67.9	43.9
(CaO)${}_n$$E_{\mathrm{rel}}$ / meV/CaO	0.0	53.1	172.9	56.6	82.2	127.7
(SrO)${}_n$$E_{\mathrm{rel}}$ / meV/SrO	0.0	102.9	173.3	50.2	96.5	113.9
(BaO)${}_n$$E_{\mathrm{rel}}$ / meV/BaO	0.0	69.9	127.8	39.3	103.9	58.5
$\mathbf{11}$
	AXXX	BBBA	CXXX	XAAC	XCCX	XXXB
(MgO)${}_n$$E_{\mathrm{rel}}$ / meV/MgO	0.0	1.1	2.4	N/A	106.8	7.9
(CaO)${}_n$$E_{\mathrm{rel}}$ / meV/CaO	N/A	6.7	128.9	0.0	28.5	45.7
(SrO)${}_n$$E_{\mathrm{rel}}$ / meV/SrO	N/A	3.2	127.0	0.0	22.9	35.2
(BaO)${}_n$$E_{\mathrm{rel}}$ / meV/BaO	N/A	0.0	92.1	13.7	N/A	12.0
$\mathbf{12}$
	ABBC	BAAA	CXXX	DCCX	XXXB
(MgO)${}_n$$E_{\mathrm{rel}}$ / meV/MgO	0.0	30.5	49.8	56.1	N/A
(CaO)${}_n$$E_{\mathrm{rel}}$ / meV/CaO	54.7	0.0	203.2	70.3	N/A
(SrO)${}_n$$E_{\mathrm{rel}}$ / meV/SrO	52.2	0.0	189.5	64.1	N/A
(BaO)${}_n$$E_{\mathrm{rel}}$ / meV/BaO	29.0	0.0	109.9	N/A	3.94

shows structures and energies for PBEsol LM, which are found to be ranked within the top 3 lowest energy LM for at least one of the clusters (alkaline earth oxide, M = Mg, Ca, Sr and Ba and sizes $n=4$ to 12); the energies (per MO unit) are relative to the corresponding GM. These structures are labelled with letters to indicate their energy ranking for (MgO)${}_n$, (CaO)${}_n$, (SrO)${}_n$ and (BaO)${}_n$ (in that order), A being the GM, B the second-lowest, etc.; for example, a structure which is the GM for all four compounds will be labelled AAAA and one which is the GM for (CaO)${}_n$ and third-lowest energy for the other three compounds is labeled CACC. If a structure is not among the three most stable ones for a given oxide, the designated letter will be X.

For sizes $n=3k$, it is possible to construct cuboid clusters composed of face sharing $n=4$ cuboid units and hexagonal barrel shaped clusters composed of k parallel $n=3$ hexagonal rings. Comparing the configurations found for GM, the most striking observation is that calcium oxide, strontium oxide and barium oxide prefer cuboid cuts from the NaCl-rocksalt structure for sizes $n=3k$ , while the barrel is the predicted GM configuration for magnesium oxide.

Considering the top three structures for each size, both the rocksalt cuts (cuboid and non-cuboid clusters composed of face-sharing $n=4$ cuboid building blocks ) and barrel motifs appear for all four oxides. One structural motif that is seen more frequently for compounds like zinc oxide is the so called bubble; atoms are all three coordinated and, typically, there are six tetragonal and $n-4$ hexagonal faces. Although the GM for sizes 4 to 7 (the cube-, drum- and clam-like configurations, respectively) can be classified as bubbles, the number of bubble configurations that are ranked within the top three typically decreases with increasing cation size in the alkali earth oxides as these become less stable with respect to the GM with increasing cluster size. We identify configurations 4-AAAA, 5-CBAC, 7-AAAB, 8-AXXC, 9-BCXX, 10-CXXX, 11-CXXX and 12-CXXX (see also 16-CXXX) to be bubble LM for (MgO)${}_n$. We can already identify from the labels that far less bubble LM are in the three lowest energy configurations for (CaO)${}_n$ (4 total), (SrO)${}_n$ (only 3) and (BaO)${}_n$ (4 total); all these configurations will be very small clusters where there are smaller numbers of total available configurations.

Comparing the nanoclusters of the four alkaline earth oxides, magnesium oxide is more likely to adopt the more open structures composed of the lower three coordinated sites than the six-coordinated sites found within the bulk phase. The three lowest energy configurations for (BaO)${}_8$, on the other hand, nicely demonstrate this typical trend: the order of stability increases with an increase in the total number of bonds (or average coordination number) and, simultaneously, the order of stability increases with an increase in density (decrease in openness, or number of hexagonal faces that become an edge-sharing pair of tetragonal faces). Configuration 8-BAAA is a (counting atoms) $2\times 2\times 4$ cuboid bulk cut and can be considered as two parallel atomic layers, just one bond length apart, of three tetragonal rings. Configuration 8-XBBB has one less bond in each of the two $2\times 4$ layers, and represents structures composed of two parallel atomic layers, still only one bond length apart, that do not only contain tetragons (in this example, each of the two sequences of three tetragonal faces become one tetragonal and one hexagonal face). Configuration 8-AXXC has a further bond reduction between parallel layers; the original 8-BAAA configuration has four sides of three tetragonal faces, each becoming one tetragonal and one hexagonal face, and in doing so creating a larger void in the centre of the cluster (than the combined volume within the (BaO)${}_4$ cuboid and (BaO)${}_6$ drum, as in configuration 8-XBBB). Only for (MgO)${}_n$, the compound with the smallest cation, is the bubble structure the GM and the intermediate 8-XBBB configuration found for (BaO)${}_8$ is unstable for MgO, indicating that perhaps there are more stable LM overall for larger-cation clusters.

For $n=13$, all oxides’ GMs except barium oxide’s adopt a bulk cut structure—more specifically, all adopt a $3\times 3\times 3$ bulk cut with one corner atom removed but (MgO)${}_{13}$ is different, in that it adopts the one with M in the centre, while (CaO)${}_{13}$ and (SrO)${}_{13}$ show a preference for O in the centre. In the case of (BaO)${}_{13}$, if the initial starting DFT geometry resembled the rocksalt cut similar to that shown for (CaO)${}_{13}$, then the resulting relaxed configuration would be the GM amorphous structure shown in

Table 2. Lowest energy local minima (LM) for (MO)${}_n$, $n=13$ to 18 and 24. The first, second, third and fourth character in the labels indicate the rank found for when M = Mg, Ca, Sr, and Ba, respectively, where A implies the global minimum, B the 2nd lowest LM, C the 3rd and X implies that the LM is outside of the top three. For each LM, only one representative configuration is shown for all compounds, with colour representations Mg, Ca, Sr, Ba and . A stick is shown if an oxygen anion is within the first coordination shell of a cation (typically less than 2.5 Å  for Mg and 2.85 Å  for Ba). In the case of $n=24$, the letters in brackets denote PBESol0 results for (BaO)${}_{24}$.

n	Structures/Labels
13
	ABXX	BAAX	CCXX	XXBX	XXXA	XXXB	XXXC
(MgO)${}_n$ $E_{\mathrm{rel}}$ / meV/MgO	0.0	26.3	57.9	245.4	190.8	8.8	13.3
(CaO)${}_n$ $E_{\mathrm{rel}}$ / meV/CaO	47.4	0.0	98.0	153.2	203.2	N/A	N/A
(SrO)${}_n$ $E_{\mathrm{rel}}$ / meV/SrO	58.4	0.0	76.1	52.6	101.8	N/A	N/A
(BaO)${}_n$ $E_{\mathrm{rel}}$ / meV/BaO	73.1	N/A	56.3	N/A	0.0	N/A	N/A
14
	ABCX	BXXX	CXXX	XAAA	XCXB	XXBX	XXXC
(MgO)${}_n$ $E_{\mathrm{rel}}$ / meV/MgO	0.0	4.0	9.8	25.5	60.5	32.0	N/A
(CaO)${}_n$ $E_{\mathrm{rel}}$ / meV/CaO	13.2	58.6	N/A	0.0	42.7	N/A	45.0
(SrO)${}_n$ $E_{\mathrm{rel}}$ / meV/SrO	11.1	57.3	N/A	0.0	29.8	8.0	33.7
(BaO)${}_n$ $E_{\mathrm{rel}}$ / meV/BaO	27.5	34.0	9.1	0.0	4.4	N/A	8.9
15
		AXXX	BAAA	CCCX	XBBX	XXXB	XXXC
(MgO)${}_n$ $E_{\mathrm{rel}}$ / meV/MgO		0.0	21.5	38.4	82.4	N/A	N/A
(CaO)${}_n$ $E_{\mathrm{rel}}$ / meV/CaO		137.7	0.0	48.3	39.0	N/A	N/A
(SrO)${}_n$ $E_{\mathrm{rel}}$ / meV/SrO		120.1	0.0	45.8	26.3	N/A	N/A
(BaO)${}_n$ $E_{\mathrm{rel}}$ / meV/BaO		73.5	0.0	N/A	N/A	3.8	14.7
16
		AAAA	BCBC	CXXX	XBXX	XXCB
(MgO)${}_n$ $E_{\mathrm{rel}}$ / meV/MgO		0.0	24.1	114.3	N/A	N/A	N/A
(CaO)${}_n$ $E_{\mathrm{rel}}$ / meV/CaO		0.0	65.1	N/A	62.9	N/A	N/A
(SrO)${}_n$ $E_{\mathrm{rel}}$ / meV/SrO		0.0	62.3	N/A	N/A	78.1	N/A
(BaO)${}_n$ $E_{\mathrm{rel}}$ / meV/BaO		0.0	N/A	N/A	N/A	34.3	47.1
17
	ACXX	BAAX	CXXX	XBXX	XXBX	XXCA	XXXB	XXXC
(MgO)${}_n$ $E_{\mathrm{rel}}$ / meV/MgO	0.0	40.2	43.7	95.6	N/A	110.5	N/A	74.5
(CaO)${}_n$ $E_{\mathrm{rel}}$ / meV/CaO	18.6	0.0	47.1	12.4	56.3	49.1	N/A	117.0
(SrO)${}_n$ $E_{\mathrm{rel}}$ / meV/SrO	52.6	0.0	46.5	31.3	24.0	24.9	N/A	113.8
(BaO)${}_n$ $E_{\mathrm{rel}}$ / meV/BaO	128.8	100.0	52.0	57.7	N/A	0.0	12.0	23.4
18
		AAAX	BXXX	CBBA	XCCX	XXXB	XXXC
(MgO)${}_n$$E_{\mathrm{rel}}$ / meV/MgO		0.0	46.3	61.0	76.0	218.2	N/A
(CaO)${}_n$$E_{\mathrm{rel}}$ / meV/CaO		0.0	112.5	56.4	97.8	221.4	N/A
(SrO)${}_n$$E_{\mathrm{rel}}$ / meV/SrO		0.0	83.3	29.7	68.4	141.7	N/A
(BaO)${}_n$$E_{\mathrm{rel}}$ / meV/BaO		31.4	33.1	0.0	50.3	6.0	20.8
24
	AAAX(A)	BBBX	CXXX	XCXX	XXCX	XXXA(B)	XXXB(C)	XXXC
(MgO)${}_n$$E_{\mathrm{rel}}$ / meV/MgO	0.0	93.4	105.4	N/A	N/A	N/A	N/A	N/A
(CaO)${}_n$$E_{\mathrm{rel}}$ / meV/CaO	0.0	107.6	145.5	137.3	N/A	N/A	N/A	N/A
(SrO)${}_n$$E_{\mathrm{rel}}$ / meV/SrO	0.0	80.0	117.1	N/A	111.9	N/A	N/A	N/A
(BaO)${}_n$$E_{\mathrm{rel}}$ / meV/BaO	13.9	25.8	55.4	N/A	N/A	0.0	1.0	7.9

for (BaO)${}_{13}$ (13-XXXA). For both larger and smaller BaO clusters, however, bulk cuts are found (for $n=11$, the bulk cut cluster is ranked third). For $n=14$, all GM are bulk cuts apart from magnesium oxide where, given the $n=6$ cuboid fragment is now less stable than the $n=6$ drum, the GM is composed of two parallel atomic layers, one bond length apart, each containing one hexagonal ring (see discussion above about (BaO)${}_8$ LM). In the case of $n=15$, again all except magnesium oxide adopt the rocksalt cut structure, with (MgO)${}_{15}$ forming a long hexagonal barrel. In $n=17$ clusters, a structure that is partially composed of a 8-membered ring barrel (17-ACXX) is found to be the GM for (MgO)${}_{17}$ and also the third-lowest energy structure of the calcium oxide cluster.

Cuboid clusters are only a subset of LM configurations that resemble cuts from the rocksalt structure. Some insight can be gained by comparing the additional exposed surfaces of our non-cuboid bulk-cut clusters with those of the perfect cuboid cuts. In the latter, we only have six surfaces that are effectively finite (001) bulk-terminated surfaces. In the case of 11-XAAC and 15-XBBX, the additional face is equivalent to the (011) bulk-terminated surface while for 13-AVXX and 13-BAAX, the equivalent surfaces are (111). This leads to 3-coordinated non-corner atoms, which appear to be favoured less when larger cations are present. For $n=15$, the difference between the GM configuration for (MgO)${}_{15}$ and the other three oxides is more noticeable as the (MgO)${}_{15}$ GM is the hexagonal barrel composed of five stacked hexagonal rings, rather than a bulk cut from the rocksalt phase. The cuboid for $n=15$, composed of $2\times 3\times 5$ atoms, is the GM for (CaO)${}_{15}$, (SrO)${}_{15}$ and (BaO)${}_{15}$ and second-lowest for (MgO)${}_{15}$; the (011) terminated bulk cut 15-XBBX is only a top 3 structure for (CaO)${}_{15}$ and (SrO)${}_{15}$. For $n=16$ and, most importantly $n=18$ and $n=24$, as at these sizes it is again possible to form a barrel motif, magnesium oxide clusters also preferentially adopt a cuboid, rocksalt cut structure. The barrel is the second-lowest energy structure for (MgO)${}_{18}$ and while it is not ranked in the top 10 structures for (MgO)${}_{24}$, many of the lowest-energy structures are partially barrel-like. The case of $n=18$ is also noteworthy as there are two possible cuboid configurations composed of either $4\times 3\times 3$ or $6\times 3\times 2$ atoms. This will be discussed in more detail below.

The stability of a configuration will increase with increasing average coordination but decrease with any resulting increase in strain. A resulting dipole across the cluster can also affect the stability of that configuration, and as we will see, the degree to which each cation can polarize to screen, or counter this, will likewise influence the ranking of configurations. Of these factors, coordination number and the calculation of dipoles are straightforward to compute, so this data, along with the second-order energy differences, are now reported.

3.2. Second-Order Energies and Structural Motifs

The second-order energy differences between the GM clusters for $n=5$ to 17 are plotted below. The second-order energy difference of a cluster size n is defined as

$$\Delta E=E\left(n\right)-\frac{1}{2}(E(n+1)+E(n-1)),$$

where $E\left(n\right)$ is the energy of the lowest-energy structure of size n for a given compound. $\Delta E$ provides a measure of relative stability of cluster sizes. As $E\left(n\right)$ is the GM of a particular size n, the minima of $\Delta E$ represent local size stabilities.

These second-order energy differences are presented here as two figures, Figure 1 for magnesium oxide clusters and Figure 2 for clusters of the other three compounds, as their second-order energies were very similar. All second-order energy differences are also tabulated in

Table 3. Second-order energy differences ($\Delta E$/meV) for tentative global minima (MO)${}_n$ cluster energies of sizes n = 5–17.

$\mathit{n}$	M = Mg	M = Ca	M = Sr	M = Ba
5	196.2	242.1	220.2	178.1
6	−246.0	−227.3	−198.1	−139.0
7	105.9	131.1	116.9	73.9
8	−10.6	−58.3	−63.0	−61.0
9	−122.1	−51.5	−24.4	21.7
10	60.9	12.7	−2.3	−22.0
11	47.7	52.4	45.0	18.7
12	−113.4	−94.6	−86.8	−13.7
13	49.8	59.3	73.7	−6.5
14	42.1	13.4	−6.0	12.8
15	−45.4	−17.3	−8.2	6.8
16	−30.1	−62.8	−55.2	−29.1
17	63.9	104.1	75.3	10.3

.

The trend discussed in Section 3.1 for magnesium oxide clusters is echoed in Figure 1: the structural motif adopted by most the structures with negative second-order energies is that of the barrel ($n=6,9,12$ and 15). The $2\times 4\times 4$ cuboid rocksalt cut GM configuration of (MgO)${}_{16}$, 16-AAAA, is relatively more stable than its neighbours.

Figure 2 shows the second-order energy differences for GM nanoclusters with M = Ca, Sr, Ba. The structures for n with negative second-order energies are typically the same for all three, so only ball and stick models of the SrO configurations are shown. There are examples where the GM configuration is different for the compound with the largest cation ($n=7,11,13$ and 18) and where all three oxides differ ($n=5$ and 17). All GM configurations, however, with an even value of n or with a value of $n=9$ have a negative or close to zero second-order energy for all three compounds, which corresponds to sizes where the construction of a cuboid bulk cut is feasible. The only non-cuboid structure (intermediate between the $2\times 3\times 4$ ($n=12$) and $2\times 3\times 5$ ($n=15$) cuboids) appearing here is the $n=14$ bulk cut, with negative second-order energies for (CaO)${}_{14}$ and (SrO)${}_{14}$ only. Typically, the magnitude of the second-order energies is smallest for GM clusters of (BaO)${}_n$ and largest for (CaO)${}_n$.

For sizes $n=8$ to 10, the GM structures are cuboids with increasing surface area ($14,16,18$ tetragons) or decreasing surface area per atom ($14/8$, $16/9$, $18/10$), but with the middle size cuboid maximising its volume per atom ($3/8$, $4/9$ and $4/10$ $n=4$ cuboids, respectively). However, from R${}^2$ analysis of surface area vs. energy of structures, we found little to no correlation. Sizes $n=14$ to 16 are another three bulk cut structures (although in the case of $n=14$ not cuboid), which all have negative second-order energies for some of the metal oxides, but not all.

3.3. Coordination Numbers and Deformation

The average coordination number in GM clusters against n is plotted in Figure 3. The average coordination number is typically lowest (where the same structural motif is not adopted for the GM configurations across all compounds) in magnesium oxide GM nanoclusters. This is unsurprising given that the coordination number will inherently be lower for barrel shapes than in rocksalt cuts as the maximum coordination number in a barrel is 4, compared to 6 in the case of an atom in the centre of a cuboid rocksalt cut. As discussed above, some higher energy LM structures (the second- and third-lowest energy LM) of (MgO)${}_n$ clusters tend to have an even lower average coordination number; the perfect bubble structures (see, for example, structures 11-CXXX and 12-CXXX) have atoms that are all three-coordinated. Configurations can also be constructed from tetragonal face sharing $n=6$ drums and n = 9, 12, 15... barrels, which would increase the average coordination. The smallest of these ($n=10$ composed of two drums with four four-coordinated atoms (10-XXXC); n = 13 composed of three drums with eight four-coordinated atoms; n = 15 composed of two $n=9$ barrels with two five-coordinated atoms) are either less stable or actually unstable. For example, the n =10 cluster can either open out to form a bubble or collapse to form the $2\times 2\times 5$ cuboid (10-AAAA). However, when combined with face sharing n = 4 cuboid clusters, a number of the LM shown in Table 1 and Table 2 can be constructed. When the barium oxide clusters’ GM is different to that of (CaO)${}_n$ and (SrO)${}_n$, its average coordination number is also typically smaller; here, this occurs when n is odd, i.e., sizes 11, 13, and 17, the latter two being armorphous configurations.

When looking at sizes $n=8$ to 10 for clusters containing one of the three largest cations, the $n=9$ second-order energy makes an interesting case to examine more closely. The compound with the smallest cation, Ca${}^{2+}$, favours $n=9$ relatively strongly, and has a positive second-order energy for $n=10$. In stark contrast, the compound with the largest cation, Ba${}^{2+}$, has a positive value for $n=9$ and favours $n=8$ and 10. Completing this trend, although closer to the value for calcium oxide, $\Delta E\left(9\right)$ for strontium oxide lies in between those calculated for the oxides of calcium and barium. The competing factors in these cuboids are the average number of dangling bonds and therefore to the average coordination number, which also has a minimum for $n=9$, and the dipole moment, which is effectively zero for $n=8$ and 10 but non-zero for $n=9$, as this has planes that contain an odd number of atoms. Hence, it appears that it is more favourable for Ca atoms to maximise their average coordination number, whilst the creation of a dipole appears most unfavourable for barium oxide. A similar trend becomes apparent with $n=14$ to 16; the polar $n=15$ cluster is most stable for calcium oxide clusters and least stable for barium oxide ones.

For clusters containing the three larger alkaline cations, it is also apparent upon comparing Figure 2 and Figure 3 that the local minima in the average coordination numbers ($n=7,11,13,17$) match the local maxima in the second-order energies. Alternatively, the GM structures that are energetically more stable than their neighbouring sizes tend to have a higher average coordination number. In the case of (MgO)${}_n$, a lower average coordination number is found for the barrel-shaped GM clusters with a size that is more stable than the average of its nearest neighbours (i.e., sizes $n=6,9,12$ and 15). This trend ends once the size of the cluster passes the transition point for bulk-cut GM.

Examining why and how exactly magnesium oxide is different in its preference for barrel shapes in smaller clusters, it is found that the $2\times 4\times 4$ cuboid GM configuration of (MgO)${}_{16}$ is relatively more stable than its neighbours, which includes the (MgO)${}_{15}$ barrel. This is indicative that the bulk transition, where magnesium oxide clusters start adopting bulk-like structures as opposed to barrels, occurs around this size. However, we note that, in the case of $n=15$, the $2\times 3\times 5$ cuboid configuration, although ranked second, is still $\sim 0.32$ eV higher in energy than the barrel. The local minimum of $\Delta E$ at $n=16$ rather than 15 is perhaps more to do with the relatively low stability of $n=17$, a size where no perfect barrel nor cuboid cut is possible, and the perfect bubbles of this size have low symmetry. Note that the GM for (MgO)${}_{17}$ is a defective (along one edge) $3\times 3\times 3$ bulk cut, whereas the GM for (MgO)${}_{14}$ is a defective (along one of the shortest edges) $2\times 3\times 4$ bulk cut.

It has been previously reported [24] that the dipole moment for the $4\times 3\times 3$ (MgO)${}_{18}$ cuboid configuration is expected to be rather high since, as discussed above, it contains planes that have an odd number of atoms, so we looked at the dipoles reported in our DFT outputs. Note that there is no significant dipole moment for the perfect $6\times 3\times 2$ cuboid configurations, and that the $9\times 2\times 2$ configurations were much higher in energy for all four oxides and should also not have a significant dipole moment. The dipole moments for all four $n=18$ clusters with the $4\times 3\times 3$ cuboid configuration are reported in

Table 4. Dipole moments of $4\times 3\times 3$ ($n=18$) cuboid clusters of magnesium, calcium, strontium and barium oxides as calculated using the PBEsol functional in FHI-aims.

Cluster	(MgO)${}_{18}$	(CaO)${}_{18}$	(SrO)${}_{18}$	(BaO)${}_{18}$
Dipole moment/D	16.2	14.9	13.7	6.0

; the magnesium oxide, calcium oxide and strontium oxide structures are the GM but barium oxide preferred the non-polar structure. The dipole moment decreases with an increase in cation size, counter to naïve arguments based on interatomic distances.

The degree of polarisation has previously been related to the acuteness of the cation–anion–cation bond angles in nanoclusters [23]—trends in both this and coordination numbers map quite well onto these angles for small clusters. We compared the angles between adjacent short contacts we found for $n=2$ to four GM structures to those found the corresponding ideal shapes (90 degrees for the $n=2$ square, 120 for the $n=3$ hexagon and 90 again for the $n=4$ cube). The absolute deviations of the angles are shown in Figure 4. For reference as to how this looks in specific clusters, see the $n=4$ structures in Table 1, where the (MgO)${}_4$ and (BaO)${}_4$ structures are deformed in opposite ways.

In the case of magnesium oxide, the Mg–O–Mg angles were more acute than the expected angle (and correspondingly O–Mg–O angles were wider). For all other cases, M–O–M angles were wider than expected, with a clear overall trend of this angle opening up and the O–M–O angle closing with an increase in cation size. The closest to ideal angles is therefore calcium oxide.

3.4. Dipole Moments

Although for the same polar structure and assuming formal point charges you would get a greater dipole moment when the spacing between charged layers is increased, it is evident from comparing the data in Table 4 that the dipole moment decreases with cation size and actually drops by more than a factor of 2 between strontium oxide and barium oxide. Why, then, is the polar $n=18$ cuboid cluster the GM for three of the alkaline oxides and not for barium oxide? Assuming formal point charges of $\pm 2$ is clearly inaccurate particularly as the cations have very different polarizabilities: Ba${}^{2+}$ ions are much more polarizable than the other metal ions [30] (actually the polarizability of Ba${}^{2+}$ is about twice that of Sr${}^{2+}$). Due to the higher polarizability, the orbitals can typically deform more easily and more mixing occurs. Through this, the dipole across the cluster can be more readily reduced for barium oxide clusters than for the other alkaline oxide polar cuboid clusters. However, one must not forget the influence of other factors; for example, how strong the penalty for low-coordinated atoms is. This penalty is presumably stronger in BaO given the larger cation can potentially accommodate a higher coordination and, therefore, acts to reverse what is found given the average coordination of the GM for (BaO)${}_{18}$ is lower than that of the GM predicted for the other three. Comparing the atom sites in the two GM $n=18$ bulk cuts, although they have the same number of corner sites, the non-polar cut that is adopted by (BaO)${}_{18}$ has four more edge sites (and fewer face and bulk sites). Thus, the average atom in the non-polar cut has more space for electronic polarisation and this effect outweighs the combination of other factors to result in the non-polar cut to be the GM for (BaO)${}_{18}$ (but clearly not dominant enough for the $9\times 2\times 2$ cuboid bulk cut to be ranked first).

Connecting the polarisation data with acuteness of M–O–M angles, the trends in both dipole moment and coordination numbers are reflected here as they were for lanthanum fluoride clusters [23]. Additionally, the acuteness of M–O–M angles may also shed light on the preference for different bulk cuts for $n=13$ (see Table 2). It also appears that calcium oxide clusters might be expected to also adopt structures that are least distorted from ideal rocksalt cuts, in line with its favourable energetics even for non-cuboid cuts. This result is in line with expectations based on polarizabilities. In the case of magnesium oxide, the anion is much more polarizable than the cation, and therefore more likely to “move out”. As the cation size is increased, the cation polarizability is also increased, and therefore the larger cations are more likely to pucker out. This does suggest that these two effects balance out most effectively for calcium oxide. Earlier the second-order energies for $n=9$ and $n=15$ were shown to increase down the group (CaO→SrO→BaO), suggesting that the polar structure is relatively more stable if the cation is less polarizable and the bonds are shorter. The degree of freedom, or space, for electronic polarisation provides a more satisfactory explanation as to why the $3\times 3\times 2$ cuboid bulk cut is predicted to be less stable than the average of the neighbouring sized non-polar $4\times 2\times 2$ and $5\times 2\times 2$ cuboid bulk cuts if the cations are barium, whereas the reverse is predicted for either calcium or strontium. Moreover, the same argument can be used to explain relative change in the rank of the polar $5\times 3\times 2$ cuboid, 15-BAAA, bulk cut; its second-order energy is not lower than that of the $n=16$ non-polar bulk cut for any oxide, and the $n=15$ cuboid cut structure is relatively most stable with calcium as the cation and least stable with barium. However, comparing to the $n=14$ non-cuboid cut reveals that its polar nature is penalised most strongly for BaO, while it is preferred the most over the 14-XAAA structure by CaO.

3.5. Selecting Targets for Nanofabrication

When trying to determine whether a particular structure will be dominant in experiments, two factors need to be considered. The first of these is how stable a particular GM configuration is relative to GM configurations of neighbouring sizes, which was discussed above after presenting graphs of the second-order energies as a function of both size and cation. The second is how likely it is that other structures of the same cluster size will also be found; metastable structures that are thermodynamically accessible at non-zero temperature. This has been visualised here for all four alkaline earth oxides by means of a “density of structures” plot, or a LM density plot, as a function of energy per MO unit for each compound (all LM energies reported relative to their respective GM energies) with sizes $n=8$ to 18 and 24. Note that we also applied thermal smearing corresponding to a temperature of 100 K to generate these curves. Curves reflecting a temperature of 300 K are available in the supporting information.

3.5.1. Magnesium Oxide Clusters

As can be seen in the magnesium oxide structure density plot (Figure 5), for $n=10$, 13 and 17, none of the $n=10,13$ and 17 configurations have a lower energy per MgO unit than the corresponding $n-1$ GM configuration. Thus, we expect that clusters of (MgO)${}_{10}$, (MgO)${}_{13}$ and (MgO)${}_{17}$ are less likely (anticipate a smaller peak in mass spectra for each of these sizes). These sizes match the positive (disfavourable) second-order energies, whereas we find a local minimum in these at $n=9,12$ and 16.

Returning to the LM density plots for (MgO)${}_n$, GM clusters of size $n=9,13,15,16,18$ and 24 have a significant energy gap before the second lowest LM of that respective size. Of these, $n=15$ and 16 still have alternative structures relatively close in energy that at modest temperatures may also be formed in significant quantity (relative to the quantity of the GM configuration for that size); see density of states data. We can discard $n=13$ (see previous paragraph). These cluster sizes all, particularly (MgO)${}_9$, make interesting targets for size-selected synthesis as they are likely to be dominated by only one atomic configuration for each size, which includes both barrel-shaped and cuboid bulk-cut clusters as good synthesis targets.

Finally, although it is a local minimum in the second-order energy difference, (MgO)${}_{12}$ has a number of low energy metastable LM configurations close in energy to the GM. The hexagonal barrel (GM), $4\times 3\times 2$ bulk-cut, the high symmetry (T${}_h$) sodalite bubble, and a structure that combines fragments of both the barrel and bulk-cut motifs (cf. configuration 12-DCCX), are all very close to each other in energy. It would be interesting to try and investigate if all four structures are the dominant configurations found for this size when synthesized.

3.5.2. Clusters of Calcium, Strontium and Barium Oxide

The equivalent figures to Figure 5 can be found in the Supplementary Material (Figures S1–S3). In summary, Figure 6 shows a heat map for all four alkaline earth oxides, which indicates structures that could be of experimental interest. Black squares indicate sizes that are unlikely to be observed at all because they are particularly high in energy compared to size $n-1$ clusters; when only one structure is thermally accessible (at ∼100 K), the size is marked in orange—these might be especially interesting as structures that can be synthesised without by-products. Alternatively, for method validation, the sizes marked in burgundy might be of interest, as they possess multiple thermally accessible structures (again, at a reference temperature of 100 K), and it might be interesting if the sets of structures predicted here are also all found in experiments.

The temperature of 100 K was kept as the choice here as previous experiments [20] were conducted at similar temperatures. Equivalent plots for a temperature of 300K are also available in the Supplementary Material.

SrO has the most sizes with uniquely low-energy GM—perhaps it could be a good starting point for non-size selected fabrication of very small nanoparticles, as there is a fairly low number of likely structures overall. Generally, this is likely to be because all these SrO structures are bulk cuts and SrO seems to have the highest likelihood to adopt stable bulk cut structures that have edges other than (001).

From the density of structures plot for barium oxide (see Supplementary Material), it is evident that, even with a uniquely low-energy GM, on average, (BaO)${}_n$ clusters tend to have LM that are much closer in energy to each other and to the GM than LM clusters of the other three compounds.

3.6. Nanoclusters of Size $n=12$

As mentioned above, (MgO)${}_{12}$ is not only a relatively stable size compared to its neighbouring GM, but it also has a number of very low energy metastable LM configurations. These LM configurations with similar energy include three high-symmetry structures: the hexagonal barrel (GM), the $4\times 3\times 2$ bulk-cut, and the $T_h$ bubble. The changes in the energies of the low energy LM for the $n=12$ nanoclusters as a function of cation are shown in Figure 7.

As can be seen in Figure 7, the bulk cut geometry is the only one that is consistently low in energy for all four oxides. The barrel shape cluster is the GM for (MgO)${}_{12}$, and slightly higher in energy (but still in the three lowest-energy LM) for BaO and SrO, but using it as a starting geometry for CaO converged to a different shape. The $T_d$ bubble, which was third in energy in magnesium oxide clusters, becomes higher in energy for (CaO)${}_{12}$ and then (SrO)${}_{12}$, and in the case of (BaO)${}_{12}$ was not found using our starting structures. This further highlights how MgO clusters behave uniquely in this series and how moving to larger cations again increases how much a higher coordination number is preferred.

3.7. Comparison with Previous Results

One experiment that our results can be compared against is mass spectrometry, but this needs to be considered with great care since experiments will typically involve charged clusters, whereas we have only examined neutral clusters. Moreover, mass spectrometry only gives insight into likely cluster sizes and sub-unit sizes, rather than the structures of the clusters. However, it can nevertheless aid in the interpretation and validation of computational results. Mass spectrometric studies on the alkaline earth oxides indicate especially high stability of the $n=3k$ magnesium oxide fragments [7], but $n=2k$ (MgO)${}_n^{+}$ peaks have also been detected alongside the $n=3k$ ones [8] (albeit weaker). For calcium oxide, $n=2k$ fragments seemed to appear more frequently [9], indicating that four atom building blocks are perhaps favoured. This correlates strongly with the structures, which had low second-order energies: in the case of CaO, they were all $n=2k$ bulk cuts, while, for (MgO)${}_n$, the $n=2k$ fragments correspond to bulk cuts (they can be interpreted as square building units) and the $n=3k$ fragments are from clusters formed of parallel hexagonal rings, which form barrel-like configurations.

The trends for magnesium oxide clusters (as well as the general region where the bulk transition occurs) are also generally in line with previous computational results [10,11,12,13,14,15,16,17], which typically report clusters of selected sizes or sizes up to $n=12$. A recent study on (CaO)${}_n$ clusters [19] data-mined from (MgO)${}_n$ geometries also found that cuboid structures were energetically more favourable for calcium oxide clusters than for magnesium oxide clusters. Although their study also included constructed cuboid cuts, barrels and multiple barrels, they do not report all non-cuboid bulk cuts, including our GM found for $n=11$ (11-XAAC) and 14 (14-XAAA) as well as two LM, 11-XCCX and 13-ABXX, reported here in Table 1 and Table 2. In their original magnesium oxide study [18], which used a tree growth-hybrid genetic algorithm [31], they reported the same GM structures that were found here for all sizes except for $n=11$. Given we have employed a different density functional, it is not surprising that there is some discrepancy. Our PBEsol-GM configuration, 11-AXXX, is reported as their second lowest B3LYP-LM (147 meV) higher than their B3LYP-GM), whereas their GM configuration (cf. 11-XXXB) is 7.9 meV/MgO higher in energy, as measured using PBEsol, than our GM. Other differences are also found in the low-lying LM; for example, for size $n=5$, we report three rather than two non-planar candidate structures. Particular configurations may not be reported in one of the studies because of a large change in their rank upon the change in the choice of the functional (in an extreme case, the LM may become unstable) or because the configurations were genuinely missed by one of the studies (which is more likely to occur for large n). In Ref. [19], a number of different energy functions, including CCSD(T), were compared by calculating the energy differences between the smallest B3LYP GM configuration and their larger sized B3LYP tentative GM. The main premise in this comparison is that the CCSD(T) level of theory provides the best available reference to date, which crucially depends on inclusion of diffuse and trained polarisation functions in the basis sets for an accurate description of the polarisation effects. These features are important in dealing with clusters of ionic systems that expose under-coordinated anionic atoms. The DFT methods in fact converge much better with the basis set and the numerical basis functions with accurate behaviour in the orbital tails and near cusp regions (employed here) are practically at the basis set limit. To aid future comparisons between studies, we have uploaded our configurations into the HIVE online database [3]. Importantly for our predictions as to which configurations are more likely to be isolated in experiments, we have focused on finding GM that are much lower in energy than LM of similar size compared to the energy change that is likely to occur when changing the energy functional.

One of the studies on (MgO)${}_n$ mentioned earlier, which also includes comparison with IR spectra [21], goes up to $n=16$; they suggest that the experimentally found structure, which is also the most stable structure thermodynamically for $n=16$, is not the bulk cut, but rather the structure which for us is second-lowest in energy (16-BCBC). However, they go on to suggest that both structures are likely to form in experiments and that their data is in line with this. Our data supports this also. When two structures are very close in energy, inaccuracies in choice of functional and basis set are likely to change their ranking, but both structures will still be likely to form in experiment.

Comparison with other ionic compounds with the same stoichiometry can give additional insight. For example, in previous computational studies of alkali halides, one paper presented DFT results for barrel and rocksalt cut structures for small (MX)${}_n$ clusters of alkali halides lithium fluoride, sodium chloride and potassium bromide [32]; these calculations suggested that for all three the lower energy structure of the two was the barrel one with $n=9$. The authors described elsewhere a corresponding result for (LiF)${}_6$ [33]. In all of these compounds, the anion’s ionic radius is much larger than the cation’s [34], making the most similar to those of magnesium oxide in terms of this ratio as well as structure.

An alkali halide that is perhaps of interest in comparison to barium oxide in particular is potassium fluoride: anions are ordinarily much larger in radius than cations due to the outermost electrons being less tightly bound (as their nuclear charge is relatively smaller and more shielded), but in both barium oxide and potassium fluoride, the cations are large and the anions small, leading to a cation:anion radius ratio of ∼1 [34]. Previous research has shown that in KF there is also a preference for the bulk cut structure [12]. Combining this with our results for the alkaline earth oxides, it appears that, overall, the relative stability of rocksalt cuts (compared to barrels) is a higher structure when the cation size is increased and/or anion size is decreased.

As reported here, the dipole moment of equivalent clusters decreases with an increase in cation size, and the similarity in structures for similar anion:cation ratios in alkali halides points toward trends in various properties being perhaps more universal.

4. Conclusions

We have predicted thermodynamically stable structures for nanoclusters of magnesium, calcium and strontium oxide. Candidate structures were successfully data mined from our previous structures of barium oxide clusters. As previously found for barium oxide, GM for clusters of calcium and strontium oxide adopted structures resembling cuts of the rocksalt phase for sizes where cuboids were possible. In contrast, magnesium oxide clusters adopted hexagonal barrel-like structures up to a size of 30 atoms, but also displayed higher stability of rocksalt-like structures beyond this size. The most obvious trend in these motifs was the change in coordination number with cation size. Recall that magnesium oxide clusters generally had the lowest coordination number of all alkaline earth oxides in its GMs (see Figure 3) as well as in their low-lying LM. Additional strain (steric effects) caused by increasing coordination of each atom is greater for the smaller cation, likewise the 2D hexagonal sheet (the structure obtained in the limit of large n for bubble structures) is less stable for the more polarisable larger cations.

From our analysis, the cluster sizes that are the most promising synthesis targets based on their relative stability compared to smaller clusters as well as other possible structures of the same size cluster are: $n=9,15,16,18$ and 24 for (MgO)${}_n$, $n=8,9,12,16,18$ and 24 for (CaO)${}_n$ and $8,9,10,12,15,16,18$ and 24 for (SrO)${}_n$.