Molecular Engineering of High Energy Barrier in Single-Molecule Magnets Based on [MoIII(CN)7]4− and V(II) Complexes
Abstract
:1. Introduction
2. Results and Discussion
2.1. Electronic Structure of [MoIII(CN)7]4− Complex
2.2. Anisotropic Spin Coupling MoIII–CN–VII
2.3. Estimate of Anisotropic Exchange Parameters
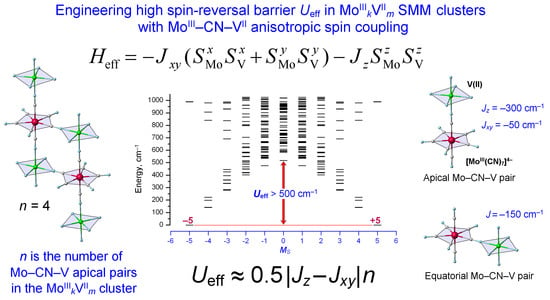
2.4. Spin Energy Spectra of MoIIIkVIIm Clusters: Engineering of High Energy Barrier
3. Method and Computation Details
4. Conclusions
Acknowledgments
Conflicts of Interest
References
- Sessoli, R.; Gatteschi, D.; Caneschi, A.; Novak, M.A. Magnetic bistability in a metal-ion cluster. Nature 1993, 365, 141–143. [Google Scholar] [CrossRef]
- Sessoli, R.; Tsai, H.L.; Schake, A.R.; Wang, S.Y.; Vincent, J.B.; Folting, K.; Gatteschi, D.; Christou, G.; Hendrickson, D.N. High-spin molecules: [Mn12O12(O2CR)16(H2O)4]. J. Am. Chem. Soc. 1993, 115, 1804–1816. [Google Scholar] [CrossRef]
- Gatteschi, D.; Sessoli, R. Quantum tunneling of magnetization and related phenomena in molecular materials. Angew. Chem. Int. Ed. 2003, 42, 268–297. [Google Scholar] [CrossRef] [PubMed]
- Coulon, C.; Miyasaka, H.; Clérac, R. Single-Molecule Magnets and Related Phenomena. In Structure and Bonding; Winpenny, R., Ed.; Springer: Berlin, Germany, 2006; Volume 122. [Google Scholar]
- Gatteschi, D.; Sessoli, R.; Villain, J. Molecular Nanomagnets; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Gao, S. Molecular Nanomagnets and Related Phenomena; Springer: New York, NY, USA, 2015; Volume 164. [Google Scholar]
- Milios, C.J.; Winpenny, R.E.P. Cluster-based single-molecule magnets. In Molecular Nanomagnets and Related Phenomena; Gao, S., Ed.; Springer: Berlin, Germany, 2015; Volume 164, pp. 1–109. [Google Scholar]
- Ardavan, A.; Blundell, S.J. Storing quantum information in chemically engineered nanoscale magnets. J. Mater. Chem. 2009, 19, 1754–1760. [Google Scholar] [CrossRef]
- Leuenberger, M.N.; Loss, D. Quantum computing in molecular magnets. Nature 2001, 410, 789–793. [Google Scholar] [CrossRef] [PubMed]
- Aromi, G.; Aguilà, D.; Gamez, P.; Luis, F.; Roubeau, O. Design of magnetic coordination complexes for quantum computing. Chem. Soc. Rev. 2012, 41, 537–546. [Google Scholar] [CrossRef] [PubMed]
- Wedge, C.J.; Timco, G.A.; Spielberg, E.T.; George, R.E.; Tuna, F.; Rigby, S.; McInnes, E.J.L.; Winpenny, R.E.P.; Blundell, S.J.; Ardavan, A. Chemical engineering of molecular qubits. Phys. Rev. Lett. 2012, 108, 107204. [Google Scholar] [CrossRef] [PubMed]
- Pedersen, K.S.; Ariciu, A.; McAdams, S.; Weihe, H.; Bendix, J.; Tuna, F.; Piligkos, S. Toward Molecular 4f Single-Ion Magnet Qubits. J. Am. Chem. Soc. 2016, 138, 5801–5804. [Google Scholar] [CrossRef] [PubMed]
- Rocha, A.R.; García-Suarez, V.M.; Bailey, S.W.; Lambert, C.J.; Ferrer, J.; Sanvito, S. Towards Molecular Spintronics. Nat. Mater. 2005, 4, 335–339. [Google Scholar] [CrossRef] [PubMed]
- Bogani, L.; Wernsdorfer, W. Molecular spintronics using single-molecule magnets. Nat. Mater. 2008, 7, 179–186. [Google Scholar] [CrossRef] [PubMed]
- Waldmann, O. A criterion for the anisotropy barrier in single-molecule magnets. Inorg. Chem. 2007, 46, 10035–10037. [Google Scholar] [CrossRef] [PubMed]
- Ruiz, E.; Cirera, J.; Cano, J.; Alvarez, S.; Loose, C.; Kortus, J. Can large magnetic anisotropy and high spin really coexist? Chem. Commun. 2008, 1, 52–54. [Google Scholar] [CrossRef]
- Neese, F.; Pantazis, D.A. What is not required to make a single molecule magnet. Faraday Discuss. 2011, 148, 229–238. [Google Scholar] [CrossRef] [PubMed]
- Sessoli, R.; Powell, A.K. Strategies towards single molecule magnets based on lanthanide ions. Coord. Chem. Rev. 2009, 253, 2328–2341. [Google Scholar] [CrossRef]
- Sorace, L.; Benelli, J.R.; Gatteschi, D. Lanthanides in molecular magnetism: old tools in a new field. Chem. Soc. Rev. 2011, 40, 3092–3105. [Google Scholar] [CrossRef] [PubMed]
- Rinehart, J.D.; Long, J.R. Exploiting single-ion anisotropy in the design of f-element single-molecule magnets. Chem. Sci. 2011, 2, 2078–2085. [Google Scholar] [CrossRef]
- Layfield, R.A.; Murugesu, M. Lanthanides and Actinides in Molecular Magnetism; Wiley-VCH: Weinheim, Germany, 2015. [Google Scholar]
- Ishikawa, N.; Sugita, M.; Ishikawa, T.; Koshihara, S.; Kaizu, Y. Lanthanide double-decker complexes functioning as magnets at the single-molecular level. J. Am. Chem. Soc. 2003, 125, 8694–8695. [Google Scholar] [CrossRef] [PubMed]
- Luzon, J.; Sessoli, R. Lanthanides in molecular magnetism: So fascinating, so challenging. Dalton Trans. 2012, 41, 13556–13567. [Google Scholar] [CrossRef] [PubMed]
- Woodruff, D.N.; Winpenny, R.E.P.; Layfield, R.A. Lanthanide Single-Molecule Magnets. Chem. Rev. 2013, 113, 5110–5148. [Google Scholar] [CrossRef] [PubMed]
- Layfield, R.A. Organometallic single-molecule magnets. Organometallics 2014, 33, 1084–1099. [Google Scholar] [CrossRef]
- Tang, J.; Zhang, P. Lanthanide Single-Molecule Magnets; Springer: Berlin, Germany, 2015. [Google Scholar]
- Liddle, S.T.; van Slageren, J. Improving f-element single molecule magnets. Chem. Soc. Rev. 2015, 44, 6655–6669. [Google Scholar] [CrossRef] [PubMed]
- Habib, F.; Murugesu, M. Lessons learned from dinuclear lanthanide nano-magnets. Chem. Soc. Rev. 2013, 42, 3278–3288. [Google Scholar] [CrossRef] [PubMed]
- Rinehart, J.D.; Fang, M.; Evans, W.J.; Long, J.R. A N23-Radical-Bridged Terbium Complex Exhibiting Magnetic Hysteresis at 14 K. J. Am. Chem. Soc. 2011, 133, 14236–14239. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.-C.; Liu, J.-L.; Ungur, L.; Liu, J.; Li, Q.-W.; Wang, L.-F.; Ni, Z.-P.; Chibotaru, L.F.; Chen, X.-M.; Tong, M.-L. Symmetry-Supported Magnetic Blocking at 20 K in Pentagonal Bipyramidal Dy(III) Single-Ion Magnets. J. Am. Chem. Soc. 2016, 138, 2829–2837. [Google Scholar] [CrossRef] [PubMed]
- Ding, Y.S.; Chilton, N.F.; Winpenny, R.E.P.; Zheng, Y.Z. On Approaching the Limit of Molecular Magnetic Anisotropy: A Near-Perfect Pentagonal Bipyramidal Dysprosium(III) Single-Molecule Magnet. Angew. Chem. Int. Ed. 2016, 55, 16071–16074. [Google Scholar] [CrossRef] [PubMed]
- Guo, F.S.; Day, B.M.; Chen, Y.C.; Tong, M.L.; Mansikkamäki, A.; Layfield, R.A. A dysprosium metallocene single-molecule magnet functioning at the axial limit. Angew. Chem. Int. Ed. 2017, 56, 11445–11449. [Google Scholar] [CrossRef] [PubMed]
- Goodwin, C.A.P.; Ortu, F.; Reta, D.; Chilton, N.F.; Mills, D.P. Molecular magnetic hysteresis at 60 kelvin in dysprosocenium. Nature 2017, 548, 439–442. [Google Scholar] [CrossRef] [PubMed]
- Milios, C.J.; Vinslava, A.; Wernsdorfer, W.; Moggach, S.; Parsons, S.; Perlepes, S.P.; Christou, G.; Brechin, E.K. A record Anisotropy Barrier for a Single-molecule Magnet. J. Am. Chem. Soc. 2007, 129, 2754–2755. [Google Scholar] [CrossRef] [PubMed]
- Craig, G.A.; Murrie, M. 3D single-ion magnets. Chem. Soc. Rev. 2015, 44, 2135–2147. [Google Scholar] [CrossRef] [PubMed]
- Frost, J.M.; Harriman, K.L.M.; Murugesu, M. The rise of 3-d single-ion magnets in molecular magnetism: Towards materials from molecules. Chem. Sci. 2016, 7, 2470–2491. [Google Scholar] [CrossRef] [PubMed]
- Zadrozny, J.M.; Xiao, D.J.; Long, J.R.; Atanasov, M.; Neese, F.; Grandjean, F.; Long, G.J. Mossbauer Spectroscopy as a Probe of Magnetization Dynamics in the Linear Iron(I) and Iron(II) Complexes [Fe(C(SiMe3)3)2]1−/0. Inorg. Chem. 2013, 52, 13123–13131. [Google Scholar] [CrossRef] [PubMed]
- Yao, X.-N.; Du, J.-Z.; Zhang, Y.-Q.; Leng, X.-B.; Yang, M.-W.; Jiang, S.-D.; Wang, Z.-X.; Ouyang, Z.-W.; Deng, L.; Wang, B.-W.; et al. Two-Coordinate Co(II) Imido Complexes as Outstanding Single-Molecule Magnets. J. Am. Chem. Soc. 2017, 139, 373–380. [Google Scholar] [CrossRef] [PubMed]
- Bar, A.K.; Pichon, C.; Sutter, J.-P. Magnetic anisotropy in two- to eight-coordinated transition–metal complexes: Recent developments in molecular magnetism. Coord. Chem. Rev. 2016, 308, 346–380. [Google Scholar] [CrossRef]
- Ruamps, R.; Batchelor, L.J.; Guillot, R.; Zakhia, G.; Barra, A.L.; Wernsdorfer, W.; Guihéry, N.; Mallah, T. Ising-type magnetic anisotropy and single molecule magnet behaviour in mononuclear trigonal bipyramidal Co(II) complexes. Chem. Sci. 2014, 5, 3418–3424. [Google Scholar] [CrossRef]
- Ruamps, R.; Maurice, R.; Batchelor, L.J.; Boggio-Pasqua, M.; Guillot, R.; Barra, A.L.; Liu, J.; Bendeif, E.-E.; Pillet, S.; Hill, S.; et al. Giant Ising-Type Magnetic Anisotropy in Trigonal Bipyramidal Ni(II) Complexes: Experiment and Theory. J. Am. Chem. Soc. 2013, 135, 3017–3026. [Google Scholar] [CrossRef] [PubMed]
- Novikov, V.V.; Pavlov, A.A.; Nelyubina, Y.V.; Boulon, M.-E.; Varzatskii, O.A.; Voloshin, Y.Z.; Winpenny, R.E.P. A Trigonal Prismatic Mononuclear Cobalt(II) Complex Showing Single-Molecule Magnet Behavior. J. Am. Chem. Soc. 2015, 137, 9792–9795. [Google Scholar] [CrossRef] [PubMed]
- Morrison, C.A.; Leavitt, R.P. Spectroscopic Properties of Triply Ionized Lanthanides in Transparent Host Crystals. In Handbook on the Physics and Chemistry of Rare Earths; Elsevier: Amsterdam, The Netherlands, 1982; Volume 5, pp. 461–692. [Google Scholar]
- Ungur, L.; Chibotaru, L.F. Strategies toward High-Temperature Lanthanide-Based Single-Molecule Magnets. Inorg. Chem. 2016, 55, 10043–10056. [Google Scholar] [CrossRef] [PubMed]
- Mironov, V.S.; Chibotaru, L.F.; Ceulemans, A. Mechanism of a Strongly Anisotropic MoIII–CN–MnII Spin–Spin Coupling in Molecular Magnets Based on the [Mo(CN)7]4− Heptacyanometalate: A New Strategy for Single-Molecule Magnets with High Blocking Temperatures. J. Am. Chem. Soc. 2003, 125, 9750–9760. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mironov, V.S. New approaches to the problem of high-temperature single-molecule magnets. Dokl. Phys. Chem. 2006, 408, 130–136. [Google Scholar] [CrossRef]
- Mironov, V.S. Origin of Dissimilar Single-Molecule Magnet Behavior of Three MnII2MoIII Complexes Based on [MoIII(CN)7]4− Heptacyanomolybdate: Interplay of MoIII–CN–MnII Anisotropic Exchange Interactions. Inorg. Chem. 2015, 54, 11339–11355. [Google Scholar] [CrossRef] [PubMed]
- Bennett, M.V.; Long, J.R. New Cyanometalate Building Units: Synthesis and Characterization of [Re(CN)7]3− and [Re(CN)8]3−. J. Am. Chem. Soc. 2003, 125, 2394–2395. [Google Scholar] [CrossRef] [PubMed]
- Samsonenko, D.G.; Paulsen, C.; Lhotel, E.; Mironov, V.S.; Vostrikova, K.E. [MnIII(Schiff base)]3[ReIV(CN)7], highly anisotropic 3D coordination framework: Synthesis, crystal structure, magnetic investigations, and theoretical analysis. Inorg. Chem. 2014, 53, 10217–10231. [Google Scholar] [CrossRef] [PubMed]
- Bendix, J.; Steenberg, P.; Sotofte, I. Isolation and Molecular Structure of Hexacyanoruthenate(III). Inorg. Chem. 2003, 42, 4510–4512. [Google Scholar] [CrossRef] [PubMed]
- Albores, P.; Slep, L.D.; Baraldo, L.M.; Baggio, R.; Garland, M.T.; Rentschler, E. Crystal Structure and Electronic and Magnetic Properties of Hexacyanoosmate(III). Inorg. Chem. 2006, 45, 2361–2363. [Google Scholar] [CrossRef] [PubMed]
- Mironov, V.S. Trigonal bipyramidal spin clusters with orbitally degenerate 5d cyano complexes [OsIII(CN)6]3–, prototypes of high-temperature single-molecule magnets. Dokl. Phys. Chem. 2007, 415, 199–204. [Google Scholar] [CrossRef]
- Dreiser, J.; Pedersen, K.S.; Schnegg, A.; Holldack, K.; Nehrkorn, J.; Sigrist, M.; Tregenna-Piggott, P.; Mutka, H.; Weihe, H.; Mironov, V.S.; et al. Three-Axis Anisotropic Exchange Coupling in the Single-Molecule Magnets NEt4[MnIII2(5-Brsalen)2(MeOH)2MIII(CN)6] (M = Ru, Os). Chem. Eur. J. 2013, 19, 3693–3701. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.-Y.; Avendaño, C.; Dunbar, K.R. Molecular magnetic materials based on 4d and 5d transition metals. Chem. Soc. Rev. 2011, 40, 3213–3238. [Google Scholar] [CrossRef] [PubMed]
- Qian, K.; Huang, X.-C.; Zhou, C.; You, X.-Z.; Wang, X.-Y.; Dunbar, K.R. A Single-Molecule Magnet Based on Heptacyanomolybdate with the Highest Energy Barrier for a Cyanide Compound. J. Am. Chem. Soc. 2013, 135, 13302–13305. [Google Scholar] [CrossRef] [PubMed]
- Wu, D.-Q.; Shao, D.; Wei, X.-Q.; Shen, F.-X.; Shi, L.; Kempe, D.; Zhang, Y.-Z.; Dunbar, K.R.; Wang, X.-Y. Reversible On–Off Switching of a Single-Molecule Magnet via a Crystal-to-Crystal Chemical Transformation. J. Am. Chem. Soc. 2017, 139, 11714–11717. [Google Scholar] [CrossRef] [PubMed]
- Freedman, D.E.; Jenkins, D.M.; Long, J.R. Strong magnetic exchange coupling in the cyano-bridged coordination clusters [(PY5Me2)4V4M(CN)6]5+ (M = Cr, Mo). Chem. Commun. 2009, 4829–4831. [Google Scholar] [CrossRef] [PubMed]
- Pinkowicz, D.; Southerland, H.; Wang, X.-Y.; Dunbar, K.R. Record Antiferromagnetic Coupling for a 3d/4d Cyanide-Bridged Compound. J. Am. Chem. Soc. 2014, 136, 9922–9924. [Google Scholar] [CrossRef] [PubMed]
- Ruiz, E.; Rodríguez-Fortea, A.; Alvarez, S.; Verdaguer, M. Is it possible to get high Tc magnets with prussian blue analogues? A theoretical prospect. Chem. Eur. J. 2005, 11, 2135–2144. [Google Scholar] [CrossRef] [PubMed]
- Gunter, M.J.; Berry, K.J.; Murray, K.S. A Model for the Cyanide Form of Oxidized Cytochrome Oxidase: An Iron(III)/Copper(II) Porphyrin Complex Displaying Ferromagnetic Coupling. J. Am. Chem. Soc. 1984, 106, 4227–4235. [Google Scholar] [CrossRef]
- Langley, S.K.; Wielechowski, D.P.; Vieru, V.; Chilton, N.F.; Moubaraki, B.; Abrahams, B.F.; Chibotaru, L.F.; Murray, K.S. A {CrIII2DyIII2} Single-Molecule Magnet: Enhancing the Blocking Temperature through 3d Magnetic Exchange. Angew. Chem. Int. Ed. 2013, 52, 12014–12019. [Google Scholar] [CrossRef] [PubMed]
- Langley, S.K.; Wielechowski, D.P.; Vieru, V.; Chilton, N.F.; Moubaraki, B.; Chibotaru, L.F.; Murray, K.S. Modulation of slow magnetic relaxation by tuning magnetic exchange in {Cr2Dy2} single molecule magnets. Chem. Sci. 2014, 5, 3246–3256. [Google Scholar] [CrossRef]
- Hursthouse, M.B.; Maijk, K.M.A.; Soares, A.M.; Gibson, J.F.; Griffith, W.P. The X-ray crystal structure of NaK3[Mo(CN)7]·2H2O and the structure of its anion in aqueous solution. Inorg. Chim. Acta 1980, 45, L81–L82. [Google Scholar] [CrossRef]
- Larionova, J.; Clérac, R.; Sanchiz, J.; Kahn, O.; Golhen, S.; Ouahab, L. Ferromagnetic Ordering, Anisotropy, and Spin Reorientation for the Cyano-Bridged Bimetallic Compound Mn2(H2O)5Mo(CN)7·4H2O (α Phase). J. Am. Chem. Soc. 1998, 120, 13088–13095. [Google Scholar] [CrossRef]
- Larionova, J.; Kahn, O.; Gohlen, S.; Ouahab, L.; Clérac, R. Structure, Ferromagnetic Ordering, Anisotropy, and Spin Reorientation for the Two-Dimensional Cyano-Bridged Bimetallic Compound K2Mn3(H2O)6[Mo(CN)7]2·6H2O. J. Am. Chem. Soc. 1999, 121, 3349–3356. [Google Scholar] [CrossRef]
- Wang, Q.-L.; Southerland, H.; Li, J.-R.; Prosvirin, A.V.; Zhao, H.; Dunbar, K.R. Crystal-to-Crystal Transformation of Magnets Based on Heptacyanomolybdate(III) Involving Dramatic Changes in Coordination Mode and Ordering Temperature. Angew. Chem. Int. Ed. 2012, 51, 9321–9324. [Google Scholar] [CrossRef] [PubMed]
- Holmes, S.M.; Girolami, G.S. Sol–Gel Synthesis of KVII[CrIII(CN)6]·2H2O: A Crystalline Molecule-Based Magnet with a Magnetic Ordering Temperature above 100 °C. J. Am. Chem. Soc. 1999, 121, 5593–5594. [Google Scholar] [CrossRef]
- Tomono, K.; Tsunobuchi, Y.; Nakabayashi, K.; Ohkoshi, S. Vanadium(II) Heptacyanomolybdate(III)-Based Magnet Exhibiting a High Curie Temperature of 110 K. Inorg. Chem. 2010, 49, 1298–1300. [Google Scholar] [CrossRef] [PubMed]
- Mironov, V.S.; Bazhenova, T.A.; Manakin, Y.V.; Lyssenko, K.A.; Talantsev, A.D.; Yagubskii, E.B. A new Mo(IV) complex with the pentadentate (N3O2) Schiff-base ligand: the first non-cyanide pentagonal–bipyramidal paramagnetic 4d complex. Dalton Trans. 2017, 46, 14083–14087. [Google Scholar] [CrossRef] [PubMed]






© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mironov, V.S. Molecular Engineering of High Energy Barrier in Single-Molecule Magnets Based on [MoIII(CN)7]4− and V(II) Complexes. Inorganics 2018, 6, 58. https://doi.org/10.3390/inorganics6020058
Mironov VS. Molecular Engineering of High Energy Barrier in Single-Molecule Magnets Based on [MoIII(CN)7]4− and V(II) Complexes. Inorganics. 2018; 6(2):58. https://doi.org/10.3390/inorganics6020058
Chicago/Turabian StyleMironov, Vladimir S. 2018. "Molecular Engineering of High Energy Barrier in Single-Molecule Magnets Based on [MoIII(CN)7]4− and V(II) Complexes" Inorganics 6, no. 2: 58. https://doi.org/10.3390/inorganics6020058
APA StyleMironov, V. S. (2018). Molecular Engineering of High Energy Barrier in Single-Molecule Magnets Based on [MoIII(CN)7]4− and V(II) Complexes. Inorganics, 6(2), 58. https://doi.org/10.3390/inorganics6020058