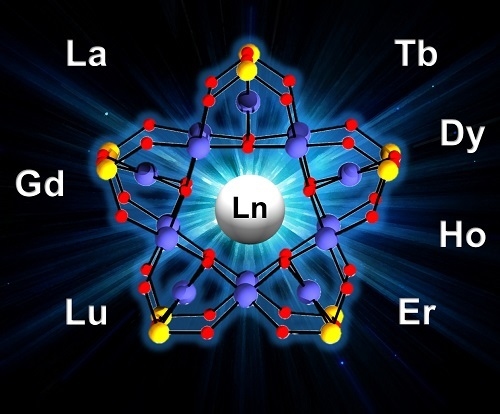
Exploring High-Symmetry Lanthanide-Functionalized Polyoxopalladates as Building Blocks for Quantum Computing
Abstract
:1. Introduction
2. Results and Discussion
2.1. Structural and Electronic Properties
2.2. Ligand Field Analysis
3. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hill, S.; Edwards, R.S.; Aliaga-Alcalde, N.; Christou, G. Quantum Coherence in an Exchange-Coupled Dimer of Single-Molecule Magnets. Science 2003, 302, 1015–1018. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cerletti, V.; Coish, W.A.; Gywat, O.; Loss, D. Recipes for spin-based quantum computing. Nanotechnology 2005, 16, R27. [Google Scholar] [CrossRef]
- Bertaina, S.; Gambarelli, S.; Mitra, T.; Tsukerblat, B.; Müller, A.; Barbara, B. Quantum oscillations in a molecular magnet. Nature 2008, 453, 203–206. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Stamp, P.C.E.; Gaita-Ariño, A. Spin-based quantum computers made by chemistry: Hows and whys. J. Mater. Chem. 2009, 19, 1718–1730. [Google Scholar] [CrossRef]
- Baldoví, J.J.; Cardona-Serra, S.; Clemente-Juan, J.M.; Coronado, E.; Gaita-Ariño, A.; Palii, A. Rational Design of Single-Ion Magnets and Spin Qubits Based on Mononuclear Lanthanoid Complexes. Inorg. Chem. 2012, 51, 12565–12574. [Google Scholar] [CrossRef] [PubMed]
- Atzori, M.; Morra, E.; Tesi, L.; Albino, A.; Chiesa, M.; Sorace, L.; Sessoli, R. Quantum Coherence Times Enhancement in Vanadium(IV)-based Potential Molecular Qubits: The Key Role of the Vanadyl Moiety. J. Am. Chem. Soc. 2016, 138, 11234–11244. [Google Scholar] [CrossRef] [PubMed]
- Gaita-Ariño, A.; Prima-García, H.; Cardona-Serra, S.; Escalera-Moreno, L.; Rosaleny, L.E.; Baldoví, J.J. Coherence and organisation in lanthanoid complexes: From single ion magnets to spin qubits. Inorg. Chem. Front. 2016, 3, 568–577. [Google Scholar] [CrossRef]
- Schleich, W.P. Quantum physics: Engineering decoherence. Nature 2000, 403, 256–257. [Google Scholar] [CrossRef] [PubMed]
- Goodwin, C.A.P.; Ortu, F.; Reta, D.; Chilton, N.F.; Mills, D.P. Molecular magnetic hysteresis at 60 kelvin in dysprosocenium. Nature 2017, 548, 439–442. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Guo, F.-S.; Day, B.M.; Chen, Y.-C.; Tong, M.-L.; Mansikkamäki, A.; Layfield, R.A. A Dysprosium Metallocene Single-Molecule Magnet Functioning at the Axial Limit. Angew. Chem. Int. Ed. 2017, 56, 11445–11449. [Google Scholar] [CrossRef] [PubMed]
- Zadrozny, J.M.; Niklas, J.; Poluektov, O.G.; Freedman, D.E. Millisecond Coherence Time in a Tunable Molecular Electronic Spin Qubit. ACS Cent. Sci. 2015, 1, 488–492. [Google Scholar] [CrossRef] [PubMed]
- Bader, K.; Dengler, D.; Lenz, S.; Endeward, B.; Jiang, S.-D.; Neugebauer, P.; van Slageren, J. Room temperature quantum coherence in a potential molecular qubit. Nat. Commun. 2014, 5, 5304. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Donati, F.; Rusponi, S.; Stepanow, S.; Wäckerlin, C.; Singha, A.; Persichetti, L.; Baltic, R.; Diller, K.; Patthey, F.; Fernandes, E.; et al. Magnetic remanence in single atoms. Science 2016, 352, 318–321. [Google Scholar] [CrossRef] [PubMed]
- Escalera-Moreno, L.; Baldoví, J.J.; Gaita-Ariño, A.; Coronado, E. Spin states, vibrations and spin relaxation in molecular nanomagnets and spin qubits: A critical perspective. Chem. Sci. 2018, 9, 3265–3275. [Google Scholar] [CrossRef] [PubMed]
- Clemente-Juan, J.M.; Coronado, E.; Gaita-Ariñoa, A. Magnetic polyoxometalates: From molecular magnetism to molecular spintronics and quantum computing. Chem. Soc. Rev. 2012, 41, 7464–7478. [Google Scholar] [CrossRef] [PubMed]
- Cardona-Serra, S.; Clemente-Juan, J.M.; Coronado, E.; Gaita-Ariño, A.; Camón, A.; Evangelisti, M.; Luis, F.; Martínez-Pérez, M.J.; Sesé, J. Lanthanoid Single-Ion Magnets Based on Polyoxometalates with a 5-fold Symmetry: The Series [LnP5W30O110]12− (Ln3+ = Tb, Dy, Ho, Er, Tm, and Yb). J. Am. Chem. Soc. 2012, 134, 14982–14990. [Google Scholar] [CrossRef] [PubMed]
- Shiddiq, M.; Komijani, D.; Duan, Y.; Gaita-Ariño, A.; Coronado, E.; Hill, S. Enhancing coherence in molecular spin qubits via atomic clock transitions. Nature 2016, 531, 348–351. [Google Scholar] [CrossRef] [PubMed]
- Baldoví, J.J.; Cardona-Serra, S.; Clemente-Juan, J.M.; Coronado, E.; Gaita-Ariño, A.; Prima-García, H. Coherent manipulation of spin qubits based on polyoxometalates: The case of the single ion magnet [GdW30P5O110]14−. Chem. Commun. 2013, 49, 8922–8924. [Google Scholar] [CrossRef] [PubMed]
- Baldoví, J.J.; Duan, Y.; Bustos, C.; Cardona-Serra, S.; Gouzerh, P.; Villanneau, R.; Gontard, G.; Clemente-Juan, J.M.; Gaita-Ariño, A.; Giménez-Saiz, C.; et al. Single ion magnets based on lanthanoid polyoxomolybdate complexes. Dalton Trans. 2016, 45, 16653–16660. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Baldoví, J.J.; Rosaleny, L.E.; Ramachandran, V.; Christian, J.; Dalal, N.S.; Clemente-Juan, J.M.; Yang, P.; Kortz, U.; Gaita-Ariño, A.; Coronado, E. Molecular spin qubits based on lanthanide ions encapsulated in cubic polyoxopalladates: Design criteria to enhance quantum coherence. Inorg. Chem. Front. 2015, 2, 893–897. [Google Scholar] [CrossRef]
- Delferro, M.; Graiff, C.; Elviri, L.; Predieri, G. Self-assembly of polyoxoselenitopalladate nanostars [Pd15(μ3-SeO3)10(μ3-O)10Na]9− and their supramolecular pairing in the solid state. Dalton Trans. 2010, 39, 4479–4481. [Google Scholar] [CrossRef] [PubMed]
- Lin, Z.-G.; Wang, B.; Cao, J.; Chen, B.-K.; Gao, Y.-Z.; Chi, Y.-N.; Xu, C.; Huang, X.-Q.; Han, R.-D.; Su, S.-Y.; et al. Cation-Induced Synthesis of New Polyoxopalladates. Inorg. Chem. 2012, 51, 4435–4437. [Google Scholar] [CrossRef] [PubMed]
- Izarova, N.V.; Biboum, R.N.; Keita, B.; Mifsud, M.; Arends, I.W.C.E.; Jameson, G.B.; Kortz, U. Self-assembly of star-shaped heteropoly-15-palladate(II). Dalton Trans. 2009, 9385–9387. [Google Scholar] [CrossRef] [PubMed]
- Izarova, N.V.; Pope, M.T.; Kortz, U. Noble metals in polyoxometalates. Angew. Chem. Int. Ed. 2012, 51, 9492–9510. [Google Scholar] [CrossRef] [PubMed]
- Kondinski, A.; Parac-Vogt, T.P. Keggin Structure, Quō Vādis? Front. Chem. 2018, 6, 346. [Google Scholar] [CrossRef] [PubMed]
- Yang, P.; Kortz, U. Discovery and Evolution of Polyoxopalladates. Acc. Chem. Res. 2018, 51, 1599–1608. [Google Scholar] [CrossRef] [PubMed]
- Kondinski, A.; Monakhov, K.Y. Breaking the Gordian Knot in the Structural Chemistry of Polyoxometalates: Copper(II)–Oxo/Hydroxo Clusters. Chem. Eur. J. 2017, 23, 7841–7852. [Google Scholar] [CrossRef] [PubMed]
- Büchner, O. Münzmetalle mit und in komplexen Anionen: Synthese, Struktur und Eigenschaften. Ph.D. Thesis, Carl von Ossietzky Universität Oldenburg, Oldenburg, Germany, 2005. Available online: https://oops.uni-oldenburg.de/id/eprint/63 (accessed on 1 April 2018).
- Yang, P.; Xiang, Y.; Lin, Z.; Lang, Z.; Jiménez-Lozano, P.; Carbó, J.J.; Poblet, J.M.; Fan, L.; Hu, C.; Kortz, U. Discrete Silver(I)-Palladium(II)-Oxo Nanoclusters, {Ag4Pd13} and {Ag5Pd15}, and the Role of Metal-Metal Bonding Induced by Cation Confinement. Angew. Chem. Int. Ed. 2016, 55, 15766–15770. [Google Scholar] [CrossRef] [PubMed]
- Xu, F.; Scullion, R.A.; Yan, J.; Miras, H.N.; Busche, C.; Scandurra, A.; Pignataro, B.; Long, D.; Cronin, L. A Supramolecular Heteropolyoxopalladate {Pd15} Cluster Host Encapsulating a {Pd2} Dinuclear Guest: [PdII2⊂{H7PdII15O10(PO4)10}]9−. J. Am. Chem. Soc. 2011, 133, 4684–4686. [Google Scholar] [CrossRef] [PubMed]
- Te Velde, G.; Bickelhaupt, F.M.; Baerends, E.J.; Guerra, C.F.; Van Gisbergen, S.J.A.; Snijders, J.G.; Ziegler, T.J. Chemistry with ADF. Comput. Chem. 2001, 22, 931–967. [Google Scholar] [CrossRef]
- Izarova, N.; Lin, Z.; Yang, P.; Kondinski, A.; Vankova, N.; Heine, T.; Kortz, U. The polyoxo-22-palladate(II), [Na2PdII22O12(AsVO4)15(AsVO3OH)]25−. Dalton Trans. 2016, 45, 2394–2398. [Google Scholar] [CrossRef] [PubMed]
- Kondinski, A.; Vankova, N.; Schinle, F.; Jäger, P.; Hampe, O.; Kortz, U.; Heine, T. How Counterions Affect the Solution Structure of Polyoxoaurates: Insights from UV–Vis Spectral Simulations and Electrospray Mass Spectrometry. Eur. J. Inorg. Chem. 2014, 3771–3778. [Google Scholar] [CrossRef]
- Izarova, N.; Kondinski, A.; Vankova, N.; Heine, T.; Jäger, P.; Schinle, F.; Hampe, O.; Kortz, U. The mixed gold-palladium polyoxo-noble-metalate, [NaAuIII4PdII8O8(AsO4)8]11−. Chem. Eur. J. 2014, 20, 8556–8560. [Google Scholar] [CrossRef] [PubMed]
- Barsukova-Stuckart, M.; Izarova, N.V.; Barrett, R.; Wang, Z.; van Tol, J.; Kroto, H.W.; Dalal, N.S.; Keita, B.; Heller, D.; Kortz, U. 3d Metal Ions in Highly Unusual Eight-Coordination: The Phosphate-Capped Dodecapalladate(II) Nanocube. Chem. Eur. J. 2012, 18, 6167–6171. [Google Scholar] [CrossRef] [PubMed]
- Shannon, R.D. Revised Effective Ionic Radii and Systematic Studies of Interatomic Distances in Halides and Chalcogenides. Acta Cryst. 1976, A32, 751–767. [Google Scholar] [CrossRef]
- Baldoví, J.J.; Borrás-Almenar, J.J.; Clemente-Juan, J.M.; Coronado, E.; Gaita-Ariño, A. Modeling the properties of lanthanoid single-ion magnets using an effective point-charge approach. Dalton Trans. 2012, 41, 13705–13710. [Google Scholar] [CrossRef] [PubMed]
- Baldoví, J.J.; Cardona-Serra, S.; Clemente-Juan, J.M.; Coronado, E.; Gaita-Ariño, A.; Palii, A. SIMPRE: A software package to calculate crystal field parameters, energy levels, and magnetic properties on mononuclear lanthanoid complexes based on charge distributions. J. Comput. Chem. 2013, 34, 1961–1967. [Google Scholar] [CrossRef]
- Baldoví, J.J.; Duan, Y.; Morales, R.; Gaita-Ariño, A.; Ruiz, E.; Coronado, E. Rational Design of Lanthanoid Single-Ion Magnets: Predictive Power of the Theoretical Models. Chem. Eur. J. 2016, 22, 13532–13539. [Google Scholar] [CrossRef] [PubMed]
- Baldoví, J.J.; Gaita-Ariño, A.; Coronado, E. Modeling the magnetic properties of lanthanide complexes: Relationship of the REC parameters with Pauling electronegativity and coordination number. Dalton Trans. 2015, 44, 12535–12538. [Google Scholar] [CrossRef] [PubMed]
- Rinehart, J.D.; Long, J.R. Exploiting single-ion anisotropy in the design of f-element single-molecule magnets. Chem. Sci. 2011, 2, 2078–2085. [Google Scholar] [CrossRef]
- Becke, A.D. A multicenter numerical integration scheme for polyatomic molecules. J. Chem. Phys. 1988, 88, 2547–2553. [Google Scholar] [CrossRef]
- Franchini, M.; Philipsen, P.H.T.; Visscher, L. The Becke Fuzzy Cells Integration Scheme in the Amsterdam Density Functional Program Suite. J. Comput. Chem. 2013, 34, 1819–1827. [Google Scholar] [CrossRef] [PubMed]
- Vosko, S.H.; Wilk, L.; Nusair, M. Accurate spin-dependent electron liquid correlation energies for local spin density calculations: A critical analysis. Can. J. Phys. 1980, 58, 1200–1211. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef]
- Perdew, J.P. Density-functional approximation for the correlation energy of the inhomogeneous electron gas. Phys. Rev. B Condens. Matter Mater. Phys. 1986, 33, 8822–8824. [Google Scholar] [CrossRef]
- Van Lenthe, E.; Baerends, E.J. Optimized Slater-type basis sets for the elements 1–118. J. Comput. Chem. 2003, 24, 1142–1156. [Google Scholar] [CrossRef] [PubMed]
- Lenthe, E.V.; Baerends, E.J.; Snijders, J.G. Relativistic regular two-component Hamiltonians. J. Chem. Phys. 1993, 99, 4597–4610. [Google Scholar] [CrossRef]
- Pye, C.C.; Ziegler, T. An implementation of the conductor-like screening model of solvation within the Amsterdam density functional package. Theor. Chem. Acc. 1999, 101, 396–408. [Google Scholar] [CrossRef]
- Stephens, P.J.; Devlin, F.J.; Chabalowski, C.F.; Frisch, M. Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields. J. Phys. Chem. 1994, 98, 11623–11627. [Google Scholar] [CrossRef]
- Poblet, J.M.; López, X. Computational Methods: Heteropolyoxoanions. In Encyclopedia of Inorganic and Bioinorganic Chemistry; Scott, R.A., Ed.; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- Barsukova-Stuckart, M.; Izarova, N.V.; Barrett, R.A.; Wang, Z.; van Tol, J.; Kroto, H.W.; Dalal, N.S.; Jiménez-Lozano, P.; Carbó, J.J.; Poblet, J.M.; et al. Polyoxopalladates Encapsulating 8-Coordinated Metal Ions, [MO8PdII12L8]n− (M = Sc3+, Mn2+, Fe3+, Co2+, Ni2+, Cu2+, Zn2+, Lu3+; L = PhAsO32−, PhPO32−, SeO32−). Inorg. Chem. 2012, 51, 13214–13228. [Google Scholar] [CrossRef] [PubMed]
- Lang, Z.; Yang, P.; Lin, Z.; Yan, L.; Li, M.-X.; Carbó, J.J.; Kortz, U.; Poblet, J.M. Size and charge effect of guest cations in the formation of polyoxopalladates: A theoretical and experimental study. Chem. Sci. 2017, 8, 7862–7872. [Google Scholar] [CrossRef] [PubMed]
- Kondinski, A.; Heine, T.; Monakhov, K.Yu. Rotational Isomerism, Electronic Structures, and Basicity Properties of “Fully-Reduced” V14-type Heteropolyoxovanadates. Inorg. Chem. 2016, 55, 3777–3788. [Google Scholar] [CrossRef] [PubMed]
- Fernández, J.A.; López, X.; Bo, C.; de Graaf, C.; Baerends, E.J.; Poblet, J.M. Polyoxometalates with Internal Cavities: Redox Activity, Basicity, and Cation Encapsulation in [Xn+P5W30O110](15−n)− Preyssler Complexes, with X = Na+, Ca2+, Y3+, La3+, Ce3+, and Th4+. J. Am. Chem. Soc. 2007, 129, 12244–12253. [Google Scholar] [CrossRef] [PubMed]
- Rudowicz, C.; Chung, C.Y. The generalization of the extended Stevens operators to higher ranks and spins, and a systematic review of the tables of the tensor operators and their matrix elements. J. Phys. Condens. Matter 2004, 16, 5825–5847. [Google Scholar] [CrossRef]
- Rudowicz, C. Transformation relations for the conventional Okq and normalised O’kq Stevens operator equivalents with k = 1 to 6 and −k ≤ q ≤ k. J. Phys. C Solid State Phys. 1985, 18, 1415–1430. [Google Scholar] [CrossRef]
- Rudowicz, C. Transformation relations for the conventional Okq and normalised O’kq Stevens operator equivalents with k = 1 to 6 and −k ≤ q ≤ k. J. Phys. C Solid State Phys. 1985, 18, 3837. [Google Scholar] [CrossRef]
- Ryabov, I.D. On the Generation of Operator Equivalents and the Calculation of Their Matrix Elements. J. Magn. Reson. 1999, 140, 141–145. [Google Scholar] [CrossRef] [PubMed]
- Stevens, K.W.H. Matrix Elements and Operator Equivalents Connected with the Magnetic Properties of Rare Earth Ions. Proc. Phys. Soc. 1952, 65, 209. [Google Scholar] [CrossRef]
- Edvardsson, S.; Klinterberg, M. Role of the electrostatic model in calculating rare-earth crystal-field parameters. J. Alloy. Comp. 1998, 275–277, 230–233. [Google Scholar] [CrossRef]



© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baldoví, J.J.; Kondinski, A. Exploring High-Symmetry Lanthanide-Functionalized Polyoxopalladates as Building Blocks for Quantum Computing. Inorganics 2018, 6, 101. https://doi.org/10.3390/inorganics6040101
Baldoví JJ, Kondinski A. Exploring High-Symmetry Lanthanide-Functionalized Polyoxopalladates as Building Blocks for Quantum Computing. Inorganics. 2018; 6(4):101. https://doi.org/10.3390/inorganics6040101
Chicago/Turabian StyleBaldoví, José J., and Aleksandar Kondinski. 2018. "Exploring High-Symmetry Lanthanide-Functionalized Polyoxopalladates as Building Blocks for Quantum Computing" Inorganics 6, no. 4: 101. https://doi.org/10.3390/inorganics6040101
APA StyleBaldoví, J. J., & Kondinski, A. (2018). Exploring High-Symmetry Lanthanide-Functionalized Polyoxopalladates as Building Blocks for Quantum Computing. Inorganics, 6(4), 101. https://doi.org/10.3390/inorganics6040101