Next Article in Journal / Special Issue
Electronic Structure of Cubane-Like Vanadium–Nitrogen Cationic Clusters [V4N4]+ and [V6N6]+
Previous Article in Journal
Electrochemical and Computational Insights into the Reduction of [Fe2(CO)6{µ-(SCH2)2GeMe2}] Hydrogenase H-Cluster Mimic
Previous Article in Special Issue
Comparative Study of Complexes of Rare Earths and Actinides with 2,6-Bis(1,2,4-triazin-3-yl)pyridine
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Inorganics
Volume 7
Issue 4
10.3390/inorganics7040051
inorganics-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

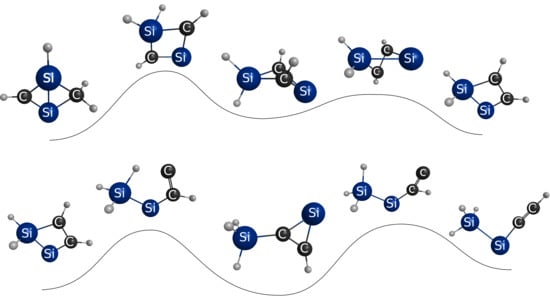
The Lowest-Energy Isomer of C2Si2H4 Is a Bridged Ring: Reinterpretation of the Spectroscopic Data Based on DFT and Coupled-Cluster Calculations

by
Jesse J. Lutz
1,* and
Larry W. Burggraf
2
1
ORISE Fellow Residing at Department of Engineering Physics, Air Force Institute of Technology, Wright-Patterson Air Force Base, Dayton, OH 45433-7765, USA
2
Department of Engineering Physics, Air Force Institute of Technology, Wright-Patterson Air Force Base, Dayton, OH 45433-7765, USA
*
Author to whom correspondence should be addressed.
Inorganics 2019, 7(4), 51; https://doi.org/10.3390/inorganics7040051
Submission received: 28 February 2019 / Revised: 2 April 2019 / Accepted: 3 April 2019 / Published: 11 April 2019
(This article belongs to the Special Issue Applications of Density Functional Theory in Inorganic Chemistry)
Browse Figures
Versions Notes

Abstract

:
The lowest-energy isomer of C 2 Si 2 H 4 is determined by high-accuracy ab initio calculations to be the bridged four-membered ring 1,2-didehydro-1,3-disilabicyclo[1.1.0]butane (1), contrary to prior theoretical and experimental studies favoring the three-member ring silylsilacyclopropenylidene (2). These and eight other low-lying minima on the potential energy surface are characterized and ordered by energy using the CCSD(T) method with complete basis set extrapolation, and the resulting benchmark-quality set of relative isomer energies is used to evaluate the performance of several comparatively inexpensive approaches based on many-body perturbation theory and density functional theory (DFT). Double-hybrid DFT methods are found to provide an exceptional balance of accuracy and efficiency for energy-ordering isomers. Free energy profiles are developed to reason the relatively large abundance of isomer 2 observed in previous measurements. Infrared spectra and photolysis reaction mechanisms are modeled for isomers 1 and 2, providing additional insight about previously reported spectra and photoisomerization channels.

Graphical Abstract

1. Introduction

The C 2 Si 2 H 4 molecule has been the subject of very few literature studies, despite being a bicyclobutane/butadiene analog of fundamental interest. Holme et al. [1] predicted the existence of over a dozen cyclic C 2 Si 2 H 4 stationary points at the Hartree-Fock (HF) level, assigning the lowest-energy isomer as the three-membered ring silylsilacyclopropenylidene. Inclusion of correlation energy using third-order many-body perturbation theory (MBPT(3)) left the isomer ordering unchanged, though it is worth noting that a modest 6-31G(d) basis set was employed. Holme remarked that a three-membered-ring isomer seemed an “unlikely choice” due to the enhanced strain destabilization as compared with competing four-membered-ring structures. Structural compression is energetically favorable when electron-correlation stabilization dominates over strain destabilization. If this is the case for C 2 Si 2 H 4 , one might expect that the maximally compressed isomer, a bridged bicyclobutane analog, should be the global minimum. One such isomer was considered by Holme et al., but it was predicted to be over 10 kcal/mol higher in energy than silylsilacyclopropenylidene.
In the first experimental study on C 2 Si 2 H 4 , Maier et al. reported infrared (IR) measurements supplemented by density functional theory (DFT) vibrational simulations [2]. In their workup a mixture of silane structures was thermalized by pulsed flash pyrolysis at 1500 K, and the resulting mixture was rapidly frozen out in an Ar matrix at 10 K before IR characterization. Signatures of silylsilacyclopropenylidene were detected and upon further irradiation the corresponding ring-opening photolysis products were observed (i.e., (silylethynyl)silylene and ethynylsilylsilylene). Accompanying calculations were performed using the BLYP generalized-gradient approximation (GGA) exchange correlation functional (XCF) and assigned silylsilacyclopropenylidene as the global minimum, in agreement with the prediction of Holme et al. Due to this apparent agreement between theory and experiment, this assignment of the lowest-energy isomer of C 2 Si 2 H 4 has stood for over 20 years.
The purpose of the current study is to apply more sophisticated computational methods to investigate the delicate balance between electron-correlation stabilization and strain destabilization in C 2 Si 2 H 4 . Ground-state DFT methods, and their extension to excited states via time-dependent (TD) DFT [3,4,5], are the most widely-used approaches for describing electron correlation in atoms, molecules, and solids [6]. While superior to the HF self-consistent field (SCF) theory, the popular BLYP and B3LYP approaches have major shortcomings, which often result in qualitatively incorrect predictions [7]. In light of recent advancements, the default choice of XCF needs to be augmented, updated, or supplanted entirely [8]. Since it is unclear which of the hundreds of existing functionals perform best overall, several popular functionals were chosen from the BLYP [9,10], PBE [11,12], and Minnesota functional families [13,14,15,16] for evaluation in the context of the current application.
The quality of XCFs can be ranked as being on one of five rungs of Jacob’s ladder, with the fifth rung approaching the “heaven” of chemical accuracy [17]. Here the term “chemical accuracy” takes the colloquial meaning that a method is predictive to within 1 kcal/mol. Functionals including only a local density approximation to the correlation functional [18] represent the first rung, while those incorporating GGA correlation represent the second rung. After density gradients, Laplacians can be included in the mix, resulting in meta-GGA functionals, or the third rung of Jacob’s ladder [19]. Hybrid functionals are on the fourth rung of Jacob’s ladder, often referred to as hyper-GGAs, while the fifth rung of Jacob’s ladder is represented here by double-hybrid (DH) DFT methods [20,21], which semiempirically blend DFT and wave-function theory. Only functionals from the highest three rungs will be considered here.
Electron correlation can be treated within a more hierarchical framework by using wave-function methods, which, unlike DFT, are systematically improvable to the exact solution of the Schrödinger equation. In the ground state, approximations based on the coupled-cluster (CC) hierarchy [22,23,24,25,26,27] are among the most rapidly convergent approaches, with the CCSD(T) method often referred to as the “gold standard” of quantum chemistry. While expensive, CCSD(T) energies extrapolated to the complete basis set (CBS) limit are widely considered benchmark-quality for molecules near their equilibrium geometries. In situations where degeneracy is commonly encountered (e.g., when crossing transition states, when accessing excited states, or when breaking or forming bonds), CCSD(T) can fail [28], and in these cases one can instead turn to new generations of CC methods, such as the left-eigenstate completely renormalized (CR) CC method [29,30,31,32] called CR-CC(2,3). The CR-CC(2,3) approach provides an accurate description of single-bond-breaking processes [33,34], biradical and magnetic molecules [35,36], and transition states [37,38]. Excited states can be accessed in a straightforward manner using the equation of motion (EOM) CC formalism [39,40,41,42], resulting in the CR-EOMCC(2,3) approximation and its size-intensive variant δ -CR-EOMCC(2,3) [31,43,44,45,46]. Experience shows that reliable energetics are produced for ring-opening [47] and bond-rearrangement processes [48] when CR-CC(2,3) is applied on top of appropriate complete-active-space (CAS) SCF geometries. The steep O ( n 7 ) scalings of CCSD(T) and CR-CC methods prohibit their use for all but the smallest systems, but fortunately they are readily applicable to the title molecule.
The motivation for this work spans several fields. Mapping interstellar silicon reaction networks is one application [49], as C 2 Si 2 H 4 may result from bimolecular collisions between the highly-abundant acetylene and its silicon-based analog disilyne. This bimolecular reaction and subsequent isomerization can also be considered as a model system for understanding preferred bonding configurations in coordinate complexes [50], bulk silicon surface-adsorption [51], and defect-inclusion processes [52]. Many of the present modeling decisions were guided by prior benchmarking work on the structure and spectroscopy of hydrogen-free silicon carbide clusters [53,54]. This study continues along these lines, investigating the performance of various modern DFT methods by comparing against spectroscopic values and high-level computational results. The structure of the paper is as follows. The methods employed are detailed in Section 2, the results and discussion are covered in Section 3, while concluding remarks and final recommendations for density functional usage are offered in Section 4.

2. Computational Methods

Electronic structure calculations were performed using the GAMESS [55,56] and Gaussian16 [57] packages on the AFRL DSRC SGI Ice X Thunder and a local workstation. Visualizations were performed using the GaussView V6 [58] and MacMolPlt V7.3 [59] software packages. All DFT gradient calculations employed the tight JANS = 2 grid in GAMESS and the ultrafine grid in Gaussian. Grimme’s D3(BJ) empirical dispersion correction was also employed [60,61,62,63].
We employed the basis sets DZP [64], Def2-TZVP, and Def2-QZVP [65]. Ahlrichs’ triple- ζ ( n = 3 ) and quadruple- ζ ( n = 4 ) basis sets were used in conjunction with the formula of Helgaker et al. [66], E = E cbs + A n − 3 , for CBS extrapolation of the correlation energy, with the SCF component of CBS energies approximated at the HF/cc-pV5Z level. Geometry optimizations were performed at the level of theory indicated by the conventional double-forward slash notation (e.g., CCSD(T)//MBPT(2)) [67,68]. All MBPT(4) calculations correspond to the MBPT(4)-SDQ approximation, and all CR-CC(2,3) and CR-EOMCC(2,3) triples corrections correspond to the most complete “D” variant, which employs the exact Epstein-Nesbet-like denominator [69]. Core orbitals were frozen in all wave-function calculations.

3. Results

3.1. Energy-Ordering C 2 Si 2 H 4 Isomers

The full potential energy surface of C 2 Si 2 H 4 includes many energetically-similar local minima involving strained three- and four-membered heterocyclic rings. Dozens of unique cyclic species can be imagined, with some resembling cyclobutane or methylcyclopropane, but, unlike their hydrocarbon analogs, C 2 Si 2 H 4 isomers differing by a transannular hydrogen migration are often separated by only a few kcal/mol. Due to the diversity of possible bonding configurations, ranking such structures by energy demands a high-level treatment of the correlation energy and a large basis set.
Figure 1 collects structures and dipole moments for 10 low-lying C 2 Si 2 H 4 isomers characterized as PES minima using B3LYP/Def2-QZVP. Dipole moments are also provided, as derived from B2PLYP/Def2-QZVP electronic densities. Saddle-point structures of any order were discarded. Isomer 2 was previously characterized as the global minimum and isomer 6 is reported here for the first time. Isomers 1 and 2 are the focal point of this work, and they have IUPAC names 1,2-didehydro-1,3-disilabicyclo[1.1.0]butane and silylsilacyclopropenylidene, respectively [70].
Optimizations were performed with no symmetry imposed, unlike in previous studies, and consequently many of the four-membered ring structures adopted puckered configurations. This puckering caused insignificant reductions in relative isomer energies accompanied by significant increases in dipole moments. Dipole moments computed using other levels were found to be within ∼5% of the B2PLYP/Def2-QZVP values reported in Figure 1. Cartesian coordinates and cartesian decompositions of dipole moments corresponding to the B3LYP/Def2-QZVP optimized structures are available in the Supplementary Materials.
Table 1 demonstrates the basis set dependence of the relative energies of isomers 1 and 2. The small-basis MBPT(3) calculations reported by Holme et al. predicted a value of 11.6 kcal/mol, while the energy difference calculated at the CCSD(T)//MBPT(2)/Def2-TZVP level was found to be 0.0 kcal/mol. When diffuse functions were added the energy difference reduced by 1.8 kcal/mol, and it reduced 1.0 kcal/mol further in going from Def2-TZVPD to Def2-QZVP. A value of −3.4 kcal/mol was obtained after CBS extrapolation, differing by 15.0 kcal/mol from the best value reported by Holme et al. Recognizing the sensitivity of the relative energies to basis set size, the Def2-QZVP basis set was employed for all isomer-ordering geometry optimizations.
Table 2 collects relative isomer energies for the 10 structures in Figure 1 using the Def2-QZVP basis set and wave-function methods including MBPT at second-, third-, and fourth-orders, as well as CCSD and CCSD(T). All calculations were performed on structures optimized at the MBPT(2)/Def2-QZVP level, with MBPT(2)/Def2-QZVP-level zero-point vibrational energy (ZPVE) corrections included. Benchmark-quality values computed at the CCSD(T)/CBS//MBPT(2)/Def2-QZVP level, are provided in the final column of Table 2, were used to generate mean signed errors (MSE) and mean unsigned errors (MUE) for each method. Only MBPT(2) failed to achieve chemical accuracy, i.e., a MUE under 1.0 kcal/mol.
Table 3 focuses on DFT-based methods, with pure GGAs, hybrid GGAs, and double-hybrid methods based on BLYP, PBE, and Minnesota XCFs represented. At the BLYP and B3LYP levels, isomer 2 was predicted as the global minimum, consistent with the small-basis BLYP results in Ref. [2]. All other methods tested here ordered isomer 1 below 2. The M06-2X and B2-PLYP+D3 approaches ordered all ten energies correctly, while DSDPBEP86 was also very close, erring by only 0.1 kcal/mol in ordering isomers 8 and 9. Only the DH-DFT methods methods produced MUEs within chemical accuracy, on average.
Figure 2 collects temperature-dependent free-energy profiles computed using MBPT(2), B3LYP, and M06-2X in conjunction with the Def2-QZVP basis set. The study by Maier et al. described sample preparation by flash pyrolysis at 1500 K, and at this temperature all three methods place isomer 2 lowest in energy. It is thus likely that thermodynamic equilibrium of the structures was not achieved within the 10K Ar matrix preceding the IR measurements. Taking into consideration their temperature-independent enthalpic energy displacements, the free-energy profiles for each of the higher-lying isomers in Figure 2 are qualitatively very similar. The notable exception is isomer 4, which has a positive gradient when computed with MBPT(2) and a negative gradient when computed with B3LYP and M06-2X.

3.2. Infrared Spectroscopy of Low-Lying C 2 Si 2 H 4 Isomers

In Section 3.1, high-accuracy ab initio methods were employed to determine isomer 1 as the zero-temperature global PES minimum, while free-energy simulations flipped the order of the two lowest-lying isomers at the pyrolysis temperature reported by Maier et al. Assuming that a non-equilibrium mixture of isomers was present during the IR characterization performed at 10K, traces of isomer 1 may have been overlapped with peaks attributed to the dominant species, isomer 2. Broad bands of this type were noted by Maier et al. occurring at 2190 cm − 1 and 919 cm − 1 . If these peaks are attributable to isomer 1, this is supporting evidence that both isomers were measured in the non-equilibrium mixture, and helps further reconcile the past and present global minimum assignments.
Figure 3 compares simulated IR spectra with peaks reported in measurements by Maier et al. Simulated spectra were computed for isomer 1 using the CASSCF(6,6), MBPT(2), and B3LYP levels of theory with the Def2-TZVP basis set. All theoretical spectra exhibit large-intensity frequencies in good agreement with the positions of the measured broad features. Vibrational simulations are known to be insensitive to both basis-set size and correlation effects, so higher-level results were not pursued. Thus, the theoretical vibrational characterizations of isomer 1 qualitatively match the broad peaks at 2190 and 920 cm − 1 , and this warrants further analysis.
Table 4 presents a quantitative comparison of the strongest IR peaks of isomers 1 and 2. Of the three methods tested, B3LYP produces the most accurate frequencies as compared to the measured IR peaks, with all values being within 50 cm − 1 of an observed frequency. Indeed, the spectral fingerprints of the two isomers are quantitatively very similar, supporting the hypothesis that both isomers were present in the original measurements.

3.3. Photoisomerization of Low-Lying C 2 Si 2 H 4 Isomers

The experimental analysis by Maier et al. also inferred the presence of isomer 2 by monitoring photolysis products via IR spectroscopy. Irradiation with 313 or 366 nm light was found to isomerize 2 via ring-opening to form (silylethynyl)silylene (H 3 SiCCSiH) and ethynylsilylsilylene (H 3 SiSiCCH). Explicit mapping of isomerization mechanisms can be performed using intrinsic reaction coordinate (IRC) calculations to connect key stationary points on the PES. Photoisomerization mechanisms can be explored by performing vertical excitation energy (VEE) calculations on the ground-state IRC structures, though we note that this does not provide definitive proof of the mechanism since, in general, none of the considered structures are well-defined stationary points on the excited-state surfaces.
Figure 4 compares potential energy cuts for the ring-opening of isomer 2, as generated using a variety of wave-function and DFT methods. The underlying ground-state structures were generated from IRC calculations connecting isomer 2 to the observed non-cyclic product H 3 SiCCSiH. IRC calculations were performed using the CASSCF(6,6), B3LYP and M06-2X methods, in Figure 4a–c, respectively. Within each frame, other methods were applied on top of these underlying geometries.
Experimental evidence suggests that irradiation of the reactant structure leads to photoconversion, implying a negative gradient on the excited-state surface at the equilibrium geometry. All theories generated potential cuts consistent with this mechanism. Evidently the second excited state is accessed by absorption of an incident photon and the reaction proceeds by adiabatic relaxation along a negative potential gradient, eventually transitioning through a cascade of avoided crossings to form the product isomer. The wave-function and DFT results differ significantly only in the placement of the avoided crossing between the first- and second-excited states, with the EOMCC methods placing it near the reactant geometry and TDDFT methods placing it near the transition state geometry.
Figure 5 collects stationary points characterized using B3LYP/DZP and carefully connected by IRC calculations. Corresponding relative energies are also provided, though, due to the basis set size, discussion is reserved to qualitative aspects of the surface. Isomer 1 was found to be connected to isomer 2 via several transition states and intermediates involving transannular hydrogen migration and bond rearrangements. The largest barrier height separating isomers 1 and 2 is shown to be within 1–2 kcal/mol of that separating isomer 2 and the second observed photolysis product, ethynylsilylsilylene. Thus, the activation energy required to surmount barriers separating isomer 2 and products will also drive the reaction converting isomer 1 to products. The magnitude of the barrier heights excludes the possibility of thermal isomerization in normal laboratory conditions.
Maier et al. reported photoisomerization after irradiation at 313 or 366 nm, resulting in the observed non-cyclic photolysis products H 3 SiCCSiH and H 3 SiSiCCH. To confirm that these frequencies will drive photoconversion of both 1 and 2, VEEs were computed at each stationary point shown in Figure 5. Table 5 collects the computed relative ground-state energies and VEEs for each stationary point structure, with labeling preserved from Figure 1. The previously reported irradiation frequencies, converted to 91.3 and 78.1 kcal/mol, are within 10% of the predicted VEEs for isomers 1, 6, and 3. A spectrally broadened light source may photoexcite and interconvert between each of the considered cyclic isomers 1, 2, 3, and 6, eventually driving the photolysis to the observed non-cyclic products H 3 SiCCSiH and H 3 SiSiCCH.

4. Conclusions

Ten C 2 Si 2 H 4 isomers were characterized as PES minima and energy-ordered using high-level coupled-cluster calculations. Isomer 1, or 1,2-didehydro-1,3-disilabicyclo[1.1.0]butane, was assigned as the global minimum, in contrast to all existing literature on this system which favored isomer 2, or silylsilacyclopropenylidene. High-level coupled-cluster isomer energies were used to benchmark DFT methods, and BLYP and B3LYP incorrectly predicted isomer 2 as the global minimum, even when very large basis sets were employed. Many DFT methods struggled to order all ten isomer energies correctly with respect to benchmarks. Only the B2-PLYP+D3 DH-DFT method energy-ordered all isomers similarly to the benchmarks, while also producing an MUE within chemical accuracy. Among the pure and hybrid functionals tested, only M06-2X predicted the same energy ordering with respect to the benchmarks but its MUE was slightly above the chemical accuracy threshold.
Assignment of isomer 1 as the global minimum required a reinterpretation of prior experimental data to reconcile with past assignments of isomer 2 as the global minimum. Computations helped show that the frequencies of isomers 1 and 2 overlap, which likely contributed to the broad bands previously observed in the IR difference spectrum. Some PES mapping was also performed to provided insight into the mechanism of photolysis of isomers 1 and 2 to form the observed products H 3 SiCCSiH and H 3 SiSiCCH. These simulations suggested that the ultraviolet frequencies used to irradiate the sample may initiate photolysis in both isomers 1 and 2, leading to the observed products.
Taken together, these simulations provide compelling evidence that the energetically similar isomers 1 and 2 were likely both present as reactants in the measurements reported in Ref. [2]. In light of the present analysis, there exists no contradictory evidence in the literature to dismiss assignment of isomer 1 as the global minimum. In closing, isomer 1 has been identified as a prominent configuration on the global PES of a barrierless acetylene-disilyne collision, and its dipole moment is strong enough for electron binding. Thus, it may be of significance in interstellar silicon carbide reaction networks. This prospect will be investigated in a future study.

Supplementary Materials

The following are available online at https://www.mdpi.com/2304-6740/7/4/51/s1, geometries, energies, zero-point vibrational energies, and dipole moments obtained at the B3LYP/Def2-QZVP level.

Author Contributions

Conceived the project, performed all calculations, and wrote the manuscript, J.J.L.; commented on the manuscript and provided entropic insights, L.W.B.

Funding

This work was supported at the Air Force Institute of Technology (AFIT) in part by the Defense Threat Reduction Agency (Grant No. HDTRA 18-274-34), with additional funding from the DoD Quantum Science and Engineering Program. Jesse J. Lutz was supported by an appointment to the Faculty Research Participation Program at the AFIT, administered by the Oak Ridge Institute for Science and Education through an interagency agreement between the U.S. Department of Energy and AFIT. We are grateful for a grant of computer time at the U.S. Air Force Research Laboratory DoD Supercomputing Research Center and we thank Frank Duan for comments on the manuscript. The views expressed in this work are those of the authors and do not reflect the official policy or position of the United States Air Force, Department of Defense, or the United States Government.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

The following abbreviations are used in this manuscript:
DFTDensity functional theory
KSKohn-Sham
SCFSelf-consistent field
HFHartree-Fock
XCFExchange-correlation functional
LYPLee Yang Parr
PBEPerdew Berke Ernzerhof
DHDouble-hybrid
MBPTMany-body perturbation theory
DSDDispersion corrected, Spin-component scaled, Double-hybrid
TDTime-dependent
CCCoupled-cluster
CCSDCoupled-cluster with singles and doubles
CRCompletely renormalized
EOMEquation-of-motion
IRInfrared
CBSComplete basis set
CASComplete active space
ZPVEZero-point vibrational energy
MSEMean signed error
MUEMean unsigned error
IRCInternal reaction coordinate
VEEVertical excitation energies

References

  1. Holme, T.A.; Gordon, M.S.; Yabushita, S.; Schmidt, M.W. Theoretical studies of cyclic C2Si2H4 molecules. Organometallics 1984, 3, 583–586. [Google Scholar] [CrossRef]
  2. Maier, G.; Reisenauer, H.P.; Meudt, A. Silylenes of the Elemental Composition C2H4Si2: Generation and Matrix-Spectroscopic Identification. Eur. J. Org. Chem. 1998, 1998, 1291. [Google Scholar] [CrossRef]
  3. Casida, M.E. Time-Dependent Density Functional Response Theory for Molecules. In Recent Advances in Density Functional Methods; World Scientific: Singapore, 1995; pp. 155–192. [Google Scholar] [CrossRef]
  4. Casida, M.E. Jacob’s Ladder for Time-Dependent Density-Functional Theory: Some Rungs on the Way to Photochemical Heaven. In ACS Symposium Series; American Chemical Society: Washington, DC, USA, 2002; pp. 199–220. [Google Scholar] [CrossRef]
  5. Maitra, N.T. Fundamental aspects of time-dependent density functional theory. J. Chem. Phys. 2016, 144, 220901. [Google Scholar] [CrossRef]
  6. Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. B 1964, 136, 864. [Google Scholar] [CrossRef]
  7. Zhang, I.Y.; Wu, J.; Xu, X. Extending the reliability and applicability of B3LYP. Chem. Commun. 2010, 46, 3057–3070. [Google Scholar] [CrossRef] [PubMed]
  8. Kruse, H.; Goerigk, L.; Grimme, S. Why the Standard B3LYP/6-31G* Model Chemistry Should Not Be Used in DFT Calculations of Molecular Thermochemistry: Understanding and Correcting the Problem. J. Org. Chem. 2012, 77, 10824–10834. [Google Scholar] [CrossRef]
  9. Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098. [Google Scholar] [CrossRef]
  10. Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785. [Google Scholar] [CrossRef]
  11. Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
  12. Adamo, C.; Barone, V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 1999, 110, 6158–6170. [Google Scholar] [CrossRef]
  13. Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar] [CrossRef]
  14. Peverati, R.; Truhlar, D.G. Improving the Accuracy of Hybrid Meta-GGA Density Functionals by Range Separation. J. Phys. Chem. Lett. 2011, 2, 2810–2817. [Google Scholar] [CrossRef]
  15. Yu, H.S.; He, X.; Li, S.L.; Truhlar, D.G. MN15: A Kohn–Sham global-hybrid exchange–correlation density functional with broad accuracy for multi-reference and single-reference systems and noncovalent interactions. Chem. Sci. 2016, 7, 5032–5051. [Google Scholar] [CrossRef]
  16. Mardirossian, N.; Head-Gordon, M. How Accurate are the Minnesota Density Functionals for Noncovalent Interactions, Isomerization Energies, Thermochemistry, and Barrier Heights Involving Molecules Comprised of Main-Group Elements. J. Chem. Theory Comput. 2016, 12, 4303–4325. [Google Scholar] [CrossRef]
  17. Perdew, J.; Schmidt, K. Jacob’s ladder of density functional approximations for the exchange-correlation energy. In Density Functional Theory and Its Applications to Materials; Doren, V.V., Alsenoy, K.V., Geerlings, P., Eds.; AIP Conference Proceedings: Melville, NY, USA, 2001; Volume 577, pp. 1–20. [Google Scholar] [CrossRef]
  18. Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133. [Google Scholar] [CrossRef]
  19. Perdew, J.P.; Ruzsinszky, A.; Tao, J.; Staroverov, V.N.; Scuseria, G.E.; Csonka, G.I. Prescription for the design and selection of density functional approximations: More constraint satisfaction with fewer fits. J. Chem. Phys. 2005, 123, 062201. [Google Scholar] [CrossRef]
  20. Zhang, Y.; Xu, X.; Goddard, W.A. Doubly hybrid density functional for accurate descriptions of nonbond interactions, thermochemistry, and thermochemical kinetics. Proc. Natl. Acad. Sci. USA 2009, 106, 4963–4968. [Google Scholar] [CrossRef]
  21. Goerigk, L.; Grimme, S. Double-hybrid density functionals. WIREs Comput. Mol. Sci. 2014, 4, 576–600. [Google Scholar] [CrossRef]
  22. Coester, F. Bound states of a many-particle system. Nucl. Phys. 1958, 7, 421. [Google Scholar] [CrossRef]
  23. Coester, F.; Kümmel, H. Short-range correlations in nuclear wave functions. Nucl. Phys. 1960, 17, 477. [Google Scholar] [CrossRef]
  24. Čížek, J. On the correlation problem in atomic and molecular systems. Calculation of wavefunction components in Ursell-type expansion using quantum-field theoretical methods. J. Chem. Phys. 1966, 45, 4256. [Google Scholar] [CrossRef]
  25. Čížek, J. On the use of the cluster expansion and the technique of diagrams in calculations of correlation effects in atoms and molecules. Adv. Chem. Phys. 1969, 14, 35. [Google Scholar]
  26. Čížek, J.; Paldus, J. Correlation problmes in atomic and molecular systems. III. Rederivation of the coupled-pair many-electron theory using the traditional quantum chemical methods. Int. J. Quantum Chem. 1971, 5, 359. [Google Scholar] [CrossRef]
  27. Paldus, J.; Čížek, J.; Shavitt, I. Correlation problems in atomic and molecular systems. IV. Extended coupled-pair many-electron theory and its application to the BH3 molecule. Phys. Rev. A 1972, 5, 50. [Google Scholar] [CrossRef]
  28. Margraf, J.T.; Perera, A.; Lutz, J.J.; Bartlett, R.J. Single-reference coupled cluster theory for multi-reference problems. J. Chem. Phys. 2017, 147, 184101. [Google Scholar] [CrossRef]
  29. Piecuch, P.; Włoch, M. Renormalized coupled-cluster methods exploiting left eigenstates of the similarity-transformed Hamiltonian. J. Chem. Phys. 2005, 123, 224105. [Google Scholar] [CrossRef]
  30. Piecuch, P.; Włoch, M.; Gour, J.R.; Kinal, A. Single-reference, size-extensive, non-iterative coupled-cluster approaches to bond breaking and biradicals. Chem. Phys. Lett. 2006, 418, 467. [Google Scholar] [CrossRef]
  31. Włoch, M.; Lodriguito, M.D.; Piecuch, P.; Gour, J.R. Two new classes of non-iterative coupled-cluster methods derived from the method of moments of coupled-cluster equations. Mol. Phys. 2006, 104, 2149–2172. [Google Scholar]
  32. Włoch, M.; Gour, J.R.; Piecuch, P. Extension of the renormalized coupled-cluster methods exploiting left eigenstates of the similarity-transformed Hamiltonian to open-shell systems: A benchmark study. J. Phys. Chem. 2007, A111, 11359. [Google Scholar] [CrossRef]
  33. Lutz, J.J.; Piecuch, P. Performance of the completely renormalized equation-of-motion coupled-cluster method in calculations of excited-state potential cuts of water. Comput. Theor. Chem. 2014, 1040–1041, 20–34. [Google Scholar] [CrossRef]
  34. Kornobis, K.; Kumar, N.; Lodowski, P.; Jaworska, M.; Piecuch, P.; Lutz, J.J.; Wong, B.M.; Kozlowski, P.M. Electronic Structure of the S1 State in Methylcobalamin: Insight from CASSCF/MC-XQDPT2, EOM-CCSD, and TD-DFT Calculations. J. Comp. Chem. 2013, 34, 987–1004. [Google Scholar] [CrossRef]
  35. Abe, M. Diradicals. Chem. Rev. 2013, 113, 7011–7088. [Google Scholar] [CrossRef]
  36. Lutz, J.J.; Nooijen, M.; Perera, A.; Bartlett, R.J. Reference dependence of the two-determinant coupled-cluster method for triplet and open-shell singlet states of biradical molecules. J. Chem. Phys. 2018, 148, 164102. [Google Scholar] [CrossRef]
  37. Zhao, Y.; Tishchenko, O.; Gour, J.R.; Li, W.; Lutz, J.J.; Piecuch, P.; Truhlar, D.G. Thermochemical kinetics for multireference systems: Addition reactions of ozone. J. Phys. Chem. A 2009, 113, 5786–5799. [Google Scholar] [CrossRef] [PubMed]
  38. Lutz, J.J.; Hutson, J.M. Reactions between cold methyl halide molecules and alkali-metal atoms. J. Chem. Phys. 2014, 140, 014303. [Google Scholar] [CrossRef] [PubMed]
  39. Emrich, K. An extension of the coupled cluster formalism to excited-states (I). Nucl. Phys. A 1981, 351, 379–396. [Google Scholar] [CrossRef]
  40. Geertsen, J.; Rittby, M.; Bartlett, R.J. The equation-of-motion coupled-cluster method: Excitation energies of Be and CO. Chem. Phys. Lett. 1989, 164, 57–62. [Google Scholar] [CrossRef]
  41. Comeau, D.C.; Bartlett, R.J. The equation-of-motion coupled-cluster method. Applications to open- and closed-shell reference states. Chem. Phys. Lett. 1993, 207, 414–423. [Google Scholar] [CrossRef]
  42. Christiansen, O.; Koch, H.; Jørgensen, P.; Olsen, J. Excitation energies of H2O, N2 and C2 in full configuration interaction and coupled cluster theory. Chem. Phys. Lett. 1996, 256, 185–194. [Google Scholar] [CrossRef]
  43. Piecuch, P.; Włoch, M.; Lodriguito, M.; Gour, J.R. Noniterative coupled-cluster methods for excited electronic states. In Recent Advances in the Theory of Chemical and Physical Systems, Progress in Theoretical Chemistry and Physics; Wilson, S., Julien, J.P., Maruani, J., Brändas, E., Delgado-Barrio, G., Eds.; Springer: Dordrecht, The Netherlands, 2006; Volume 15, pp. 45–106. [Google Scholar]
  44. Piecuch, P.; Gour, J.R.; Włoch, M. Left-eigenstate completely renormalized equation-of-motion coupled-cluster methods: Review of key concepts, extension to excited states of open-shell systems, and comparison with electron-attached and ionized approaches. Int. J. Quantum Chem. 2009, 109, 3268–3304. [Google Scholar] [CrossRef]
  45. Fradelos, G.; Lutz, J.J.; Wesołowski, T.A.; Piecuch, P.; Włoch, M. Embedding vs supermolecular strategies in evaluating the hydrogen-bonding-induced shifts of excitation energies. J. Chem. Theory Comput. 2011, 7, 1647–1666. [Google Scholar] [CrossRef]
  46. Fradelos, G.; Lutz, J.J.; Wesołowski, T.A.; Piecuch, P.; Włoch, M. Shifts in excitation energies induced by hydrogen bonding: A comparison of the embedding and supermolecular time-dependent density functional theory calculations with the equation-of-motion coupled-cluster results. In Advances in the Theory of Quantum Systems in Chemistry and Physics, Progress in Theoretical Chemistry and Physics; Hoggan, P.E., Brändas, E.J., Maruani, J., Piecuch, P., Delgado-Barrio, G., Eds.; Springer: Dordrecht, The Netherlands, 2012; Volume 22, pp. 219–248. [Google Scholar]
  47. Lutz, J.J.; Piecuch, P. Extrapolating Potential Energy Surfaces by Scaling Electron Correlation: Isomerization of Bicyclobutane to Butadiene. J. Chem. Phys. 2008, 128, 154116. [Google Scholar] [CrossRef]
  48. Magoon, G.R.; Aguilera-Iparraguirre, J.; Green, W.H.; Lutz, J.J.; Piecuch, P.; Oluwole, O.O.; Wong, H.W. Detailed Chemical Modeling of JP-10 (exo-tetrahydrodicyclopentadiene) High Temperature Oxidation: Exploring the Role of Biradical Species in Initial Decomposition Steps. Int. J. Chem. Kinet. 2012, 44, 179–193. [Google Scholar] [CrossRef]
  49. Gobrecht, D.; Crstallo, S.; Piersanti, L.; Bromley, S.T. Nucleation of Small Silicon Carbide Dust Clusters in AGB Stars. Astrophys. J. 2017, 840, 117. [Google Scholar] [CrossRef]
  50. Mohapatra, C.; Kundu, S.; Paesch, A.N.; Herbst-Irmer, R.; Stalke, D.; Andrada, D.M.; Frenking, G.; Roesky, H.W. The Structure of the Carbene Stabilized Si2H2 May Be Equally Well Described with Coordinate Bonds as with Classical Double Bonds. J. Am. Chem. Soc. 2016, 138, 10429–10432. [Google Scholar] [CrossRef]
  51. Pecher, L.; Tonner, R. Bond Insertion at Distorted Si(001) Subsurface Atoms. Inorganics 2018, 6, 17. [Google Scholar] [CrossRef]
  52. Lutz, J.J.; Duan, X.F.; Burggraf, L.W. Semiconductor color-center structure and excitation spectra: Equation-of-motion coupled-cluster description of vacancy and transition-metal defect photoluminescence. Phys. Rev. B 2018, 97, 115108. [Google Scholar] [CrossRef]
  53. Byrd, J.N.; Lutz, J.J.; Jin, Y.; Ranasinghe, D.S.; Montgomery, J.A., Jr.; Perera, A.; Duan, X.F.; Burggraf, L.W.; Sanders, B.A.; Bartlett, R.J. Predictive coupled-cluster isomer orderings for some SinCm (m, n ≤ 12) clusters: A pragmatic comparison between DFT and complete basis limit coupled-cluster benchmarks. J. Chem. Phys. 2016, 145, 024312. [Google Scholar] [CrossRef]
  54. Lutz, J.J.; Duan, X.F.; Ranasinghe, D.S.; Jin, Y.; Margraf, J.T.; Perera, A.; Burggraf, L.W.; Bartlett, R.J. Valence and charge-transfer optical properties for some SinCm (m, n ≤ 12) clusters: Comparing TD-DFT, complete-basis-limit EOMCC, and benchmarks from spectroscopy. J. Chem. Phys. 2018, 148, 174309. [Google Scholar] [CrossRef]
  55. Schmidt, M.W.; Baldridge, K.K.; Boatz, J.A.; Elbert, S.T.; Gordon, M.S.; Jensen, J.J.; Koseki, S.; Matsunaga, N.; Nguyen, K.A.; Su, S.; et al. General atomic and molecular electronic structure system. J. Comput. Chem. 1993, 14, 1347–1363. [Google Scholar] [CrossRef]
  56. Gordon, M.S.; Schmidt, M.W. Advances in electronic structure theory: GAMESS a decade later. In Theory and Applications of Computational Chemistry, the First Forty Years; Dykstra, C.E., Frenking, G., Kim, K.S., Scuseria, G.E., Eds.; Elsevier: Amsterdam, The Netherlands, 2005; pp. 1167–1189. [Google Scholar] [CrossRef]
  57. Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian~16 Revision B.01; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
  58. Dennington, R.; Keith, T.A.; Millam, J.M. GaussView Version 6; Semichem Inc.: Shawnee Mission, KS, USA, 2016. [Google Scholar]
  59. Bode, B.M.; Gordon, M.S. MacMolPlt: A graphical user interface for GAMESS. J. Mol. Graph. Model. 1998, 16, 133–138. [Google Scholar] [CrossRef]
  60. Grimme, S. Semiempirical hybrid density functional with perturbative second-order correlation. J. Chem. Phys. 2006, 124, 034108. [Google Scholar] [CrossRef]
  61. Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
  62. Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the damping function in dispersion corrected density functional theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef]
  63. Goerigk, L.; Grimme, S. Efficient and Accurate Double-Hybrid-Meta-GGA Density Functionals—Evaluation with the Extended GMTKN30 Database for General Main Group Thermochemistry, Kinetics, and Noncovalent Interactions. J. Chem. Theory Comput. 2011, 7, 291–309. [Google Scholar] [CrossRef]
  64. Neto, A.C.; Muniz, E.P.; Centoducatte, R.; Jorge, F.E. Gaussian basis sets for correlated wave functions. Hydrogen, helium, first- and second-row atoms. J. Mol. Struct. 2005, 718, 219–224. [Google Scholar] [CrossRef]
  65. Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef]
  66. Helgaker, T.; Klopper, W.; Koch, H.; Noga, J. Basis-set convergence of correlated calculations on water. J. Chem. Phys. 1997, 106, 9639–9646. [Google Scholar] [CrossRef]
  67. Hansen, J.A.; Piecuch, P.; Lutz, J.J.; Gour, J.R. Geometries and adiabatic excitation energies of the low-lying valence states of CNC, C2N, N3 and NCO studied with the electron-attached and ionized equation-of-motion coupled-cluster methodologies. Phys. Scr. 2011, 84, 028110. [Google Scholar] [CrossRef]
  68. Ehara, M.; Piecuch, P.; Lutz, J.J.; Gour, J.R. Symmetry-Adapted-Cluster Configuration- Interaction and Equation-of-Motion Coupled-Cluster Studies of Electronically Excited States of Copper Tetrachloride and Copper Tetrabromide Dianions. Chem. Phys. 2012, 399, 94–110. [Google Scholar] [CrossRef]
  69. Piecuch, P.; Kowalski, K.; Pimienta, I.S.O.; McGuire, M.J. Recent advances in electronic structure theory: Method of moments of coupled-cluster equations and renormalized coupled-cluster approaches. Int. Rev. Phys. Chem. 2002, 21, 527–655. [Google Scholar] [CrossRef]
  70. Leigh, G.J.; Favre, H.A.; Metanomski, W.V. Principles of Chemical Nomenclature: A Guide to IUPAC Recommendations, 2011 Edition ed; Blackwell Science: Oxford, UK, 2011. [Google Scholar] [CrossRef]
Inorganics 07 00051 g001 550
Figure 1. Low-lying C 2 Si 2 H 4 isomers optimized with B3LYP/Def2-QZVP and B2-PLYP/Def2-QZVP- level dipole moments.
Figure 1. Low-lying C 2 Si 2 H 4 isomers optimized with B3LYP/Def2-QZVP and B2-PLYP/Def2-QZVP- level dipole moments.
Inorganics 07 00051 g001
Inorganics 07 00051 g002 550
Figure 2. Relative free energies of the ten isomers in Figure 1 computed using the (a) MBPT(2), (b) B3LYP, and (c) M06-2X methods. The flash pyrolysis temperature reported in Ref. [2] is marked with a vertical dotted line.
Figure 2. Relative free energies of the ten isomers in Figure 1 computed using the (a) MBPT(2), (b) B3LYP, and (c) M06-2X methods. The flash pyrolysis temperature reported in Ref. [2] is marked with a vertical dotted line.
Inorganics 07 00051 g002
Inorganics 07 00051 g003 550
Figure 3. Simulated IR spectra for isomer 1 overlaid upon measured broad features from Reference [2] assigned arbitrary intensities. Frequencies are in cm − 1 and intensities have arbitrary units.
Figure 3. Simulated IR spectra for isomer 1 overlaid upon measured broad features from Reference [2] assigned arbitrary intensities. Frequencies are in cm − 1 and intensities have arbitrary units.
Inorganics 07 00051 g003
Inorganics 07 00051 g004 550
Figure 4. Reaction profiles for the ring-opening of silylsilacyclopropenylidene (isomer 2) to (silylethynyl)silylene, as computed using (a) wave-function methods, (b) BLYP-based DFT methods, and (c) Minnesota DFT methods. Solid (▲), dashed (▼), and dotted (♦) lines (symbols) correspond to the ground, first-excited, and second-excited states, respectively.
Figure 4. Reaction profiles for the ring-opening of silylsilacyclopropenylidene (isomer 2) to (silylethynyl)silylene, as computed using (a) wave-function methods, (b) BLYP-based DFT methods, and (c) Minnesota DFT methods. Solid (▲), dashed (▼), and dotted (♦) lines (symbols) correspond to the ground, first-excited, and second-excited states, respectively.
Inorganics 07 00051 g004
Inorganics 07 00051 g005 550
Figure 5. The stationary points connecting isomers 1, 2, 3, 6 and ethynylsilylsilylene products, as optimized using B3LYP/DZP Relative energies are provided in parentheses in kcal/mol.
Figure 5. The stationary points connecting isomers 1, 2, 3, 6 and ethynylsilylsilylene products, as optimized using B3LYP/DZP Relative energies are provided in parentheses in kcal/mol.
Inorganics 07 00051 g005
Table
Table 1. Energy differences between isomers 1 and 2 in kcal/mol, calculated as Δ E = E ( 1 ) − E ( 2 ) for consistency with Ref. [1]. Optimizations and ZPVE calculations were performed at the MBPT(2) level using the basis set indicated.
Table 1. Energy differences between isomers 1 and 2 in kcal/mol, calculated as Δ E = E ( 1 ) − E ( 2 ) for consistency with Ref. [1]. Optimizations and ZPVE calculations were performed at the MBPT(2) level using the basis set indicated.
Ref. [1]CCSD(T)
Def2-TZVPDef2-TZVPDDef2-QZVPCBS 1
11.60.0−1.8−2.8−3.4
1 CBS extrapolated value; for the details of how this was computed, see the text.
Table
Table 2. Statistical evaluation of wave-function methods for determination of the relative energies of low-lying isomers of C 2 Si 2 H 4 . Isomer energies were computed as Δ E = E ( 2 ) − E ( 1 ) . All values are in kcal/mol.
Table 2. Statistical evaluation of wave-function methods for determination of the relative energies of low-lying isomers of C 2 Si 2 H 4 . Isomer energies were computed as Δ E = E ( 2 ) − E ( 1 ) . All values are in kcal/mol.
IsomerRef. [1]MBPT(2)MBPT(3)MBPT(4)CCSDCCSD(T) Benchmark 1
2−11.64.41.90.40.12.8 3.4
3−2.310.67.76.76.57.5 7.9
417.014.710.69.79.311.2 11.3
520.013.313.312.112.013.7 14.0
6-16.316.416.216.415.1 15.4
726.720.320.119.019.219.2 19.5
8-25.824.423.423.523.5 23.6
931.122.023.323.523.424.4 23.9
1038.131.129.228.428.528.7 28.8
MSE 2 -1.10.1−0.6−0.6−0.1 0.0
MUE 3 -1.70.50.80.80.2 0.0
1 Computed at the CCSD(T)/CBS//MBPT(2)/Def2-QZVP level of theory. 2 Mean signed errors computed with respect to reference CCSD(T)/CBS//MBPT(2)/Def2-QZVP values. 3 Mean unsigned errors computed with respect to reference CCSD(T)/CBS//MBPT(2)/Def2-QZVP values.
Table
Table 3. Statistical evaluation of density functional theory methods for determination of relative energies of the 10 lowest-lying isomers of C 2 Si 2 H 4 .
Table 3. Statistical evaluation of density functional theory methods for determination of relative energies of the 10 lowest-lying isomers of C 2 Si 2 H 4 .
FunctionalMSEMUE
BLYP2.63.3
B3LYP−0.91.2
B3LYP+D3−0.81.4
B2-PLYP+D30.20.6
PBE0−1.01.0
PBE0+D3−1.11.1
DSDPBEP86−0.10.4
M06L−2.33.6
MN15L−1.33.0
M06-2X−1.21.3
MN15−0.11.3
Table
Table 4. Vibrational frequencies (in cm − 1 ) as computed for isomers 1 and 2 at various levels of theory. Values for protonated species are reported above and deuterated species below. Intensities relative to the strongest band are provided in parentheses. Measured spectroscopic data are listed for comparison.
Table 4. Vibrational frequencies (in cm − 1 ) as computed for isomers 1 and 2 at various levels of theory. Values for protonated species are reported above and deuterated species below. Intensities relative to the strongest band are provided in parentheses. Measured spectroscopic data are listed for comparison.
Isomer 1Isomer 2Exp. (Ref. [2])
Computational MethodComputational Method
CASSCF(6,6)MBPT(2)B3LYPCASSCF(6,6)MBPT(2)B3LYP
2300 (1.0)2230 (1.0)2140 (1.0)2300 (0.4)2280 (0.3)2210 (0.4)2190 1
1010 (0.1)960 (0.3)980 (0.3)1030 (0.3)970 (0.3)950 (0.4)950 (0.2)
1000 (0.2)950 (0.3)950 (0.2)1020 (1.0)950 (1.0)930 (1.0)920 (1.0)
860 (0.1)820 (0.1)810 (0.1)880 (0.2)860 (0.1)840 (0.2)840 (0.2)
780 (0.1)790 (0.1)750 (0.1)820 (0.2)770 (0.1)750 (0.1)720 (0.1)
690 (0.1)760 (0.1)670 (0.1)720 (0.2)680 (0.2)670 (0.1)670 (0.1)
660 (0.1)650 (0.1)650 (0.1)700 (0.1)670 (0.1)650 (0.1)650 (0.2)
1660 (1.0)1600 (1.0)1550 (1.0)1650 (0.5)1630 (0.4)1580 (0.5)1600 1
850 (0.8)820 (0.5)830 (0.5)850 (1.0)820 (0.6)810 (0.8)800 (0.6)
780 (0.3)710 (0.3)720 (0.2)760 (1.0)710 (1.0)700 (1.0)690 (1.0)
620 (0.1)550 (0.2)540 (0.1)560 (0.3)530 (0.2)520 (0.3)520 (0.1)
1 Broad band from several overlapping species; intensity not reported in Ref. [2].
Table
Table 5. Relative energies (above) and excitation energies (below) for the C 2 Si 2 H 4 stationary points appearing in Figure 5. All values are reported in kcal/mol.
Table 5. Relative energies (above) and excitation energies (below) for the C 2 Si 2 H 4 stationary points appearing in Figure 5. All values are reported in kcal/mol.
MethodStructures
1TS-a6TS-b3TS-c2TS-dProd
B3LYP0.067.116.731.34.971.52.969.826.8
CCSD0.070.414.170.22.771.3−0.365.823.8
CR-CC(2,3)0.066.914.869.43.171.01.167.325.4
EOM-CCSD71.620.385.932.162.651.490.847.743.6
CR-EOMCC(2,3)78.928.093.938.371.160.498.056.451.6
δ -CR-EOMCC(2,3)64.39.980.022.956.945.584.843.438.7

Share and Cite

MDPI and ACS Style

Lutz, J.J.; Burggraf, L.W. The Lowest-Energy Isomer of C2Si2H4 Is a Bridged Ring: Reinterpretation of the Spectroscopic Data Based on DFT and Coupled-Cluster Calculations. Inorganics 2019, 7, 51. https://doi.org/10.3390/inorganics7040051

AMA Style

Lutz JJ, Burggraf LW. The Lowest-Energy Isomer of C2Si2H4 Is a Bridged Ring: Reinterpretation of the Spectroscopic Data Based on DFT and Coupled-Cluster Calculations. Inorganics. 2019; 7(4):51. https://doi.org/10.3390/inorganics7040051

Chicago/Turabian Style

Lutz, Jesse J., and Larry W. Burggraf. 2019. "The Lowest-Energy Isomer of C2Si2H4 Is a Bridged Ring: Reinterpretation of the Spectroscopic Data Based on DFT and Coupled-Cluster Calculations" Inorganics 7, no. 4: 51. https://doi.org/10.3390/inorganics7040051

APA Style

Lutz, J. J., & Burggraf, L. W. (2019). The Lowest-Energy Isomer of C2Si2H4 Is a Bridged Ring: Reinterpretation of the Spectroscopic Data Based on DFT and Coupled-Cluster Calculations. Inorganics, 7(4), 51. https://doi.org/10.3390/inorganics7040051

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop