Next Article in Journal
Synthesis, Structures and Chemistry of the Metallaboranes of Group 4–9 with M2B5 Core Having a Cross Cluster M–M Bond
Next Article in Special Issue
The Lowest-Energy Isomer of C2Si2H4 Is a Bridged Ring: Reinterpretation of the Spectroscopic Data Based on DFT and Coupled-Cluster Calculations
Previous Article in Journal
Bond Forming Reactions Involving Isocyanides at Diiron Complexes
Previous Article in Special Issue
Survey of the Geometric and Electronic Structures of the Key Hydrogenated Forms of FeMo-co, the Active Site of the Enzyme Nitrogenase: Principles of the Mechanistically Significant Coordination Chemistry
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Inorganics
Volume 7
Issue 3
10.3390/inorganics7030026
inorganics-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Comparative Study of Complexes of Rare Earths and Actinides with 2,6-Bis(1,2,4-triazin-3-yl)pyridine

by
Attila Kovács
*,
Christos Apostolidis
and
Olaf Walter
European Commission, Joint Research Centre (JRC), P.O. Box 2340, 76125 Karlsruhe, Germany
*
Author to whom correspondence should be addressed.
Inorganics 2019, 7(3), 26; https://doi.org/10.3390/inorganics7030026
Submission received: 20 December 2018 / Revised: 31 January 2019 / Accepted: 19 February 2019 / Published: 26 February 2019
(This article belongs to the Special Issue Applications of Density Functional Theory in Inorganic Chemistry)
Browse Figures
Versions Notes

Abstract

:
Complexes of group III metals (rare earth and actinides) with 2,6-bis(5,6-dipropyl-1,2,4-triazin-3-yl)pyridine (BTP) have been investigated by computational (DFT) and, in limited cases, by experimental (FT-IR, X-ray) techniques with the goal of determining the characteristics of metal–ligand interactions. The DFT calculations using the M062X exchange-correlation functional revealed that metal–ligand distances correlate with the ionic radii of the metals, in agreement with available X-ray diffraction results on the Sc, Y, La, U, and Pu complexes. A related blue-shift trend could be observed in seven characteristic bands in the IR spectra associated with metal–ligand vibrations. The computations uncovered considerable charge transfer interactions, particularly in the actinide complexes, as important covalent contributions to the metal–ligand bonding. The covalent character of the metal–ligand bonds decreases in the actinides, from U to Cm.

Graphical Abstract

1. Introduction

After the first synthesis of 2,6-bis(5,6-dipropyl-1,2,4-triazin-3-yl)pyridine (BTP) in 1999 [1,2], it has become one of the most powerful extractants, separating actinides (An) and lanthanides (Ln) from nuclear waste [3]. The relevant actinides in this process are the trivalent americium and curium ions, as uranium and plutonium can be removed from the waste beforehand by the PUREX process [4].
In general, complexing ligands with soft donor atoms are likely to bind more strongly to the actinides than to the lanthanides. The origin of this behavior lies in the somewhat stronger donor-acceptor abilities of the actinide 5f and 6d atomic orbitals with the molecular orbitals of the donor ligands, as compared to the 4f/5d orbitals of the lanthanides [5,6,7]. The success of BTP and its derivatives [3] was attributed partly to the soft donor nitrogen atoms in an aromatic environment. An important factor is the basicity, which can be regulated by appropriate substituents: The complexation energies [8] and the An/Ln separation factors increase with increasing BTP basicity [9]. The role of steric effects was also suggested between the [1,2,4]-triazin-3-yl versus the 2-pyridinyl rings for complexing with lanthanides [10]; due to the better steric properties of the former group, its nitrogen can approach metals with small ionic radii more closely.
Several studies have investigated the various aspects of the different binding mechanisms of BTP to actinides and lanthanides [3,6,11,12,13,14,15,16,17,18,19,20,21,22,23,24]. From them, the following theoretical studies provided the most detailed information on the electronic nature of the bonding.
Guillaumont studied the interaction of f elements with a single BTP derivative ligand in [M(MeBTP)(H2O)6]3+ complexes using density functional theory (DFT) [13]. Analysis of molecular orbitals predicted slightly stronger covalent effects in the bonding of actinides than for lanthanides, and the covalent strength decreased from U towards Am. This bonding is realized mainly in the form of charge transfer from the ligand to the empty 6d orbitals of the metals. Metal to ligand back-donation was found only for the U complex, involving a singly-occupied 5f orbital of U [13].
Complexes analogous to the structures in the present study were investigated by Petit et al. [15], by means of DFT. The bonding in those La, Gd, U, and Cm complexes was investigated by energy decomposition analysis [25] and extended by analysis of the natural atomic charges and orbital populations [26]. The interaction energy decomposed to covalent and electrostatic parts showed a particularly strong covalent contribution in the U complex, decreasing towards La, in the following order: U >> Cm > Gd >> La. The natural metal charges and valence orbitals indicated considerable BTP → M3+ donations, while notable back-donation only occurred in the case of U.
Recently, we performed a detailed joint experimental and theoretical study of the lanthanide series, Ln(BTP)3, focusing on the structural and energetic effects of “lanthanide contraction” [27]. As one of the main results, we found increasing metal–ligand interactions along the Ln series. A recent topological study of [Ln(BTP)3]3+ derivatives, by Fryer-Kanssen et al. [28], reported low charge densities at the Ln–N bond critical points (BCPs) and very small irregular variation as the series was traversed. Comparison of the integrated properties of the Eu and Gd complexes with those of Am and Cm indicated slightly larger metal-ligand covalent bonding contributions in the actinide complexes.
In the present study, we compared the properties of rare earth (Sc, Y, La, and Lu) and actinide (U, Np, Pu, Am, and Cm) BTP complexes, by means of experimental and theoretical techniques. The main part of the study consists of DFT calculations in order to elucidate the bonding differences between the three groups of metals; namely, transition metals (TM: Sc, Y), lanthanides, and actinides. Due to technical considerations and the previously-found negligible effects upon replacing the n-propyl chains of BTP by hydrogen in lanthanide BTP complexes [27], in the present theoretical modeling we used the reduced ligand molecule, denoted as BTP′. The La and Lu complexes (investigated by us, recently [27]) were recomputed with a larger valence basis set, being more comparable with the basis sets used for the other metals. The bonding properties were analyzed using the natural bond orbital (NBO) [26] and quantum theory of atoms in molecules (QTAIM) [29] model theories, providing quantitative information on the bonding. The computed results were compared with experimental X-ray diffraction (XRD) data of the Sc, Y, La, U, and Pu complexes, as well as with the FT-IR spectra of the Sc, Y, Pu, and Am complexes.

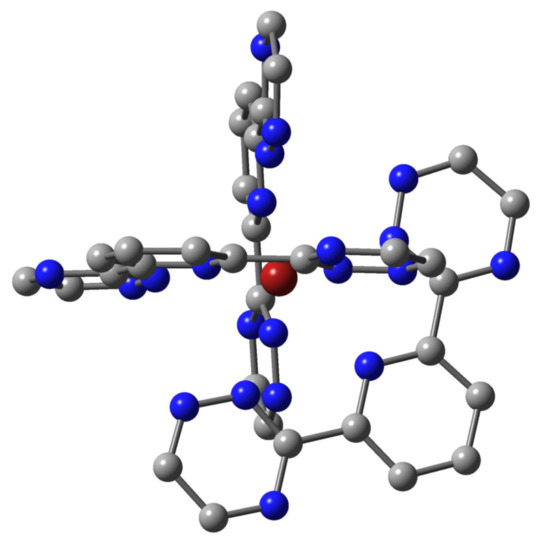
2. Results and Discussion

The trivalent metal ions form 1:3 complexes with neutral BTP-type ligands [3,14,30]. The tridentate character of BTP is manifested in three metal-nitrogen donor-acceptor bonds: One with the pyridine (N1), and two with the closest azine nitrogens (N2, N2′) (see Figure 1). In the complex molecules, three BTP ligands are arranged around the metal ion in a spherical fashion, as depicted in Figure 2. We note that this moiety has a +3 charge, which was neutralized by appropriate counter-anions in experiments.
The computations predicted D3 symmetry for the ground-state structures of the Sc and Y (and La and Lu [27]) complexes. In contrast, the computations of the five An complexes converged to slightly asymmetric structures (the Cm complex being closest to D3 symmetry), while keeping the main structural motifs, as above. Therefore, the structural characteristics of the presently studied [M(BTP′)3]3+ complex cations are in good agreement with data on metal complexes with BTP in the literature [27,30], BTP derivatives [12,31,32], and with other ligands possessing structural motifs related to BTP, in terms of symmetry and coordination behavior [3,33,34,35,36,37,38,39,40,41,42,43,44].
Selected geometrical parameters from our M062X computations and available XRD data are compared in Table 1. We note that the determined X-ray structures of the Sc, Y, and Pu complexes have large uncertainties, due to poor crystallographic quality of the samples. Nevertheless, the crystal analysis verified the structures, being isostructural to lanthanide homologues [27]. Due to the mentioned large uncertainties, a detailed discussion of the experimental structure is not feasible, thus we show only the average of the most important M–N bonds in Table 1. Additional data can be found in the Supplementary Materials (Tables S1 and S2).
The metal–nitrogen distances differ characteristically in the complexes with the various metals. In the trend, there is a good agreement between the computations and experiment. The M–N1 and M–N2 distances (representing the bonding between M and BTP) are between 2.4–2.7 Å. These distances are in the magnitude of single bonds between M and N. In fact, the experimental data agree well with the sum of the ionic radii (e.g., for La and N, the sum of ionic radii is 2.62 Å [48], while the measured distances are 2.61 and 2.59 Å, see Table 1). This is in agreement with a major ionic character of the bonding by the La3+ ion. The computed M–N distances are slightly overestimated by the applied DFT level, with respect to the experimental results. The M–N3 distance is around 3.5 Å, which is too large for any significant bonding interaction.
In Figure 3, we compare the variation of the M(III) ionic radii [46,47] and the M–N bond distances from the computed geometries. The ionic radii increase in the order Sc < Lu < Y < Cm < Am < Pu < Np < U < La. The same trend appears in the M–N bonds of the complexes. Beside the bond distances close to the sums of the ionic radii (vide supra), this is further support for the major ionic character of these metal-ligand interactions. The minor difference between the ionic radii of Lu(III) and Y(III) is also well reflected in the donor–acceptor M–N bonds of these two complexes. A small discrepancy can be observed, however, in the increase of the actinide M–N bonds, which is less pronounced than the increase in the An(III) ionic radii.
From the bonds within the BTP′ ligand, N1–C, N2–N3, and N2–C are affected by the complex formation due to changes in the electron density distribution. The largest effect can be observed for N2–C: Compared with the bond distances of the free BTP′ ligand (Table 1), it is decreased by 0.01 Å upon complex formation, while the others show changes of a few thousandths of an angstrom. In the magnitudes of change, a relation with the M–N distances was found only in the case of N1–C.
Similarly to our previous work on the lanthanide row [27], we can observe here a dependence of the relative order of the M–N1 and M–N2 distances on the M(III) ionic radii: with smaller ionic radii the M–N1 bond is shorter than M–N2, while between Y and Cm the order is changed to M–N1 > M–N2 (cf. Figure 3). The trend can be recognized in the available experimental data (Table 1). It seems that the M(III) ionic radii determine how the metal can approach the electron donor nitrogen (N1, N2, N2′): The small ions can get closer to N1, while the approach of the larger ions may be hindered by steric interactions with the triazine rings.
The variation of the metal–ligand bond distances within the complexes of group III metals is also reflected in some of the weak features in the vibrational spectra. In our previous study on Ln(BTP)3 complexes [27], we found that, as the Ln(III) ion radii shorten across the Ln row, the consequently decreasing Ln–N distances resulted in blue shifts up to 10 cm−1 (between La(BTP)3 and Lu(BTP)3) of some fundamental wavenumbers. The same feature can be observed in the available FT-IR data of the Sc, Y, Am, and Pu complexes. Notable shifts were found for seven fundamentals listed in Table 2, the largest being 14 cm−1 for the fundamental at around 470 cm−1. The shifts were reasonably reproduced by the M062X frequency calculations on the [M(BTP′)3]3+ models.
The fundamentals listed in Table 2 are complex, but all contain some contributions from the M–N vibrations. In the high-wavenumber modes, these contributions correspond mainly to stretching, while in the low-wavenumber modes, they correspond to out-of-plane (with respect to the plane of the aromatic ring) bending vibrations.
The complete set of experimental wavenumbers of the Sc, Y, Pu, and Am complexes, with assignments on the basis of DFT calculations, is given in the Supplementary Materials (Table S3). The characteristics of the observed bands correspond, in general, to those of the La complex reported in our previous study [27]. The assignment of the CF3SO3− bands agrees with IR data on rare earth trifluoromethanesulfonate crystals in the literature [49].
The electronic nature of the metal–nitrogen bonding was investigated using the natural bond orbital (NBO) [26] and quantum theory of atoms in molecules (QTAIM) [29] models. Selected calculated atomic charges, metal valence orbital populations, main charge transfer interactions, and electron density data are compiled in Table 3.
Both bonding analysis models (NBO and QTAIM) resulted in considerable positive charges of the M atoms and negative ones of N1 and N2 in the [M(BTP′)3] complexes. However, they differed somewhat in the trends: NBO predicted significantly higher atomic charges (n) of the lanthanides, compared with TM and An, and a gradually increasing trend from U to Cm. In contrast, the QTAIM charges (q) varied only within 0.15 e and showed a decreasing trend from U to Am. The close q values of the various metal groups (TM, Ln, An) are in better agreement with chemical intuition. Nevertheless, computed atomic charges are generally less suitable for the analysis of small bonding differences, as the atomic charge is a property integrated all over the atoms, lacking information on the variation of electron density distribution in different directions. Thus, the gains from the present atomic charges are the confirmations of the significant ionic character of M–N bonding and of the net BTP′→M charge transfers in the complexes, the latter reducing the positive charge of the parent M3+ ions. For analysis of bonding interactions, the electron density properties between the interacting atoms are more suitable.
The M valence orbital populations from the NBO analysis give information on the role of these atomic orbitals in the donor–acceptor interactions. As can be seen in Table 3, the valence s orbitals show only slight variation, around 0.23 e. The An 5f orbitals have a slight population increase upon the 5f subconfiguration of the parent An3+ ions. This increase is declining from Np to Cm, in agreement with the stabilization of the 5f subshell. The donor–acceptor interactions in the complexes mainly involve the valence d orbitals of the metals, as indicated by the considerable populations (0.65–0.93 e).
From the NBO analysis, the second-order perturbation energy data represents the most relevant information on the donor–acceptor interactions, modeling the energy consequences of the individual charge transfers. According to them, the majority (60–80%) of the covalent interaction is established by the lone pairs of N1 and N2 (σ-donation). We note the somewhat smaller second-order perturbation energies of the charge donation from the lone pair of N1 to M, with respect to those from N2 (see Table 3). Additional weak charge donations occur from N1–C, N2–N3, and N2–C bonding orbitals. Detailed inspection of the orbital interactions revealed that the main acceptor orbitals of the metals are the valence d orbitals, as assumed above on the basis of their populations. Considerably fewer donations occurred to the valence s orbitals, and quite small ones to the actinide 5f orbitals.
From the studied group III metals, the strongest donor–acceptor interactions were predicted for the An complexes, while the weakest were the Ln complexes. This correlates well with the significantly larger populations of the An 6d orbitals (extended by the minor increases of 5f, vide supra), as compared to those of the Ln 5d ones (see Table 3).
Noteworthy are the considerably stronger donor–acceptor interactions in the U complex (particularly the N1→M and N2→M charge transfers, see Table 3), compared to those of the other An in the study. This feature may be in relation with the largest 6d population in the U complex among the An complexes, as well as with the larger 6d orbital radii of U being more favorable for donor–acceptor interactions. With increasing atomic number (Pu–Cm), the 6d orbitals become contracted [51], and are less suitable for orbital interactions.
The covalent bonding in the An complexes also incorporates some metal-to-ligand back-donation. This interaction is very weak; the second-order perturbation energies are 10–60 times smaller than the ones of the ligand-to-metal donations. Hence, in contrast to the suggestion of Berthet et al. [3], the present NBO analyses predict only a negligible role of back-donation in the stability of these complexes. In addition, our second-order perturbation energies indicate the strongest back-donation in Pu(BTP′)33+ among the studied five An, while previously significant back-donation was reported only for U [13,15]. The metal-to-ligand back-donations in the [An(BTP′)3]3+ complexes occur from the partly occupied 5f orbitals of the actinides. No back-donation was found for the rare earths, due to a lack of appropriate donor orbitals.
The topological analysis of the electron density distribution provided useful information on the covalent interactions in the [M(BTP′)3]3+ complexes. Figure 4 depicts the bond paths, with the bond and ring critical points, and gives an overview of the chemical bonds between M3+ and BTP′. The electron densities (ρ) and their Laplacian (▽2ρ) values at the BCPs of the M–N interactions are given in Table 3. Both properties vary within a small range. The only noteworthy characteristic is the somewhat higher ρ(M,N) values of the U complex as compared to the others, in agreement with the known considerably larger charge transfer in [U(BTP′)3]3+ (vide supra).
The integrated QTAIM properties, given in Table 3, proved to be more informative. The Δ(M) data, meaning the difference between the integrated electron density in the atomic basin of M and average number of electrons localized in the atomic basin of M (the latter called the localization index), give a better representation of the bonding propensities of M than the QTAIM atomic charges (q). As was shown above, the trend in q disagrees at several points with those in the natural atomic charges (n). Consequently, it disagrees also with the covalent trend of M–N bonding, deduced on the basis of the second-order perturbation energies. The atomic charge refers to the space around the whole atom, while the bonding electron density occupies only the space between the bonded atom pairs. The latter is given by the Δ(M) difference, as the localization index means the average number of electrons belonging exclusively to M. In agreement with the expectations, the variation of the Δ(M) values shows some resemblance to the second-order perturbation energies from the NBO analyses.
Part of Δ(M) is manifested in the DI(M,N) delocalization indices (Table 3) in which the integrated parameter has helped in the elucidation of weak trends in the bonding of various lanthanide- and actinide-containing molecules [28,52,53,54,55,56,57,58,59,60]. DI quantifies the average number of electrons shared between two atoms connected by a bond path [52].
The Δ(M) and DI(M,N) values correlate well with the second-order perturbation energies, except for La: The NBO analysis predicted the smallest second-order perturbation energies for the [La(BTP′)3]3+ complex, while Δ(La) and DI(La,N) are the largest among the rare earths. On the other hand, the La > Lu trend in the integrated properties is in agreement with the recently reported one of Eu > Gd [28].
Nevertheless, the Δ(M) and DI data of Table 3 contains three important pieces of information: (i) The covalent character in the An complexes is characteristically stronger than in the rare earth ones, supporting previous conclusions [13,15,28,57]; (ii) the covalent character in the An–N bonds decreases from U to Cm, resembling the trend found in the series AnF4 [61] and AnCOT2 (An = Th–Cm) complexes [53]; and (iii) the strength of covalent interactions in the M–N1 and M–N2 bonds is comparable.
Apart from the discrepancy for La, the relevant NBO and QTAIM properties agree in the main bonding trends in the investigated [M(BTP′)3]3+ complexes.
The computed dissociation energies (De) predict the largest complex stability for Sc, with a decreasing trend down group III in the periodic system. The ranges of the computed bond dissociation energies of the two f-element rows overlap, in agreement with the known very close stabilities of related Ln and An complexes [3,6,11,12,13,14,15,16,17,18,19,20,62]. The close stabilities confirm that the weaker electrostatic interactions in the An complexes are successfully compensated by the larger donor–acceptor interactions. We note that, in both the Ln and An rows, an increasing trend of De parallel with the atomic number can be observed, in agreement with earlier reports [63,64].

3. Materials and Methods

3.1. General Preparation Procedure of the Complexes [M(BTP)3](CF3SO3)3

Approximately 45 mg (~0.06 mmol) of [M(H2O)9](CF3SO3)3 was dissolved in 1 mL EtOH, then 3 equivalents of 2,6-bis(5,6-dipropyl-1,2,4-triazin-3-yl)pyridine (~100 mg) in 1 mL EtOH (dissolved at elevated temperature) were added. On slow cooling to room temperature, the complexes formed crystals of the constitution [M(BTP)3](CF3SO3)3*EtOH (Sc without EtOH) in yields of 50–60%. Reducing the solvent volume by evaporation to a volume of ~0.3 mL, more crystals were formed completing the precipitation to yields of >90%.

3.2. Crystallography

The XRD measurements were performed on a Siemens SMART CCD 1000 diffractometer (Siemens Analytical X-ray Instruments, Inc., Karlsruhe, Germany) [65] (Sc) and a Bruker Apex II Quazar diffractometer (Bruker AXS, Inc., Madison, WI, USA) [66] (Y, Pu). Frames were collected with an irradiation time of 20 s or 10 s per frame and the ω-scan technique with Δω = 0.45° on the SMART diffractometer; whereas, on the Apex II diffractometer, a mixed ω- and ϕ-scan technique was employed for data collection, with Δω = Δϕ = 0.5° with irradiation times of 12 s per frame, appropriate to the size and diffracting abilities of the crystals. Data were integrated with SAINT, corrected to Lorentz, and polarization effects and an empirical adsorption correction with SADABS was applied. The structures were solved by direct methods and refined to an optimum R1 value with SHELX-2013 [67]. All structures here suffer from the low quality of the crystals and the resulting structures. Redetermination and collection on other crystals did not lead to better quality. Nevertheless, the structures were deposited at the Cambridge Crystallographic Data Centre with the reference CCDC numbers: CCDC 1885828 (Pu), 1885829 (Sc), and 1885830 (Y). These data can be obtained, free of charge, from the CCDC at www.ccdc.cam.ac.uk. Crystallographic details of the measured [M(BTP)3](CF3SO3)3 complexes can be found in the Supplementary Materials (Table S1).

3.3. IR Spectroscopy

IR spectroscopic measurements were performed using a Perkin Elmer Spectrum 1000 FT spectrometer (PerkinElmer, Inc., Waltham, MA, USA), on KBr pellets for the mid-IR range (4000–400 cm−1) and polyethylene pellets for the far-IR range (400–120 cm−1) with a resolution of 2 cm−1.

3.4. Computational Details

Due to the large size of BTP and the flexibility of the propyl chains, getting convergence for the open-shell actinide complexes containing the whole ligand is extremely difficult. On the other hand, it was shown that the external propyl substituents of the triazine rings have no significant effect on the complex structure [3,14]. Recently, we found also negligible effects in test calculations on lanthanide BTP complexes [27]. Therefore, we performed all our present calculations with a reduced ligand molecule replacing the n-propyl chains by hydrogen, denoted as BTP′.
The computations were performed with the Gaussian09 suite of programs [68], using the M062X [69] exchange-correlation functional in conjunction with the quasi-relativistic pseudopotentials of the Stuttgart-Cologne group. Test calculations with the D3 version of Grimme’s dispersion correction [70] indicated marginal effects of the dispersion forces (up to 0.006 Å for the M–N1 distance) and, therefore, this option was omitted. For Sc, we took the pseudopotential containing 10 electrons in the core (ECP10MDF) [71] in conjunction with the correlation consistent valence basis having a contraction scheme of [8s7p6d2f1g]/[6s5p3d2f1g] [71,72], while, for Y, the pseudopotential containing 28 electrons in the core (ECP28MWB) [73] in conjunction with the correlation consistent valence basis having a contraction scheme of [8s7p6d2f1g]/[6s5p3d2f1g] [72,73]. For La and Lu we used the 4f-in-core quasi-relativistic pseudopotentials [74,75] in conjunction with a [8s7p6d3f2g]/[6s5p5d3f2g] valence basis set treating the 5s5p5d6s orbitals [76,77]. For actinides the 5f-in-valence pseudopotentials (ECP60MWB) [78] were applied in conjunction with valence basis sets having a contraction scheme of [14s13p10d8f6g]/[10s9p5d4f3g] [79,80]. Accordingly, the An complexes and ions were computed as open-shell, and the others as closed-shell. For N, C, and H the standard 6-31G** basis set was used. The above theoretical level provided results in good agreement with the experimental FT-IR data of Ln(BTP)3(CF3SO3)3 complexes in our previous study [27]. The trends predicted by the M062X functional for the various properties were checked by B3LYP calculations, using the same basis set on the selected (Sc, La, Lu, U, and Am) complexes. The latter results (given in Table S4 in the Supplementary Materials) are in good agreement with the ones obtained with the M062X functional.
The ground state of the computed actinide complexes was verified by utilizing the STABLE keyword of the Gaussian code. The atomic charges and charge transfer properties were calculated according to natural bond orbital (NBO) theory [26] utilizing the NBO 5.9 code [81]. Due to the deficiency of the NBO 5.9 code for g functions, in these calculations the g polarization functions were omitted from the valence basis sets. The topological analysis of the electron density distribution was performed by means of the AIMAll software [82], at the same level of theory as used for the geometric optimizations.

4. Conclusions

Complexes of group III metals with 2,6-bis(5,6-dipropyl-1,2,4-triazin-3-yl)pyridine show similar structural and vibrational characteristics, despite the different M(III) ionic radii. The M–N bond distances correlate well with the ionic radii of the metals. A characteristic feature is the interchange of the relative order of the M–N1 and M–N2 distances around r(III) = 1.1 Å. This can be related to the steric conditions of the interaction with the ligand, determined by the ionic radii of the metals. The smaller metals (Sc, Lu, Y) have a stronger interaction with N1, while the larger radii of the other metals hinder the approach to the pyridine ring.
The trend of increasing M–N distances by Sc < Lu < Y < Cm < Am < Pu < Np < U < La can be recognized in the FT-IR spectra as small shifts of some bands. These blue-shifting bands can be attributed to modes including contributions from metal–ligand vibrations; mostly stretching and out-of-plane bending.
The DFT calculations revealed some important bonding characteristics of the complexes. Regardless of the similar ionic radii (and, thus, the M–N bond distances), the actinides are involved in larger charge transfer interactions with BTP than the studied lanthanides and transition metals. The main role in the process is played by the valence d orbitals, receiving the donation from the ligand. In the actinides, the spatial and energetic proximity of the 6d orbitals determine the magnitude of interaction: From the five studied actinides, these factors are the most favorable in U, explaining its considerably larger donor–acceptor interaction with BTP. Metal-to-ligand back-donation was found only for the actinides, but with very small magnitudes compared to the ligand-to-metal donation. The strength of the covalent bonding interactions decreases along the actinide row.
The NBO and QTAIM bonding models agree in the above-outlined main bonding trends in the investigated [M(BTP′)3]3+ complexes. The NBO model underestimates the covalent interactions in the lanthanides, with respect to QTAIM.

Supplementary Materials

The following are available online at https://www.mdpi.com/2304-6740/7/3/26/s1: Selected X-ray diffraction data of the crystals of [M(BTP)3](CF3SO3)3 (M = Sc, Y, Pu); a list of experimental IR data; Cartesian coordinates of the [M(BTP′)3]3+ complexes (M = Sc, Y, U, Np, Pu, Am, Cm), computed with the M062X functional; and selected properties of the complexes of M = Sc, La, Lu, U, Am obtained with the B3LYP functional.

Author Contributions

Investigation, A.K., C.A., and O.W.; writing—original draft preparation, A.K. and O.W.; writing—review and editing, A.K.

Funding

This research received no external funding.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Kolarik, Z.; Müllich, U.; Gassner, F. Selective Extraction Of Am(III) Over Eu(III) by 2,6-Ditriazolyl- and 2,6-Ditriazinylpyridines. Solvent Extr. Ion Exch. 1999, 17, 23–32. [Google Scholar] [CrossRef]
  2. Kolarik, Z.; Müllich, U.; Gassner, F. Extraction of Am(III) and Eu(III) Nitrates by 2-6-Di-(5,6-Dipropyl-1,2,4-Triazin-3-yl)Pyridines. Solvent Extr. Ion Exch. 1999, 17, 1155–1170. [Google Scholar] [CrossRef]
  3. Berthet, J.C.; Miquel, Y.; Iveson, P.B.; Nierlich, M.; Thuery, P.; Madic, C.; Ephritikhine, M. The affinity and selectivity of terdentate nitrogen ligands towards trivalent lanthanide and uranium ions viewed from the crysatl structures of the 1:3 complexes. J. Chem. Soc. Dalton Trans. 2002, 16, 3265–3272. [Google Scholar] [CrossRef]
  4. Choppin, G.; Liljenzin, J.-O.; Rydberg, J. Radiochemistry and Nuclear Chemistry; Butterworth-Heinemann: Woburn, MA, USA, 2002. [Google Scholar]
  5. Geist, A.; Hill, C.; Modolo, G.; Foreman, M.R.S.J.; Weigl, M.; Gompper, K.; Hudson, M.J. 6,6′-Bis(5,5,8,8-tetramethyl-5,6,7,8-tetrahydro-benzo[1,2,4]triazin-3-yl) [2,2′]bipyridine, an Effective Extracting Agent for the Separation of Americium(III) and Curium(III) from the Lanthanides. Solv. Extr. Ion Exch. 2006, 24, 463–483. [Google Scholar] [CrossRef]
  6. Lan, J.-H.; Shi, W.-Q.; Yuan, L.-Y.; Li, J.; Zhao, Y.-L.; Chai, Z.-F. Recent advances in computational modeling and simulations on the An(III)/Ln(III) separation process. Coord. Chem. Rev. 2012, 256, 1406–1417. [Google Scholar] [CrossRef]
  7. Neidig, M.L.; Clark, D.L.; Martin, R.L. Covalency in f-element complexes. Coord. Chem. Rev. 2013, 257, 394–406. [Google Scholar] [CrossRef]
  8. Benay, G.; Schurhammer, R.; Desaphy, J.; Wipff, G. Substituent effects on BTP’s basicity and complexation properties with LnIII lanthanide ions. New J. Chem. 2011, 35, 184–189. [Google Scholar] [CrossRef]
  9. Trumm, S.; Wipff, G.; Geist, A.; Panak, P.J.; Fanghänel, T. Optimising BTP ligands by tuning their basicity. Radiochim. Acta Int. J. Chem. Asp. Nucl. Sci. Technol. 2011, 99, 13–16. [Google Scholar] [CrossRef]
  10. Ionova, G.; Rabbe, C.; Guillaumont, R.; Ionov, S.; Madic, C.; Krupac, J.-C.; Guillaneux, D. A donor–acceptor model of Ln(III) complexation with terdentate nitrogen planar ligands. New J. Chem. 2002, 26, 234–242. [Google Scholar] [CrossRef]
  11. Panak, P.J.; Geist, A. Complexation and Extraction of Trivalent Actinides and Lanthanides by Triazinylpyridine N-Donor Ligands. Chem. Rev. 2013, 113, 1199–1236. [Google Scholar] [CrossRef] [PubMed]
  12. Iveson, P.B.; Rivière, C.; Guillaneux, D.; Niederlich, M.; Thuéry, P.; Epheritikine, M.; Madic, C. Selective complexation of uranium(III) over cerium(III) by 2,6-bis(5,6-dialkyl-1,2,4-triazin-3-yl)pyridines: 1H NMR and X-ray crystallography studies. Chem. Commun. 2001, 16, 1512–1513. [Google Scholar] [CrossRef]
  13. Guillaumont, D. Quantum Chemistry Study of Actinide(III) and Lanthanide(III) Complexes with Tridentate Nitrogen Ligands. J. Phys. Chem. A 2004, 108, 6893–6900. [Google Scholar] [CrossRef]
  14. Denecke, M.A.; Rossberg, A.; Panak, P.J.; Weigl, M.; Schimmelpfennig, B.; Geist, A. Characterization and comparison of Cm(III) and Eu(III) complexed with 2,6-di(5,6-dipropyl-1,2,4-triazin-3-yl)pyridine using EXAFS, TRFLS, and quantum-chemical methods. Inorg. Chem. 2005, 44, 8418–8425. [Google Scholar] [CrossRef] [PubMed]
  15. Petit, L.; Adamo, C.; Maldivi, P. Toward a Clear-Cut Vision on the Origin of 2,6-Di(1,2,4-triazin-3-yl)pyridine Selectivity for Trivalent Actinides: Insights from Theory. Inorg. Chem. 2006, 45, 8517–8522. [Google Scholar] [CrossRef] [PubMed]
  16. Maldivi, P.; Petit, L.; Adamo, C.; Vetere, V. Theoretical description of metal-ligand bonding within f-element complexes: A successful and necessary interplay between theory and experiment. C. R. Chimie 2007, 10, 888–896. [Google Scholar] [CrossRef]
  17. Steppert, M.; Walther, C.; Geist, A.; Fanghänel, T. Direct nano ESI time-of-flight mass spectrometric investigations on lanthanide BTP complexes in the extraction-relevant diluent 1-octanol. New J. Chem. 2009, 33, 2437–2442. [Google Scholar] [CrossRef]
  18. Kolarik, Z. Complexation and Separation of Lanthanides(III) and Actinides(III) by Heterocyclic N-Donors in Solutions. Chem. Rev. 2008, 108, 4208–4252. [Google Scholar] [CrossRef] [PubMed]
  19. Banik, N.L.; Schimmelpfennig, B.; Marquard, C.M.; Brendebach, B.; Geist, A.; Denecke, M.A. Characterization of redox sensitive plutonium(III) complexed with alkylated 2,6-ditriazinylpyridine (BTP) in organic solution. Dalton Trans. 2010, 39, 5117–5122. [Google Scholar] [CrossRef] [PubMed]
  20. Dupont, C.; Hill, C.; Suzenet, F.; Guillaumet, G. Influence of an Alkoxy Group on Bis-Triazinyl-Pyridines for Selective Extraction of Americium(III). Solv. Extract. Ion Exch. 2013, 31, 253–268. [Google Scholar] [CrossRef]
  21. Lan, J.-H.; Shi, W.-Q.; Yuan, L.-Y.; Zhao, Y.-L.; Li, J.; Chai, Z.-F. Trivalent Actinide and Lanthanide Separations by Tetradentate Nitrogen Ligands: A Quantum Chemistry Study. Inorg. Chem. 2011, 50, 9230–9237. [Google Scholar] [CrossRef] [PubMed]
  22. Lan, J.-H.; Shi, W.-Q.; Yuan, L.-Y.; Feng, Y.-X.; Zhao, Y.-L.; Chai, Z.-F. Thermodynamic Study on the Complexation of Am(III) and Eu(III) with Tetradentate Nitrogen Ligands: A Probe of Complex Species and Reactions in Aqueous Solution. J. Phys. Chem. A 2012, 116, 504–511. [Google Scholar] [CrossRef] [PubMed]
  23. Narbutt, J.; Oziminski, W.P. Selectivity of bis-triazinyl bipyridine ligands for americium(III) in Am/Eu separation by solvent extraction. Part 1. Quantum mechanical study on the structures of BTBP complexes and on the energy of the separation. Dalton Trans. 2012, 41, 14416–14424. [Google Scholar] [CrossRef] [PubMed]
  24. Narbutt, J.; Wodyński, A.; Pecul, M. The selectivity of diglycolamide (TODGA) and bis-triazine-bipyridine (BTBP) ligands in actinide/lanthanide complexation and solvent extraction separation-a theoretical approach. Dalton Trans. 2015, 44, 2657–2666. [Google Scholar] [CrossRef] [PubMed]
  25. Ziegler, T.; Rauk, A. On the calculation of bonding energies by the Hartree Fock Slater method. Theor. Chim. Acta 1977, 46, 1–10. [Google Scholar] [CrossRef]
  26. Reed, A.E.; Curtiss, L.A.; Weinhold, F. Intermolecular interactions from a natural bond orbital, donor–acceptor viewpoint. Chem. Rev. 1988, 88, 899–926. [Google Scholar] [CrossRef]
  27. Kovács, A.; Apostolidis, C.; Walter, O.; Lindqvist-Reis, P. “Lanthanide contraction” in [Ln(BTP)3](CF3SO3)3 complexes. Struct. Chem. 2015, 26, 1287–1295. [Google Scholar] [CrossRef]
  28. Fryer-Kanssen, I.; Austin, J.; Kerridge, A. Topological Study of Bonding in Aquo and Bis(triazinyl)pyridine Complexes of Trivalent Lanthanides and Actinides: Does Covalency Imply Stability? Inorg. Chem. 2016, 55, 10034–10042. [Google Scholar] [CrossRef] [PubMed]
  29. Bader, R.F.W. Atoms in Molecules. A Quantum Theory; Oxford University Press: Oxford, UK, 1990. [Google Scholar]
  30. Drew, M.G.B.; Guillaneux, D.; Hudson, M.J.; Iveson, P.B.; Russell, M.L.; Madic, C. Lanthanide(III) complexes of a highly efficient actinide(III) extracting agent—2,6-bis(5,6-dipropyl-1,2,4-triazin-3-yl)pyridine. Inorg. Chem. Commun. 2001, 4, 12–15. [Google Scholar] [CrossRef]
  31. Fedosseev, A.M.; Grigoriev, M.S.; Charushnikova, I.A.; Budantseva, N.A.; Starikova, Z.A.; Moisy, P. Synthesis, crystal structure and some properties of new perrhenate and pertechnetate complexes of Nd3+ and Am3+ with 2,6-bis(tetramethylfurano)-1,2,4-triazin-3-yl)-pyridine, tris(2-pyridylmethyl)amine and N,N′-tetraethylmalonamide. Polyhedron 2008, 27, 2007–2014. [Google Scholar] [CrossRef]
  32. Guillet, G.L.; Hyatt, I.F.D.; Hillesheim, P.C.; Abboud, K.A.; Scott, M.J. 1,2,4-Triazine-picolinamide functionalized, nonadentate chelates for the segregation of lanthanides(III) and actinides(III) in biphasic systems. New J. Chem. 2013, 37, 119–131. [Google Scholar] [CrossRef]
  33. Frost, G.H.; Hart, F.A.; Heath, C.; Hursthouse, M.B. The crystal structure of tris-(2,2′,6′,2″-terpyridyl)europium(III) perchlorate. J. Chem. Soc. D 1969, 23, 1421–1422. [Google Scholar] [CrossRef]
  34. Piquet, C.; Williams, A.F.; Bernardinelli, G.; Bunzli, J.-C. Structural and photophysical properties of lanthanide complexes with planar aromatic tridentate nitrogen ligands as luminescent building blocks for triple-helical structures. Inorg. Chem. 1993, 32, 4139–4149. [Google Scholar] [CrossRef]
  35. Mallet, C.; Thummel, R.P.; Hery, C. Conformational properties of Eu(III) complexes of 3,3′; 5,3″-polymethylene bridged derivatives of 2,2′; 6,2″-terpyridine. Inorg. Chim. Acta 1993, 210, 223–231. [Google Scholar] [CrossRef]
  36. Piguet, C.; Bunzli, J.-C.G.; Bernardinelli, G.; Bochet, C.G.; Froidevaux, P. Design of luminescent building blocks for supramolecular triple-helical lanthanide complexes. J. Chem. Soc. Dalton Trans. 1995, 1, 83–97. [Google Scholar] [CrossRef]
  37. Bardwell, D.A.; Jeffery, J.C.; Jones, P.L.; McCleverty, J.A.; Psillakis, E.; Reeves, Z.; Ward, M.D. Lanthanide complexes of the tetradentate N-donor ligand dihydrobis[3-(2-pyridyl)pyrazolyl]borate and the terdentate N-donor ligand 2,6-bis(1H-pyrazol-3-yl)pyridine: Syntheses, crystal structures and solution structures based on luminescence lifetime studies. J. Chem. Soc. Dalton Trans. 1997, 12, 2079–2086. [Google Scholar]
  38. Semenova, L.I.; Sobolev, A.N.; Skelton, B.W.; White, A.H. Structural Systematics of Rare Earth Complexes. XV Tris(2,2′:6′,2″-terpyridine)lanthanoid(III) Tris(perchlorate) Complexes. Aust. J. Chem. 1999, 52, 519–529. [Google Scholar] [CrossRef]
  39. Li, Y.; Huffman, J.C.; Flood, A.H. Can terdentate 2,6-bis(1,2,3-triazol-4-yl)pyridines form stable coordination compounds? Chem. Commun. 2007, 26, 2692–2694. [Google Scholar] [CrossRef] [PubMed]
  40. Meudtner, R.M.; Ostermeier, M.; Goddard, R.; Limberg, C.; Hecht, S. Multifunctional “Clickates” as Versatile Extended Heteroaromatic Building Blocks: Efficient Synthesis via Click Chemistry, Conformational Preferences, and Metal Coordination. Chem. Eur. J. 2007, 13, 9834–9840. [Google Scholar] [CrossRef] [PubMed]
  41. de Bettencourt-Dias, A.; Barber, P.S.; Viswanathan, S.; de Lill, D.T.; Rollett, A.; Ling, G.; Altun, S. Para-Derivatized Pybox Ligands As Sensitizers in Highly Luminescent Ln(III) Complexes. Inorg. Chem. 2010, 49, 8848–8861. [Google Scholar] [CrossRef] [PubMed]
  42. Yip, Y.-W.; Wen, H.; Wong, W.-T.; Tanner, P.A.; Wong, K.-L. Increased Antenna Effect of the Lanthanide Complexes by Control of a Number of Terdentate N-Donor Pyridine Ligands. Inorg. Chem. 2012, 51, 7013–7015. [Google Scholar] [CrossRef] [PubMed]
  43. Andreiadis, E.S.; Imbert, D.; Pecaut, J.; Demadrille, R.; Mazzanti, M. Self-assembly of highly luminescent lanthanide complexes promoted by pyridine-tetrazolate ligands. Dalton Trans. 2012, 41, 1268–1277. [Google Scholar] [CrossRef] [PubMed]
  44. Shavaleev, N.M.; Eliseeva, S.V.; Scopelliti, R.; Bunzli, J.-C.G. Tridentate Benzimidazole-Pyridine-Tetrazolates as Sensitizers of Europium Luminescence. Inorg. Chem. 2014, 53, 5171–5178. [Google Scholar] [CrossRef] [PubMed]
  45. WebElements. Available online: http://www.webelements.com (accessed on 25 February 2019).
  46. Shannon, R.D. Revised Effective Ionic Radii and Systematic Studies of Interatomic Distances in Halides and Chalcogenides. Acta Cryst. 1976, A32, 751–767. [Google Scholar] [CrossRef]
  47. Huheey, J.E.; Keiter, E.A.; Keiter, R.L. Inorganic Chemistry: Principles of Structure and Reactivity, 4th ed.; HarperCollins: New York, NY, USA, 1993. [Google Scholar]
  48. Shannon, R.D.; Prewitt, C.T. Revised values of effective ionic radii. Acta Cryst. 1970, B26, 1046–1048. [Google Scholar] [CrossRef]
  49. Paul, P.; Ghosh, M.; Neogy, D.; Mallick, P.K. Electronic and vibrational spectra of some rare earth trifluoromethanesulfonates crystals. Spectrochim. Acta A 2011, 78, 59–63. [Google Scholar] [CrossRef] [PubMed]
  50. Boys, S.F.; Bernardi, F. The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors. Mol. Phys. 1970, 19, 553–566. [Google Scholar] [CrossRef]
  51. Mann, J.B. Atomic Structure Calculations II. Hartree-Fock Wave Functions and Radial Expectation Values: Hydrogen to Lawrencium; LA-3691; Los Alamos Scientific Laboratory: Los Alamos, NM, USA, 1968. [Google Scholar]
  52. Kerridge, A. Oxidation state and covalency in f-element metallocenes (M = Ce, Th, Pu): A combined CASSCF and topological study. Dalton Trans. 2013, 42, 16428–16436. [Google Scholar] [CrossRef] [PubMed]
  53. Kerridge, A. f-Orbital covalency in the actinocenes (An = Th–Cm): Multiconfigurational studies and topological analysis. RSC Adv. 2014, 4, 12078–12086. [Google Scholar] [CrossRef]
  54. Di Pietro, P.; Kerridge, A. U–Oyl Stretching Vibrations as a Quantitative Measure of the Equatorial Bond Covalency in Uranyl Complexes: A Quantum-Chemical Investigation. Inorg. Chem. 2016, 55, 573–583. [Google Scholar] [CrossRef] [PubMed]
  55. Kaltsoyannis, N. Covalency hinders AnO2(H2O)+→AnO(OH)2+ isomerisation (An = Pa–Pu). Dalton Trans. 2016, 45, 3158–3162. [Google Scholar] [CrossRef] [PubMed]
  56. Di Pietro, P.; Kerridge, A. Ligand size dependence of U–N and U–O bond character in a series of uranyl hexaphyrin complexes: Quantum chemical simulation and density based analysis. Phys. Chem. Chem. Phys. 2017, 19, 7546–7559. [Google Scholar] [CrossRef] [PubMed]
  57. Kerridge, A. Quantification of f-element covalency through analysis of the electron density: Insights from simulation. Chem. Commun. 2017, 53, 6685–6695. [Google Scholar] [CrossRef] [PubMed]
  58. Tanti, J.; Lincoln, M.; Kerridge, A. Decomposition of d- and f-shell contributions to uranium bonding from the quantum theory of atoms in molecules: Application to uranium and uranyl halides. Inorganics 2018, 6, 88. [Google Scholar] [CrossRef]
  59. Kaltsoyannis, N. Transuranic Computational Chemistry. Chem. Eur. J. 2018, 24, 2815–2825. [Google Scholar] [CrossRef] [PubMed]
  60. Sadhu, B.; Mishra, V. The coordination chemistry of lanthanide and actinide metal ions with hydroxypyridinone-based decorporation agents: Orbital and density based analyses. Dalton Trans. 2018, 47, 16603–16615. [Google Scholar] [CrossRef] [PubMed]
  61. Wang, C.-Y.; Cheng, C.; Su, J.; Huai, P. Bonding nature of the actinide tetrafluorides AnF4 (An = Th–Cm). Mol. Phys. 2015, 113, 3450–3458. [Google Scholar] [CrossRef]
  62. Jensen, M.P.; Bond, A.H. Comparison of Covalency in the Complexes of Trivalent Actinide and Lanthanide Cations. J. Am. Chem. Soc. 2002, 124, 9870–9877. [Google Scholar] [CrossRef] [PubMed]
  63. Jackson, G.P.; King, F.L.; Goeringer, D.E.; Duckworth, D.C. Collision-induced dissociation of lanthanide oxide ions in quadrupole ion traps: Effects of bond strength and mass. Int. J. Mass Spectrom. 2002, 2016, 85–93. [Google Scholar] [CrossRef]
  64. Konings, R.J.M.; Beneš, O.; Kovács, A.; Manara, D.; Sedmidubský, D.; Gorokhov, L.; Iorish, V.S.; Yungman, V.; Shenyavskaya, E.; Osina, E. The thermodynamic properties of the f-elements and their compounds. Part II. The Lanthanide and Actinide Oxides. J. Phys. Chem. Ref. Data 2014, 43, 013101. [Google Scholar] [CrossRef]
  65. SMART, SAINT, SADABS; Siemens, Analytical X-ray Instruments Inc.: Karlsruhe, Germany, 1997.
  66. APEX2, SAINT-Plus, SADABS; Bruker AXS Inc.: Madison, WI, USA,, 2007.
  67. Sheldrick, G.M. SHELX-2013 programme package for structure solution and refinement. Acta Cryst. 2008, A64, 112–122. [Google Scholar] [CrossRef] [PubMed]
  68. Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, Revision D.01; Gaussian, Inc.: Wallingford, CT, USA, 2010. [Google Scholar]
  69. Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar]
  70. Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parameterization of density functional dispersion correction (DFT-D) for the 94 elements H–Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed]
  71. Dolg, M.; Wedig, U.; Stoll, H.; Preuss, H. Energy-adjusted ab initio pseudopotentials for the first row transition elements. J. Chem. Phys. 1987, 86, 866–872. [Google Scholar]
  72. Martin, J.M.L.; Sundermann, A. Correlation consistent valence basis sets for use with the Stuttgart–Dresden–Bonn relativistic effective core potentials: The atoms Ga–Kr and In–Xe. J. Chem. Phys. 2001, 114, 3408–3420. [Google Scholar] [CrossRef] [Green Version]
  73. Andrae, D.; Haeussermann, U.; Dolg, M.; Stoll, H.; Preuss, H. Energy-adjusted ab initio pseudopotentials for the second and third row transition elements. Theor. Chim. Acta 1990, 77, 123–141. [Google Scholar] [CrossRef]
  74. Dolg, M.; Stoll, H.; Savin, A.; Preuss, H. Energy-adjusted pseudopotentials for the rare earth elements. Theor. Chim. Acta 1989, 75, 173–194. [Google Scholar] [CrossRef]
  75. Dolg, M.; Stoll, H.; Preuss, H. A combination of quasirelativistic pseudopotential and ligand field calculations for lanthanoid compounds. Theor. Chim. Acta 1993, 85, 441–450. [Google Scholar] [CrossRef]
  76. Yang, J.; Dolg, M. Valence basis sets for lanthanide 4f-in-core pseudopotentials adapted for crystal orbital ab initio calculations. Theor. Chem. Acc. 2005, 113, 212–224. [Google Scholar] [CrossRef]
  77. Weigand, A.; Cao, X.; Yang, J.; Dolg, M. Quasirelativistic f-in-core pseudopotentials and core-polarization potentials for trivalent actinides and lanthanides: Molecular test for trifluorides. Theor. Chem. Acc. 2009, 126, 117–127. [Google Scholar] [CrossRef]
  78. Küchle, W.; Dolg, M.; Stoll, H.; Preuss, H. Energy-Adjusted Pseudopotentials for the Actinides. Parameter Sets and Test Calculations for Thorium and Thorium Monoxide. J. Chem. Phys. 1994, 100, 7535–7542. [Google Scholar] [CrossRef]
  79. Cao, X.; Dolg, M.; Stoll, H. Valence basis sets for relativistic energy-consistent small-core actinide pseudopotentials. J. Chem. Phys. 2003, 118, 487–496. [Google Scholar] [CrossRef]
  80. Cao, X.; Dolg, M. Segmented contraction scheme for small-core actinide pseudopotential basis sets. J. Mol. Struct. 2004, 673, 203–209. [Google Scholar] [CrossRef]
  81. Glendening, E.D.; Badenhoop, J.K.; Reed, A.E.; Carpenter, J.E.; Bohmann, J.A.; Morales, C.M.; Weinhold, F. NBO 5.9; Theoretical Chemistry Institute, University of Wisconsin: Madison, WI, USA, 2011. [Google Scholar]
  82. Keith, T.A. AIMAll (Version 17.11.14); TK Gristmill Software: Overland Park, KS, USA, 2017. [Google Scholar]
Inorganics 07 00026 g001 550
Figure 1. Coordination of metals to 2,6-bis(5,6-dipropyl-1,2,4-triazin-3-yl)pyridine (BTP)-type ligands.
Figure 1. Coordination of metals to 2,6-bis(5,6-dipropyl-1,2,4-triazin-3-yl)pyridine (BTP)-type ligands.
Inorganics 07 00026 g001
Inorganics 07 00026 g002 550
Figure 2. The D3 nine-fold coordination structure of the [M(BTP′)3]3+ complexes (hydrogens are not depicted).
Figure 2. The D3 nine-fold coordination structure of the [M(BTP′)3]3+ complexes (hydrogens are not depicted).
Inorganics 07 00026 g002
Inorganics 07 00026 g003 550
Figure 3. Computed M–N bond distances and the M3+ ionic radii. N1 (blue cycle) and N2 (red triangle) correspond to the pyridine and azine nitrogen, respectively (see Figure 1).
Figure 3. Computed M–N bond distances and the M3+ ionic radii. N1 (blue cycle) and N2 (red triangle) correspond to the pyridine and azine nitrogen, respectively (see Figure 1).
Inorganics 07 00026 g003
Inorganics 07 00026 g004 550
Figure 4. Topological picture presenting the bond (green) and ring (red) critical points within an M(BTP′)3+ moiety.
Figure 4. Topological picture presenting the bond (green) and ring (red) critical points within an M(BTP′)3+ moiety.
Inorganics 07 00026 g004
Table
Table 1. Selected bond distances (Å) from M062X computations and available XRD results. a
Table 1. Selected bond distances (Å) from M062X computations and available XRD results. a
Mr(III) bCalculatedX-ray
M–N1M–N2N1–CN2–N3N2–CM–N1M–N2
Sc0.8852.3962.4171.3371.3251.3332.37 ± 0.012.41 ± 0.01
Y1.0402.5162.5251.3391.3281.3342.49 ± 0.012.52 ± 0.02
La1.1722.6842.6581.3421.3281.3332.611 ± 0.0092.585 ± 0.009
Lu1.0012.5002.5091.3391.3281.334
U1.1652.627(9)2.609(10)1.342(1)1.329(1)1.335(1)2.55 ± 0.032.54 ± 0.03
Np1.152.625(5)2.612(17)1.341(1)1.328(1)1.334(0)
Pu1.142.614(8)2.604(22)1.341(1)1.328(0)1.334(0)2.58 ± 0.022.55 ± 0.04
Am1.1152.605(3)2.592(20)1.341(2)1.328(1)1.333(2)
Cm1.112.594(1)2.592(4)1.340(0)1.328(1)1.334(0)
BTP′ 1.3371.3301.344
a The computed data refer to the [M(BTP′)3]3+ species, while the XRD data refer to the [M(BTP)3](CF3SO3)3 (M = Sc, Y, La, Pu) and [U(BTP)3]I3 compounds [12]. The bond distances of slightly asymmetric structures (actinides, experimental) have been averaged; the deviation is included in the experimental error, while it is indicated by the values in parentheses in the computed results. b The ionic radii, r(III), refer to 6-coordinated M(III) ions from crystallographic studies [45,46,47].
Table
Table 2. Fundamental vibrational bands from FT-IR measurements most sensitive to the quality of metal. a
Table 2. Fundamental vibrational bands from FT-IR measurements most sensitive to the quality of metal. a
ScYPuAmMain Character b
1610, m(1660)1606, m(1657)1603, m(1655)1603, m(1656)ν(Aza), ν(Py), ν(M–N)
1585, w(1644)1583, w(1643)1580, w(1642)1580, w(1642)ν(Aza), ν(Py), ν(M–N)
1538, s(1558)1534, sh(1549)1532, s(1545)1533, s(1547)ν(Aza), ν(Py), ν(M–N)
1394, s(1431)1390, s(1428)1387, s(1426)1388, s(1427)β(CH2), ν(Aza), ν(Py), ν(M–N)
1018, m(1045)1017, w(1045)1014, m(1043)1015, m(1044)β(Aza), ν(CC)propyl, ν(M–N)
477, w(455)470, w(441)463, w(437)-(438)τ(Aza), γ(N–M)
437, sh(444)hidden(437)425, m(435)425, m(435)τ(Aza), τ(Py), γ(N–M)
a In cm−1. Computed harmonic frequencies of the [M(BTP′)3]3+ models are given in parentheses. The abbreviations for the intensities correspond to strong (s), medium (m), weak (w), and shoulder (sh). b The assignment is based on the DFT calculations on La(BTP)3(CF3SO3)3, reported in [27]. The meaning of the vibrational symbols are the following: ν, stretch; β, bend; γ, out-of-plane bend; τ, torsion. The notations Py and Aza mean pyridine and triazine, respectively.
Table
Table 3. Comparison of selected electronic properties in [M(BTP′)3]3+ complexes from natural bond orbital (NBO) and quantum theory of atoms in molecules (QTAIM) analyses. a
Table 3. Comparison of selected electronic properties in [M(BTP′)3]3+ complexes from natural bond orbital (NBO) and quantum theory of atoms in molecules (QTAIM) analyses. a
PropertyScYLaLuUNpPuAmCm
n(M)+1.76+1.89+2.14+2.04+1.60+1.64+1.76+1.84+1.86
n(N1)−0.53−0.55−0.56−0.56−0.51−0.51−0.52−0.52−0.53
n(N2)−0.35−0.37−0.38−0.38−0.34−0.35−0.34−0.35−0.36
s0.250.240.210.260.220.230.230.240.24
d0.930.750.650.680.860.780.800.810.80
f----3.094.215.126.057.03
N1(LP)→M218194140164436269264252219
N2(LP)→M252229162185444294311289257
N1–C→M566943597965686341
N2–N3→M395832466255555324
N2–C→M688255748661676452
M→Py----7101885
M→Aza----8132494
q(M)+2.15+2.26+2.24+2.19+2.35+2.25+2.21+2.20+2.21
ρ(M,N1)0.0420.0410.0390.0430.0460.0420.0420.0420.043
ρ(M,N2)0.0400.0390.0410.0420.0470.0430.0430.0440.043
▽2ρ(M,N1)0.1370.1360.1120.1470.1600.1490.1530.1530.153
▽2ρ(M,N2)0.1310.1350.1210.1440.1540.1470.1530.1550.155
Δ(M)0.990.971.110.981.501.291.261.221.17
DI(M,N1)0.200.200.220.200.290.250.250.240.23
DI(M,N2)0.190.190.220.190.280.250.250.240.23
De b340630192645305827352746281528422851
a NBO results: Natural atomic charge, n (e); selected M valence orbital populations, s, d, f (e); and second-order perturbation energy between the electron donor and acceptor moieties (kJ/mol). The energy data are averaged to one donor group in the case of ligand to metal donation, while for one pyridine (Py) and triazine (Aza) ring, respectively, in the case of metal to ligand back-donation. QTAIM results: Atomic charge, q (e); electron density and Laplacian of electron density at the BCPs, ρ and ▽2ρ (au), respectively; difference between the integrated electron density and localization index of the atomic basin of M, Δ(M) (e); delocalization index between atoms M and N, DI(M,N) (e); and dissociation energy, De (kJ/mol). b The basis set superposition errors were computed by the counterpoise method [50], and were 65, 72, and around 50 kJ/mol for Sc, Y, and Ln/An, respectively.

Share and Cite

MDPI and ACS Style

Kovács, A.; Apostolidis, C.; Walter, O. Comparative Study of Complexes of Rare Earths and Actinides with 2,6-Bis(1,2,4-triazin-3-yl)pyridine. Inorganics 2019, 7, 26. https://doi.org/10.3390/inorganics7030026

AMA Style

Kovács A, Apostolidis C, Walter O. Comparative Study of Complexes of Rare Earths and Actinides with 2,6-Bis(1,2,4-triazin-3-yl)pyridine. Inorganics. 2019; 7(3):26. https://doi.org/10.3390/inorganics7030026

Chicago/Turabian Style

Kovács, Attila, Christos Apostolidis, and Olaf Walter. 2019. "Comparative Study of Complexes of Rare Earths and Actinides with 2,6-Bis(1,2,4-triazin-3-yl)pyridine" Inorganics 7, no. 3: 26. https://doi.org/10.3390/inorganics7030026

APA Style

Kovács, A., Apostolidis, C., & Walter, O. (2019). Comparative Study of Complexes of Rare Earths and Actinides with 2,6-Bis(1,2,4-triazin-3-yl)pyridine. Inorganics, 7(3), 26. https://doi.org/10.3390/inorganics7030026

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop