The S3 State of the Oxygen-Evolving Complex: Overview of Spectroscopy and XFEL Crystallography with a Critical Evaluation of Early-Onset Models for O–O Bond Formation
Abstract
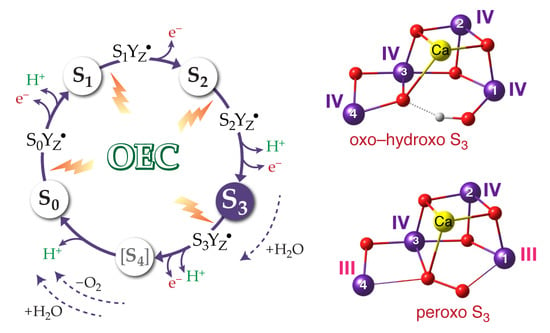
:1. Introduction
2. Geometric and Electronic Information on the S3 State
3. Spectroscopy-Consistent Computational Models for the S3 State
4. XFEL Crystallographic Models for the S3 State
5. Peroxo/Superoxo Models for the S3 State
6. Evaluation of Early-Onset O–O Bond Formation Models
6.1. Structural Features
6.2. Oxidation States and Spectroscopy
6.3. Kinetics of Substrate Exchange
6.4. Computed Energetics of Redox Isomers
7. Conclusions
Funding
Conflicts of Interest
References
- Blankenship, R.E. Molecular Mechanisms of Photosynthesis, 2nd ed.; Wiley: Chichester, UK, 2014; p. 312. [Google Scholar]
- Barber, J. Photosystem II: The water splitting enzyme of photosynthesis and the origin of oxygen in our atmosphere. Q. Rev. Biophys. 2016, 49, e14. [Google Scholar] [CrossRef] [PubMed]
- Junge, W. Oxygenic photosynthesis: History, status and perspective. Q. Rev. Biophys. 2019, 52, e1. [Google Scholar] [CrossRef] [PubMed]
- Askerka, M.; Brudvig, G.W.; Batista, V.S. The O2-Evolving Complex of Photosystem II: Recent Insights from Quantum Mechanics/Molecular Mechanics (QM/MM), Extended X-ray Absorption Fine Structure (EXAFS), and Femtosecond X-ray Crystallography Data. Acc. Chem. Res. 2017, 50, 41–48. [Google Scholar] [CrossRef]
- Pantazis, D.A. Missing Pieces in the Puzzle of Biological Water Oxidation. ACS Catal. 2018, 8, 9477–9507. [Google Scholar] [CrossRef]
- Krewald, V.; Retegan, M.; Pantazis, D.A. Principles of Natural Photosynthesis. Top. Curr. Chem. 2016, 371, 23–48. [Google Scholar] [PubMed]
- Dau, H.; Zaharieva, I.; Haumann, M. Recent developments in research on water oxidation by photosystem II. Curr. Opin. Chem. Biol. 2012, 16, 3–10. [Google Scholar] [CrossRef] [PubMed]
- Pérez-Navarro, M.; Neese, F.; Lubitz, W.; Pantazis, D.A.; Cox, N. Recent developments in biological water oxidation. Curr. Opin. Chem. Biol. 2016, 31, 113–119. [Google Scholar] [CrossRef]
- Messinger, J.; Noguchi, T.; Yano, J. Photosynthetic O2 Evolution. In Molecular Solar Fuels; Wydrzynski, T.J., Hillier, W., Eds.; The Royal Society of Chemistry: Cambridge, UK, 2012; pp. 163–207. [Google Scholar]
- Grundmeier, A.; Dau, H. Structural Models of the Manganese Complex of Photosystem II and Mechanistic Implications. Biochim. Biophys. Acta Bioenerg. 2012, 1817, 88–105. [Google Scholar] [CrossRef]
- Cox, N.; Pantazis, D.A.; Neese, F.; Lubitz, W. Biological water oxidation. Acc. Chem. Res. 2013, 46, 1588–1596. [Google Scholar] [CrossRef]
- Yano, J.; Yachandra, V. Mn4Ca Cluster in Photosynthesis: Where and How Water is Oxidized to Dioxygen. Chem. Rev. 2014, 114, 4175–4205. [Google Scholar] [CrossRef]
- Barber, J.; Tran, P.D. From natural to artificial photosynthesis. J. R. Soc. Interface 2013, 10, 20120984. [Google Scholar] [CrossRef] [PubMed]
- Barber, J. Photosynthetic energy conversion: Natural and artificial. Chem. Soc. Rev. 2009, 38, 185–196. [Google Scholar] [CrossRef] [PubMed]
- Messinger, J.; Lubitz, W.; Shen, J.-R. Photosynthesis: From natural to artificial. Phys. Chem. Chem. Phys. 2014, 16, 11810–11811. [Google Scholar] [CrossRef] [PubMed]
- Lubitz, W.; Reijerse, E.J.; Messinger, J. Solar water-splitting into H2 and O2: Design principles of photosystem II and hydrogenases. Energy Environ. Sci. 2008, 1, 15–31. [Google Scholar] [CrossRef]
- Cox, N.; Pantazis, D.A.; Neese, F.; Lubitz, W. Artificial photosynthesis: Understanding water splitting in nature. Interface Focus 2015, 5, 20150009. [Google Scholar] [CrossRef] [PubMed]
- Nocera, D.G. The Artificial Leaf. Acc. Chem. Res. 2012, 45, 767–776. [Google Scholar] [CrossRef] [PubMed]
- Kim, D.; Sakimoto, K.K.; Hong, D.; Yang, P. Artificial Photosynthesis for Sustainable Fuel and Chemical Production. Angew. Chem. Int. Ed. 2015, 54, 3259–3266. [Google Scholar] [CrossRef]
- Gust, D.; Moore, T.A.; Moore, A.L. Solar Fuels via Artificial Photosynthesis. Acc. Chem. Res. 2009, 42, 1890–1898. [Google Scholar] [CrossRef]
- Kärkäs, M.D.; Verho, O.; Johnston, E.V.; Åkermark, B. Artificial Photosynthesis: Molecular Systems for Catalytic Water Oxidation. Chem. Rev. 2014, 114, 11863–12001. [Google Scholar] [CrossRef]
- Dau, H.; Zaharieva, I. Principles, Efficiency, and Blueprint Character of Solar-Energy Conversion in Photosynthetic Water Oxidation. Acc. Chem. Res. 2009, 42, 1861–1870. [Google Scholar] [CrossRef]
- Dau, H.; Limberg, C.; Reier, T.; Risch, M.; Roggan, S.; Strasser, P. The Mechanism of Water Oxidation: From Electrolysis via Homogeneous to Biological Catalysis. ChemCatChem 2010, 2, 724–761. [Google Scholar] [CrossRef]
- Paul, S.; Neese, F.; Pantazis, D.A. Structural models of the biological oxygen-evolving complex: Achievements, insights, and challenges for biomimicry. Green Chem. 2017, 19, 2309–2325. [Google Scholar] [CrossRef]
- Kurz, P. Biomimetic Water-Oxidation Catalysts: Manganese Oxides. Top. Curr. Chem. 2016, 371, 49–72. [Google Scholar] [PubMed]
- Parent, A.R.; Sakai, K. Progress in Base-Metal Water Oxidation Catalysis. ChemSusChem 2014, 7, 2070–2080. [Google Scholar] [CrossRef] [PubMed]
- Umena, Y.; Kawakami, K.; Shen, J.-R.; Kamiya, N. Crystal Structure of the Oxygen-Evolving Photosystem II at a Resolution of 1.9 Å. Nature 2011, 473, 55–60. [Google Scholar] [CrossRef] [PubMed]
- Suga, M.; Akita, F.; Hirata, K.; Ueno, G.; Murakami, H.; Nakajima, Y.; Shimizu, T.; Yamashita, K.; Yamamoto, M.; Ago, H.; et al. Native Structure of Photosystem II at 1.95 Å Resolution Viewed by Femtosecond X-ray Pulses. Nature 2015, 517, 99–103. [Google Scholar] [CrossRef] [PubMed]
- Krewald, V.; Neese, F.; Pantazis, D.A. Resolving the Manganese Oxidation States in the Oxygen-evolving Catalyst of Natural Photosynthesis. Isr. J. Chem. 2015, 55, 1219–1232. [Google Scholar] [CrossRef]
- Krewald, V.; Retegan, M.; Cox, N.; Messinger, J.; Lubitz, W.; DeBeer, S.; Neese, F.; Pantazis, D.A. Metal Oxidation States in Biological Water Splitting. Chem. Sci. 2015, 6, 1676–1695. [Google Scholar] [CrossRef] [PubMed]
- Dau, H.; Haumann, M. Eight Steps Preceding O–O Bond Formation in Oxygenic Photosynthesis—A Basic Reaction Cycle of the Photosystem II Manganese Complex. Biochim. Biophys. Acta Bioenerg. 2007, 1767, 472–483. [Google Scholar] [CrossRef] [PubMed]
- Schlodder, E.; Witt, H.T. Stoichiometry of Proton Release from the Catalytic Center in Photosynthetic Water Oxidation—Reexamination by a Glass Electrode Study at pH 5.5–7.2. J. Biol. Chem. 1999, 274, 30387–30392. [Google Scholar] [CrossRef]
- Klauss, A.; Haumann, M.; Dau, H. Alternating Electron and Proton Transfer Steps in Photosynthetic Water Oxidation. Proc. Natl. Acad. Sci. USA 2012, 109, 16035–16040. [Google Scholar] [CrossRef]
- Klauss, A.; Haumann, M.; Dau, H. Seven Steps of Alternating Electron and Proton Transfer in Photosystem II Water Oxidation Traced by Time-resolved Photothermal Beam Deflection at Improved Sensitivity. J. Phys. Chem. B 2015, 119, 2677–2689. [Google Scholar] [CrossRef] [PubMed]
- Siegbahn, P.E.M. Water oxidation mechanism in photosystem II, including oxidations, proton release pathways, O–O bond formation and O2 release. Biochim. Biophys. Acta Bioenerg. 2013, 1827, 1003–1019. [Google Scholar] [CrossRef] [PubMed]
- Siegbahn, P.E.M. Structures and energetics for O2 formation in photosystem II. Acc. Chem. Res. 2009, 42, 1871–1880. [Google Scholar] [CrossRef] [PubMed]
- Sproviero, E.M.; Gascon, J.A.; McEvoy, J.P.; Brudvig, G.W.; Batista, V.S. Quantum mechanics/molecular mechanics study of the catalytic cycle of water splitting in photosystem II. J. Am. Chem. Soc. 2008, 130, 3428–3442. [Google Scholar] [CrossRef]
- Guo, Y.; Li, H.; He, L.-L.; Zhao, D.-X.; Gong, L.-D.; Yang, Z.-Z. The open-cubane oxo–oxyl coupling mechanism dominates photosynthetic oxygen evolution: A comprehensive DFT investigation on O–O bond formation in the S4 state. Phys. Chem. Chem. Phys. 2017, 19, 13909–13923. [Google Scholar] [CrossRef]
- Pecoraro, V.L.; Baldwin, M.J.; Caudle, M.T.; Hsieh, W.-Y.; Law, N.A. A proposal for water oxidation in photosystem II. Pure Appl. Chem. 1998, 70, 925–929. [Google Scholar] [CrossRef] [Green Version]
- Vrettos, J.S.; Limburg, J.; Brudvig, G.W. Mechanism of photosynthetic water oxidation: Combining biophysical studies of photosystem II with inorganic model chemistry. Biochim. Biophys. Acta Bioenerg. 2001, 1503, 229–245. [Google Scholar] [CrossRef]
- Yamaguchi, K.; Takahara, Y.; Fueno, T. Ab-Initio Molecular Orbital Studies of Structure and Reactivity of Transition Metal–Oxo Compounds. In Applied Quantum Chemistry; Smith, V.H., Jr., Scheafer, H.F., III, Morokuma, K., Eds.; D. Reidel: Boston, MA, USA, 1986; pp. 155–184. [Google Scholar]
- Siegbahn, P.E.M.; Crabtree, R.H. Manganese oxyl radical intermediates and O–O bond formation in photosynthetic oxygen evolution and a proposed role for the calcium cofactor in photosystem II. J. Am. Chem. Soc. 1999, 121, 117–127. [Google Scholar] [CrossRef]
- Renger, G. Mechanistic and structural aspects of photosynthetic water oxidation. Physiol. Plant. 1997, 100, 828–841. [Google Scholar] [CrossRef]
- Renger, G. Coupling of electron and proton transfer in oxidative water cleavage in photosynthesis. Biochim. Biophys. Acta Bioenerg. 2004, 1655, 195–204. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Renger, G. Oxidative photosynthetic water splitting: Energetics, kinetics and mechanism. Photosynth. Res. 2007, 92, 407–425. [Google Scholar] [CrossRef] [PubMed]
- Suga, M.; Akita, F.; Sugahara, M.; Kubo, M.; Nakajima, Y.; Nakane, T.; Yamashita, K.; Umena, Y.; Nakabayashi, M.; Yamane, T.; et al. Light-Induced Structural Changes and the Site of O=O bond Formation in PSII Caught by XFEL. Nature 2017, 543, 131–135. [Google Scholar] [CrossRef] [PubMed]
- Kern, J.; Chatterjee, R.; Young, I.D.; Fuller, F.D.; Lassalle, L.; Ibrahim, M.; Gul, S.; Fransson, T.; Brewster, A.S.; Alonso-Mori, R.; et al. Structures of the Intermediates of Kok’s Photosynthetic Water Oxidation Clock. Nature 2018, 563, 421–425. [Google Scholar] [CrossRef] [PubMed]
- Isobe, H.; Shoji, M.; Shen, J.-R.; Yamaguchi, K. Chemical Equilibrium Models for the S3 State of the Oxygen-Evolving Complex of Photosystem II. Inorg. Chem. 2016, 55, 502–511. [Google Scholar] [CrossRef] [PubMed]
- Pushkar, Y.; Davis, K.M.; Palenik, M.C. Model of the Oxygen Evolving Complex Which is Highly Predisposed to O–O Bond Formation. J. Phys. Chem. Lett. 2018, 9, 3525–3531. [Google Scholar] [CrossRef]
- Corry, T.A.; O’Malley, P.J. Evidence of O–O Bond Formation in the Final Metastable S3 State of Nature’s Water Oxidizing Complex Implying a Novel Mechanism of Water Oxidation. J. Phys. Chem. Lett. 2018, 9, 6269–6274. [Google Scholar] [CrossRef]
- Yamaguchi, K.; Shoji, M.; Isobe, H.; Yamanaka, S.; Kawakami, T.; Yamada, S.; Katouda, M.; Nakajima, T. Theory of chemical bonds in metalloenzymes XXI. Possible mechanisms of water oxidation in oxygen evolving complex of photosystem II. Mol. Phys. 2018, 116, 717–745. [Google Scholar] [CrossRef]
- Isobe, H.; Shoji, M.; Suzuki, T.; Shen, J.-R.; Yamaguchi, K. Spin, Valence, and Structural Isomerism in the S3 State of the Oxygen-Evolving Complex of Photosystem II as a Manifestation of Multimetallic Cooperativity. J. Chem. Theory Comput. 2019, 15, 2375–2391. [Google Scholar] [CrossRef]
- Glöckner, C.; Kern, J.; Broser, M.; Zouni, A.; Yachandra, V.; Yano, J. Structural Changes of the Oxygen-evolving Complex in Photosystem II during the Catalytic Cycle. J. Biol. Chem. 2013, 288, 22607–22620. [Google Scholar] [CrossRef]
- Liang, W.; Roelofs, T.A.; Cinco, R.M.; Rompel, A.; Latimer, M.J.; Yu, W.O.; Sauer, K.; Klein, M.P.; Yachandra, V.K. Structural Change of the Mn Cluster during the S2→S3 State Transition of the Oxygen-Evolving Complex of Photosystem II. Does It Reflect the Onset of Water/Substrate Oxidation? Determination by Mn X-ray Absorption Spectroscopy. J. Am. Chem. Soc. 2000, 122, 3399–3412. [Google Scholar] [CrossRef] [PubMed]
- Haumann, M.; Müller, C.; Liebisch, P.; Iuzzolino, L.; Dittmer, J.; Grabolle, M.; Neisius, T.; Meyer-Klaucke, W.; Dau, H. Structural and Oxidation State Changes of the Photosystem II Manganese Complex in Four Transitions of the Water Oxidation Cycle (S0→S1, S1→S2, S2→S3, and S3,4→S0) Characterized by X-ray Absorption Spectroscopy at 20 K and Room Temperature. Biochemistry 2005, 44, 1894–1908. [Google Scholar] [CrossRef] [PubMed]
- Messinger, J.; Robblee, J.H.; Bergmann, U.; Fernandez, C.; Glatzel, P.; Visser, H.; Cinco, R.M.; McFarlane, K.L.; Bellacchio, E.; Pizarro, S.A.; et al. Absence of Mn-centered oxidation in the S2→S3 Transition: Implications for the mechanism of photosynthetic water oxidation. J. Am. Chem. Soc. 2001, 123, 7804–7820. [Google Scholar] [CrossRef]
- Iuzzolino, L.; Dittmer, J.; Dörner, W.; Meyer-Klaucke, W.; Dau, H. X-ray Absorption Spectroscopy on Layered Photosystem II Membrane Particles Suggests Manganese-Centered Oxidation of the Oxygen-Evolving Complex for the S0–S1, S1–S2, and S2–S3 Transitions of the Water Oxidation Cycle. Biochemistry 1998, 37, 17112–17119. [Google Scholar] [CrossRef] [PubMed]
- Dau, H.; Iuzzolino, L.; Dittmer, J. The Tetra-Manganese Complex of Photosystem II During its Redox Cycle—X-ray Absorption Results and Mechanistic Implications. Biochim. Biophys. Acta Bioenerg. 2001, 1503, 24–39. [Google Scholar] [CrossRef]
- Dau, H.; Haumann, M. The Manganese Complex of Photosystem II in its Reaction Cycle–Basic Framework and Possible Realization at the Atomic Level. Coord. Chem. Rev. 2008, 252, 273–295. [Google Scholar] [CrossRef]
- Dau, H.; Liebisch, P.; Haumann, M. The manganese complex of oxygenic photosynthesis: Conversion of five-coordinated Mn(III) to six-coordinated Mn(IV) in the S2–S3 transition is implied by XANES simulations. Phys. Scr. 2005, 2005, 844. [Google Scholar] [CrossRef]
- Zaharieva, I.; Chernev, P.; Berggren, G.; Anderlund, M.; Styring, S.; Dau, H.; Haumann, M. Room-Temperature Energy-Sampling Kβ X-ray Emission Spectroscopy of the Mn4Ca Complex of Photosynthesis Reveals Three Manganese-Centered Oxidation Steps and Suggests a Coordination Change Prior to O2 Formation. Biochemistry 2016, 55, 4197–4211. [Google Scholar] [CrossRef] [PubMed]
- Schuth, N.; Zaharieva, I.; Chernev, P.; Berggren, G.; Anderlund, M.; Styring, S.; Dau, H.; Haumann, M. Kα X-ray Emission Spectroscopy on the Photosynthetic Oxygen-Evolving Complex Supports Manganese Oxidation and Water Binding in the S3 State. Inorg. Chem. 2018, 57, 10424–10430. [Google Scholar] [CrossRef] [PubMed]
- Zaharieva, I.; Dau, H.; Haumann, M. Sequential and Coupled Proton and Electron Transfer Events in the S2 → S3 Transition of Photosynthetic Water Oxidation Revealed by Time-Resolved X-ray Absorption Spectroscopy. Biochemistry 2016, 55, 6996–7004. [Google Scholar] [CrossRef]
- Matsukawa, T.; Mino, H.; Yoneda, D.; Kawamori, A. Dual-Mode EPR Study of New Signals from the S3-State of Oxygen-Evolving Complex in Photosystem II. Biochemistry 1999, 38, 4072–4077. [Google Scholar] [CrossRef] [PubMed]
- Ioannidis, N.; Petrouleas, V. Electron Paramagnetic Resonance Signals from the S3 State of the Oxygen-Evolving Complex. A Broadened Radical Signal Induced by Low-Temperature Near-Infrared Light Illumination. Biochemistry 2000, 39, 5246–5254. [Google Scholar] [CrossRef] [PubMed]
- Sanakis, Y.; Sarrou, J.; Zahariou, G.; Petrouleas, V. Q-band Electron Paramagnetic Resonance studies of the S3 state of the OEC of Photosystem II. In Photosynthesis: Energy from the Sun; Allen, J.F., Gantt, E., Golbeck, J.H., Osmond, B., Eds.; Springer: Dordrecht, The Netherlands, 2008; pp. 479–482. [Google Scholar]
- Boussac, A.; Sugiura, M.; Rutherford, A.W.; Dorlet, P. Complete EPR Spectrum of the S3-State of the Oxygen-Evolving Photosystem II. J. Am. Chem. Soc. 2009, 131, 5050–5051. [Google Scholar] [CrossRef] [PubMed]
- Cox, N.; Retegan, M.; Neese, F.; Pantazis, D.A.; Boussac, A.; Lubitz, W. Electronic Structure of the Oxygen-Evolving Complex in Photosystem II Prior to O–O Bond Formation. Science 2014, 345, 804–808. [Google Scholar] [CrossRef]
- Hatakeyama, M.; Ogata, K.; Fujii, K.; Yachandra, V.K.; Yano, J.; Nakamura, S. Structural Changes in the S3 State of the Oxygen Evolving Complex in Photosystem II. Chem. Phys. Lett. 2016, 651, 243–250. [Google Scholar] [CrossRef]
- Noguchi, T. FTIR detection of water reactions in the oxygen-evolving centre of photosystem II. Philos. Trans. R. Soc. B 2008, 363, 1189–1195. [Google Scholar] [CrossRef] [PubMed]
- Möbius, K.; Lubitz, W.; Cox, N.; Savitsky, A. Biomolecular EPR Meets NMR at High Magnetic Fields. Magnetochemistry 2018, 4, 50. [Google Scholar] [CrossRef]
- Hillier, W.; Wydrzynski, T. Substrate water interactions within the Photosystem II oxygen evolving complex. Phys. Chem. Chem. Phys. 2004, 6, 4882–4889. [Google Scholar] [CrossRef]
- Hillier, W.; Wydrzynski, T. 18O-Water exchange in photosystem II: Substrate binding and intermediates of the water splitting cycle. Coord. Chem. Rev. 2008, 252, 306–317. [Google Scholar] [CrossRef]
- Cox, N.; Messinger, J. Reflections on substrate water and dioxygen formation. Biochim. Biophys. Acta Bioenerg. 2013, 1827, 1020–1030. [Google Scholar] [CrossRef] [Green Version]
- Pace, R.J.; Jin, L.; Stranger, R. What Spectroscopy Reveals Concerning the Mn Oxidation Levels in the Oxygen Evolving Complex of Photosystem II: X-ray to Near Infra-Red. Dalton Trans. 2012, 41, 11145–11160. [Google Scholar] [CrossRef]
- Petrie, S.; Stranger, R.; Pace, R.J. What Mn K β Spectroscopy Reveals Concerning the Oxidation States of the Mn Cluster in Photosystem II. Phys. Chem. Chem. Phys. 2017, 19, 27682–27693. [Google Scholar] [CrossRef]
- Dasgupta, J.; Ananyev, G.M.; Dismukes, G.C. Photoassembly of the water-oxidizing complex in photosystem II. Coord. Chem. Rev. 2008, 252, 347–360. [Google Scholar] [CrossRef]
- Vinyard, D.J.; Ananyev, G.M.; Dismukes, G.C. Photosystem II: The Reaction Center of Oxygenic Photosynthesis. Annu. Rev. Biochem. 2013, 82, 577–606. [Google Scholar] [CrossRef]
- Davis, K.M.; Palenik, M.C.; Yan, L.; Smith, P.F.; Seidler, G.T.; Dismukes, G.C.; Pushkar, Y.N. X-ray Emission Spectroscopy of Mn Coordination Complexes Toward Interpreting the Electronic Structure of the Oxygen-Evolving Complex of Photosystem II. J. Phys. Chem. C 2016, 120, 3326–3333. [Google Scholar] [CrossRef]
- Boussac, A.; Rutherford, A.W.; Sugiura, M. Electron transfer pathways from the S2-states to the S3-states either after a Ca2+/Sr2+ or a Cl−/I− exchange in Photosystem II from Thermosynechococcus elongatus. Biochim. Biophys. Acta Bioenerg. 2015, 1847, 576–586. [Google Scholar] [CrossRef]
- Boussac, A.; Ugur, I.; Marion, A.; Sugiura, M.; Kaila, V.R.I.; Rutherford, A.W. The low spin-high spin equilibrium in the S2-state of the water oxidizing enzyme. Biochim. Biophys. Acta Bioenerg. 2018, 1859, 342–356. [Google Scholar] [CrossRef]
- Sanakis, Y.; Ioannidis, N.; Sioros, G.; Petrouleas, V. A Novel S = 7/2 Configuration of the Mn Cluster of Photosystem II. J. Am. Chem. Soc. 2001, 123, 10766–10767. [Google Scholar] [CrossRef] [PubMed]
- Ioannidis, N.; Nugent, J.H.A.; Petrouleas, V. Intermediates of the S3 State of the Oxygen-Evolving Complex of Photosystem II. Biochemistry 2002, 41, 9589–9600. [Google Scholar] [CrossRef]
- Boussac, A.; Sugiura, M.; Inoue, Y.; Rutherford, A.W. EPR Study of the Oxygen Evolving Complex in His-Tagged Photosystem II from the Cyanobacterium Synechococcus elongatus. Biochemistry 2000, 39, 13788–13799. [Google Scholar] [CrossRef] [PubMed]
- Petrouleas, V.; Koulougliotis, D.; Ioannidis, N. Trapping of Metalloradical Intermediates of the S-States at Liquid Helium Temperatures. Overview of the Phenomenology and Mechanistic Implications. Biochemistry 2005, 44, 6723–6728. [Google Scholar] [CrossRef] [PubMed]
- Ioannidis, N.; Zahariou, G.; Petrouleas, V. Trapping of the S2 to S3 State Intermediate of the Oxygen-Evolving Complex of Photosystem II. Biochemistry 2006, 45, 6252–6259. [Google Scholar] [CrossRef] [PubMed]
- Chrysina, M.; Zahariou, G.; Sanakis, Y.; Ioannidis, N.; Petrouleas, V. Conformational changes of the S2YZ· intermediate of the S2 to S3 transition in photosystem II. J. Photochem. Photobiol. B 2011, 104, 72–79. [Google Scholar] [CrossRef] [PubMed]
- Havelius, K.G.V.; Sjöholm, J.; Ho, F.; Mamedov, F.; Styring, S. Metalloradical EPR Signals from the YZ·S-State Intermediates in Photosystem II. Appl. Magn. Reson. 2010, 37, 151–176. [Google Scholar] [CrossRef]
- Havelius, K.G.V.; Su, J.-H.; Han, G.; Mamedov, F.; Ho, F.M.; Styring, S. The formation of the split EPR signal from the S3 state of Photosystem II does not involve primary charge separation. Biochim. Biophys. Acta Bioenerg. 2011, 1807, 11–21. [Google Scholar] [CrossRef] [PubMed]
- Pantazis, D.A.; Ames, W.; Cox, N.; Lubitz, W.; Neese, F. Two Interconvertible Structures that Explain the Spectroscopic Properties of the Oxygen-Evolving Complex of Photosystem II in the S2 State. Angew. Chem. Int. Ed. 2012, 51, 9935–9940. [Google Scholar] [CrossRef] [PubMed]
- Isobe, H.; Shoji, M.; Yamanaka, S.; Umena, Y.; Kawakami, K.; Kamiya, N.; Shen, J.R.; Yamaguchi, K. Theoretical illumination of water-inserted structures of the CaMn4O5 cluster in the S2 and S3 states of oxygen-evolving complex of photosystem II: Full geometry optimizations by B3LYP hybrid density functional. Dalton Trans. 2012, 41, 13727–13740. [Google Scholar] [CrossRef]
- Bovi, D.; Narzi, D.; Guidoni, L. The S2 State of the Oxygen-Evolving Complex of Photosystem II Explored by QM/MM Dynamics: Spin Surfaces and Metastable States Suggest a Reaction Path Towards the S3 State. Angew. Chem. Int. Ed. 2013, 52, 11744–11749. [Google Scholar] [CrossRef]
- Dismukes, G.C.; Siderer, Y. Intermediates of a polynuclear manganese center involved in photosynthetic oxidation of water. Proc. Natl. Acad. Sci. USA 1981, 78, 274–278. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Casey, J.L.; Sauer, K. EPR detection of a cryogenically photogenerated intermediate in photosynthetic oxygen evolution. Biochim. Biophys. Acta Bioenerg. 1984, 767, 21–28. [Google Scholar] [CrossRef]
- Zimmermann, J.L.; Rutherford, A.W. EPR studies of the oxygen-evolving enzyme of Photosystem II. Biochim. Biophys. Acta Bioenerg. 1984, 767, 160–167. [Google Scholar] [CrossRef]
- De Paula, J.C.; Brudvig, G.W. Magnetic properties of manganese in the photosynthetic oxygen-evolving complex. J. Am. Chem. Soc. 1985, 107, 2643–2648. [Google Scholar] [CrossRef]
- Askerka, M.; Wang, J.; Vinyard, D.J.; Brudvig, G.W.; Batista, V.S. S3 State of the O2-Evolving Complex of Photosystem II: Insights from QM/MM, EXAFS, and Femtosecond X-ray Diffraction. Biochemistry 2016, 55, 981–984. [Google Scholar] [CrossRef]
- Li, X.; Siegbahn, P.E.M.; Ryde, U. Simulation of the isotropic EXAFS spectra for the S2 and S3 structures of the oxygen evolving complex in photosystem II. Proc. Natl. Acad. Sci. USA 2015, 112, 3979–3984. [Google Scholar] [CrossRef]
- Beckwith, M.A.; Ames, W.; Vila, F.D.; Krewald, V.; Pantazis, D.A.; Mantel, C.; Pecaut, J.; Gennari, M.; Duboc, C.; Collomb, M.-N.; et al. How accurately can Extended X-ray Absorption Spectra be Predicted from First Principles? Implications for Modeling the Oxygen-Evolving Complex in Photosystem II. J. Am. Chem. Soc. 2015, 137, 12815–12834. [Google Scholar] [CrossRef]
- Chernev, P.; Zaharieva, I.; Rossini, E.; Galstyan, A.; Dau, H.; Knapp, E.-W. Merging Structural Information from X-ray Crystallography, Quantum Chemistry, and EXAFS Spectra: The Oxygen-Evolving Complex in PSII. J. Phys. Chem. B 2016, 120, 10899–10922. [Google Scholar] [CrossRef]
- Beal, N.J.; Corry, T.A.; O’Malley, P.J. A Comparison of Experimental and Broken Symmetry Density Functional Theory (BS-DFT) Calculated Electron Paramagnetic Resonance (EPR) Parameters for Intermediates Involved in the S2 to S3 State Transition of Nature’s Oxygen Evolving Complex. J. Phys. Chem. B 2018, 122, 1394–1407. [Google Scholar] [CrossRef]
- Krewald, V.; Neese, F.; Pantazis, D.A. On the Magnetic and Spectroscopic Properties of High-Valent Mn3CaO4 Cubanes as Structural Units of Natural and Artificial Water Oxidizing Catalysts. J. Am. Chem. Soc. 2013, 135, 5726–5739. [Google Scholar] [CrossRef]
- Krewald, V.; Retegan, M.; Neese, F.; Lubitz, W.; Pantazis, D.A.; Cox, N. Spin State as a Marker for the Structural Evolution of Nature’s Water-Splitting Catalyst. Inorg. Chem. 2016, 55, 488–501. [Google Scholar] [CrossRef]
- Retegan, M.; Krewald, V.; Mamedov, F.; Neese, F.; Lubitz, W.; Cox, N.; Pantazis, D.A. A Five-Coordinate Mn(IV) Intermediate in Biological Water Oxidation: Spectroscopic Signature and a Pivot Mechanism for Water Binding. Chem. Sci. 2016, 7, 72–84. [Google Scholar] [CrossRef]
- Retegan, M.; Cox, N.; Lubitz, W.; Neese, F.; Pantazis, D.A. The First Tyrosyl Radical Intermediate Formed in the S2–S3 Transition of Photosystem II. Phys. Chem. Chem. Phys. 2014, 16, 11901–11910. [Google Scholar] [CrossRef]
- Narzi, D.; Bovi, D.; Guidoni, L. Pathway for Mn-Cluster Oxidation by Tyrosine-Z in the S2 State of Photosystem II. Proc. Natl. Acad. Sci. USA 2014, 111, 8723–8728. [Google Scholar] [CrossRef]
- Gupta, R.; Taguchi, T.; Lassalle-Kaiser, B.; Bominaar, E.L.; Yano, J.; Hendrich, M.P.; Borovik, A.S. High-spin Mn–oxo complexes and their relevance to the oxygen-evolving complex within photosystem II. Proc. Natl. Acad. Sci. USA 2015, 112, 5319–5324. [Google Scholar] [CrossRef]
- Sugiura, M.; Tibiletti, T.; Takachi, I.; Hara, Y.; Kanawaku, S.; Sellés, J.; Boussac, A. Probing the role of Valine 185 of the D1 protein in the Photosystem II oxygen evolution. Biochim. Biophys. Acta Bioenerg. 2018, 1859, 1259–1273. [Google Scholar] [CrossRef]
- Vinyard, D.J.; Khan, S.; Askerka, M.; Batista, V.S.; Brudvig, G.W. Energetics of the S2 State Spin Isomers of the Oxygen-Evolving Complex of Photosystem II. J. Phys. Chem. B 2017, 121, 1020–1025. [Google Scholar] [CrossRef]
- Oyala, P.H.; Stich, T.A.; Stull, J.A.; Yu, F.; Pecoraro, V.L.; Britt, R.D. Pulse Electron Paramagnetic Resonance Studies of the Interaction of Methanol with the S2 State of the Mn4O5Ca Cluster of Photosystem II. Biochemistry 2014, 53, 7914–7928. [Google Scholar] [CrossRef]
- Pérez Navarro, M.; Ames, W.M.; Nilsson, H.; Lohmiller, T.; Pantazis, D.A.; Rapatskiy, L.; Nowaczyk, M.M.; Neese, F.; Boussac, A.; Messinger, J.; et al. Ammonia binding to the oxygen-evolving complex of photosystem II identifies the solvent-exchangeable oxygen bridge (μ-oxo) of the manganese tetramer. Proc. Natl. Acad. Sci. USA 2013, 110, 15561–15566. [Google Scholar] [CrossRef] [Green Version]
- Oyala, P.H.; Stich, T.A.; Debus, R.J.; Britt, R.D. Ammonia Binds to the Dangler Manganese of the Photosystem II Oxygen Evolving Complex. J. Am. Chem. Soc. 2015, 137, 8829–8837. [Google Scholar] [CrossRef]
- Lohmiller, T.; Krewald, V.; Pérez Navarro, M.; Retegan, M.; Rapatskiy, L.; Nowaczyk, M.M.; Boussac, A.; Neese, F.; Lubitz, W.; Pantazis, D.A.; et al. Structure, ligands and substrate coordination of the oxygen-evolving complex of photosystem II in the S2 state: A combined EPR and DFT study. Phys. Chem. Chem. Phys. 2014, 16, 11877–11892. [Google Scholar] [CrossRef]
- Askerka, M.; Vinyard, D.J.; Brudvig, G.W.; Batista, V.S. NH3 Binding to the S2 State of the O2-Evolving Complex of Photosystem II: Analogue to H2O Binding during the S2→S3 Transition. Biochemistry 2015, 54, 5783–5786. [Google Scholar] [CrossRef]
- Retegan, M.; Pantazis, D.A. Interaction of methanol with the oxygen-evolving complex: Atomistic models, channel identification, species dependence, and mechanistic implications. Chem. Sci. 2016, 7, 6463–6476. [Google Scholar] [CrossRef]
- Retegan, M.; Pantazis, D.A. Differences in the Active Site of Water Oxidation among Photosynthetic Organisms. J. Am. Chem. Soc. 2017, 139, 14340–14343. [Google Scholar] [CrossRef] [PubMed]
- Marchiori, D.A.; Oyala, P.H.; Debus, R.J.; Stich, T.A.; Britt, R.D. Structural Effects of Ammonia Binding to the Mn4CaO5 Cluster of Photosystem II. J. Phys. Chem. B 2018, 122, 1588–1599. [Google Scholar] [CrossRef]
- Schuth, N.; Liang, Z.; Schonborn, M.; Kussicke, A.; Assuncao, R.; Zaharieva, I.; Zilliges, Y.; Dau, H. Inhibitory and Non-Inhibitory NH3 Binding at the Water-Oxidizing Manganese Complex of Photosystem II Suggests Possible Sites and a Rearrangement Mode of Substrate Water Molecules. Biochemistry 2017, 56, 6240–6256. [Google Scholar] [CrossRef]
- Wang, J.; Askerka, M.; Brudvig, G.W.; Batista, V.S. Crystallographic Data Support the Carousel Mechanism of Water Supply to the Oxygen-Evolving Complex of Photosystem II. ACS Energy Lett. 2017, 2, 2299–2306. [Google Scholar] [CrossRef]
- Capone, M.; Bovi, D.; Narzi, D.; Guidoni, L. Reorganization of Substrate Waters between the Closed and Open Cubane Conformers during the S2 to S3 Transition in the Oxygen Evolving Complex. Biochemistry 2015, 54, 6439–6442. [Google Scholar] [CrossRef]
- Shoji, M.; Isobe, H.; Yamaguchi, K. QM/MM Study of the S2 to S3 Transition Reaction in the Oxygen-Evolving Complex of Photosystem II. Chem. Phys. Lett. 2015, 636, 172–179. [Google Scholar] [CrossRef]
- Ugur, I.; Rutherford, A.W.; Kaila, V.R.I. Redox-coupled substrate water reorganization in the active site of Photosystem II—The role of calcium in substrate water delivery. Biochim. Biophys. Acta Bioenerg. 2016, 1857, 740–748. [Google Scholar] [CrossRef]
- Capone, M.; Narzi, D.; Bovi, D.; Guidoni, L. Mechanism of Water Delivery to the Active Site of Photosystem II along the S2 to S3 Transition. J. Phys. Chem. Lett. 2016, 7, 592–596. [Google Scholar] [CrossRef]
- Young, I.D.; Ibrahim, M.; Chatterjee, R.; Gul, S.; Fuller, F.D.; Koroidov, S.; Brewster, A.S.; Tran, R.; Alonso-Mori, R.; Kroll, T.; et al. Structure of Photosystem II and Substrate Binding at Room Temperature. Nature 2016, 540, 453–457. [Google Scholar] [CrossRef]
- Wang, J.; Askerka, M.; Brudvig, G.W.; Batista, V.S. Insights into Photosystem II from Isomorphous Difference Fourier Maps of Femtosecond X-ray Diffraction Data and Quantum Mechanics/Molecular Mechanics Structural Models. ACS Energy Lett. 2017, 2, 397–407. [Google Scholar] [CrossRef]
- Siegbahn, P.E.M. Computational investigations of S3 structures related to a recent X-ray free electron laser study. Chem. Phys. Lett. 2017, 690, 172–176. [Google Scholar] [CrossRef]
- Robertazzi, A.; Galstyan, A.; Knapp, E.W. Can oxidation states and the protonation pattern of oxomanganese complexes be recognized from their structures? CrystEngComm 2011, 13, 6369–6372. [Google Scholar] [CrossRef]
- Galstyan, A.; Robertazzi, A.; Knapp, E.W. Oxygen–Evolving Mn Cluster in Photosystem II: The Protonation Pattern and Oxidation State in the High–Resolution Crystal Structure. J. Am. Chem. Soc. 2012, 134, 7442–7449. [Google Scholar] [CrossRef]
- Brown, I.D.; Altermatt, D. Bond-valence parameters obtained from a systematic analysis of the Inorganic Crystal Structure Database. Acta Cryst. 1985, B41, 244–247. [Google Scholar] [CrossRef]
- Gagné, O.C.; Hawthorne, F.C. Comprehensive derivation of bond-valence parameters for ion pairs involving oxygen. Acta Cryst. 2015, B71, 562–578. [Google Scholar] [CrossRef]
- Askerka, M.; Vinyard, D.J.; Wang, J.; Brudvig, G.W.; Batista, V.S. Analysis of the Radiation-Damage-Free X-ray Structure of Photosystem II in Light of EXAFS and QM/MM Data. Biochemistry 2015, 54, 1713–1716. [Google Scholar] [CrossRef]
- Amin, M.; Badawi, A.; Obayya, S.S. Radiation Damage in XFEL: Case study from the oxygen-evolving complex of Photosystem II. Sci. Rep. 2016, 6, 36492. [Google Scholar] [CrossRef]
- Amin, M.; Askerka, M.; Batista, V.S.; Brudvig, G.W.; Gunner, M.R. X-ray Free Electron Laser Radiation Damage through the S-State Cycle of the Oxygen-Evolving Complex of Photosystem II. J. Phys. Chem. B 2017, 121, 9382–9388. [Google Scholar] [CrossRef]
- Clausen, J.; Winkler, S.; Hays, A.-M.A.; Hundelt, M.; Debus, R.J.; Junge, W. Photosynthetic water oxidation in Synechocystis sp. PCC6803: Mutations D1-E189K, R and Q are without influence on electron transfer at the donor side of photosystem II. Biochim. Biophys. Acta Bioenerg. 2001, 1506, 224–235. [Google Scholar] [CrossRef]
- Becke, A.D. Density-Functional Thermochemistry. III. The Role of Exact Exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron-Density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Becke, A.D. Density-Functional Exchange-Energy Approximation with Correct Asymptotic-Behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef]
- Perdew, J.P. Density-Functional Approximation for the Correlation-Energy of the Inhomogeneous Electron-Gas. Phys. Rev. B 1986, 33, 8822–8824. [Google Scholar] [CrossRef]
- Reiher, M.; Salomon, O.; Artur Hess, B. Reparameterization of hybrid functionals based on energy differences of states of different multiplicity. Theor. Chem. Acc. 2001, 107, 48–55. [Google Scholar] [CrossRef]
- Salomon, O.; Reiher, M.; Hess, B.A. Assertion and validation of the performance of the B3LYP* functional for the first transition metal row and the G2 test set. J. Chem. Phys. 2002, 117, 4729–4737. [Google Scholar] [CrossRef]
- Davis, K.M.; Sullivan, B.T.; Palenik, M.C.; Yan, L.; Purohit, V.; Robison, G.; Kosheleva, I.; Henning, R.W.; Seidler, G.T.; Pushkar, Y. Rapid Evolution of the Photosystem II Electronic Structure during Water Splitting. Phys. Rev. X 2018, 8, 041014. [Google Scholar] [CrossRef]
- Staroverov, V.N.; Scuseria, G.E.; Tao, J.; Perdew, J.P. Comparative Assessment of a New Nonempirical Density Functional: Molecules and Hydrogen-Bonded Complexes. J. Chem. Phys. 2003, 119, 12129–12137. [Google Scholar] [CrossRef]
- Hillier, W.; Messinger, J.; Wydrzynski, T. Kinetic determination of the fast exchanging substrate water molecule in the S3 state of photosystem II. Biochemistry 1998, 37, 16908–16914. [Google Scholar] [CrossRef]
- Hillier, W.; Wydrzynski, T. The Affinities for the Two Substrate Water Binding Sites in the O2 Evolving Complex of Photosystem II Vary Independently during S-State Turnover. Biochemistry 2000, 39, 4399–4405. [Google Scholar] [CrossRef]
- Hillier, W.; Wydrzynski, T. Oxygen ligand exchange at metal sites—Implications for the O2 evolving mechanism of photosystem II. Biochim. Biophys. Acta Bioenerg. 2001, 1503, 197–209. [Google Scholar] [CrossRef]
- Nilsson, H.; Rappaport, F.; Boussac, A.; Messinger, J. Substrate–water exchange in photosystem II is arrested before dioxygen formation. Nat. Commun. 2014, 5, 4305. [Google Scholar] [CrossRef]
- Siegbahn, P.E.M. Substrate water exchange for the oxygen evolving complex in PSII in the S1, S2, and S3 states. J. Am. Chem. Soc. 2013, 135, 9442–9449. [Google Scholar] [CrossRef]
- Renger, G. Mechanism of light induced water splitting in Photosystem II of oxygen evolving photosynthetic organisms. Biochim. Biophys. Acta Bioenerg. 2012, 1817, 1164–1176. [Google Scholar] [CrossRef] [Green Version]
- Orio, M.; Pantazis, D.A.; Petrenko, T.; Neese, F. Magnetic and Spectroscopic Properties of Mixed Valence Manganese(III, IV) Dimers: A Systematic Study Using Broken Symmetry Density Functional Theory. Inorg. Chem. 2009, 48, 7251–7260. [Google Scholar] [CrossRef]
- Pantazis, D.A.; Orio, M.; Petrenko, T.; Zein, S.; Bill, E.; Lubitz, W.; Messinger, J.; Neese, F. A New Quantum Chemical Approach to the Magnetic Properties of Oligonuclear Transition-Metal Complexes: Application to a Model for the Tetranuclear Manganese Cluster of Photosystem II. Chem. Eur. J. 2009, 15, 5108–5123. [Google Scholar] [CrossRef]
- Krewald, V.; Neese, F.; Pantazis, D.A. Redox potential tuning by redox-inactive cations in nature’s water oxidizing catalyst and synthetic analogues. Phys. Chem. Chem. Phys. 2016, 18, 10739–10750. [Google Scholar] [CrossRef]
- Krewald, V.; Pantazis, D.A. Understanding and tuning the properties of redox-accumulating manganese helicates. Dalton Trans. 2016, 45, 18900–18908. [Google Scholar] [CrossRef]
- Cramer, C.J.; Truhlar, D.G. Density functional theory for transition metals and transition metal chemistry. Phys. Chem. Chem. Phys. 2009, 11, 10757–10816. [Google Scholar] [CrossRef]
- Neese, F. Prediction of Molecular Properties and Molecular Spectroscopy with Density Functional Theory: From Fundamental Theory to Exchange-Coupling. Coord. Chem. Rev. 2009, 253, 526–563. [Google Scholar] [CrossRef]
- Orio, M.; Pantazis, D.A.; Neese, F. Density Functional Theory. Photosynth. Res. 2009, 102, 443–453. [Google Scholar] [CrossRef] [PubMed]
- Neese, F.; Ames, W.; Christian, G.; Kampa, M.; Liakos, D.G.; Pantazis, D.A.; Roemelt, M.; Surawatanawong, P.; Ye, S.F. Dealing with complexity in open-shell transition metal chemistry from a theoretical perspective: Reaction pathways, bonding, spectroscopy, and magnetic properties. Adv. Inorg. Chem. 2010, 62, 301–349. [Google Scholar]
- Tsipis, A.C. DFT flavor of coordination chemistry. Coord. Chem. Rev. 2014, 272, 1–29. [Google Scholar] [CrossRef]
- Chan, G.K.-L.; Sharma, S. The Density Matrix Renormalization Group in Quantum Chemistry. Annu. Rev. Phys. Chem. 2011, 62, 465–481. [Google Scholar] [CrossRef] [PubMed]
- Marti, K.H.; Reiher, M. New Electron Correlation Theories for Transition Metal Chemistry. Phys. Chem. Chem. Phys. 2011, 13, 6750–6759. [Google Scholar] [CrossRef] [PubMed]
- Marti, K.H.; Ondík, I.M.; Moritz, G.; Reiher, M. Density matrix renormalization group calculations on relative energies of transition metal complexes and clusters. J. Chem. Phys. 2008, 128, 014104. [Google Scholar] [CrossRef]
- Roemelt, M.; Pantazis, D.A. Multireference Approaches to Spin-State Energetics of Transition Metal Complexes Utilizing the Density Matrix Renormalization Group. Adv. Theory Simul. 2019, 1800201. [Google Scholar] [CrossRef]
- Paul, S.; Cox, N.; Pantazis, D.A. What Can We Learn from a Biomimetic Model of Nature’s Oxygen-Evolving Complex? Inorg. Chem. 2017, 56, 3875–3888. [Google Scholar] [CrossRef]
- Zhang, C.; Chen, C.; Dong, H.; Shen, J.-R.; Dau, H.; Zhao, J. A synthetic Mn4Ca-cluster mimicking the oxygen-evolving center of photosynthesis. Science 2015, 348, 690–693. [Google Scholar] [CrossRef]
- Harris, T.V.; Kurashige, Y.; Yanai, T.; Morokuma, K. Ab initio Density Matrix Renormalization Group Study of Magnetic Coupling in Dinuclear Iron and Chromium Complexes. J. Chem. Phys. 2014, 140, 054303. [Google Scholar] [CrossRef]
- Roemelt, M.; Krewald, V.; Pantazis, D.A. Exchange Coupling Interactions from the Density Matrix Renormalization Group and N-Electron Valence Perturbation Theory: Application to a Biomimetic Mixed-Valence Manganese Complex. J. Chem. Theory Comput. 2018, 14, 166–179. [Google Scholar] [CrossRef] [PubMed]
- Kawakami, T.; Miyagawa, K.; Sharma, S.; Saito, T.; Shoji, M.; Yamada, S.; Yamanaka, S.; Okumura, M.; Nakajima, T.; Yamaguchi, K. UNO DMRG CAS CI Calculations of Binuclear Manganese Complex Mn(IV)2O2(NHCHCO2)4: Scope and Applicability of Heisenberg Model. J. Comput. Chem. 2018, 40, 333–341. [Google Scholar] [CrossRef] [PubMed]
- Pantazis, D.A. Meeting the Challenge of Magnetic Coupling in a Triply-Bridged Chromium Dimer: Complementary Broken-Symmetry Density Functional Theory and Multireference Density Matrix Renormalization Group Perspectives. J. Chem. Theory Comput. 2019, 15, 938–948. [Google Scholar] [CrossRef] [PubMed]
- Guo, S.; Watson, M.A.; Hu, W.; Sun, Q.; Chan, G.K.-L. N-Electron Valence State Perturbation Theory Based on a Density Matrix Renormalization Group Reference Function, with Applications to the Chromium Dimer and a Trimer Model of Poly(p-Phenylenevinylene). J. Chem. Theory Comput. 2016, 12, 1583–1591. [Google Scholar] [CrossRef]
- Freitag, L.; Knecht, S.; Angeli, C.; Reiher, M. Multireference Perturbation Theory with Cholesky Decomposition for the Density Matrix Renormalization Group. J. Chem. Theory Comput. 2017, 13, 451–459. [Google Scholar] [CrossRef] [PubMed]
- Radoń, M. Spin-State Energetics of Heme-Related Models from DFT and Coupled Cluster Calculations. J. Chem. Theory Comput. 2014, 10, 2306–2321. [Google Scholar] [CrossRef] [PubMed]
- Radoń, M.; Gassowska, K.; Szklarzewicz, J.; Broclawik, E. Spin-State Energetics of Fe(III) and Ru(III) Aqua Complexes: Accurate ab Initio Calculations and Evidence for Huge Solvation Effects. J. Chem. Theory Comput. 2016, 12, 1592–1605. [Google Scholar] [CrossRef]
- Radoń, M. Benchmarking quantum chemistry methods for spin-state energetics of iron complexes against quantitative experimental data. Phys. Chem. Chem. Phys. 2019, 21, 4854–4870. [Google Scholar] [CrossRef] [PubMed]
- Feldt, M.; Phung, Q.M.; Pierloot, K.; Mata, R.A.; Harvey, J.N. Limits of Coupled-Cluster Calculations for Non-Heme Iron Complexes. J. Chem. Theory Comput. 2019, 15, 922–937. [Google Scholar] [CrossRef] [PubMed]
- Riplinger, C.; Neese, F. An efficient and near linear scaling pair natural orbital based local coupled cluster method. J. Chem. Phys. 2013, 138, 034106. [Google Scholar] [CrossRef]
- Saitow, M.; Becker, U.; Riplinger, C.; Valeev, E.F.; Neese, F. A new near-linear scaling, efficient and accurate, open-shell domain-based local pair natural orbital coupled cluster singles and doubles theory. J. Chem. Phys. 2017, 146, 164105. [Google Scholar] [CrossRef] [PubMed]
- Senn, H.M.; Thiel, W. QM/MM Methods for Biomolecular Systems. Angew. Chem. Int. Ed. 2009, 48, 1198–1229. [Google Scholar] [CrossRef] [PubMed]
- Quesne, M.G.; Borowski, T.; de Visser, S.P. Quantum Mechanics/Molecular Mechanics Modeling of Enzymatic Processes: Caveats and Breakthroughs. Chem. Eur. J. 2016, 22, 2562–2581. [Google Scholar] [CrossRef] [PubMed]
- Sproviero, E.M.; Gascon, J.A.; McEvoy, J.P.; Brudvig, G.W.; Batista, V.S. QM/MM models of the O2-evolving complex of photosystem II. J. Chem. Theory Comput. 2006, 2, 1119–1134. [Google Scholar] [CrossRef]
- Retegan, M.; Neese, F.; Pantazis, D.A. Convergence of QM/MM and cluster models for the spectroscopic properties of the oxygen-evolving complex in photosystem II. J. Chem. Theory Comput. 2013, 9, 3832–3842. [Google Scholar] [CrossRef]
- Shoji, M.; Isobe, H.; Yamanaka, S.; Umena, Y.; Kawakami, K.; Kamiya, N.; Shen, J.-R.; Nakajima, T.; Yamaguchi, K. Theoretical modelling of biomolecular systems I. Large-scale QM/MM calculations of hydrogen-bonding networks of the oxygen evolving complex of photosystem II. Mol. Phys. 2015, 113, 359–384. [Google Scholar] [CrossRef]










| S3 Model [30] | 55Mn |Aiso| | |||
|---|---|---|---|---|
| S3H-1 | −86 (Mn1) | −76 (Mn2) | −34 (Mn3) | 27 (Mn4) |
| S3H-2 | −99 (Mn2) | −88 (Mn1) | −29 (Mn4) | 20 (Mn3) |
| Exp. [68] | −99 (Mn1 or Mn2) | −96 (Mn1 or Mn2) | −26 (Mn3 or Mn4) | ≤5 (Mn3 or Mn4) |
| S3 Model [50] | 55Mn |Aiso| | |||
|---|---|---|---|---|
| peroxo-A | −130 (Mn4) | 83 (Mn1) | −72 (Mn3) | −68 (Mn2) |
| peroxo-B | −128 (Mn4) | −109 (Mn3) | 85 (Mn1) | −58 (Mn2) |
| peroxo-C | −103 (Mn4) | −83 (Mn3) | −45 (Mn1) | 22 (Mn2) |
| Exp. [68] | −99 (Mn1 or Mn2) | −96 (Mn1 or Mn2) | −26 (Mn3 or Mn4) | ≤5 (Mn3 or Mn4) |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pantazis, D.A. The S3 State of the Oxygen-Evolving Complex: Overview of Spectroscopy and XFEL Crystallography with a Critical Evaluation of Early-Onset Models for O–O Bond Formation. Inorganics 2019, 7, 55. https://doi.org/10.3390/inorganics7040055
Pantazis DA. The S3 State of the Oxygen-Evolving Complex: Overview of Spectroscopy and XFEL Crystallography with a Critical Evaluation of Early-Onset Models for O–O Bond Formation. Inorganics. 2019; 7(4):55. https://doi.org/10.3390/inorganics7040055
Chicago/Turabian StylePantazis, Dimitrios A. 2019. "The S3 State of the Oxygen-Evolving Complex: Overview of Spectroscopy and XFEL Crystallography with a Critical Evaluation of Early-Onset Models for O–O Bond Formation" Inorganics 7, no. 4: 55. https://doi.org/10.3390/inorganics7040055
APA StylePantazis, D. A. (2019). The S3 State of the Oxygen-Evolving Complex: Overview of Spectroscopy and XFEL Crystallography with a Critical Evaluation of Early-Onset Models for O–O Bond Formation. Inorganics, 7(4), 55. https://doi.org/10.3390/inorganics7040055