Next Article in Journal
σ-Holes vs. Buildups of Electronic Density on the Extensions of Bonds to Halogen Atoms
Next Article in Special Issue
Covalent Si–H Bonds in the Zintl Phase Hydride CaSiH1+x (x ≤ 1/3)
Previous Article in Journal
Recent Progress on Catalysts for the Positive Electrode of Aprotic Lithium-Oxygen Batteries †
Previous Article in Special Issue
Low-Temperature Ordering in the Cluster Compound (Bi8)Tl[AlCl4]3
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Inorganics
Volume 7
Issue 6
10.3390/inorganics7060070
inorganics-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

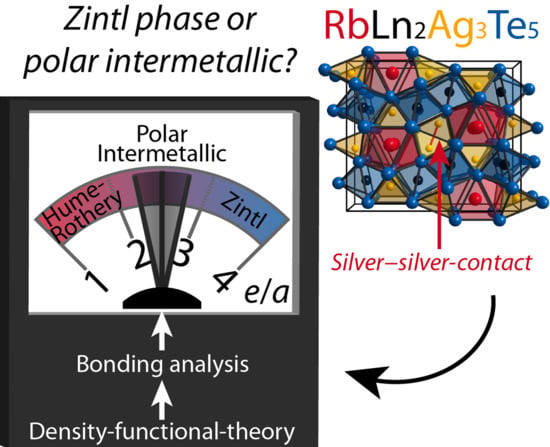
Revealing the Nature of Chemical Bonding in an ALn2Ag3Te5-Type Alkaline-Metal (A) Lanthanide (Ln) Silver Telluride

by
Kai C. Göbgen
1,
Kai S. Fries
1,
Fabian C. Gladisch
1,
Richard Dronskowski
1,2,3 and
Simon Steinberg
1,*
1
Institute of Inorganic Chemistry, RWTH Aachen University, Landoltweg 1, D-52074 Aachen, Germany
2
Jülich-Aachen Research Alliance (JARA-FIT and -HPC), RWTH Aachen University, Landoltweg 1, D-52074 Aachen, Germany
3
Hoffmann Institute of Advanced Materials, Shenzhen Polytechnic, 7098 Liuxian Blvd, Nanshan District, Shenzhen 518055, China
*
Author to whom correspondence should be addressed.
Inorganics 2019, 7(6), 70; https://doi.org/10.3390/inorganics7060070
Submission received: 24 April 2019 / Revised: 23 May 2019 / Accepted: 27 May 2019 / Published: 31 May 2019
(This article belongs to the Special Issue Structure, Properties, and Bonding in Solid State Compounds)
Browse Figures
Versions Notes

Abstract

:
Although the electronic structures of several tellurides have been recognized by applying the Zintl-Klemm concept, there are also tellurides whose electronic structures cannot be understood by applications of the aforementioned idea. To probe the appropriateness of the valence-electron transfers as implied by Zintl-Klemm treatments of ALn2Ag3Te5-type tellurides (A = alkaline-metal; Ln = lanthanide), the electronic structure and, furthermore, the bonding situation was prototypically explored for RbPr2Ag3Te5. The crystal structure of that type of telluride is discussed for the examples of RbLn2Ag3Te5 (Ln = Pr, Nd), and it is composed of tunnels which are assembled by the tellurium atoms and enclose the rubidium, lanthanide, and silver atoms, respectively. Even though a Zintl-Klemm treatment of RbPr2Ag3Te5 results in an (electron-precise) valence-electron distribution of (Rb+)(Pr3+)2(Ag+)3(Te2−)5, the bonding analysis based on quantum-chemical means indicates that a full electron transfer as suggested by the Zintl-Klemm approach should be considered with concern.

Graphical Abstract

1. Introduction

The understanding and, furthermore, the tailored design of the physical properties for a given solid-state material requires a proper knowing of its electronic (band) structure [1,2]. In addition, the knowledge of the total (electronic) energy, which is evaluated from the electronic (band) structure computations for a given material, also provides valuable information about the structural preferences and, hence, stability trends for such a substance [3,4]. The total energy of a given material depends on two elementary energetic contributions, that are, the site energy and the bond energy [2]. Although the energy arising from the bonds within a given solid-state material plays an important role with regard to its total energy, the interpretation of the nature of bonding has still remained challenging for one particular class of solid-state materials, i.e., intermetallic phases [5]. Yet, certain concepts, e.g., those stated by Hume-Rothery [6,7,8] or Zintl and Klemm [9,10,11], help to understand the distributions of valence-electrons in some intermetallics. On the other hand, more recent research [1,12] on polar intermetallic compounds revealed the existence of polyanionic or polycationic units (“clusters”) which are combined with monoatomic counterions, but are electron-poorer relative to Zintl phases.
Among the group of intermetallic compounds, tellurides have attracted an enormous interest because of the employments as materials for diverse applications including thermoelectric energy conversion [13,14,15] or data storage [16,17,18]. The distributions of the valence-electrons in the tellurides have been typically described by applying the Zintl-Klemm concept [19,20]; however, the application of the latter to certain tellurides containing low-dimensional tellurium fragments resulted in the assignments of non-electron-precise charges to the tellurium atoms [20]. In that connection, recent research [21,22] on the electronic structures of certain tellurides, i.e., LaCuxTe2 (0.28 ≤ x ≤ 0.50), Gd3Cu2Te7, and Ag5−xTe3 (−0.25 ≤ x ≤ 1.44), indicated that the valence-electron transfers as suggested by Zintl-Klemm treatments should be taken with a grain of salt. In fact, analyzing the nature of bonding for the aforementioned tellurides revealed the presence of strong rare-earth–tellurium as well as transition-metal–tellurium bonding interactions being in stark contrast to the (complete) valence-electron transfers as assumed by Zintl-Klemm treatments. The outcome of these examinations stimulated our impetus to determine the electronic structures and, furthermore, the nature of bonding for tellurides, which are expected to comprise rather ionic interactions, but also the aforementioned mixed-metal interactions.
In the quest for tellurides, which are estimated to show rather ionic as well as mixed-metal interactions, the group of the quaternary alkaline-metal rare-earth transition-metal tellurides has attracted our interest. Previous research on the group of the quaternary tellurides has focused on exploring the formations [23,24] of charge density waves, the effectiveness [25,26,27,28] for thermoelectric energy conversion, and the magnetic [29] properties. In this contribution, we examine the electronic structure and, furthermore, the nature of bonding for one representative of the ALn2Ag3Te5-type (A = alkaline-metal; Ln = lanthanide), whose crystal structure will be described for the examples of RbLn2Ag3Te5 (Ln = Pr, Nd).

2. Results and Discussion

The quaternary RbLn2Ag3Te5 (Ln = Pr, Nd; Table 1) were obtained as high-yield products from reactions of the respective lanthanides, silver, and tellurium in the presence of rubidium chloride, which was used as a reactive flux [30] (see Section 3.1). Both tellurides are isostructural to the recently reported [28] RbLn2Ag3Te5 (Ln = Sm, Gd–Dy), which are related to smaller unit cell volumes relative to the herein reported tellurides as a consequence of the lanthanide contraction [31]. A comparison of the unit cell volumes of RbLn2Ag3Te5 (Ln = Pr, Nd; Table 1) to those of the cesium-containing analogues [28], i.e., CsLn2Ag3Te5 (Ln = Pr, Nd), reveals that the unit cells of the rubidium-containing tellurides are smaller because of an increased atomic radius [32] from rubidium (2.20 Å) to cesium (2.44 Å). To provide an insight into the structural features for this type of telluride, the crystal structures of the quaternary RbLn2Ag3Te5 (Ln = Pr, Nd) will be inspected in detail in the following.

2.1. Structural Details

RbLn2Ag3Te5 (Ln = Pr, Nd) crystallize with the orthorhombic space group Cmcm (Table 1 and Table 2) and their crystal structures are composed of one-dimensional tunnels (Figure 1), which are assembled by the tellurium atoms and enclose the rubidium, silver, and lanthanide atoms. More specifically, the rubidium atoms reside in the centers of bicapped trigonal tellurium prisms, [Rb@Te8], that are condensed via their triangular faces to linear [ Rb @ Te 8 ] ∞ 1 chains parallel to the a-axis. Each [Rb@Te8] unit shares six edges with six nearest neighboring tellurium octahedra enclosing the lanthanide atoms, [Ln@Te6]. The [Ln@Te6] units are connected via common edges to [ Ln @ Te 6 ] ∞ 1 double chains, while the silver atoms occupy the tetrahedral voids located between the [ Rb @ Te 8 ] ∞ 1 chains and [ Ln @ Te 6 ] ∞ 1 double chains. The tetrahedral [Ag@Te4] units encapsulating the Ag5 atoms (Wyckoff position 8f) join edges and vertices with neighboring [Ag5@Te4] units to construct [ Ag 5 @ Te 4 ] ∞ 1 double chains parallel to the a-axis. Additionally, the tellurium tetrahedra encompassing the Ag6 atoms (Wyckoff position 4c), [Ag6@Te4], are connected via common tellurium atoms to neighboring units within the [ Ag 6 @ Te 4 ] ∞ 1 chains as well as nearby [ Ag 5 @ Te 4 ] ∞ 1 double chains. A closer topological inspection of the [ Ag 5 @ Te 4 ] ∞ 1 double chains reveals the presence of relatively short Ag5–Ag5 contacts (see Table 3). Considering the covalent atomic radii [32] of silver (1.45 Å), such short Ag–Ag separations of ~2.95 Å suggest the presence of Ag–Ag bonding interactions; however, an application of the Zintl-Klemm concept [9,10,11] to RbLn2Ag3Te5 (Ln = Pr, Nd) leads to a formal (electron-precise) valence-electron-distribution of (Rb+)(Ln3+)2(Ag+)3(Te2−)5 disregarding the presence of Ag–Ag bonds. To determine the actual nature of bonding for this telluride, we followed up with a prototypical examination of the electronic band structure for RbPr2Ag3Te5.

2.2. Electronic Structure and Chemical Bonding Analysis

An examination of the densities-of-states (DOS) curves for RbPr2Ag3Te5 (Figure 2) reveals that the occupied states close to the Fermi level, EF, originate to a large extent from the Ag-d and Te-p atomic orbitals beside minor contributions from the Pr-d states. This outcome implies that the majority of the valence electrons and, hence, bonding interactions reside between the Ag–Te, Pr–Te, and Ag–Ag contacts. A further integration of the energy regions near EF also bares that the contributions arising from the Rb-s bands are rather negligible (not shown in Figure 2). Accordingly, one may infer that rubidium acts as a one-electron donor in the telluride. Because the Fermi level in RbPr2Ag3Te5 falls in a band gap of 0.93 eV, an electronically favorable situation is achieved for this telluride. Furthermore, the presence of the band gap at the Fermi level is in full accordance with the formal valence-electron distribution as proposed by the application of the Zintl-Klemm concept. Yet, there are the Ag–Ag separations of ~2.95 Å suggesting the presence of Ag–Ag bonding interactions which are not predicted by a Zintl-Klemm treatment.
To provide an insight into the bonding situation in RbPr2Ag3Te5, we followed up with an examination of the crystal orbital Hamilton population curves (COHP; Figure 2) and their respective integrated values (Table 3). In this context, the cumulative –ICOHP/cell values, i.e., the sums of the negative ICOHP/bond values of all nearest neighboring contacts within one unit cell, were projected as percentages of the net bonding capabilities for each sort of interaction to identify roles of the diverse interactions in overall bonding—a procedure that has been largely employed elsewhere [21,22,33,34,35,36].
A comparison of all –ICOHP/bond values bares that the largest values correspond to the heteroatomic Pr–Te and Ag–Te interactions, which contribute 43.7% (Pr–Te) and 53.7% (Ag–Te) to the total bonding capabilities. Therefore, it may be concluded that the vast majority of the bonding populations is located between the Pr–Te and Ag–Te interactions. The Rb–Te interactions are related to rather small –ICOHP/bond values, which contribute 1.1% to the net bonding capabilities. Under consideration of previous research [37,38] on the electronic structures of alkaline-metal-containing polar intermetallics, this outcome suggests that the Rb–Te interactions should be considered as ionic interactions, while the Pr–Te and Ag–Te interactions should be regarded as rather strong, polar, mixed-metal bonds. This outcome also indicates that a full valence-electron transfer as proposed by an application of the Zintl-Klemm concept should be regarded with suspicion—a consequence which has also been identified by recent explorations of the electronic structures of rare-earth transition-metal tellurides [22] as well as silver tellurides [21]. The homoatomic Ag–Ag interactions change from bonding to considerable antibonding states at −4.41 eV, which may be regarded as attributes of the d10–d10 closed-shell [39,40] interactions; however, the Ag–Ag –ICOHP values are indicative of a net bonding character for these interactions. Because of the rather low bond frequency of the Ag–Ag separations, these interactions solely contribute 1.5% to the net bonding capabilities.

3. Materials and Methods

3.1. Syntheses

RbLn2Ag3Te5 (Ln = Pr, Nd) were obtained from reactions of the respective rare-earth-elements (smart-elements®, Vienna, Austria, Pr: 99.9%, Nd: 99.9%), silver (Alfa®, Haverhill, MA, USA, ≥99.99%), and tellurium (Merck®, Darmstadt, Germany, >99%) in the presence of rubidium chloride (Sigma Aldrich®, St. Louis, MO, USA, 99.8%), which was employed as a reactive [30] flux. Powders of the rare-earth elements were obtained from filing large ingots, whose surfaces were polished prior to every use. All reactants were stored and handled in an argon-filled glove box with strict exclusion of air and moisture (MBraun®, Garching, Germany; O2 < 0.1 ppm by volume; H2O < 0.3 ppm by volume). In the glove box, mixtures of 0.3 mmol Ln, 0.45 mmol Ag, 0.75 mmol Te, and 0.5 mmol RbCl were first weighed, then pesteled and, finally, loaded in one-side-closed silica tubes, which were subsequently flame-sealed under a dynamic vacuum of at least 2 × 10−3 mbar. The samples were heated using computer-controlled tube furnaces and the following temperature program: heat to 400 °C in 5 h, slowly warm up to 850 °C with a rate of 10 °C/h, keep that temperature for 100 h, slowly cool to 300 °C with a rate of 2 °C/h, and equilibrate to room temperature within 25 h. The excess flux was removed with the aid of deionized water, and the products appeared as grey powders containing small crystals. Phase analyses based on powder X-ray diffraction techniques (see Figure 3 and Section 3.2) revealed that the products, which remained stable in air for at least two weeks, were obtained in high yields. Further research, which has been conducted under similar conditions and started from the reactants holmium, silver, tellurium, and a RbCl/LiCl flux, resulted in the identification of the respective holmium-containing telluride (a = 4.52(1) Å; b = 16.14(4) Å; c = 18.30(4) Å).

3.2. X-ray Diffraction Studies and Determinations of the Crystal Structures

Sets of powder X-ray diffraction (PXRD) data were collected to identify the yields of RbLn2Ag3Te5 (Ln = Pr, Nd) and feasible side-products by comparing the measured PXRD patterns to those which were simulated for RbLn2Ag3Te5 (Ln = Pr, Nd) and plausible side-products. To measure the samples, the obtained products were first finely ground and, then, dispersed on Mylar sheets with grease, which were fixed between split aluminum rings. The sets of PXRD data were collected at room temperature with the aid of a STOE StadiP diffractometer (Stoe® & Cie, Darmstadt, Germany; area detector; Cu Kα radiation; λ = 1.54059 Å). The WinXPow software package [45] was utilized for control of the measurements and further processing of the measured PXRD patterns, while phase analyses were conducted using the Match! [46] code.
For the collections of the sets of single-crystal X-ray intensity data, samples were selected from the bulk, mounted on capillaries with grease and, finally, transferred to a Bruker APEX CCD diffractometer (Bruker Inc.®, Madison, WI, USA; Mo Kα radiation; λ = 0.71073 Å). The diffractometer was employed for initial inspections of the quality of the samples and the collections of the X-ray intensity data at room temperature. The programs SAINT+ and SADABS [47] were employed for the integrations of the raw X-ray intensity data and multi-scan absorption corrections, respectively. Applications of the reflection conditions to the collected X-ray intensity data were accomplished with the XPREP [48] algorithms and indicated space group Cmcm (no. 63) for both tellurides. The structures were solved using direct methods (SHELXS-97 [49]) in the aforementioned space group, while the structure refinements, which also included anisotropic atomic displacement parameters for all sites, were carried out in full matrix least-squares on F2 with the SHELXL-2014 [49,50] code. CCDC 1911953 and 1911960 contain the crystallographic data for this paper (see Supplementary Materials). These data can also be obtained free of charge via http://www.ccdc.cam.ac.uk/conts/retrieving.html or from the CCDC, 12 Union Road, Cambridge CB2 1EZ, UK; Fax: +44-1223-336033; E-Mail: [email protected].

3.3. Computational Details

Full structural optimizations (lattice parameters and atomic positions) and electronic band structure computations for RbPr2Ag3Te5 were accomplished utilizing the projector augmented wave (PAW) method [51] as implemented in the Vienna ab initio Simulation Package [52,53,54,55,56] (VASP). Correlation and exchange were depicted by the generalized gradient approximation of Perdew, Burke, and Ernzerhof (GGA–PBE [57]), while the energy cutoff of the plane-wave basis set was 500 eV and a mesh of 12 × 3 × 3 k-points was used to sample the first Brillouin zone. All computations were considered converged once the energy differences between two iterative steps of the electronic (and ionic) relaxations fell below 10−8 (and 10−6) eV/cell.
A chemical bonding analysis of RbPr2Ag3Te5 was accomplished based on the crystal orbital Hamilton population (COHP [36,58]) method, in which the off-site projected DOS are weighted with the respective Hamilton matrix elements to identify bonding, non-bonding, and antibonding interactions. The COHP curves and the corresponding integrated values (ICOHP) were computed utilizing the tight-binding linear-muffin-tin orbital (TB-LMTO) method in the atomic sphere approximation (ASA) [59,60,61] and employing the von Barth-Hedin [62] exchange-correlation functional. The Wigner-Seitz (WS) radii were automatically generated, while empty spheres were included to accomplish optimal approximations of full potentials. The following orbitals were employed as basis sets in the computations (downfolded [63] orbitals in parentheses): Rb-5s/(-5p)/(-4d)/(-4f); Pr-6s/(-6p)/-5d; Ag-5s/-5p/-4d/(-4f); Te-5s/-5p/(-5d)/(-4f) with the corresponding WS radii (Å): Rb, 4.73; Pr, 3.58; Ag, 2.86–2.89; Te, 3.24–3.35. The praseodymium 4f states were treated as core-like states—a procedure that has been widely used elsewhere [34,35,64,65]. More specifically, the aforementioned handling of the rare-earth-metal 4f states has been substantiated by previous explorations [34,35,65,66,67] on the electronic structures of rare-earth-containing compounds. Namely, the bands corresponding to the rare-earth-metal 4f atomic orbitals are typically related to modest dispersions and, hence, are rather localized such that these states scarcely participate in overall bonding. Reciprocal space integrations were achieved employing the tetrahedron method [68] with a 12 × 12 × 6 k-points set.

4. Conclusions

The appropriateness of valence-electron transfers as proposed by Zintl-Klemm treatments has been probed for tellurides which crystallize with the ALn2Ag3Te5-type of structure (A = alkaline-metal; Ln = lanthanide). The crystal structure of that type of telluride has been described for the examples of the previously unknown RbLn2Ag3Te5 (Ln = Pr, Nd) containing tunnels which are constituted by the tellurium atoms and encapsulate the rubidium, lanthanide, and silver atoms, respectively. Although an application of the Zintl-Klemm concept to RbLn2Ag3Te5 (Ln = Pr, Nd) leads to an electron-precise valence-electron distribution of (Rb+)(Ln3+)2(Ag+)3(Te2−)5, yet, the bonding analysis based on the COHP method indicates that a full electron transfer as suggested by such a Zintl-Klemm treatment should be considered with concern. In fact, the majority of the bonding population is located between the Pr–Te and Ag–Te contacts showing characteristics of strong, polar mixed-metal bonds, while the Rb–Te interactions may be regarded as rather ionic bonds. Even though the Ag–Ag interactions change from bonding to antibonding states below the Fermi level as a consequence of closed-shell interactions, an integration of the –COHP curves for these homoatomic interactions indicates a net bonding character.

Supplementary Materials

The following are available online at https://www.mdpi.com/2304-6740/7/6/70/s1: CIF and checkCIF files.

Author Contributions

K.C.G., K.S.F., and F.C.G. conducted the syntheses, while the crystal structure solutions and refinements were carried out by K.C.G.; S.S. accomplished the electronic structure computations, independently designed and supervised the project. The manuscript was written with input from all authors (K.C.G., K.S.F., F.C.G., R.D., and S.S.), who approved the final version of the manuscript.

Funding

This research was funded by the Verband der Chemischen Indstrie e.V., Frankfurt, Germany (FCI; F.C.G. and S.S.), Liebig-Stipend, as well as the German Research Foundation, Bonn, Germany (DFG; K.S.F. and R.D.), SFB 917 “Nanoswitches”.

Acknowledgments

The authors also wish to thank Tobias Storp and Björn Faßbänder for the collections of the SCXRD and PXRD data, respectively, and the IT Center of RWTH Aachen for the provided computational resources (JARA-HPC project jara0167).

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Gladisch, F.C.; Steinberg, S. Revealing Tendencies in the Electronic Structures of Polar Intermetallic Compounds. Crystals 2018, 8, 80. [Google Scholar] [CrossRef]
  2. Miller, G.J. The “Coloring Problem” in Solids: How It Affects Structure, Composition and Properties. Eur. J. Inorg. Chem. 1998, 1998, 523–536. [Google Scholar] [CrossRef]
  3. Gautier, R.; Zhang, X.; Hu, L.; Yu, L.; Lin, Y.; Sunde, T.O.L.; Chon, D.; Poeppelmeier, K.R.; Zunger, A. Prediction and accelerated laboratory discovery of previously unknown 18-electron ABX compounds. Nat. Chem. 2015, 7, 308–316. [Google Scholar] [CrossRef] [Green Version]
  4. Curtarolo, S.; Hart, G.L.W.; Nardelli, M.B.; Mingo, N.; Sanvito, S.; Levy, O. The high-throughput highway to computational materials design. Nat. Mater. 2013, 12, 191–201. [Google Scholar] [CrossRef] [PubMed]
  5. Nesper, R. Bonding Patterns in Intermetallic Compounds. Angew. Chem. Int. Ed. Engl. 1991, 30, 789–817. [Google Scholar] [CrossRef]
  6. Jones, H. The phase boundaries in binary alloys, part 2: The theory of the α, β phase boundaries. Proc. Phys. Soc. 1937, 49, 250–257. [Google Scholar] [CrossRef]
  7. Massalski, T.B.; Mizutani, U. Electronic Structure of Hume-Rothery Phases. Prog. Mater. Sci. 1978, 22, 151–262. [Google Scholar] [CrossRef]
  8. Mizutani, U.; Sato, H. The Physics of the Hume-Rothery Electron Concentration Rule. Crystals 2017, 7, 9. [Google Scholar] [CrossRef]
  9. Zintl, E. Intermetallische Verbindungen. Angew. Chem. 1939, 52, 1–6. [Google Scholar] [CrossRef]
  10. Schäfer, H.; Eisenmann, B.; Müller, W. Zintl Phases: Transitions between Metallic and Ionic Bonding. Angew. Chem. Int. Ed. 1973, 12, 694–712. [Google Scholar] [CrossRef]
  11. Miller, G.J.; Schmidt, M.W.; Wang, F.; You, T.-S. Quantitative Advances in the Zintl-Klemm Formalism. In Structure and Bonding; Fässler, T., Ed.; Springer Publishers: Berlin/Heidelberg, Germany, 2011; Volume 139, pp. 1–55. [Google Scholar]
  12. Corbett, J.D. Exploratory Synthesis: The Fascinating and Diverse Chemistry of Polar Intermetallic Phases. Inorg. Chem. 2010, 49, 13–28. [Google Scholar] [CrossRef] [PubMed]
  13. Toberer, E.S.; May, A.F.; Snyder, G.J. Zintl Chemistry for Designing High Efficiency Thermoelectric Materials. Chem. Mater. 2010, 22, 624–634. [Google Scholar] [CrossRef]
  14. Snyder, G.J.; Toberer, E.S. Complex thermoelectric materials. Nat. Mater. 2008, 7, 105–114. [Google Scholar] [CrossRef] [PubMed]
  15. Sootsman, J.R.; Chung, D.Y.; Kanatzidis, M.G. New and Old Concepts in Thermoelectric Materials. Angew. Chem. Int. Ed. 2009, 48, 8616–8639. [Google Scholar] [CrossRef] [PubMed]
  16. Wuttig, M.; Yamada, N. Phase-change materials for rewriteable data storage. Nat. Mater. 2007, 6, 824–832. [Google Scholar] [CrossRef] [PubMed]
  17. Lencer, D.; Salinga, M.; Grabowski, B.; Hickel, T.; Neugebauer, J.; Wuttig, M. A map for phase-change materials. Nat. Mater. 2008, 7, 972–977. [Google Scholar] [CrossRef]
  18. Wuttig, M.; Raoux, S. The Science and Technology of Phase Change Materials. Z. Anorg. Allg. Chem. 2012, 638, 2455–2465. [Google Scholar] [CrossRef]
  19. Böttcher, P. Tellurium-Rich Tellurides. Angew. Chem. Int. Ed. Engl. 1988, 27, 759–772. [Google Scholar] [CrossRef]
  20. Papoian, G.A.; Hoffmann, R. Hypervalent Bonding in One, Two, and Three Dimensions: Extending the Zintl-Klemm Concept to Nonclassical Electron-Rich Networks. Angew. Chem. Int. Ed. 2000, 39, 2408–2448. [Google Scholar] [CrossRef]
  21. Göbgen, K.C.; Gladisch, F.C.; Steinberg, S. The Mineral Stützite: a Zintl-Phase or Polar Intermetallic? A Case Study Using Experimental and Quantum-Chemical Techniques. Inorg. Chem. 2018, 57, 412–421. [Google Scholar] [CrossRef]
  22. Gladisch, F.C.; Steinberg, S. Revealing the Nature of Bonding in Rare-Earth Transition-Metal Tellurides by Means of Methods Based on First Principles. Eur. J. Inorg. Chem. 2017, 2017, 3395–3400. [Google Scholar] [CrossRef]
  23. Malliakas, C.D.; Kanatzidis, M.G. Charge Density Waves in the Square Nets of Tellurium of AMRETe4 (A = K, Na; M = Cu, Ag; RE = La, Ce). J. Am. Chem. Soc. 2007, 129, 10675–10677. [Google Scholar] [CrossRef]
  24. Patschke, R.; Heising, J.; Kanatzidis, M.; Brazis, P.; Kannewurf, C.R. KCuCeTe4: A New Intergrowth Rare Earth Telluride with an Incommensurate Superstructure Associated with a Distorted Square Net of Tellurium. Chem. Mater. 1998, 10, 695–697. [Google Scholar] [CrossRef]
  25. Patschke, R.; Brazis, P.; Kannewurf, C.R.; Kanatzidis, M. K2Ag3CeTe4: A Semiconducting Tunnel Framework Made from the Covalent “Link-Up” of [Ag2CeTe4]3− Layers with Ag. Inorg. Chem. 1998, 37, 6562–6563. [Google Scholar] [CrossRef]
  26. Patschke, R.; Brazis, P.; Kannewurf, C.R.; Kanatzidis, M. Rb2Cu3CeTe5: A quaternary semiconducting compound with a two-dimensional polytelluride framework. J. Mater. Chem. 1998, 8, 2587–2589. [Google Scholar] [CrossRef]
  27. Meng, C.-Y.; Chen, H.; Wang, P.; Chen, L. Syntheses, Structures, and Magnetic and Thermoelectric Properties of Double-Tunnel Tellurides: AxRE2Cu6−xTe6 (A = K–Cs; RE = La–Nd). Chem. Mater. 2011, 23, 4910–4919. [Google Scholar] [CrossRef]
  28. Meng, C.-Y.; Chen, H.; Wang, P. Syntheses, Structures, and Physical Properties of CsRE2Ag3Te5 (RE = Pr, Nd, Sm, Gd–Er) and RbRE2Ag3Te5 (RE = Sm, Gd–Dy). Inorg. Chem. 2014, 53, 6893–6903. [Google Scholar] [CrossRef]
  29. Babo, J.-M.; Choi, E.S.; Albrecht-Schmitt, T.E. Synthesis, Structure, Magnetism, and Optical Properties of Cs2Cu3DyTe4. Inorg. Chem. 2012, 51, 11730–11735. [Google Scholar] [CrossRef]
  30. Janka, O.; Pöttgen, R. Reactive Fluxes. In Handbook of Solid State Chemistry; Dronskowski, R., Kikkawa, S., Stein, A., Eds.; Wiley-VCH: Weinheim, Germany, 2017. [Google Scholar]
  31. Cotton, S. Lanthanide and Actinide Chemistry; John Wiley & Sons Ltd.: Chichester, England, 2006. [Google Scholar]
  32. Cordero, B.; Gómez, V.; Platero-Prats, A.; Revés, M.; Echeverría, J.; Cremades, E.; Barragán, F.; Alvarez, S. Covalent radii revisited. Dalton Trans. 2008, 2008, 2832–2838. [Google Scholar] [CrossRef]
  33. Steinberg, S.; Brgoch, J.; Miller, G.J.; Meyer, G. Identifying a Structural Preference in Reduced Rare-Earth Metal Halides by Combining Experimental and Computational Techniques. Inorg. Chem. 2012, 51, 11356–11364. [Google Scholar] [CrossRef] [Green Version]
  34. Steinberg, S.; Card, N.; Mudring, A.-V. From the Ternary Eu(Au/In)2 and EuAu4(Au/In)2 with Remarkable Au/In Distributions to a New Structure Type: The Gold-Rich Eu5Au16(Au/In)6 Structure. Inorg. Chem. 2015, 54, 8187–8196. [Google Scholar] [CrossRef]
  35. Smetana, V.; Steinberg, S.; Mudryk, Y.; Pecharsky, V.; Miller, G.J.; Mudring, A.-V. Cation-Poor Complex Metallic Alloys in Ba(Eu)-Au-Al(Ga) Systems: Identifying the Keys that Control Structural Arrangements and Atom Distributions at the Atomic Level. Inorg. Chem. 2015, 54, 10296–10308. [Google Scholar] [CrossRef]
  36. Steinberg, S.; Dronskowski, R. The Crystal Orbital Hamilton Population (COHP) Method as a Tool to Visualize and Analyze Chemical Bonding in Intermetallic Compounds. Crystals 2018, 8, 225. [Google Scholar] [CrossRef]
  37. Smetana, V.; Steinberg, S.; Mudring, A.-V. Layered Structures and Disordered Polyanionic Nets in the Cation-Poor Polar Intermetallics CsAu1.4Ga2.8 and CsAu2Ga2.6. Cryst. Growth Des. 2017, 17, 693–700. [Google Scholar] [CrossRef]
  38. Davaasuren, B.; Dashjav, E.; Rothenberger, A. Synthesis and Characterization of the Ternary Telluroargentate K4[Ag18Te11]. Z. Anorg. Allg. Chem. 2014, 640, 2939–2944. [Google Scholar] [CrossRef]
  39. Jansen, M. Homoatomic d10–d10 Interactions: Their Effects on Structure and Chemical and Physical Properties. Angew. Chem. Int. Ed. Engl. 1987, 26, 1098–1110. [Google Scholar] [CrossRef]
  40. Pyykkö, P. Strong Closed-Shell Interactions in Inorganic Chemistry. Chem. Rev. 1997, 97, 597–636. [Google Scholar] [CrossRef]
  41. Dreele, R.B.; Eyring, L.; Bowman, A.L.; Yamell, J.L. Refinement of the crystal structure of Pr7O12 by powder neutron diffraction. Acta Crystallogr. Sect. B 1975, 31, 971–974. [Google Scholar] [CrossRef]
  42. Wang, R.; Steinfink, H.; Bradley, W.F. The crystal structure of lanthanum telluride and tellurium-deficient neodymium telluride. Inorg. Chem. 1966, 5, 142–145. [Google Scholar] [CrossRef]
  43. Stöwe, K. Crystal structure, magnetic properties and band gap measurements of NdTe(2−x) (x = 0.11(1)). Z. Kristallogr. 2001, 216, 215–224. [Google Scholar] [CrossRef]
  44. Adenis, C.; Langer, V.; Lindqvist, O. Reinvestigation of the structure of tellurium. Acta Crystallogr. Sect. C 1989, 45, 941–942. [Google Scholar] [CrossRef]
  45. WinXPow Version 2.23; STOE & Cie GmbH: Darmstadt, Germany, 2008.
  46. Match! Vers. 3.8.0.137; Crystal Impact GbR: Bonn, Germany, 2019.
  47. SAINT+ and SADABS; Bruker AXS Inc.: Madison, WI, USA, 2009.
  48. XPREP, Version 6.03; Bruker AXS Inc.: Madison, WI, USA, 2014.
  49. Sheldrick, G.M. A short history of SHELX. Acta Crystallogr. Sect. A Found. Crystallogr. 2008, 64, 112–122. [Google Scholar] [CrossRef]
  50. Sheldrick, G.M. Crystal structure refinement with SHELXL. Acta Crystallogr. Sect. C Struct. Chem. 2015, 71, 3–8. [Google Scholar] [CrossRef]
  51. Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B Condens. Matter Mater. Phys. 1994, 50, 17953–17979. [Google Scholar] [CrossRef] [Green Version]
  52. Kresse, G.; Marsman, M.; Furthmüller, J. Vienna Ab Initio Simulation Package (VASP), The Guide; Computational Materials Physics, Faculty of Physics, Universität Wien: Vienna, Austria, 2014. [Google Scholar]
  53. Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B Condens. Matter Mater. Phys. 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
  54. Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
  55. Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B Condens. Matter Mater. Phys. 1993, 47, 558–561. [Google Scholar] [CrossRef]
  56. Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B Condens. Matter Mater. Phys. 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
  57. Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [Green Version]
  58. Dronskowski, R.; Blöchl, P.E. Crystal Orbital Hamilton Populations (COHP). Energy-Resolved Visualization of Chemical Bonding in Solids Based on Density-Functional Calculations. J. Phys. Chem. 1993, 97, 8617–8624. [Google Scholar] [CrossRef]
  59. Andersen, O.K. Linear methods in band theory. Phys. Rev. B Condens. Matter Mater. Phys. 1975, 12, 3060–3083. [Google Scholar] [CrossRef] [Green Version]
  60. Andersen, O.K.; Jepsen, O. Explicit, First-Principles Tight-Binding Theory. Phys. Rev. Lett. 1984, 53, 2571–2574. [Google Scholar] [CrossRef]
  61. Krier, G.; Jepsen, O.; Burkhardt, A.; Andersen, O.K. TB-LMTO-ASA Program, 4.7 ed.; Max-Planck-Institut für Festkörperforschung: Stuttgart, Germany, 1995. [Google Scholar]
  62. von Barth, U.; Hedin, L. A local exchange-correlation potential for the spin polarized case: I. J. Phys. C Solid State Phys. 1972, 5, 1629–1642. [Google Scholar] [CrossRef]
  63. Lambrecht, W.R.L.; Andersen, O.K. Minimal basis sets in the linear muffin-tin orbital method: Application to the diamond-stucture crystals C, Si, and Ge. Phys. Rev. B Condens. Matter Mater. Phys. 1986, 34, 2439–2449. [Google Scholar] [CrossRef]
  64. Steinberg, S.; Bell, T.; Meyer, G. Electron Counting Rules and Electronic Structure in Tetrameric Transition-Metal (T)-Centered Rare-Earth (R) Cluster Complex Halides (X). Inorg. Chem. 2015, 54, 1026–1037. [Google Scholar] [CrossRef]
  65. Bigun, I.; Steinberg, S.; Smetana, V.; Mudryk, Y.; Kalychak, Y.; Havela, L.; Pecharsky, V.; Mudring, A.-V. Magnetocaloric Behavior in Ternary Europium Indides EuT5In: Probing the Design Capability of First-Principles-Based Methods on the Multifacted Magnetic Materials. Chem. Mater. 2017, 29, 2599–2614. [Google Scholar] [CrossRef]
  66. Provino, A.; Steinberg, S.; Smetana, V.; Paramanik, U.; Manfrinetti, P.; Dhar, S.K.; Mudring, A.-V. Gold in the Layered Structures of R3Au7Sn3: From Relativity to Versatility. Cryst. Growth Des. 2016, 16, 5657–5668. [Google Scholar] [CrossRef]
  67. Li, W.-L.; Ertural, C.; Bogdanovski, D.; Li, J.; Dronskowski, R. Chemical Bonding of Crystalline LnB6 (Ln = La–Lu) and Its Relationship with Ln2B8 Gas-Phase Complexes. Inorg. Chem. 2018, 57, 12999–13008. [Google Scholar] [CrossRef]
  68. Blöchl, P.E.; Jepsen, O.; Andersen, O.K. Improved tetrahedron method for Brillouin-zone integrations. Phys. Rev. B Condens. Matter Mater. Phys. 1994, 49, 16223–16233. [Google Scholar] [CrossRef]
Inorganics 07 00070 g001 550
Figure 1. View on the unit cell of RbLn2Ag3Te5 (Ln = Pr, Nd) along a: the crystal structures of the tellurides are composed of tunnels which are assembled by the tellurium atoms and enclose the rubidium, lanthanide, and silver atoms, respectively. The diverse types of tellurium (blue) polyhedra surrounding the rubidium (red), lanthanide (black), and silver atoms (orange) are shown in the insets.
Figure 1. View on the unit cell of RbLn2Ag3Te5 (Ln = Pr, Nd) along a: the crystal structures of the tellurides are composed of tunnels which are assembled by the tellurium atoms and enclose the rubidium, lanthanide, and silver atoms, respectively. The diverse types of tellurium (blue) polyhedra surrounding the rubidium (red), lanthanide (black), and silver atoms (orange) are shown in the insets.
Inorganics 07 00070 g001
Inorganics 07 00070 g002 550
Figure 2. Densities-of-states (DOS) and crystal orbital Hamilton population (COHP) curves of RbPr2Ag3Te5: the Fermi level, EF, is given by the black horizontal line, while the atom-projected DOS (blue) of praseodymium, silver, and tellurium are shown in (a)–(c), respectively. Additionally, the orbital-projected DOS (red) which provide the largest contributions to the states near EF for a given sort of atom have been included.
Figure 2. Densities-of-states (DOS) and crystal orbital Hamilton population (COHP) curves of RbPr2Ag3Te5: the Fermi level, EF, is given by the black horizontal line, while the atom-projected DOS (blue) of praseodymium, silver, and tellurium are shown in (a)–(c), respectively. Additionally, the orbital-projected DOS (red) which provide the largest contributions to the states near EF for a given sort of atom have been included.
Inorganics 07 00070 g002
Inorganics 07 00070 g003 550
Figure 3. Measured and simulated powder X-ray diffraction patterns of (a) RbPr2Ag3Te5 and (b) RbNd2Ag3Te5: reflections corresponding to the by-products, i.e., Pr7O12 [41], NdTe1.8 [42,43], and tellurium [44], have been denoted by the different triangles.
Figure 3. Measured and simulated powder X-ray diffraction patterns of (a) RbPr2Ag3Te5 and (b) RbNd2Ag3Te5: reflections corresponding to the by-products, i.e., Pr7O12 [41], NdTe1.8 [42,43], and tellurium [44], have been denoted by the different triangles.
Inorganics 07 00070 g003
Table
Table 1. Details of the crystal structure investigations and refinements for RbLn2Ag3Te5 (Ln = Pr, Nd).
Table 1. Details of the crystal structure investigations and refinements for RbLn2Ag3Te5 (Ln = Pr, Nd).
FormulaRbPr2Ag3Te5RbNd2Ag3Te5
from wt.1328.901335.56
space groupCmcm (no. 63)
a (Å)4.618(2)4.607(2)
b (Å)16.014(7)16.031(7)
c (Å)18.644(8)18.594(8)
volume (Å3)1378.7(10)1373.1(10)
Z4
density (calc.), g/cm36.4026.461
μ (mm−1)24.94625.513
F (000)22242232
θ range (°)2.19−25.762.19−25.67
index ranges−5 ≤ h ≤ 5
−18 ≤ k ≤ 19
−22 ≤ l ≤ 22		−5 ≤ h ≤ 5
−19 ≤ k ≤ 18
−20 ≤ l ≤ 22
reflections collected42033900
independent reflections774762
refinement methodfull-matrix least-squares on F2
data/restraints/parameters774/0/37762/0/37
goodness-of-fit on F21.161.15
final R indices [I > 2σ(I)]R1 = 0.036; wR2 = 0.081R1 = 0.066; wR2 = 0.156
R indices (all data)R1 = 0.040; wR2 = 0.082R1 = 0.068; wR2 = 0.158
Rint0.0680.098
largest diff. peak and hole, e−/Å31.99 and −3.903.25 and −6.84
Table
Table 2. Atomic positions and equivalent anisotropic displacement parameters for RbPr2Ag3Te5 and RbNd2Ag3Te5.
Table 2. Atomic positions and equivalent anisotropic displacement parameters for RbPr2Ag3Te5 and RbNd2Ag3Te5.
AtomPositionxyzUeq, Å2
RbPr2Ag3Te5
Pr18f00.3096(1)0.5945(1)0.0114(2)
Te28f½0.4421(1)0.6232(1)0.0124(3)
Te38f00.3289(1)0.4264(1)0.0110(3)
Te44c00.2389(1)¾0.0128(3)
Ag58f00.0864(1)0.5275(1)0.0208(3)
Ag64c½0.3360(1)¾0.0229(4)
Rb74c00.5587(1)¾0.0227(5)
RbNd2Ag3Te5
Nd18f00.3095(1)0.5945(1)0.0071(4)
Te28f½0.4417(1)0.6230(1)0.0084(4)
Te38f00.3281(1)0.4265(1)0.0071(4)
Te44c00.2390(1)¾0.0082(5)
Ag58f00.0865(1)0.5281(1)0.0161(5)
Ag64c½0.3359(2)¾0.0185(6)
Rb74c00.5587(2)¾0.0182(7)
Table
Table 3. Distances, numbers of bonds, –ICOHP/bond values, average –ICOHP/bond values, cumulative –ICOHP/cell, and percentage contributions to the net bonding capability of the diverse contacts in RbPr2Ag3Te5.
Table 3. Distances, numbers of bonds, –ICOHP/bond values, average –ICOHP/bond values, cumulative –ICOHP/cell, and percentage contributions to the net bonding capability of the diverse contacts in RbPr2Ag3Te5.
InteractionDistance (Å)No. of Bonds–ICOHP/bond
(eV/bond)		Ave. –ICOHP/bond
(eV/bond)		Cum. –ICOHP/cell%
Pr1‒Te23.182(1)161.1031.12353.89243.7
Pr1‒Te33.150(2)81.363
Pr1‒Te33.225(1)160.936
Pr1‒Te43.112(2)81.295
Rb7‒Te23.796(2)160.0450.0451.4251.1
Rb7‒Te33.749(2)80.038
Rb7‒Te43.696(2)80.050
Ag5‒Ag52.952(2)40.4550.4551.8191.5
Ag5‒Te22.846(2)81.3851.38166.26553.7
Ag5‒Te22.919(2)80.930
Ag5‒Te32.812(1)161.412
Ag6‒Te22.913(2)81.323
Ag6‒Te42.783(2)81.821

Share and Cite

MDPI and ACS Style

Göbgen, K.C.; Fries, K.S.; Gladisch, F.C.; Dronskowski, R.; Steinberg, S. Revealing the Nature of Chemical Bonding in an ALn2Ag3Te5-Type Alkaline-Metal (A) Lanthanide (Ln) Silver Telluride. Inorganics 2019, 7, 70. https://doi.org/10.3390/inorganics7060070

AMA Style

Göbgen KC, Fries KS, Gladisch FC, Dronskowski R, Steinberg S. Revealing the Nature of Chemical Bonding in an ALn2Ag3Te5-Type Alkaline-Metal (A) Lanthanide (Ln) Silver Telluride. Inorganics. 2019; 7(6):70. https://doi.org/10.3390/inorganics7060070

Chicago/Turabian Style

Göbgen, Kai C., Kai S. Fries, Fabian C. Gladisch, Richard Dronskowski, and Simon Steinberg. 2019. "Revealing the Nature of Chemical Bonding in an ALn2Ag3Te5-Type Alkaline-Metal (A) Lanthanide (Ln) Silver Telluride" Inorganics 7, no. 6: 70. https://doi.org/10.3390/inorganics7060070

APA Style

Göbgen, K. C., Fries, K. S., Gladisch, F. C., Dronskowski, R., & Steinberg, S. (2019). Revealing the Nature of Chemical Bonding in an ALn2Ag3Te5-Type Alkaline-Metal (A) Lanthanide (Ln) Silver Telluride. Inorganics, 7(6), 70. https://doi.org/10.3390/inorganics7060070

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop