SABER: A Model-Agnostic Postprocessor for Bias Correcting Discharge from Large Hydrologic Models

Abstract

Hydrologic modeling is trending toward larger spatial and temporal domains, higher resolutions, and less extensive local calibration and validation. Thorough calibration and validation are difficult because the quantity of observations needed for such scales do not exist or is inaccessible to modelers. We present the Stream Analysis for Bias Estimation and Reduction (SABER) method for bias correction targeting large models. SABER is intended for model consumers to apply to a subset of a larger domain at gauged and ungauged locations and address issues with data size and availability. SABER extends frequency-matching postprocessing techniques using flow duration curves (FDC) at gauged subbasins to be applied at ungauged subbasins using clustering and spatial analysis. SABER uses a “scalar” FDC (SFDC), a ratio of simulated to observed FDC, to characterize biases spatially, temporally, and for varying exceedance probabilities to make corrections at ungauged subbasins. Biased flows at ungauged locations are corrected with the scalar values from the SFDC. Corrected flows are refined to fit a Gumbel Type 1 distribution. We present the theory, procedure, and validation study in Colombia. SABER reduces biases and improves composite metrics, including Nash Sutcliffe and Kling Gupta Efficiency. Recommendations for future work and a discussion of limitations are provided.

1. Introduction

Advances in hydrologic modeling capabilities have led to the development of hydrometeorological models with large spatial domains, increased spatial and temporal resolutions, and longer lead times for forecasts [1]. Many of the models are of a continental-scale or larger and entered an operational phase within the last 20 years. Some examples include the North American Land Data Assimilation System (NLDAS) [2] and Global Land Data Assimilation System (GLDAS) [3] land-surface models produced by the National Aeronautics and Space Administration (NASA); the United States’ National Water Model [4] produced by the National Oceanic and Atmospheric Administration (NOAA); the European Flood Awareness System (EFAS) and Global Flood Awareness System (GloFAS) [5] both produced by the Joint Research Centre; the GEOGloWS ECMWF Streamflow (GES) [6,7,8] model produced by the Group on Earth Observations Global Water Sustainability (GEOGloWS) program; and Water Global Assessment and Prognosis (WaterGAP2) [9] produced by the University of Kessel in Germany. Each of these models uses different approaches and inputs to produce forecasts and hindcasts for several hydrologic variables. Their results have been used in a myriad of water-related activities, such as reservoir operations, water supply forecasting, agricultural planning, groundwater sustainability studies, flood mapping, and water quality modeling [10,11,12,13,14,15].

Despite using the best available calibration and validation techniques, large-scale models are generally not fully calibrated for all regions in which they operate. Their large spatial extents require an extensive amount of in situ observed data for a full calibration. These models are generally calibrated using a relatively small set of available observed data, and these data do not cover the model’s full spatial and temporal domains. This can cause biases, especially in regions poorly represented during calibration. GloFAS, for instance, was calibrated using only 1287 stations, many selected from the Global Runoff Data Centre (GRDC) discharge dataset, which has records for approximately 8000 locations [16]. WaterGAP2 was calibrated at the outlets of 1319 basins, which represent about half the global drainage area and a fraction of the available gauges [17].

As it is infeasible, if not impossible, to fully calibrate continental or global scale models, a common approach is to perform bias correction. There is extensive literature on hydrologic model bias correction methods [18,19,20,21,22]. These bias correction approaches can be generally classified as preprocessors or postprocessors, which adjust model inputs or outputs, respectively [23]. Preprocessor approaches frequently focus on adjusting precipitation and temperature inputs. They may include many methods such as spatial and temporal interpolation, downscaling of coarse data, data imputation, and statistical regressions [24,25,26,27]. Remote sensing datasets and platforms such as Google Earth Engine are increasingly available to provide higher quality model inputs and make preprocessors easier to implement [28]. Postprocessor approaches typically use forms of regression with measured data, including frequency or distribution matching, multivariate statistical analysis, and machine learning regression, to map biased model outputs to bias-corrected values [29,30,31,32]. Machine learning-centered approaches for bias correction postprocessors and related analysis are particularly common in recent publications [33,34,35,36].

The two major challenges to bias correction are, first, a lack of sufficient observed discharge data for calibration and, second, the practical computational difficulties in accessing and processing data from many agencies with disparate data management practices. Both challenges become more difficult to address as the spatial and temporal resolutions increase and the domains expand.

The first challenge is the shortage of observed discharge data. On a global scale, there are relatively few in situ hydrologic measurement stations with publicly available data [37]. The most comprehensive and publicly-available global-scale discharge database is maintained by the Global Runoff Data Centre (GRDC), with approximately 10,000 locations worldwide [38,39]. Other countries and organizations monitor discharge, such as the NWIS (National Water Information System) network in the United States [40]. The national networks are often not included in the GRDC, may not be shared publicly, may require licenses or fees, are not available online, or are otherwise difficult to access programmatically [37,41,42]. GRDC and country-level gauge databases are not uniformly spatially distributed, with more gauges generally available in wealthier countries and on larger rivers or near highly populated areas [41]. Many stations have gaps in their records or are no longer operating. Many have gaps or have inaccurate measurements—particularly during high-flow events, which can temporarily disable gauges or alter river channels and affect gauge accuracy [42,43,44]. Gauges often only record river stage or water surface elevation because developing rating curves to convert the stage to discharge is difficult and time intensive. Stage data may not be useful to hydrologic models that generally ignore channel geometry and predict discharge rather than stage. Additionally, some gauges only report monthly statistics rather than daily averages, which are more useful for modelers.

The second large challenge to bias correction is the practical difficulty in accessing the observed discharge data that are available to modelers. Available discharge measurements are subjected to quality control processes before being published, which can create significant lags between measurement and publication. Furthermore, each organization has different preferred computer systems and file formats for storing and disseminating data. The issue compounds for hundreds to thousands of gauges operated by dozens of organizations. These differences, especially differences in data access methods, result in non-trivial barriers to automatically retrieving and processing the observations. GloFAS and GEOGloWS, for example, produce new discharge forecasts daily. Their global scale creates challenges to providing bias-corrected forecasts in near-real-time.

In general, published bias correction preprocessor methods are intended to be implemented by modelers who have direct access to model inputs and outputs and the ability to run additional model simulations after adjusting model inputs and parameters. The model developers that build global-scale models often do not have access to enough observation data for calibration or may not perform additional refinements if more data become available. The developers of global-scale models are generally not the ultimate model users. The target audience for such models is hydrometeorological agencies, scientists, or engineers at local or national levels. These model users may have a better understanding of local watersheds and have additional observation data but do not have the access or expertise required to modify the model and its inputs or to execute model runs when bias correction is needed.

For these reasons, we developed a bias correction approach for large-scale models that we consider model-agnostic postprocessors (MAPs). MAPs do not need access to input datasets or tailoring for specific modeling methods (i.e., they are model agnostic instead of model specific). MAPs can be performed on model results after the model run and do not require additional model runs or integration with the model’s computer systems (i.e., they are postprocessors instead of preprocessors). A MAP approach can be run and rerun as additional observed data become available without being tied to the model’s execution schedule. The MAP qualities favor local model users who may have data that the modelers do not have or were too difficult to ingest, hindering data assimilation or bias correction preprocessor methods. The local user can continuously implement and refine bias corrections without modifying the model. The MAP approach empowers the model user and thereby makes global models more applicable to local-scale decisions.

We present the SABER (Stream Analysis for Bias Estimation and Reduction) method for hydrologic model bias correction. SABER combines spatial analysis and machine learning clustering algorithms, and a frequency-matching approach. SABER mitigates, in part, the practical and computational challenges to global model bias correction. SABER seeks to meet the goals of a MAP bias corrector. SABER differs from many published approaches because it is meant to be used by model users rather than the model developers. In addition, SABER provides a method to extend bias correction to ungauged areas in a physically explainable and defensible manner, which we validate through a case study. Uncertainty in model results at ungauged subbasins decreases confidence in using global model results for local-scale applications. Extending corrections regionally to ungauged subbasins has a high potential for impact on global models, such as GloFAS and GES, where results may exhibit local bias, but local users cannot modify the global models.

We describe the minimum data requirements, theory, and procedure for the SABER method. We validate SABER on a hindcast for the Magdalena River in Colombia from GES, which covers the period of 1980 through 2021. We discuss possibilities for applying and using SABER with global hydrologic models currently in development.

2. Materials and Methods

2.1. Overview

SABER extends a frequency-matching technique using flow duration curves (FDC) to correct flows based on flows and exceedance probabilities of the observed and simulated discharge data at the same location [30,45,46,47]. Many similar forms of frequency matching are documented in the literature. SABER uses spatial analysis, machine learning clustering, and statistical analysis to both create a framework for applying the method to ungauged stream reaches and to improve the bias correction performance. As a final step, SABER compares the corrected flows to the Gumbel distribution to verify that the upper and lower probability flows are not unrealistically distorted. The procedure is explained in the following subsections. An open-source Python package that implements SABER is available through GitHub [48]. The code is not specific to the analysis presented in this paper and may be applied to many models and watersheds.

SABER requires two vector spatial datasets and several discharge datasets. While model agnostic, SABER is most easily applied to hydrologic models with a vector spatial representation of the stream network (polyline stream centerlines and polygon subbasin and watershed boundary outlines). This is true even if the core computations of the model are performed on a mesh or grid since the vector datasets are more easily and automatically analyzed through computer code. To use the provided Python package that implements SABER, we recommend the open-source standard Geopackage format [49]. The following datasets are required:

• The subbasins or catchments (vector polygons) in the watershed as used by the hydrologic model. A stream centerlines (vector polylines) dataset is helpful but not essential. Each feature should have the following attributes at minimum:
  • A unique identifier (integer or alphanumeric) shared by each subbasin and stream reach pair. Ideally, this number is the identifier used by the hydrologic model, but it can be randomly generated.
  • The identifier number of the next subbasin downstream (to facilitate faster network analysis).
  • The Strahler stream order [50,51].
  • The cumulative drainage area for the subbasin in the same area units reported by the gauges.
  • The (x, y) coordinates of the outlet. If the outlet is not easily determined computationally, the centroid of the reach can be substituted.
• Hindcast or simulated historical discharge for each of the subbasins/streams in the model for as long as is available. It should be converted to the same units as the observed discharge, if necessary.
• The location of each available river gauging station (vector points). Each feature should have the following attributes at minimum:
  • The name or other unique identifier (integer or alphanumeric) assigned to the gauge.
  • The total drainage area upstream of the gauge.
  • The ID of the subbasin/stream in the model whose outlet is measured by that gauge. If the gauge does not align with a subbasin’s outlet, the user decides which subbasin it should be applied to by considering its location in relation to the model’s reporting points.
• Observed discharge for each gauge for as long as is available.

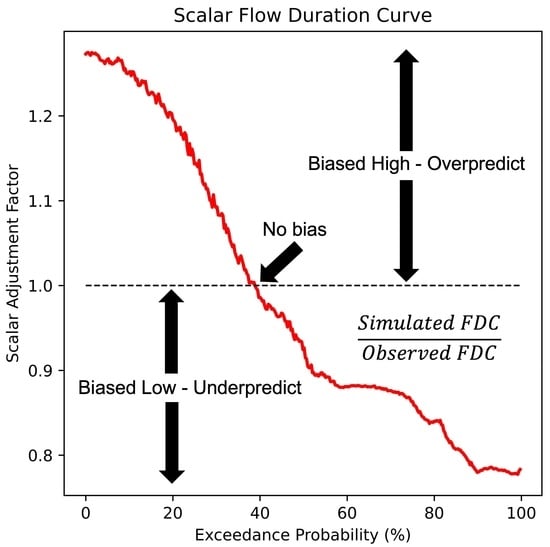
2.2. Frequency Matching and Scalar Flow Duration Curves

Figure 1 presents the basic frequency-matching process applied to subbasins that have observed data [30,47,49]. The data shown were synthetically generated for the figure. On the left (Panels 1 and 4) are simulated (solid blue line), observed (solid green line), and bias-corrected (solid red line) hydrographs. On the right (Panels 2 and 3) are simulated (blue lines) and observed (green lines) FDC. The first step is collecting the simulated discharge data (Panel 1). Next, SABER calculates the FDC of the simulated discharge data (Panel 2). The arrow labeled Step 1 represents calculating the exceedance probability for the indicated point on the hydrograph. This is repeated for each flow to create the FDC curve in Panel 2. Next, SABER computes the FDC for the observed discharge data (solid green line, Panel 3). The arrow labeled Step 2 represents matching the simulated flow with an observed flow for the same exceedance probability. Finally, the arrow labeled Step 3 represents replacing the simulated flow with the frequency (exceedance probability) matched observed flow. The preceding steps are repeated for all simulated flows to create the bias-corrected hydrograph (solid red line, Panel 4). This process assumes that the modeled data can be accurately used to calculate exceedance probabilities and only needs to remove the bias evident in the flow magnitudes.

SABER accounts for biases that vary temporally. A model may perform better during wet or dry seasons resulting in biases that vary throughout the year. To include the temporally variable model performance in the bias correction, SABER divides the simulated and observed data into temporal subsets. We chose to use monthly subsets of the modeled data, making 12 groups from January through December, based on our previous work [46]. The temporal groups capture seasonal variations that could be lost in an annual curve. We assume the biases are relatively consistent across all the years, which contribute to the monthly curves. The frequency matching approach is applied to each simulated value, but the FDC used for the correction changes depending on the date of the simulated value.

For subbasins without gauges, SABER generalizes the known biases with the novel scalar flow duration curve (SFDC). The SFDC is the ratio of the simulated to observed FDC at a gauged location. The SFDC has exceedance probability on the X-axis like a typical FDC. On the Y-axis, the SFDC has the ratio of simulated divided by observed discharge value and thus is a scalar, unitless value. Each of the ratios is referred to as a scalar adjustment factor (SAF). The SFDC is the calculated SAF plotted against each exceedance probability creating a continuous curve. As with the frequency matching with gauge data, SABER generates an SFDC for each month using the observed and simulated data at a gauge. Figure 2 shows the same modeled and observed FDC used in Figure 1 in Panel 1 (left side) next to the ratio of the curves, the SFDC, on Panel 2 (right side). The dashed black line (where the SAF is equal to one) marks the dividing line between biased high (over predicting) and biased low (under predicting).

The SFDC characterizes model behavior for different exceedance probabilities. Models overpredict when the SFDC is greater than 1 (i.e., biased high), are approximately correct when the SFDC is close to 1 (i.e., unbiased), and underpredict when the SFDC is less than 1 (i.e., biased low). The SFDC is also calculated and applied monthly to capture temporally varying biases.

SABER applies the SFDC to the ungauged, simulated data to generate bias-corrected data. This procedure follows the same steps as the general frequency matching method except substituting an SFDC curve that was matched to the ungauged area in place of the observed FDC. Thus, each flow is mapped to a SAF rather than a flow value. To generate the bias-corrected values, the simulated discharge is divided by the SAF, the ratio of simulated to observed discharge for a given exceedance probability. Equivalently, the biased simulated value is multiplied by the ratio of observed to simulated values for that exceedance probability. This is mathematically illustrated in Equation (1). $Q_C$ is the bias-corrected flow. $Q_B$ is the biased flow in an ungauged location. $SAF$ is the ratio of the simulated to observed flow, for the same exceedance probability and month as $Q_B$, at the gauge location selected as a pair for the ungauged location.

$$Q_C=\frac{Q_B}{SAF}$$

(1)

In a practical sense, SABER extends previous bias correction work through a novel process of pairing each ungauged subbasin with a gauged subbasin and introducing the SFDC as a tool for characterizing and correcting bias. If a subbasin contains a gauge, SABER applies the FDC frequency-matching technique adapted from previous researchers. If the subbasin is ungauged, SABER uses spatial analysis and clustering algorithms to determine which gauge best represents the biases found in the ungauged basin and uses the SFDC for bias correction. SABER implements physically explainable and defensible methods to pair gauged subbasins with ungauged subbasins so that the process is transparent and justifiable. This allows users to review and edit the automatically determined pairs of gauged and ungauged subbasins.

2.3. Identifying Flow Regime Patterns

SABER identifies groups of subbasins with similar flow regimes using machine learning clustering on the simulated FDCs. The clusters identify watersheds that behave similarly across the temporal range of the simulated data. SABER clusters the modeled data because we lack observed data and local expertise to cluster based on the observed discharge or other properties. SABER determines groups by analyzing the FDCs of the simulated data for each stream reach and grouping those that are similar. The groups are one of the criteria used when determining which ungauged subbasins should be paired with the limited number of subbasins with observed data when extrapolating the bias corrections.

There are many methods for clustering data and for calculating the similarity between time series or other sequences of data [52]. SABER uses the k-means clustering algorithm with the dynamic time warping measure of similarity rather than Euclidean distances, which is the typical metric for k-means [53,54,55]. Dynamic time warping was originally applied to audio processing, but we selected it because it performs well in matching the curve shapes, which is our goal [56]. SABER applies a z-scale transform, also known as a standard scaler, to the FDC before clustering since we are interested in patterns in watershed responses rather than absolute discharge values. Standard scaling converts each discharge to a value representing the number of standard deviations from the mean by subtracting the mean and dividing by the standard deviation. For most rivers in our case study, the transform reduces the range of values to lie predominantly between −2 and 4.

Figure 3 shows an example of clusters created by SABER. The red line shows the location of the centroid of the cluster, with the black lines representing the other subbasin FDC curves included in the cluster. The clustering is based on the curve shape in normalized space, which is visually evident in the different curve clusters.

SABER uses the knee method to automatically choose the optimal number of clusters to create [57,58]. The knee method computes k-clusters, where k is the number of clusters for a range of k values and tracks the residual error for each. The knee point is the point of maximum inflection on a plot of error versus the number of clusters. It represents the point of diminishing returns with each increase in k, the number of clusters, and produces minimal additional descriptive power for the dataset. We found that computing between 2 and 10 clusters was sufficient to find the knee point in the regions where we experimented during the research process. Figure 4 presents a plot showing the knee point for a set of clusters.

Some subbasins in the group will have gauge discharge data, and some will not. Ideally, each cluster should contain several gauged subbasins. The gauges in the group are used to characterize the bias for the streams presumed to behave similarly. However, depending on the number and spatial distribution of gauges within a region, this may not be possible. If no gauged subbasins are within a cluster, the rest of the SABER procedure can be applied, and pairs of gauged and ungauged subbasins can still be extrapolated. There will be weaker justification for the corrections made in those cases and, therefore, greater uncertainty.

2.4. Identifying Spatial Relationships

SABER identifies spatial correlations using spatial and network analysis. The purpose of the analysis is to identify portions of watersheds that are likely to share similar biases because of their location or other features that affect water routing. The intuition for the analysis is that subbasins that are hydraulically connected on the stream network (i.e., upstream or downstream of each other) or which are close together may experience similar biases. We assume subbasins that are connected or close together are more likely to have similar channel cross-sections, slopes, soil types, and land uses compared to subbasins that are farther away [59]. When adjacent subbasins are within the same tributary area, they are more likely to receive runoff from the same sources, such as precipitation, snowmelt, or groundwater, which may have been inaccurately predicted and contribute to bias.

The first SABER spatial operation is to determine which subbasins have gauges on the stream or at the outlet. SABER pairs these subbasins with the gauges they contain.

Next, SABER uses network analysis to identify the subbasins that are directly upstream and downstream of the gauge. We assume that because these subbasins are directly hydraulically connected to gauged subbasins, they should exhibit similar biases to those present at the gauge. Since flow regime patterns can change along the river network, we limit this assumption to only subbasins upstream or downstream of the gauge of the same Strahler stream order. The model biases may be similar in other subbasins, but the confidence of the assumption degrades with distance from the gauge, upstream or downstream. We limit the assumption based on stream order because the tributaries may not share the same characteristics and biases as the gauged subbasin.

2.5. Pairing Gauged and Ungauged Subbasins

SABER assigns a gauged subbasin to each of the ungauged subbasins using the results of the clustering and geospatial analysis. Each gauged subbasin can be paired with multiple ungauged subbasins. SABER makes these assignments using the following criteria, presented in order of the strongest to weakest physically explainable justification for assuming the ungauged basin shares the same biases as the gauged basin.

• Hydraulic connectivity. Choose a gauge for the ungauged basin that is directly upstream or downstream of a gauge on a stream of the same Strahler order. If multiple gauges exist, choose the closest gauge in terms of distance along the stream network. If no matches are found, proceed to the next selection criterion.
• Clustered basin. Choose a gauge from the same FDC cluster as the ungauged basin. If only one gauge exists in the cluster, use that gauge for the ungauged subbasins. If multiple matches are found, proceed to the following criteria to determine which of those gauges is the best fit. If no matches are found, use the following criteria to choose a gauge from all gauges in the watershed.
• Stream order. Choose a gauge from a stream that has the same stream order as the ungauged stream. If no matches are found, look for gauges within one stream order class of the ungauged basin and repeat. If there is one option, use that gauge. If no gauges meet this criterion, skip this step and use the next criterion. If multiple matches are found, use the next selection criterion to choose between those options.
• Drainage area. Choose the gauged subbasin with the drainage area closest to that of the ungauged subbasin. If multiple gauges are within 5% of the target drainage area, proceed to the next selection criterion.
• Proximity. From the remaining possibilities, pick the gauge located closest, in geodesic distance rather than distance along the stream network, to the outlet of the ungauged basin’s outlet.

2.6. Applying Corrections and Statistical Refinements

Occasionally, applying these scalar factors can result in corrected discharge values that are impractically large. This can occur because of the variation in flow values and the potential for incorrect matches between gauged and ungauged subbasins. This occurs because of inherent uncertainties in attempting to bias-correct ungauged areas. To identify and mitigate these errors, SABER compares the bias-corrected flows against values that are statistically likely to determine if flow values seem reasonable. Specifically, SABER compares the distribution of corrected flows against a Gumbel Type 1 distribution, which is commonly used for estimating high-flow values [60,61,62]. SABER replaces flows with a return period of 100 years or larger with the 100-year discharge predicted by the Gumbel Type 1 distribution. Choosing the 100-year return period threshold was subjective. However, the longest historical simulations of discharge are less than 50 years long (the ERA5 model forcings, for instance, begin in 1979), so we chose 100 years as a default value. The decision could be a point of experimentation and calibration when applying SABER to areas where local observations suggest larger floods have been captured in the observed data.

3. Results

3.1. Case Study Design

We validated SABER using GES hindcast results in the Magdalena River Basin in Colombia. Figure 5 contains a map of the study area with the GES stream network shown by the solid blue lines and the location of the river gauges marked by red dots. There are 233 gauges in the Magdalena basin that record discharge. The river gauges are operated by the Institute of Hydrology, Meteorology and Environmental Studies (Instituto de Hidrología, Meteorología y Estudios Ambientales—IDEAM). The gauges have varied periods of record, and some contain gaps. Daily average discharge is available for each gauge. The GES hindcast data provides daily average discharge, and we used the period from 1 January 1980 through 31 December 2021. We obtained the hindcast data from the model developers in bulk netCDF format and extracted time series for each of the 2326 subbasins [63,64]. The watershed has several dams and diversions that are not simulated by the GES model and contribute to the model’s bias on some stream reaches.

We randomly reserved approximately half of the gauge locations, not half the measurements, for validation. We choose half the locations rather than half the measurements since a key element of the method is justifying subbasins (i.e., locations) that should be paired together for bias correction. We used SABER to bias correct all the subbasins and then computed error metrics.

We evaluated the performance of SABER using the Mean Error (ME) and Mean Absolute Percent Error (MAPE) metrics [65,66]. We report several other supplementary metrics common in the hydrology literature, including the Nash Sutcliffe Efficiency (NSE) [67], Kling Gupta Efficiency (KGE) [68,69], Mean Absolute Error (MAE), and Normalized Root Mean Square Error (NRMSE). Many of these metrics, such as NSE or KGE, can only be used to compare different results at a single location and cannot be used to compare results at different locations, though this is commonly performed in the literature [66]. These additional metrics also indicate bias, and we included them for additional insight into GES model performance before and after bias correction.

We calculate and report metrics for three conditions at each location reserved for validation. The first condition compares the unaltered model results against the observations. This represents the baseline performance of the model at the validation points with no bias corrections applied. The next condition is the bias-corrected results produced using the SFDC calculated and applied by the SABER algorithm. This estimates the performance of the bias correction at the ungauged subbasins. The third condition is bias-corrected results using the observed data at those locations and the direct frequency-matching approach. These results estimate the performance of SABER at gauged subbasins and should be the best possible result when using SABER since observed data for that location are used. These corrections are only possible for gauged subbasins. If SABER is successful, the bias-corrected data should show less bias than the original GES model results. The bias-corrected data using SFDC extrapolations (condition two) will be less biased than the original data but will likely have more bias than when using observed data and direct frequency matching for bias correction (condition three).

3.2. Bias Reduction Statistics

Figure 6 shows box plots of the mean error results that are summarized in

Table 1. Mean error summary statistics for the Magdalena River.

Statistic	GES Model Results	SFDC Corrected Results	Freq. Matched Results
n	109	109	109
Max.	10,994.75	23,596.18	19,984.16
75%	129.08	29.74	4.42
Median	23.61	2.36	1.16
25%	7.34	−6.64	−2.46
Min.	−196.76	−327.08	−125.95

. From left to right in Figure 6, the figure first shows the GES model results (Raw Model results), then bias-corrected results using the SFDC assigned to those points (SFDC Corrected), then bias-corrected results using observed data frequency matching (Frequency Matched).

To determine if the various tests were different, we performed a t-test for the hypothesis of equal means. When we compared the mean error results of the raw GES model data and the SFDC-corrected results, the p-value was approximately 0.12. This is not statistically significant using the traditional 0.05 threshold (95% confidence). There are, however, approximately 20 outliers with a mean error above 400 m³/s (cubic meters per second) or below −200 m³/s, which skew many statistic calculations and the significance calculation. While the means may not be statistically different, the variances and range of the errors are greatly reduced after bias correction. Each box plot from left to right shows a decrease in the median ME and a narrower interquartile range (IQR). The best results were produced by the frequency-matched corrections, followed by SFDC corrected, and, finally, the raw model results. We interpret this as the SABER method providing a substantial reduction in model bias in ungauged subbasins (SFDC Corrected) but not as much as is possible when gauged data are available (Frequency Matched).

As model bias decreases, the ME should trend towards zero. The median ME is 23.61 m³/s for the raw modeled data, is 2.36 m³/s when corrected using the SFDC corrections and is 1.16 m³/s when directly using the frequency-matching technique with the observed data at those locations. The IQR and other statistics trend toward zero for each test from left to right on the plot. This indicates that both the overall bias, indicated by the median ME, and the variance in bias between subbasins, shown by the range of the box plot, are decreasing. The subbasins in the original model data had widely varying ME, and the corrected data have more similarities between subbasins.

We calculated other error metrics to analyze the performance of the GES results before and after bias correction. The statistics were calculated for all stream segments included in the test set, and the median value across all points is reported in

Table 2. Magdalena River median error metrics for each test group.

Metric	GES Model Results	SFDC Corrected Results	Freq. Matched Results	Target Value
ME	23.61	2.36	1.16	0
MAPE	258.62	92.40	88.40	0
MAE	54.86	29.80	24.40	0
NRMSE	2.10	1.24	1.12	0
KGE	−0.66	0.04	0.16	1
NSE	−8.22	−0.92	−0.82	1

. Box plots of the MAPE and KGE metrics are included in Figure 7 and Figure 8, respectively.

The ME (Figure 6) and KGE (Figure 8) show a substantial reduction in variance and improved median values after bias correction, while the MAPE (Figure 7) is still large. The GES model’s MAPE is 258.62% and approximately 90% when corrected with either the SFDC or frequency matching methods. These values are still extremely large. The explanation for the large values is the high resolution of the GES stream network [6]. In the study area, 1164 of the 2326 subbasins are of stream order 1, with an average drainage area of 153 km². The small drainage area subbasins have small discharges near zero for many months of the year. Small errors in discharge yield large percent errors when the discharge is small.

Removing model bias should also reveal a trend in composite metrics, such as KGE and NSE, which have a maximum value of one. However, since these are composite measures of multiple aspects of a model’s performance, we expected that correcting bias will have diminishing returns when the bias has largely been removed. The model’s other sources of error then become the principal reason for the lower composite score and thus plateau even as additional observed discharge data become available. This effect is apparent in the columns of the table. There is a relatively large increase in the model performance for each metric between the column reporting GES Model Results vs. SFDC Corrected Results. By comparison, there is a relatively smaller increase in performance for each metric between the SFDC Corrected Results columns and the Frequency Matched Results column. Though the improvement in KGE plateaus, the median KGE increases from −0.66 to just above 0 for both the SFDC and frequency matching columns. A naïve simulation using the average observed value as a constant produces a KGE of −0.41 [70]. The SABER-corrected values are above zero, which is above −0.41, which indicates the median corrected subbasin has some predictive skill.

3.3. Spatial Trends in Performance

The clustering analysis and use of the knee method determined that the optimal number of clusters for the Magdalena watershed was four. Figure 9 shows a map of each of the subbasins in the watershed as delineated by the GES model. Subbasins colored in orange either contain a gauge or were paired with a gauge for bias correction because they are upstream or downstream of a gauge. The remaining subbasins are colored according to the cluster to which they were assigned.

Figure 10 shows the performance of the SABER algorithm in each of the three conditions of the validation tests (refer to Figure 5 for a map of stream and gauge locations). Each map marks the locations of 50% of the gauges reserved for validation, and they are colored in intervals according to the KGE values calculated at each location. Locations with a KGE value below −10 are colored red with values in the interval [−10, −5] for simpler visualization. We plotted the KGE rather than ME or MAPE because the range of values for KGE is more compatible with visualizing via colors. The leftmost map shows the original model results. Most of the gauges, particularly along the western boundary and in the center of the watershed, have values below zero, which are colored yellow, orange, or red. Most of these points increased their KGE to be above zero, colored green, using both the SFDC extrapolated corrections and frequency matching with the observed data. The shift in color indicates an improvement in the model performance after correction. This is supported by the summary statistics shown in Table 2, which lists the median values for KGE as −0.66 before bias correction and as 0.04 and 0.16, respectively, for the two bias-corrected trials. The gauges that showed improvement were generally river segments with a smaller stream order and with smaller contributing drainage areas.

In contrast, a few points decreased in KGE to the red colored interval [−10, −5]. The points are found at the northern end of the watershed near the outlet and the south-central area. The decrease in model performance near the outlet is most likely because those gauges measure the largest discharges in the watershed. The random selection of gauges to reserve for the validation happened to select most of the gauges that measure flows of that size. The clustering and network analysis could not adequately determine SAF, which place flows in the proper order of magnitude, because there were no gauges available to characterize biases on the larger streams. The points at the south end of the watershed had values that originally performed well with a KGE above 0. In these instances, the best available gauge and SFDC, according to SABER’s procedure, indicated that the flows needed to be increased. The magnitude of the SAF corrections was too large, and the flows were amplified, creating more bias. Both instances highlight the need for gauges that span the watershed spatially and cover river segments of all sizes.

3.4. Hydrograph Analysis

We compared the uncorrected, SFDC-corrected, frequency-matching corrected, and observed hydrographs. Figure 11 presents two hydrograph plots for a subbasin with representative results. Both hydrographs come from the results of the same subbasin. The case study corrected the simulated discharge between 1980 and 2021, but the plots show a ten-year period from 2000 to 2010 (top panel) and a one-year period from 2006 to 2007 (bottom panel) for clarity. The uncorrected GES model results are shown in blue, the SFDC-corrected values in orange, the frequency-matched values in green, and the observed discharge in red. The written analysis refers to the bottom panel.

In this subbasin, the uncorrected discharge (blue line) is biased high since it is consistently above the observed discharge (red line). The SFDC-corrected discharge (orange) is always below the uncorrected discharge. It is usually between the uncorrected and observed discharge, which means it has less bias. Occasionally the SFDC line is overcorrected and plots below the observed line. The SFDC, frequency matched (green), and observed lines are extremely similar for approximately six months between May and November. The SFDC correction performs the best in this subbasin for that six-month period. In the other six months, the frequency-matched hydrograph is closer than the SFDC hydrograph to the observed hydrograph. This means that the frequency matching performed better than the SFDC corrections for about half the year. Throughout the whole year, both the SFDC and frequency-matched hydrographs show a reduction in bias and, therefore, an improvement over the original model results.

4. Discussion and Limitations

We identified at least six areas for future research to improve the performance of SABER and address the current limitations of the bias correction process.

First, we used monthly FDCs to capture the temporally varying biases, which we assumed was a reasonable way to temporally divide the data. Indeed, monthly divisions may adequately capture seasonal variations and were sufficient to reduce the GES model’s bias in the presented case study. However, the groupings could be either too fine or coarse to accurately capture trends in all watersheds. Other groupings, such as quarterly or months that correspond to local wet and dry seasons, could be substituted. Wet seasons can begin and finish early or late in some years and cause the naïve monthly groups to inaccurately capture trends and probabilities. Groups that capture the typical wet and dry seasons might better characterize the flow regimes during those months and should be investigated.

Second, the clustering approaches used to characterize trends spatially can be improved. In particular, the SABER approach may become impractical to scale up as models grow in spatial or temporal extent and resolution. For instance, the largest hydrologic model in terms of volume of data produced are the United States National Water Model [4]. Its retrospective dataset (currently version 2.1) in netCDF format consumes about 17 terabytes of computer disc space [64,71,72,73]. The clustering algorithms implemented by SABER may not easily scale to that volume of data; even when applied to regional subsets of the model. Incremental k-means training techniques, code optimizations, data preprocessing workflows, or alternative clustering approaches may be necessary for models with such spatial and temporal resolution. We recommend these approaches be explored because we hypothesize they will be more robust and easily applied and may enhance the performance of SABER.

Third, the presented methods and case study do not quantify the minimum amount of data necessary to implement SABER, nor how sensitive the method is to the amount of available data. Indeed, we found that such an analysis depends on the hydrologic model and the geographic region of the watershed since bias may vary spatially. General statements about minimum data requirements and sensitivity are difficult to justify because of that variability. The SABER method depends on having sufficient gauges to characterize the model biases throughout the area of interest. We posit that how well the gauges can characterize biases is a function of the same properties used in the SABER decision-making process. For instance, the gauges should be relatively well spatially distributed across the watershed area, and measure river reaches of different stream orders. Like statistical scenarios involving forecasting, clustering, or extrapolation, we expect that SABER will perform better when the available gauges more fully span the range of possible values for each parameter. Future developments on SABER should investigate the method’s sensitivity to the quantity of available data. The investigation needs to be nuanced enough to identify the value of gauged data based on the properties and characteristics of the gauges. That analysis, even if it is model specific, may suggest strategies for more wisely placing new gauges and leveraging limited local capacity for operating river gauges.

Fourth, SABER does not enforce the conservation of mass between subbasins. Connected river segments will receive similar SAFs, but this does not guarantee that the flows are continuous between segments or that a valid water balance calculation is possible. Though not unusual for bias corrections methods, SABER has the effect of reducing the bias in subbasins individually rather than collectively. One of the original motivations for developing SABER was needing to bias correct without the ability to execute model runs. That objective precludes implementing a river routing component to smooth the differences between connected segments. Section 3.3 found that a few gauge points experienced a decrease in performance after the SABER method. While we were unable to identify a specific reason or watershed characteristic that led to SABER incorrectly adjusting flows, the basins could still be identified after performing the corrections. We hypothesize that adding a step that calculates a water balance progressing through the stream network would identify the seemingly “random” basins where flows become too large or too small and creates a discontinuity in discharge and the calculated metrics. When these basins are identified, we propose implementing a method to enforce the conservation of mass by smoothing discontinuities. The solution could include averaging or interpolating between streams with higher confidence in the water balance calculation.

Fifth, the clustering and pairing procedures depend heavily on spatial relationships. SABER only indirectly accounts for watershed characteristics such as land use and land cover, soil types, or slope because it is correcting results from some underlying hydrologic model. The presented case study, however, is evidence that substantial bias reduction is possible without such data. Nevertheless, there are many global datasets that measure the listed hydrologic properties and that are likely the same or comparable to those used by the modelers. Google Earth Engine alone has a large catalog of such datasets and makes querying those datasets at a catchment scale relatively simple [74,75,76,77]. Including these data would increase the complexity and difficulty of the SABER method, but the results would be more physically explainable and justifiable. There are many methods to include these data and enhance or replace the presented procedures for the clustering process as justification to improve the pairing process or both. These options should be explored.

Finally, SABER currently does not provide special treatment to subbasins that have flow control structures. The subbasins downstream of a diversion, dam, retention basin, or lakes, are likely to exhibit flow regimes and biases that are different from the rest of the watershed. Human intervention creates an artificial rather than natural flow regime. This violates the assumption that the modeled data can be clustered and spatially correlated with characterizing biases. Previous research showed that frequency matching performs well in subbasins that contain dams and have observed data [45,46]. We have not investigated the performance of SABER on a global model that tries to account for such features. In the case study, some of the locations where the performance of the bias correction degrades were downstream of flow control structures. We propose the development of an additional step in the spatial analysis and basin pairing procedure that separately handles subbasins that contain or are downstream of dams, reservoirs, or similar features.

5. Conclusions

We presented a new postprocessing method, Stream Analysis for Bias Estimation and Reduction (SABER), for bias-correcting hydrologic models. The unique contribution of this method is its extension of previous work on frequency matching to ungauged subbasins using the novel scalar flow duration curve (SFDC) and a clustering and spatial analysis procedure. The SFDC characterizes model biases temporally, spatially, and for varying flow exceedance probabilities. The novel SFDC is used to characterize and correct biases in all ungauged subbasins through a physically explainable sequence of steps informed by machine learning clustering and geospatial analysis. This approach extends a relatively small number of gauge locations and the total number of observations to more subbasins. We describe this approach as model agnostic, which means it requires no access to the hydrologic model’s code, forcings, or other datasets so it can be applied to any hydrologic model. It is a postprocessor that is applied to model results in a computationally efficient way targeting the model consumer rather than the model developer. With such features, our method lends itself well to automating bias correction of large-scale hydrologic models on regional scales.

We tested SABER in a case study of the Magdalena River in Colombia using the GEOGloWS ECMWF Streamflow model. We showed that SABER effectively removes bias from modeled discharge by reducing the mean error and mean absolute percent error. Additionally, SABER improves model performance measured by several other metrics, including increasing the Kling Gupta and Nash Sutcliffe Efficiency. We presented a statistical analysis of the performance of SABER using these results. We discussed several limitations and areas for future work on SABER, including investigating alternative methods for temporally characterizing biases, optimizations and improvements to the k-means clustering implementation, the need for sensitivity analysis of each hydrologic model, enforcing conservation of mass, including datasets to characterize subbasin properties, and special considerations for reservoirs and diversions.