Design of an Automatically Controlled Multi-Axis Stretching Device for Mechanical Evaluations of the Anterior Eye Segment
Abstract
:1. Introduction
2. Materials and Methods
2.1. Mechanical Design
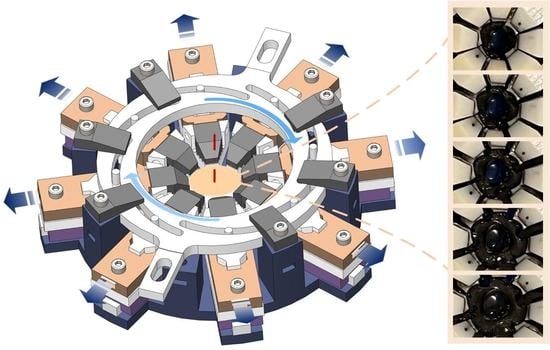
2.1.1. Stretcher
2.1.2. Gear System
2.1.3. Stretching Force Sensing
2.2. Electronics and Control
2.3. Experimental Measurement
2.3.1. Calibration of the Resistance Force
2.3.2. Validation Experiment Based on Spring Stretching
2.3.3. Feasibility Test Using Porcine Eyes
3. Results
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pierscionek, B.K.; Regini, J.W. The gradient index lens of the eye: An opto-biological synchrony. Prog. Retin. Eye Res. 2012, 31, 332–349. [Google Scholar] [CrossRef] [PubMed]
- Wang, K.; Pierscionek, B.K. Biomechanics of the human lens and accommodative system: Functional relevance to physiological states. Prog. Retin. Eye Res. 2019, 71, 114–131. [Google Scholar] [CrossRef] [PubMed]
- Bron, A.J.; Tripathi, R.C.; Tripathi, B.J. Wolf ’s Anatomy of the Eye and Orbit, 8th ed.; Hodder Education Publishers: London, UK, 1997. [Google Scholar]
- Werner, L.; Trindade, F.; Pereira, F.; Werner, L. Physiology of Accommodation and Presbyopia. Arq. Bras. Oftalmol. 2000, 63, 503–509. [Google Scholar]
- Charman, W.N. The eye in focus: Accommodation and presbyopia. Clin. Exp. Optom. 2008, 91, 207–225. [Google Scholar] [CrossRef]
- Streeten, B.W. Te zonular insertion: A scanning electron microscopic study. Investig. Ophthalmol. Vis. Sci. 1977, 16, 364–375. [Google Scholar]
- Wang, K.; Venetsanos, D.; Wang, J.; Pierscionek, B.K. Gradient moduli lens models: How material properties and application of forces can affect deformation and distributions of stress. Sci. Rep. 2016, 6, 31171. [Google Scholar] [CrossRef] [Green Version]
- Glasser, A.; Campbell, M.C. Biometric, optical and physical changes in the isolated human crystalline lens with age in relation to presbyopia. Vision Res. 1999, 39, 1991–2015. [Google Scholar] [CrossRef] [Green Version]
- Wilde, G.; Burd, H.; Judge, S. Shear modulus data for the human lens determined from a spinning lens test. Exp. Eye Res. 2012, 97, 36–48. [Google Scholar] [CrossRef] [Green Version]
- Chai, C.K.; Burd, H.J.; Wilde, G.S. Shear modulus measurement on isolated human lens nuclei. Exp. Eye. Res. 2012, 103, 78–81. [Google Scholar] [CrossRef]
- Heys, K.R.; Cram, S.L.; Truscott, R.J. Massive increase in the stifness of the human lens nucleus with age: The basis for presbyopia? Mol. Vis. 2004, 10, 956–963. [Google Scholar]
- Schachar, R.A.; Chan, R.W.; Fu, M. Viscoelastic shear properties of the fresh porcine lens. Br. J. Ophthalmol. 2007, 91, 366–368. [Google Scholar] [CrossRef] [Green Version]
- Schachar, R.A.; Chan, R.W.; Fu, M. Viscoelastic properties of fresh human lenses under 40 years of age: Implications for the aetiology of presbyopia. Br. J. Ophthalmol. 2011, 95, 1010–1013. [Google Scholar] [CrossRef] [PubMed]
- Beers, A.P.A.; van der Heijde, G.L. In vivo Determination of the Biomechanical Properties of the Component Elements of the Accommodation Mechanism. Vision Res. 1994, 34, 2897–2905. [Google Scholar] [CrossRef] [PubMed]
- Beers, A.P.A.; van der Heijde, G.L. Age Related Changes in the Accommodation mechanism. Optom. Vis. Sci. 1996, 73, 235–242. [Google Scholar] [CrossRef] [PubMed]
- Krag, S.; Andreassen, T.T. Mechanical properties of the human lens capsule. Prog. Retin. Eye Res. 2003, 22, 749–767. [Google Scholar] [CrossRef]
- Fisher, R.F. Elastic constants of the human lens capsule. J. Physiol. 1969, 201, 198. [Google Scholar] [CrossRef]
- Burd, H.J.; Wilde, G.S.; Judge, S.J. An improved spinning lens test to determine the stiffness of the human lens. Exp. Eye Res. 2011, 92, 28–39. [Google Scholar] [CrossRef] [Green Version]
- Pierscionek, B.K.; Weale, R.A. Presbyopia- a maverick of human ageing. Arch. Gerontol. Geriatr. 1995, 20, 229–240. [Google Scholar] [CrossRef]
- Pierscionek, B.K.; Weale, R.A. The optics of the eye-lens and lenticular senescence, a review. Doc. Ophthalmol. 1995, 89, 321–335. [Google Scholar] [CrossRef]
- Schachar, R.A. Growth patterns of fresh human crystalline lenses measured by in vitro photographic biometry. J. Anat. 2005, 206, 575–580. [Google Scholar] [CrossRef]
- Brown, N. The Change in Lens Curvature with Age. Exp. Eye Res. 1974, 19, 175–183. [Google Scholar] [CrossRef] [PubMed]
- Domínguez-Vicent, A.; Monsálvez-Romín, D.; Esteve-Taboada, J.J.; Montés-Micó, R.; Ferrer-Blasco, T. Effect of age in the ciliary muscle during accommodation: Sectorial analysis. J. Optom. 2019, 12, 14–21. [Google Scholar] [CrossRef] [PubMed]
- Fisher, R.F. The force of contraction of the human ciliary muscle during accommodation. J. Physiol. 1977, 270, 51–74. [Google Scholar] [CrossRef]
- Fisher, R.F. The elastic constants of the human lens. J. Physiol. 1971, 212, 147–180. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, K.; Venetsanos, D.T.; Wang, J.; Pierscionek, B.K. Combined use of parallel-plate compression and finite element modeling to analyze the mechanical properties of intact porcine lens. J. Mech. Med. Biol. 2018, 18, 1840013. [Google Scholar] [CrossRef] [Green Version]
- Pierscionek, B.K. Age-related response of human lenses to stretching forces. Exp. Eye Res. 1995, 60, 325–332. [Google Scholar] [CrossRef] [PubMed]
- Pau, H.; Kranz, J. The increasing sclerosis of the human lens with age and its relevance to accommodation and presbyopia. Graefes. Arch. Clin. Exp. Ophthalmol. 1991, 229, 294–296. [Google Scholar] [CrossRef] [PubMed]
- Weeber, H.A.; Eckert, G.; Pechhold, W.; van der Heijde, R.G.L. Stiffness gradient in the crystalline lens. Graefes. Arch. Clin. Exp. Ophthalmol. 2007, 245, 1357–1366. [Google Scholar] [CrossRef] [Green Version]
- Hollman, K.W.; O’Donnell, M.; Erpelding, T.N. Mapping elasticity in human lenses using bubble-based acoustic radiation force. Exp. Eye Res. 2007, 85, 890–893. [Google Scholar] [CrossRef] [Green Version]
- Erpelding, T.N.; Hollman, K.W.; O’Donnell, M. Mapping age-related elasticity changes in porcine lenses using bubble-based acoustic radiation force. Exp. Eye Res. 2007, 84, 332–341. [Google Scholar] [CrossRef] [Green Version]
- Besner, S.; Scarcelli, G.; Pineda, R.; Yun, S.H. In vivo brillouin analysis of the aging crystalline lens. Investig. Ophthalmol. Vis. Sci. 2016, 57, 5093–5100. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bailey, S.T.; Twa, M.D.; Gump, J.C.; Venkiteshwar, M.; Bullimore, M.A.; Sooryakumar, R. Light-scattering study of the normal human eye lens: Elastic properties and age dependence. IEEE Trans. Biomed. Eng. 2010, 57, 2910–2917. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, K.; Venetsanos, D.T.; Hoshino, M.; Uesugi, K.; Yagi, N.; Pierscionek, B.K. A modelling approach for investigating opto-mechanical relationships in the human eye lens. IEEE Trans Biomed. Eng. 2020, 67, 999–1006. [Google Scholar] [CrossRef] [PubMed]
- Scarcelli, G.; Kim, P.; Yun, S.H. In vivo measurement of age-related stiffening in the crystalline lens by Brillouin optical microscopy. Biophys. J. 2011, 101, 1539–1545. [Google Scholar] [CrossRef] [Green Version]
- Pierscionek, B.K. In vitro alteration of human lens curvatures by radial stretching. Exp. Eye Res. 1993, 57, 629–635. [Google Scholar] [CrossRef] [PubMed]
- Cortés, L.P.; Burd, H.J.; Montenegro, G.A.; D’Antin, J.C.; Mikielewicz, M.; Barraquer, R.I.; Michael, R. Experimental protocols for Ex vivo lens stretching tests to investigate the biomechanics of the human accommodation apparatus. Investig. Ophthalmol. Vis. Sci. 2015, 56, 2926–2932. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Reilly, M.A.; Hamilton, P.D.; Ravi, N. Dynamic multi-arm radial lens stretcher: A robotic analog of the ciliary body. Exp. Eye Res. 2008, 86, 157–164. [Google Scholar] [CrossRef]
- Ehrmann, K.; Ho, A.; Parel, J.M. Ex vivo accommodation simulator II: Concept and preliminary results. Ophthalmic. Technol. XIV 2004, 5314, 48. [Google Scholar]
- Michael, R.; Mikielewicz, M.; Gordillo, C.; Montenegro, G.A.; Pinilla Cortés, L.; Barraquer, R.I. Elastic properties of human lens zonules as a function of age in presbyopes. Investig. Ophthalmol. Vis. Sci. 2012, 53, 6109–6114. [Google Scholar] [CrossRef]
- Nankivil, D.; Heilman, B.M.; Durkee, H.; Manns, F.; Ehrmann, K.; Kelly, S.; Arrieta-Quintero, E.; Parel, J.M. The zonules selectively alter the shape of the lens during accommodation based on the location of their anchorage points. Investig. Ophthalmol. Vis. Sci. 2015, 56, 1751–1760. [Google Scholar] [CrossRef] [Green Version]
- Webb, J.N.; Dong, C.; Bernal, A.; Scarcelli, G. Simulating the Mechanics of Lens Accommodation via a Manual Lens Stretcher. J. Vis. Exp. 2018, 132, e57162. [Google Scholar] [CrossRef] [PubMed]
- Reilly, M.A.; Hamilton, P.D.; Perry, G.; Ravi, N. Comparison of the behavior of natural and refilled porcine lenses in a robotic lens stretcher. Exp. Eye Res. 2009, 88, 483–494. [Google Scholar] [CrossRef] [PubMed]
- Manns, F.; Parel, J.M.; Denham, D.; Billotte, C.; Ziebarth, N.; Borja, D.; Fernandez, V.; Aly, M.; Arrieta, E.; Ho, A.; et al. Optomechanical response of human and monkey lenses in a lens stretcher. Investig. Ophthalmol. Vis. Sci. 2007, 48, 3260–3268. [Google Scholar] [CrossRef] [PubMed]
- Reilly, M.; Ravi, N. Microindentation of the young porcine ocular lens. J. Biomech. Eng. 2009, 131, 044502. [Google Scholar] [CrossRef]
- Reilly, M.A.; Martius, P.; Kumar, S.; Burd, H.J.; Stachs, O. The mechanical response of the porcine lens to a spinning test. Z. Med. Phys. 2016, 26, 127–135. [Google Scholar] [CrossRef]
- Gokhin, D.S.; Nowak, R.B.; Kim, N.E.; Arnett, E.E.; Chen, A.C.; Sah, R.L.; Clark, J.I.; Fowler, V.M. Tmod1 and CP49 synergize to control the fiber cell geometry, transparency, and mechanical stiffness of the mouse lens. PLoS ONE 2012, 7, 48734. [Google Scholar] [CrossRef] [Green Version]
- Baradia, H.; Nikahd, N.; Glasser, A. Mouse lens stiffness measurements. Exp. Eye Res. 2010, 91, 300–307. [Google Scholar] [CrossRef]
- Wu, C.; Han, Z.; Wang, S.; Li, J.; Singh, M.; Liu, C.H.; Aglyamov, S.; Emelianov, S.; Manns, F.; Larin, K.V. Assessing age-related changes in the biomechanical properties of rabbit lens using a coaligned ultrasound and optical coherence elastography system. Investig. Ophthalmol. Vis. Sci. 2015, 56, 1292–1300. [Google Scholar] [CrossRef] [Green Version]
- Wang, Q.; Zhu, Y.; Shao, M.; Liu, H.; Chen, S.; Chen, X.; Alizad, A.; Fatemi, M.; Zhang, X. In vivo assessment of the mechanical properties of crystalline lenses in a rabbit model using ultrasound elastography: Effects of ultrasound frequency and age. Exp. Eye Res. 2019, 184, 258–265. [Google Scholar] [CrossRef]








Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, K.; Qiu, Z.; Xie, Y.; Cai, S.; Zhao, Y.; Pierscionek, B.K.; Guo, J.; Fan, Y. Design of an Automatically Controlled Multi-Axis Stretching Device for Mechanical Evaluations of the Anterior Eye Segment. Bioengineering 2023, 10, 142. https://doi.org/10.3390/bioengineering10020142
Wang K, Qiu Z, Xie Y, Cai S, Zhao Y, Pierscionek BK, Guo J, Fan Y. Design of an Automatically Controlled Multi-Axis Stretching Device for Mechanical Evaluations of the Anterior Eye Segment. Bioengineering. 2023; 10(2):142. https://doi.org/10.3390/bioengineering10020142
Chicago/Turabian StyleWang, Kehao, Ziyan Qiu, Yiping Xie, Shuo Cai, Yang Zhao, Barbara K. Pierscionek, Jiangzhen Guo, and Yubo Fan. 2023. "Design of an Automatically Controlled Multi-Axis Stretching Device for Mechanical Evaluations of the Anterior Eye Segment" Bioengineering 10, no. 2: 142. https://doi.org/10.3390/bioengineering10020142
APA StyleWang, K., Qiu, Z., Xie, Y., Cai, S., Zhao, Y., Pierscionek, B. K., Guo, J., & Fan, Y. (2023). Design of an Automatically Controlled Multi-Axis Stretching Device for Mechanical Evaluations of the Anterior Eye Segment. Bioengineering, 10(2), 142. https://doi.org/10.3390/bioengineering10020142