Effect of Nonlinear Elasticity on the Swelling Behaviors of Highly Swollen Polyelectrolyte Gels
Abstract
:1. Introduction
2. Theoretical Description of the Equilibrium Swelling State
2.1. Estimation of the Elastic Pressure
2.2. Estimation of the Mixing Pressure
2.3. Estimation of the Ionic Pressure
2.4. Estimation of the Swelling Ratio Q by the Flory–Rehner Model Considering the Gibbs–Donnan Effect and Manning’s Counterion Condensation Effect (the FRGDM Model)
3. Results and Discussion
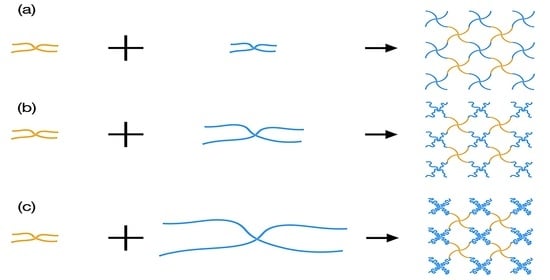
3.1. Fabrication of Tetra-PAA-PEG Gels with Tuned Neutral Segment Lengths
3.2. Effect of the Neutral Segment Length on the Swelling Behavior
3.3. Effect of the Neutral Segment Length on the Mechanical Properties
3.4. Effect of the Finite Extensibility of the Polymer Chains on the Swelling Behavior
4. Conclusions
5. Materials and Methods
5.1. Fabrication of the Tetra-PAA-PEG Gels
5.2. Rheological Measurements after Gelation
5.3. Swelling Experiments
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Shibayama, M.; Ikkai, F.; Inamoto, S.; Nomura, S.; Han, C.C. PH and Salt Concentration Dependence of the Microstructure of Poly (N-Isopropylacrylamide-Co-Acrylic acid) Gels. J. Chem. Phys. 1996, 105, 4358–4366. [Google Scholar] [CrossRef]
- Liu, X.; Tong, Z.; Hu, O. Swelling Equilibria of Hydrogels with Sulfonate Groups in Water and in Aqueous Salt Solutions. Macromolecules 1995, 28, 3813–3817. [Google Scholar] [CrossRef]
- Jeon, C.H.; Makhaeva, E.E.; Khokhlov, A.R. Swelling Behavior of Polyelectrolyte Gels in the Presence of Salts. Macromol. Chem. Phys. 1998, 199, 2665–2670. [Google Scholar] [CrossRef]
- Horkay, F.; Basser, P.J. Ionic and PH Effects on the Osmotic Properties and Structure of Polyelectrolyte Gels. J. Polym. Sci. Part B Polym. Phys. 2008, 46, 2803–2810. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rička, J.; Tanaka, T. Swelling of Ionic Gels: Quantitative Performance of the Donnan Theory. Macromolecules 1984, 17, 2916–2921. [Google Scholar] [CrossRef]
- Flory, P.J. Principles of Polymer Chemistry; Cornell University Press: Ithaca, NY, USA, 1953; ISBN 0801401348. [Google Scholar]
- Flory, P.J.; Rehner, J. Statistical Mechanics of Cross-Linked Polymer Networks II. Swelling. J. Chem. Phys. 1943, 11, 521–526. [Google Scholar] [CrossRef]
- Flory, P.J. Thermodynamics of High Polymer Solutions. J. Chem. Phys. 1942, 10, 51–61. [Google Scholar] [CrossRef]
- Huggins, M.L. Thermodynamic Properties of Solutions of Long-Chain Compounds. Ann. N. Y. Acad. Sci. 1942, 43, 1–32. [Google Scholar] [CrossRef]
- Donnan, F.G. Theorie der Membrangleichgewichte und Membranpotentiale bei Vorhandensein von nicht dialysierenden Elektrolyten. Ein Beitrag zur physikalisch-chemischen Physiologie. Z. für Elektrochem. und Angew. Phys. Chem. 1911, 17, 572–581. [Google Scholar]
- Aalaie, J.; Vasheghani-Farahani, E. Swelling Behavior of Sulfonated Polyacrylamide Nanocomposite Hydrogels in Electrolyte Solutions: Comparison of Theoretical and Experimental Results. Iran. Polym. J. 2012, 21, 175–183. [Google Scholar] [CrossRef]
- Çaykara, T.; Akçakaya, İ. Synthesis and Network Structure of Ionic Poly (N,N-Dimethylacrylamide-co-Acrylamide) Hydrogels: Comparison of Swelling Degree with Theory. Eur. Polym. J. 2006, 42, 1437–1445. [Google Scholar] [CrossRef]
- Drozdov, A.D. Swelling of pH-Responsive Cationic Gels: Constitutive Modeling and Structure-Property Relations. Int. J. Solids Struct. 2015, 64, 176–190. [Google Scholar] [CrossRef]
- Okay, O.; Sariisik, S.B. Swelling Behavior of Poly(Acrylamide-co-Sodium Acrylate) Hydrogels in Aqueous Salt Solutions: Theory versus Experiments. Eur. Polym. J. 2000, 36, 393–399. [Google Scholar] [CrossRef]
- Höpfner, J.; Richter, T.; Košovan, P.; Holm, C.; Wilhelm, M. Seawater Desalination via Hydrogels: Practical Realisation and First Coarse Grained Simulations. Intell. Hydrogels 2013, 140, 140. [Google Scholar]
- Katchalsky, A.; Michaeli, I. Polyelectrolyte Gels in Salt Solutions. J. Polym. Sci. 1955, 15, 69–86. [Google Scholar] [CrossRef]
- Manning, G.S. Limiting Laws and Counterion Condensation in Polyelectrolyte solutions I. Colligative Properties. J. Chem. Phys. 1969, 51, 924–933. [Google Scholar] [CrossRef]
- Pochard, I.; Boisvert, J.-P.; Malgat, A.; Daneault, C. Donnan Equilibrium and the Effective Charge of Sodium Polyacrylate. Colloid Polym. Sci. 2001, 279, 850–857. [Google Scholar] [CrossRef]
- Molina, M.J.; Gómez-Antón, M.R.; Piérola, I.F. pH-Dependence of the Swelling Capacity of Poly(N-vinylimidazole) Hydrogels. Macromol. Chem. Phys. 2002, 203, 2075–2082. [Google Scholar] [CrossRef]
- Molina, M.J.; Gómez-Antón, M.R.; Piérola, I.F. Determination of the Parameters Controlling Swelling of Chemically Cross-Linked pH-Sensitive Poly(N-vinylimidazole) Hydrogels. J. Phys. Chem. B 2007, 111, 12066–12074. [Google Scholar] [CrossRef] [PubMed]
- Zeldovich, K.B.; Khokhlov, A.R. Osmotically Active and Passive Counterions in Inhomogeneous Polymer Gels. Macromolecules 1999, 32, 3488–3494. [Google Scholar] [CrossRef]
- Fujiyabu, T.; Yoshikawa, Y.; Chung, U.I.; Sakai, T. Structure-Property Relationship of a Model Network Containing Solvent. Sci. Technol. Adv. Mater. 2019, 20, 608–621. [Google Scholar] [CrossRef] [Green Version]
- Kamata, H.; Li, X.; Chung, U.I.; Sakai, T. Design of Hydrogels for Biomedical Applications. Adv. Healthc. Mater. 2015, 4, 2360–2374. [Google Scholar] [CrossRef]
- Sakai, T.; Matsunaga, T.; Yamamoto, Y.; Ito, C.; Yoshida, R.; Suzuki, S.; Sasaki, N.; Shibayama, M.; Chung, U.I. Design and Fabrication of a High-Strength Hydrogel with Ideally Homogeneous Network Structure from Tetrahedron-Like Macromonomers. Macromolecules 2008, 41, 5379–5384. [Google Scholar] [CrossRef]
- Tang, J.; Katashima, T.; Li, X.; Mitsukami, Y.; Yokoyama, Y.; Sakumichi, N.; Chung, U.; Shibayama, M.; Sakai, T. Swelling Behaviors of Hydrogels with Alternating Neutral/Highly Charged Sequences. Macromolecules 2020, 53, 8244–8254. [Google Scholar] [CrossRef]
- Li, J.; Suo, Z.; Vlassak, J.J. A Model of Ideal Elastomeric Gels for Polyelectrolyte Gels. Soft Matter 2014, 10, 2582–2590. [Google Scholar] [CrossRef]
- Orakdogen, N.; Boyacı, T. Non-Gaussian Elasticity and Charge Density-Dependent Swelling of Strong Polyelectrolyte Poly(N-Isopropylacrylamide-Co-Sodium Acrylate) Hydrogels. Soft Matter 2017, 13, 9046–9059. [Google Scholar] [CrossRef] [PubMed]
- Ozmen, M.M.; Okay, O. Non-Gaussian Elasticity of Poly (2-acrylamido-2-methylpropane Sulfonic Acid) Gels. Polym. Bull. 2004, 52, 83–90. [Google Scholar] [CrossRef]
- Orakdogen, N.; Boyaci, T. Finite Extensibility and Deviation from Gaussian Elasticity of Dimethylacrylamide-Based Gels with Different Charge Density: Insight into pH/Solvent-Dependent Swelling and Surfactant Interactions. Polymer 2017, 132, 306–324. [Google Scholar] [CrossRef]
- Yoshikawa, Y.; Sakumichi, N.; Chung, U.; Sakai, T. Negative Energy Elasticity in a Rubber-Like Gel. Phys. Rev. X 2021. Accepted. [Google Scholar]
- Donnan, F.G.; Guggenheim, E.A. Die genaue thermodynamik der membrangleichgewichte. Z. Phys. Chem. 1932, 162A, 346–360. [Google Scholar] [CrossRef]
- Procter, H.R.; Wilson, J.A. XXXV. —The Acid–Gelatin Equilibrium. J. Chem. Soc. Trans. 1916, 109, 307–319. [Google Scholar] [CrossRef] [Green Version]
- Shibayama, M.; Tanaka, T. Volume Phase Transition and Related Phenomena of Polymer Gels. Adv. Polym. Sci. 1993, 109, 1–62. [Google Scholar]
- Treloar, L.R.G. The Elasticity of a Network of Long-Chain Molecules—II. Trans. Faraday Soc. 1943, 39, 241–246. [Google Scholar] [CrossRef]
- Treloar, L.R.G. The Physics of Rubber Elasticity; Oxford University Press: Oxford, UK, 1975; ISBN 0191523305. [Google Scholar]
- Donnan, F.G. The Theory of Membrane Equilibria. Chem. Rev. 1924, 1, 73–90. [Google Scholar] [CrossRef]
- Fowler, R.H.; Guggenheim, E.A. Statistical Thermodynamics; Cambridge University Press: Cambridge, UK, 1939. [Google Scholar]
- Oosawa, F. A Simple Theory of Thermodynamic Properties of Polyelectrolyte Solutions. J. Polym. Sci. 1957, 23, 421–430. [Google Scholar] [CrossRef]
- Kotin, L.; Nagasawa, M. Chain Model for Polyelectrolytes. VII. Potentiometric Titration and Ion Binding in Solutions of Linear Polyelectrolytes. J. Chem. Phys. 1962, 36, 873–879. [Google Scholar] [CrossRef]
- Manning, G.S.; Ray, J. Counterion Condensation Revisited. J. Biomol. Struct. Dyn. 1998, 16, 461–476. [Google Scholar] [CrossRef] [PubMed]
- Flory, P.J. Theory of Elasticity of Polymer Networks. The Effect of Local Constraints on Junctions. J. Chem. Phys. 1977, 66, 5720–5729. [Google Scholar] [CrossRef]
- James, H.M.; Guth, E. Statistical Thermodynamics of Rubber Elasticity. J. Chem. Phys. 1953, 21, 1039–1049. [Google Scholar] [CrossRef]
- Flory, P.J. Molecular Theory of Rubber Elasticity. Polymer 1979, 20, 1317–1320. [Google Scholar] [CrossRef]
- Matsunaga, T.; Sakai, T.; Akagi, Y.; Chung, U.I.; Shibayama, M. Structure Characterization of Tetra-PEG Gel by Small-Angle Neutron Scattering. Macromolecules 2009, 42, 1344–1351. [Google Scholar] [CrossRef]
- Cohen, Y.; Prevysh, V. The Structure of the Interpolymer Complex of Poly(Ethylene Oxide) and Poly(Acrylic Acid) in Water–Dioxane Mixtures. Acta Polym. 1998, 49, 539–543. [Google Scholar] [CrossRef]
- Khutoryanskiy, V.V.; Dubolazov, A.V.; Nurkeeva, Z.S.; Mun, G.A. pH Effects in the Complex Formation and Blending of Poly(Acrylic Acid) with Poly(Ethylene Oxide). Langmuir 2004, 20, 3785–3790. [Google Scholar] [CrossRef] [PubMed]
- Yu, X.; Tanaka, A.; Tanaka, K.; Tanaka, T. Phase Transition of a Poly (Acrylic Acid) Gel Induced by Polymer Complexation. J. Chem. Phys. 1992, 97, 7805–7808. [Google Scholar] [CrossRef]
- Horkay, F.; Tasaki, I.; Basser, P.J. Osmotic Swelling of Polyacrylate Hydrogels in Physiological Salt Solutions. Biomacromolecules 2000, 1, 84–90. [Google Scholar] [CrossRef]
- Wall, F.T. Statistical Thermodynamics of Rubber. II. J. Chem. Phys. 1942, 10, 485–488. [Google Scholar] [CrossRef]
- Gent, A.N. A New Constitutive Relation for Rubber. Rubber Chem. Technol. 1996, 69, 59–61. [Google Scholar] [CrossRef]
- Rivlin, R.S. Large Elastic Deformations of Isotropic Materials IV. Further Developments of the General Theory. Philos. Trans. R. Soc. Lond. A 1948, 241, 379–397. [Google Scholar]
- Hoshino, K.I.; Nakajima, T.; Matsuda, T.; Sakai, T.; Gong, J.P. Network Elasticity of a Model Hydrogel as a Function of Swelling Ratio: From Shrinking to Extreme Swelling States. Soft Matter 2018, 14, 9693–9701. [Google Scholar] [CrossRef] [Green Version]
- Oshima, K.; Fujimoto, T.; Minami, E.; Mitsukami, Y. Model Polyelectrolyte Gels Synthesized by End-Linking of Tetra-Arm Polymers with Click Chemistry: Synthesis and Mechanical Properties. Macromolecules 2014, 47, 7573–7580. [Google Scholar] [CrossRef]
- Yoshikawa, Y.; Sakumichi, N.; Chung, U.I.; Sakai, T. Connectivity Dependence of Gelation and Elasticity in AB-Type Polymerization: An Experimental Comparison of the Dynamic Process and Stoichiometrically Imbalanced Mixing. Soft Matter 2019, 15, 5017–5025. [Google Scholar] [CrossRef] [PubMed]
- Hayashi, K.; Okamoto, F.; Hoshi, S.; Katashima, T.; Zujur, D.C.; Li, X.; Shibayama, M.; Gilbert, E.P.; Chung, U.; Ohba, S.; et al. Fast-Forming Hydrogel with Ultralow Polymeric Content as an Artificial Vitreous Body. Nat. Biomed. Eng. 2017, 1, 1–7. [Google Scholar] [CrossRef]








Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, J.; Katashima, T.; Li, X.; Mitsukami, Y.; Yokoyama, Y.; Chung, U.-i.; Shibayama, M.; Sakai, T. Effect of Nonlinear Elasticity on the Swelling Behaviors of Highly Swollen Polyelectrolyte Gels. Gels 2021, 7, 25. https://doi.org/10.3390/gels7010025
Tang J, Katashima T, Li X, Mitsukami Y, Yokoyama Y, Chung U-i, Shibayama M, Sakai T. Effect of Nonlinear Elasticity on the Swelling Behaviors of Highly Swollen Polyelectrolyte Gels. Gels. 2021; 7(1):25. https://doi.org/10.3390/gels7010025
Chicago/Turabian StyleTang, Jian, Takuya Katashima, Xiang Li, Yoshiro Mitsukami, Yuki Yokoyama, Ung-il Chung, Mitsuhiro Shibayama, and Takamasa Sakai. 2021. "Effect of Nonlinear Elasticity on the Swelling Behaviors of Highly Swollen Polyelectrolyte Gels" Gels 7, no. 1: 25. https://doi.org/10.3390/gels7010025
APA StyleTang, J., Katashima, T., Li, X., Mitsukami, Y., Yokoyama, Y., Chung, U. -i., Shibayama, M., & Sakai, T. (2021). Effect of Nonlinear Elasticity on the Swelling Behaviors of Highly Swollen Polyelectrolyte Gels. Gels, 7(1), 25. https://doi.org/10.3390/gels7010025