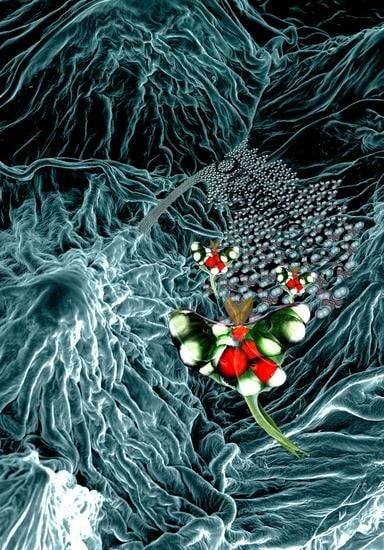
Supramolecular Fractal Growth of Self-Assembled Fibrillar Networks
Abstract
:1. Introduction
2. Results and Discussion
3. Conclusions
4. Materials and Methods
4.1. Sample Preparation
4.2. Microscopy and Image Analysis
4.3. Small Deformation Rheology
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| SAFiNs | Self-assembled fibrillar networks |
| DBS | 1,3:2,4-Dibenzylidene sorbitol |
| PEG | Polyethylene glycol |
| Df | Fractal dimension |
| Db | Box-counting fractal dimension |
| d | Euclidean dimension |
| LMOGs | Low-molecular-mass organogelators |
| PPG | Polypropylene glycol |
| z | Branching rate |
| ζ | Segment length |
| l | Distance within the Euclidian embedding space |
| Nε | The count of foreground, white pixels |
| ε | Box size |
| PT | Percentile Thresholded |
| CWB | Corrected White Balance |
| BPCA | Ballistic particle–cluster aggregation |
| g | number of fractal shell in Caylee tree |
| R | Distance from the origin to the gth tree shell |
| M | Mass of the fractal |
| ξ | Chemical distance |
| Dξ | Fractal dimension in chemical space |
| Xcr | Crystallinity |
| t | Time |
| D | Bulk crystal growth dimension |
| k | Rate constant |
| φ | Crystal volume fraction |
| ηsp | Specific viscosity |
| F | Shape factor |
| η* | Complex viscosity of the system |
| ηo | Initial solvent viscosity |
References
- von Koch, H. Sur une courbe continue sans tangente, obtenue par une construction géométrique élémentaire. Ark. Mat. Astron. Fys. 1904, 1, 681–702. [Google Scholar]
- Sierpiński, W. Sur une courbe cantorienne qui contient une image biunivoquet et continue detoute courbe don nee. Comptes Rendus Acad. Sci. 1916, 162, 629–632. [Google Scholar]
- Liu, X.Y.; Sawant, P.D. Determination of the fractal characteristic of nanofiber-network formation in supramolecular Materials. ChemPhysChem 2002, 4, 374–377. [Google Scholar] [CrossRef]
- Tahavvor, A.R. Modeling of frost crystal growth over a flat plate using artificial neural networks and fractal geometries. Heat Mass Transf. 2017, 53, 813–823. [Google Scholar] [CrossRef]
- Co, E.D.; Marangoni, A.G. Colloidal networks of fat crystals. Adv. Colloid Interface Sci. 2019, 273, 102035. [Google Scholar] [CrossRef]
- Shin, S.; Gu, M.-L.; Yu, C.-Y.; Jeon, J.; Lee, E.; Choi, T.-L. Polymer self-assembly into unique fractal nanostructures in solution by a one-shot synthetic procedure. J. Am. Chem. Soc. 2018, 140, 475–482. [Google Scholar] [CrossRef] [PubMed]
- Matheson, A.B.; Koutsos, V.; Dalkas, G.; Euston, S.; Clegg, P. Microstructure of β-sitosterol:γ-oryzanol edible organogels. Langmuir 2017, 33, 4537–4542. [Google Scholar] [CrossRef]
- Lupi, F.R.; Mancina, V.; Baldino, N.; Parisi, O.I.; Scrivano, L.; Gabriele, D. Effect of the monostearate/monopalmitate ratio on the oral release of active agents from monoacylglycerol organogels. Food Funct. 2018, 9, 3278–3290. [Google Scholar] [CrossRef]
- Shaikh, H.; Rho, J.Y.; Macdougall, L.J.; Gurnani, P.; Lunn, A.M.; Yang, J.; Huband, S.; Mansfield, E.D.H.; Peltier, R.; Perrier, S. Hydrogel and organogel formation by hierarchical self-assembly of cyclic peptides nanotubes. Chem.–A Eur. J. 2018, 24, 19066–19074. [Google Scholar] [CrossRef]
- Chen, J.-Y.; Komeily-Nia, Z.; Fan, L.-P.; Li, Z.-Y.; Yuan, B.; Tang, B.; Li, J.-L. Manipulating the fractal fiber network of a molecular gel with surfactants. J. Colloid Interface Sci. 2018, 526, 356–365. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. Fractals and the Geomenty of Nature; W.H. Freeman: New York, NY, USA, 1983; Volume 173. [Google Scholar]
- Li, J.-L.; Yuan, B.; Liu, X.-Y.; Wang, X.-G.; Wang, R.-Y. Kinetically controlled homogenization and transformation of crystalline fiber netwroks in supramolecular materials. Cryst. Growth Des. 2011, 11, 3227–3234. [Google Scholar] [CrossRef]
- Rogers, M.A.; Marangoni, A.G. Non-isothermal nucleation and crystallization of 12-hydroxystearic acid in vegetable oils. Cryst. Growth Des. 2008, 8, 4596–4601. [Google Scholar] [CrossRef]
- Löfman, M.; Lahtinen, M.; Pettersson, M.; Sievänen, E. Insights into localized manipulation of organogel-related microcrystalline spherulite formation. Colloids Surf. A Physicochem. Eng. Asp. 2015, 474, 18–28. [Google Scholar] [CrossRef]
- Boncheva, M.G.M.W. Making things by self assembly. MRS Bull. 2005, 30, 736–742. [Google Scholar] [CrossRef] [Green Version]
- Yan, N.; Xu, Z.; Diehn, K.K.; Raghavan, S.R.; Fang, Y.; Weiss, R. How do liquid mixtures solubilize insoluble gelators? Self-assembly properties of pyrenyl-linker-glucono gelators in tetrahydrofuran-water mixtures. JACS 2013, 135, 8989–8999. [Google Scholar] [CrossRef] [PubMed]
- Ajayaghosh, A.; Praveen, V.K. π-Organogels of self-assembled p-phenylenevinylenes: Soft materials with distinct size, shape, and functions. Acc. Chem. Res. 2007, 40, 644–656. [Google Scholar] [CrossRef]
- Farbi, D.; Guan, J.; Cesaro, A. Crystallisation and melting behaviour of poly (3-hydroxybutyrate) in dilute solution: Towards an understanding of physical gels. Thermochim. Acta 1998, 321, 3–16. [Google Scholar]
- Becerril, J.; Escuder, B.; Miravet, J.F.; Gavara, R.; Luis, S.V. Understanding the expression of molecular chirality in the self-assembly of a peptidomimetic organogelator. Eur. J. Org. Chem. 2005, 2005, 481–485. [Google Scholar] [CrossRef]
- Brizard, A.; Oda, R.; Huc, I. Chirality effects in self-assembled fibrillar networks. Top. Is Curr. Chem. 2005, 256, 167–215. [Google Scholar]
- Edwards, W.; Smith, K.D. Chiral assembly preferences and directing effects in supramolecular two-component organogels. Gels 2018, 4, 31. [Google Scholar] [CrossRef] [Green Version]
- Grahame, D.A.S.; Olauson, C.; Lam, R.S.H.; Pedersen, T.; Borondics, F.; Abraham, S.; Weiss, R.G.; Rogers, M.A. Influence of chirality on the modes of self-assembly of 12-hydroxystearic acid in molecular gels of mineral oil. Soft Matter 2011, 7, 7359–7365. [Google Scholar] [CrossRef]
- Ihara, H.; Sakurai, T.; Yamada, T.; Hashimoto, T.; Takafuji, M.; Sagawa, T.; Hachisako, H. Chirality control of self-assembling organogels from a lipophilic l-glutamide derivative with metal chlorides. Langmuir 2002, 18, 7120–7123. [Google Scholar] [CrossRef]
- Marchesan, S.; Easton, C.D.; Styan, K.E.; Waddington, L.J.; Kushkaki, F.; Goodall, L.; McLean, K.M.; Forsythe, J.S.; Hartley, P.G. Chirality effects at each amino acid position on tripeptide self-assembly into hydrogel biomaterials. Nanoscale 2014, 6, 5172–5180. [Google Scholar] [CrossRef] [PubMed]
- Peng, J.; Liu, K.; Liu, J.; Zhang, Q.; Feng, X.; Fang, Y. New dicholesteryl-based gelators: Chirality and spacer length effect. Langmuir 2008, 24, 2992–3000. [Google Scholar] [CrossRef] [PubMed]
- Abraham, S.; Lan, Y.; Lam, R.S.H.; Grahame, D.A.S.; Kim, J.J.H.; Weiss, R.G.; Rogers, M.A. Influence of positional isomers on the macroscale and nanoscale architectures of aggregates of racemic hydroxyoctadecanoic acids in their molecular gel, dispersion, and solid states. Langmuir 2012, 28, 4955–4964. [Google Scholar] [CrossRef] [PubMed]
- Mukhopadhyay, P.; Iwashita, Y.; Shirakawa, M.; Kawano, S.-I.; Fujita, N.; Shinkai, S. Spontaneous colorimetric sensing of the positional isomers of dihydroxynaphthalene in a 1D organogel matrix. Angew. Chem. Int. Ed. 2006, 45, 1592–1595. [Google Scholar] [CrossRef]
- Pal, A.; Abraham, S.; Rogers, M.A.; Dey, J.; Weiss, R.G. Comparison of dipolar, H-bonding, and dispersive interactions on gelation efficiency of positional isomers of keto and hydroxy substituted octadecanoic acids. Langmuir 2013, 29, 6467–6475. [Google Scholar] [CrossRef]
- Rogers, M.A.; Abraham, S.; Bodondics, F.; Weiss, R.G. Positional isomers of hydroxyoctadecanoic acid molecular gels and dispersions influence crystallization kinetics and activation energies. Cryst. Growth Des. 2012, 12, 5497–5504. [Google Scholar] [CrossRef]
- Abdallah, D.J.; Lu, L.; Weiss, R.G. Thermoreversible organogels from alkane gelators with one hetero-atom. Chem. Mater. 1999, 11, 2907–2911. [Google Scholar] [CrossRef]
- George, M.; Tan, G.; John, V.T.; Weiss, R.G. Urea and thiourea derivatives as low molecular-mass organogelators. Chem.–A Eur. J. 2005, 11, 3243–3254. [Google Scholar] [CrossRef]
- George, M.; Weiss, R.G. Primary alkyl amines as latent gelators and their organogel adducts with neutral triatomic molecules. Langmuir 2003, 19, 1017–1025. [Google Scholar] [CrossRef]
- Singh, A.; Auzanneau, F.-I.; Corradini, M.G.; Grover, G.; Weiss, R.G.; Rogers, M.A. Molecular nuances governing the self-assembly of 1,3:2,4-dibenzylidene-d-sorbitol. Langmuir 2017, 33, 10907–10916. [Google Scholar] [CrossRef]
- Rogers, M.A.; Weiss, R.G. Systematic modifications of alkane-based molecular gelators and the consequences to the structures and properties of their gels. New J. Chem. 2015, 39, 785–799. [Google Scholar] [CrossRef]
- He, Y.; Zhao, H.; Yao, M.; Weiss, R.G. Complex new materials from simple chemistry: Combining an amino-substituted polysiloxane and carboxylic acids. J. Polym. Sci. Part A Polym. Chem. 2017, 2017, 3851–3861. [Google Scholar] [CrossRef]
- Yan, N.; Xu, Z.; Diehn, K.K.; Raghavan, S.R.; Fang, Y.; Weiss, R.G. Pyrenyl-linker-glucono gelators. Correlations of gel properties with gelator structures and characterization of solvent effects. Langmuir 2013, 29, 793–805. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; de Kruijff, R.M.; Lovrak, M.; Guo, X.; Eelkema, R.; van Esch, J.H. Access to metastable gel states using seeded self-assembly of low molecular weight gelators. Angew. Chem. Int. Ed. 2019, 58, 3800–3803. [Google Scholar] [CrossRef] [PubMed]
- Okesola, B.O.; Vieira, V.M.P.; Cornwell, D.J.; Whitelaw, N.K.; Smith, D.K. 1,3:2,4-dibenzylidene-d-sorbitol (DBS) and its derivatives–efficient, versatile and industrially-relevant low-molecular-weight gelators with over 100 years of history and a bright future. Soft Matter 2015, 11, 4768–4787. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.; Fei, J.; Wang, A.; Cui, W.; Zhu, P.; Li, J. Transformation of dipeptide-based organogels into chiral crystals by cryogenic treatment. Angew. Chem. Int. Ed. 2017, 56, 2660–2663. [Google Scholar] [CrossRef] [PubMed]
- Diehn, K.K.; Oh, H.; Hashemipour, R.; Weiss, R.G.; Raghavan, S.R. Insights into organogelation and its kinetics from hansen solubility parameters. Toward a priori predictions of molecular gelation. Soft Matter 2014, 10, 2632–2640. [Google Scholar] [CrossRef] [PubMed]
- Gao, J.; Wu, S.; Rogers, M.A. Harnessing hansen solubility parameters to predict organogel formation. J. Mater. Chem. 2012, 22, 12651. [Google Scholar] [CrossRef]
- Lan, Y.; Corradini, M.G.; Liu, X.; May, T.E.; Borondics, F.; Weiss, R.G.; Rogers, M.A. Comparing and correlating solubility parameters governing the self-assembly of molecular gels using 1,3:2,4-dibenzylidene sorbitol as the gelator. Langmuir 2014, 30, 14128–14142. [Google Scholar] [CrossRef] [PubMed]
- van Esch, J.H. We can design molecular, but do we understand them? Langmuir 2008, 25, 8392–8394. [Google Scholar] [CrossRef]
- van Esch, J.; Feringa, B.L. New functional materials based on self-assembling organogels: From serendipity towards design. Angew. Chem. Int. Ed. 2000, 39, 2263–2266. [Google Scholar] [CrossRef]
- Liu, S.; Yu, W.; Zhou, C. Solvents effects in the formation and viscoelasticity of DBS organogels. Soft Matter 2013, 2013, 864–874. [Google Scholar] [CrossRef]
- Lai, W.-C.; Wu, C.-H. Studies on the self-assembly of neat DBS and DBS/PPG organogels. J. Appl. Polym. Sci. 2010, 115, 1113–1119. [Google Scholar] [CrossRef]
- Wilder, E.A.; Hall, C.K.; Khan, S.A.; Spontak, R.J. Effects of composition and matrix polarity on network development in organogels of poly(ethylene glycol) and dibenzylidene sorbitol. Langmuir 2003, 19, 6004–6013. [Google Scholar] [CrossRef]
- Mercurio, D.J.; Spontak, R.J. Morphological characteristics of 1,3:2,4-dibenzylidene sorbitol/poly(propylene glycol) organogels. J. Phys. Chem. 2001, 105, 2091–2098. [Google Scholar] [CrossRef]
- Weiss, R.G.; Terech, P. Molecular Gels. Materials with Self-Assembled Fibrillar Networks; Springer: Dordrecht, The Netherlands, 2006. [Google Scholar]
- Lan, Y.; Corradini, M.G.; Weiss, R.G.; Raghavanc, S.R.; Rogers, M.A. To gel or not to gel: Correlating molecular gelation with solvent parameters. Chem. Soc. Rev. 2015. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.Y.; Sawant, P.D. Formation kinetics of fractal nanofiber networks in organogels. Appl. Phys. Lett. 2001, 19, 3518–3520. [Google Scholar] [CrossRef]
- Liu, X.-Y.; Sawant, P.D.; Tan, W.B.; Noor, I.B.M.; Pramesti, C.; Chem, B.H. Creating new supramolecular materials by architecture of three-dimensional nanocrystal fiber networks. JACS 2002, 124, 15055–15063. [Google Scholar] [CrossRef]
- Avrami, M. Kinetics of phase change. III granulation, phase change, and microstructure. J. Chem. Phys. 1941, 9, 177–184. [Google Scholar] [CrossRef]
- Avrami, M. Kinetics of phase change. II transformation-time relations for random distribution of nuclei. J. Chem. Phys. 1940, 8, 212–226. [Google Scholar] [CrossRef]
- Avrami, M. Kinetics of phase change. I general theory. J. Chem. Phys. 1939, 7, 1103–1112. [Google Scholar] [CrossRef]
- Vicsek, T. Fractal Growth Phenomena; World Scientific: Singapore, 1992; p. 528. [Google Scholar]
- Langer, J.S. Dendrites, viscous fingers, and the theory of pattern formation. Science 1989, 243, 1150–1156. [Google Scholar] [CrossRef] [PubMed]
- Ben-Jacob, E.; Garik, P. The formation of patterns in non-equilibrium growth. Nature 1990, 343, 523–530. [Google Scholar] [CrossRef] [Green Version]
- Terech, P.; Pasquier, D.; Bordas, V.; Rossat, C. Rheological properties and structural correlations in molecular gels. Langmuir 2000, 16, 4485–4494. [Google Scholar] [CrossRef]
- Vandewalle, N.; Ausloos, M. Construction and properties of fractal trees with tunable dimension: The interplay of geometry and physics. Phys. Rev. E 1997, 55, 94. [Google Scholar] [CrossRef]
- Havlin, S.; Nossal, R.; Trus, B. Cluster growth model for treelike structures. Phys. Rev. A 1985, 32, 3829. [Google Scholar] [CrossRef]
- Gisler, T.; Ball, R.C.; Weitz, D.A. Strain hardening of fractal colloidal gels. Phys. Rev. Lett. 1999, 82, 1064–1067. [Google Scholar] [CrossRef]
- Rafe, A.; Razavi, S.M.A. Scaling law, fractal analysis and rheological characteristics of physical gels cross-linked with sodium trimetaphosphate. Food Hydrocoll. 2017, 62, 58–65. [Google Scholar] [CrossRef]
- Lazzari, S.; Nicoud, L.; Jaquet, B.; Lattuada, M.; Morbidelli, M. Fractal-like structures in colloid science. Adv. Colloid Interface Sci. 2016, 235, 1–13. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yu, R.; Lin, N.; Yu, W.; Liu, X.Y. Crystal networks in supramolecular gels: Formation kinetics and mesoscopic engineering principles. CrystEngComm 2015, 17, 7986–8010. [Google Scholar] [CrossRef]
- Lam, R.; Rogers, M.A.; Marangoni, A.G. Thermo-mechanical method for the determination of the fractal dimension of fat crystal networks. J. Therm. Anal. Calorim. 2009, 98, 7–12. [Google Scholar] [CrossRef]
- Liu, X.Y.; Sawant, P.D. Mechanism of the formation of self-organized microstructures in soft functional materials. Adv. Mater. 2002, 14, 421–426. [Google Scholar] [CrossRef]
- Liu, X.Y.; van den Berg, B.E.P.G.; Zauner, A.R.A.; Bennema, P. Can a foreign particle cause surface instability? J. Phys. Chem. B 2000, 104, 11942–11949. [Google Scholar] [CrossRef]
- Liu, X.Y.; Maiwa, K.; Tsukamoto, K. Heterogeneous two-dimensional nucleation and growth kinetics. J. Chem. Phys. 1997, 106, 1870–1879. [Google Scholar] [CrossRef]
- Havlin, S.; Trus, B.; Weiss, G.H.; Ben-Avraham, D. The chemical distance distribution in percolation clusters. J. Phys. A Math. Gen. 1985, 18, L247. [Google Scholar] [CrossRef] [Green Version]
- Hiemenz, P.C.; Rajagopalan, R. Principles of Colloid and Surface Chemistry; CRC Press: Boca Raton, FL, USA, 1997. [Google Scholar]
- Danker, G.; Misbah, C. Rheology of a dilute suspension of vesicles. Phys. Rev. Lett. 2007, 98, 088104. [Google Scholar] [CrossRef] [PubMed]
- Einstein, A. Eine neue Bestimmung der Moleküldimensionen. Ann. Phys. 1906, 324, 289–306. [Google Scholar] [CrossRef] [Green Version]
- Einstein, A. Berichtigung zu meiner Arbeit: “Eine neue Bestimmung der Moleküldimensionen”. Ann. Phys. 1911, 339, 591–592. [Google Scholar] [CrossRef] [Green Version]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nasr, P.; Leung, H.; Auzanneau, F.-I.; Rogers, M.A. Supramolecular Fractal Growth of Self-Assembled Fibrillar Networks. Gels 2021, 7, 46. https://doi.org/10.3390/gels7020046
Nasr P, Leung H, Auzanneau F-I, Rogers MA. Supramolecular Fractal Growth of Self-Assembled Fibrillar Networks. Gels. 2021; 7(2):46. https://doi.org/10.3390/gels7020046
Chicago/Turabian StyleNasr, Pedram, Hannah Leung, France-Isabelle Auzanneau, and Michael A. Rogers. 2021. "Supramolecular Fractal Growth of Self-Assembled Fibrillar Networks" Gels 7, no. 2: 46. https://doi.org/10.3390/gels7020046
APA StyleNasr, P., Leung, H., Auzanneau, F. -I., & Rogers, M. A. (2021). Supramolecular Fractal Growth of Self-Assembled Fibrillar Networks. Gels, 7(2), 46. https://doi.org/10.3390/gels7020046