Dynamic Analysis and Design Optimization of a Drag-Based Vibratory Swimmer
Abstract
:1. Introduction
2. Materials and Methods
2.1. Averaging of Piecewise-Smooth Systems with High Frequency Inputs
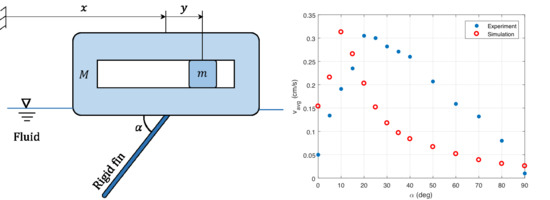
2.2. The Vibratory Swimmer: Dynamic Analysis and Averaging
2.3. Optimization of a Class of Vibratory Systems
2.4. Numerical Simulation of Hydrodynamic Forces Acting on a Rigid, Inclined Fin
3. Results
3.1. The Vibratory Swimmer with an Asymmetric Added Mass
3.2. Experiments
4. Discussion
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Proof of Theorem 1
References
- Meerkov, S.M. Principle of Vibrational Control: Theory and Applications. IEEE Trans. Autom. Control 1980, AC-25, 755–762. [Google Scholar] [CrossRef]
- Bellman, R.E.; Bentsman, J.; Meerkov, S.M. Vibrational Control of Nonlinear Systems: Vibrational Stabilizability. IEEE Trans. Autom.Control 1986, AC-31, 710–716. [Google Scholar] [CrossRef]
- Bellman, R.E.; Bentsman, J.; Meerkov, S.M. Vibrational Control of Nonlinear Systems: Vibrational Controllability and Transient Behavior. IEEE Trans. Autom. Control 1986, AC-31, 717–724. [Google Scholar] [CrossRef]
- Di Bernardo, M.; Budd, C.J.; Champneys, A.R.; Kowalczyk, P. Piecewise-smooth Dynamical Systems; Applied Mathematical Sciences; Springer: London, UK, 2008. [Google Scholar]
- Khalil, H.K. Nonlinear Systems; Prentice-Hall, Inc.: Upper Saddle River, NJ, USA, 1996. [Google Scholar]
- Guckenheimer, J.; Holmes, P. Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields; Applied Mathematical Sciences; Springer: New York, NY, USA, 1983. [Google Scholar]
- Sanders, J.A.; Verhulst, F. Averaging Methods in Nonlinear Dynamical Systems; Applied Mathematical Sciences; Springer: New York, NY, USA, 1985. [Google Scholar]
- Bullo, F.; Lewis, A.D. Geometric Control of Mechanical Systems; Texts in Applied Mathematics; Springer: New York, NY, USA, 2005. [Google Scholar]
- Blekhman, I.I. Vibrational Mechanics; World Scientific Publishing Co.: Singapore, 2000. [Google Scholar]
- Thomsen, J.J. Vibrations and Stability; Springer: Berlin, Germay, 2003. [Google Scholar]
- Fidlin, A. Nonlinear Oscillations in Mechanical Engineering; Springer: Heidelberg, Germay, 2006. [Google Scholar]
- Vela, P.A.; Burdick, J.W. Control of underactuated mechanical systems with drift using higher-order averaging theory. In Proceedings of the IEEE Conference on Decision and Control, Maui, HI, USA, 9–12 December 2003; pp. 3111–3117. [Google Scholar]
- Vela, P.A.; Burdick, J.W. A general Averaging Theory via Series Expansions. Am. Control Conf. 2003, 1530–1535. [Google Scholar] [CrossRef] [Green Version]
- Vela, P.A.; Morgansen, K.A.; Burdick, J.W. Underwater locomotion from oscillatory shape deformations. In Proceedings of the IEEE Conference on Decision and Control, Las Vegas, NV, USA, 10–13 December 2002; pp. 2074–2080. [Google Scholar]
- Morgansen, K.A.; Triplett, B.I.; Klein, D.J. Geometric Methods for Modeling and Control of Free-Swimming Fin-Actuated Underwater Vehicles. IEEE Trans. Robot. 2007, 23, 1184–1199. [Google Scholar] [CrossRef]
- Wood, R.J. The First Takeoff of a Biologically Inspired At-Scale Robotic Insect. IEEE Trans. Robot. 2008, 24, 341–347. [Google Scholar] [CrossRef]
- Abbott, J.J.; Peyer, K.E.; Lagomarsino, M.C.; Zhang, L.; Dong, L.; Kaliakatsos, I.K.; Nelson, B.J. How Should Microrobots Swim? Int. J. Robot. Res. 2009, 28, 1434–1447. [Google Scholar] [CrossRef]
- Kelly, S.D.; Murray, R.M. Modeling Efficient Pisciform Swimming for Control. Int. J. Robust Nonlinear Control 2000, 10, 217–241. [Google Scholar] [CrossRef]
- Tahmasian, S.; Allen, D.W.; Woolsey, C.A. On Averaging and Input Optimization of High-Frequency Mechanical Control Systems. J. Vib. Control 2018, 24, 937–955. [Google Scholar] [CrossRef]
- Taha, H.E.; Hajj, M.R.; Nayfeh, A.H. Wing Kinematics Optimization for Hovering Micro Air Vehicles Using Calculus of Variation. J. Aircr. 2013, 50, 610–614. [Google Scholar] [CrossRef]
- Huang, H.; Chao, Q.; Sakar, M.S.; Nelson, B.J. Optimization of Tail Geometry for the Propulsion of Soft Microrobots. IEEE Robot. Autom. Lett. 2017, 2, 727–732. [Google Scholar] [CrossRef]
- Taha, H.E.; Hajj, M.R.; Nayfeh, A.H. Flight dynamics and control of flapping-wing MAVs: A review. Nonlinear Dyn. 2012, 70, 907–939. [Google Scholar] [CrossRef]
- Gerdes, J.W.; Gupta, S.K.; Wilkerson, S.A. A Review of Bird-Inspired Flapping Wing Miniature Air Vehicle Designs. J. Mech. Robot. 2012, 4, 021003. [Google Scholar] [CrossRef] [Green Version]
- Roper, D.T.; Sharma, S.; Sutton, R.; Culverhouse, P. A review of Developments Towards Biologically Inspired Propulsion Systems for Autonomous Underwater Vehicles. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2011, 225, 77–96. [Google Scholar] [CrossRef]
- Diller, E.; Sitti, M. Micro-Scale Mobile Robotics. Found. Trends Robot. 2013, 2, 143–259. [Google Scholar] [CrossRef]
- Ehlers, K.M.; Koiller, J. Micro-swimming Without Flagella: Propulsion by Internal Structures. Regul. Chaotic Dyn. 2011, 16, 623–652. [Google Scholar] [CrossRef]
- Childress, S.; Spagnolie, S.E.; Tokieda, T. A Bug on a Raft: Recoil Locomotion in a Viscous Fluid. J. Fluid Mech. 2011, 669, 527–556. [Google Scholar] [CrossRef] [Green Version]
- Quillen, A.C.; Askari, H.; Kelley, D.H.; Friedmann, T.; Oakes, P.W. A Coin Vibrational Motor Swimming at Low Reynolds Number. Regul. Chaotic Dyn. 2016, 21, 902–917. [Google Scholar] [CrossRef] [Green Version]
- Vetchanin, E.V.; Mamaev, I.S.; Tenenev, V.A. The Self-Propulsion of a Body with Moving Internal Masses in a Viscous Fluid. Regul. Chaotic Dyn. 2013, 18, 100–117. [Google Scholar] [CrossRef]
- Tallapragada, P.; Kelly, S.D. Self-Propulsion of Free Solid Bodies with Internal Rotors via Localized Singular Vortex Shedding in Planar Ideal Fluids. Eur. Phys. J. 2015, 224, 3185–3197. [Google Scholar] [CrossRef]
- Chernous’ko, F.L. The Optimal Periodic Motions of a Two-Mass System in a Resistant Medium. J. Appl. Math. Mech. 2008, 72, 116–125. [Google Scholar] [CrossRef]
- Bolotnik, N.N.; Figurina, T.Y.; Chernous’ko, F.L. Optimal Control of the Rectilinear Motion of a Two-Body System in a Resistive Medium. J. Appl. Math. Mech. 2012, 76, 1–14. [Google Scholar] [CrossRef]
- Chernousko, F.L.; Bolotnik, N.N.; Figurina, T.Y. Optimal Control of Vibrationally Excited Locomotion Systems. Regul. Chaotic Dyn. 2013, 18, 85–99. [Google Scholar] [CrossRef]
- Burns, J.A. Introduction to the Calculus of Variations and Control with Modern Applications; Applied Mathematics and Nonlinear Science Series; Chapman and Hall/CRC: Boca Raton, FL, USA, 2014. [Google Scholar]











© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tahmasian, S.; Jafaryzad, A.; Bulzoni, N.L.; Staples, A.E. Dynamic Analysis and Design Optimization of a Drag-Based Vibratory Swimmer. Fluids 2020, 5, 38. https://doi.org/10.3390/fluids5010038
Tahmasian S, Jafaryzad A, Bulzoni NL, Staples AE. Dynamic Analysis and Design Optimization of a Drag-Based Vibratory Swimmer. Fluids. 2020; 5(1):38. https://doi.org/10.3390/fluids5010038
Chicago/Turabian StyleTahmasian, Sevak, Arsam Jafaryzad, Nicolas L. Bulzoni, and Anne E. Staples. 2020. "Dynamic Analysis and Design Optimization of a Drag-Based Vibratory Swimmer" Fluids 5, no. 1: 38. https://doi.org/10.3390/fluids5010038
APA StyleTahmasian, S., Jafaryzad, A., Bulzoni, N. L., & Staples, A. E. (2020). Dynamic Analysis and Design Optimization of a Drag-Based Vibratory Swimmer. Fluids, 5(1), 38. https://doi.org/10.3390/fluids5010038