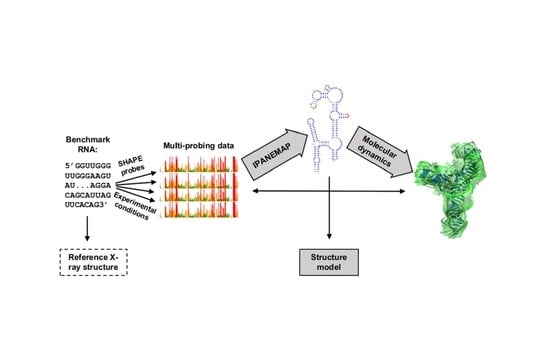
Progress toward SHAPE Constrained Computational Prediction of Tertiary Interactions in RNA Structure
Abstract
:1. Introduction
2. Material and Methods
2.1. RNA Preparation
2.2. Melting Curves
2.3. SHAPE Probing
2.4. Comparison of Two Probing Profiles
2.5. Nucleotide Clustering
2.6. All-Atom Molecular Dynamics Simulations
2.7. Definition of the Parameters
3. Results
3.1. Probing DiLCrz Structure in Presence or Absence of Mg2+ Ions
3.2. Structure Characterisation by Thermal Denaturation
3.3. Molecular Dynamics Analysis
3.4. Using Probing Data for Secondary Structure Modeling
4. Discussion
4.1. DiLCrz Hierarchical Thermal Unfolding
4.2. Molecular Dynamics Shed Light on Unexpected Reactivity
4.3. Informing Prediction Software to Integrate Pseudoknots and Other Tertiary Motifs
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Availability
References
- Kehr, J.; Kragler, F. Long distance RNA movement. New Phytol. 2018, 218, 29–40. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Flynn, R.A.; Pedram, K.; Malaker, S.A.; Batista, P.J.; Smith, B.A.H.; Johnson, A.G.; George, B.M.; Majzoub, K.; Villalta, P.W.; Carette, J.E.; et al. Small RNAs are modified with N-glycans and displayed on the surface of living cells. Cell 2021, 184, 3109–3124.e22. [Google Scholar] [CrossRef] [PubMed]
- Langdon, E.M.; Qiu, Y.; Niaki, A.G.; McLaughlin, G.A.; Weidmann, C.A.; Gerbich, T.M.; Smith, J.A.; Crutchley, J.M.; Termini, C.M.; Weeks, K.M.; et al. mRNA structure determines specificity of a polyQ-driven phase separation. Science 2018, 360, 922–927. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Iserman, C.; Roden, C.A.; Boerneke, M.A.; Sealfon, R.S.G.; McLaughlin, G.A.; Jungreis, I.; Fritch, E.J.; Hou, Y.J.; Ekena, J.; Weidmann, C.A.; et al. Genomic RNA Elements Drive Phase Separation of the SARS-CoV-2 Nucleocapsid. Mol. Cell 2020, 80, 1078–1091.e6. [Google Scholar] [CrossRef]
- Beaudoin, J.-D.; Novoa, E.M.; Vejnar, C.E.; Yartseva, V.; Takacs, C.M.; Kellis, M.; Giraldez, A.J. Analyses of mRNA structure dynamics identify embryonic gene regulatory programs. Nat. Struct. Mol. Biol. 2018, 25, 677–686. [Google Scholar] [CrossRef]
- Mustoe, A.M.; Busan, S.; Rice, G.M.; Hajdin, C.E.; Peterson, B.K.; Ruda, V.M.; Kubica, N.; Nutiu, R.; Baryza, J.L.; Weeks, K.M. Pervasive Regulatory Functions of mRNA Structure Revealed by High-Resolution SHAPE Probing. Cell 2018, 173, 181–195.e18. [Google Scholar] [CrossRef] [Green Version]
- Watts, J.M.; Dang, K.K.; Gorelick, R.J.; Leonard, C.W.; Bess, J.W., Jr.; Swanstrom, R.; Burch, C.L.; Weeks, K.M. Architecture and secondary structure of an entire HIV-1 RNA genome. Nature 2009, 460, 711. [Google Scholar] [CrossRef] [Green Version]
- Dethoff, E.A.; Boerneke, M.A.; Gokhale, N.S.; Muhire, B.M.; Martin, D.P.; Sacco, M.T.; McFadden, M.J.; Weinstein, J.B.; Messer, W.B.; Horner, S.M.; et al. Pervasive tertiary structure in the dengue virus RNA genome. Proc. Natl. Acad. Sci. USA 2018, 115, 11513–11518. [Google Scholar] [CrossRef] [Green Version]
- Koculi, E.; Cho, S.S.; Desai, R.; Thirumalai, D.; Woodson, S.A. Folding path of P5abc RNA involves direct coupling of secondary and tertiary structures. Nucleic Acids Res. 2012, 40, 8011–8020. [Google Scholar] [CrossRef] [Green Version]
- Deigan, K.E.; Li, T.W.; Mathews, D.H.; Weeks, K.M. Accurate SHAPE-directed RNA structure determination. Proc. Natl. Acad. Sci. USA 2009, 106, 97–102. [Google Scholar] [CrossRef] [Green Version]
- Washietl, S.; Hofacker, I.L.; Stadler, P.F.; Kellis, M. RNA folding with soft constraints: Reconciliation of probing data and thermodynamic secondary structure prediction. Nucleic Acids Res. 2012, 40, 4261–4272. [Google Scholar] [CrossRef] [Green Version]
- Brunel, C.; Romby, P. Probing RNA structure and RNA-ligand complexes with chemical probes. In Methods in Enzymology; Elsevier BV: Amsterdam, The Netherlands, 2000; Volume 318, pp. 3–21. [Google Scholar]
- McGinnis, J.L.; Dunkle, J.A.; Cate, J.H.D.; Weeks, K.M. The Mechanisms of RNA SHAPE Chemistry. J. Am. Chem. Soc. 2012, 134, 6617–6624. [Google Scholar] [CrossRef] [Green Version]
- Frezza, E.; Courban, A.; Allouche, D.; Sargueil, B.; Pasquali, S. The interplay between molecular flexibility and RNA chemical probing reactivities analyzed at the nucleotide level via an extensive molecular dynamics study. Methods 2019, 162–163, 108–127. [Google Scholar] [CrossRef]
- Pinamonti, G.; Bottaro, S.; Micheletti, C.; Bussi, G. Elastic network models for RNA: A comparative assessment with molecular dynamics and SHAPE experiments. Nucleic Acids Res. 2015, 43, 7260–7269. [Google Scholar] [CrossRef] [Green Version]
- Mlýnský, V.; Bussi, G. Molecular dynamics simulations reveal an interplay between SHAPE reagent binding and RNA flexibility. J. Phys. Chem. Lett. 2018, 9, 313–318. [Google Scholar] [CrossRef] [Green Version]
- Zubradt, M.; Gupta, P.; Persad, S.; Lambowitz, A.M.; Weissman, J.S.; Rouskin, S. DMS-MaPseq for genome-wide or targeted RNA structure probing in vivo. Nat. Methods 2017, 14, 75–82. [Google Scholar]
- Lucks, J.B.; Mortimer, S.A.; Trapnell, C.; Luo, S.; Aviran, S.; Schroth, G.P.; Pachter, L.; Doudna, J.A.; Arkin, A.P. Multiplexed RNA structure characterization with selective 2′-hydroxyl acylation analyzed by primer extension sequencing (SHAPE-Seq). Proc. Natl. Acad. Sci. USA 2011, 108, 11063–11068. [Google Scholar] [CrossRef] [Green Version]
- Watters, K.E.; Yu, A.M.; Strobel, E.J.; Settle, A.H.; Lucks, J.B. Characterizing RNA structures in vitro and in vivo with selective 2′-hydroxyl acylation analyzed by primer extension sequencing (SHAPE-Seq). Methods 2016, 103, 34–48. [Google Scholar] [CrossRef]
- Flynn, R.A.; Zhang, Q.C.; Spitale, R.C.; Lee, B.; Mumbach, M.; Chang, H.Y. Transcriptome-wide interrogation of RNA secondary structure in living cells with icSHAPE. Nat. Protoc. 2016, 11, 273–290. [Google Scholar] [CrossRef] [Green Version]
- Ziv, O.; Gabryelska, M.M.; Lun, A.T.L.; Gebert, L.F.R.; Sheu-Gruttadauria, J.; Meredith, L.W.; Liu, Z.-Y.; Kwok, C.K.; Qin, C.-F.; MacRae, I.J.; et al. COMRADES determines in vivo RNA structures and interactions. Nat. Methods 2018, 15, 785–788. [Google Scholar] [CrossRef]
- Cheng, C.Y.; Chou, F.-C.; Das, R. Modeling Complex RNA Tertiary Folds with Rosetta. In Methods in Enzymology; Elsevier BV: Amsterdam, The Netherlands, 2015; Volume 553, pp. 35–64. [Google Scholar]
- Smola, M.J.; Rice, G.M.; Busan, S.; Siegfried, N.A.; Weeks, K.M. Selective 2′-hydroxyl acylation analyzed by primer extension and mutational profiling (SHAPE-MaP) for direct, versatile and accurate RNA structure analysis. Nat. Protoc. 2015, 10, 1643. [Google Scholar] [CrossRef]
- Leontis, N.B.; Stombaugh, J.; Westhof, E. The non-Watson-Crick base pairs and their associated isostericity matrices. Nucleic Acids Res. 2002, 30, 3497–3531. [Google Scholar] [CrossRef]
- Meyer, M.; Nielsen, H.; Olieric, V.; Roblin, P.; Johansen, S.D.; Westhof, E.; Masquida, B. Speciation of a group I intron into a lariat capping ribozyme. Proc. Natl. Acad. Sci. USA 2014, 111, 7659–7664. [Google Scholar] [CrossRef] [Green Version]
- Beckert, B.; Nielsen, H.; Einvik, C.; Johansen, S.D.; Westhof, E.; Masquida, B. Molecular modelling of the GIR1 branching ribozyme gives new insight into evolution of structurally related ribozymes. EMBO J. 2008, 27, 667–678. [Google Scholar] [CrossRef] [Green Version]
- Mathews, D.H. Using an RNA secondary structure partition function to determine confidence in base pairs predicted by free energy minimization. RNA 2004, 10, 1178–1190. [Google Scholar] [CrossRef] [Green Version]
- Mathews, D.H.; Burkard, M.E.; Freier, S.M.; Wyatt, J.R.; Turner, D.H. Predicting oligonucleotide affinity to nucleic acid targets. RNA 1999, 5, 1458–1469. [Google Scholar] [CrossRef] [Green Version]
- Turner, D.H.; Mathews, D.H. NNDB: The nearest neighbor parameter database for predicting stability of nucleic acid secondary structure. Nucleic Acids Res. 2009, 38, D280–D282. [Google Scholar] [CrossRef]
- Watkins, A.M.; Rangan, R.; Das, R. FARFAR2: Improved De Novo Rosetta Prediction of Complex Global RNA Folds. Struct. 2020, 28, 963–976.e6. [Google Scholar] [CrossRef]
- Watkins, A.M.; Geniesse, C.; Kladwang, W.; Zakrevsky, P.; Jaeger, L.; Das, R. Blind prediction of noncanonical RNA structure at atomic accuracy. Sci. Adv. 2018, 4, eaar5316. [Google Scholar] [CrossRef] [Green Version]
- Boniecki, M.J.; Lach, G.; Dawson, W.; Tomala, K.; Lukasz, P.; Soltysinski, T.; Rother, K.M.; Bujnicki, J.M. SimRNA: A coarse-grained method for RNA folding simulations and 3D structure prediction. Nucleic Acids Res. 2016, 44, e63. [Google Scholar] [CrossRef]
- Rybarczyk, A.; Szostak, N.; Antczak, M.; Zok, T.; Popenda, M.; Adamiak, R.; Blazewicz, J.; Szachniuk, M. New in silico approach to assessing RNA secondary structures with non-canonical base pairs. BMC Bioinform. 2015, 16, 276. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Antczak, M.; Zablocki, M.; Żok, T.; Rybarczyk, A.; Blazewicz, J.; Szachniuk, M. RNAvista: A webserver to assess RNA secondary structures with non-canonical base pairs. Bioinform. 2019, 35, 152–155. [Google Scholar] [CrossRef] [PubMed]
- Parisien, M.; Major, F. The MC-Fold and MC-Sym pipeline infers RNA structure from sequence data. Nat. Cell Biol. 2008, 452, 51–55. [Google Scholar] [CrossRef] [PubMed]
- Sloma, M.F.; Mathews, D.H. Base pair probability estimates improve the prediction accuracy of RNA non-canonical base pairs. PLoS Comput. Biol. 2017, 13, e1005827. [Google Scholar] [CrossRef] [Green Version]
- Siederdissen, C.H.Z.; Bernhart, S.H.; Stadler, P.F.; Hofacker, I. A folding algorithm for extended RNA secondary structures. Bioinform. 2011, 27, i129–i136. [Google Scholar] [CrossRef]
- Lyngsø, R.B.; Pedersen, C.N.S. RNA Pseudoknot Prediction in Energy-Based Models. J. Comput. Biol. 2000, 7, 409–427. [Google Scholar] [CrossRef]
- Sheikh, S.; Backofen, R.; Ponty, Y. Impact of the energy model on the complexity of RNA folding with pseudoknots. In Human-Computer Interaction—INTERACT 2011; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 2012; pp. 321–333. [Google Scholar]
- Jabbari, H.; Wark, I.; Montemagno, C. RNA secondary structure prediction with pseudoknots: Contribution of algorithm versus energy model. PLoS ONE 2018, 13, e0194583. [Google Scholar] [CrossRef] [Green Version]
- Rivas, E.; Eddy, S.R. A dynamic programming algorithm for RNA structure prediction including pseudoknots11Edited by I. Tinoco. J. Mol. Biol. 1999, 285, 2053–2068. [Google Scholar] [CrossRef]
- Jabbari, H.; Condon, A. A fast and robust iterative algorithm for prediction of RNA pseudoknotted secondary structures. BMC Bioinform. 2014, 15, 147. [Google Scholar] [CrossRef] [Green Version]
- Hajdin, C.E.; Bellaousov, S.; Huggins, W.; Leonard, C.W.; Mathews, D.H.; Weeks, K.M. Accurate SHAPE-directed RNA secondary structure modeling, including pseudoknots. Proc. Natl. Acad. Sci. USA 2013, 110, 5498–5503. [Google Scholar] [CrossRef] [Green Version]
- Xayaphoummine, A.; Bucher, T.; Thalmann, F.; Isambert, H. Prediction and statistics of pseudoknots in RNA structures using exactly clustered stochastic simulations. Proc. Natl. Acad. Sci. USA 2003, 100, 15310–15315. [Google Scholar] [CrossRef] [Green Version]
- Miao, Z.; Adamiak, R.W.; Blanchet, M.-F.; Boniecki, M.; Bujnicki, J.M.; Chen, S.-J.; Cheng, C.; Chojnowski, G.; Chou, F.-C.; Cordero, P.; et al. RNA-Puzzles Round II: Assessment of RNA structure prediction programs applied to three large RNA structures. RNA 2015, 21, 1066–1084. [Google Scholar] [CrossRef] [Green Version]
- Miao, Z.; Adamiak, R.W.; Antczak, M.; Batey, R.T.; Becka, A.J.; Biesiada, M.; Boniecki, M.J.; Bujnicki, J.M.; Chen, S.-J.; Cheng, C.Y.; et al. RNA-Puzzles Round III: 3D RNA structure prediction of five riboswitches and one ribozyme. RNA 2017, 23, 655–672. [Google Scholar] [CrossRef] [Green Version]
- Miao, Z.; Adamiak, R.W.; Antczak, M.; Boniecki, M.J.; Bujnicki, J.; Chen, S.-J.; Cheng, C.Y.; Cheng, Y.; Chou, F.-C.; Das, R.; et al. RNA-Puzzles Round IV: 3D structure predictions of four ribozymes and two aptamers. RNA 2020, 26, 982–995. [Google Scholar] [CrossRef]
- Deforges, J.; Chamond, N.; Sargueil, B. Structural investigation of HIV-1 genomic RNA dimerization process reveals a role for the Major Splice-site Donor stem loop. Biochimie 2012, 94, 1481–1489. [Google Scholar] [CrossRef]
- De Bisschop, G.; Sargueil, B. RNA Footprinting Using Small Chemical Reagents. Funct. Proteom. 2021, 2323, 13–23. [Google Scholar] [CrossRef]
- Karabiber, F.; McGinnis, J.L.; Favorov, O.V.; Weeks, K.M. QuShape: Rapid, accurate, and best-practices quantification of nucleic acid probing information, resolved by capillary electrophoresis. RNA 2012, 19, 63–73. [Google Scholar] [CrossRef] [Green Version]
- Van Der Spoel, D.; Lindahl, E.; Hess, B.; Groenhof, G.; Mark, A.E.; Berendsen, H.J.C. GROMACS: Fast, flexible, and free. J. Comput. Chem. 2005, 26, 1701–1718. [Google Scholar] [CrossRef]
- Abraham, M.J.; Murtola, T.; Schulz, R.; Páll, S.; Smith, J.C.; Hess, B.; Lindahl, E. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 2015, 1–2, 19–25. [Google Scholar] [CrossRef] [Green Version]
- Hess, B.; Kutzner, C.; Van Der Spoel, D.; Lindahl, E. GROMACS 4: Algorithms for highly efficient, load-balanced, and scalable molecular simulation. J. Chem. Theory Comput. 2008, 4, 435–447. [Google Scholar] [CrossRef] [Green Version]
- Pronk, S.; Páll, S.; Schulz, R.; Larsson, P.; Bjelkmar, P.; Apostolov, R.; Shirts, M.R.; Smith, J.C.; Kasson, P.M.; van der Spoel, D.; et al. GROMACS 4.5: A high-throughput and highly parallel open source molecular simulation toolkit. Bioinformatics 2013, 29, 845–854. [Google Scholar] [CrossRef]
- Pérez, A.; Marchán, I.; Svozil, D.; Sponer, J.; Cheatham, T.E.; Laughton, C.A.; Orozco, M. Refinement of the AMBER force field for nucleic acids: Improving the description of alpha/gamma conformers. Biophys. J. 2017, 92, 3817–3829. [Google Scholar] [CrossRef] [Green Version]
- Šponer, J.; Bussi, G.; Krepl, M.; Banáš, P.; Bottaro, S.; Cunha, R.A.; Gil-Ley, A.; Pinamonti, G.; Poblete, S.; Jurečka, P.; et al. RNA structural dynamics as captured by molecular simulations: A comprehensive overview. Chem. Rev. 2018, 118, 4177–4338. [Google Scholar] [CrossRef] [Green Version]
- Horn, H.W.; Swope, W.C.; Pitera, J.W. Characterization of the TIP4P-Ew water model: Vapor pressure and boiling point. J. Chem. Phys. 2005, 123, 194504. [Google Scholar] [CrossRef]
- Joung, I.S.; Cheatham, T.E. Determination of alkali and halide monovalent ion parameters for use in explicitly solvated biomolecular simulations. J. Phys. Chem. B 2008, 112, 9020–9041. [Google Scholar] [CrossRef] [Green Version]
- Besseová, I.; Otyepka, M.; Réblová, K.; Sponer, J. Dependence of A-RNA simulations on the choice of the force field and salt strength. Phys. Chem. Chem. Phys. PCCP 2009, 11, 10701–10711. [Google Scholar] [CrossRef]
- Allnér, O.; Nilsson, L.; Villa, A. Magnesium Ion–Water Coordination and Exchange in Biomolecular Simulations. J. Chem. Theory Comput. 2012, 8, 1493–1502. [Google Scholar] [CrossRef] [Green Version]
- Cunha, R.A.; Bussi, G. Unraveling Mg2+–RNA binding with atomistic molecular dynamics. RNA 2017, 23, 628–638. [Google Scholar] [CrossRef] [Green Version]
- Darden, T.; York, D.; Pedersen, L. Particle mesh Ewald: An N⋅log(N) method for Ewald sums in large systems. J. Chem. Phys. 1993, 98, 10089–10092. [Google Scholar] [CrossRef] [Green Version]
- Essmann, U.; Perera, L.; Berkowitz, M.; Darden, T.; Lee, H.; Pedersen, L.G. A smooth particle mesh Ewald method. J. Chem. Phys. 1995, 103, 8577–8593. [Google Scholar] [CrossRef] [Green Version]
- Hess, B.; Bekker, H.; Berendsen, H.J.C.; Fraaije, J.G.E.M. LINCS: A linear constraint solver for molecular simulations. J. Comput. Chem. 1997, 18, 1463–1472. [Google Scholar] [CrossRef]
- Harvey, S.C.; Tan, R.K.-Z.; Cheatham, T.E. The flying ice cube: Velocity rescaling in molecular dynamics leads to violation of energy equipartition. J. Comput. Chem. 1998, 19, 726–740. [Google Scholar] [CrossRef]
- Berendsen, H.J.C.; Postma, J.P.M.; Van Gunsteren, W.F.; Di Nola, A.; Haak, J.R. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 1984, 81, 3684–3690. [Google Scholar] [CrossRef] [Green Version]
- Bussi, G.; Donadio, D.; Parrinello, M. Canonical sampling through velocity rescaling. J. Chem. Phys. 2007, 126, 014101. [Google Scholar] [CrossRef] [Green Version]
- Parrinello, M.; Rahman, A. Polymorphic transitions in single crystals: A new molecular dynamics method. J. Appl. Phys. 1981, 52, 7182–7190. [Google Scholar] [CrossRef]
- Lisi, V.; Major, F. A comparative analysis of the triloops in all high-resolution RNA structures reveals sequence structure relationships. RNA 2007, 13, 1537–1545. [Google Scholar] [CrossRef] [Green Version]
- Lemieux, S.; Major, F. RNA canonical and non-canonical base pairing types: A recognition method and complete repertoire. Nucleic Acids Res. 2002, 30, 4250–4263. [Google Scholar] [CrossRef] [Green Version]
- Gendron, P.; Lemieux, S.; Major, F. Quantitative analysis of nucleic acid three-dimensional structures. J. Mol. Biol. 2001, 308, 919–936. [Google Scholar] [CrossRef] [Green Version]
- Leontis, N.B.; Westhof, E. Geometric nomenclature and classification of RNA base pairs. RNA 2001, 7, 499–512. [Google Scholar] [CrossRef] [Green Version]
- Lu, X.-J.; Bussemaker, H.J.; Olson, W.K. DSSR: An integrated software tool for dissecting the spatial structure of RNA. Nucleic Acids Res. 2015, 43, e142. [Google Scholar] [CrossRef] [Green Version]
- Marzec, C.J.; Day, L.A. An exact description of five-membered ring configurations. I. Parameterization via an amplitude S, an angle gamma, the pseudorotation amplitude q and phase angle P, and the bond lengths. J. Biomol. Struct. Dyn. 1993, 10, 1091–1123. [Google Scholar] [CrossRef]
- Westhof, E.; Sundaralingam, M. A method for the analysis of puckering disorder in five-membered rings: The relative mobilities of furanose and proline rings and their effects on polynucleotide and polypeptide backbone flexibility. J. Am. Chem. Soc. 1983, 105, 970–976. [Google Scholar] [CrossRef]
- Lavery, R.; Moakher, M.; Maddocks, J.H.; Petkeviciute, D.; Zakrzewska, K. Conformational analysis of nucleic acids revisited: Curves+. Nucleic Acids Res. 2009, 37, 5917–5929. [Google Scholar] [CrossRef] [Green Version]
- Busan, S.; Weidmann, C.A.; Sengupta, A.; Weeks, K.M. Guidelines for SHAPE Reagent Choice and Detection Strategy for RNA Structure Probing Studies. Biochemistry 2019, 58, 2655–2664. [Google Scholar] [CrossRef] [Green Version]
- Rice, G.; Leonard, C.W.; Weeks, K.M. RNA secondary structure modeling at consistent high accuracy using differential SHAPE. RNA 2014, 20, 846–854. [Google Scholar] [CrossRef] [Green Version]
- Butcher, S.E.; Burke, J.M. Structure-mapping of the Hairpin Ribozyme: Magnesium-dependent folding and evidence for tertiary interactions within the ribozyme-substrate complex. J. Mol. Biol. 1994, 244, 52–63. [Google Scholar] [CrossRef]
- Horiya, S.; Li, X.; Kawai, G.; Saito, R.; Katoh, A.; Kobayashi, K.; Harada, K. RNA LEGO: Magnesium-dependent formation of specific RNA assemblies through kissing interactions. Chem. Biol. 2003, 10, 645–654. [Google Scholar] [CrossRef] [Green Version]
- Lipfert, J.; Doniach, S.; Das, R.; Herschlag, D. Understanding nucleic Acid–Ion interactions. Annu. Rev. Biochem. 2014, 83, 813–841. [Google Scholar] [CrossRef] [Green Version]
- Tan, Z.-J.; Chen, S.-J. Importance of diffuse metal ion binding to RNA. Met. Ions Life Sci. 2011, 9, 101–124. [Google Scholar]
- Lorenz, R.; Bernhart, S.H.F.; Zu Siederdissen, C.H.; Tafer, H.; Flamm, C.; Stadler, P.F.; Hofacker, I.L. ViennaRNA Package 2.0. Algorithms Mol. Biol. 2011, 6, 26. [Google Scholar] [CrossRef]
- Mathews, D.H. RNA Secondary structure analysis using RNA structure. Curr. Protoc. Bioinform. 2006, 13, 12.6.1–12.6.14. [Google Scholar] [CrossRef]
- Silvers, R.; Keller, H.; Schwalbe, H.; Hengesbach, M. Differential scanning fluorimetry for monitoring RNA stability. Chem. BioChem. 2015, 16, 1109–1114. [Google Scholar] [CrossRef]
- Nielsen, H.; Westhof, E.; Johansen, S. An mRNA Is Capped by a 2′, 5′ Lariat Catalyzed by a Group I-Like Ribozyme. Science 2005, 309, 1584–1587. [Google Scholar] [CrossRef] [Green Version]
- Saaidi, A.; Allouche, D.; Regnier, M.; Sargueil, B.; Ponty, Y. IPANEMAP: Integrative probing analysis of nucleic acids empowered by multiple accessibility profiles. Nucleic Acids Res. 2020, 48, 8276–8289. [Google Scholar] [CrossRef]
- Deforges, J.; de Breyne, S.; Ameur, M.; Ulryck, N.; Chamond, N.; Saaidi, A.; Ponty, Y.; Ohlmann, T.; Sargueil, B. Two ribosome recruitment sites direct multiple translation events within HIV1 Gag open reading frame. Nucleic Acids Res. 2017, 45, 7382–7400. [Google Scholar] [CrossRef]
- Banerjee, A.R.; Jaeger, J.A.; Turner, D.H. Thermal unfolding of a group I ribozyme: The low-temperature transition is primarily disruption of tertiary structure. Biochemistry 1993, 32, 153–163. [Google Scholar] [CrossRef]
- Brion, P.; Michel, F.; Renée, S.; Westhof, E. Analysis of the cooperative thermal unfolding of the td intron of bacteriophage T4. Nucleic Acids Res. 1999, 27, 2494–2502. [Google Scholar] [CrossRef]
- Jaeger, L.; Westhof, E.; Michel, F. Monitoring of the cooperative unfolding of the sunY Group I intron of bacteriophage t4: The active form of the suny ribozyme is stabilized by multiple interactions with 3′ terminal intron components. J. Mol. Biol. 1993, 234, 331–346. [Google Scholar] [CrossRef]
- Wilkinson, K.A.; Merino, E.J.; Weeks, K.M. RNA SHAPE Chemistry reveals nonhierarchical interactions dominate equilibrium structural transitions in tRNAAsp transcripts. J. Am. Chem. Soc. 2005, 127, 4659–4667. [Google Scholar] [CrossRef]
- Strulson, C.A.; Boyer, J.A.; Whitman, E.E.; Bevilacqua, P.C. Molecular crowders and cosolutes promote folding cooperativity of RNA under physiological ionic conditions. RNA 2014, 20, 331–347. [Google Scholar] [CrossRef] [Green Version]
- Choi, S.; Park, C.; Kim, K.E.; Kim, K.K. An in vitro technique to identify the RNA binding-site sequences for RNA-binding proteins. BioTechniques 2017, 63, 28–33. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gasser, C.; Gebetsberger, J.; Gebetsberger, M.; Micura, R. SHAPE probing pictures Mg2+-dependent folding of small self-cleaving ribozymes. Nucleic Acids Res. 2018, 46, 6983–6995. [Google Scholar] [CrossRef] [PubMed]
- Steen, K.-A.; Rice, G.M.; Weeks, K.M. Fingerprinting Noncanonical and Tertiary RNA Structures by Differential SHAPE Reactivity. J. Am. Chem. Soc. 2012, 134, 13160–13163. [Google Scholar] [CrossRef] [PubMed] [Green Version]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
De Bisschop, G.; Allouche, D.; Frezza, E.; Masquida, B.; Ponty, Y.; Will, S.; Sargueil, B. Progress toward SHAPE Constrained Computational Prediction of Tertiary Interactions in RNA Structure. Non-Coding RNA 2021, 7, 71. https://doi.org/10.3390/ncrna7040071
De Bisschop G, Allouche D, Frezza E, Masquida B, Ponty Y, Will S, Sargueil B. Progress toward SHAPE Constrained Computational Prediction of Tertiary Interactions in RNA Structure. Non-Coding RNA. 2021; 7(4):71. https://doi.org/10.3390/ncrna7040071
Chicago/Turabian StyleDe Bisschop, Grégoire, Delphine Allouche, Elisa Frezza, Benoît Masquida, Yann Ponty, Sebastian Will, and Bruno Sargueil. 2021. "Progress toward SHAPE Constrained Computational Prediction of Tertiary Interactions in RNA Structure" Non-Coding RNA 7, no. 4: 71. https://doi.org/10.3390/ncrna7040071
APA StyleDe Bisschop, G., Allouche, D., Frezza, E., Masquida, B., Ponty, Y., Will, S., & Sargueil, B. (2021). Progress toward SHAPE Constrained Computational Prediction of Tertiary Interactions in RNA Structure. Non-Coding RNA, 7(4), 71. https://doi.org/10.3390/ncrna7040071