Modelling and Optimization of Operational Setpoint Parameters for Maximum Fermentative Biohydrogen Production Using Box-Behnken Design
Abstract
:1. Introduction
2. Materials and Methods
2.1. Inoculum Development
2.2. Experimental Design
2.3. Substrates and Pretreatment
2.4. Fermentation Process
2.5. Analytical Procedures
2.6. General Model
3. Results and Discussion
3.1. The Linear Interactive Effect of Parameters on Biohydrogen Production
3.2. Development of Model for Optimization of Biohydrogen Production
3.2.1. Model Analysis Based on Input Parameters
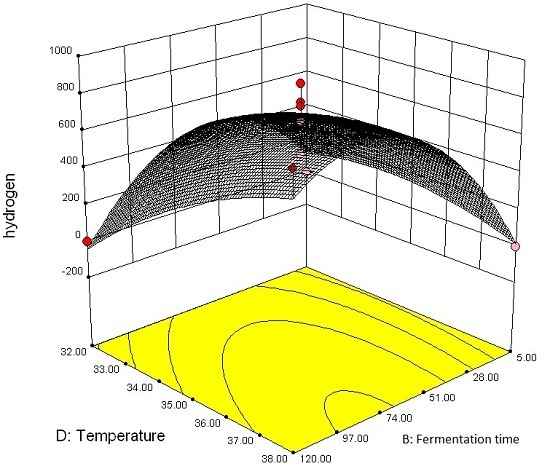
3.2.2. Effect of Parameter Interaction on Biohydrogen Production Response
3.3. Modelling and Optimization of Setpoint Parameters Using Box-Behnken Design
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Wang, J.L.; Wan, W. Effect of temperature on fermentative hydrogen production by mixed cultures. Int. J. Hydrog. Energy 2008, 33, 5392–5397. [Google Scholar] [CrossRef]
- Xing, D.F.; Ren, N.Q.; Wang, A.J.; Li, Q.B.; Feng, Y.J.; Ma, F. Continuous hydrogen production of auto-aggregative Ethanoligenens harbinense YUAN-3 under non-sterile condition. Int. J. Hydrog. Energy 2008, 33, 2137–2146. [Google Scholar] [CrossRef]
- Yang, H.J.; Shen, J.Q. Effect of ferrous iron concentration on anaerobic bio-hydrogen production from soluble starch. Int. J. Hydrog. Energy 2006, 31, 2137–2146. [Google Scholar] [CrossRef]
- Sekoai, P.T.; Gueguim Kana, E.B. Semi-pilot scale production of hydrogen from organic fraction of solid municipal waste and electricity generation from process effluents. Biomass Bioenergy 2014, 60, 156–163. [Google Scholar] [CrossRef]
- Lotfy, W.; Ghanem, K.M.; Helow, E.R. Citric acid by a novel Aspergillus niger isolate: II. Optimization of process parameters through statistical experimental designs. Bioresour. Technol. 2007, 98, 3470–3477. [Google Scholar] [CrossRef] [PubMed]
- He, G.Q.; Chen, Q.H.; Ju, X.J.; Shi, N.D. Improved elastase production by Bacillus sp. EL3140-further optimization and kinetics studies of culture medium for batch fermentation. J. Zhejiang Univ. Sci. 2004, 5, 149–156. [Google Scholar] [CrossRef] [PubMed]
- Haltrich, D.; Preiss, M.; Steiner, W. Optimization of a culture medium for increased xylanase production by a wild strain of Schizophyllum commune. Enzyme Microbiol. Technol. 1993, 15, 854–860. [Google Scholar] [CrossRef]
- Box, G.E.P.; Behnken, D.W. Some new three level designs for the study of quantitative variables. Technometrics 1960, 2, 455–475. [Google Scholar] [CrossRef]
- Haaland, P.D. Experimental Design in Biotechnology; Marcel Dekker: New York, NY, USA, 1989. [Google Scholar]
- Box, G.E.; Hunter, W.G.; Hunter, J.S. Statistical for Experimenters; John Wiley & Sons: Hoboken, NJ, USA, 1978. [Google Scholar]
- Strobel, R.J.; Nakatsukasa, W.M. Response surface for optimization Saccharopolyspora spinosa, a novel macrolide producer. J. Indian Microbiol. 1993, 11, 121–127. [Google Scholar] [CrossRef]
- Swanson, T.R.; Carroll, J.O.; Britto, R.A.; Durhart, D.J. Development and field confirmation of a mathematical model for amyloglucosidase/pollulanase saccharafication. Starch 1986, 38, 382–387. [Google Scholar] [CrossRef]
- Dhillon, G.S.; Brar, S.K.; Verma, M.; Tygi, R.D. Apple pomace ultrafiltration sludge—A novel substrate for fungal bioproduction of citric acid: Optimisation studies. Food Chem. 2011, 128, 864–871. [Google Scholar] [CrossRef]
- Nath, K.; Muthukumar, M.; Kumar, A.; Das, D. Kinetics of two stage fermentation process for the production of hydrogen. Int. J. Hydrog. Energy 2008, 33, 1195–1203. [Google Scholar] [CrossRef]
- Argun, H.; Kargi, F.; Kapdan, I.K.; Oztekin, R. Bio hydrogen production by dark fermentation of wheat powder solution: Effects of C/N and C/P ratio on hydrogen yield and formation rate. Int. J. Hydrog. Energy 2008, 33, 1813–1819. [Google Scholar] [CrossRef]
- Rorke, D.; Gueguim Kana, E.B. Biohydrogen process development on waste sorghum (Sorghum bicolor) leaves: Optimization of saccharafication, hydrogen production and preliminary scale up. Int. J. Hydrog. Energy 2016, 41, 12941–12952. [Google Scholar] [CrossRef]
- Mafuleka, S.; Gueguim Kana, E.B. Modelling and optimization of xylose and glucose production from Napier grass using hybrid pre-treatment techniques. Biomass Bioenergy 2015, 77, 200–208. [Google Scholar] [CrossRef]
- O-Thong, S.; Prasertsan, P.; Intrasungkha, N.; Dhamwichukorn, S.; Birkeland, N.K. Optimization of simultaneous thermophilic fermentative hydrogen production and COD reduction from palm oil mill effluent by Thermoanaerobacterium-rich sludge. Int. J. Hydrog. Energy 2008, 33, 1221–1231. [Google Scholar] [CrossRef]
- Sekoai, P.T.; Gueguim Kana, E.B. A two-stage modelling and optimization of biohydrogen production from a mixture of agro-municipal waste. Int. J. Hydrog. Energy 2013, 38, 8657–8663. [Google Scholar] [CrossRef]
- Chong, M.L.; Rahim, R.A.; Shirai, Y.; Hassan, M.A. Biohydrogen production by Clostridium butyricum EB6 from palm oil mill effluent. Int. J. Hydrog. Energy 2009, 34, 746–771. [Google Scholar] [CrossRef] [Green Version]
- Myers, R.H.; Montgomery, D.C. Response Surface Methodology: Process and Product Optimization Using Designed Experiments; John Wiley & Sons: Hoboken, NJ, USA, 1995. [Google Scholar]
- Moodley, P.; Gueguim Kana, E.B. Optimization of xylose and glucose production from sugarcane leaves (Saccharum officinarum) using hybrid pretreatment techniques and assessment for hydrogen generation at semi-pilot scale. Int. J. Hydrog. Energy 2015, 40, 3859–3867. [Google Scholar] [CrossRef]
- Wu, J.H.; Lin, C.Y. Biohydrogen production by mesophilic fermentation of food wastewater. Water Sci. Technol. 2004, 49, 223–228. [Google Scholar] [PubMed]
- Sinha, P.; Pandey, A. An evaluative report and challenges for fermentative biohydrogen production. Int. J. Hydrog. Energy 2011, 36, 7460–7478. [Google Scholar] [CrossRef]
- Mu, Y.; Wang, G.; Yu, H.Q. Response surface methodological analysis on bio hydrogen production by enriched anaerobic cultures. Enzyme Microbiol. Technol. 2006, 38, 905–913. [Google Scholar] [CrossRef]
- Wang, G.; Mu, Y.; Yu, H.Q. Response surface analysis to evaluate the influence of pH, temperature and substrate concentration on the acidogenesis of sucrose-rich wastewater. Biochem. Eng. J. 2005, 23, 175–184. [Google Scholar] [CrossRef]
- Khanal, S.K.; Chen, W.H.; Li, L.; Sung, S. Biological hydrogen production: Effects of pH and intermediate products. Int. J. Hydrog. Energy 2004, 29, 1123–1131. [Google Scholar] [CrossRef]
- Zhang, T.; Liu, H.; Fang, H.H.P. Biohydrogen production from starch in wastewater under thermophilic conditions. J. Environ. Manag. 2003, 69, 49–56. [Google Scholar] [CrossRef]
- Chen, C.C.; Lin, C.Y.; Lin, M.C. Acid-base enrichment enhances anaerobic hydrogen production process. Appl. Microbiol. Biotechnol. 2002, 58, 224–228. [Google Scholar] [PubMed]
- Hussy, I.; Hawkes, F.R.; Dinsdale, R.; Hawkes, D.L. Continuous fermentative hydrogen production from a wheat starch coproduct by mixed microflora. Biotechnol. Bioeng. 2003, 84, 619–629. [Google Scholar] [CrossRef] [PubMed]
- Cheng, X.Y.; Liu, C.Z. Hydrogen production via thermophilic fermentation of cornstalk by Clostridium thermocellum. Energy Fuels 2011, 25, 1714–1720. [Google Scholar] [CrossRef]
- Lay, J.J. Modelling and optimization of anaerobic digested sludge converting starch to hydrogen. Biotechnol. Bioeng. 2000, 68, 269–278. [Google Scholar] [CrossRef]
- Li, C.L.; Fang, H.H.P. Fermentative hydrogen production from wastewater and solid wastes by mixed cultures. Crit. Rev. Environ. Sci. Technol. 2007, 37, 1–39. [Google Scholar] [CrossRef]
- Van Ginkel, S.W.; Oh, S.E.; Logan, B.E. Bio hydrogen gas production from food processing and domestic wastewaters. Int. J. Hydrog. Energy 2005, 30, 1535–1542. [Google Scholar] [CrossRef]
- De Gioannis, G.; Muntoni, A.; Polettini, A.; Pomi, R. A review of dark fermentative hydrogen production from biodegradable municipal waste fractions. Waste Manag. 2013, 33, 1345–1361. [Google Scholar] [CrossRef] [PubMed]
- Sewsynker, Y.; Gueguim Kana, E.G. Modelling of biohydrogen generation in microbial electrolysis cells (MECs) using a committee of artificial neural networks (ANNs). Biotechnol. Biotechnol. Equip. 2015, 29, 1208–1215. [Google Scholar] [CrossRef]
- Faloye, F.D.; Gueguim Kana, E.B.; Schmidt, S. Optimization of biohydrogen inoculum development via a hybrid pH and microwave treatment technique—Semi pilot scale production assessment. Int. J. Hydrog. Energy 2014, 39, 5607–5616. [Google Scholar] [CrossRef]






| Run | PW | FT | pH | Temp | H2 Yield |
|---|---|---|---|---|---|
| 1 | 10 | 62.5 | 8 | 35 | 89.8 |
| 2 | 10 | 120 | 5.5 | 35 | 111.3 |
| 3 | 25 | 5 | 3 | 35 | 0.5 |
| 4 | 40 | 120 | 5.5 | 35 | 214.2 |
| 5 | 40 | 5 | 5.5 | 35 | 30.9 |
| 6 | 25 | 5 | 8 | 35 | 50.4 |
| 7 | 25 | 120 | 8 | 35 | 58.6 |
| 8 | 25 | 120 | 3 | 35 | 48.7 |
| 9 | 10 | 5 | 5.5 | 35 | 10.5 |
| 10 | 25 | 62.5 | 3 | 38 | 139.5 |
| 11 | 25 | 120 | 5.5 | 38 | 405.0 |
| 12 | 40 | 62.5 | 5.5 | 38 | 495.5 |
| 13 | 25 | 5 | 5.5 | 38 | 0 |
| 14 | 10 | 62.5 | 5.5 | 38 | 0 |
| 15 | 25 | 62.5 | 8 | 38 | 528.0 |
| 16 | 40 | 62.5 | 8 | 35 | 474.5 |
| 17 | 25 | 62.5 | 5.5 | 35 | 373.0 |
| 18 | 25 | 62.5 | 5.5 | 35 | 245.5 |
| 19 | 25 | 62.5 | 5.5 | 35 | 333.0 |
| 20 | 25 | 62.5 | 5.5 | 35 | 384.5 |
| 21 | 10 | 62.5 | 3 | 35 | 0 |
| 22 | 40 | 62.5 | 8 | 35 | 275.0 |
| 23 | 25 | 62.5 | 5.5 | 35 | 432.5 |
| 24 | 25 | 62.5 | 3 | 32 | 10.0 |
| 25 | 25 | 5 | 5.5 | 32 | 0 |
| 26 | 10 | 62.5 | 5.5 | 32 | 61.0 |
| 27 | 25 | 62.5 | 8 | 32 | 310.0 |
| 28 | 40 | 62.5 | 5.5 | 32 | 277.0 |
| 29 | 25 | 120 | 5.5 | 32 | 0 |
| Source | SS | df | MS | F-Value | p-Value | R2 |
|---|---|---|---|---|---|---|
| Model | 2,890,000 | 14 | 207,000 | 3.75 | 0.0094 | 0.7895 |
| A | 738,000 | 1 | 738,000 | 13.4 | 0.0026 | |
| B | 183,000 | 1 | 183,000 | 3.33 | 0.0895 | |
| C | 138,000 | 1 | 138,000 | 2.51 | 0.1357 | |
| D | 277,000 | 1 | 277,000 | 5.03 | 0.0415 | |
| AB | 6972.25 | 1 | 0.13 | 0.7273 | ||
| AC | 88,209 | 1 | 1.6 | 0.2263 | ||
| AD | 79,242.25 | 1 | 1.44 | 0.2502 | ||
| BC | 1296 | 1 | 0.024 | 0.8803 | ||
| BD | 164,000 | 1 | 2.98 | 0.1064 | ||
| CD | 7832.25 | 1 | 7832.25 | 0.7117 | ||
| A2 | 130,000 | 1 | 2.36 | 0.1465 | ||
| B2 | 1,150,000 | 1 | 20.9 | 0.0004 | ||
| C2 | 156,000 | 1 | 2.84 | 0.1141 | ||
| D2 | 60,602.16 | 1 | 1.1 | 0.3119 |
| Factor | CE | df | SE | 95% CIL | 95% CIH | VIF |
|---|---|---|---|---|---|---|
| Intercept | 707.4 | 1 | 104.95 | 482.31 | 932.49 | |
| A | 248 | 1 | 67.74 | 102.7 | 393.3 | 1 |
| B | 123.58 | 1 | 67.74 | −21.71 | 268.88 | 1 |
| C | 107.25 | 1 | 67.74 | −38.05 | 252.55 | 1 |
| D | 152 | 1 | 67.74 | 6.7 | 297.3 | 1 |
| AB | 41.75 | 1 | 117.34 | −209.91 | 293.41 | 1 |
| AC | −148.5 | 1 | 117.34 | −400.16 | 103.16 | 1 |
| AD | 140.75 | 1 | 117.34 | −110.91 | 392.41 | 1 |
| BC | −18 | 1 | 117.34 | −269.66 | 233.66 | 1 |
| BD | 202.5 | 1 | 117.34 | −49.16 | 454.16 | 1 |
| CD | 44.25 | 1 | 117.34 | −207.41 | 295.91 | 1 |
| A2 | −141.66 | 1 | 92.14 | −339.28 | 55.97 | 1.08 |
| B2 | −421.28 | 1 | 92.14 | −618.91 | −223.66 | 1.08 |
| C2 | −155.28 | 1 | 92.14 | −352.91 | 42.34 | 1.08 |
| D2 | −96.66 | 1 | 92.14 | −294.28 | 100.97 | 1.08 |
© 2016 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sekoai, P.T. Modelling and Optimization of Operational Setpoint Parameters for Maximum Fermentative Biohydrogen Production Using Box-Behnken Design. Fermentation 2016, 2, 15. https://doi.org/10.3390/fermentation2030015
Sekoai PT. Modelling and Optimization of Operational Setpoint Parameters for Maximum Fermentative Biohydrogen Production Using Box-Behnken Design. Fermentation. 2016; 2(3):15. https://doi.org/10.3390/fermentation2030015
Chicago/Turabian StyleSekoai, Patrick T. 2016. "Modelling and Optimization of Operational Setpoint Parameters for Maximum Fermentative Biohydrogen Production Using Box-Behnken Design" Fermentation 2, no. 3: 15. https://doi.org/10.3390/fermentation2030015
APA StyleSekoai, P. T. (2016). Modelling and Optimization of Operational Setpoint Parameters for Maximum Fermentative Biohydrogen Production Using Box-Behnken Design. Fermentation, 2(3), 15. https://doi.org/10.3390/fermentation2030015