Shedding Light on the Effect of Uncertainties in the Seismic Fragility Analysis of Existing Concrete Dams
Abstract
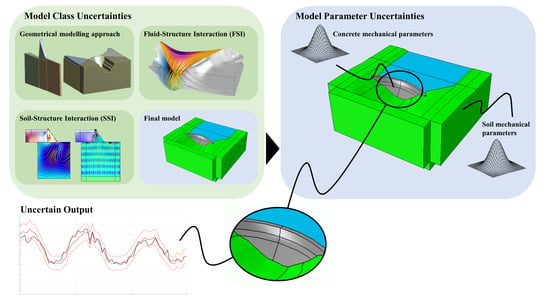
:1. Introduction
2. Source of Uncertainties Involved in the Seismic Analysis of Existing Concrete Gravity Dams
3. Seismic Fragility Assessment of Existing Concrete Gravity Dams
4. Illustrative Application: The Effect of Epistemic Uncertainties on the Seismic Fragility Analysis of Existing Concrete Gravity Dams
4.1. The Dam
4.2. The Numerical Model
- Hardening branch: if ,
- First softening branch: if ,
- Second softening branch: if ,
4.3. Uncertainty Quantification (UQ) in the Modal Analysis of Concrete Dams
4.4. Fragility Analysis
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- International Commission on Large Dams (ICOLD). World Register of Dams; Technical Report; ICOLD: Paris, France, 2003. [Google Scholar]
- Zhang, L.; Peng, M.; Chang, D.; Xu, Y. Dam Failure Mechanisms and Risk Assessment; John Wiley & Sons Singapore Pte. Ltd.: Hoboken, NJ, USA, 2016; p. 476. [Google Scholar]
- Hall, J.F. The dynamic and earthquake behaviour of concrete dams: Review of experimental behaviour and observational evidence. Soil Dyn. Earthq. Eng. 1988, 7, 58–121. [Google Scholar] [CrossRef]
- Hariri-Ardebili, M.A. Risk, Reliability, Resilience (R3) and beyond in dam engineering: A state-of-the-art review. Int. J. Disaster Risk Reduct. 2018, 31, 806–831. [Google Scholar] [CrossRef]
- Galambos, T.V. Load and resistance factor design. Eng. J. Am. Inst. Steel Constr. 1981, 18, 74–82. [Google Scholar]
- Moehle, J.; Deierlein, G.G. A framework methodology for performance-based earthquake engineering. In Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, BC, Canada, 1–6 August 2004. [Google Scholar]
- Bozorgnia, Y.; Bertero, V.V. Earthquake Engineering: From Engineering Seismology to Performance-Based Engineering; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- European Committee for Standardization (CEN). EN 1990:2002—Basis of Structural Design; Technical Report; CEN: Brussels, Belgium, 2002. [Google Scholar]
- Madsen, H.O.; Krenk, S.; Lind, N.C. Methods of Structural Safety; Dover Publications, Inc.: Mineola, NY, USA, 2006. [Google Scholar]
- Porter, K.A. An Overview of PEER’s Performance-Based Earthquake Engineering Methodology. In Proceedings of the 9th International Conference on Applications of Statistics and Probability in Civil Engineering, San Francisco, CA, USA, 6–9 July 2003. [Google Scholar]
- Ciano, M.; Gioffrè, M.; Grigoriu, M. The role of intensity measures on the accuracy of seismic fragilities. Probabilistic Eng. Mech. 2020, 60, 103041. [Google Scholar] [CrossRef]
- Hariri-Ardebili, M.A.; Saouma, V.E. Collapse Fragility Curves for Concrete Dams: Comprehensive Study. J. Struct. Eng. 2016, 142, 04016075. [Google Scholar] [CrossRef]
- Federal Emergency Management Agency (FEMA). FEMA 93—Federal Guidelines for Dam Safety; Technical Report; FEMA: Washington, DC, USA, 2004. [Google Scholar]
- Hariri-Ardebili, M.A. Performance Based Earthquake Engineering of Concrete Dams. Ph.D. Thesis, University of Colorado, Boulder, CO, USA, 2015. [Google Scholar]
- Der Kiureghian, A.; Ditlevsen, O. Aleatory or epistemic? Does it matter? Struct. Saf. 2009, 31, 105–112. [Google Scholar] [CrossRef]
- Faber, M.H. On the Treatment of Uncertainties and Probabilities in Engineering Decision Analysis. J. Offshore Mech. Arct. Eng. 2005, 127, 243–248. [Google Scholar] [CrossRef]
- Huang, Y.; Shao, C.; Wu, B.; Beck, J.L.; Li, H. State-of-the-art review on Bayesian inference in structural system identification and damage assessment. Adv. Struct. Eng. 2018, 22, 1329–1351. [Google Scholar] [CrossRef]
- Andreini, M.; Falco, A.D.; Marmo, G.; Mori, M.; Sevieri, G. Modelling issues in the structural analysis of existing concrete gravity dams. In Proceedings of the 85th ICOLD Annual Meeting, Prague, Czech Republic, 3–7 July 2017; pp. 363–383. [Google Scholar]
- De Falco, A.; Mori, M.; Sevieri, G. Simplified Soil-Structure Interaction models for concrete gravity dams. In Proceedings of the 6th European Conference on Computational Mechanics (ECCM 6) and the 7th European Conference on Computational Fluid Dynamics (ECFD 7), Glasgow, UK, 11–15 June 2018; pp. 2269–2280. [Google Scholar]
- De Falco, A.; Mori, M.; Sevieri, G. Soil-Structure Interaction modeling for the dynamic analysis of concrete gravity dams. In Proceedings of the COMPDYN 2019, 7th International Conference on Computational Methods in Structural Dynamics and Earthquake Engineering, Crete, Greece, 24–26 June 2019. [Google Scholar]
- De Falco, A.; Mori, M.; Sevieri, G. Bayesian updating of concrete gravity dams model parameters using static measurements. In Proceedings of the 6th European Conference on Computational Mechanics (ECCM 6) and the 7th European Conference on Computational Fluid Dynamics (ECFD 7), Glasgow, UK, 11–15 June 2018. [Google Scholar]
- Westergaard, H.M. Water pressures on dams during earthquakes. Trans. Am. Soc. Civ. Eng. 1933, 98, 418–433. [Google Scholar]
- Liu, Q.H.; Tao, J. The perfectly matched layer for acoustic waves in absorptive media. J. Acoust. Soc. Am. 1997, 102, 2072–2082. [Google Scholar] [CrossRef]
- Astley, R.J. Infinite elements. In Computational Acoustics of Noise Propagation in Fluids—Finite and Boundary Element Methods; Marburg, S., Nolte, B., Eds.; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar] [CrossRef]
- Wolf, J.P. Dynamic Soil-Structure Interaction; Prentice-Hall: Upper Saddle River, NJ, USA, 1985; p. 466. [Google Scholar]
- Sevieri, G.; De Falco, A. Dynamic Structural Health Monitoring for concrete gravity dams based on the Bayesian inference. J. Civ. Struct. Health Monit. 2020, 380, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Marsili, F.; Croce, P.; Friedman, N.; Formichi, P.; Landi, F. Seismic Reliability Assessment of a Concrete Water Tank Based on the Bayesian Updating of the Finite Element Model. ASCE-ASME J. Risk Uncert. Eng. Syst. Part B Mech. Eng. 2017, 3, 021004. [Google Scholar] [CrossRef]
- Hadamard, J. Lectures on Cauchy’s Problem in Linear Partial Differential Equations; Dover publications, INC: Mineola, NY, USA, 1923. [Google Scholar]
- De Falco, A.; Girardi, M.; Pellegrini, D.; Robol, L.; Sevieri, G. Model parameter estimation using Bayesian and deterministic approaches: The case study of the Maddalena Bridge. Procedia Struct. Integr. 2018, 11, 210–217. [Google Scholar] [CrossRef]
- Box, G.E.P.; Tiao, G.C. Bayesian Inference in Statistical Analysis; Wiley-Interscience: Hoboken, NJ, USA, 1992; p. 608. [Google Scholar]
- Sevieri, G.; Andreini, M.; De Falco, A.; Matthies, H.G. Concrete gravity dams model parameters updating using static measurements. Eng. Struct. 2019, 196, 109231. [Google Scholar] [CrossRef]
- Xiu, D. Numerical Methods for Stochastic Computations; Princeton University Press: Princeton, NJ, USA, 2010; p. 142. [Google Scholar]
- Kennedy, R.P.; Ravindra, M.K. Seismic fragilities for nuclear power plant risk studies. Nucl. Eng. Des. 1984, 79, 47–68. [Google Scholar] [CrossRef]
- Huo, Y.; Zhang, J. Effects of pounding and skewness on seismic responses of typical multispan highway bridges using the fragility function method. J. Bridge Eng. 2013, 18, 499–515. [Google Scholar] [CrossRef]
- Choe, D.E.; Gardoni, P.; Rosowsky, D.; Haukaas, T. Probabilistic capacity models and seismic fragility estimates for RC columns subject to corrosion. Reliab. Eng. Syst. Saf. 2008, 93, 383–393. [Google Scholar] [CrossRef]
- de Araújo, J.M.; Awruch, A.M. Probabilistic finite element analysis of concrete gravity dams. Adv. Eng. Softw. 1998, 29, 97–104. [Google Scholar] [CrossRef]
- Tekie, P.B.; Ellingwood, B.R. Seismic fragility assessment of concrete gravity dams. Earthq. Eng. Struct. Dyn. 2003, 32, 2221–2240. [Google Scholar] [CrossRef]
- Lin, L.; Adams, J. Lessons for the fragility of Canadian hydropower components under seismic loading. In Proceedings of the Ninth Canadian Conference on Earthquake Engineering, Ottawa, ON, Canada, 26–29 June 2007; pp. 1762–1771. [Google Scholar]
- Applied Technology Council. ATC-13: Earthquake Damage Evaluation Data for California; Technical Report; Applied Technology Council: Redwood City, CA, USA, 1985. [Google Scholar]
- Mirzahossein Kashani, S.; Ghaemian, M. Seismic fragility assessment of concrete gravity dams. In Proceedings of the 29th Annual USSD Conference, Nashville, TN, USA, 20–24 April 2009. [Google Scholar]
- Lupoi, A.; Callari, C. A probabilistic method for the seismic assessment of existing concrete gravity dams. Struct. Infrastruct. Eng. Maint. Manag. Life-Cycle Des. Perform. 2012, 8, 37–41. [Google Scholar] [CrossRef]
- Hebbouche, A.; Bensaibi, M.; Mroueh, H. Seismic Fragility and uncertainty Analysis of Concrete Gravity Dams under Near-Fault Ground Motions. Civ. Environ. Res. 2013, 5, 123–129. [Google Scholar]
- Ghanaat, Y.; Hashimoto Philip, S.; Zuchuat, O.; Kennedy, R.P. Seismic fragility of Muhlberg dam using nonlinear analysis with Latin Hypercube Simulation. In Proceedings of the 31st Annual USSD Conference, San Diego, CA, USA, 11–15 April 2011. [Google Scholar]
- Vamvatsikos, D.; Allin Cornell, C. Incremental dynamic analysis. Earthq. Eng. Struct. Dyn. 2002, 31, 491–514. [Google Scholar] [CrossRef]
- Ghanaat, Y.; Patev, R.C.; Chudgar, A.K. Seismic fragility analysis of concrete gravity dams. In Proceedings of the 15th World Conference on Earthquake Engineering, Lisbon, Portugal, 24–28 September 2012. [Google Scholar]
- Ghanaat, Y.; Patev, R.C.; Chudgar, A.K. Seismic fragility for risk assessment of concrete gravity dams. In Proceedings of the 2015 USSD Annual Conference, Louisville, KY, USA, 13–17 April 2015; pp. 645–660. [Google Scholar]
- Kadkhodayan, V.; Meisam Aghajanzadeh, S.; Mirzabozorg, H. Seismic Assessment of Arch Dams Using Fragility Curves. Civ. Eng. J. 2015, 1, 14–20. [Google Scholar] [CrossRef]
- Ghanaat, Y. Failure modes approach to safety evaluation of dams. In Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, BC, Canada, 1–6 August 2004. [Google Scholar]
- Bernier, C.; Padgett, J.E.; Proulx, J.; Paultre, P. Seismic fragility of concrete gravity dams with modeling parameter uncertainty and spacial variation. J. Struct. Eng. 2014, 142. [Google Scholar]
- Bernier, C.; Padgett, J.E.; Proulx, J.; Paultre, P. Seismic Fragility of Concrete Gravity Dams with Spatial Variation of Angle of Friction: Case Study. J. Struct. Eng. 2016, 142, 05015002. [Google Scholar] [CrossRef]
- Hariri-Ardebili, M.A.; Saouma, V.E.; Porter, K.A. Quantification of seismic potential failure modes in concrete dams. Earthq. Eng. Struct. Dyn. 2016, 45, 979–997. [Google Scholar] [CrossRef]
- U.S. Army Corps of Engineers (USACE). Earthquake Design and Evaluation of Concrete Hydraulic Structures; United States Army Crops of Engineers (USACE): Washington, DC, USA, 2007. [Google Scholar]
- U.S. Army Corps of Engineers (USACE). Time-History Dynamic Analysis of Concrete Hydraulic Structures; United States Army Crops of Engineers (USACE): Washington, DC, USA, 2003. [Google Scholar]
- Hariri-Ardebili, M.A.; Saouma, V.E. Probabilistic seismic demand model and optimal intensity measure for concrete dams. Struct. Saf. 2016, 59, 67–85. [Google Scholar] [CrossRef]
- Jalayer, F.; Ebrahimian, H.; Miano, A.; Manfredi, G.; Sezen, H. Analytical fragility assessment using unscaled ground motion records. Earthq. Eng. Struct. Dyn. 2017, 46, 2639–2663. [Google Scholar] [CrossRef]
- Hariri-Ardebili, M.A.; Saouma, V.E. Sensitivity and uncertainty quantification of the cohesive crack model. Eng. Fract. Mech. 2016, 155, 18–35. [Google Scholar] [CrossRef]
- Hariri-Ardebili, M.A.; Seyed-Kolbadi, S.M.; Saouma, V.E.; Salamon, J.; Rajagopalan, B. Random finite element method for the seismic analysis of gravity dams. Eng. Struct. 2018, 171, 405–420. [Google Scholar] [CrossRef]
- ABAQUS. ABAQUS Version 6.14—Documentation Manual. Technical Report. 2014. Available online: http://ivt-abaqusdoc.ivt.ntnu.no:2080/texis/search/?query=wetting&submit.x=0&submit.y=0&group=bk&CDB=v6.14 (accessed on 29 January 2020).
- Lee, J.H.; Fenves, G.L. Plastic-damage model for cyclic loading of concrete structures. J. Eng. Mech. 1998, 124, 892–900. [Google Scholar] [CrossRef]
- Sevieri, G. The Seismic Assessment of Existing Concrete Gravity Dams: FE Model Uncertainty Quantification and Reduction. Ph.D. Thesis, University of Pisa & Technical University of Braunschweig, Braunschweig, Germany, 2019. [Google Scholar]
- Hillerborg, A.; Modéer, M.; Petersson, P.E. Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements. Cem. Concr. Res. 1976, 6, 773–781. [Google Scholar] [CrossRef]
- Omidi, O.; Valliappan, S.; Lotfi, V. Seismic cracking of concrete gravity dams by plastic-damage model using different damping mechanisms. Finite Elem. Anal. Des. 2013, 63, 80–97. [Google Scholar] [CrossRef]
- The Mathworks Inc. MATLAB; MathWorks: Natick, MA, USA, 2016. [Google Scholar]
- Rosić, B.; Matthies, H.G. Sparse bayesian polynomial chaos approximations of elasto-plastic material models. In Proceedings of the XIV International Conference on Computational Plasticity, Fundamentals and Applications, Barcelona, Spain, 5–7 September 2017; pp. 256–267. [Google Scholar]
- Sobol’, I. Sensitivity Estimates for Nonlinear Mathematical Models. Math. Model. Comput. Exp. 1993, 1, 407–414. [Google Scholar] [CrossRef]
- Sudret, B. Global sensitivity analysis using polynomial chaos expansions. Reliab. Eng. Syst. Saf. 2008, 93, 964–979. [Google Scholar] [CrossRef]
- Liel, A.B.; Haselton, C.B.; Deierlein, G.G.; Baker, J.W. Incorporating modeling uncertainties in the assessment of seismic collapse risk of buildings. Struct. Saf. 2009, 31, 197–211. [Google Scholar] [CrossRef]
- Sooch, G.S.; Bagchi, A. A New Iterative Procedure for Deconvolution of Seismic Ground Motion in Dam-Reservoir-Foundation Systems. J. Appl. Math. 2014, 2014, 287605. [Google Scholar] [CrossRef] [Green Version]
- Iervolino, I.; Galasso, C.; Cosenza, E. REXEL: Computer aided record selection for code-based seismic structural analysis. Bull. Earthq. Eng. 2010, 8, 339–362. [Google Scholar] [CrossRef]








| [°] | |||
|---|---|---|---|
| 36.31 | 0.1 | 1.16 | 0.66 |
| [Mpa] | [kg/] | [Mpa] | [kg/] | [Mpa] | [kg/] | [Mpa] | [Mpa] | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | 34,620 | 0.16 | 2270 | 21,000 | 0.16 | 1800 | 7000 | 0.22 | 1800 | 16.7 | 2 |
| s.d. | 12,498 | 0.06 | 189.17 | 9545 | 0.07 | - | 3181.8 | 0.1 | - | 5.16 | 1.1 |
| 1 | ||||
| 0 | 1 | |||
| 0.83 | 0.83 | 1 | ||
| 0.83 | 0.83 | 0.9 | 1 |
| # | Event | Year | Station ID | Mw | Epicentral Distance [km] | EC8 Site Class |
|---|---|---|---|---|---|---|
| 1 | Campano Lucano | 1980 | ST96 | 6.9 | 32 | A |
| 2 | Friuli | 1976 | ST20 | 6.5 | 23 | A |
| 3 | Campano Lucano | 1980 | ST98 | 6.9 | 25 | A |
| 4 | Bingol | 2003 | ST539 | 6.3 | 14 | A |
| 5 | South Iceland | 2000 | ST2558 | 6.4 | 5 | A |
| 6 | Duzce 1 | 1999 | ST1252 | 7.2 | 34 | A |
| 7 | Tabas | 1978 | ST54 | 7.3 | 12 | A |
| 8 | Umbria Marche | 1997 | ST238 | 6 | 21 | A |
| 9 | Montenegro | 1979 | ST64 | 6.9 | 21 | A |
| 10 | Basso Tirreno | 1978 | ST49 | 6 | 34 | A |
| 11 | Golbasi | 1986 | ST161 | 6 | 29 | A |
| 12 | Duzce 1 | 1999 | ST3136 | 7.2 | 23 | A |
| 13 | South Iceland | 2000 | ST2556 | 6.5 | 35 | A |
| 14 | Izmit | 1999 | ST575 | 7.6 | 9 | A |
| 15 | Friuli | 1976 | ST36 | 6 | 28 | A |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sevieri, G.; De Falco, A.; Marmo, G. Shedding Light on the Effect of Uncertainties in the Seismic Fragility Analysis of Existing Concrete Dams. Infrastructures 2020, 5, 22. https://doi.org/10.3390/infrastructures5030022
Sevieri G, De Falco A, Marmo G. Shedding Light on the Effect of Uncertainties in the Seismic Fragility Analysis of Existing Concrete Dams. Infrastructures. 2020; 5(3):22. https://doi.org/10.3390/infrastructures5030022
Chicago/Turabian StyleSevieri, Giacomo, Anna De Falco, and Giovanni Marmo. 2020. "Shedding Light on the Effect of Uncertainties in the Seismic Fragility Analysis of Existing Concrete Dams" Infrastructures 5, no. 3: 22. https://doi.org/10.3390/infrastructures5030022
APA StyleSevieri, G., De Falco, A., & Marmo, G. (2020). Shedding Light on the Effect of Uncertainties in the Seismic Fragility Analysis of Existing Concrete Dams. Infrastructures, 5(3), 22. https://doi.org/10.3390/infrastructures5030022