Figure 1.
Ice types: rime ice, clear ice, and mixed-ice. (Photo credit: NASA, adapted from [
8]).
Figure 1.
Ice types: rime ice, clear ice, and mixed-ice. (Photo credit: NASA, adapted from [
8]).
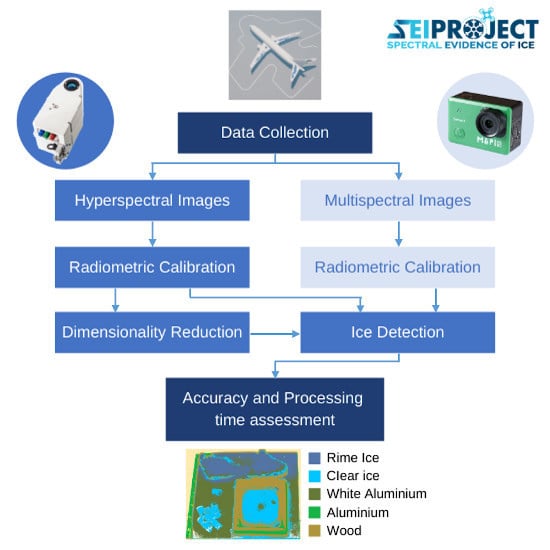
Figure 2.
Methodology workflow.
Figure 2.
Methodology workflow.
Figure 3.
Example of annotated image with reference data. Training set sample (a) and validation set sample (b).
Figure 3.
Example of annotated image with reference data. Training set sample (a) and validation set sample (b).
Figure 4.
Screen graph on a sample image. Zoom of the ‘elbow’.
Figure 4.
Screen graph on a sample image. Zoom of the ‘elbow’.
Figure 5.
First principal component eigenvalues plot.
Figure 5.
First principal component eigenvalues plot.
Figure 6.
Second principal component eigenvalues plot.
Figure 6.
Second principal component eigenvalues plot.
Figure 7.
Third principal component eigenvalues plot.
Figure 7.
Third principal component eigenvalues plot.
Figure 8.
RF validation curve for maximum depth (on the left) and maximum number of trees (on the right).
Figure 8.
RF validation curve for maximum depth (on the left) and maximum number of trees (on the right).
Figure 9.
SVM validation curve for the maximum number of samples.
Figure 9.
SVM validation curve for the maximum number of samples.
Figure 10.
The classification results on Test_1 with SVM. (a) Original classified hypercube, (b) reduced classified hypercube-27 bands, (c) reduced classified hypercube-10 bands, and (d) PC classified hypercube.
Figure 10.
The classification results on Test_1 with SVM. (a) Original classified hypercube, (b) reduced classified hypercube-27 bands, (c) reduced classified hypercube-10 bands, and (d) PC classified hypercube.
Figure 11.
The classification results on Test_1 with SVM. (a) RGN classified images and (b) RGBN classified images.
Figure 11.
The classification results on Test_1 with SVM. (a) RGN classified images and (b) RGBN classified images.
Table 1.
Sensor specifications: the Senop Rikola hyperspectral camera and the MAPIR Survey3N multispectral camera.
Table 1.
Sensor specifications: the Senop Rikola hyperspectral camera and the MAPIR Survey3N multispectral camera.
| Camera | Senop Rikola | MAPIR Survey3N |
|---|
| Lens optics | H 36.5°, V 36.5° | H 41° HFOV (47 mm) |
| Spectral range | 500–900 nm | 550–850 nm |
| Spectral channels | 380 | 3 |
| Spectral resolution | 1 nm | - |
| Shutter type | Global | Rolling |
| Focal length | 9 mm | 8.25 mm |
| Image resolution | 1010 × 1010 pixels | 4000 × 3000 pixels |
| Pixel size | 5.5 μm | 1.55 μm |
| Weight | 720 g | 75.4 g |
| Dimensions | 172.7 × 89 × 77 mm | 59 × 41.5 × 36 mm |
| Cost | ≈60,000€ | ≈700€ |
Table 2.
Hyperspectral and multispectral reference samples per class.
Table 2.
Hyperspectral and multispectral reference samples per class.
| Class | Hyperspectral Samples (Pixels) | Multispectral Samples (Pixels) |
|---|
| Rime ice | 10,156 | 101,797 |
| Clear ice | 10,457 | 104,819 |
| White aluminum | 11,632 | 116,588 |
| Aluminum | 3580 | 35,912 |
| Wood | 10,896 | 93,624 |
| Floor tile | 19,812 | 198,572 |
| White reference panel | 9545 | 95,672 |
| Black reference panel | 16,024 | 160,617 |
| 21% grey reference panel | 12,980 | 130,089 |
| 27% grey reference panel | 10,670 | 106,949 |
| Average pixels per class | 10,523 | 104,058 |
Table 3.
Principal component analysis (PCA): example of eigenvalue and cumulative variance in percentage on a single sample image.
Table 3.
Principal component analysis (PCA): example of eigenvalue and cumulative variance in percentage on a single sample image.
| Component | Percent % | Cumulative% |
|---|
| 1 | 80.0010 | 80.0010 |
| 2 | 8.4818 | 88.4828 |
| 3 | 1.8341 | 90.3169 |
| 4 | 0.9935 | 91.3104 |
| 5 | 0.5888 | 91.8992 |
Table 4.
Band selection for the three principal components (PC) in the representative tests (Test1, Test2, Test6, Test10).
Table 4.
Band selection for the three principal components (PC) in the representative tests (Test1, Test2, Test6, Test10).
| Principal Component | Test1 | Test2 | Test6 | Test10 |
|---|
| 1 | 1, 3–7, 25, 32–38 | 1, 3–6, 14, 33–37 | 1, 3–6, 32–37 | 4, 5, 32–34, 36, 37 |
| 2 | 80–85 | 80–85 | 78–89 | 83–89 |
| 3 | 35–37 | 35–37 | 35–37 | 35–37, 86–89 |
Table 5.
Training accuracy (on the left) and validation accuracy (on the right) for random forest (RF) tree depth optimization. R_i stands for rime ice, C_i for clear ice, and W_a for white aluminum. In yellow, the selected optimized hyperparameter.
Table 5.
Training accuracy (on the left) and validation accuracy (on the right) for random forest (RF) tree depth optimization. R_i stands for rime ice, C_i for clear ice, and W_a for white aluminum. In yellow, the selected optimized hyperparameter.
| D_Trees | Training Accuracy (%) | Validation Accuracy (%) |
|---|
| R_i | C_i | W_a | Overall | R_i | C_i | W_a | Overall |
|---|
| 5 | 73.6842 | 91.0615 | 74.7475 | 92.5425 | 42.4802 | 92.9577 | 64.8855 | 85.5371 |
| 10 | 80.1887 | 98.8636 | 92.9412 | 97.0971 | 44.4992 | 94.9346 | 69.5067 | 87.7175 |
| 15 | 78.8018 | 98.8506 | 93.4524 | 96.8969 | 43.128 | 95.0083 | 68.9602 | 87.0574 |
| 20 | 84.6535 | 93.956 | 93.8547 | 97.2472 | 41.2747 | 94.108 | 68.7908 | 86.6773 |
| 25 | 79.3427 | 97.1429 | 93.4911 | 96.8468 | 42.2256 | 92.5159 | 68.932 | 86.5173 |
| 30 | 81.6038 | 99.422 | 95.3757 | 97.2472 | 43.6863 | 95.7816 | 70.8692 | 87.83 |
Table 6.
Training accuracy (on the left) and validation accuracy (on the right) optimization of RF number of trees. R_i stands for rime ice, C_i for clear ice, and W_a for white aluminum. In yellow the selected optimized hyperparameter is shown.
Table 6.
Training accuracy (on the left) and validation accuracy (on the right) optimization of RF number of trees. R_i stands for rime ice, C_i for clear ice, and W_a for white aluminum. In yellow the selected optimized hyperparameter is shown.
| N_Trees | Training Accuracy (%) | Validation Accuracy (%) |
|---|
| R_i | C_i | W_a | Overall | R_i | C_i | W_a | Overall |
|---|
| 5 | 85,3403 | 96.5909 | 91.0053 | 97.1471 | 39.0855 | 93.9542 | 66.8908 | 86.0172 |
| 10 | 83.3333 | 99.422 | 95.4802 | 97.5475 | 41.1854 | 93.9344 | 67.7368 | 86.6573 |
| 15 | 82.381 | 99.422 | 94.2529 | 97.3974 | 45.4699 | 95.1604 | 71.3681 | 87.9587 |
| 20 | 80.7512 | 98.3051 | 95.2663 | 97.2472 | 43.2602 | 94.2122 | 71.205 | 87.2575 |
| 25 | 85.8586 | 97.2067 | 95.0549 | 97.6977 | 42.8571 | 93.4959 | 72.0339 | 87.3253 |
| 30 | 82.6923 | 97.7011 | 93.2203 | 97.1972 | 44.0476 | 94.3548 | 71.1538 | 87.8743 |
| 35 | 86.8687 | 99.4253 | 95.6522 | 97.998 | 44.081 | 93.75 | 70.892 | 87.3375 |
| 40 | 83.0846 | 96.4912 | 90.3226 | 96.9469 | 42.1217 | 94.2997 | 68.7988 | 86.5973 |
| 45 | 81.6425 | 98.8506 | 92.1348 | 97.0971 | 42.6404 | 95.098 | 69.9681 | 87.4375 |
| 50 | 81.6038 | 99.422 | 95.3757 | 97.2472 | 43.6863 | 95.7816 | 70.8692 | 87.83 |
Table 7.
Processing time for the training in RF using different values of tree depth (on the left) and the number of trees (on the right). In yellow the time for training the model with the selected optimized hyperparameter is shown.
Table 7.
Processing time for the training in RF using different values of tree depth (on the left) and the number of trees (on the right). In yellow the time for training the model with the selected optimized hyperparameter is shown.
| D_Trees | Processing Time | N_Trees | Processing Time |
|---|
| 5 | 34″ | 5 | 14″ |
| 10 | 31″ | 10 | 26″ |
| 15 | 26″ | 15 | 32″ |
| 20 | 26″ | 20 | 31″ |
| 25 | 27″ | 25 | 32″ |
| 30 | 33″ | 30 | 29″ |
| - | - | 35 | 33″ |
| - | - | 40 | 30″ |
| - | - | 45 | 33″ |
| - | - | 50 | 33″ |
Table 8.
Training accuracy (on the left) and validation accuracy (on the right) optimization of support vector machine (SVM) number of the sample. R_i stands for rime ice, C_i for clear ice, and W_a for white aluminum. In yellow the selected optimized hyperparameter is shown.
Table 8.
Training accuracy (on the left) and validation accuracy (on the right) optimization of support vector machine (SVM) number of the sample. R_i stands for rime ice, C_i for clear ice, and W_a for white aluminum. In yellow the selected optimized hyperparameter is shown.
| N_Samples | Training Accuracy (%) | Validation Accuracy (%) |
|---|
| R_i | C_i | W_a | Overall | R_i | C_i | W_a | Overall |
|---|
| 100 | 77.6744 | 97.7401 | 92.1687 | 96.3964 | 56.6879 | 99.1667 | 72.4719 | 91.4671 |
| 250 | 86.8687 | 97.7401 | 96.7568 | 97.9980 | 46.8354 | 96.4567 | 74.5247 | 89.7206 |
| 500 | 86.6667 | 1.0000 | 94.6237 | 97.9479 | 44.7059 | 95.2756 | 73.1707 | 88.6228 |
| 750 | 93.5135 | 99.4382 | 98.4615 | 99.0490 | 51.8644 | 93.9623 | 90.9091 | 90.9182 |
| 1000 | 91.8919 | 98.895 | 97.3822 | 98.7487 | 52.8571 | 92.6740 | 89.0000 | 91.0679 |
| 2000 | 91.5344 | 1.0000 | 97.8836 | 98.9990 | 49.6815 | 93.8697 | 89.4444 | 89.8204 |
| 5000 | 97.1910 | 1.0000 | 98.4925 | 99.5996 | 52.9825 | 92.8058 | 91.1917 | 91.3673 |
Table 9.
Processing time for the training in SVM using different values of sample size. In yellow the time for training the model with the selected optimized hyperparameter is shown.
Table 9.
Processing time for the training in SVM using different values of sample size. In yellow the time for training the model with the selected optimized hyperparameter is shown.
| N_Samples | Processing Time |
|---|
| 100 | 2′8″ |
| 250 | 12′26″ |
| 500 | 24′51″ |
| 750 | 47′21″ |
| 1000 | 1h18′2″ |
| 2000 | 1h33′36″ |
| 5000 | 3h4′25″ |
Table 10.
Training accuracy (on the left) and validation accuracy (on the right) RF tree depth and the number of trees optimization. R_i stands for rime ice, C_i for clear ice, and W_a for white aluminum. The test name is defined as xx_yy, where xx is the number of trees, yy is the depth. In yellow the selected optimized hyperparameter is shown.
Table 10.
Training accuracy (on the left) and validation accuracy (on the right) RF tree depth and the number of trees optimization. R_i stands for rime ice, C_i for clear ice, and W_a for white aluminum. The test name is defined as xx_yy, where xx is the number of trees, yy is the depth. In yellow the selected optimized hyperparameter is shown.
| Test (xx_yy) | Training Accuracy (%) | Validation Accuracy (%) |
|---|
| R_i | C_i | W_a | Overall | R_i | C_i | W_a | Overall |
|---|
| 50_30 | 70.5078 | 66.9162 | 56.3398 | 81.6832 | 55.3701 | 68.7615 | 60.2531 | 77.1311 |
| 50_40 | 69.8004 | 67.3592 | 56.2977 | 816582 | 54.1104 | 67.8014 | 60.6952 | 77.0461 |
| 50_50 | 69.5568 | 67.5865 | 55.8317 | 81.5282 | 53.0954 | 68.4173 | 60.8929 | 77.2861 |
| 50_60 | 70.0849 | 67.6036 | 54.2184 | 81.4681 | 53.5284 | 68.5125 | 60.6882 | 77.6211 |
| 75_30 | 68.8278 | 67.2374 | 55.5764 | 81.4281 | 53.9481 | 67.9496 | 60.4317 | 77.1311 |
| 75_40 | 69.9799 | 67.5952 | 56.2234 | 81.7932 | 53.4521 | 68.7778 | 59.3454 | 76.9912 |
| 75_50 | 69.5681 | 66.3261 | 55.0188 | 81.5732 | 53.0235 | 67.9594 | 59.4336 | 77.0561 |
| 75_60 | 68.8259 | 66.6204 | 53.4672 | 81.2381 | 54.9031 | 68.4853 | 61.2722 | 77.3711 |
| 100_30 | 67.2472 | 67.9566 | 54.3531 | 81.4881 | 56.2536 | 69.6554 | 61.6554 | 77.8161 |
| 100_40 | 71.1968 | 67.5524 | 56.8807 | 81.8782 | 54.2343 | 69.0955 | 60.4542 | 77.6161 |
| 100_50 | 70.6303 | 67.463 | 57.5832 | 81.3081 | 54.5098 | 68.7132 | 61.0991 | 77.3811 |
| 100_60 | 69.8595 | 67.5313 | 55.8442 | 81.3281 | 54.0376 | 69.2891 | 60.8715 | 77.5611 |
| 125_30 | 68.8588 | 66.3749 | 54.7497 | 81.2081 | 53.224 | 69.2393 | 59.2529 | 77.4511 |
| 125_40 | 69.0385 | 67.5875 | 55.7325 | 81.7182 | 52.5876 | 69.8535 | 60.451 | 77.6211 |
| 125_50 | 69.5795 | 67.8422 | 56.7398 | 81.7282 | 53.6558 | 69.1431 | 59.2657 | 77.3261 |
| 125_60 | 691205 | 66.6516 | 55.627 | 81.4181 | 53.7237 | 69.7354 | 60.792 | 77.7861 |
Table 11.
Processing time for the training in RF using different values of tree depth and the number of trees. In yellow the time for training the model with the selected optimized hyperparameter is shown.
Table 11.
Processing time for the training in RF using different values of tree depth and the number of trees. In yellow the time for training the model with the selected optimized hyperparameter is shown.
| Test | Processing Time |
|---|
| 50_30 | 2′59″ |
| 50_40 | 2′54″ |
| 50_50 | 2′57″ |
| 50_60 | 3′4″ |
| 75_30 | 4′50″ |
| 75_40 | 5′8″ |
| 75_50 | 5′4″ |
| 75_60 | 5′13″ |
| 100_30 | 6′55″ |
| 100_40 | 7′23″ |
| 100_50 | 7′25″ |
| 100_60 | 7′24″ |
| 125_30 | 9′23″ |
| 125_40 | 8′58″ |
| 125_50 | 9′1″ |
| 125_60 | 9′25″ |
Table 12.
Training accuracy (on the left) and validation accuracy (on the right) optimization of SVM number of the sample. R_i stands for rime ice, C_i for clear ice, and W_a for white aluminum. In yellow the selected optimized hyperparameter is shown.
Table 12.
Training accuracy (on the left) and validation accuracy (on the right) optimization of SVM number of the sample. R_i stands for rime ice, C_i for clear ice, and W_a for white aluminum. In yellow the selected optimized hyperparameter is shown.
| N_Samples | Training Accuracy (%) | Validation Accuracy (%) |
|---|
| R_i | C_i | W_a | Overall | R_i | C_i | W_a | Overall |
|---|
| 500 | 67.8201 | 62.1644 | 54.3074 | 80.9231 | 51.924 | 64.772 | 60.339 | 75.9512 |
| 1000 | 67.1179 | 64.2766 | 57.4959 | 80.463 | 51.8227 | 66.7797 | 62.0635 | 76.6062 |
| 1500 | 66.7683 | 64.8352 | 54.526 | 80.213 | 52.5362 | 67.6934 | 61.0333 | 77.0711 |
| 2000 | 68.616 | 66.6042 | 54.0258 | 80.283 | 53.9737 | 68.603 | 61.3453 | 77.0461 |
Table 13.
Processing time for the training in SVM using different values of the number of samples. In yellow the time for training the model with the selected optimized hyperparameter is shown.
Table 13.
Processing time for the training in SVM using different values of the number of samples. In yellow the time for training the model with the selected optimized hyperparameter is shown.
| N_Samples | Processing Time |
|---|
| 500 | 24′47″ |
| 1000 | 50′47″ |
| 1500 | 1h5′43″ |
| 2000 | 1h23′20″ |
Table 14.
Accuracy and processing time on the original dataset with random forest. R_i stands for rime ice, C_i for clear ice, and W_a for white aluminum.
Table 14.
Accuracy and processing time on the original dataset with random forest. R_i stands for rime ice, C_i for clear ice, and W_a for white aluminum.
| Test | Accuracy (%) | Processing Time |
|---|
| R_i | C_i | W_a | Overall |
|---|
| Test_1 | 41.7311 | 96.3272 | 69.0852 | 87.3775 | 13′22″ |
| Test_2 | 46.3158 | 96.3636 | 70.9497 | 88.8378 | 14′38″ |
| Test_6 | 53.2446 | 81.6364 | 69.1238 | 86.9974 | 12′37″ |
| Test_10 | 43.3428 | 52.7938 | 59.5405 | 81.5763 | 16′9″ |
Table 15.
Accuracy and processing time on the original dataset with SVM. R_i stands for rime ice, C_i for clear ice, and W_a for white aluminum.
Table 15.
Accuracy and processing time on the original dataset with SVM. R_i stands for rime ice, C_i for clear ice, and W_a for white aluminum.
| Test | Accuracy (%) | Processing Time |
|---|
| R_i | C_i | W_a | Overall |
|---|
| Test_1 | 50.4886 | 95.1975 | 88.0297 | 90.39 | 15′2″ |
| Test_2 | 56.6781 | 97.0843 | 82.5337 | 91.91 | 16′48″ |
| Test_6 | 56.5801 | 80.2994 | 72.5888 | 88.39 | 15′4″ |
| Test_10 | 63.1236 | 55.4054 | 64.4209 | 84.54 | 21′29″ |
Table 16.
Accuracy and processing time on the reduced hypercube (27 and 10 bands) with RF. R_i stands for rime ice, C_i for clear ice, and W_a for white aluminum.
Table 16.
Accuracy and processing time on the reduced hypercube (27 and 10 bands) with RF. R_i stands for rime ice, C_i for clear ice, and W_a for white aluminum.
| Bands N° | Test | Accuracy (%) | Processing Time |
|---|
| R_i | C_i | W_a | Overall |
|---|
| 27 | Test_1 | 41.7047 | 92.7769 | 69.1438 | 82.5365 | 25″ |
| Test_2 | 52.2158 | 93.28 | 74.6367 | 86.0572 | 28″ |
| Test_6 | 40.4255 | 70.997 | 67.0165 | 80.3561 | 31″ |
| Test_10 | 34.1797 | 54.2955 | 56.0549 | 76.3753 | 30″ |
| 10 | Test_1 | 43.5185 | 95.4392 | 69.9213 | 80.8962 | 24″ |
| Test_2 | 50.1825 | 94.8074 | 74.7238 | 83.2366 | 27″ |
| Test_6 | 38.9886 | 80.3754 | 59.7285 | 77.0154 | 26″ |
| Test_10 | 30.7018 | 57.7818 | 56.6897 | 73.0546 | 29″ |
Table 17.
Accuracy and processing time on the reduced hypercube (27 and 10 bands) with SVM. R_i stands for rime ice, C_i for clear ice, and W_a for white aluminum.
Table 17.
Accuracy and processing time on the reduced hypercube (27 and 10 bands) with SVM. R_i stands for rime ice, C_i for clear ice, and W_a for white aluminum.
| Bands N° | Test | Accuracy (%) | Processing Time |
|---|
| R_i | C_i | W_a | Overall |
|---|
| 27 | Test_1 | 45.2203 | 94.4217 | 70.1794 | 82.84 | 1′33″ |
| Test_2 | 62.4833 | 96.7882 | 72.6236 | 87.32 | 1′52″ |
| Test_6 | 53.3607 | 84.0215 | 68.2892 | 82.18 | 1′58″ |
| Test_10 | 45.7447 | 61.0082 | 59.3465 | 78.02 | 1′57″ |
| 10 | Test_1 | 44.1153 | 94.9749 | 70.038 | 79.37 | 1′35″ |
| Test_2 | 48.8522 | 96.144 | 72.9124 | 80.84 | 1′43″ |
| Test_6 | 49.3736 | 84.3806 | 67.8459 | 78.89 | 1′42″ |
| Test_10 | 33.6364 | 61.4594 | 55.3836 | 72.78 | 1′40″ |
Table 18.
Accuracy and processing time on the PC images with RF. R_i stands for rime ice, C_i for clear ice, and W_a for white aluminum.
Table 18.
Accuracy and processing time on the PC images with RF. R_i stands for rime ice, C_i for clear ice, and W_a for white aluminum.
| Test | Accuracy (%) | Processing Time |
|---|
| R_i | C_i | W_a | Overall |
|---|
| Test_1 | 37.8215 | 94.8214 | 65.92 | 75.8552 | 34″ |
| Test_2 | 41.1435 | 75.6241 | 78.6325 | 73.5947 | 39″ |
| Test_6 | 33.5897 | 68.3121 | 57.9747 | 69.4139 | 39″ |
| Test_10 | 46.1314 | 54.9505 | 72.1607 | 70.9542 | 41″ |
Table 19.
Accuracy and processing time on the PC images with SVM. R_i stands for rime ice, C_i for clear ice, and W_a for white aluminum.
Table 19.
Accuracy and processing time on the PC images with SVM. R_i stands for rime ice, C_i for clear ice, and W_a for white aluminum.
| Test | Accuracy (%) | Processing Time |
|---|
| R_i | C_i | W_a | Overall |
|---|
| Test_1 | 42.4956 | 95.3888 | 68.2451 | 78.16 | 59″ |
| Test_2 | 42.7742 | 81.6558 | 80.7923 | 78.24 | 1′5″ |
| Test_6 | 45.1613 | 77.8899 | 64.8072 | 76.05 | 1′16″ |
| Test_10 | 45.9184 | 56.5625 | 71.4886 | 72.29 | 1′48″ |
Table 20.
Accuracy and processing time on the RGN (red, green, and near infrared) images with RF. R_i stands for rime ice, C_i for clear ice, and W_a for white aluminum.
Table 20.
Accuracy and processing time on the RGN (red, green, and near infrared) images with RF. R_i stands for rime ice, C_i for clear ice, and W_a for white aluminum.
| Test | Accuracy (%) | Processing Time |
|---|
| R_i | C_i | W_a | Overall |
|---|
| Test_1 | 54.9565 | 69.7936 | 60.7158 | 77.6311 | 6′40″ |
| Test_2 | 36.1789 | 42.5788 | 35.2851 | 47.9226 | 6′36″ |
| Test_6 | 25.2031 | 33.7942 | 8.2353 | 30.9185 | 6′30″ |
| Test_10 | 34.7062 | 33.3841 | 44.8087 | 41.34 | 7′5″ |
Table 21.
Accuracy and processing time on the RGN images with SVM. R_i stands for rime ice, C_i for clear ice, and W_a for white aluminum.
Table 21.
Accuracy and processing time on the RGN images with SVM. R_i stands for rime ice, C_i for clear ice, and W_a for white aluminum.
| Test | Accuracy (%) | Processing Time |
|---|
| R_i | C_i | W_a | Overall |
|---|
| Test_1 | 52.2795 | 67.3587 | 63.1305 | 76.9362 | 22′13″ |
| Test_2 | 34.8404 | 41.2713 | 32.8609 | 46.8527 | 23′9″ |
| Test_6 | 25.8493 | 35.6347 | 10.6874 | 30.6135 | 23′55″ |
| Test_10 | 40.3123 | 37.1409 | 42.4566 | 42.375 | 25′21″ |
Table 22.
Accuracy and processing time on the RGBN(red, green, blue, near-infrared) image with RF and SVM. R_i stands for rime ice, C_i for clear ice, and W_a for white aluminum.
Table 22.
Accuracy and processing time on the RGBN(red, green, blue, near-infrared) image with RF and SVM. R_i stands for rime ice, C_i for clear ice, and W_a for white aluminum.
| Classifier | Accuracy (%) | Processing Time |
|---|
| R_i | C_i | W_a | Overall |
|---|
| RF | 57.9867 | 54.2284 | 83.7163 | 84.495 | 4′49″ |
| SVM | 62.3726 | 57.3843 | 88.1515 | 86.695 | 8′18″ |