Numerical Modelling of Bond Strength in Overmoulded Thermoplastic Composites
Abstract
:1. Introduction
2. Materials and Methods
2.1. Specimen Manufacturing and Cross-Tension Test
2.2. Overmoulding Simulation
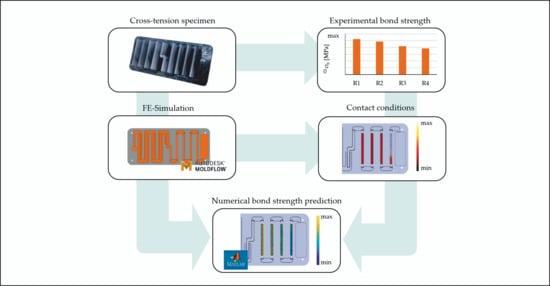
2.3. Workflow of Data Processing
2.4. Bond Strength Modelling Approach
3. Results and Discussion
3.1. Cross-Tension Test
3.2. Numerical Results
3.2.1. Simulation of Injection Moulding
3.2.2. Autohesion
3.2.3. Intimate Contact
3.2.4. Bond Strength
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A


References
- Verein Deutscher Ingenieure e.V. Werkstoffinnovationen für Nachhaltige Mobilität und Energieversorgung; Verein Deutscher Ingenieure: Düsseldorf, Germany, 2014. [Google Scholar]
- Siebenpfeiffer, W. Leichtbau-Technologien im Automobilbau. Werkstoffe-Fertigung-Konzepte; Springer (ATZ/MTZ-Fachbuch): Wiesbaden, Germany, 2014. [Google Scholar] [CrossRef]
- Gude, M.; Just, G.; Kaufhold, J.; Müller, M.; Stegelmann, M.; Meschut, G.; Gerkens, M.; Zäh, M.F.; Hofmann, D.; Greitemann, J.; et al. Chancen und Herausforderungen im Ressourceneffizienten Leichtbau für Die Elektromobilität. Forelstudie; Institut für Leichtbau und Kunststofftechnik (ILK) Technische Universität Dresden: Dresden, Germany, 2015; Available online: http://edok01.tib.uni-hannover.de/edoks/e01fb17/883204193.pdf (accessed on 7 May 2021).
- Akkerman, R.; Bouwman, M.; Wijskamp, S. Analysis of the Thermoplastic Composite Overmolding Process: Interface Strength. Front. Mater. 2020, 7. [Google Scholar] [CrossRef]
- Valverde, M.A.; Kupfer, R.; Wollmann, T.; Kawashita, L.F.; Gude, M.; Hallett, S.R. Influence of component design on features and properties in thermoplastic overmoulded composites. Compos. Part A Appl. Sci. Manuf. 2020, 132, 105823. [Google Scholar] [CrossRef]
- Geiger, M.; Ehrenstein, G.W. Werkstoff- und Prozessoptimierte Herstellung Flächiger Kunststoff-Kunststoff und Kunststoff-Metall-Verbundbauteile. Robuste, Verkürzte Prozessketten für Flächige Leichtbauteile; Lehrstuhl für Kunststofftechnik und Lehrstuhl für Mustererkennung; Meisenbach: Bamberg, Germany, 2003. [Google Scholar]
- Schijve, W.; Francato, G. New thermoplastic composite solutions for automotive lightweighting. JEC Compos. Mag. 2016, 103, 96–98. [Google Scholar]
- Behrens, B.A.; Bohne, F.; Lorenz, R.; Arndt, H.; Hübner, S.; Micke-Camuz, M. Numerical and Experimental Investigation of GMT Compression Molding and Fiber Displacement of UD-Tape Inserts. Procedia Manuf. 2020, 47, 11–16. [Google Scholar] [CrossRef]
- Behrens, B.A.; Raatz, A.; Hübner, S.; Bonk, C.; Bohne, F.; Bruns, C.; Micke-Camuz, M. Automated Stamp Forming of Continuous Fiber Reinforced Thermoplastics for Complex Shell Geometries. Procedia CIRP 2017, 66, 113–118. [Google Scholar] [CrossRef] [Green Version]
- Hopmann, C.; Michaeli, W. Einführung in die Kunststoffverarbeitung; 7. Aufl. s.l.; Carl Hanser Fachbuchverlag: München, Germany, 2015. [Google Scholar]
- Behrens, B.A.; Hübner, S.; Chugreev, A.; Neumann, A.; Grbic, N.; Schulze, H.; Lorenz, R.; Micke, M.; Bohne, F. Development and numerical validation of combined forming processes for production of hybrid parts. In Technologies for Economical and Functional Lightweight Design; Dröder, K., Vietor, T., Eds.; Springer Vieweg: Berlin, Germany, 2018. [Google Scholar]
- Bonefeld, D.; Giehl, S.; Haspel, J.; Jäschke, A.; Lahr, R.; Obermann, C.; Schmeer, S.; Schmuck, M.; Würtele, M. Kombination von Thermoplast-Spritzguss und Thermoformen kontinuierlich faserverstärkter Thermoplaste für Crashelemente (SpriForm). In BMBF-Forschungsbericht; Bundesministerium für Bildung und Forschung (BMBF): Berlin, Germany, 2011. [Google Scholar]
- Ye, L.; Ageorges, C. Engineering Materials and Processes. In Fusion Bonding of Polymer Composites; Springer Ltd.: London, UK, 2002. [Google Scholar]
- Hummel, S.; Knorr, L.; Karlinger, P.; Schemme, M. Eine Frage der Haftung. In Kunststoffe; Carl Hanser Verlag GmbH & Co. KG: München, Germany, 2017. [Google Scholar]
- Al-Sheyyab, A.; Müller, T.; Kühnert, I.; Schmachtenberg, E. Kurzer Prozess bei hybriden Strukturen. In Kunststoffe; Carl Hanser Verlag GmbH & Co. KG: München, Germany, 2007. [Google Scholar]
- Liebsch, A.; Koshukow, W.; Gebauer, J.; Kupfer, R.; Gude, M. Overmoulding of consolidated fibre-reinforced thermoplastics-increasing the bonding strength by physical surface pre-treatments. Procedia CIRP 2019, 85, 212–217. [Google Scholar] [CrossRef]
- Hürkamp, A.; Gellrich, S.; Ossowski, T.; Beuscher, J.; Thiede, S.; Herrmann, C.; Dröder, K. Combining Simulation and Machine Learning as Digital Twin for the Manufacturing of Overmolded Thermoplastic Composites. JMMP 2020, 4, 92. [Google Scholar] [CrossRef]
- Giusti, R.; Lucchetta, G. Analysis of the welding strength in hybrid polypropylene composites as a function of the forming and overmolding parameters. Polym. Eng. Sci. 2018, 58, 592–600. [Google Scholar] [CrossRef]
- Beuscher, J.P.; Schnurr, R.; Gabriel, F.; Kühn, M.; Dröder, K. Mould-integrated heating technology for efficient and appropriate processing of fibre-reinforced thermoplastics. Procedia CIRP 2019, 85, 133–140. [Google Scholar] [CrossRef]
- Loos, A.C.; Dara, P.H. Processing of Thermoplastic Matrix Composites. In Review of Progress in Quantitative Nondestructive Evaluation; Thompson, D.O., Chimenti, D.E., Eds.; Review of Progress in Quantitative Nondestructive Evaluation; Springer: Boston, MA, USA, 1987; pp. 1257–1265. [Google Scholar]
- Lee, W.I.; Springer, G.S. A Model of the Manufacturing Process of Thermoplastic Matrix Composites. J. Compos. Mater. 1987, 21, 1017–1055. [Google Scholar] [CrossRef]
- Mantell, S.C.; Springer, G.S. Manufacturing Process Models for Thermoplastic Composites. J. Compos. Mater. 1992, 26, 2348–2377. [Google Scholar] [CrossRef]
- Loos, A.C.; Li, M.C. Non-Isothermal Autohesion Model for Amorphous Thermoplastic Composites. J. Thermoplast. Compos. Mater. 1994, 7, 280–310. [Google Scholar] [CrossRef]
- Chao, M.; Gillespie, J.W., Jr. The Influence of Healing and Bondline Thickness on the Mechanical Performance of Fusion-Bonded Thermoplastic Composite Joints. Mov. Forw. 50 Years Leadersh. Adv. Mater. 1994, 39, 2023–2037. [Google Scholar]
- Shi, H.; Villegas, I.F.; Bersee, H.E.N. Modelling of heat transfer and consolidation for thermoplastic composites resistance welding. In Proceedings of the 18th International Conference on Composites Materials, Jeju, Korea, 21–26 August 2011. [Google Scholar]
- Großmann, J. Einfluß von Plasmabehandlungen auf die Haftfestigkeit vakuumtechnisch hergestellter Polymer-Metall-Verbunde. Ph.D. Thesis, Friedrich-Alexander-Universität Erlangen-Nürnberg, Erlangen, Germany, 2009. [Google Scholar]
- Wool, R.P.; O’Connor, K.M. A theory crack healing in polymers. J. Appl. Phys. 1981, 52, 5953–5963. [Google Scholar] [CrossRef]
- Wool, R.P.; O’Connor, K.M. Time dependence of crack healing. J. Polym. Sci. B Polym. Lett. Ed. 1982, 20, 7–16. [Google Scholar] [CrossRef]
- Khan, M.A.; Mitschang, P.; Schledjewski, R. Identification of some optimal parameters to achieve higher laminate quality through tape placement process. Adv. Polym. Technol. 2010, 29, 98–111. [Google Scholar] [CrossRef]
- Tierney, J.; Gillespie, J.W., Jr. Modeling of In Situ Strength Development for the Thermoplastic Composite Tow Placement Process. J. Compos. Mater. 2006, 40, 1487–1506. [Google Scholar] [CrossRef]
- Hürkamp, A.; Gellrich, S.; Dér, A.; Herrmann, C.; Dröder, K.; Thiede, S. Machine learning and simulation-based surrogate modeling for improved process chain operation. Int. J. Adv. Manuf. Technol. 2021. [Google Scholar] [CrossRef]
















| Variable Parameters | Set 1 “Low” | Set 2 “Ref1” | Set 3 “HiMelt” | Set 4 “Ref2” | Set 5 “Ref3” | Set 6 “HiOrg” | |
|---|---|---|---|---|---|---|---|
| Temperature of organo sheet | 50 | 50 | 50 | 80 | 80 | 160 | |
| Temperature melt | 240 | 240 | 280 | 240 | 280 | 240 | |
| Tool temperature | 50 | 50 | 50 | 80 | 80 | 50 | |
| Holding pressure | [bar] | 600 | 900 | 900 | 900 | 900 | 900 |
| Constant parameters | |||||||
| Pressure-switchover | [%] | 90 | |||||
| Holding time | [s] | 10 | |||||
| Injection speed | [cm3s−1] | 50 | |||||
| Cooling time | [s] | 30 | |||||
| 220 °C | 240 °C | 260 °C | 280 °C | |
|---|---|---|---|---|
| Welding time | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Behrens, B.-A.; Dröder, K.; Brunotte, K.; Wester, H.; Hürkamp, A.; Ossowski, T.; Lorenz, R. Numerical Modelling of Bond Strength in Overmoulded Thermoplastic Composites. J. Compos. Sci. 2021, 5, 164. https://doi.org/10.3390/jcs5070164
Behrens B-A, Dröder K, Brunotte K, Wester H, Hürkamp A, Ossowski T, Lorenz R. Numerical Modelling of Bond Strength in Overmoulded Thermoplastic Composites. Journal of Composites Science. 2021; 5(7):164. https://doi.org/10.3390/jcs5070164
Chicago/Turabian StyleBehrens, Bernd-Arno, Klaus Dröder, Kai Brunotte, Hendrik Wester, André Hürkamp, Tim Ossowski, and Ralf Lorenz. 2021. "Numerical Modelling of Bond Strength in Overmoulded Thermoplastic Composites" Journal of Composites Science 5, no. 7: 164. https://doi.org/10.3390/jcs5070164
APA StyleBehrens, B. -A., Dröder, K., Brunotte, K., Wester, H., Hürkamp, A., Ossowski, T., & Lorenz, R. (2021). Numerical Modelling of Bond Strength in Overmoulded Thermoplastic Composites. Journal of Composites Science, 5(7), 164. https://doi.org/10.3390/jcs5070164