Pulsed Dielectric Barrier Discharges for Gas-Phase Composition Control: A Simulation Model

Featured Application

Control or at least prediction of the gas-phase composition in atmospheric pressure cold plasmas is very important to evaluate the potential of plasma treatments, which could be considered in several applications, from health and environmental processes targeting hazard agents to the production of advanced materials through suitable surface functionalization.

Abstract

We present results obtained from the numerical simulation of the gas-phase chemical kinetics in atmospheric pressure air non-equilibrium plasmas. In particular, we addressed the effect of the pulsed operation mode of a planar dielectric barrier discharge. As conjectured, the large difference in the time scales involved in the fast dissociation of molecules in plasmas and their subsequent reactions to produce stable chemical species makes the presence of a continuously repeated plasma production stage unnecessary and a waste of electrical power and efficiency. The results on NOx remediation, ozone production, water vapor and ammonia dissociation are discussed. A few comparisons with experimental findings in a dielectric barrier discharge reactor already used for applications are also briefly addressed. Our results clearly indicate a pattern for the optimization of the discharge using a carefully designed repetition rate and duty cycle.

1. Introduction

Dielectric barrier discharges (DBDs) are a widely employed device to obtain non-equilibrium plasmas at or near atmospheric pressure, with a limited power consumption [1,2,3,4,5]. Their main feature is the autoregulation of the electric current intensity and of the gas temperature, which is obtained by avoiding any direct pattern through the gas gap joining the electrodes, usually interposing some dielectric materials between them. The discharge electric current is regulated by its delivery of charges accumulating on the insulating surfaces, counterbalancing the externally applied electric fields and quenching the electrical breakdown [1]. At or near atmospheric pressure, the discharge develops into narrow filaments where an ionizing wave is propagating along their axis, usually having small transverse sizes. The duration of the discharge process is usually very short, whereas the charge density could be quite high [1]. The steady-state operations required by applications can be achieved by a repetition, on average, periodical, of such discharge events filling, in the best case uniformly, the gas gap. To remove the charge accumulated in the discharge region and its surrounding surfaces, the discharge is normally sustained by applying an oscillating voltage to one of the electrodes at kHz frequencies, although different waveforms of HV signals and even unipolar pulses can be employed. In the simplest situation, the changing sign voltage dissipates away the charge deposited on the dielectric surfaces, and a new filament with the current flowing in the other way could originate from the same location on the insulating material. What we would like to point out is that each discharge is very brief, with intervals of dead time between one event and another. On the other side, they appear as separated also regarding the space location, since, at least in small gaps, they develop in very slim channels (with typical radii R about a hundred micrometers [2]), whereas their separation is generally much larger, in the order of the gap size and so a few millimeters [1,2].

The relevant observation, concerning our topic, is that in such an environment, the local gas-phase composition is controlled both by the happening of one of the discharge paths (usually a very fast phenomenon) and by the duration of the quiet time intervals between two consecutive events. At later times, diffusion, both perpendicular and parallel to the discharge filament paths, leads to mixing and leveling of the gas phase, followed by the macroscopic diffusion, or advection if present, from the whole discharge region. The main topic we would like to investigate here is whether the interplay between the two phases could be altered and somewhat directed by delivering the discharges in time bunches, using suitable duty cycles, a task that could be provided by advanced pulsed HV generators [6,7].

To this purpose we reformulated our previous model, which simulates the chemical kinetics of atmospheric pressure discharges produced by DBD devices [8,9], in order to embody the effect of a pulsed operation mode on the gas phase composition. We then studied a few suitable cases, where pulsed operation could have an impact.

The paper is structured as follows. First, we present the numerical simulation of the chemical kinetics in the gas phase of a single air microdischarge. Then, we discuss the results of the numerical study of pulsed operation in a DBD reactor, taking into account the effects of multiple discharges and duty cycles on the development of the gas-phase chemistry. We then present some case studies. In particular, we discuss the dynamics of ozone, one of the main discharge outputs, and how this is modified by the pulsed operation mode. In the context of volatile organic compound (VOC) remediation, we discuss the prospect of abatement of nitrogen oxides by pulsed DBD. Finally, using an extended model suitable for simulations of plasmas in humid air, we present some observations concerning the chemical kinetics of water vapor and ammonia in a pulsed DBD reactor.

In the end, we discuss the findings of an experimental campaign, aimed at VOC remediation and air purification [10,11]. Targeted simulations, mirroring, at best, the experimental conditions, were performed to compare actual results with the numerical predictions.

Many results about DBD in air have been collected both from the experimental and from theoretical points of view. About the latter, the simulation of the chemical and physical phenomena characterizing DBD plasmas in air is not trivial. Three main methods have been applied to simulate non-thermal plasmas [12]: the kinetic approach [13], the fluid one [14,15] and some global models [16]. Ozone production in a surface DBD was studied by using a simple parametric model in [17]. The model was validated against some experimental ozone density measurements. They also observed ozone depletion through quenching reactions at a high power level. Another paper studied the chemical species concentration produced in a surface DBD reactor in humid air. The simulation comprised more than 600 reaction paths [18]. Another parametric model [19], based on a limited reaction paths of 36 reactions, was used to study the interplay between O₃ and NOx evolutions in a plasma actuator device. Another approach proposed a two-stage model, including the discharge and the afterglow, to study the main plasma chemistry processes of atmospheric pressure air plasmas including 103 reaction paths [20]. Modeling of nanosecond pulse discharges in atmospheric pressure mixtures is focused mainly on the very short timescales of the discharge development and its effects, for instance, in energy applications [21].

2. Materials and Methods

Our aim was to develop a framework suitable to investigate the gas-phase composition of an atmospheric pressure discharge, as it develops in a DBD reactor. Multiple breakdown events happen and repeat in different, but partially superimposing, space locations and times. The main point is whether this superposition could be exploited to control the evolution of the discharge gas-phase composition, thus tailoring the production or destruction rate of specific targeted compounds. The first step was to formulate a simplified model that allows one to simulate the microdischarge formation [8]. Then, we addressed the task to take into account the effects arising from the reiterated applications of several discharge events according to some definite spatial and temporal patterns.

As already mentioned, the electric discharge in DBD is made up of narrow current filaments, each having lifetimes of a few nanoseconds. They can be modeled as isolated events in time and space. Several models [22,23,24,25] and many experimental details [26,27,28,29,30] have been collected to obtain a picture of the formation, development and propagation of these events, which show a remarkable common character, even in different kind of DBDs [1]. The development of the discharge filaments is guided by the electron avalanche multiplication that happens in the strong field ahead of the ionizing wave (which could reach values of about 5–15 × 10⁶ V/m) and typically travels very fast (with velocities in the 10⁵–10⁶ m/s range). The discharge filament body then consists of a thin channel of weakly ionized gas, almost quasi-neutral (with densities n+~n⁻ of the order of 10¹³–10¹⁵ cm⁻³). When the spreading ionization area reaches the insulator material that prevents the direct contact with the cathode pole, the conductive ionized gas supports a small electrical current, which quickly decays because of the nearby space charge located at the dielectric surface [1].

With this in mind, we could focus on what happens at a fixed position along the discharge filament path. The picture is that the electric field will increase very quickly from its local unperturbed value as the ionizing wave approaches and then it decays almost as fast to the much smaller value it assumes in the filament channel. In fact, it should be remembered that at high pressures, electrons move along the electric field at the drift velocity and almost instantaneously (ν_m⁻¹~0.3 ps, ν_E⁻¹~50 ps [31]) reach a mean energy determined by the amplitude of the field there. This behavior will control both the filament propagation and the ionization strength. On the other hand, ion inertia keeps them practically still and substantially cold, almost at the set temperature. The effect then will be that of an ionizing wave quickly propagating between the two dielectric surfaces, with the local charge density increasing as the wave passes by. This affects not only the formation of the discharge filament but also the chemical composition of its gas phase. Indeed, from the chemical kinetics point of view, the process can be seen as consisting of an almost instantaneous phase, during which energetic electrons produce new electrons and ions, but also atoms and more generally radicals, out of the impact dissociation processes on the initial gas-phase molecules. This event is followed by a phase in which electrons cool down very quickly and reach lower temperatures, effectively ending the efficient fragmentation conditions. It should be pointed out that existing models could be used to predict the distribution and the intensity of the electric field pulses during their movement in the gas gap, depending on the electrode geometry and initial gas-phase composition [11,22]. The general picture, however, shows that the dependence from the position along the filament path is not so large, apart from the region near the dielectric surface. So, in order to keep complexity small, we chose to neglect such differences and formulated the model assuming uniformity along the filament path. To greatly simplify the geometry, the filament body was idealized as that of a thin cylinder, with a circular cross-section. The numerical value of the radius has to be considered as one of the free, tunable parameters of the simulation, even if we considered a value of 100 µm as the reference, as discussed above [31]. The cylinder height, which corresponds to the discharge gap, was set to 0.8 mm, somewhat typical and equal to a few previously performed laboratory experiments [32]. A second approximation was introduced to treat the ionizing wave. In the model, it was idealized as a pulse of the electric field strength uniform in the head of the developing filament. The pulse is, therefore, characterized only by an electric field amplitude E_max and by the duration τ_s of it (about 2 ns, based on the model in ref. [11]). Although a bit rough, such a simplification embodies all the relevant phenomena for our aims. This saves a lot of time and reduces complexity, since we do not have to recalculate the ionization and dissociation rates during the ionizing wave passage. A tricky point needs a little more clarification. At the start of the simulation, as the ionizing wave arrives, the electron density starts to increase very strongly, almost exponentially. Because of this behavior, the total amount of ions and radicals produced during the wave passage is set mainly by the actual value reached by the electron density at the end of the pulse [9]. In practice, it happens to be largely independent from the time length of the ionizing wave and from the initial electron density. So, the value of τ_s was fixed to 2 ns in these simulations. The truly variable parameter was then the electron density reached after the passage of the ionizing wave. As a reference, we considered a density of 1.2 × 10¹⁴ cm⁻³, based on the typical charge transported by microdischarges, of about 0.7 nC [10,33]. This value is also in the same range of other reported results [34]. A discussion of the effect of the electron density on the chemical kinetics of the discharges can be found in our previous works [8,9].

Thanks to the approximations introduced, the model can be classified, from a chemical engineering point of view, as a well-mixed reactor with cylindrical geometry [35]. A further approximation is applied to treat the spatial profiles of the concentrations of the different chemical species. Because of the assumed uniformity along the filament axis, diffusion along this direction is neglected and concentrations are independent from the axial coordinate. The transverse profile of the concentration is described in terms of the normal modes dictated by the geometry (here, as already stated, a cylindrical one) [36]. The gas-phase composition in the reactor is determined by the concentrations of the different N species considered by the model, which now only depend on time. Their time evolution is controlled by the balance between the chemical reactions involving the reactive species and the transport processes. It could be calculated by integrating each balance equation for the density n_k of the kth species:

$$\frac{\mathrm{d}{\mathrm{n}}_k}{\mathrm{dt}}={\sum }_{i<j=1}^{N}K(i+j\to k){\mathrm{n}}_i{n}_j-{\sum }_{\mathrm{i},\mathrm{j}=1}^N \mathrm{K}(k+i\to j){\mathrm{n}}_k{n}_i+\frac{D_k}{{\Lambda }_k^2}{n}_k$$

Here, K is the reaction rates for the gas-phase reactions, including those involving electrons and ions, whereas D and Λ are the diffusion coefficient and effective length [25]. In particular, the coefficient Λ depends only on geometrical factors and on the sticking coefficient S of each chemical species [35]. Adsorption on the dielectric barrier could easily be included but, because of the much smaller extension of the filament radius with respect to the discharge gap, it turns out to be negligible, apart from ions. Since all the coefficients are constant, the abovementioned equations form a system of coupled differential equations, which has been integrated by using an adaptive Runge–Kutta routine [8].

The choice of ions and molecules to be included in the model was based on existing experimental data based on emission spectroscopy or mass spectroscopy. For atmospheric air, here, we considered only oxygen and nitrogen species in a 20:80 mixture. A set of 10 neutral, including different nitrogen oxides, 10 metastables (atomic nitrogen N* = N(²D), N** = N(²P), molecular nitrogen N2* = N₂(A ³Σ_u⁺), N2** = N₂(B ³Π_g), N2*** = N₂(C ³Π_u), N2**** = N₂(a ¹Σ_u⁻), atomic oxygen O* = O(¹D), O** = O(¹S) and molecular ox-ygen O2* = O₂(a ¹Δ_g), O2** = O₂(b ¹Σ_g⁺)) and 9 charged, species was included in the simulations presented here. Rate constants for neutral gas phase, charge exchange and ion recombination reactions were taken from literature referenced in [8,9]. A strict cold plasma approximation was used. So, reaction rates for ions as well as neutral species are evaluated at a set temperature, that is, 300 K, even if this could be changed if needed for comparison with experiments. In atmospheric pressure air plasmas, neutral rates also depend on the vibrational states of molecules, in particular those of nitrogen molecules [37,38]. This aspect could be taken partially into account considering the mean energy associated with vibrational states (usually referred to as the vibrational temperature) and updating the reaction rates accordingly [9,39]. Such a rough approximation avoids an overwhelming multiplication of the species numbers and of often largely unknown reaction rates, by separately considering the individual vibrational states. From the previous discussion, the central role played by electron impact reactions is clear, whose rates used in this study were already discussed in our previous works [8,9]. For simplicity, such rate constants were evaluated assuming a Maxwellian energy distribution function for electrons, described then by only one parameter, their temperature T_e. This could be better thought of as a determination of the mean electron energy, which, in turn, is linked to the local electric field value through the Boltzmann equation [31]. This value should be used in order to make a direct comparison between this simulation and other ones or with the experimental measurements [34]. So, instead of a specific value of the electric field strength E_max in the ionizing wave pulse, we considered an electron temperature value of 4 eV as reference [8]. In the afterglow, after the ionizing wave passage, the electric field is much smaller [22] and so is the energy of the electrons, which was approximated by the set temperature [8]. A discussion of the effect of the electron temperature during the discharge pulse on the chemical kinetics can be found in our previous works [8,9]. Together with the electron density, those are the two main parameters used to perform simulations and are discussed below. Further, a total of 410 reactions and 43 diffusion processes were taken into account in the simulations.

3. Results

In order to grasp the relevant time scales in the build-up of the plasma gas phase, we present the results of a simulation that models the evolution of a single discharge happening once. Both neutral and ion species densities are shown as a function of time, respectively, in Figure 1a for stable species, Figure 1b for charged species and Figure 1c for metastable neutral states. Throughout the paper, we will use double logarithm scales. This allows us to appreciate the evolution of minority ions and molecules and their build-up times. It also permits us to appreciate the effects of the fast ionizing wave together with the slower features connected with chemical reactions, repetitions and diffusion processes.

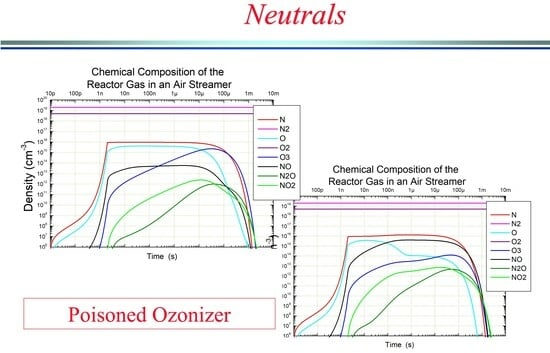
As might be expected, during the time length τ_s (2 ns) needed for the ionizing pulse sweep, O and N atoms are produced, in the dissociation from parent molecules by electron collisions (oxygen atom density exceeds nitrogen, as predicted at the chosen value of the electron temperature). Subsequently, the development of the gas phase starts. It turns out that ozone is continuously produced until its density reaches the same order of that of the atoms. Afterwards, atomic oxygen density decays, as atoms are substituted by ozone as the main product in the gas phase. Ozone exceeds oxygen atoms after some time at 11 µs. The peak density reached by ozone was about 1.1 × 10¹⁵ cm⁻³ after about 32 µs. Subsequently, the diffusion processes kick in. They are able to sweep away the whole modified gas phase in milliseconds. Nitrogen oxides accumulate too, albeit at a somewhat slower rate because of the lower reactivity of nitrogen, always remaining as a minority in the gas phase. The composition of the charged species is much more complex. First of all, the temporal dynamics of charged species appears to be faster than that of neutrals. This is mostly due to the higher rates of ion–ion recombination, charge exchange reactions and of electron attachment. As expected, all the charged species increase almost exponentially during the streamer development time (2 ns). Afterwards, the total charge density begins to decrease because of recombination. Another two processes then occur to modify the charged gas phase. In the presence of oxygen, after the pulse ends, when the electron temperature decreases below about 2 eV, electrons are quickly removed due to attachment processes. Under the reported setting, the O₂¯ molecule turns out to be the main negative ion and the overcoming happens after just 14 ns. On the other hand, positive charged species composition is mainly determined by charge exchange reactions on the still majority N₂ and O₂ molecules. They quickly remove atomic ions and leave O₄⁺ as the majority ion. In our condition, this substitution is even readier than that of electrons. Subsequently, ion density, both positively and negatively charged species, displays the same trend: a decrease in time (formally described by a power-law that appears as a straight line in our logarithm scale pictures) controlled by the ion–ion recombination process, followed by a decay due to diffusion towards the dielectric surfaces (formally described by a negative exponential curve), when density decreases at such low values that recombination becomes negligible with respect to transport. At the minority level, we also observe a brief time window where the formation of NO⁺ ions is observed, together with its subsequent removal. Excited molecules are produced during the passage of the ionization wave, just as ions and dissociated atoms. Most of them are quickly quenched by reactions in the gas phase or radiative decay after the end of the ionization phase. Metastable states (narrowly excited states that cannot radiatively decay because they have only forbidden transitions, which make their lifetimes much longer) and other weakly interacting states remain in the discharge gas phase. Their lifetime is, thus, determined by the slower quenching reactions. The most lasting are metastable molecular oxygen states, which accumulate in the discharge gas phase. In the end, they are removed by diffusion together with all the other stable discharge products. We could also observe that metastable atomic states start accumulating only after the production of a suitable amount of the parent atoms and remain as a minority in the chosen conditions.

When the discharge happens more times, that is, we introduce a repetition at a defined frequency (above the kHz range), the interplay between the dissociation and formation of oxygen atoms and the reactions in the gas phase leading to the ozone production is exposed. The density of the same neutral and charged species considered before is displayed in the same logarithm scale as a function of time in Figure 2, considering a repetition period of 25 µs. For ease of comparison, only the densities calculated at the end of each discharge are reported on the graph at later times. These conditions correspond to a symmetric DBD fed by a supply with a 20 kHz sinusoidal HV signal, where the discharges happen and repeat in each half cycle. This broadly corresponds to the experimental conditions we investigated previously [14,16]. We discussed the effect of the repetition frequency on the chemical kinetics evolution of discharges in our previous papers [9]. The first observation is that after a very small number of repetitions, in the order of ten, the gas phase reaches a steady composition at the end of each discharge. Since the repetition rate chosen is longer than the ozone overcoming times, this is the species that dominates the gas phase. More specifically, an equilibrium is reached between the ozone produced in the post-discharge phases and that removed by diffusion or destroyed in the discharges. Under such conditions, ozone reaches a steady-state concentration of about 4.7 × 10¹⁵ cm⁻³ (about 180 ppm), whereas atomic nitrogen and oxygen densities are ten-times smaller and nitrogen oxides more than one hundred less. The same picture is also reported for charged and excited species. Although the overall behavior is similar to that already reported, we noticed that minority negative ions could accumulate because of the repetitions. As for the metastable states, accumulation happens only, as expected, for the species whose quenching time is long enough with respect to the repetition period. A deeper analysis shows that the key timing is whether the repetition frequency allows the multiple discharges to happen after the overcoming of atomic oxygen by ozone but before the diffusion has kicked in. By tuning the time interval between multiple discharges, it is possible to define an optimal periodicity under which the ozone flow outside the discharge region is maximal. This condition roughly corresponds to the one when the maximal concentration is reached at the end of the discharge. However, this condition is not considered to be the best production of ozone achievable, since one could observe that the multiple repetitions of discharges also have the effect to destroy a fraction of the ozone formed in the time after the previous discharge. This is the way we are able to consider whether a duty cycle operation mode could affect and possible increase, for instance, the ozone production. On the other hand, continuous operation implies steady energy injection and, thus, consumption, even where sufficient active species are already present and not really needed to increase stable species, notably ozone build-up.

3.1. Efficient Ozone Production

There is substantial interest in the efficient production of ozone for practical applications. Oxidation by ozone is quite efficient. In fact, it was employed in water treatment as a powerful cleaning agent [40,41]. Many more applications of ozone have been proposed or introduced in medical treatments and in food sector applications. It was observed that, already, brief treatment times and small amounts of ozone are able to control infective agents, be it bacteria, molds, yeasts, viruses or other parasites. The ozone treatments were considered as a tool for contaminant inactivation on products, such as meat, eggs, fish, fruits, vegetables and dry foods [42,43]. Ozone has also been proposed in health treatments, for instance, in skin or other biological tissue, as an antimicrobial agent [44]. Other medical applications include dentistry, for example [45].

When considering a model for pulsed operation mode, we need to make some definite choices describing the kind of device setup that will be the object of the simulation. In order to maintain the overall geometry implemented in the previously developed software, we define a cylindrical gas gap (like that one between two symmetric, equally insulated electrodes, consisting of a couple of parallel plates). The idealized device has an active volume made of a cylinder, with a diameter of 35 mm and a height of 0.8 mm. According to an idealized parallel plane geometry, the electric field is considered as constant in intensity and directed parallel to the cylinder axis in the whole discharge volume. Microdischarges in the form of thin channels aligned to the axis, like those discussed in the previous section, are thought to repeat with the same probability. This applies to each position in the considered discharge volume, ignoring any edge effect. The model will consider an effective repetition rate, which is connected by the period between subsequent active phases of the applied voltage. The effective rate value, however, is set by the ratio between the microdischarge-affected volume and that of the whole device and also by the number of microdischarges during each active phase. This could be rationalized as a model where all the microdischarges are equal to an average, typical one, which is uniquely defined by its assumed plasma parameters (the same employed in the model discussed). Such a physical agent acts with a fixed, constant repetition rate, and the same evolution is thought to happen at each position in the discharge volume (a so-called zero-dimensional model of plasma) [23]. It could appear as a roughly idealized simplification of the realistic device operations, but we feel that it does not overlook the relevant evolution and it makes it easier to check what is the overall imprint of plasma parameters as they act on the discharge and device performances. As a matter of fact, a sort of uniformization of the gas gap composition is also present in the experiments because of diffusion processes. Also, the great number of microdischarges and voltage cycles involved at different locations in the device volume produces a smearing of the overall performance. This is true even if experiments confirm that each microdischarge has non-negligible variability in terms of amplitude, duration and delay between subsequent events [32]. In any case, when considering a specific location in the discharge gap, it is possible that no plasma filaments pass through it in some of the cycles. Although addressing this requires a dedicated model and suitable experimental information, we think that the discussion about the effects of a duty cycle, that we now undertake, can shed light even on this more complicated situation. As implied by the previous sentences, we included diffusion processes outside the device volume, consisting of mainly radial transport. They were added to the model in a straightforward way, just as the diffusion outside the single streamer channel [36]. These simulations lead to results that are broadly in agreement with the evolution shown in Figure 2. So, the whole gap region reaches a steady composition with an equilibrium between outwards diffusion and the production of ozone and other compounds due to the repeated discharge processes.

We were then in the position to introduce an ideal pulse operation. Again, a few simplifications were implemented. The operating mode was imagined as consisting of a fixed number of equal active periods separated by quiet intervals. Based on the duration of the on (τ_on) and off (τ_off) periods, we can define a duty cycle, which was used as a figure of merit of the process. It is not surprising that the densities of the neutral species in the gas phase show an evolution that broadly reproduces that already observed in continuous operation simulations. The important novelty is that, during the periods without discharges, ozone and nitrogen oxides accumulate, while oxygen and nitrogen atoms are consumed, as in the case of a single discharge afterglow. We were happy to note that the equilibrium was reached again in a few repetitions of duty cycles, generally less than some tens. This allowed us to maintain the simulation length and machine times relatively affordably. The concentration reached by ozone at the end of the last pause period was estimated and is displayed in Figure 3 as a function of the pause period duration. It could be grasped how the ozone concentration increases with respect to the continuous repetition mode, with an optimal pause duration, before it decreases for much longer pauses. When considered as a function of the power absorbed by the DBD reactor, the effect is even more impressive, with a huge increase in the production efficiency and energy saving. Another quite interesting result lies in the ozone concentration, becoming almost independent from the duration of the on period; in our case, it was tested between 250 and 2000 μs. This arises from the steady state reached after a small number of repetitions. Any prolongation of the active time is not needed.

3.2. NOx Remediation

The removal of NO and other nitrogen oxides from environment is a relevant problem concerning pollution control [46]. Nitrogen oxides stay in the low atmosphere for several days and enter cycles producing ozone, causing smog. Nitrogen oxides are mainly produced as a by-product in combustion processes in free air. For instance, in diesel engine exhaust, NO can reach 200–500 ppm and NO₂ 50 ppm [47]. On the other hand, understanding the capability of plasma treatment in the dissociation of such molecules can provide some insight into the much more complex pattern involved in the plasma interaction with more harmful volatile compounds. So, we slightly modified our simulations to consider the effect of plasma on a gas phase composed of air contaminated by small levels of nitrogen oxides. In order to speed up the calculations, we neglected the contribution to dissociation given by excited states, for which the precise reaction rates with nitrogen oxides are also poorly known. No diffusion of contaminants from outside is considered here to allow the system to reach chemical equilibrium. Such a process kicks in, however, only at late times, considering discharge repetition times (here 20 kHz, but several kHz generally). In Figure 4, we display the results of a simulation, with a continuous compared with a pulsed discharge. As we found previously [39], NO could be removed and transformed into ozone and, to a smaller extent, to other more oxidated states. In the reported simulations, we used the same plasma parameters as above, but we started from a gas phase containing 500 ppm of NO, that is, a density of 1.3 × 10¹⁶ cm⁻³. After a few discharges, NO started to decline and was almost completely removed in a short period, oxidated initially by O atoms and then, when atomic radicals disappeared, consumed in reactions with ozone and NO₂. In the final state, it was substituted mainly by ozone (about 10 ppm). A small amount of NO₂ (1.6 ppm) and N₂O (0.8 ppm) was produced too, while other oxides did not form with appreciable concentration. The NO equilibrium level decreased to 0.8 ppm. From the figure, it could also be appreciated that transition in the gas phase takes more time with respect to those involved in ozone formation. From the time evolution point of view, we observe that, while the transition from oxygen atoms to ozone happens after about 10 μs, NO transition to ozone starts only after 175 μs, and equilibrium is reached after about 0.5 ms. The overall effect of the duty cycle is not immediately perceivable. However, a closer look reveals its effects. Part of the NO equilibrium concentration is built up by the plasma itself. In this case, the application of a 50% duty cycle (see Figure 4) could improve the reduction in the NO level (here, 0.1 and 0.5 ppm after the off/on phases), besides cutting to half the energy consumed.

3.3. Water Vapor Dissociation

A step forward could be performed by extending the modeling to perform simulations of a humid air plasma gas phase. This required a substantial expansion of both the number of species considered and of their reaction database [24,48]. Based again on available experimental information, we gathered a set, including 20 neutral and 21 charged states, with 667 reactions. In a preliminary effort, again, excited molecules were excluded. Here, we present only a few results to demonstrate the potential of the model. The density of the neutral and charged species is displayed in a log-log scale as a function of time in Figure 5, using the same parameters already shown for the dry air simulations but now with a water vapor partial pressure of 1 mbar. A pattern similar to dry air conditions could also be recognized in the wet atmosphere. After a few microseconds, the main product remains as ozone, whereas the charge phase consists primarily of oxygen positive and negative ions. However, here, the 0.1% concentration of water vapor is sufficient to deeply affect the details. NO⁺ and H₃O⁺ ions become significant and slowly add to the ion phase, while, albeit only partially, OH⁻ negative ions grow. Hydrogen ions remain as the minority, and a small amount of ammonia NH₄⁺ also formed. We could then inspect the behavior of the neutral ga -phase, as displayed in Figure 5a. The main chemical kinetics effect remains the reaction of atomic oxygen to produce mainly ozone, with some concentration of nitrogen oxides. In wet air, however, even starting with such a limited amount of water vapor is sufficient to alter the evolution. Ozone formation is somewhat inhibited, reaching only 10 ppm concentration. The production of hydrogen or ammonia appears not to be favored, with only a trace of HNO molecules slowly building up. Atomic oxygen, but also atomic hydrogen and oxydril radicals, react and are consumed. The other main components of the gas phase then become nitrogen oxides (N₂O, NO and NO₂ mainly, compared to NO₃ and N₂O₅) and hydrogenated water (O₂H favored more than H₂O₂ itself), whose limited reactivity allows for accumulation. At higher initial water vapor concentrations, ozone is substituted by those compounds in the final neutral gas phase. This pattern of chemical kinetics appears to be substantially solid. It could be traced by increasing water vapor concentration or the neutral gas temperature, which allows us to investigate even larger wet conditions as vapor pressure is increased. The transition from dry to wet air plasma conditions, characterized by the substitution of ozone and nitrogen oxide ions in favor of species originated from water, can be set at around 1% water vapor concentration. How this pattern is modified by applying a pulsed regime of discharges could be observed from the trends displayed in Figure 6.

A duty cycle of 5:5 and 2:8 on/off discharges was applied. As could be guessed, the final gas phase looks similar, but we observe, once more, an increase in the final output of ozone using a lower amount of energy for the electrical discharges. The efficiency is higher by 65% and 150% in the two instances.

3.4. Ammonia Treatment

As a by-product of the wet air chemical kinetics environment, our simulations allow us to discuss another interesting point. As stated before, a meaningful description of the plasma gas phase includes hydrogen and ammonia compounds too. So, the model could also be used to discuss the chemical kinetics of discharges containing ammonia in the initial mixture. This chemical could be harmful at high concentrations, and it is produced in a variety of processes, both natural and industrial [49]. This could also provide some insight into the much more complex pattern involved in the plasma interaction with more harmful volatile compounds.

The results of the simulation are displayed in Figure 7, where the density of the neutral species is reported in a log-log scale as a function of time. In the bottom frame, a duty cycle of 2:8 on/off discharges was applied and compared with a continuous discharge. The modeling was evaluated with the same parameters already shown for the dry and wet air simulations but with an ammonia partial pressure of about 0.2 mbar, corresponding to 22 ppm [24].

The equilibrium gas phases look similar, and ammonia is consumed to produce mainly ozone and water vapor and its radicals. On the other hand, ammonia radicals (majority NH₂) as well as nitrogen oxides (majority NO₂ and N₂O) reach only small concentrations. Even smaller is the more harmful nytroxyl radical HNO. So, the plasma remediation process appears to be quite clean and efficient too. As already observed, the application of the duty cycle is substantially lower than the amount of energy necessary for the transformation of the same quantity of ammonia by the electrical discharge. The efficiency is higher by 67% by using the 2:8 duty cycle. The simulation also provides interesting features in the evolution of the neutral and charged gas phase, which helps in understanding the reaction pattern of ammonia, with substantial room for treatment process improvement.

3.5. Addressing Air Purification Treatments

Finally, we discuss the use of such modeling in a more realistic environment, linked to existing plasma devices and processes. The aim was to draw a comparison with the findings of an experimental campaign, aiming at VOC remediation and air purification [11,50]. The device and its properties are discussed elsewhere [10], so we briefly report only the relevant features needed to implement a few targeted simulations. The discharges happen at the surface of a stacked set of Teflon plates. Electrodes consists of five parallel, equally spaced metal strips, 75 mm long, glued and exposed on the upper surface, while an insulated metal plate on the lower surface acts as a ground electrode. This configuration is typical of surface DBD, used previously to study ion wind and plasma aerodynamics [16]. An air flow (14 L/s) is maintained in a pipe (12 cm diameter) streaming along the electrodes, so that discharges happen mostly transverse to the flow direction. The discharge repetition rate was 4 kHz.

As for the simulations, the model could be formulated as a plug-flow reactor [32]. Within this approximation, the transverse non-homogeneities in the electric field strength and in the plasma filament are not considered. Based on the experimental flow rate, the global exposure time to plasma was then 60 ms. The streamer channel was considered to be rectangular, with a 100 μm square section, to simplify the treatment of diffusion and covering the inter-electrode space. Diffusion and reactions onto the dielectric surfaces are to be considered here. However, since the discharge repetition frequency is substantially larger than the crossing time of the microdischarge channel, the system could be modeled as a repetition of independent discharge events, just as we have discussed. The peak electron density was estimated from experimental data on the charge transported by the microdischarges [10].

The result of the simulation is displayed in Figure 8, where the density of the neutral and charged species is reported in a log-log scale as a function of time. It could be observed that the relevant trends in the evolution of the gas phase are similar to those obtained in the symmetric DBD setup discussed previously. So, this kind of simulation can also be used as a guide in more complex and realistic experimental geometries and setups. More detailed comparisons between experiments and simulations will be addressed in future dedicated work.

4. Discussion and Conclusions

We presented several issues that could be analyzed in the framework of chemical kinetics simulations of dielectric barrier discharge plasmas. In particular, we focused on the role of pulsed operation in the control of the evolution of the discharge gas phase. We demonstrated that interesting effects could be achieved when the pulse times are comparable with the relevant scales for the formation of stable molecular species. We discussed instances relative to ozone, nitrogen oxides, water vapor and ammonia.

Taking a more general point of view, simplified but reasonably fast simulations of the plasma chemical kinetics can bring fruitful information about the pattern taken by the gas-phase evolution, which could aid in the experimental campaign and help to design the device (electrode spacing and number, relative to the flow rate to be processed) and the operating conditions. As in this work, carefully designed duty cycles help to substantially reduce the electrical power consumption and to boost the process efficiency, possibly achieving an economic viability of plasma processing, this being the main brake to the spreading of this kind of technology [1].