Achieving Optimal Reactive Power Compensation in Distribution Grids by Using Industrial Compensation Systems
Abstract
:1. Introduction
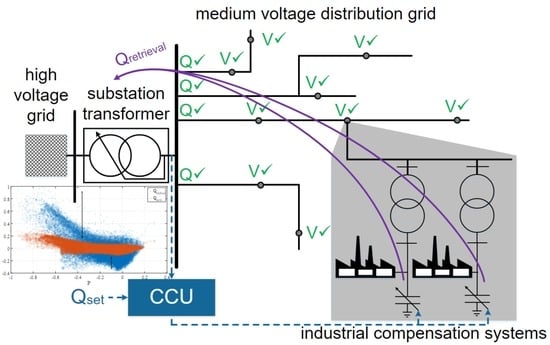
2. Investigation of the Reactive Power Potential of Industrial Compensation Systems
- base load consumers within their industrial grid, which obtain inductive reactive power and
- continually switched-in compensation steps of the ICS.
3. A Central Optimal Reactive Power Control Strategy
- transforming the model to an economic optimization by changing the objective function to a minimization of the costs of and setting the compliance of the reactive power exchange as a restriction;
- setting cost limits by modelling additional restrictions;
- using multi-objective techniques; or
- performing economical optimization afterwards.
4. An Application Example
- Analysis of the functionality at steady-state conditions and achieving the reactive power objectives and
- Impact on and compliance of the voltage limitations and load flow capacities.
4.1. Description of the Simulation Parameters
- existence of real measured P- and Q-data with a 10-second resolution for each low-voltage load and generation unit, which are implemented in the grid model.
- The grid topology is a typical medium-voltage ring structure and
- the territory of supply is a rural industry area with high load penetration and a typical environment of the six measured industrial companies
4.2. Presentation of the Achievements
4.3. Review of the Constraints
5. Conclusions
Author Contributions
Funding

Data Availability Statement
Conflicts of Interest
References
- The German Bundestag. Renewable Energy Sources Act (EEG 2021); Federal Ministry of Justice: Berlin, Germany, 2022.
- The German Bundestag. Atomic Energy Act on the Peaceful Utilization of Atomic Energy and the Protection against Its Hazards (AtG); Federal Ministry of Justice: Berlin, Germany, 2021.
- The German Bundestag. Coal–Fired Power Generation Termination Act (KVBG); Federal Ministry of Justice: Berlin, Germany, 2021.
- 50Hertz Transmission GmbH; Amprion GmbH; Tennet TSO GmbH; TransnetBW GmbH. Bewertung der Systemstabilität, Begleitdokument zum Netzentwicklungsplan Strom 2030, Version 2019, zweiter Entwurf; 50Hertz Transmission GmbH: Berlin, Germany; Amprion GmbH: Dortmund, Germany; Tennet TSO GmbH: Bayreuth, Germany; TransnetBW GmbH: Stuttgart, Germany, 2019. (In German) [Google Scholar]
- The European Parliament and the Council of the European Union. Directive (EU) 2019/944 of the European Parliament and of the Council of 5 June 2019 on Common Rules for the Internal Market for Electricity and Amending Directive 2012/27/EU; Official Journal of the European Union: Brussel, Belgium, 2019.
- The European Parliament and the Council of the European Union. Regulation (EU) 2019/943 of the European Parliament and of the Council of 5 June 2019 on the Internal Market for Electricity; Official Journal of the European Union: Brussel, Belgium, 2019.
- The German Bundestag. German Energy Industry Act (EnWG); Federal Ministry of Justice: Berlin, Germany, 2022.
- Zhang, W.; Tolbert, L.M. Survey of reactive power planning methods, Institute of Electrical and Electronics Engineers. IEEE Power Eng. Soc. Gen. Meet. 2005, 2, 1430–1440. [Google Scholar]
- Zhang, W.; Li, F.; Tolbert, L.M. Review of Reactive Power Planning: Objectives, Constraints, and Algorithms. IEEE Trans. Power Electron. 2007, 22, 2177–2186. [Google Scholar] [CrossRef] [Green Version]
- Soma, G.G. Optimal Sizing and Placement of Capacitor Banks in Distribution Networks Using a Genetic Algorithm. Electricity 2021, 2, 187–204. [Google Scholar] [CrossRef]
- Yuvaraj, T.; Devabalaji, K.R.; Prabaharan, N.; Haes Alhelou, H.; Manju, A.; Pal, P.; Siano, P. Optimal Integration of Capacitor and Distributed Generation in Distribution System Considering Load Variation Using Bat Optimization Algorithm. Energies 2021, 14, 3548. [Google Scholar] [CrossRef]
- Kingston, R.; Baghzouz, Y. Power factor and harmonic compensation in industrial power systems with nonlinear loads. In Proceedings of the Industrial and Commercial Power Systems Conference, Irvine, CA, USA, 1–5 May 1994. [Google Scholar]
- Ekel, P.; Ansuj, S.; Schinzinger, R.; Prakhovnik, A.; Razumovsky, O. Automation of reactive power compensation in industrial power systems. In Proceedings of the IEEE International Conference on Control and Applications, Glasgow, UK, 24–26 August 1994. [Google Scholar]
- Putman, R.E.; Huff, F.C.; Pal, J.K. Optimal reactive power control for industrial power networks. IEEE Trans. Ind. Appl. 1999, 35, 506–514. [Google Scholar] [CrossRef]
- Glöckler, C.; Harms, Y.; Hau, M.; Jost, D.; Löwer, L.; Stock, D.; Wecker, M.; Wessel, A. IMOWEN-Integration großer Mengen On- und Offshore erzeugter Windenergie in das elektrische Netz durch intelligente Netzanalyse und Clusterbetriebsführung: Schlussbericht; Fraunhofer-Institut für Energiewirtschaft und Energiesystemtechnik IEE: Kassel, Germany, 2018. (In German) [Google Scholar]
- Małaczek, M.; Wasiak, I. Control of low voltage microgrid in autonomous operation mode. In Proceedings of the 2016 Electric Power Networks (EPNet), Szklarska Poreba, Poland, 19–21 September 2016. [Google Scholar]
- Andrychowicz, M.; Olek, B. Energy storing vs. generation curtailment—The measures for controlling renewable generation. In Proceedings of the 2017 14th International Conference on the European Energy Market (EEM), Dresden, Germany, 6–9 June 2017. [Google Scholar]
- Grab, R.; Köppe, H.; Schuster, M. PV-Wind-Symbiose-Ausnutzung der sich ergänzenden Eigenschaften von PV- und Wind-Kraftwerken hinsichtlich Spannungsqualität und der Bereitstellung von Wirk- und Blindleistung: Schlussbericht zum Verbundvorhaben; Fraunhofer ISE: Freiburg im Breisgau, Germany, 2019. (In German) [Google Scholar]
- VDE-AR-N 4105:2018-11; Generators Connected to the Low-Voltage Distribution Network-Technical Requirements for the Connection to and Parallel Operation with Low-Voltage Distribution Networks. FNN: Berlin, Germany, 2018.
- VDE-AR-N 4110:2018-11; Technical Requirements for the Connection and Operation of Customer Installations to the Medium Voltage Network (TAR Medium Voltage). FNN: Berlin, Germany, 2018.
- VDE-AR-N 4120:2018-11; Technical Requirements for the Connection and Operation of Customer Installations to the High Voltage Network (TAR High Voltage). FNN: Berlin, Germany, 2018.
- Brückl, O.; Haslbeck, M. Beitrag industrieller Blindleistungs-Kompensationsanlagen und -Verbraucher für ein innovatives Blindleistungs-Management in der Stromversorgung Deutschlands; ZVEI-Zentralverband Elektrotechnik- und Elektronikindustrie e. V., Fachverband Starkstromkondensatoren: Frankfurt, Germany, 2013. (In German) [Google Scholar]
- Carpentier, J. Contribution á l’étude du dispatching économique. Bull. Société Fr. Électriciens 1962, 3, 431–447. (In French) [Google Scholar]
- Dommel, H.; Tinney, W. Optimal Power Flow Solutions. IEEE Trans. Power Appar. Syst. 1968, 87, 1866–1876. [Google Scholar] [CrossRef]
- Stephen, F.; Steponavičė, I.; Rebennack, S. Optimal Power Flow: A bibliographic survey I. Energy Syst. 2012, 3, 221–258. [Google Scholar]
- Stephen, F.; Steponavičė, I.; Rebennack, S. Optimal Power Flow: A bibliographic survey II. Energy Syst. 2012, 3, 259–289. [Google Scholar]
- Buksh, W.; Grothey, A.; McKinnon, K.I.M.; Trodden, P.A. Local Solutions of the Optimal Power Flow Problem. IEEE Trans. Power Syst. 2013, 28, 4780–4788. [Google Scholar] [CrossRef] [Green Version]
- Qiu, Z.; Deconinck, G.; Belmans, R. A literature survey of Optimal Power Flow problems in the electricity market context. In Proceedings of the 2009 IEEE/PES Power Systems Conference and Exposition, Seattle, WA, USA, 15–18 March 2009. [Google Scholar]
- Molzahn, D.K.; Dörfler, F.; Sandberg, H.; Low, S.H.; Chakrabarti, S.; Baldick, R.; Lavaei, J. A Survey of Distributed Optimization and Control Algorithms for Electric Power Systems. IEEE Trans Smart Grid 2017, 8, 2941–2962. [Google Scholar] [CrossRef]
- Granville, S. Optimal reactive dispatch through interior point methods. IEEE Trans. Power Syst. 1994, 9, 136–146. [Google Scholar] [CrossRef]
- Wu, Q.H.; Ma, J.T. Power system optimal reactive power dispatch using evolutionary programming. IEEE Trans. Power Syst. 1995, 10, 1243–1249. [Google Scholar] [CrossRef] [PubMed]
- Dai, C.; Chen, W.; Zhu, Y.; Zhang, X. Seeker Optimization Algorithm for Optimal Reactive Power Dispatch. IEEE Trans. Power Syst. 2009, 24, 1218–1231. [Google Scholar]
- Syah, R.; Faghri, S.; Nasution, M.K.; Davarpanah, A.; Jaszczur, M. Modeling and Optimization of Wind Turbines in Wind Farms for Solving Multi-Objective Reactive Power Dispatch Using a New Hybrid Scheme. Energies 2021, 14, 5919. [Google Scholar] [CrossRef]
- Nagarajan, K.; Parvathy, A.K.; Rajagopalan, A. Multi-objective optimal reactive power dispatch using levy interior search algorithm. Int. J. Electr. Eng. Inform. 2020, 12, 547–570. [Google Scholar] [CrossRef]
- Das, D.B.; Patvardhan, C. Reactive power dispatch with a hybrid stochastic search technique. Int. J. Electr. Power Energy Syst. 2002, 24, 731–736. [Google Scholar]
- Tudose, A.M.; Picioroaga, I.I.; Sidea, D.O.; Bulac, C. Solving Single- and Multi-Objective Optimal Reactive Power Dispatch Problems Using an Improved Salp Swarm Algorithm. Energies 2021, 14, 1222. [Google Scholar] [CrossRef]
- Tao, Q.; Wang, D.; Yang, B.; Liu, H.; Yan, S. Voltage control of distribution network with distributed generation based on Voltage Sensitivity Matrix. In Proceedings of the 2018 IEEE International Conference on Energy Internet (ICEI), Bejing, China, 21–25 May 2018. [Google Scholar]
- Rauch, J.; Brückl, O. Entwicklung eines Regelverfahrens für einen optimierten und zentralen Blindleistungsabruf zur Beeinflussung des Blindleistungshaushalts von Mittelspannungsverteilnetzen unter Einhaltung von Netzrestriktionen. In Proceedings of the Konferenz Zukünftige Stromnetze, Berlin, Germany, 30–31 January 2019. (In German). [Google Scholar]
- Zhu, J. Optimization of Power System Operation; John Wiley & Sons: New Jersey, NJ, USA, 2009. [Google Scholar]
- Molver, I.; Chowdhury, S. Investigation of the Impact of Grid-integrated Distributed Generation on MV Network Voltage using Load Flow Sensitivities. In Proceedings of the 2019 IEEE PES/IAS PowerAfrica, Abuja, Nigeria, 20–23 August 2019. [Google Scholar]
- Haslbeck, M. Planerische Bestimmung von Randbedingungen zur Steuerung von Blindleistungsquellen an Knoten von Mittelspannungsnetzen. Ph.D. Thesis, Clausthal University of Technology, Clausthal-Zellerfeld, Germany, 2020. (In German). [Google Scholar]
- Rauch, J.; Klitsman, M.; Haslbeck, M.; Brückl, O. Entwicklung von Methoden zur Prognose der Blindleistungsbilanz von Mittelspannungsnetzen zur Steuerung eines dezentralen Blindleistungsabrufs. In Proceedings of the Zukünftige Stromnetze, Berlin, Germany, 30–31 January 2018. (In German). [Google Scholar]
- Haslbeck, M.; Kreuzer, R.; Rauch, J.; Brückl, O.; Günther, A.; Bäsmann, R.; Rietsche, H.; Tempelmeier, A. SyNErgie-Systemoptimierendes Netz- und Energiemanagement für die Verteilungsnetze der Zukunft: SyNErgie-Stromnetze Forschungsinitiative der Bundesregierung: Schlussbericht; Ostbayerische Technische Hochschule Regensburg FENES: Regensburg, Germany, 2018. (In German) [Google Scholar]
- Rauch, J. Entwicklung eines Regelverfahrens für einen optimierten und zentralen Blindleistungsabruf zur Beeinflussung des Blindleistungshaushalts von Mittelspannungsnetzen unter Einhaltung von Netzrestriktionen. Master’s Thesis, Ostbayerische Technische Hochschule Regensburg, Regensburg, Germany, 2018. (In German). [Google Scholar]
- DIN EN 50160:2011-02; Voltage Characteristics of Electricity Supplied by Public Electricity Networks. DIN e.V.-Beuth Verlag: Berlin, Germany, 2011.











| Notation | Description | Unit |
|---|---|---|
| Time-dependent reactive power behavior of plant i at the substation transformer | var | |
| Time-dependent reactive power provision of all installed ICSs at plant | var | |
| Installed reactive power of all ICSs at plant i | var |
| ID | Sector/Type | Max. Measured Effective Power Consumption in kW | in Kvar | Measurement Period in Days | Measurement Resolution |
|---|---|---|---|---|---|
| B1 | printing company | 2193 | 1000 | 20 | 1-second |
| B2 | university | 5872 | 2205 | 22 | 1-minute |
| B3 | automotive supplier | 1359 | 1150 | 21 | 1-second |
| B4 | manufacturing | 263 | 325 | 22 | 1-second |
| B5 | machine building | 1192 | 1150 | 46 | 1-second |
| B6 | manufacturing | 7623 | 7075 | 242 | 1-minute |
| Minimal Non-Simultaneous Reactive Power Potential | Minimal Simultaneous Reactive Power Potential | Minimal Compensational Effect in Application | |||
|---|---|---|---|---|---|
| Total in Kvar | Total in Kvar | Change in % | Total in Kvar | Change in % | |
| Inductive | 636 | 1388 | 118.2 | 1500 | 135.8 |
| Capacitive | −5993 | −6955 | 16.1 | −5168 | −13.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rauch, J.; Brückl, O. Achieving Optimal Reactive Power Compensation in Distribution Grids by Using Industrial Compensation Systems. Electricity 2023, 4, 78-95. https://doi.org/10.3390/electricity4010006
Rauch J, Brückl O. Achieving Optimal Reactive Power Compensation in Distribution Grids by Using Industrial Compensation Systems. Electricity. 2023; 4(1):78-95. https://doi.org/10.3390/electricity4010006
Chicago/Turabian StyleRauch, Johannes, and Oliver Brückl. 2023. "Achieving Optimal Reactive Power Compensation in Distribution Grids by Using Industrial Compensation Systems" Electricity 4, no. 1: 78-95. https://doi.org/10.3390/electricity4010006
APA StyleRauch, J., & Brückl, O. (2023). Achieving Optimal Reactive Power Compensation in Distribution Grids by Using Industrial Compensation Systems. Electricity, 4(1), 78-95. https://doi.org/10.3390/electricity4010006