Randomness and Entropy Production
Share This Topical Collection
Editor
 Prof. Dr. Thomas Dittrich
Prof. Dr. Thomas Dittrich
 Prof. Dr. Thomas Dittrich
Prof. Dr. Thomas Dittrich
E-Mail
Website
Collection Editor
Departamento de Física, Universidad Nacional de Colombia, Bogotá 111321, Colombia
Interests: complex classical and quantum dynamics; semiclassical methods; quantum randomness
Topical Collection Information
Dear Colleagues,
Information and randomness are intimately related concepts. This topical collection is intended to analyze their relationship at depth. It should offer a forum to explore and discuss the idea that random processes and disorder in space and time are, above all, sources of entropy. Fundamental questions arise, such as: Can randomness be quantified by a positive production of information? How can we distinguish “true randomness” from deterministic chaos? Where and how can unpredictable phenomena be traced down to deeper sources of randomness, for example in microscopic processes? In physics, the first notion of entropy is the thermodynamic, calorimetric notion, which does not fully overlap with the notions of information and randomness, except for well-controlled situations such as thermodynamic equilibrium states. For instance, the randomness exhibited by macroscopic and many-body systems is qualitatively distinct from chaos in systems with a few degrees of freedom. Which role does it play in thermalization? Randomness in quantum systems is considered the last stronghold of fundamental unpredictability. How can it be reconciled with entropy conservation in unitary quantum mechanics? There are important applications in fields beyond mathematics and physics, such as the stochastic nature of biomolecular reactions and of biological phenomena in general, or the limits of predictability of neural information processing. We believe that the production of entropy can provide us with a unifying approach to these diverse topics.
Papers on recent original research in mathematics and logics, in physics and the neighboring sciences, but also in philosophy are cordially invited. Reviews from a novel perspective are welcome, too. The Special Issue is intended for a wide audience, so contributions should be accessible to a multidisciplinary readership.
Prof. Dr. Thomas Dittrich
Collection Editor
Manuscript Submission Information
Manuscripts should be submitted online at www.mdpi.com by registering and logging in to this website. Once you are registered, click here to go to the submission form. Manuscripts can be submitted until the deadline. All submissions that pass pre-check are peer-reviewed. Accepted papers will be published continuously in the journal (as soon as accepted) and will be listed together on the collection website. Research articles, review articles as well as short communications are invited. For planned papers, a title and short abstract (about 100 words) can be sent to the Editorial Office for announcement on this website.
Submitted manuscripts should not have been published previously, nor be under consideration for publication elsewhere (except conference proceedings papers). All manuscripts are thoroughly refereed through a single-blind peer-review process. A guide for authors and other relevant information for submission of manuscripts is available on the Instructions for Authors page. Entropy is an international peer-reviewed open access monthly journal published by MDPI.
Please visit the Instructions for Authors page before submitting a manuscript.
The Article Processing Charge (APC) for publication in this open access journal is 2600 CHF (Swiss Francs).
Submitted papers should be well formatted and use good English. Authors may use MDPI's
English editing service prior to publication or during author revisions.
Keywords
- randomness
- algorithmic complexity
- determinism
- unpredictability
- causality
- chaos
- thermalization
- quantum randomness
- quantum measurement
- pseudorandom number generation
- gambling games
- thermodynamic equilibrium
- non-equilibrium phenomena
- genetic mutation
Published Papers (3 papers)
Open AccessArticle
MRNG: Accessing Cosmic Radiation as an Entropy Source for a Non-Deterministic Random Number Generator
by
Stefan Kutschera, Wolfgang Slany, Patrick Ratschiller, Sarina Gursch and Håvard Dagenborg
Viewed by 2387
Abstract
Privacy and security require not only strong algorithms but also reliable and readily available sources of randomness. To tackle this problem, one of the causes of single-event upsets is the utilization of a non-deterministic entropy source, specifically ultra-high energy cosmic rays. An adapted
[...] Read more.
Privacy and security require not only strong algorithms but also reliable and readily available sources of randomness. To tackle this problem, one of the causes of single-event upsets is the utilization of a non-deterministic entropy source, specifically ultra-high energy cosmic rays. An adapted prototype based on existing muon detection technology was used as the methodology during the experiment and tested for its statistical strength. Our results show that the random bit sequence extracted from the detections successfully passed established randomness tests. The detections correspond to cosmic rays recorded using a common smartphone during our experiment. Despite the limited sample, our work provides valuable insights into the use of ultra-high energy cosmic rays as an entropy source.
Full article
►▼
Show Figures
Open AccessArticle
Rate of Entropy Production in Stochastic Mechanical Systems
by
Gregory S. Chirikjian
Cited by 1 | Viewed by 2915
Abstract
Entropy production in stochastic mechanical systems is examined here with strict bounds on its rate. Stochastic mechanical systems include pure diffusions in Euclidean space or on Lie groups, as well as systems evolving on phase space for which the fluctuation-dissipation theorem applies, i.e.,
[...] Read more.
Entropy production in stochastic mechanical systems is examined here with strict bounds on its rate. Stochastic mechanical systems include pure diffusions in Euclidean space or on Lie groups, as well as systems evolving on phase space for which the fluctuation-dissipation theorem applies, i.e., return-to-equilibrium processes. Two separate ways for ensembles of such mechanical systems forced by noise to reach equilibrium are examined here. First, a restorative potential and damping can be applied, leading to a classical return-to-equilibrium process wherein energy taken out by damping can balance the energy going in from the noise. Second, the process evolves on a compact configuration space (such as random walks on spheres, torsion angles in chain molecules, and rotational Brownian motion) lead to long-time solutions that are constant over the configuration space, regardless of whether or not damping and random forcing balance. This is a kind of potential-free equilibrium distribution resulting from topological constraints. Inertial and noninertial (kinematic) systems are considered. These systems can consist of unconstrained particles or more complex systems with constraints, such as rigid-bodies or linkages. These more complicated systems evolve on Lie groups and model phenomena such as rotational Brownian motion and nonholonomic robotic systems. In all cases, it is shown that the rate of entropy production is closely related to the appropriate concept of Fisher information matrix of the probability density defined by the Fokker–Planck equation. Classical results from information theory are then repurposed to provide computable bounds on the rate of entropy production in stochastic mechanical systems.
Full article
Open AccessFeature PaperArticle
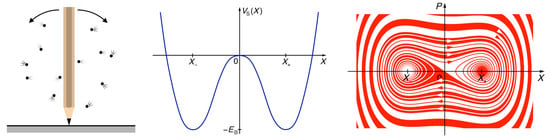
Toppling Pencils—Macroscopic Randomness from Microscopic Fluctuations
by
Thomas Dittrich and Santiago Peña Martínez
Cited by 6 | Viewed by 3168
Abstract
We construct a microscopic model to study discrete randomness in bistable systems coupled to an environment comprising many degrees of freedom. A quartic double well is bilinearly coupled to a finite number
N of harmonic oscillators. Solving the time-reversal invariant Hamiltonian equations of
[...] Read more.
We construct a microscopic model to study discrete randomness in bistable systems coupled to an environment comprising many degrees of freedom. A quartic double well is bilinearly coupled to a finite number
N of harmonic oscillators. Solving the time-reversal invariant Hamiltonian equations of motion numerically, we show that for
, the system exhibits a transition with increasing coupling strength from integrable to chaotic motion, following the Kolmogorov-Arnol’d-Moser (KAM) scenario. Raising
N to values of the order of 10 and higher, the dynamics crosses over to a quasi-relaxation, approaching either one of the stable equilibria at the two minima of the potential. We corroborate the irreversibility of this relaxation on other characteristic timescales of the system by recording the time dependences of autocorrelation, partial entropy, and the frequency of jumps between the wells as functions of
N and other parameters. Preparing the central system in the unstable equilibrium at the top of the barrier and the bath in a random initial state drawn from a Gaussian distribution, symmetric under spatial reflection, we demonstrate that the decision whether to relax into the left or the right well is determined reproducibly by residual asymmetries in the initial positions and momenta of the bath oscillators. This result reconciles the randomness and spontaneous symmetry breaking of the asymptotic state with the conservation of entropy under canonical transformations and the manifest symmetry of potential and initial condition of the bistable system.
Full article
►▼
Show Figures