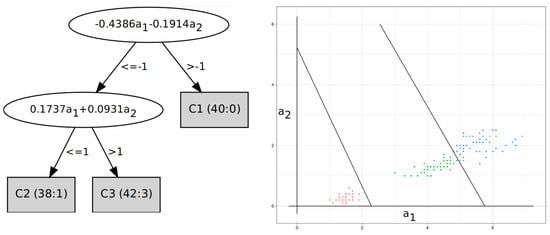
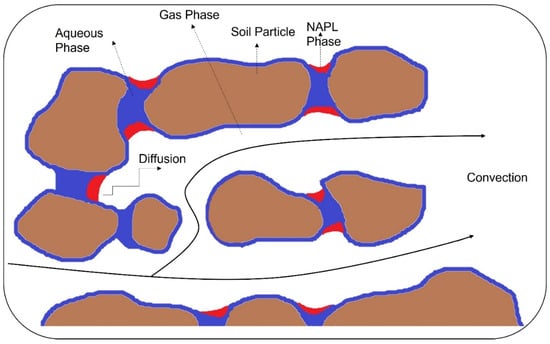
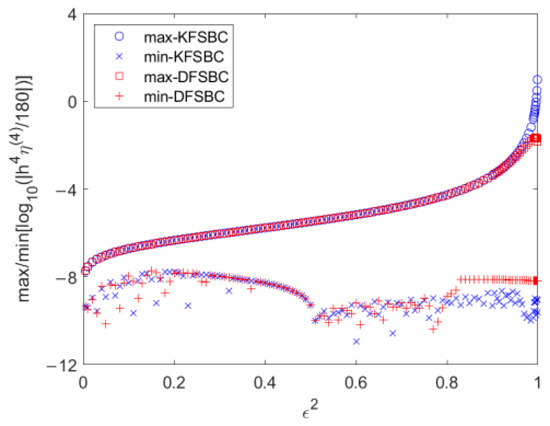
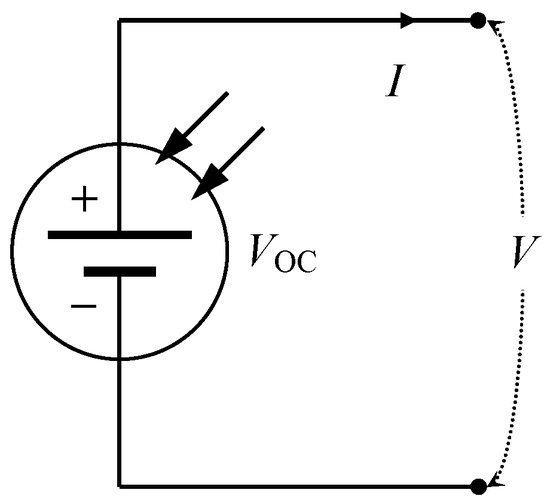
Feature Papers in Mathematical and Computational Applications 2024 (Closed)
A topical collection in Mathematical and Computational Applications (ISSN 2297-8747).
Viewed by 11822Editors
Interests: numerical analysis and scientific computing; reduced order modelling and methods; efficient reduced-basis methods for parametrized PDEs and a posteriori error estimation; computational fluid dynamics: aero-naval-mechanical engineering; blood flows (haemodynamics); environmental fluid dynamics; multi-physics; software in computational science and engineering
Special Issues, Collections and Topics in MDPI journals
Interests: multi-objective optimization; evolutionary computation (genetic algorithms and evolution strategies); numerical analysis; engineering applications
Special Issues, Collections and Topics in MDPI journals
Interests: modeling of offshore structures and offshore structural components; structural theories of plates and applied mathematical modeling; mechanics of solids and structures; study of composite laminated structures and advanced composite materials; fracture mechanics and crack propagation and initiation; applied numerical methods such as finite element method and mesh-free element method
Special Issues, Collections and Topics in MDPI journals
Topical Collection Information
Dear Colleagues,
We are pleased to announce that the journal Mathematical and Computational Applications is presently compiling a collection of papers submitted exclusively by our Editorial Board Members (EBMs) and outstanding scholars in this research field.
The purpose of this collection is to publish a set of papers that typify the most insightful and influential original articles or reviews in which our EBMs discuss key topics in the field. We expect these papers to be widely read and highly influential. All papers in this collection will be collected into a printed book edition that will be extensively promoted.
Prof. Dr. Gianluigi Rozza
Dr. Oliver Schütze
Dr. Nicholas Fantuzzi
Collection Editors
Manuscript Submission Information
Manuscripts should be submitted online at www.mdpi.com by registering and logging in to this website. Once you are registered, click here to go to the submission form. Manuscripts can be submitted until the deadline. All submissions that pass pre-check are peer-reviewed. Accepted papers will be published continuously in the journal (as soon as accepted) and will be listed together on the collection website. Research articles, review articles as well as short communications are invited. For planned papers, a title and short abstract (about 100 words) can be sent to the Editorial Office for announcement on this website.
Submitted manuscripts should not have been published previously, nor be under consideration for publication elsewhere (except conference proceedings papers). All manuscripts are thoroughly refereed through a single-blind peer-review process. A guide for authors and other relevant information for submission of manuscripts is available on the Instructions for Authors page. Mathematical and Computational Applications is an international peer-reviewed open access semimonthly journal published by MDPI.
Please visit the Instructions for Authors page before submitting a manuscript. The Article Processing Charge (APC) for publication in this open access journal is 1400 CHF (Swiss Francs). Submitted papers should be well formatted and use good English. Authors may use MDPI's English editing service prior to publication or during author revisions.
Keywords
- applied mathematics
- classical mechanics
- computational fluid dynamics
- computational techniques
- differential equations
- dynamical systems
- evolutionary algorithms
- finite element methods
- machine learning and data mining
- mathematical modelling
- neural networks
- numerical analysis
- numerical simulation
- optimization and control
- statistics