Computational Fluid Simulation of Fibrinogen around Dental Implant Surfaces
Abstract
:1. Introduction
2. Result
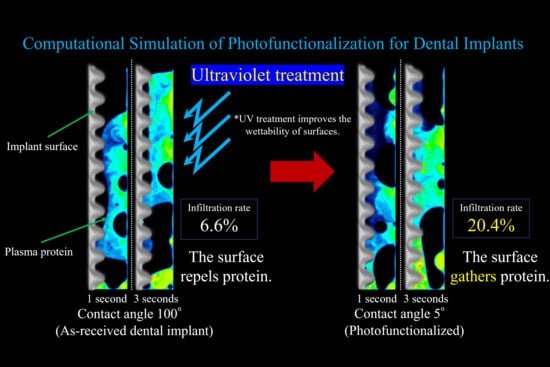
2.1. Fibrinogen Infiltration to the Interfacial Zone of Implants with Different Contact Angles
2.2. Blood Plasma Infiltration to the Interfacial Zone of Implants with Different Contact Angles
2.3. Correlation of Fibrinogen Infiltration and Blood Plasma Infiltration Around Implants
3. Discussion
4. Materials and Methods
4.1. Geometrical Model
4.2. Mesh Generation
4.3. Numerical Methods for Blood Flow Simulation
4.4. Numerical Methods for Fibrinogen Flow Simulation
4.5. Numerical Conditions
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| CAIS | Contact angle between implant surface and blood plasma |
| CFD | Computational fluid dynamics |
References
- Boucari, A.; Francius, G. AFM force spectroscopy of the fibrinogen adsorption process onto dental implants. J. Biomed. Mater. Res. 2006, 78, 466–472. [Google Scholar] [CrossRef]
- Jenney, C.R.; Anderson, J.M. Adsorbed serum proteins responsible for surface dependent human macrophage behaviour. J. Biomed. Mater. Res. 2000, 49, 435–447. [Google Scholar] [CrossRef]
- Tang, L.; Eaton, J.W. Fibrin (ogen) mediates acute inflammatory responses to biomaterials. J. Exp. Med. 1993, 178, 2147–2156. [Google Scholar] [CrossRef] [Green Version]
- Trindade, R.; Albrektsson, A.; Tengvall, P. Foreign body reaction to biomaterials: On mechanisms for buildup and breakdown of osseointegration. Clin. Implant Dent. Relat. Res. 2016, 18, 192–203. [Google Scholar] [CrossRef]
- Beguin, S.; Kumar, R. Thrombin, fibrin and platelets: A resonance loop in which von Willebrand factor is a necessary link. Thromb. Haemost. 1997, 78, 590–594. [Google Scholar] [CrossRef]
- Kumar, R.; Beguin, S.; Hemker, H.C. The influence of fibrinogen and fibrin on thrombin generation-evidence for feedback activation of the clotting system clot bound thrombin. Thromb. Haemost. 1994, 72, 713–721. [Google Scholar] [CrossRef]
- Tzoneva, R.; Heuchel, M.; Groth, T. Fibrinogen adsorption and platelet interactions on polymer membranes. J. Biomater. Sci. Polym. Ed. 2002, 13, 1033–1050. [Google Scholar] [CrossRef]
- Khodakaram, T.A.; Mehrabani, D.; Shaterzadeh-Yazdi, H. An overview on autologous fibrin glue in bone tissue engineering of maxillofacial surgery. Dent. Res. J. (Isfahan) 2017, 14, 79–86. [Google Scholar]
- Leighton, Y.; Weber, B.; Rosas, E. Autologous fibrin glue with collagen carrier during maxillary sinus lift procedure. J. Craniofac. Surg. 2019, 30, 843–845. [Google Scholar] [CrossRef] [PubMed]
- Lüers, S.; Seitz, C.; Laub, M. Contact angle measurement on dental implants. Biomed. Tech. 2014, 59, 91–95. [Google Scholar]
- Yan, G.; Ying, L.; Lei, Z. The effect of different wavelength UV photofunctionalization on micro-arc oxidized titanium. PLoS ONE 2013, 8, e68086. [Google Scholar]
- Ogawa, T. Ultraviolet photofunctionalization of titanium implants. Int. J. Oral Maxillofac. Implants 2014, 29, 95–102. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Aita, H.; Hori, N.; Takeuchi, M. The effect of ultraviolet functionalization of titanium on integration with bone. Biomaterials 2009, 30, 1015–1025. [Google Scholar] [CrossRef] [PubMed]
- Verri, F.R.; Santiago Júnior, J.F.; Almeida, D.A.D.F. Three-dimensional finite element analysis of anterior single implant-supported prostheses with different bone anchorages. Sci. World J. 2015, 2015. [Google Scholar] [CrossRef]
- Tamai, N.; Hirota, M.; Iwai, T. Evaluation of influence factors to reduce mechanical stress on the marginally resected mandibular bone against dental implant-supported occlusion. J. Hard Tissue Biol. 2018, 27, 11–16. [Google Scholar] [CrossRef] [Green Version]
- Pirmoradian, M.; Naeeni, H.A.; Firouzbakht, M. Finite element analysis and experimental evaluation on stress distribution and sensitivity of dental implants to assess optimum length and thread pitch. Comput. Methods Programs Biomed. 2020, 187, 105258. [Google Scholar] [CrossRef]
- Zhong, L.; Zhang, J.M.; Su, B. Application of patient-specific computational fluid dynamics in coronary and intra-cardiac flow simulations: Challenges and opportunities. Front. Physiol. 2018, 9, 742. [Google Scholar] [CrossRef]
- Shin, E.; Kim, J.J.; Lee, S. Hemodynamics in diabetic human aorta using computational fluid dynamics. PLoS ONE 2018, 13, e0202671. [Google Scholar] [CrossRef]
- Zhang, D.; Xu, P.; Qiao, H. Carotid DSA based CFD simulation in assessing the patient with asymptomatic carotid stenosis: A preliminary study. Biomed. Eng. Online 2018, 7, 31. [Google Scholar] [CrossRef] [Green Version]
- Razavi, S.E.; Farhangmehr, V.; Zendeali, N. Numerical investigation of the blood flow through the middle cerebral artery. BioImpacts 2018, 8, 195–200. [Google Scholar] [CrossRef]
- James, M.E.; Papavassiliou, D.V.; O’Rear, E.A. Use of computational fluid dynamics to analyze blood flow, hemolysis and sublethal damage to red blood cells in a bileaflet artificial heart valve. Fluids 2019, 4, 19. [Google Scholar] [CrossRef] [Green Version]
- Att, W.; Hori, N.; Takeuchi, M. Time-dependent degradation of titanium osteoconductivity: An implication of biological aging of implant materials. Biomaterials 2009, 30, 5352–5363. [Google Scholar] [CrossRef] [PubMed]
- Hori, N.; Att, W.; Ueno, T. Age-dependent degradation of the protein adsorption capacity of titanium. J. Dent. Res. 2009, 88, 663–667. [Google Scholar] [CrossRef] [PubMed]
- Hori, N.; Ueno, T.; Suzuki, T. Ultraviolet light treatment for the restoration of age-related degradation of titanium bioactivity. Int. J. Oral Maxillofac. Implants 2010, 25, 49–62. [Google Scholar]
- Suzuki, T.; Hori, N.; Att, W. Ultraviolet treatment overcomes time-related degrading bioactivity of titanium. Tissue Eng. Part A 2009, 15, 3679–3688. [Google Scholar] [CrossRef]
- Suzuki, T.; Kubo, K.; Hori, N. Nonvolatile buffer coating of titanium to prevent its biological aging and for drug delivery. Biomaterials 2010, 31, 4818–4828. [Google Scholar] [CrossRef]
- Att, W.; Hori, N.; Iwasa, F. The effect of UV-photofunctionalization on the time-related bioactivity of titanium and chromium-cobalt alloys. Biomaterials 2009, 30, 4268–4276. [Google Scholar] [CrossRef]
- Lee, J.H. The biological aging of titanium implants. Implant Dent. 2012, 21, 415–421. [Google Scholar] [CrossRef]
- Saita, M.; Ikeda, T.; Yamada, M. UV photofunctionalization promotes nano-biomimetic apatite deposition on titanium. Int. J. Nanomed. 2016, 11, 223–234. [Google Scholar]
- Iwasa, F.; Hori, N.; Ueno, T. Enhancement of osteoblast adhesion to UV-photofunctionalized titanium via an electrostatic mechanism. Biomaterials 2010, 31, 2717–2727. [Google Scholar] [CrossRef]
- Hori, N.; Ueno, T.; Minamikawa, H. Electrostatic control of protein adsorption on UV-photofunctionalized titanium. Acta Biomater. 2010, 6, 4175–4180. [Google Scholar] [CrossRef] [PubMed]
- The Physics Factbook. Available online: https://hypertextbook.com/facts/2004/MichaelShmukler.shtml (accessed on 1 December 2019).
- Lanotte, L. Red cells’ dynamic morphologies govern blood shear thinning under microcirculatory flow conditions. Proc. Natl. Acad. Sci. USA 2016, 113, 13289–13294. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mottaghy, K.; Hahn, A. Interfacial tension of some biological fluids: A comparative study. J. Clin. Chem. Clin. Biochem. 1981, 19, 267–271. [Google Scholar] [CrossRef] [PubMed]
- Nauman, J.V. Diffusion of insulin-like growth factor-1 and ribonuclease through fibrin gels. Biophys. J. 2007, 92, 4444–4450. [Google Scholar] [CrossRef] [Green Version]
- Wufsus, A.R.; Macera, N.E.; Neeves, K.B. The hydraulic permeability of blood clots as a function of fibrin and platelet density. Biophys. J. 2013, 104, 1812–1823. [Google Scholar] [CrossRef] [Green Version]
- Harkness, J.; Whittington, R.B. The viscosity of human blood plasma: In change in disease and on the exhibition of drugs. Rheol. Acta 1971, 10, 55–60. [Google Scholar] [CrossRef]
- Lorna, T.S.; John, R.M. Determination of serum and blood densities. Anal. Chem. 1979, 51, 1577–1578. [Google Scholar]









| Time Stage | 5° | 30° | 50° | 70° | 100° |
|---|---|---|---|---|---|
| Early stage | 0.6 mg (1.00) | 0.4 mg (0.67) | 0.5 mg (0.83) | 0.5 mg (0.83) | 0.3 mg (0.50) |
| Mid stage | 1.7 mg (1.00) | 1.2 mg (0.71) | 1.3 mg (0.76) | 1.1 mg (0.65) | 0.6 mg (0.35) |
| Late stage | 2.6 mg (1.00) | 2.1 mg (0.81) | 1.9 mg (0.73) | 1.7 mg (0.65) | 0.7 mg (0.27) |
| Time Stage | 5° | 30° | 50° | 70° | 100° |
|---|---|---|---|---|---|
| Early stage | 2388 mg (1.00) | 2218 mg (0.93) | 2114 mg (0.89) | 1846 mg (0.77) | 742 mg (0.31) |
| Mid stage | 2377 mg (1.00) | 2371 mg (1.00) | 2295 mg (0.97) | 1902 mg (0.80) | 721 mg (0.30) |
| Late stage | 2413 mg (1.00) | 2322 mg (0.96) | 2279 mg (0.94) | 1974 mg (0.82) | 805 mg (0.33) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kitajima, H.; Hirota, M.; Iwai, T.; Hamajima, K.; Ozawa, R.; Hayashi, Y.; Yajima, Y.; Iida, M.; Koizumi, T.; Kioi, M.; et al. Computational Fluid Simulation of Fibrinogen around Dental Implant Surfaces. Int. J. Mol. Sci. 2020, 21, 660. https://doi.org/10.3390/ijms21020660
Kitajima H, Hirota M, Iwai T, Hamajima K, Ozawa R, Hayashi Y, Yajima Y, Iida M, Koizumi T, Kioi M, et al. Computational Fluid Simulation of Fibrinogen around Dental Implant Surfaces. International Journal of Molecular Sciences. 2020; 21(2):660. https://doi.org/10.3390/ijms21020660
Chicago/Turabian StyleKitajima, Hiroaki, Makoto Hirota, Toshinori Iwai, Kosuke Hamajima, Ryotaro Ozawa, Yuichiro Hayashi, Yasuharu Yajima, Masaki Iida, Toshiyuki Koizumi, Mitomu Kioi, and et al. 2020. "Computational Fluid Simulation of Fibrinogen around Dental Implant Surfaces" International Journal of Molecular Sciences 21, no. 2: 660. https://doi.org/10.3390/ijms21020660
APA StyleKitajima, H., Hirota, M., Iwai, T., Hamajima, K., Ozawa, R., Hayashi, Y., Yajima, Y., Iida, M., Koizumi, T., Kioi, M., Mitsudo, K., & Ogawa, T. (2020). Computational Fluid Simulation of Fibrinogen around Dental Implant Surfaces. International Journal of Molecular Sciences, 21(2), 660. https://doi.org/10.3390/ijms21020660