1. Introduction
Recently, the linear motor has attracted more attentions in subway applications due to the following advantages: (1) the direct production of thrust force; (2) smaller turning radius and less requirement of cross-sectional area of a tunnel; (3) better climbing ability and faster acceleration; and (4) less maintenance and lower noise [
1,
2,
3,
4,
5]. Compared with the linear induction motor, which has been already employed in some subway projects [
6,
7], the permanent-magnet linear motor (PMLM) is always gone in actual subway applications in spite of its high efficiency and high power factor [
8,
9,
10]. One important reason is the expensive construction cost since the permanent-magnets or armature windings must be equipped in the stator (rail) of the conventional PMLM. However, this problem can be solved by the primary PMLM (PPMLM) since both the permanent-magnets and armature windings can be mounted in the mover of PPMLM [
11,
12,
13,
14,
15]. Generally, existing topologies of PPMLM can be divided into three main categories: double-salient type [
11], flux-switching type [
12,
13,
14], and flux reversal type [
15].
Compared with PPMLM itself, the control has received less attention while it is important for the successful application of PPMLM in subway fields in the future. Due to a fast dynamic response and the simple structure, the direct thrust force control (DTFC) has attracted more attentions for PMLM [
16]. In order to enhance the reliability, a fault-tolerant DTFC is proposed for the flux reversal PMLM with open-end windings [
17]. To cope with current sensor failures, an improved DTFC scheme is proposed for PPMLM using only a single direct current (DC)-link current sensor [
18]. Comparing with DTFC, the average switching frequency of model predictive control (MPC) can be significantly reduced while the MPC also inherits the advantages of the fast dynamic response and simple structure [
19]. However, the MPC of PMLM has not received its deserved attention. That is why the MPC is investigated for PPMLM in this paper.
Finite control set MPC (FCS-MPC) is the original form of MPC, which takes full advantage of the discrete feature of voltage source inverter (VSI) [
20,
21]. Firstly, the values of control variables are predicted by each candidate voltage vector (VV) according to the discrete-time state-space model. Secondly, a cost function is designed by involving the errors between the reference and predictive values of control variables. Finally, the optimal VV is determined by minimizing the value of the cost function. According to the selected control variables, various FCS-MPCs have been proposed. In motor drives, model predictive torque/thrust control (MPTC) and model predictive current control (MPCC) are two main categories. In MPTC, stator flux and electromagnetic torque/thrust force are selected as the control variables [
22]. However, these control variables usually cannot be measured directly, and they are often observed by mathematical methods. Besides, a weighting factor is usually required in cost function since the selected control variables have different units. In MPCC, direct- and quadrature-axis currents are selected as the control variables, which can be measured directly and no weighting factor is required [
23].
As is known, high computation cost is the common challenge of FCS-MPC. For example, seven current predictions and same cost function calculations are required to determine the optimal VV for three-phase motor drives [
24]. Furthermore,
Nn VVs will be evaluated for an
N-level
n-phase VSI. Obviously, the computation cost is significantly increased. The heavy computation cost will require longer calculation time, and then reduces the average switching frequency of the VSI, especially in multi-phase motor or multi-motor drives. Consequently, some methods have been proposed to reduce the computation cost of FCS-MPC. In [
25], only the VVs with single switch state changed are considered for a five-leg dual-motor system. Compared with the conventional FCS-MPC, the amount of candidate VVs is reduced from 31 to 10. In [
26], several predefined constraints are designed and the candidate VVs are reduced from 64 to 16 in the six-phase VSI supplied system. In the induction motor drive with asymmetrical dual three-phase winding, only 12 largest active VVs and zero VVs are considered [
27]. However, the system performances using aforementioned simplified FCS-MPCs are usually affected since these modified solutions are not equivalent to the original ones. An equivalent simplified MPTC is proposed for PM motor drives, in which the deadbeat concept is involved and the candidate VVs are reduced from 7 to 4 [
28].
However, to the best of authors’ knowledge, there is no literature to present an equivalent simplified MPCC for not only rotary permanent-magnet synchronous motor (PMSM) drives but also PMLM drives. The main contribution of this paper is to propose an equivalent MPCC for the PPMLM traction systems in subway applications, in which a shortest distance principle is designed and the cost function is eliminated. As a result, the computation cost can be further reduced comparing with the modified MPTC in [
28] while the performances of PPMLM traction systems are not affected. It should be emphasized that the proposed MPCC is novel for not only PMLM drives but also rotary PMSM drives, and the PPMLM traction system is just taken as an example to present the proposed MPCC in this paper. This paper contains six sections. The studied PPMLM traction system is described in
Section 2. The two MPCCs are introduced in
Section 3. Equivalence analysis of two MPCCs is conducted in
Section 4. The theoretical analysis is verified by experiment results in
Section 5. Finally, some conclusions are drawn in
Section 6.
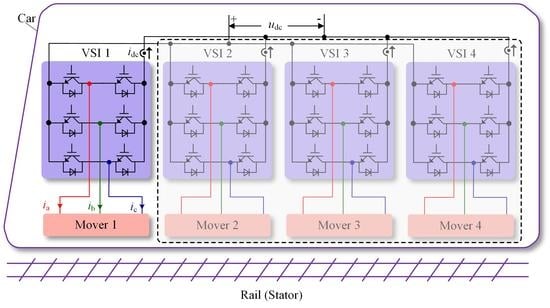
2. Studied PPMLM Traction System
The studied PPMLM is composed of a primary mover and secondary stator as illustrated in
Figure 1. Both the permanent-magnets and armature windings are equipped in movers. As is shown in
Figure 1, the middle of stator teeth is defined as the
d-axis with the maximum PM flux linkage. Meanwhile, the primary position is defined as the
q-axis where PM flux linkage is minimum (zero).
τs is the stator pole pitch, and the distance between two axes is
τs/4. When the positive permanent-magnet flux linkage in phase-A winding is maximum, the corresponding primary position
θe is defined as zero.
According to the previous definition, the voltage equation of the studied PPMLM in
dq coordinate system is expressed as:
with
where
Rs and
Ls are the mover resistance and inductance;
ψPM is the permanent-magnet flux linkage;
ud,
uq and
id,
iq are the synchronous voltage and current components, respectively;
ψd and
ψq are the synchronous flux linkage components; and
vm is the mover speed.
The thrust force
Fe can be deduced as:
The motion equation is designed as:
where
Fl is the load force;
mt is the weight of PPMLM;
B is the friction coefficient.
The studied PPMLM is fed by a two-level VSI, which is illustrated in
Figure 2. The VSI consists of six power switches. The switch state
sx of
xth leg is defined as:
The VV of the VSI is defined as [
sa sb sc]. All candidate VVs of VSI are presented in
Table 1.
3. Two MPCCs for PPMLM
To clarify the description, the conventional and proposed MPCCs were defined as MPCC-I and MPCC-II in this paper, respectively. To simplify the analysis, two assumptions were given as follows: (1) the variation of mover speed vm could be neglected in one sampling period Ts; (2) the phase inductance Ls, the phase resistance Rs, and the peak value of PM flux linkage ψPM are considered unchanged during the entire operation.
3.1. MPCC-I
MPCC-I for the PPMLM traction system is shown in
Figure 3, which contains two main modules: current model prediction and cost function calculation. In this paper, the average primary position
was used in the model prediction, which is determined by
. The primary position
θe can be detected by the linear encoder.
(1) Current model prediction:
In MPCC-I, synchronous currents of PPMLM are selected as control variables to calculate their predictive values. Substituting (2) into (1) gives:
According to the discrete time state-space model and Euler’s prediction formula, the current differential can be simplified as:
In this paper, the superscripts p and m indicate predictive and measured quantities; the symbol k indicates the kth sampling period.
Substituting (7) into (6) gives the predictive currents:
with
where
and
are the predictive synchronous currents by using the VV
Un, respectively.
T3s/2r is the transformation matrix from
abc coordinate system to
d-q coordinate system;
udc is the dc bus voltage;
udn and
uqn are the synchronous components of the VV
Un, respectively. The measured synchronous currents
and
can be calculated from the measured phase currents (
,
,
) and the primary position
θe(
k).
(2) Cost function calculation:
According to (8), the cost function of MPCC-I is designed as:
where
is the reference
q-axis current. According to the difference between the reference speed
and the actual value
,
can be obtained from the automatic speed regulator (ASR).
is the reference
d-axis current, which is set as 0. The optimal VV
Uop is selected to minimize
Jn:
3.2. MPCC-II
MPCC-II for the PPMLM traction system is shown in
Figure 4, which contains two main modules: deadbeat prediction and sector determination.
(1) Deadbeat prediction:
It is assumed in this module that the reference currents
and
can be achieved in next sampling period. In other words, the predictive synchronous currents
and
should be equal to
and
, respectively. Substituting these equivalent relationships into (8) gives the reference synchronous voltages
and
:
with
However, the reference synchronous voltages
and
usually cannot be achieved since the candidate VVs of VSI are discrete as listed in
Table 1.
(2) Sector determination:
To simplify the analysis, the distance of the VV
Un is defined as
Ln:
According to (13) and (15), the selection of the optimal VV
Uop becomes to find the VV with the shortest distance, which was defined as the shortest distance principle in this paper. According to (10), seven Park transformations from
abc coordinate system to
dq coordinate system (
udn,
uqn) must be implemented to determine the optimal VV. To reduce the computation burden of coordinate transformation,
dq components are expressed by
αβ components:
Substituting (16) and (17) into (15) gives:
where
uαn and
uβn are the
α- and
β-axis components of the VV
Un, respectively. The values of
uαn and
uβn are discrete, and they are listed in
Table 2. According to (18), only one inverse Park transformation is implemented from
dq coordinate system (
,
) to
αβ coordinate system (
,
):
Comparing (18) with (15), the computation burden of (18) is significantly reduced. Comparing with the MPTC [
28], the prediction amount has reduced from 4 to 1 by using MPCC-II, and the computation burden can be further reduced.
According to (18), a new cost function is developed as:
The optimal VV
Uop is selected to minimize
λn:
Based on the shortest distance principle, the distribution of the reference voltage vector
U* was divided into seven sectors (Sector 0–6), as illustration in
Figure 5.
Un was chosen as the optimal VV when the reference voltage vector
U* was located in Sector
n. Especially, the central hexagon with radial length
udc/3 is Sector 0, and one zero VV was chosen by minimum switching actions principle. To reduce the computation burden, a fast determination method of the optimal VV was designed for MPCC-II.
Firstly, the phase angle
φ and the magnitude
U* of the reference voltage vector
are determined as:
Secondly, the direction code
M of the reference voltage vector
is determined according to the value of
φ:Thirdly, the relationship between the reference voltage vector
and the central hexagon as shown in
Figure 5 is determined by:
According to (24), the reference voltage vector locates in the central hexagon if H = 0; otherwise, the reference voltage vector locates outside of the central hexagon.
Finally, the optimal VV
Uop is determined as:
4. Equivalence Analysis
The difference between two MPCCs is how to determine the optimal VV. For MPCC-I, the optimal VV is determined by the cost function (11), which can minimize the value of (11). As is listed in
Table 1, there are eight VVs. If two zero VVs are considered as same, the number of candidate VVs can be reduced to 7. Therefore, seven different current groups [
,
] can be predicted, and the cost function (11) will be calculated seven times. In some degree, MPCC-I is similarly like classical PWM. On the other hand, the reference synchronous voltages
and
are calculated by (13), and then the optimal VV can be determined by the location of the reference synchronous voltages in
Figure 5. In fact, MPCC-II has referred to the SVM theory. However, both MPCCs can select the same optimal VV, and the equivalence of two MPCCs was analyzed in this section.
Comparing (13) with (26), the voltage error can be calculated by:
Consequently, the initial form (11) can be simplified as:
According to (15) and (18), (28) can be rewritten as:
According to (20) and (29), two cost function formulas can be expressed as:
According to (30), MPCC-I and MPCC-II will select the same optimal VV. Hence, both MPCCs are equivalent.
5. Experimental Validation
To verify the effectiveness of the proposed MPCC, the hardware should be able to measure the dc bus voltage, two phase currents and the primary position. There was no special requirement for the software. According to the hardware/software requirements, a test bench was designed as illustrated in
Figure 6, and the parameters of the studied PPMLM are listed in
Table 3. A dSPACE DS1103 controller was adopted to execute the control algorithm. DC bus voltage was measured by a voltage sensor (LEM LV25-P, LEM, Geneva, Switzerland). Phase currents are sensed by two current sensors (LEM LA55-P/SP50, LEM, Geneva, Switzerland). The primary position was detected by the linear encoder. The VSI was manufactured by Infineon, and its switch states were determined by the dSPACE DS1103 controller. The sampling frequency was 20 kHz. To compare the two MPCCs, several experiments were carried out.
5.1. Steady-State Experiment
In this experiment, the steady-state performances of two MPCCs were compared. The reference speed was respectively set as 0.3 m/s and 0.6 m/s, and experimental results are respectively illustrated in
Figure 7 and
Figure 8. According to the experimental results, speed, synchronous currents, and phase currents were compared in
Table 4. It can be found in
Table 4 that MPCC-I and MPCC-II had nearly the same performance regarding speed, synchronous currents, and phase currents.
In the steady-state operation, the implement times of MPCC-I and MPCC-II in one sampling period were 12 μs and 9 μs, respectively. Hence, the computation burden could be reduced by 25% if MPCC-II was employed.
5.2. Speed Response Experiment
In this experiment, the speed response performances of two MPCCs were compared. The reference speed was changed between 0.3 m/s and 0.6 m/s. The experimental results are shown in
Figure 9 and
Figure 10. The integral time absolute error (ITAE) was introduced in this paper to evaluate the transient performances. The rising time of MPCC-I and MPCC-II were respectively 0.1649 s (ITAE value: 0.00743 m∙s) and 0.1650 s (ITAE value: 0.00746 m·s), while the falling time were respectively 0.1388 s (ITAE value: 0.00402 m·s) and 0.1391 s (ITAE value: 0.00400 m·s). The dynamic performances of synchronous currents and phase currents were also the same in two MPCCs. Hence, both MPCCs nearly demonstrated the same speed response performance.
5.3. Thrust Force Response Experiment
In this experiment, the thrust force response performances of both MPCCs were compared. The reference thrust force was increased from −100 N to 100 N, and then returned to −100 N.
Figure 11 shows the experimental results. It can be found in
Figure 11 that both MPCC-I and MPCC-II had fast thrust force response. The rising and falling time of MPCC-I were respectively 4.43 m·s (ITAE value: 0.00538 N·s
2) and 3.30 m·s (ITAE value: 0.00339 N·s
2) while those of MPCC-II were respectively 4.39 m·s (ITAE value: 0.00542 N·s
2) and 3.31 m·s (ITAE value: 0.00341 N·s
2). Hence, MPCC-I and MPCC-II had nearly the same thrust force response.
5.4. Comparison of VV Selection
Both MPCCs run at the same time in this experiment but only the command signals of MPCC-II were implemented by the VSI. In other words, the command signals of MPCC-I were generated only for comparison instead of implementation. The reference speed was changed between 0.3 m/s and 0.6 m/s. Experimental results are illustrated in
Figure 12, in which the numbers 0–7 respectively represent
U0–
U7. It can be found in
Figure 12 that both MPCCs always selected the same VV no matter in transient- or steady-state operations. Therefore, the equivalence of both MPCC was well verified.
5.5. Motor Parameter Variation
It is well known that MPCC is sensitive to the accuracy of the motor modeling, unmatched parameters, uncertainties, and disturbances. Therefore, compensation actions are usually necessary if high-performances are required. However, the purpose of this paper was to provide a simple but equivalent MPCC. Hence, there were no compensation actions taken in this paper. Some details about parameter compensation of MPCC can be found in [
23]. In this subsection, the simplification and equivalence of MPCC-II were evaluated considering the motor parameter variation. As an example, 150% of the rated mover inductance and 50% of the rated mover resistance were considered in this experiment, and the experimental results are illustrated in
Figure 13 and
Figure 14. According to the experimental results, the performances of both MPCCs are compared in
Table 5 and
Table 6. It can be found in the two previous tables that MPCC-I and MPCC-II still had nearly the same performances.
6. Conclusions
For the reduction of the computation burden, a simple but equivalent solution was proposed for the MPCC of PPMLM traction systems. In the proposed MPCC, a continuous reference VV was predicted, and the optimal VV was determined according to the shortest distance principle instead of the cost function. Though the performances of the proposed MPCC were not enhanced in terms of precision, robustness, and dynamics, the computation cost could be significantly reduced, which achieved the target of this paper. The simplification and the equivalence of the proposed MPCC were verified by experimental results. Although the proposed MPCC was designed for PPMLM originally, it is also novel for the rotary PMSM. From the viewpoint of the implementation, there is no difference between the PMLM and the rotary PMSM.