New High-Efficiency Resonant O-Type Devices as the Promising Sources of Microwave Power

Abstract

New O-type high-power vacuum resonant microwave devices are considered in this study: COM klystrons, CSM klystrons and resotrodes. All these devices can output a large amount of power (up to units of MW and higher) with an efficiency of up to 90%. Such devices are promising microwave sources for industrial microwave technologies as well as for microwave energy. The principle of GSP-equivalence for klystrons is described herein, allowing a complete physical analog of this device with other parameters to be created. The existing mathematical and computer models of klystrons are analyzed. The processes of stage-by-stage optimization and the embedding procedure, which leads to COM and to CSM klystrons, are considered. Resotrodes, IOT-type devices with energy regeneration in the input circuit, are also considered. It is shown that these devices can combine high power with an efficiency of up to 90% and a gain of more than 30 dB. Resotrodes with 0-regeneration can be effective sources of radio frequency (RF) power in the range of 20 to 200 MHz. Resotrodes with 2π-regeneration are an effective source of RF/microwave energy in the range of 200 MHz to 1000 MHz.

1. Introduction

Powerful vacuum microwave devices have existed and been developed since the 1930s. From the moment of their introduction until recently, such devices have mainly been used for radar and communication. Other applications of one of these devices (the magnetron) are defrosting food and cooking in household microwave stoves.

Some applications of vacuum microwave devices have been discovered relatively recently. In the 1960s, charged particle accelerators appeared that used microwave fields for acceleration. In the 1970s, medical microwave devices began to appear, including medical accelerators, microwave scalpels, among others.

Recently, industrial technologies using microwave energy have begun to be developed. These include, for example, technologies for defrosting large volumes of products in defrosters [1], for the radiation sterilization of products and materials, for sintering ceramics, for drying wood [2], and so on.

The development potential of industrial microwave technologies is very large. For example, several years ago, successful experiments were conducted to produce artificial sandstone from crushed sand. This is a building material that can compete with concrete in mass production. Foam glass is another building material that can be efficiently produced using microwave technology. There is also the possibility of deep oil refining using microwave technologies.

Another area with great potential for development is microwave energetics. This is a set of technologies utilizing microwave radiation for wireless energy transmission. Energy can be transferred to hard-to-reach places, to mountainous areas, to remote islands, to polar stations, and so on. In addition, energy can be transferred from the earth to aircrafts and spacecrafts. In the long term, the reverse process is possible via the transfer of energy to Earth from solar panels located in space.

Classification of existing high-power vacuum electronic devices (Figure 1), amplifiers and generators of microwave power, can be carried out by taking two basic characteristics into account: the type of interaction of the microwave field with the electronic flow (O-type, M-type, gyrotron type) and the nature of the microwave vibrations (traveling wave or standing wave). As examples, Figure 1 shows the most typical representatives of each class.

In contrast to devices with a traveling wave, the interactions of electron beams with microwave fields in O-type resonant devices are local and realized in the gaps of resonators, the values of which are significantly less than the wavelength.

O-type resonant devices can be divided into two classes: devices with velocity modulation (klystron type) and devices with emission modulation (IOT type). The first class includes various modifications of klystrons, while devices of the second class have several names: klystrodes, inductive output tubes (IOTs), tristrodes, among others.

Figure 2 represents the simplified schism of standard klystrons and IOTs.

Klystrons and IOTs are the powerful microwave amplifiers (i.e., transformers of a small input microwave signal to a large output). The output signal receives energy from a DC source or a pulsed electrical power source (modulator). The electron beam is accelerated via the voltage of the electrical source, then bunched and decelerated by the microwave field. Slowing down, the electron beam gives away its kinetic energy to the microwave field. This process can be considered the transformation of DC or pulsed power into microwave power, and therefore klystrons and IOTs can be considered microwave power sources. Klystrons and IOTs are currently widely used for powering particle accelerators and in medical equipment, but their promotion in the field of mass industrial technologies and energy is hindered by their lack of efficiency.

Recently, several publications have proposed and investigated new variants of O-type resonant devices based on computer models: COM klystrons [3,4,5,6,7,8,9], CSM klystrons [9,10,11,12] and resotrodes [13,14,15,16,17]. It has been shown that the efficiency of such devices can reach 90%.

Table 1. Comparison of standard klystrons with COM and CSM ones.

Parameter	Standard	COM	CSM
Number of cavities	5–8	7–8	10–12
Harmonic cavities	No or one 2nd harmonic cavity	No	3–4 cavities of 2nd harmonic and 1–2 cavities of 3rd harmonic
Length	standard length	~1.6·(standard length)	~standard length
Bandwidth	0.5–5%	0.5–5%	0.5–5%
Work frequency	400–30,000 MHz	400–30,000 MHz	400–30,000 MHz
Gain	40–60 dB	40–60 dB	40–60 dB
Efficiency	<70%	up to 90%	up to 90%

and

Table 2. Comparison of IOTs with resotrodes.

Parameter	IOT	Resotrode with 0-Regeneration	Resotrode with 2π-Regeneration
Number of cavities	2	2	3–4
Multi gap cavities	No	2-gaps cavity	3-gaps cavity with far-spaced gaps
Harmonic cavities	No	No	2nd or 3rd harmonic cavity
Broadband amplifier	yes	no	no
Work frequency	400–1000 MHz	40–200 MHz	200–1000 MHz
Gain	<20 dB	35 dB and more	35 dB and more
Efficiency	<70%	up to 90%	up to 90%

compare the main characteristics of the standard and new devices.

We use the term “standard length” instead of a specific numeric value, since the length depends on the operating frequency, current and voltage. If the values of these parameters are set, the “standard length” becomes a specific number.

A big length is a problem for frequencies under 1000 MHz (standard length is recognized as about 2 m or more in these cases). Thus, devices can be very large and expensive. COM klystrons are 60% longer than the standard length (see Table 1), meaning that they are even longer and even more expensive. As the operating frequency increases, the standard length decreases proportionally, reaching values of 15–20 cm at 10 GHz. For such high frequencies, increasing the length in COM klystrons is an advantage, since it allows the problem of heat removal to be solved.

The main disadvantage of CSM klystrons is their more complex design, which includes cavities of the second and third harmonics. This disadvantage becomes more significant with increases in work frequency.

Thus, in the lower part of the microwave range (up to about 5 GHz), it is advisable that CSM klystrons be used, while COM klystrons are optimal for higher frequencies.

In general, the main disadvantages of COM and CSM klystrons are their larger dimensions (for COM), complicated designs, and increased costs. The main advantage of these klystrons is their heightened efficiency.

Unlike IOT, resotrodes use the regeneration of microwave power in the input circuit. This inevitably narrows the gain band. Therefore, the main drawback of resotrodes is the inability to use them as broadband amplifiers (Table 2). When using a resotrode as the source of microwave power, this drawback does not manifest itself. The main advantage of resotrodes in comparison with IOTs is the ability to provide high gain at high output power with high efficiency.

The purpose of this paper is to review the latest achievements in the field of modeling and to research new O-type resonant microwave devices that could be used for the development of industrial microwave technologies and microwave energetics.

2. Efficiency of Resonant Microwave Devices of O-Type

Both in industrial microwave technologies and in microwave power engineering, it is essential to achieve high efficiency values.

For example, in power systems, no more than 10–12% is lost during transportation and transmission (i.e., the total efficiency of power systems is about 90%). When implementing microwave power systems, efficiency must be at least 90%, which means that the efficiency of devices and devices included in such systems must be at least 90%.

In industrial microwave technologies, an increase in efficiency from 60% to 90% (1.5 times) will reduce the cost of electricity consumed by the same 1.5 times. This can turn some promising, but currently unprofitable, technologies into cost-effective ones. At the same time, the power of additional cooling equipment will be reduced by four times, which will result in additional savings.

For all these applications, high efficiency must be combined with high power output.

Efficiency is one of the main output parameters of the device and is defined as the ratio of useful to consumed power:

$$\eta =\frac{P_{useful}}{P_{supply}}$$

(1)

Depending on the interpretation of the concepts “useful power” and “spent power”, different definitions of efficiency are possible. In the Equation (1), P_useful refers to the microwave power transmitted to the load, and P_suply refers to the power of the power source spent on beam acceleration. This definition corresponds to the term “load efficiency”.

In this study we also use the term “electronic efficiency”, in which P_suply is defined as above, while P_useful refers to the microwave energy transmitted by the electron beam to the microwave field in the output cavity. Electronic efficiency is always higher than load efficiency. In resonant microwave devices of the O-type, as a rule, these two values differ by less than 1%, but sometimes the difference can be several percent.

For a long time during the development of O-type resonant microwave devices, efficiency was given less priority compared with other output parameters such as output power and bandwidth. The 2005 SLAC report [18] showed a graph of the increase in the pulsed power of klystrons, revealing that the power grew exponentially over the period from 1940 to 2000, reaching a level of 1 GW by 2000. This process is still ongoing.

As for efficiency, there have been no similar dynamics in improving this parameter. The efficiency of a multi-cavity klystron of 50% was achieved at the turn of the 1950s–60s, and since then then no significant increase in the average efficiency of manufactured klystrons has been achieved.

During the second half of the 20th century, several single klystrons with a fairly high efficiency were created. Among them, we should note the 50 kW CW klystron developed by E. L. Lien in 1970 [19,20], which has an efficiency of 75%, and a klystron with an efficiency of more than 80% (electronic efficiency of about 90%) that was developed by S. V. Lebedinsky in 1979 [21].

Devices with emission modulation have had an efficiency of 50–60% since the beginning of their development in the 1980s. Among these devices, we should note the tristrod [22,23] (an IOT with an additional bunching cavity), created by V. A. Tsarev (RF, NGO “Contact”) in 1998. This device had a measured efficiency of about 90%.

These devices were unique, and these results have not been repeated by anyone until now.

Most of the currently manufactured klystrons do not reach an efficiency level of 65%, and only three of the manufactured devices (Figure 3) have an efficiency of about 70%. These are the TH-1801 from Thales, E-3736 from Toshiba, and VKL-8301 from CPI.

3. Klystron Parameters and the GSP Equivalence Principle

Before we talk about the possibility of increasing the efficiency of klystrons, we will analyze the main parameters that define the device design and power mode.

The set of these parameters can be divided into two groups, which we will call “group A” and “group B”.

Group A includes parameters that are selected a priori based on the technical requirements for the device and general physical considerations. These are the main frequency f₀, the accelerating voltage U₀, the total current I₀, the number of electron beams N_b, the number of cavities n, the working harmonics, the gap values l_g, the R/O factors of the cavities ρ, the proper Q-factors of the cavities Q_0i, the beam radii r_b, the canal radii r_c, among others. The index i means the number of the cavity or the stage. If all the parameters of group A are set, we will say that the basic design of the device is set.

Group B consists of all other parameters of the device, which include the natural frequencies f_i and the loaded Q-factors of the cavities Q_i, the length of the drifts l_ci and the input power P_in. Group B can be narrowed if the values of some of the listed parameters must be fixed in accordance with technical requirements. For example, in a narrow-band klystron, the Q-factors of the intermediate cavities can be set equal to their own Q-factors, and, accordingly, they will not be included in group B.

If complex electrodynamic systems and multi-band cavities are used in klystron stages, the number of parameters will increase.

A complete set of input parameters of groups A and B that are enough for the development of the device will be called the complete set of parameters.

We will now determine the number of optimization parameters for an n-stage klystron consisting only of the standard stages (with a single single-gap cavity that is excited at only one frequency). The parameters of group B are n detunings, n Q-factors (including the loaded Q–factors of the input and output cavities), n−1 drifts and the input power. As such, there are 3n parameters. Some of these parameters may not be included in the optimization or, accordingly, in group B. For example, if all the intermediate cavities are detuned far beyond the band, then their Q-factors can be set equal to their own Q-factors and fixed. The number of parameters disabled from optimization will not exceed n2, since the loaded Q-factors of the input and output cavities should remain in optimization. Thus, the number of parameters in group B for the n-cavity klystron are in the range from 2n + 2 to 3n. That is, from 12 to 15 parameters are obtained for the five cavity klystron, and for the 16 to 21 parameters are obtained for the seven cavity klystron.

The number of parameters is reduced after reducing them to a dimensionless form.

When writing formulas, we will use two types of normalization, the first of which is the fundamental normalization [24], which is obtained by dividing physical quantities by the quantities of the same dimension made up of fundamental physical constants: the charge of the electron, the mass of the electron, the speed of light and the dielectric constant. Values for this normalization are shown in

Table 3. Values for fundamental normalization.

Name	Designation/Formula	Value
Charge of the electron	e	1.60 × 10−19 Kl
Mass of the electron	me	9.11 × 10−31 kg
Speed of light	c	3.0 × 108 m/c
Dielectric constant	ε0	8.85 × 10−12 F/m
Fundamental voltage	$U_e=\frac{m_e·c^2}{e}$	511 kV
Fundamental current	$I_e=\frac{m_e·c^3·{\epsilon }_0}{e}$	1.36 kA
Fundamental perveance	$K_e={\epsilon }_0·\sqrt{\frac{e}{m_e}}$	$3.7\frac{\mathsf{\mu }\mathrm{A}}{{\mathrm{V}}^{\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}$
Fundamental impedance	$Z_e=\frac{1}{c·{\epsilon }_0}$	377 Ohm

.

We will denote the fundamental-normalized (f. n.) values by underlining them from below. For example, $\underset{\_}{U}=\frac{U}{U_e}$ (f. n. voltage), $\underset{\_}{I}=\frac{I}{I_e}$ (f. n. current), $\underset{\_}{v}=\frac{v}{c}$ (f. n. speed), and so on.

The second, “functional” normalization is obtained by dividing physical quantities by quantities of the same dimension, which are made up of the main functional parameters of the device: output power, accelerating voltage and main frequency (

Table 4. Values for functional normalization.

Name	Designation/Formula	Dimention
Beam power	P0	W
Accelerating voltage	U0	V
Main frequency	f0or${\omega }_0=2\pi f_0$	c−1
Beam speed	$v_0=c·\sqrt{1-\frac{1}{{\left({\underset{\_}{U}}_0+1\right)}^2}}$	m/c
Duration of one radian of the microwave field	$t_{norm}=\frac{1}{{\omega }_0}$	c
Distance that the beam passes during one radian of the microwave field	$l_{norm}=\frac{v_{norm}}{{\omega }_0}$	m
Beam impedance	$R_{norm}=\frac{U_0{}^2}{P_0}$	Ohm

).

Functionally normalized values will be denoted by two asterisks at the bottom for example, $\underset{\ast \ast }{f}=\frac{f}{f_0}$, $\underset{\ast \ast }{z}=\frac{z}{l_{norm}}$, $\underset{\ast \ast }{Z}=\frac{Z}{R_{norm}}$, $\underset{\ast \ast }{t}={\omega }_0·t$, etc.

In the process of functional normalization, the parameters of group A turn into dimensionless complexes [25] (similarity criteria), the number of which is three less than the number of initial parameters.

The first of these dimensionless complexes is the relativistic perveance assigned to a single beam of a multi-beam (MB) klystron:

$${\underset{\_}{K}}_{rel}=\frac{{\underset{\_}{P}}_0}{{\underset{\_}{U}}_0{}^{5/2}{\left(1+\frac{{\underset{\_}{U}}_0}{2}\right)}^{3/2}{N}_b}$$

(2)

In addition, dimensionless complexes are the normalized length of the gap (the angle of passage through the gap),

$$\Theta =\frac{{\omega }_0·l_g}{c\sqrt{1-\frac{1}{{\left(1+{\underset{\_}{U}}_0\right)}^2}}}$$

(3)

the gap form factor,

$$\mu =\frac{l_g}{2r_c}$$

(4)

the coefficient of filling the channel with a beam,

$$\alpha =\frac{r_b}{r_c}$$

(5)

and the excitation parameter [24], which has the meaning of the “natural” bandwidth of the device,

$$\nu =\frac{\rho ·P_0}{U_0{}^2}$$

(6)

The parameters of group “B” are converted to dimensionless lengths of drifts,

$$\underset{\ast \ast }{l_{ci}}=\frac{l_{ci}}{l_{norm}}$$

(7)

to the relative detuning of cavities,

$${\delta }_{fi}=\frac{f_i-f_0}{f_0}$$

(8)

and to the normalized input power,

$$\underset{\ast \ast }{P_{in}}=\frac{P_{in}}{P_0}$$

(9)

The number of parameters in group B does not change during the normalization process.

The general scaling principle (GSP; transcription as “global scaling principle” was also used in publications [25]) is the statement that two klystrons with the same values of dimensionless Parameters (2)–(9) are physically equivalent. All processes of the grouping and selection of energy occur in these two devices in the same way. These two devices will have the same dimensionless output characteristics, including the same efficiency. At the same time, such klystrons can differ greatly in the level of output power, the number of beams, the accelerating voltage, the operating frequency and other basic dimensional characteristics.

The GSP principle splits the set of all existing klystrons and all klystrons that may be developed in the future into equivalence classes. Each equivalence class is defined by five parameters (Parameters (2)–(6)).

Note that of Parameters (2)–(6), only Parameters (2) and (6) are free. Although optimization for Parameters (3)–(5) is not usually performed, their values are chosen close to the known conditionally optimal values $\mu \simeq 1$, $\alpha \simeq 0.5$ and $\Theta \simeq 1.2÷1.4$, and do not deviate significantly from these value, since such a deviation leads to a deliberately suboptimal construction. Thus, Parameters (3)–(5) can be considered fixed.

Consider an equivalence class given by two parameters ${\underset{\_}{K}}_{rel}$ and $\nu$, assuming that each of the parameters $\mu$, $\alpha$ and $\Theta$ is in some reasonable range near the optimal value. This class of klystron equivalence will be called the $K-\nu$ class.

Each $K-\nu$ class is represented by a dot on the $K-\nu$ diagram.

In Figure 4, klystrons that are currently produced by various manufacturers are divided into three groups according to level of efficiency, and are marked on two $K-\nu$ diagrams. In the right-hand diagram, the abscissas axis is replaced by the normal perveance $K=\frac{P_0}{U_0{}^{5/2}·N_b}$ instead of the relativistic perveance (Parameter (2)).

The sample includes devices of different frequency ranges (from 400 MHz to 30 GHz), different levels of output power (from 3 kW to 80 MW) and different numbers of beams (from 1 to 42).

All klystrons are divided into three groups: high efficiency (60–70%), medium efficiency (40–60%) and low efficiency (less than 40%).

Klystrons with low and medium efficiency are distributed evenly across the diagram, while klystrons with high efficiency are concentrated in the region of relativistic perveance 0.2–0.3. This range is optimal in terms of efficiency.

The GSP principle makes it easier to develop new high-performance klystrons if their analogues already belong to the same class. To do this, it is enough to recalculate all the parameters, leaving the dimensionless values (Parameters (2)–(9)) constant. In this case, GSP modeling avoids a long, complex and expensive process of computer optimization of the device. The method of such recalculation is described in [24]. The limitations of using GSP modeling are also discussed there.

4. Methods of Klystron Modeling and Optimization

If there are no suitable GSP analogues (and no analogues for efficiency above 70%), it is necessary to optimize the parameters of group B using a mathematical model implemented in the form of a computer code.

Currently, developers use several computer codes that simulate the operations of klystrons. The most appropriate codes are based on particles-in-cell (PIC) models [26], which were initially developed for modeling processes in plasma, then adapted for electrovacuum devices.

Klystron developers actively use two universal PIC packages: the MAGIC code [27], developed by the American firm Orbital ATK, and the CST studio suit code [28], produced by the German company CST.

However, it should be noted that universal PIC codes do not consider the specifics of microwave devices, so the calculation process for them are extremely expensive. On an office PC, the calculation of one specific device variant with fixed frequency and input power values is a day or more. This process can only be performed on high-performance supercomputers. At the same time, the computing process itself not only requires a lot of resources, but also a lot of data preparation, and any changes to the data are associated with significant difficulties. For example, in order to change a cavity’s detuning, it is necessary to repeatedly change its size, select a new frequency value, rebuild the computational grid, and only then perform the calculation process with the new frequency. This complexity of changing data makes it impossible to optimize the parameters of devices using universal PIC codes, even on supercomputers.

Note that, despite the huge computational complexity of universal PIC codes, their use does not guarantee a reliable result. Although the methodological error in such codes can be practically reduced to zero by shredding the computational grid and increasing the number of particles, this cannot be said about the computational error, which, on the contrary, often begins to increase under these conditions. The computational error is shown as “numerical noise”, the presence of which is usually estimated visually. At the same time, there are neither sufficiently reliable mechanisms for recognizing computational noise, nor universal ways to suppress it. Usually such noise is suppressed by heuristic manipulations such as changes in boundary conditions (deterioration of wall conductivity), adding virtual absorbers, and so on. It is obvious that such actions change the model of the system, and, consequently, lead to a deterioration in the adequacy of modeling the original system.

However, universal non-stationary 2D/3D PIC codes are currently the main recognized criterion for the accuracy of results obtained by other computational methods.

In addition to universal PIC codes, quite a lot of special computing codes have been developed that are adapted to microwave devices of one type or another.

Let’s look at the features of such codes on the example of the TESLA (USA) code, created by a group of specialists from several scientific organizations in the United States. As follows from the description in [29], for example, the TESLA code uses the separation of the microwave fields of cavities and fields (coulomb and microwave) in the region of beam motion. The crosslinking of these fields in the gap area occurs on the continuation of the inner surface of the drift pipe. This separation corresponds to the specifics of the klystron and allows us to separate the problems of electrodynamics (modeling of microwave fields in the cavity) and electronics (beam bunching, interaction of the beam with microwave fields). This, in turn, leads to the possibility of using different scales of computational grids in the cavity region and in the interaction region, while accordingly leading to the possibility of a significant reduction in the number of particles and a consequent reduction in calculation time. The calculation time for one option under the TESLA code is 10–20 min on a personal computer. This is too much to optimize on a PC, but on multiprocessor supercomputers, optimization can be performed using this code. It should be noted, however, that due to the simplifying assumptions used in the construction of the model, the question of the methodological error of the results remains open. For example, in the results given in [29], the discrepancy between the results of TESLA and MAGIC seems significant.

One of the latest developments of adapted codes is the KlyC/1.5 code (CERN, Geneva, Switzerland) [30], developed by I. Syrachev and J. Cai. This code allows you to model the operation of a klystron in approximations 1D and 1.5 D (one-dimensional motion with a bundle). According to the authors, the difference between the results of KlyC-1.5 D and CST is no more than 1%. The calculation time for a single variant using the KlyC-1.5 D code with seven layers depends very much on the device being modeled, but is usually at least 30–40 min on a PC. This is too much for full multiparametric optimization, which requires tens or even hundreds of thousands of calculations [31].

In order to combine high performance with high adequacy, a new class of klystron models was developed called “discrete-analytical models” [32].

Discrete-analytical models appeared as a reasonable compromise between analytical and numerical approaches in the construction of a mathematical model of the device. This compromise is achieved by splitting the structure of the device or processes occurring in it into conditionally autonomous parts, building models for these parts in the form of analytical dependencies and coupling these dependencies.

Thus, the core of the mathematical model is a set of analytical dependencies, while the rest of the model structure, including the method of coupling these dependencies, is formed on the basis of numerical algorithms.

The numerical algorithms can also be used in the process of forming the core to determine the numerical parameters that are included in the core of model. In this case, the gain of time is achieved because the process of the numerical determination of parameters (the process of “learning”) is separated from the model operation process.

In addition to the speed and adequacy of the model, the optimization method itself is an important factor for successful optimization of klystron parameters.

The main feature of any klystron goal function constructed on the basis of efficiency is the existence of a multidimensional “quasi-optimal” variety of an unknown a priori structure, characterized by a weak and non-monotonic change in the objective function with a very large (10¹² or more) number of local extremes [31].

As one of the simplest examples of movement through such a variety, we can cite the process of tuning the klystron input cavity while increasing the input power so that the amplitude of the microwave voltage in the input gap does not change. In this case, the efficiency of the klystron due to changes in the phase of the input voltage will change, but very slightly and non-monotonously. The trajectory of changes in the detuning and the input power in the parameter space forms a curve, a one-dimensional quasi-optimal variety. If you add a loaded Q-factor to these two parameters and change all three parameters at once so that the microwave amplitude in the input gap does not change, you will get a two-dimensional quasi-optimal variety. As the number of parameters increases, there are more and more opportunities to change them without significantly changing the efficiency, but it is very difficult to find all such variations a priori (i.e., the structure and dimension of a quasi-optimal manifold are unknown in advance).

This structure of the target function makes it useless to use any optimization method aimed at finding a single local extremum, which explains the fact that most researchers using optimization have always achieved local results without getting a procedure that would allow them to approach the global extremum with a guarantee (even for a very long time).

To overcome these difficulties, a method of macro-steps was developed [31] that includes probing a relatively large working area in the parameter space, finding the local extremes closest to the best points obtained as a result of probing, selecting one of these local extremes and moving to a new working area. The macro-steps method allows for multi-parameter optimization and provides hope for achieving a global maximum of the goal function. To increase the guarantee of achieving the global extremum, the macro-steps method must be supplemented with an appropriate method of structural optimization, as will be discussed in more detail later.

The KlypWin computer code was developed based on the discrete-analytical klystron model and the macro-steps method [33]. It takes less than 1 s to calculate one version of the device using KlypWin.

A comparison of the calculation results for the KlypWin and Magic codes conducted by David Constable in 2013–2016 for 10 klystrons synthesized as part of the work of the international High Efficiency Klystron Activity (HEIKA) group [7] is shown in Figure 5, Figure 6 and Figure 7.

Note that each point by the MAGIC code in Figure 6 and Figure 7 requires more than a day of computer time, while a similar point by the KlypWin requires only 0.3 s. As you can see from the figures, the difference in results for all 10 devices does not exceed 5%. The results show that KlypWin can be considered an adequate code for modeling klystrons. At the same time, its speed makes it possible to perform global multi-parameter optimization.

5. COM and CSM Klystrons are Promising Power Sources in the Centimeter Range

Based on the KlypWin code, a large set of studies has been conducted over the past decade on the possibility of achieving the maximum efficiency values in klystrons [4,5,6,7,8,9,10,11,12,24]. In the course of these studies, it was found that maximum efficiency values were achieved with two bunching modes: the core oscillation method (COM) [4,5,6,7,8,9] and the core stabilization method (CSM) [9,10,11,12].

As was found in the course of research, in order to reliably achieve the global extremum of the target function, the macro-steps method must be supplemented with a suitable structural optimization method. Structural optimization refers to the process of gradually complicating the structure of a device, starting with the simplest structure. After each stage of structural complexity, global optimization is performed using the macro-steps method. The process that includes structural optimization of this type and global optimization by the method of macro-steps is called full optimization [34].

Klystrons with extreme efficiency values are obtained as a result of two possible processes of full optimization.

The first full optimization process is called stage-by-stage optimization [24] and was first described in [4]. The process begins with the formation of a two-cavity klystron based on a given prototype (a set of parameters of group A). This two-cavity klystron is optimized, after which another stage is added to the optimal two-cavity klystron, and it turns into a three-cavity klystron. For the resulting three-cavity klystron, the optimal input power is found, then global optimization is performed for all parameters in a wide range of their changes. The resulting optimal three-cavity klystron is converted into a four-cavity klystron by adding another stage, the global optimization process is started again, and so on. Starting with a three-cavity klystron, adding a new stage is performed by duplicating the second stage. The process stops when, after adding a new stage and performing optimization, the efficiency stops increasing (it comes to saturation).

The stage-by-stage optimization process is shown for a C-band klystron with an output power of 8.5 MW, as shown in Figure 8.

In addition to efficiency, the figure shows two other key parameters. The first one is the saturation of the bunch [5], which reflects the proportion of electrons caught in the bunch at the entrance to the output gap. The second parameter is lumped bunching length (LBL) [4], which is describe in the

Table 5. Bunching dimensionless values.

Name	Designation/Formula	Description
Total normalized length of the bunching [4]	$\underset{\ast \ast }{l}=\frac{\omega ·l}{v_0}$	Normalized total length of all drifts and gaps
Parameter of the convection wave [24]	${\Omega }_p$	Ratio of the electron beam convective wave frequency and the microwave frequency
Lumped bunching length (LBL)	$l_{\Omega }={\Omega }_p·\underset{\ast \ast }{l}$	Number of radians of the convective wave that fit over the bunching length

.

The left part shows the change in the bunching process (phase trajectories) as the number of stages increases. The upper-right corner shows the change in efficiency (1), bunch saturation (2) and LBL (3) depending on the number of stages.

In the stage-by-stage optimization process, only standard stages are added, which include a simple single-gap cavity and a single drift. Accordingly, all klystrons obtained during this process have a standard configuration (i.e., they do not contain multi-gap cavities and cavities of higher harmonics).

All klystrons resulting from stage-by-stage optimization are characterized by the same non-monotonic character of bunching.

For the core particles of a bunch, this mode is oscillatory: these particles approach the center of the bunch, then move away from it. For particles of anti-bunch [5], the oscillatory nature of the motion is changed to a monotone. It is in this bunching mode that the klystron of the standard configuration reaches the maximum saturation of the bunch at a given frequency.

In turn, the saturation of the bunch is one of the main and most difficult factors to achieve in order to obtain maximum efficiency.

The key parameter that ensures the maximum saturation of the bunch is the LBL, which must be increased 1.6–1.8 times compared to known prototypes to increase the bunch saturation. The length of the device increases accordingly.

The fact that the stage-by-stage optimization of various prototypes that differ significantly from each other leads to the same nature of bunching and to similar values of the LBL and efficiency, allows us to speak about the fundamental nature of both the bunching mode itself and the LBL as the main parameters that characterize the bunching mode. This bunching mode was named core oscillation method (COM) [5].

All COM klystrons synthesized during full stage-by-stage optimization are characterized by efficiency from 85% to 90%, and the result practically does not depend on the prototype used, in particular, on its power. Thus, powerful COM klystrons with high efficiency can be developed for use in industrial microwave technologies and in microwave power engineering.

The second method of full optimization is called the embedding procedure. In this case, the optimal three-cavity COM klystron is selected as the initial option. Then, the total length is fixed, and new cavities are inserted between the existing ones. As shown by the research, only the first harmonic does not affect the efficiency in this case during the insertion of cavities, and efficiency remains at the level of 70%. To increase efficiency, it is necessary to alternate the cavities of the first harmonic with the cavities of the second harmonic, and to achieve an efficiency of about 90% it is necessary to include at least one cavity of the third harmonic. An explanation of this fact is given in [9,24].

Note that second harmonic cavities are used in the development of many klystrons. As a rule, developers have been limited to one such cavity, but in rare cases their number has increased to two or three. In this regard, we can mention the works of I. A. Guzilov, which were devoted to the development of BAK-bunching [35].

We could not find information about the use of third harmonic cavities in commercially produced klystrons. High-efficiency klystron models based on third harmonic cavities were constructed in [36,37] by Chiara Marelli (ESS) and Igor Syratcev (CERN).

The embedding procedure results differ significantly from COM bunching. There are no fluctuations in the core of the bunch; instead, the core stabilizes and attains a monospeed. Peripheral electrons due to voltage harmonics acquire a high relative velocity, which is quickly extinguished when these electrons approach the core of the bunch. After the speed is extinguished, these electrons replenish the stabilized core of the bunch. This process is called the core stabilization method (CSM). It provides a high saturation of the bunch, but at a much shorter length than COM. At the same time, the total number of cavities increases in comparison with COM klystrons. The optimal COM klystron has seven to eight cavities, while in the optimal CSM klystron the number of cavities increases to 10 or 11. The problem of arranging cavities in this case turns out to be solved, because the cavities of the second and third harmonics are relatively small.

The results of the synthesis of CSM klystron at a frequency of 800 MHz and a pulse power of 20 MW are shown in Figure 9. The numbers of working harmonics of the cavities are signed above the diagram of phase trajectories.

Another high-efficiency bunching mode is possible, which combines the characteristics of COM and CSM modes and makes it possible to realize an efficiency of about 90%. This mode is called COM2. It is implemented only when an additional second harmonic signal is applied to the input. The klystron buncher in this case contains either two-frequency cavities operating on both the first and second harmonics, or alternating cavities of the first and second harmonics. The length of the LBL is less than that of COM klystrons, but longer than that of CSM klystrons. COM2 klystrons are described in more detail in [24].

Some synthesized COM and CSM klystrons are shown in Figure 9, where the numbering of the prototypes from [24] are used. As can be seen from the K-ν diagram, high efficiency values are obtained for klystrons with a beam perveance from 0.2 to 0.4. The synthesized klystrons do not correspond to the empirical dependence [38] of the maximum efficiency on the perveance, shown by the inclined straight line in the right part of Figure 10.

COM and CSM klystrons with an efficiency of about 90% can be considered as promising sources of microwave power for industrial applications and for microwave energetics.

6. Resotrode with 0-Regeneration

In devices with emission modulation (IOTs), it is possible to realize sufficiently high efficiency values by reducing the length of the clot (cutoff angle). This reduces both the output power and the gain.

A new class of devices called resotrodes can achieve high efficiency with high output power and a high gain value [13]. These devices are sources of RF/microwave power for the upper RF range (20–200 MHz), for the lower microwave range (300–1000 MHz) and for the boundaries of RF/microwave bands (200–300 MHz).

In devices with emission modulation, the electronic gun and input cavity are combined within the same design.

There are three possible variants of this combination, as shown in Figure 11.

Classical IOTs use variant (a), multi-beam IOTs use variant (b).

One of the disadvantages of IOTs is the low gain, which does not usually exceed 20 dB. Another disadvantage is the need to place the control grid very close to the cathode to obtain even this gain, which significantly complicates the technology and reduces the reliability of the device. This problem is particularly significant in multi-beam devices (MB IOTs), since it is necessary to achieve the same cathode-grid distance for all cathodes at a distance of 0.2 mm or less. Moreover, this same small distance must be implemented in the “hot mode”, considering the thermal expansion.

Most commercially produced IOT devices have a single-beam grid design (Figure 11a). The first multi-beam grid structures appeared in the late 1990s (Figure 11b).

The constructions in Figure 11c, as far as is known, were not used for the development of industrial designs of IOTs. This is because the ratio of the absolute values of the grid voltage to anode in this design cannot be less than an amount equal to about 1/4 to obtain a sufficiently high efficiency. Thus, the ratio of the amplitude of the input signal to the amplitude of the output signal must also be about 1/4, which leads to a very low gain (5–6 dB).

For relatively low frequencies (20–200 MHz), a new device with emission modulation has been proposed, corresponding to the scheme Figure 11c and using energy regeneration in the input circuit. This device is called a resotrode (names “resotrod” and “rezotrod” [13] have also been used in publications).

An essential feature of the resotrode that allows the disadvantages of IOTs to be overcome is the ability to implement a high gain at a relatively high value of the voltage amplitude in the input gap (in the cathode-grid gap).

This possibility appears because the control electrode–anode gap is the second gap of the two-gap input cavity, which operates on antiphase-type vibrations. However, the degree of compensation (regeneration) in such a design depends significantly on the angle of passage of the cathode–anode: the higher the angle of passage, the smaller the regeneration. At frequencies above 200 MHz, the compensation becomes incomplete and quickly drops as the frequency increases.

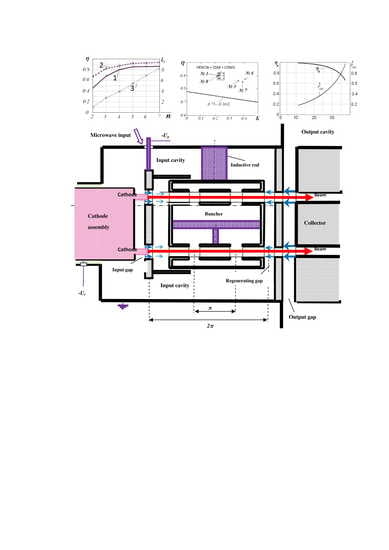
The general scheme of a resotrode with 0-regeneration (assuming that the angle of passage through a pair of input gaps, including the regenerating gap, is close to zero) is shown in Figure 12.

The anode-collector gap is the gap of the output cavity. The control electrode is current-less, because the instantaneous dynamic value of the potential on it is always negative (c- or d-lamp operation mode).

Thus, the current flows only in the cathode-collector circuit and, therefore, only this circuit should be designed for high power. It should be noted that when working in amplification mode at time intervals when the signal is absent, the cathode is locked, and the current does not flow to the collector, which ensures the efficiency of the device and reduces the thermal load on the collector.

In a general sense we will use “a resotrode” to refer to any devices with emission modulation that has full or excessive electronic load compensation in the input circuit.

Thus, name “resotrode” can apply not only to the construction in Figure 11c, but also to the type in Figure 11b with the appropriate compensation.

7. Evaluation of the Efficiency and Gain of a Resotrode

Unlike the klystron output parameters, a resotrode can be quantified with relatively simple analytical relations. Further refinement of these estimates is possible within the framework of computer 2D/3D modeling only.

We assume that the angles of passage of the electrons through all the gaps are small ${\Theta }_d\ll 1$, and that the electronic load operates at full compensation, in which the amplitudes of the microwave voltage in the first and second gaps of the input cavities are the same. In this case, the electron velocities will correspond to the static potential of the anode after entering the anode hole (i.e., the bunch will be strictly monospeed).

As shown by klystron studies, a narrow monospeed bunch can be slowed down to zero speed, and, if the gap is narrow, full braking is provided by zero detuning and a microwave voltage amplitude equal to the accelerating voltage.

The instantaneous voltage at the control electrode must be negative, which implies a condition of $U_1\le U_g$, where $U_1$ is the amplitude of the microwave voltage in the input gap, and $U_g$ is the absolute value of the constant voltage at the control electrode (offset voltage) relative to the cathode. On the other hand, a decrease in the microwave amplitude at a given offset leads to a sharp decrease in the current and, consequently, the power of the device. It follows that the next equality is optimal:

$$U_1=U_g$$

(10)

In the output gap at small angles of flight, the amplitude of the microwave voltage $U_2$ at zero detuning cannot be made greater than the accelerated voltage $U_0$, because this will lead to electron reflections. On the other hand, if $U_2<U_0$, then the bunch will not be completely stopped (i.e., under this condition, the efficiency will not be maximum). This leads to the conclusion that for zero detuning, equality $U_2=U_0$ is optimal. Next, we assume that the output cavity detuning is zero.

The input cell of resotrode (Figure 12) is a three-electrode electron gun, which is characterized by the cutoff potential $U_{sh}$ (i.e., the value of the control electrode negative potential $-U_{sh}$ at which the anode current ceases to go). The relative value of the cutoff potential is determined by the shape of the electrodes and the relative distances between them. In the grid-free constructions (Figure 11c), the value $\underset{\ast \ast }{U_{sh}}=\frac{U_{sh}}{U_0}$ is bound from below by the values 0.12–0.15. Next, we assume that the value $\underset{\ast \ast }{U_{sh}}$ is set.

Under Equation (10), the instantaneous voltage at the gap between the cathode and the control electrode has the form $u_{in}\left(\underset{\ast \ast }{t}\right)=U_g·\left(1-\cos \left(\underset{\ast \ast }{t}\right)\right)$, and the width of the bunch is determined by the ratio

$$k_{sh}=\frac{U_g}{U_{sh}}$$

(11)

which will then be called the cutoff coefficient.

From the bottom of Figure 13, it follows that the normalized width $\underset{\ast \ast }{{\tau }_b}$ of the bunch is related to the cutoff coefficient $k_{sh}$ by the ratio

$$\underset{\ast \ast }{{\tau }_b}=2\arccos \left(1-\frac{1}{k_{sh}}\right)$$

(12)

Let us consider the deceleration of a single-speed bunch of width (Equation (12)) by the field of an infinitely thin gap of the output cavity with zero detuning. When such a bunch passes through the gap, the instantaneous value of the microwave voltage changes from the amplitude value $U_0$ corresponding to the center of the bunch, to some value $U_b$ corresponding to the edges of the bunch (Figure 13, upper).

The electronic efficiency can be calculated as the ratio of the interaction power to the beam power,

$${\eta }_e=\frac{1}{U_0{I}_0}·\frac{1}{\underset{\ast \ast }{{\tau }_b}}·{\displaystyle \underset{-\raisebox{1ex}{$\underset{\ast \ast }{{\tau }_b}$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}{\overset{\raisebox{1ex}{$\underset{\ast \ast }{{\tau }_b}$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}{\int }}{U}_0·\cos \left(s\right)}·I\left(s\right)ds$$

(13)

If we bring the current outside the integral, using the averaging theorem and assuming approximately that this average current is equal to $I_0$ (calculations for various forms of bunches show that the error of this approximation does not exceed 2%), then from Equation (13) we get an expression for the electronic efficiency of the resotrode ${\eta }_e=\frac{\sin \left(\underset{\ast \ast }{{\tau }_b}/2\right)}{\underset{\ast \ast }{{\tau }_b}/2}$.

Given Equation (12), we finally get

$${\eta }_e=\frac{\sqrt{2k_{sh}-1}}{k_{sh}·\arccos \left(1-\frac{1}{k_{sh}}\right)}$$

(14)

The dependencies defined by Equations (12) and (14) are shown in Figure 14. From these dependencies, it follows that to obtain the maximum efficiency values (90% and higher), the cutoff coefficient values $k_{sh}>4$ are required, which correspond to the value of the normalized width of the bunch $\underset{\ast \ast }{{\tau }_b}<\frac{\pi }{2}$.

Now let us estimate the gain of the resotrode.

In the mode of full electronic load compensation, the input power is equal to the power of the input cavity’s own losses (i.e., $P_{in}=\frac{U_1{}^2}{2·{\rho }_1·Q_1}$, where ${\rho }_1$ is the R/Q factor, and $Q_1$ is the input cavity’s own O-factor).

Representing the output power as $P_{out}={\eta }_e·U_0·I_0$, we find that

$$\frac{P_{out}}{P_{in}}=2{\eta }_e·\nu ·Q_1·{\left(\frac{U_0}{U_g}\right)}^2$$

(15)

where $\nu$ is the output gap excitation parameter defined by Equation (6). Substituting Equations (11) and (14) into Equation (15) and proceeding to the logarithmic recording of the gain, we finally get

$$Ku=10·\log \left(\frac{2·\nu ·Q_1}{\underset{\ast \ast }{U_{sh}{}^2}}\frac{\sqrt{2k_{sh}-1}}{k_{sh}{}^3·\arccos \left(1-\frac{1}{k_{sh}}\right)}\right)$$

(16)

Since the resotrode is essentially a high-perveance device, the characteristic values of the excitation parameter $\nu$ are 0.1 and higher. The own Q-factor can be obtained from 2000 to 5000.

Let’s compare the resulting formula with the gain formula for the classical IOT design, which can be written as

$$Ku=10·\log \left(\frac{1}{\underset{\ast \ast }{U_{sh}}·k_{sh}}\frac{1}{1+\frac{k_{sh}\underset{\ast \ast }{U_{sh}}}{\nu ·Q_1}}\right)$$

(17)

or, for large values of its own Q-factor, in the form

$$Ku=10·\log \left(\frac{U_0}{U_g}\right))$$

(18)

Graphs of the gain dependence for resotrode with parameters $\underset{\ast \ast }{U_{sh}}=0.15$, $Q_1=2000$, $\nu =0.1$ and for IOTs with the same values $Q_1$ and $\nu$ are shown in Figure 15. As you can see from the graphs, the resotrode has a gain of about 40 dB at $k_{sh}=1$ (a bunch of duration π), the gain decreases as $k_{sh}$ increases, but even at $k_{sh}=5$ (a bunch of duration 0.4 π) the gain remains more than 25 dB. In a grid-less IOT (lower graph), the gain is equal to 9 dB if $k_{sh}=1$, but falls to almost zero if $k_{sh}=5$. Only when using a very fine-grained grid ($\underset{\ast \ast }{U_{sh}}=0.001$) can the gain exceed 20 dB.

The dependence of electronic efficiency of a resotrode on gain is shown in Figure 16, from which it follows that at a gain of 30 dB in a resotrode you can achieve an electronic efficiency of about 90%.

It should be noted that when the cutoff increases due to a decrease in the pulse duration, the output power of the device also decreases. In Figure 16 the output power is normalized to the output power of $k_{sh}=1$ (i.e., when the offset voltage of the gain is equal to the cutoff voltage).

From the graphs, we can conclude that the optimal choice is a gain of 25–30 dB, which corresponds to a cutoff coefficient from 3 to 5.

In general, the obtained analytical estimates suggest that the combination of high efficiency with high gain is possible in resonant microwave devices with emission modulation.

8. Possible Designs and Applications of Resotrodes with 0-Regeneration

Resotrodes are modular devices that can be represented as a set of functional cells.

One of the first studied designs of a resotrode for a range of 27–40 MHz included flat cells with tape cathodes. These cells can form various devices that differ in the number of cells and their layouts within a single design.

Research has been conducted to determine the parameters of the optimal functional electron-optical cell of a device, including the sizes and shapes of the electrodes, and their potentials.

Cell synthesis was performed using an electron-optical code according to the “gun-anti-gun” scheme (Figure 17). First, a gun was synthesized that provides a laminar uniform beam in the center of the anode hole (Figure 17a). Next, a “mirror” system was synthesized containing a virtual supposed “issue” of the beam from the collector surface. This beam was gradually transformed into a uniform laminar beam in the process of moving to the center of the anode hole (Figure 17B), where these two beams were sewed. The functional cell synthesized as a result of calculations (Figure 17c) consisted of a linear cathode 0.8 mm thick and 50 mm long with a 1.3-mm radius of the curvature of the emitting surface, a control electrode protruding 0.3 mm above the cathode surface, an anode with a narrow (0.7 mm) input groove and an external part expanding (up to 3 mm) to the collector and a collector with an anti-dynatron grid.

The synthesized cell was quite versatile and, depending on the basic requirements for the device, provided a possibility for implementing various electrostatic potentials on the electrodes and various values of RF voltage amplitudes. For example, by setting the potential of the control electrode at −300 V, the anode potential at +1.2 kV and the collector potential at +300 V, an HF power source of 1–2 kW can be created at a frequency of 27 or 40 MHz and powered directly from the supply mains (without a power transformer) based on the 12 cells considered. Such a source would be very useful for creating high-volume household RF stoves of 60–80 L or more with uniform volumetric heating. Having realized the potentials of 1 kV on the control electrode and +4 kV on the anode and the collector, it is possible to create a power source of 100 kW for industrial heating installations on the basis of the same 12 cells, as well as a continuous power source of 1 MW on the basis of 120 cells (when the voltage increases, the number of cells decreases by the law of degree 5/2).

Based on the synthesized optimal cell, the design of the vacuum part of the resotrode was developed, containing 12 azimuth-oriented functional cells. The control electrode was a molybdenum cylinder with slotted longitudinal grooves, the anode was made of a copper cylinder and the collector had a special prefabricated anti-dynatron structure that absorbed almost all secondary electrons [24].

As a result of the research, the following patterns were established:

• The synthesized electron-cell is minimally critical to small changes in the shape of the electrodes, the distances between them and the applied potentials (i.e., with small (up to 5%) changes in the specified parameters, the electron trajectory practically does not change and the current passage remains complete). This stability ensure the stable operation of the device despite errors in the manufacture of parts, errors in the assembly of components and thermal care.
• The linearity of the amplitude characteristic of the device in the average RF range (tens of MHz) is preserved up to the maximum value of the input signal amplitude.
• The efficiency of the device in monoharmonic mode with a normalized width of the clot about 2 rad. more than 80%. It is possible to obtain maximum efficiency values (close to 100%) when the cut-off angle is reduced.
• The conditions of monotron excitation of the common-phase type of vibrations (the main parasitic type), as well as other (higher) types of parasitic vibrations are not fulfilled. Thus, the device does not generate spurious vibrations.

In addition to the flat design, a resotrode design with cylindrical beams has also been studied. This design uses magnetics, and focuses on permanent magnets.

The design of such a device with the possibility of wide-range frequency tuning from 20 to 150 MHz has been considered, for which the general design is described in [24].

As a result of numerical simulation, V. N. Kozlov [24] showed that a functional cell with a convex cathode is optimal for such a device, since it reduces the locking potential (Figure 18).

Currently, there are no powerful and efficient microwave power sources in the 50–150 MHz range. Traditional microwave devices—magnetrons, klystrons, and TWTs—would be too large in this range, and standard IOTs would have too small a gain. However, this range is the most attractive for solving problems of uniform volumetric heating in industrial processes (e.g., oil distillation, production of building materials, water desalination, etc.).

For effective uniform volumetric heating, it is necessary that the size of the object being heated be somewhat (but not much) less than half the wavelength. Shorter waves inevitably lead to the appearance of zeros in the spatial distribution of the microwave field and, consequently, to uneven heating. Longer waves lead to the need to increase the amplitude of the RF (microwave) field strength and, consequently, to the occurrence of breakouts. The characteristic size of objects that need to be heated during technological processes is about a meter, requiring the wavelength of the microwave field for effective heating to be 2–3 m in order to achieve the frequency range mentioned above. This uniform volumetric heating can be used, for example, for the manufacture of new environmentally friendly materials (foam glass, artificial Sandstone, etc.), for deep oil refining, and for other applications. A design with a direct connection of the resotrode collector to the capacitive electrode of the heating chamber is possible. In this case, heating will be produced not only by the microwave field, but also by the heat of the heated collector (i.e., double microwave and convection heating will be provided).

9. Resotrode with 2π -Regeneration

Based on the given design, low-frequency resotrode can be moved it to a higher-frequency region using scaling, but this procedure will lead to a significant decrease in output power.

Indeed, if all dimensions are reduced in proportion to the wavelength, the emitting area will decrease in proportion to the square of the wavelength, and the total current and power of the device will decrease accordingly. In addition, correct scaling requires the saving value of the beam’s perveance, which leads to an additional decrease in voltage and, consequently, in power.

Attempts to compensate for decreases in input power by increasing the voltage while maintaining the distance will lead to an increase in the current density from the cathode (and therefore to a decrease in the durability of the device) and to a risk of electrical breakdowns in the area of the input cavity.

An increase in the emission area without changing the voltage can lead to a decrease in the R/Q factor of the cavity, and will runs into restrictions on the transverse dimensions of the capacitive part of the cavity of the permissible fraction of the wavelength.

If you increase the voltage while increasing the gaps, then the 0-regeneration condition is violated, which requires that the angle of passage from the cathode to the anode be close to zero.

The relationship between the frequency and the maximum output power of the resotrode with a 0-regeneration is determined by a scaling formula, which implies that using such a device at frequencies less than 200 MHz is impractical.

Thus, to create a powerful microwave source at a frequency greater than 200 MHz, the ideas underlying the resotrode must be corrected.

For operation in the area of hundreds of MHz, a different device scheme was proposed [15], as shown in Figure 19.

This device is called a resotrode with 2π-regeneration, because the optimal angle of passage between the main (accelerating) and regenerating (braking) gaps of the input cavity become 2π instead of 0. The input cavity turns out to be a three-gap cavity, in which the first gap is the main one, and the third one is the regenerating one. The microwave voltage in the second gap is common to the voltage in the first gap, but its amplitude must be small (the gap is “off”). This shutdown is provided by an additional large capacity that provides the microwave closure of this gap to the central bushing.

Between the second and third gaps there is a drift distance enough for the location of at least one additional bunching cavity. When using a two-gap bunching cavity or higher harmonics cavities (i.e., second and third harmonics), two or even three bunching gaps can be placed here. This makes it possible to significantly improve the quality of the bunch, reduce its length and ensure the speed distribution corresponds to the converging bunch [24].

The idea of additional bunching in devices with emission modulation was previously proposed and successfully implemented by V. A. Tsarev [22,23], A. D. Sushkov and V. K. Fedyaev [39] in devices called a tristrod and a tryston, respectively.

Note the main features of the resotrode with 2π-regeneration.

The distance between the first (forming) and third (regenerating) gaps of the input cavity does not depend on the “cathode–anode” distance, so the beam perveance is not related to the pass angle (i.e., the electron-optical parameters (current and voltage) and the pass angle that provide regeneration do not depend on each other). This is the main feature of the design, which makes it possible to work in the high-frequency area.

On the other hand, in contrast to a resotrode with 0-regeneration, the bunch at the entrance to the anode hole is not monospeed, since its speed is modulated by the input signal. This circumstance does not allow such a device to be implemented in a completely grid-free version (Figure 11c), because in this case, even with a minimum offset voltage equal to the cutoff voltage, the speed modulation would be too large and would lead to a scattering of the bunch when it moves to the regenerating gap.

Thus, for a resotrode with 2π-regeneration, it is necessary to use the scheme of Figure 11b. However, in contrast to the classic MB IOTs, the grid can be much more large-scaled and, for flat cathodes, a set of monocrystalline graphite “whiskers” laid in parallel in a row on the control electrode can be used as such a grid. This design of the grid (common to all beams) will significantly simplify the technology and avoid misaligned deformations due to thermal care.

The size of the grid cells is determined by the allowable value of the input signal amplitude, which in resotrodes, unlike IOTs, is not the main factor determining the gain.

The estimates of the efficiency and gain of a resotrode with 0-regeneration made in Section 7 require adjustments to apply them to a resotrode with 2π-regeneration.

In a resotrode with 2π-regeneration, the width of the bunch during its formation and at the entrance to the regenerating gap will differ due to additional bunching. The result of this bunching can be estimated based on the results obtained for klystrons. Under the condition that the width of the bunch, in accordance with Equation (12) and Figure 14, becomes smaller (i.e., the bunch, according to the terminology used for klystrons, becomes fully saturated (FS)). Further bunching of the FS-bunch is primarily related to the transformation of its velocity function. It is necessary to acquire the bunch that comes together and ensures the most effective braking in the exit gap. In this case, the output cavity itself must be detuned to the left. In the klystron, the necessary transformation of the velocity function is performed in the gap of last cavity of buncher, which is located close enough to the output gap. However, the bunch comes into this gap close to the monospeed. In a resotrode with 2π-regeneration, the original velocity function has a different form: the center of the bunch has a maximum velocity that falls to the edges (Figure 20). Further transformation of such a bunch in the drift without additional impact would lead to additional bunching of the front part of the bunch and to the unbunching and lagging of its rear part (i.e., to the formation of a kind of “comet”).

To prevent this, it is necessary to correct the shape of the velocity function (e.g., by using a cavity of the second or third harmonic tuned to the proper resonance (Figure 20)). Thus, the buncher must contain at least one higher harmonic cavity and one main harmonic cavity. If the bunch width is small, the main harmonic cavity can be replaced with a second harmonic cavity that is detuned to the right (Figure 21).

Thus, in a resotrode with 2π-regeneration, a converging FS-bunch can be formed, which allows to an efficiency of 90% or more to be obtained.

As for the gain factor, the rating (Equation (15)) applies for it in the mode of full electronic load compensation. Since the ratio is at least 10 in the grid design, the gain factor should be at least 30 dB even for small gain factors.

For the currently active large hadron collider (LHC), the frequency of 400 MHz is the main frequency, and it is assumed that this frequency will also be used for the FCC (future circular collider) and CLIC (compact linear collider). Currently, klystrons are used as microwave sources for the LHC. Resotrodes with 2π-regeneration have significant advantages over such a klystron: lower supply voltage, higher efficiency and significantly smaller dimensions. You can lower the voltage of a klystron by switching to a multi-beam design. As shown in Section 5, this can significantly increase efficiency, as seen with the COM and CSM klystrons. But the size (and, consequently, the weight and cost) of the klystron cannot be significantly reduced.

A resotrode with 2π–regeneration at the frequency of 400 MHz seems to be a much more promising microwave source than the klystron.

Currently, the first preliminary stage of designing a resotrode with 2π-regeneration at a frequency of 400 MHz and an output power of 300 kV in a continuous mode has been carried out.

Dr. Igor Syratchev [16] at CERN conducted a complete electrodynamic simulation of such an instrument using HFSS code and built a 3D model of it. The results of this work are shown in Figure 22.

The general electrodynamic design of the device (Figure 22) includes an three-phase input cavity that provides bunch formation and energy regeneration, a buncher, an output cavity with a coaxial output of energy through a capacitive connection, as well as blocking filters in the cathode circuit and in the control electrode circuit.

The input cavity has four inductive rods that provide a working antiphase (relative to the third gap to the first two) type of oscillation.

The buncher is modeled with two possible variants, both of which have a two-gap cavity of the main frequency and cavities of harmonics. In the first case, an antiphase type of oscillation is excited in the two-gap cavity, and the gaps are located at a distance of π from each other, which makes it possible to implement bunching phases of the microwave voltage in both gaps. In the second case, the cavity of the third harmonic is tuned to a resonance that corrects the velocity function in accordance with Figure 20, while the cavity of the second harmonic forms a converging bunch in accordance with Figure 21.

Important electrodynamic elements of the device are the resonant choke filters developed by I. Syratchev [16], which ensure the absence of microwave radiation through the power supply chain on the working-type vibrations, simultaneously suppressing parasitic types of vibrations. Note that the filter in the control electrode circuit is also a communication element for the input signal, the suppression of parasitic vibrations is provided by their low loaded Q-factor and grid-less and gridded designs of the resotrode were both considered.

A grid-less design, as already noted, requires a microwave amplitude that is too large for the input gap.

As shown by preliminary calculations, an amplitude of at least 30% of the accelerating voltage requires to ensure the duration of the bunch π/2, which is an unacceptably high value. However, even with this amplitude, a gain of at least 25 dB is obtained, although a preferable option is a sparse grid that provides a gain of more than 35 dB in full-compensation mode. Note that if you switch from the full compensation mode to the excess compensation mode, making the amplitude of the microwave voltage in the regenerating gap greater than the total amplitude in the first gap, you can increase the gain indefinitely until you switch to the generation mode.

The question of the possibility of using a resotrode in the generation mode remains open until studies of the stability of such a mode are conducted.

A general 3D model of a resotrode with 2π-regeneration at 400 MHz and 300 kW in a continuous mode was made by I. Syrachev [16], as shown in Figure 23.

This device is described in more detail in [16,24]. Although this device was modeled as a microwave source for the LHC, it can also be used for other purposes: for defrosters, for wood drying devices and for other industrial technologies, as well as for advanced microwave energetic devices.

10. Conclusions

In this study, new types of resonant microwave O-type samples are considered including COM klystrons, CSM klystrons and resotrodes, which can combine high output power with an efficiency of up to 90%.

The modeling and research of COM and CSM klystrons has been made possible by the development of mathematical modeling and optimization methods; in particular, by the development of a discrete-analytical klystron model, the macro-steps method for global multiparametric optimization, the stage-by-stage method and the embedding procedure for full structural optimization.

It was shown that the synthesized optimal variants of high-performance multipath klystrons can be transformed into equivalent devices corresponding to other values of output power, voltage and number of beams without performing a new optimization, thanks to the GSP-parameter conversion procedure.

The results of the synthesis of COM and CSM klystrons are presented. It is shown that for various prototypes, klystrons were created with an efficiency of about 90%. COM and CSM klystrons can be considered as promising sources of microwave energy for industrial microwave technologies and microwave energy.

COM klystrons are characterized by an increased ratio of the length of the device to the wavelength, so they are optimal microwave sources for the relatively short-wave part of the microwave range from 3 to 10 GHz.

In CSM klystrons, the relative length is fixed and equal to the length of the optimal three-cavity COM klystron. Therefore, CSM klystrons are optimal sources of microwave power for a range from hundreds of MHz to 3 GHz.

For devices with emission modulation, it is shown that it is possible to achieve a combination of high efficiency with high gain within the design of a new microwave device called a resotrode.

Two types of resotrodes are considered: one with 0-regeneration for frequencies of 20–200 MHz and one with 2π-regeneration for frequencies of 200–1000 MHz.

Possible designs of resotrodes with 0-regeneration based on a universal functional cell are shown. Systems of uniform volumetric RF/microwave heating of large-sized objects based on resotrodes with 0-regeneration are proposed.

The design of a resotrode with 2π-regeneration at 400 MHz with an output power of 300 kW in continuous mode is proposed.

All these devices can be used to power modern colliders, for industrial microwave heating installations for various purposes and for advanced wireless power transmission devices.

Currently, leading klystron manufacturers are trying to implement the ideas of COM and CSM bunching by modifying their existing klystron designs. This leads to an increase in efficiency of several percent. The maximum efficiency values of about 90% can only be realized based on a new design initially calculated for the appropriate bunching mode. The development of such a new design is very expensive, so COM and CSM klystrons that fully correspond to the theory have not yet been created. The same problems apply to resotrodes. Their development requires not only the creation of a new design, but also a thorough study of the regenerative amplification mode with a possible transition to the generator mode. This a fundamental experimental investigation which is still waiting in the wings.