Constitutive Models for the Prediction of the Hot Deformation Behavior of the 10%Cr Steel Alloy
Abstract
:1. Introduction
2. Experimental Procedure
3. Constitutive Models
3.1. Modified JC Model
3.2. Strain-Compensated Arrhenius Model
3.3. Artificial Neural Network Models
4. Results and Discussion
4.1. Flow Stress Behavior
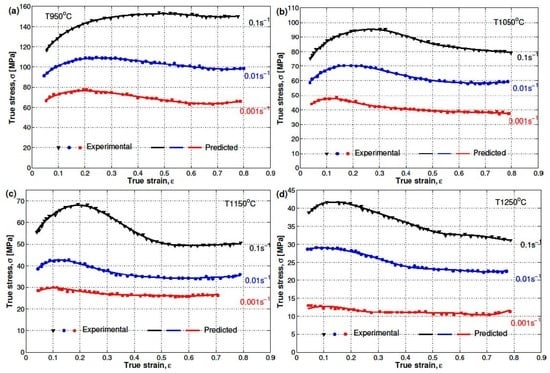
4.2. Modified JC Model
4.3. Strain-Compensated Arrhenius Model
4.4. Artificial Neural Network Models
4.5. Comparative Study between the Modified JC, Strain-Compensated Arrhenius, and Developed ANN Models
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Abe, F. Research and development of heat-resistant materials for advanced USC power plants with steam temperatures of 700 C and above. Engineering 2015, 1, 211–224. [Google Scholar] [CrossRef]
- Cui, H.; Sun, F.; Chen, K.; Zhang, L.; Wan, R.; Shan, A.; Wu, J. Precipitation behavior of Laves phase in 10% Cr steel X12CrMoWVNbN10-1-1 during short-term creep exposure. Mater. Sci. Eng. A 2010, 527, 7505–7509. [Google Scholar] [CrossRef]
- Xu, Y.; Wang, M.; Wang, Y.; Gu, T.; Chen, L.; Zhou, X.; Ma, Q.; Liu, Y.; Huang, J. Study on the nucleation and growth of Laves phase in a 10% Cr martensite ferritic steel after long-term aging. J. Alloys Compd. 2015, 621, 93–98. [Google Scholar] [CrossRef]
- Bendick, W.; Ring, M. Creep rupture strength of tungsten-alloyed 9–12% Cr steels for piping in power plants. Steel Res. 1996, 67, 382–385. [Google Scholar] [CrossRef]
- Tao, X.; Gu, J.; Han, L. Characterization of precipitates in X12CrMoWVNbN10-1-1 steel during heat treatment. J. Nucl. Mater. 2014, 452, 557–564. [Google Scholar] [CrossRef]
- Rao, K.; Prasad, Y.; Suresh, K. Materials modeling and simulation of isothermal forging of rolled AZ31B magnesium alloy: anisotropy of flow. Mater. Des. 2011, 32, 2545–2553. [Google Scholar] [CrossRef]
- Yu, Z.Q.; Zhou, G.S.; Tuo, L.F.; Song, C.F. Optimization of extrusion process parameters of Incoloy028 alloy based on hot compression test and simulation. Trans. Nonferrous Met. Soc. China 2017, 27, 2464–2473. [Google Scholar] [CrossRef]
- Zhou, L.; Huang, Z.; Wang, C.; Zhang, X.; Xiao, B.; Ma, Z. Constitutive flow behaviour and finite element simulation of hot rolling of SiCp/2009Al composite. Mech. Mater. 2016, 93, 32–42. [Google Scholar] [CrossRef]
- Johnson, G.R. A constitutive model and data for materials subjected to large strains, high strain rates, and high temperatures. In Proceedings of the 7th International Symposium on Ballistics, The Hague, The Netherlands, 19–21 April 1983; pp. 541–547. [Google Scholar]
- Johnson, G.R.; Cook, W.H. Fracture characteristics of three metals subjected to various strains, strain rates, temperatures and pressures. Eng. Fract. Mech. 1985, 21, 31–48. [Google Scholar] [CrossRef]
- Li, H.Y.; Wang, X.F.; Duan, J.Y.; Liu, J.J. A modified Johnson–Cook model for elevated temperature flow behavior of T24 steel. Mater. Sci. Eng. A 2013, 577, 138–146. [Google Scholar] [CrossRef]
- Zhao, Y.; Sun, J.; Li, J.; Yan, Y.; Wang, P. A comparative study on Johnson–Cook and modified Johnson–Cook constitutive material model to predict the dynamic behavior laser additive manufacturing FeCr alloy. J. Alloys Compd. 2017, 723, 179–187. [Google Scholar] [CrossRef]
- He, A.; Xie, G.; Zhang, H.; Wang, X. A comparative study on Johnson–Cook, modified Johnson–Cook and Arrhenius-type constitutive models to predict the high temperature flow stress in 20CrMo alloy steel. Mater. Des. (1980–2015) 2013, 52, 677–685. [Google Scholar] [CrossRef]
- Zhang, D.N.; Shangguan, Q.Q.; Xie, C.J.; Liu, F. A modified Johnson–Cook model of dynamic tensile behaviors for 7075-T6 aluminum alloy. J. Alloys Compd. 2015, 619, 186–194. [Google Scholar] [CrossRef]
- Buzyurkin, A.; Gladky, I.; Kraus, E. Determination and verification of Johnson–Cook model parameters at high-speed deformation of titanium alloys. Aerosp. Sci. Technol. 2015, 45, 121–127. [Google Scholar] [CrossRef]
- Shokry, A. On the constitutive modeling of a powder metallurgy nanoquasicrystalline Al93 Fe3Cr2Ti2 alloy at elevated temperatures. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 118. [Google Scholar] [CrossRef]
- Samantaray, D.; Mandal, S.; Bhaduri, A. A comparative study on Johnson–Cook, modified Zerilli–Armstrong and Arrhenius-type constitutive models to predict elevated temperature flow behaviour in modified 9Cr–1Mo steel. Comput. Mater. Sci. 2009, 47, 568–576. [Google Scholar] [CrossRef]
- Chen, L.; Zhao, G.; Yu, J. Hot deformation behavior and constitutive modeling of homogenized 6026 aluminum alloy. Mater. Des. 2015, 74, 25–35. [Google Scholar] [CrossRef]
- Lin, Y.; Chen, X.M.; Liu, G. A modified Johnson–Cook model for tensile behaviors of typical high-strength alloy steel. Mater. Sci. Eng. A 2010, 527, 6980–6986. [Google Scholar] [CrossRef]
- Shokry, A. A Modified Johnson–Cook Model for Flow Behavior of Alloy 800H at Intermediate Strain Rates and High Temperatures. J. Mater. Eng. Perform. 2017, 26, 5723–5730. [Google Scholar] [CrossRef]
- Tao, Z.J.; Fan, X.G.; He, Y.; Jun, M.; Heng, L. A modified Johnson–Cook model for NC warm bending of large diameter thin-walled Ti–6Al–4V tube in wide ranges of strain rates and temperatures. Trans. Nonferrous Met. Soc. China 2018, 28, 298–308. [Google Scholar] [CrossRef]
- He, J.; Chen, F.; Wang, B.; Zhu, L.B. A modified Johnson–Cook model for 10% Cr steel at elevated temperatures and a wide range of strain rates. Mater. Sci. Eng. A 2018, 715, 1–9. [Google Scholar] [CrossRef]
- Jonas, J.; Sellars, C.; Tegart, W.M. Strength and structure under hot-working conditions. Metall. Rev. 1969, 14, 1–24. [Google Scholar]
- Mostafaei, M.; Kazeminezhad, M. Hot deformation behavior of hot extruded Al–6Mg alloy. Mater. Sci. Eng. A 2012, 535, 216–221. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, B.; Baoxiang, Z. Effect of initial microstructure on the hot compression deformation behavior of a 2219 aluminum alloy. Mater. Des. 2012, 34, 15–21. [Google Scholar] [CrossRef]
- Zhu, A.; Chen, J.I.; Zhou, L.; Luo, L.; Qian, L.; Zhang, L.; Zhang, W. Hot deformation behavior of novel imitation-gold copper alloy. Trans. Nonferrous Met. Soc. China 2013, 23, 1349–1355. [Google Scholar] [CrossRef]
- Slooff, F.; Zhou, J.; Duszczyk, J.; Katgerman, L. Constitutive analysis of wrought magnesium alloy Mg–Al4–Zn1. Scr. Mater. 2007, 57, 759–762. [Google Scholar] [CrossRef]
- Shalbafi, M.; Roumina, R.; Mahmudi, R. Hot deformation of the extruded Mg–10Li–1Zn alloy: Constitutive analysis and processing maps. J. Alloys Compd. 2017, 696, 1269–1277. [Google Scholar] [CrossRef]
- Zhang, Y.; Sun, H.; Volinsky, A.A.; Tian, B.; Song, K.; Wang, B.; Liu, Y. Hot workability and constitutive model of the Cu-Zr-Nd alloy. Vacuum 2017, 146, 35–43. [Google Scholar] [CrossRef]
- Wang, Y.; Peng, J.; Zhong, L.; Pan, F. Modeling and application of constitutive model considering the compensation of strain during hot deformation. J. Alloys Compd. 2016, 681, 455–470. [Google Scholar] [CrossRef]
- Wu, H.; Wen, S.; Huang, H.; Wu, X.; Gao, K.; Wang, W.; Nie, Z. Hot deformation behavior and constitutive equation of a new type Al–Zn–Mg–Er–Zr alloy during isothermal compression. Mater. Sci. Eng. A 2016, 651, 415–424. [Google Scholar] [CrossRef]
- Sabokpa, O.; Zarei-Hanzaki, A.; Abedi, H.; Haghdadi, N. Artificial neural network modeling to predict the high temperature flow behavior of an AZ81 magnesium alloy. Mater. Des. 2012, 39, 390–396. [Google Scholar] [CrossRef]
- Haghdadi, N.; Zarei-Hanzaki, A.; Khalesian, A.; Abedi, H. Artificial neural network modeling to predict the hot deformation behavior of an A356 aluminum alloy. Mater. Des. 2013, 49, 386–391. [Google Scholar] [CrossRef]
- Sellars, C.M.; McTegart, W. On the mechanism of hot deformation. Acta Metall. 1966, 14, 1136–1138. [Google Scholar] [CrossRef]
- Han, Y.; Qiao, G.; Sun, J.; Zou, D. A comparative study on constitutive relationship of as-cast 904L austenitic stainless steel during hot deformation based on Arrhenius-type and artificial neural network models. Comput. Mater. Sci. 2013, 67, 93–103. [Google Scholar] [CrossRef]
- Zener, C.; Hollomon, J.H. Effect of strain rate upon plastic flow of steel. J. Appl. Phys. 1944, 15, 22–32. [Google Scholar] [CrossRef]
- Ashtiani, H.R.; Shahsavari, P. A comparative study on the phenomenological and artificial neural network models to predict hot deformation behavior of AlCuMgPb alloy. J. Alloys Compd. 2016, 687, 263–273. [Google Scholar] [CrossRef]
- Haykin, S. Neural Networks: A Comprehensive Foundation; Prentice Hall PTR: Upper Saddle River, NJ, USA, 1994. [Google Scholar]
- Christodoulou, C.; Georgiopoulos, M. Applications of Neural Networks in Electromagnetics; Artech House, Inc.: Norwood, MA, USA, 2000. [Google Scholar]
- Matlab. Choose a Multilayer Neural Network Training Function. MathWorks. 2018. Available online: https://www.mathworks.com/help/deeplearning/ug/choose-a-multilayer-neural-network-training-function.html (accessed on 10 December 2018).
- Saracoglu, Ö.G. An artificial neural network approach for the prediction of absorption measurements of an evanescent field fiber sensor. Sensors 2008, 8, 1585–1594. [Google Scholar] [CrossRef]
- Gowid, S.; Dixon, R.; Ghani, S. Performance Comparison Between Fast Fourier Transform-Based Segmentation, Feature Selection, and Fault Identification Algorithm and Neural Network for the Condition Monitoring of Centrifugal Equipment. J. Dyn. Syst. Meas. Control. 2017, 139, 061013. [Google Scholar] [CrossRef]
- Li, H.Y.; Li, Y.H.; Wang, X.F.; Liu, J.J.; Wu, Y. A comparative study on modified Johnson–Cook, modified Zerilli–Armstrong and Arrhenius-type constitutive models to predict the hot deformation behavior in 28CrMnMoV steel. Mater. Des. 2013, 49, 493–501. [Google Scholar] [CrossRef]
- Trimble, D.; O’Donnell, G.E. Constitutive modelling for elevated temperature flow behaviour of AA7075. Mater. Des. 2015, 76, 150–168. [Google Scholar] [CrossRef]
- Phaniraj, M.P.; Lahiri, A.K. The applicability of neural network model to predict flow stress for carbon steels. J. Mater. Process. Technol. 2003, 141, 219–227. [Google Scholar] [CrossRef]
- Srinivasulu, S.; Jain, A. A comparative analysis of training methods for artificial neural network rainfall–runoff models. Appl. Soft Comput. 2006, 6, 295–306. [Google Scholar] [CrossRef]












| Material Constant | (MPa) | ||||||
|---|---|---|---|---|---|---|---|
| Value | 165.57 | 0.13 | 0.0852 | 0.1042 | −0.0609 | −1.9365 | −1.9648 |
| Assessment Method | 17 × 17 Neurons NN Using SCG | 18 Neurons NN Using LM | ||
|---|---|---|---|---|
| All Data | Testing Data | All Data | Testing Data | |
| Min. error | −3.013 | −3.013 | −1.800 | −1.800 |
| Max. error | 6.417 | 6.417 | 1.294 | 1.231 |
| MAE | 0.811 | 1.010 | 0.334 | 0.374 |
| RMSE | 1.082 | 1.344 | 0.441 | 0.474 |
| Model | R | AARE (%) | RMSE (MPa) |
|---|---|---|---|
| Modified JC | 0.99184 | 9.367 | 4.690 |
| Strain compensated Arrhenius | 0.98838 | 7.557 | 5.531 |
| Developed ANN using SCG | 0.99955 | 1.908 | 1.082 |
| Developed ANN using LM | 0.99992 | 0.748 | 0.441 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shokry, A.; Gowid, S.; Kharmanda, G.; Mahdi, E. Constitutive Models for the Prediction of the Hot Deformation Behavior of the 10%Cr Steel Alloy. Materials 2019, 12, 2873. https://doi.org/10.3390/ma12182873
Shokry A, Gowid S, Kharmanda G, Mahdi E. Constitutive Models for the Prediction of the Hot Deformation Behavior of the 10%Cr Steel Alloy. Materials. 2019; 12(18):2873. https://doi.org/10.3390/ma12182873
Chicago/Turabian StyleShokry, Abdallah, Samer Gowid, Ghias Kharmanda, and Elsadig Mahdi. 2019. "Constitutive Models for the Prediction of the Hot Deformation Behavior of the 10%Cr Steel Alloy" Materials 12, no. 18: 2873. https://doi.org/10.3390/ma12182873
APA StyleShokry, A., Gowid, S., Kharmanda, G., & Mahdi, E. (2019). Constitutive Models for the Prediction of the Hot Deformation Behavior of the 10%Cr Steel Alloy. Materials, 12(18), 2873. https://doi.org/10.3390/ma12182873