Experimental Analysis of Perimeter Shear Strength of Composite Sandwich Structures
Abstract
:1. Introduction
2. Materials and Methods
3. Results
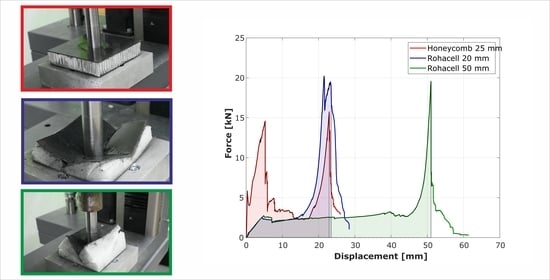
3.1. Results for Specimen Number 1
3.2. Results for Specimen Number 2
3.3. Results for Specimen Number 3
3.4. Results Comparison
4. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tsai, S.W.; Hahn, H.T. Introduction to Composite Materials, 2nd ed.; Routledge: Abingdo, UK, 2018. [Google Scholar]
- Jones, J.G. Marine Applications of Advanced Fibre-Reinforced Composites; Elsevier BV: Amsterdam, The Netherlands, 2016. [Google Scholar]
- Baker, A.A.; Scott, M.L. Composite materials for aircraft structures, 3rd ed.; AIAA/American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2016; ISBN 978-1-62410-326-1. [Google Scholar]
- Liu, N.; Ren, X.; Lua, J. An isogeometric continuum shell element for modeling the nonlinear response of functionally graded material structures. Compos. Struct. 2020, 237, 111893. [Google Scholar] [CrossRef]
- Liu, N.; Jeffers, A.E. Isogeometric analysis of laminated composite and functionally graded sandwich plates based on a layerwise displacement theory. Compos. Struct. 2017, 176, 143–153. [Google Scholar] [CrossRef]
- Birman, V.; Kardomateas, G.A. Review of current trends in research and applications of sandwich structures. Compos. Part B Eng. 2018, 142, 221–240. [Google Scholar] [CrossRef]
- Bezazi, A.; El Mahi, A.; Berthelot, J.-M.; Bezzazi, B. Experimental analysis of behavior and damage of sandwich composite materials in three-point bending. Part 1. Static tests and stiffness degradation at failure studies. Strength Mater. 2007, 39, 170–177. [Google Scholar] [CrossRef] [Green Version]
- Galletti, G.G.; Vinquist, C.; Es-Said, O.S. Theoretical design and analysis of a honeycomb panel sandwich structure loaded in pure bending. Eng. Fail. Anal. 2008, 15, 555–562. [Google Scholar] [CrossRef]
- Tsang, P.; Lagace, P. Failure mechanisms of impact-damaged sandwich panels under uniaxial compression. In Proceedings of the 35th Structures, Structural Dynamics, and Materials Conference, Hilton Head, SC, USA, 18–20 April 1994. [Google Scholar]
- Liu, T.; Hou, S.; Nguyen, X.; Han, X. Energy absorption characteristics of sandwich structures with composite sheets and bio coconut core. Compos. Part B Eng. 2017, 114, 328–338. [Google Scholar] [CrossRef]
- Nguyen, M.; Jacombs, S.; Thomson, R.; Hachenberg, D.; Scott, M. Simulation of impact on sandwich structures. Compos. Struct. 2005, 67, 217–227. [Google Scholar] [CrossRef]
- Hwang, Y.; Lacy, T.E. Numerical Estimates of the Compressive Strength of Impact-damaged Sandwich Composites. J. Compos. Mater. 2006, 41, 367–388. [Google Scholar] [CrossRef]
- Zhang, T.; Yan, Y.; Li, J.; Luo, H. Low-velocity impact of honeycomb sandwich composite plates. J. Reinf. Plast. Compos. 2015, 35, 8–32. [Google Scholar] [CrossRef]
- Stanczak, M.; Fras, T.; Blanc, L.; Pawlowski, P.; Rusinek, A. Blast-Induced Compression of a Thin-Walled Aluminum Honeycomb Structure—Experiment and Modeling. Metals 2019, 9, 1350. [Google Scholar] [CrossRef] [Green Version]
- Tomasiewicz, J.; Czarnocki, P. Wing-to-fuselage attachment fitting for composite airframes: Experimental and finite element analysis. Compos. Theory Pract. 2016, 16, 61–66. [Google Scholar]
- Orkisz, M.; Święch, Ł.; Zacharzewski, J. Fatigue tests of motor glider wing’s composite spar. Maint. Reliab. 2012, 14, 228–232. [Google Scholar]
- Song, K.-I.; Choi, J.-Y.; Kweon, J.-H.; Choi, J.-H.; Kim, K.S. An experimental study of the insert joint strength of composite sandwich structures. Compos. Struct. 2008, 86, 107–113. [Google Scholar] [CrossRef]
- Bois, C.; Wargnier, H.; Wahl, J.-C.; Le Goff, E. An analytical model for the strength prediction of hybrid (bolted/bonded) composite joints. Compos. Struct. 2013, 97, 252–260. [Google Scholar] [CrossRef]
- Dawood, M.; Ballew, W.; Seiter, J. Enhancing the resistance of composite sandwich panels to localized forces for civil infrastructure and transportation applications. Compos. Struct. 2011, 93, 2983–2991. [Google Scholar] [CrossRef]
- Hamilton, L.; Joyce, P.J.; Forero, C.; McDonald, M. Production of a Composite Monocoque Frame for a Formula SAE Racecar. SAE Tech. Pap. Ser. 2013. [Google Scholar] [CrossRef]
- Sturm, R.; Klett, Y.; Kindervater, C.; Voggenreiter, H. Failure of CFRP airframe sandwich panels under crash-relevant loading conditions. Compos. Struct. 2014, 112, 11–21. [Google Scholar] [CrossRef] [Green Version]
- Greń, K.; Szatkowski, P.; Chłopek, J. Characteristics of failure mechanisms and shear strength of sandwich composites. Compos. Theory Pract 2016, 16, 255–259. [Google Scholar]
- Mostafa, A.; Shankar, K.; Morozov, E. Insight into the shear behaviour of composite sandwich panels with foam core. Mater. Des. 2013, 50, 92–101. [Google Scholar] [CrossRef]
- Schubel, P.M.; Luo, J.-J.; Daniel, I.M. Impact and post impact behavior of composite sandwich panels. Compos. Part A Appl. Sci. Manuf. 2007, 38, 1051–1057. [Google Scholar] [CrossRef]
- Jones, R.M. Mechanics of Composite Materials; Taylor & Francis: Philadelphia, PA, USA, 1999. [Google Scholar]
- Vasiliev, V.V.; Morozov, E.V. Advanced Mechanics of Composite Materials and Structures; Elsevier: Amsterdam, The Netherlands, 2018. [Google Scholar]
- Królikowski, W. Wydawnictwo Naukowe PWN Polimerowe kompozyty konstrukcyjne; Wydawnictwo Naukowe PWN: Warszawa, Poland, 2017. [Google Scholar]
- Meraghni, F.; Desrumaux, F.; Benzeggagh, M. Mechanical behaviour of cellular core for structural sandwich panels. Compos. Part A Appl. Sci. Manuf. 1999, 30, 767–779. [Google Scholar] [CrossRef]
- Wadley, H.N.G. Fabrication and structural performance of periodic cellular metal sandwich structures. Compos. Sci. Technol. 2003, 63, 2331–2343. [Google Scholar] [CrossRef]
- Hou, S.; Li, Q.; Long, S.; Yang, X.; Li, W. Crashworthiness design for foam filled thin-wall structures. Mater. Des. 2009, 30, 2024–2032. [Google Scholar] [CrossRef]
- Xiong, J.; Ma, L.; Pan, S.; Wu, L.; Papadopoulos, J.; Vaziri, A. Shear and bending performance of carbon fiber composite sandwich panels with pyramidal truss cores. Acta Mater. 2012, 60, 1455–1466. [Google Scholar] [CrossRef]
- Hou, S.; Zhao, S.; Ren, L.; Han, X.; Li, Q. Crashworthiness optimization of corrugated sandwich panels. Mater. Des. 2013, 51, 1071–1084. [Google Scholar] [CrossRef]
- Li, T.; Wang, L. Bending behavior of sandwich composite structures with tunable 3D-printed core materials. Compos. Struct. 2017, 175, 46–57. [Google Scholar] [CrossRef]
- Bauchau, O.A.; Craig, J.I. Structural Analysis: With Applications to Aerospace Structures; Solid Mechanics and Its Applications; Springer: New York, NY, USA, 2009. [Google Scholar]
- Szilard, R. Theory and Analysis of Plates: Classical and Numerical Methods; Civil Engineering and Engineering Mechanics Series; Prentice-Hall: Englewood Cliffs, NJ, USA, 1973. [Google Scholar]
- Ugural, A.C.; Ugural, A.C. Stresses in Beams, Plates, and Shells, 3rd ed.; (CRC Series in Computational Mechanics and Applied Analysis); CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Carlsson, L.A.; Kardomateas, G.A. Structural and Failure Mechanics of Sandwich Composites; Solid Mechanics and Its Applications; Springer: New York, NY, USA, 2011. [Google Scholar]
- Laminating Resin MGS L285; Hexion Speciality Chemicals GmbH: Stuttgart, Germany. 2016. Available online: https://m.aircraftspruce.com/catalog/pdf/mgs285tech.pdf (accessed on 23 September 2020).
- Aluminum Honeycomb Core—Technical Data Sheet for All Types; Euro-Composites: Echternach, Luxembourg. 2013. Available online: https://www.nzcomposites.com/site/nzcomposites/Aluminium%20Honeycomb%20Core.pdf (accessed on 23 September 2020).
- Product Information Rohacell IG-F; Evonik Resource Efficiency GmbH: Essen, Germany. 2020. Available online: http://www.relicom.ru/images/upload/en/1589/ROHACELL_IG_IG-F_Product_Information.pdf (accessed on 23 September 2020).













| Density | (g/cm3) | 1.18–1.20 |
| Flexural Strength | (N/mm2) | 110–120 |
| Young’s Modulus | (kN/mm2) | 3.0–3.3 |
| Tensile Strength | (N/mm2) | 70–80 |
| Compressive Strength | (N/mm2) | 120–140 |
| Impact Strength | (kJ/m2) | 45–55 |
| Mechanical Properties | Unit | Honeycomb Aluminium | Rohacell 31 IG-F |
|---|---|---|---|
| Density | (kg/m3) | 130 | 32 ± 7 |
| Compressive strength | (MPa) | 7 | 0.4 |
| Compressive longitudinal elastic modulus | (MPa) | - | 17 |
| Compressive strength | (MPa) | 3.38 | - |
| Shear strength in the plane along the longitudinal direction | (MPa) | 4 | 2.4 |
| Shear modulus in the plane along the longitudinal direction | (MPa) | 550 | 13 |
| Shear strength in the plane along the transverse direction | (MPa) | 2.5 | 2.4 |
| Shear modulus in the plane along the transverse direction | (MPa) | 350 | 13 |
| Tensile strength | (MPa) | - | 1 |
| Tensile longitudinal elastic modulus | (MPa) | - | 36 |
| Operational temperature | (°C) | from −55 °C to 177 °C | Up to 130 °C |
| Specimen | 1st peak | 2nd peak | ||
|---|---|---|---|---|
| Force (N) | Displacement (mm) | Force (N) | Displacement (mm) | |
| Specimen 1 (honeycomb 25 mm) | 14,576 | 5.27 | 15,744 | 22.93 |
| Specimen 2 (Rohacell 20 mm) | 20,201 | 21.53 | 19,505 | 23.27 |
| Specimen 1 (Rohacell 50 mm) | 19,572 | 51.01 | - | - |
| Specimen | EA (J) | EA/δ (J/mm) | EA/ρδ (J m2/kg) |
|---|---|---|---|
| Specimen 1 (honeycomb 25 mm) | 123.7 | 4.95 | 38.1 |
| Specimen 2 (Rohacell 20 mm) | 125.7 | 6.29 | 196.4 |
| Specimen 1 (Rohacell 50 mm) | 150.4 | 3.01 | 94.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Święch, Ł.; Kołodziejczyk, R.; Stącel, N. Experimental Analysis of Perimeter Shear Strength of Composite Sandwich Structures. Materials 2021, 14, 12. https://doi.org/10.3390/ma14010012
Święch Ł, Kołodziejczyk R, Stącel N. Experimental Analysis of Perimeter Shear Strength of Composite Sandwich Structures. Materials. 2021; 14(1):12. https://doi.org/10.3390/ma14010012
Chicago/Turabian StyleŚwięch, Łukasz, Radosław Kołodziejczyk, and Natalia Stącel. 2021. "Experimental Analysis of Perimeter Shear Strength of Composite Sandwich Structures" Materials 14, no. 1: 12. https://doi.org/10.3390/ma14010012
APA StyleŚwięch, Ł., Kołodziejczyk, R., & Stącel, N. (2021). Experimental Analysis of Perimeter Shear Strength of Composite Sandwich Structures. Materials, 14(1), 12. https://doi.org/10.3390/ma14010012