Mass Transfer Principles in Column Percolation Tests: Initial Conditions and Tailing in Heterogeneous Materials
Abstract
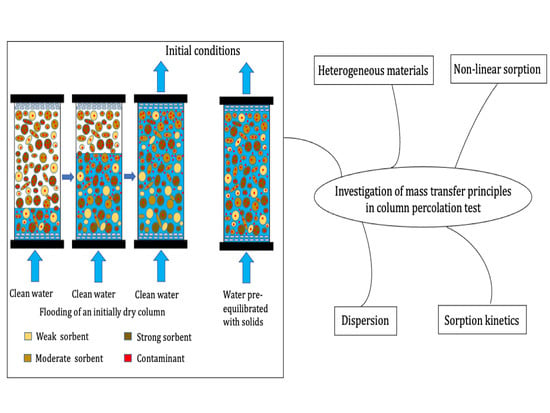
:1. Introduction
2. Theory and Background
2.1. Local Equilibrium: The Advection—Dispersion Equation
2.2. Desorption Kinetics Limited by Film Diffusion
2.3. Desorption Limited by Intraparticle Pore Diffusion
2.4. Set-Up of “Numerical” Column Tests
3. Results and Discussion
3.1. Impact of Initial Conditions on Leaching
3.2. Initial Conditions and Leaching with Mass Transfer Limitations
3.3. Nonlinear Sorption Isotherms
3.4. Impact of Heterogeneous Sample Composition
4. Summary and Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Empirical Relationships for the Estimation of Sherwood Numbers
Appendix B. Film Diffusion Coupled to Advective-Dispersive Transport

Appendix C. Intraparticle Pore Diffusion Coupled to Advective-Dispersive Transport
Appendix D. Length of the Mass Transfer Zone () for the First Order Analytical Solution
Appendix D.1. Analytical Solution Based on the Film Diffusion Model
Appendix D.2. Analytical Solution Based on the Intraparticle Pore Diffusion Model
Appendix D.3. Comparison of Analytical and Numerical Solution and Estimation of Mass Transfer Zone Length ()

Appendix E. Comparison of Analytical and Numerical Solution (Code Verification)


References
- Röhler, K.; Haluska, A.A.; Susset, B.; Liu, B.; Grathwohl, P. Long-term behavior of PFAS in contaminated agricultural soils in Germany. J. Contam. Hydrol. 2021, 241, 103812. [Google Scholar] [CrossRef] [PubMed]
- Löv, Å.; Larsbo, M.; Sjöstedt, C.; Cornelis, G.; Gustafsson, J.P.; Kleja, D.B. Evaluating the ability of standardised leaching tests to predict metal(loid) leaching from intact soil columns using size-based elemental fractionation. Chemosphere 2019, 222, 453–460. [Google Scholar] [CrossRef] [PubMed]
- Inui, T.; Hori, M.; Takai, A.; Katsumi, T. Column percolation tests for evaluating the leaching behavior of marine sediment containing non-anthropogenic arsenic. In Proceedings of the 8th International Congress on Environmental Geotechnics (from 28th October to 1st November 2018 in Hangzhou, China); Zhan, L., Chen, Y., Bouazza, A., Eds.; Springer: Singapore, 2019; Volume 1. ICEG 2018, Environmental Science and Engineering. [Google Scholar] [CrossRef]
- Kalbe, U.; Bandow, N.; Bredow, A.; Mathies, H.; Piechotta, C. Column leaching tests on soils containing less investigated organic pollutants. J. Geochem. Explor. 2014, 147, 291–297. [Google Scholar] [CrossRef]
- Zhu, Y.; Hu, Y.; Guo, Q.; Zhao, L.; Li, L.; Wang, Y.; Hu, G.; Wibowo, H.; Francesco, D.M. The effect of wet treatment on the distribution and leaching of heavy metals and salts of bottom ash from municipal solid waste incineration. Environ. Eng. Sci. 2021. ahead of print. [Google Scholar] [CrossRef]
- Kumar, A.; Samadder, S.R.; Kumar, V. Assessment of groundwater contamination risk due to fly ash leaching using column study. Environ. Earth Sci. 2019, 78, 18. [Google Scholar] [CrossRef]
- Chan, W.P.; Ren, F.; Dou, X.; Yin, K.; Chang, V.W.C. A large-scale field trial experiment to derive effective release of heavy metals from incineration bottom ashes during construction in land reclamation. Sci. Total Environ. 2018, 637, 182–190. [Google Scholar] [CrossRef] [PubMed]
- Di Gianfilippo, M.; Costa, G.; Verginelli, I.; Gavasci, R.; Lombardi, F. Analysis and interpretation of the leaching behaviour of waste thermal treatment bottom ash by batch and column tests. Waste Manag. 2016, 56, 216–228. [Google Scholar] [CrossRef]
- Tsiridis, V.; Petala, M.; Samaras, P.; Sakellaropoulos, G.P. Evaluation of interactions between soil and coal fly ash leachates using column percolation tests. Waste Manag. 2015, 43, 255–263. [Google Scholar] [CrossRef]
- Lange, C.N.; Flues, M.; Hiromoto, G.; Boscov, M.E.G.; Camargo, I.M.C. Long-term leaching of As, Cd, Mo, Pb, and Zn from coal fly ash in column test. Environ. Monit. Assess. 2019, 191, 602. [Google Scholar] [CrossRef]
- Liu, B.; Li, J.; Wang, Z.; Zeng, Y.; Ren, Q. Long-term leaching characterization and geochemical modeling of chromium released from AOD slag. Environ. Sci. Pollut. Res. 2020, 27, 921–929. [Google Scholar] [CrossRef]
- Schwab, O.; Bayer, P.; Juraske, R.; Verones, F.; Hellweg, S. Beyond the material grave: Life Cycle Impact Assessment of leaching from secondary materials in road and earth constructions. Waste Manag. 2014, 34, 1884–1896. [Google Scholar] [CrossRef]
- Diotti, A.; Galvin, A.P.; Piccinali, A.; Plizzari, G.; Sorlini, S. Chemical and leaching behavior of construction and demolition wastes and recycled aggregates. Sustainability 2020, 12, 10326. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, J.; Li, B.; Zhou, N.; Xiao, X.; Li, M.; Zhu, C. Environmental behavior of construction and demolition waste as recycled aggregates for backfilling in mines: Leaching toxicity and surface subsidence studies. J. Hazard. Mater. 2020, 389, 121870. [Google Scholar] [CrossRef] [PubMed]
- Bandow, N.; Finkel, M.; Grathwohl, P.; Kalbe, U. Influence of flow rate and particle size on local equilibrium in column percolation tests using crushed masonry. J. Mater. Cycles Waste Manag. 2019, 21, 642–651. [Google Scholar] [CrossRef]
- Butera, S.; Hyks, J.; Christensen, T.H.; Astrup, T.F. Construction and demolition waste: Comparison of standard up-flow column and down-flow lysimeter leaching tests. Waste Manag. 2015, 43, 386–397. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, P.; Brown, K.; Branch, J.; van der Sloot, H.; Meeussen, J.; Delapp, R.; Um, W.; Kosson, D. Development of a geochemical speciation model for use in evaluating leaching from a cementitious radioactive waste form. Environ. Sci. Technol. 2021, 55, 8642–8653. [Google Scholar] [CrossRef]
- Molleda, A.; López, A.; Cuartas, M.; Lobo, A. Release of pollutants in MBT landfills: Laboratory versus field. Chemosphere 2020, 249, 126145. [Google Scholar] [CrossRef]
- Grathwohl, P.; van der Sloot, H. Groundwater risk assessment at contaminated sites (GRACOS): Test methods and modelling approaches. In Groundwater Science and Policy; Quevauviller, P., Ed.; RSC Publishing: Cambridge, UK, 2007. [Google Scholar]
- Susset, B.; Grathwohl, P. Leaching standards for mineral recycling materials—A harmonized regulatory concept for the upcoming German Recycling Decree. Waste Manag. 2011, 31, 201–214. [Google Scholar] [CrossRef] [PubMed]
- Grathwohl, P.; Susset, B. Comparison of percolation to batch and sequential leaching tests: Theory and data. Waste Manag. 2009, 29, 2681–2688. [Google Scholar] [CrossRef] [PubMed]
- Grathwohl, P. On equilibration of pore water in column leaching tests. Waste Manag. 2014, 34, 908–918. [Google Scholar] [CrossRef]
- Grathwohl, P.; Reinhard, M. Desorption of Trichloroethylene in Aquifer Material: Rate Limitation at the Grain Scale. Environ. Sci. Technol. 1993, 27, 2360–2366. [Google Scholar] [CrossRef]
- Rügner, H.; Kleineidam, S.; Grathwohl, P. Long term sorption kinetics of phenanthrene in aquifer materials. Environ. Sci. Technol. 1999, 33, 1645–1651. [Google Scholar] [CrossRef]
- Wang, G.; Kleineidam, S.; Grathwohl, P. Sorption/desorption reversibility of phenanthrene in soils and carbonaceous materials. Environ. Sci. Technol. 2007, 41, 1186–1193. [Google Scholar] [CrossRef]
- Finkel, M.; Grathwohl, P. Impact of pre-equilibration and diffusion limited release kinetics on effluent concentration in column leaching tests: Insights from numerical simulations. Waste Manag. 2017, 63, 58–73. [Google Scholar] [CrossRef] [PubMed]
- Kleineidam, S.; Rügner, H.; Grathwohl, P. Impact of grain scale heterogeneity on slow sorption kinetics. Environ. Toxicol. Chem. 1999, 18, 1673–1678. [Google Scholar] [CrossRef]
- Jäger, R.; Liedl, R. Prognose der Sorptionskinetik organischer Schadstoffe in heterogenem Aquifermaterial (Predicting sorption kinetics of organic contaminants in heterogeneous aquifer material). Grundwasser 2000, 5, 57–66. [Google Scholar] [CrossRef]
- Xiao, Y.; Feng, Z.; Huang, X.; Huang, L.; Chen, Y.; Wang, L.; Long, Z. Recovery of rare earths from weathered crust elution-deposited rare earth ore without ammonia-nitrogen pollution: I. leaching with magnesium sulfate. Hydrometallurgy 2015, 153, 58–65. [Google Scholar] [CrossRef]
- Yin, K.; Chan, W.P.; Dou, X.; Lisak, G.; Chang, V.W.C. Kinetics and modeling of trace metal leaching from bottom ashes dominated by diffusion or advection. Sci. Total Environ. 2020, 719, 137203. [Google Scholar] [CrossRef] [PubMed]
- Ogata, A.; Banks, R.B. A solution of the differential equation of longitudinal dispersion in porous media. In Professional Paper; Geological Survey (U.S.): Washington, DC, USA, 1961; pp. A1–A7. [Google Scholar]
- Boving, T.; Grathwohl, P. Matrix diffusion coefficients in sandstones and limestones: Relationship to permeability and porosity. J. Contam. Hydrol. 2001, 53, 85–100. [Google Scholar] [CrossRef]
- Kalbe, U.; Berger, W.; Eckardt, J.; Simon, F.G. Evaluation of leaching and extraction procedures for soil and waste. Waste Manag. 2008, 28, 1027–1038. [Google Scholar] [CrossRef]
- Kalbe, U.; Berger, W.; Simon, F.G.; Eckardt, J.; Christoph, G. Results of interlaboratory comparisons of column percolation tests. J. Hazard. Mater. 2007, 148, 714–720. [Google Scholar] [CrossRef]
- Liu, Y.; Illangasekare, T.H.; Kitanidis, P.K. Long-term mass transfer and mixing-controlled reactions of a DNAPL plume from persistent residuals. J. Contam. Hydrol. 2014, 157, 11–24. [Google Scholar] [CrossRef]
- Naka, A.; Yasutaka, T.; Sakanakura, H.; Kalbe, U.; Watanabe, Y.; Inoba, S.; Takeo, M.; Inui, T.; Katsumi, T.; Fujikawa, T.; et al. Column percolation test for contaminated soils- Key factors for standardization. J. Hazard. Mater. 2016, 320, 326–340. [Google Scholar] [CrossRef] [Green Version]
- Arters, D.C.; Fan, L.S. Experimental methods and correlation of solid-liquid mass transfer in fluidized beds. Chem. Eng. Sci. 1990, 45, 965–975. [Google Scholar] [CrossRef]
- Blasius, H. Grenzschichten in Flüssigkeiten mit kleiner Reibung (The boundary layers in fluids with little friction). J. Appl. Math. Phys. 1908, 56, 1–37. [Google Scholar]
- Calderbank, P.H.; Moo-Young, M.B. The continuous phase heat and mass transfer properties of dispersions. Chem. Eng. Sci. 1995, 50, 3921–3934. [Google Scholar] [CrossRef]
- Kirwan, J.; Armenante, P.M. Mass transfer to microparticle systems. Chem. Eng. Sci. 1989, 44, 2781–2796. [Google Scholar] [CrossRef]
- Levins, D.M.; Glastonbury, J.R. Application of Kolmogorofff’s theory to particle-liquid mass transfer in agitated vessels. Chem. Eng. Sci. 1972, 27, 537–543. [Google Scholar] [CrossRef]
- Mao, H.; Chisti, Y.; Moo-Young, M. Multiphase hydrodynamics and solid-liquid mass transfer in an external-loop airlift reactor- a comparative study. Chem. Eng. Commun. 1992, 113, 1–13. [Google Scholar] [CrossRef]
- Ohashi, H.; Sugawara, T.; Kikuchi, K.I. Mass transfer between particles and liquid in solid-liquid two-phase flow through vertical tubes. J. Chem. Eng. Jpn. 1981, 14, 489–491. [Google Scholar] [CrossRef] [Green Version]
- Sherwood, T.K.; Pigford, R.L.; Wilke, R.L. “Mass Transfer”; McGraw-Hill: New York, NY, USA, 1975. [Google Scholar]
- Cirpka, O.A. Solute and heat transport. In Lecture Notes “Environmental Modeling 2”; 2020; (unpublished, University of Tübingen). [Google Scholar]
- Liedl, R.; Ptak, T. Modelling of diffusion-limited retardation of contaminants in hydraulically and lithologically nonuniform media. J. Contam. Hydrol. 2003, 66, 239–259. [Google Scholar] [CrossRef]











| Property | Symbol (Unit) | Reference and [Alternative Values] |
|---|---|---|
| Net column length | (cm) | 30 |
| Inner column diameter | (cm) | 5.46 |
| Total volume of column | 0.70 | |
| Dry solid density | (kg L−1) | 2.60 |
| Inter-granular porosity | n (-) | 0.45 |
| Intraparticle porosity | (-) | 0.05 |
| Solid mass in column | (kg) | 1 |
| Liquid to solid ratio in column | (L kg−1) | 0.31 |
| Initial concentration in solid phase | (µg kg−1) | 1000 |
| Contact time | (h) | 5 |
| Dispersivity | (m) | [0, 0.03] |
| Water flow velocity | v (m s−1) | 1.67 × 10−5 |
| Aqueous diffusion coefficient | (m2 s−1) | 1 × 10−9 |
| Particle diameters | (µm) | [63, 2000] |
| Distribution coefficients | (L kg−1) | [0.1, 1, 10, 100] |
| Freundlich coefficients | (µg kg−1:(µg L−1)1/n) | [1.58, 7.94, 39.81] |
| Freundlich exponent | 0.7 | |
| Sherwood number | (-) | [2.1, 2.6] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, B.; Finkel, M.; Grathwohl, P. Mass Transfer Principles in Column Percolation Tests: Initial Conditions and Tailing in Heterogeneous Materials. Materials 2021, 14, 4708. https://doi.org/10.3390/ma14164708
Liu B, Finkel M, Grathwohl P. Mass Transfer Principles in Column Percolation Tests: Initial Conditions and Tailing in Heterogeneous Materials. Materials. 2021; 14(16):4708. https://doi.org/10.3390/ma14164708
Chicago/Turabian StyleLiu, Binlong, Michael Finkel, and Peter Grathwohl. 2021. "Mass Transfer Principles in Column Percolation Tests: Initial Conditions and Tailing in Heterogeneous Materials" Materials 14, no. 16: 4708. https://doi.org/10.3390/ma14164708
APA StyleLiu, B., Finkel, M., & Grathwohl, P. (2021). Mass Transfer Principles in Column Percolation Tests: Initial Conditions and Tailing in Heterogeneous Materials. Materials, 14(16), 4708. https://doi.org/10.3390/ma14164708