Stress–Strain Field in an Innovative Metallic Dam Gate Used to Control the Water Flow
Abstract
:1. Introduction
2. Description of the Dam Gates
- own weight, including the weight of the piles, screed, dams, bridge, and other mechanical equipment;
- horizontal and vertical hydrostatic pressure;
- static and dynamic under-pressure;
- ice pressure (if applicable);
- the pressure of the alluvium;
- wave pressure;
- earthquake loads—inertial component and hydrodynamic component;
- loads due to temperature variations;
- wind action;
- forces caused by traction or braking on the tracks.
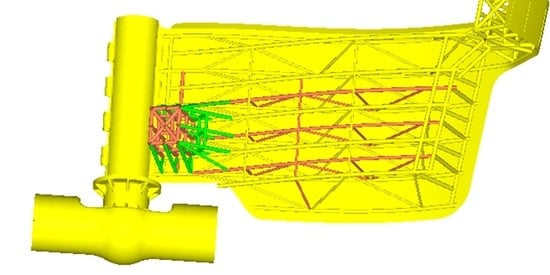
3. FEA Model Used to Analyze Different Load Design Scenarios
4. Results
- ❑
- The maximum stress for both cases analyzed exceeds the stress limit. In this situation, the design must be improved until this criterion is accomplished. The place of occurrence of the maximum stress is on the structure of bars. The values obtained on cases are the following:
- -
- Case 1: Stress = 390.54 [MPa]
- -
- Case 2: Stress = 661.61 [MPa].
- ❑
- Solutions proposed to reduce the stress in the assembly:
- -
- Strengthening the reinforcing bar system by increasing the thickness of the bars or their cross sections.
- -
- Application of a honeycomb plate system especially in the area close to the pole where the highest displacements obtained stresses in the structure.
- -
- Use of lighter materials (aluminum alloys or composite) to reduce the weight of the gate assembly (on the current design, a subassembly located on one side or the other of the column has 77.5 tons). By reducing the weight, lower inertias of the system will be obtained, especially for the situations of shock closing of the gates.
- -
- It is recommended to continue the static analysis scenarios with a dynamic analysis to take into account the average speed of a water stream.
- ❑
- The maximum resultant stress on the second case analyzed (the worst case) is reduced from 661 MPa to 352 MPa, which is 50%.
- ❑
- The global displacement magnitude is also reduced from 77 mm to 20 mm.
- -
- Strengthening the reinforcing bar system by increasing the thickness of the bars or their cross sections, especially for the bars that have a level of stress that exceeds the yield.
- -
- Application of a honeycomb plate system especially in the area close to the pole to increase the stiffness and reduce the global displacement.
5. Conclusions
- ❑
- The principal target was to minimize the maximum stress in the gate structure as much as possible using some of the hypothetical scenarios considered and described above.
- ❑
- The local maximum resultant stress close to the pole zone, in the second case analyzed (the worst case), was reduced from 352 Mpa to 263 Mpa, which is 25%.
- ❑
- The maximum stress moved to the other zone faraway from the polem and the maximum value was 426.7 MPa.
- -
- Strengthening the reinforcing bar system by increasing the thickness of the bars or their cross sections, especially for the bars that have a level of stress that exceed the yield.
- -
- In the zone with max stress, some additional short bars with a reinforcement role in the local zone can be applied.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cozzolino, L.; Cimorelli, L.; Pianese, D. The analytic solution of the Shallow-Water Equations with partially open sluice-gates: The dam-break problem. Adv. Water Resour. 2015, 80, 90–102. [Google Scholar] [CrossRef]
- Pratiwi, V.; Kusuma, M.S.B.; Kardhana, H.; Farid, M. Experimental Study of Dam Break Flow generated by the Flap Gate in Horizontal Channel. Int. J. Geomate 2020, 19, 19–26. [Google Scholar] [CrossRef]
- Noël, B.; Soares-Frazão, S.; Zech, Y. Computation of the ‘Isolated Obstruction Test Case’ and the ‘Model City Experiment’ Benchmarks, IMPACT Investigation of Extreme Flood Processes and Uncertainty. In Proceedings of the 3rd Project Workshop, Louvain-la Neuve, Belgium, 6–7 November 2003. [Google Scholar]
- Aleixo, R.; Soares-Frazao, S.; Zech, Y. Before the Dam Breaks: Analysis of the Flow behind a Downward Moving Gate. In Proceedings of the 8th International Conference on Fluvial Hydraulics (RIVER FLOW 2016), St Louis, MO, USA, 11–14 July 2016; Proceedings Paper. pp. 436–442. [Google Scholar]
- Chen, C.; Fu, X.L.; Xu, P. A Preliminary Investigation of Numerical Model for Dam Break Wave Flume. In Proceedings of the 2nd International Workshop on Renewable Energy and Development (IWRED 2018), Guilin, China, 20–22 April 2018; Proceedings Paper. Volume 153, p. 032031. [Google Scholar] [CrossRef]
- Von Hafen, H.; Goseberg, N.; Stolle, J.; Nistor, I. Gate-Opening Criteria for Generating Dam-Break Waves. J. Hydraul. Eng. 2019, 145, 04019002. [Google Scholar] [CrossRef]
- Ye, Z.T.; Zhao, X.Z.; Deng, Z.Z. Numerical investigation of the gate motion effect on a dam break flow. J. Mar. Sci. Technol. 2016, 21, 579–591. [Google Scholar] [CrossRef]
- Stolle, J.; Ghodoosipour, B.; Derschum, C.; Nistor, I.; Petriu, E.; Goseberg, N. Swing gate generated dam-break waves. J. Hydraul. Res. 2019, 57, 675–687. [Google Scholar] [CrossRef]
- Anami, K.; Ishii, N. In-Air and in-Water Natural Vibrations of Folsom Dam Radial Gate in California. Experimental Mechanics, VOLS 1 AND 2, Book Subtitle Advances in Design, Testing and Analysis. In Proceedings of the 11th International Conference on Experimental Mechanics, Oxford, UK, 24–28 August 1998; Proceedings Paper. pp. 29–34. [Google Scholar]
- Tian, X.; van Overloop, P.J.; Negenborn, R.R.; van de Giesen, N. Operational flood control of a low-lying delta system using large time step Model Predictive Control. Adv. Water Resour. 2015, 75, 1–13. [Google Scholar] [CrossRef]
- Querner, E.P.; Mioduszewski, W.; Povilaitis, A.; Slesicka, A. Modelling Peatland Hydrology: Three Cases from Northern Europe. Pol. J. Environ. Stud. 2010, 19, 149–159. [Google Scholar]
- Ahmad, M.U.; Birdsall, D.B. The Environmental Impact of Dams. In Proceedings of the 1st International Conference on New/Emerging Concepts for Rivers (RIVERTECH96), Chicago, IL, USA, 22–26 September 1996; Proceedings Paper. pp. 77–83. [Google Scholar]
- Heitefuss, C.; Karopoulos, C. Strategies for the Rehabilitation of the Bottom Outlet of Mornos Dam/Greece. In Proceedings of the ICOLD European Symposium on Dams in a European Context, Geiranger, Norway, 25–27 June 2001; Proceedings Paper. pp. 419–428. [Google Scholar]
- Adi, H.P.; Wahyudi, S.I.; Ni’am, M.F. Decision Support System for Selecting Type of Moveable Dam Gate to Handle Tidal Flood Issued (A Case Study in The Parid River, Cilacap, Indonesia). In Proceedings of the 2nd International Conference on Sustainable Infrastructure (ICSI), Yogyakarta, Indonesia, 28–29 October 2019; Volume 1625, p. 012043. [Google Scholar] [CrossRef]
- Javanshir, I.; Javanshir, N.; Barmaki, R.; Mahmoodi, M. Modeling of the fluid-induced vibrations in sliding gate dams. J. Vibroeng. 2015, 17, 478–486. [Google Scholar]
- Ng, F.C.; Abas, A.; Abustan, I.; Rozainy, Z.M.R.; Abdullah, M.Z.; Jamaludin, A.B.; Kon, S.M. Effect of the Gap Height of Radial Gate on the Volumetric Flow Rate in Dam. In Proceedings of the 1st International Conference on Aerospace and Mechanical Engineering (AeroMech17), Batu Ferringhi, Malaysia, 21–22 November 2017; Volume 370, p. 012062. [Google Scholar] [CrossRef]
- Daneshmand, F.; Adamowski, J.; Liaghat, T. Bottom outlet dam flow: Physical and numerical modeling. Proc. Inst. Civ. Eng. Water Manag. 2014, 167, 176–184. [Google Scholar] [CrossRef]
- Zienkievicz, O.C.; Taylor, R.L.; Nithiarasu, H. Finite Element Method in Fluid Dynamics; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Reddy, J.N.; Gartling, D.K. The Finite Element Method in Heat Transfer and Fluid Dynamics (Applied and Computational Mechanics); CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Pirroneau, O. Finite Element Methods for Fluids; Wiley: Hoboken, NJ, USA, 1990. [Google Scholar]
- Yang, S.; Wang, B.; Guo, Y.K.; Zhang, J.M.; Chen, Y.L. Gate-Opening Criterion for Generating Dam-Break Flow in Non-Rectangular Wet Bed Channels. Energies 2020, 13, 6280. [Google Scholar] [CrossRef]
- Aleixo, R.; Soares-Frazao, S.; Altinakar, M.; Zech, Y. The Gate Removal Effect in the Initial Instants of the Dam-break Flow. In Proceedings of the 35th World Congress of the International-Association-for-Hydro-Environment-Engineering-and-Research (IAHR), Chengdu, China, 8–13 September 2013; Proceedings Paper. Volumes I and II, pp. 1329–1338. [Google Scholar]
- Yamini, O.A.; Mousavi, S.H.; Kavianpour, M.R.; Ghaleh, R.S. Hydrodynamic Performance and Cavitation Analysis in Bottom Outlets of Dam Using CFD Modelling. Adv. Civ. Eng. 2021, 2021, 5529792. [Google Scholar] [CrossRef]
- Gu, S.L.; Zheng, X.P.; Ren, L.Q.; Xie, H.W.; Huang, Y.F.; Wei, J.H.; Shao, S.D. SWE-SPHysics Simulation of Dam Break Flows at South-Gate Gorges Reservoir. Water 2017, 9, 387. [Google Scholar] [CrossRef] [Green Version]
- Patev, R.C.; Putcha, C.S. Risk Analysis Methodologies for Dam Gates and Operating Equipment. In Proceedings of the 23rd Annual United-States-Society-on-Dams Conference, Charleston, SC, USA, 14–18 April 2003; Proceedings Paper. pp. 199–209. [Google Scholar]
- Vlase, S.; Teodorescu, P.P.; Itu, C.; Scutaru, M.L. Elasto-Dynamics of a Solid with a General “Rigid” Motion using FEM Model. Part II. Analysis of a Double Cardan Joint. Rom. J. Phys. 2013, 58, 882–892. [Google Scholar]
- Vlase, S.; Nastac, C.; Marin, M.; Mihalcica, M. A Method for the Study of the Vibration of Mechanical Bars Systems with Symmetries. Acta Tech. Napocensis. Ser. Appl. Math. Mech. Eng. 2017, 60, 539–544. [Google Scholar]
- Scutaru, M.L.; Vlase, S.; Marin, M.; Modrea, A. New analytical method based on dynamic response of planar mechanical elastic systems. Bound. Value Probl. 2020, 2020, 104. [Google Scholar] [CrossRef]
- Vlase, S.; Marin, M.; Scutaru, M.L.; Munteanu, R. Coupled transverse and torsional vibrations in a mechanical system with two identical beams. AIP Adv. 2017, 7, 065301. [Google Scholar] [CrossRef]
- Scutaru, M.L.; Vlase, S. Some Properties of Motion Equations Describing the Nonlinear Dynamical Response of a Multibody System with Flexible Elements. J. Appl. Math. 2012, 2012, 628503. [Google Scholar] [CrossRef] [Green Version]
- Negrean, I.; Crisan, A.V.; Vlase, S. A New Approach in Analytical Dynamics of Mechanical Systems. Symmetry 2021, 12, 95. [Google Scholar] [CrossRef] [Green Version]
- Vlase, S.; Teodorescu-Draghicescu, H.; Calin, M.R.; Serbina, L. Simulation of the elastic properties of some fibre-reinforced composite laminates under off-axis loading system. Optoelectron. Adv. Mater.-Rapid Commun. 2011, 5, 424–429. [Google Scholar]
- Hughes, T.J.R. Finite Element Method; Dover Publication, Inc.: Mineola, NY, USA, 2000. [Google Scholar]





















Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Itu, C.; Vlase, S. Stress–Strain Field in an Innovative Metallic Dam Gate Used to Control the Water Flow. Materials 2022, 15, 2689. https://doi.org/10.3390/ma15072689
Itu C, Vlase S. Stress–Strain Field in an Innovative Metallic Dam Gate Used to Control the Water Flow. Materials. 2022; 15(7):2689. https://doi.org/10.3390/ma15072689
Chicago/Turabian StyleItu, Calin, and Sorin Vlase. 2022. "Stress–Strain Field in an Innovative Metallic Dam Gate Used to Control the Water Flow" Materials 15, no. 7: 2689. https://doi.org/10.3390/ma15072689
APA StyleItu, C., & Vlase, S. (2022). Stress–Strain Field in an Innovative Metallic Dam Gate Used to Control the Water Flow. Materials, 15(7), 2689. https://doi.org/10.3390/ma15072689