The Non-Steady State Growth of Pearlite outside the Hultgren Extrapolation
Abstract
:1. Introduction
2. Materials and Experimental Procedure
3. Results and Discussion
4. Conclusions
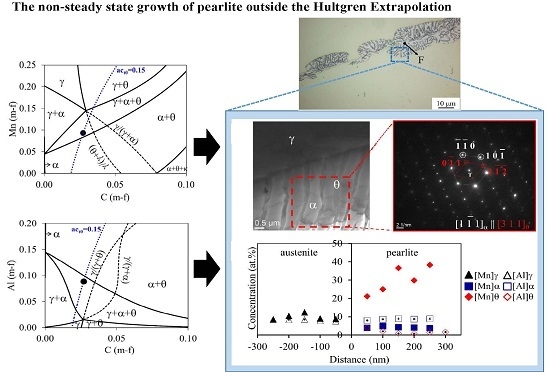
- Pearlite can nucleate from a much wider span of average austenite carbon concentrations than those defined by the Hultgren extrapolation, provided that some amount of the more favourable proeutectoid phase is present. Once initiated, pearlite can grow into austenite having any composition inside the α + θ two-phase field and the γ + α + θ three-phase field. As has been reported previously by the authors [16,19], the flux balance ahead of the interface allows lamellar pearlite formation outside Hultgren extrapolation.
- The experimental ATEM measurements allow us to conclude that Mn increases in Al-steel during transformation in both ferrite and cementite, reaching the full equilibrium value after 13 days. On the other hand, in the case of Al-steel, the Al content in cementite is negligible, as was expected due to its low solubility. The concentration of Al in ferrite remains approximately constant and close to the LE values.
- The change in carbon activity in Al-steel is smaller than that for the Mn-steel in the same (γ + α + θ) three-phase region of the corresponding phase diagram, which explains the lower driving force for the pearlite reaction.
- All these results allow us to conclude that divergent pearlite can be observed not only when the alloy composition lies within the (γ + α + θ), but also when the change in carbon activity is large enough to make the divergent microstructure noticeable.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hillert, M. Analysis of the effect of alloying elements on the pearlite reaction. In International Conference on Solid-Solid Phase Transformations, Warrendale, PA, USA, 1982; Aaronson Hubert, I., Laughlin David, E., Sekerka Robert, F., Wayman, C.M., Eds.; TMS-AIME: Warrendale, PA, USA, 1982; pp. 789–806. [Google Scholar]
- Mehl, R.F.; Hagel, W.C. The austenite: Pearlite reaction. Prog. Met. Phys. 1956, 6, 74–134. [Google Scholar] [CrossRef]
- Hultgren, A. Isothermal transformation of austenite. Trans. ASM 1947, 39, 915–1005. [Google Scholar]
- Sharma, R.C.; Purdy, G.R.; Kirkaldy, J.S. Kinetics of the pearlite reaction in Fe-C-Cr. Metall. Trans. A 1979, 10, 1129–1139. [Google Scholar] [CrossRef]
- Razik, N.A.; Lorimer, G.W.; Ridley, N. An investigation of manganese partitioning during the austenite-pearlite transformation using analytical electron microscopy. Acta Metall. 1974, 22, 1249–1258. [Google Scholar] [CrossRef]
- Razik, N.A.; Lorimer, G.W.; Ridley, A. Chromium partitioning during the austenite-pearlite transformation. Metall. Trans. A 1976, 7, 209–214. [Google Scholar] [CrossRef]
- Tewari, S.; Sharma, R. The effect of alloying elements on pearlite growth. Metall. Mater. Trans. A 1985, 16, 597–603. [Google Scholar] [CrossRef]
- Smallman, R.E. Modern Physical Metallurgy; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Martin, J.W. Concise Encyclopedia of the Structure of Materials; Elsevier: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Hutchinson, C.R.; Hackenberg, R.E.; Shiflet, G.J. The growth of partitioned pearlite in Fe-C-Mn steels. Acta Mater. 2004, 52, 3565–3585. [Google Scholar] [CrossRef]
- Cahn, J.W.; Hagel, W.G. Divergent pearlite in a manganese eutectoid steel. Acta Metall. 1963, 11, 561–574. [Google Scholar] [CrossRef]
- Gilmour, J.B.; Purdy, G.R.; Kirkaldy, J.S. Thermodynamics controlling the proeutectoid ferrite transformations in Fe-C-Mn alloys. Metall. Trans. 1972, 3, 1455–1464. [Google Scholar] [CrossRef]
- Coates, D.E. Diffusion-controlled precipitate growth in ternary systems I. Metall. Trans. A 1972, 3, 1203–1212. [Google Scholar] [CrossRef]
- Coates, D.E. Diffusion-controlled precipitate growth in ternary systems II. Metall. Trans. A 1973, 4, 1077–1086. [Google Scholar] [CrossRef]
- Bhadeshia, H.; Honeycombe, R. Steels: Microstructure and Properties: Microstructure and Properties; Elsevier Science: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Aranda, M.M.; Rementeria, R.; Poplawsky, J.; Urones-Garrote, E.; Capdevila, C. The role of C and Mn at the austenite/pearlite reaction front during non-steady-state pearlite growth in a Fe-C-Mn steel. Scr. Mater. 2015, 104, 67–70. [Google Scholar] [CrossRef]
- Mehl, R. Hardenability of Alloy Steels; ASM International: Cheveland, OH, USA, 1939; pp. 1–65. [Google Scholar]
- Liu, Z.Q.; Miyamoto, G.; Yang, Z.G.; Furuhara, T. Volume fractions of proeutectoid ferrite/pearlite and their dependence on prior austenite grain size in hypoeutectoid Fe-Mn-C alloys. Metall. Mater. Trans. A 2013, 44, 5456–5467. [Google Scholar] [CrossRef]
- Aranda, M.M.; Rementeria, R.; Capdevila, C.; Hackenberg, R.E. Can pearlite form outside of the hultgren extrapolation of the Ae3 and Acm phase boundaries? Metall. Mater. Trans. A 2016, 47, 649–660. [Google Scholar] [CrossRef]
- Isaichev, I.V. Orientation of cementite in tempered carbon steel. Zh Sakharnoi Promst 1947, 17, 835–838. [Google Scholar]
- Czarski, A.; Skowronek, T.; Osuch, W. Influence of orientation relationship between ferrite and cementite in pearlite on stability of cementite plates. Metall. Foundry Eng. 2007, 33, 41–49. [Google Scholar] [CrossRef]
- Zhang, M.X.; Kelly, P.M. The morphology and formation mechanism of pearlite in steels. Mater. Charact. 2009, 60, 545–554. [Google Scholar] [CrossRef]
- Zhang, G.H.; Wei, R.; Enomoto, M.; Suh, D.W. Growth kinetics of proeutectoid ferrite in Fe-0.1C-1.5Mn-1Si quaternary and Fe-0.1C-1.5Mn-1Si-0.2Al quinary alloys. Metall. Mater. Trans. A 2012, 43, 833–842. [Google Scholar] [CrossRef]
- Zhang, G.-H.; Heo, Y.-U.; Song, E.-J.; Suh, D.-W. Kinetic transition during the growth of proeutectoid ferrite in Fe-C-Mn-Si quaternary steel. Met. Mater. Int. 2013, 19, 153–158. [Google Scholar] [CrossRef]
- Jang, Y.; Phaniraj, M.P.; Kim, D.-I.; Shim, J.-H.; Huh, M.-Y. Effect of aluminum content on the microstructure and mechanical properties of hypereutectoid steels. Metall. Mater. Trans. A 2010, 41, 2078–2084. [Google Scholar] [CrossRef]
- Leslie, W.C.; Rauch, G.C. Precipitation of carbides in low-carbon Fe-Al-C alloys. Metall. Trans. A 1978, 9, 343–349. [Google Scholar] [CrossRef]
- Cahn, J.; Hagel, W. Theory of the pearlite reaction. In Decomposition of Austenite by Diffusional Processes, New York, 1962; Zackey, Z., Aaronson, H., Eds.; Interscience: New York, NY, USA, 1962; pp. 131–192. [Google Scholar]






| Steel | Unit | C | Mn | Al | Fe |
|---|---|---|---|---|---|
| Al-steel | wt % | 0.63 | 9.82 | 4.60 | bal. |
| at % | 2.74 | 9.30 | 8.86 | bal. | |
| Mn-steel | wt % | 0.65 | 9.72 | - | bal. |
| at % | 2.98 | 9.66 | - | bal. |
| Alloy (wt %) | T (°C) | act0 | actF | Δac | a* | Δμ (J·mol−1) | Reference |
|---|---|---|---|---|---|---|---|
| Fe–0.6C–5.2Mn | 650 | 0.250 | 0.182 | −0.068 | 0.728 | −2439 | [11] |
| Fe–0.6C–5.2Mn | 625 | 0.300 | 0.156 | −0.144 | 0.520 | −4869 | [11] |
| Fe–1C–5Mn | 680 | 0.420 | 0.214 | −0.206 | 0.509 | −5339 | [27] |
| Fe–0.6C–4.7Mn | 650 | 0.260 | 0.182 | −0.078 | 0.700 | −2744 | [10] |
| Fe–0.55C–5.4Mn | 625 | 0.270 | 0.156 | −0.114 | 0.577 | −4080 | [10] |
| Fe–0.49C–6.3Mn | 600 | 0.270 | 0.132 | −0.138 | 0.489 | −5197 | [10] |
| Fe–0.42C–6.8Mn | 575 | 0.265 | 0.109 | −0.156 | 0.411 | −6256 | [10] |
| Fe–0.66C–9.74Mn | 600 | 0.320 | 0.130 | −0.190 | 0.406 | −6543 | [16] |
| Fe–0.6C–9.8Mn–4.6Al | 670 | 0.150 | 0.130 | −0.020 | 0.867 | −1123 | CW ** |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martin-Aranda, M.; Rementeria, R.; Hackenberg, R.; Urones-Garrote, E.; Tsai, S.P.; Yang, J.R.; Capdevila, C. The Non-Steady State Growth of Pearlite outside the Hultgren Extrapolation. Materials 2016, 9, 998. https://doi.org/10.3390/ma9120998
Martin-Aranda M, Rementeria R, Hackenberg R, Urones-Garrote E, Tsai SP, Yang JR, Capdevila C. The Non-Steady State Growth of Pearlite outside the Hultgren Extrapolation. Materials. 2016; 9(12):998. https://doi.org/10.3390/ma9120998
Chicago/Turabian StyleMartin-Aranda, Maria, Rosalia Rementeria, Robert Hackenberg, Esteban Urones-Garrote, Shao Pu Tsai, Jen Ren Yang, and Carlos Capdevila. 2016. "The Non-Steady State Growth of Pearlite outside the Hultgren Extrapolation" Materials 9, no. 12: 998. https://doi.org/10.3390/ma9120998
APA StyleMartin-Aranda, M., Rementeria, R., Hackenberg, R., Urones-Garrote, E., Tsai, S. P., Yang, J. R., & Capdevila, C. (2016). The Non-Steady State Growth of Pearlite outside the Hultgren Extrapolation. Materials, 9(12), 998. https://doi.org/10.3390/ma9120998