VIIRS Reflective Solar Bands Calibration Progress and Its Impact on Ocean Color Products
Abstract
:1. Introduction
2. VIIRS Sensor Data Records
3. RSB Calibration Methodology and Performance
3.1. SD and SDSM Calibration
3.2. Lunar Calibration
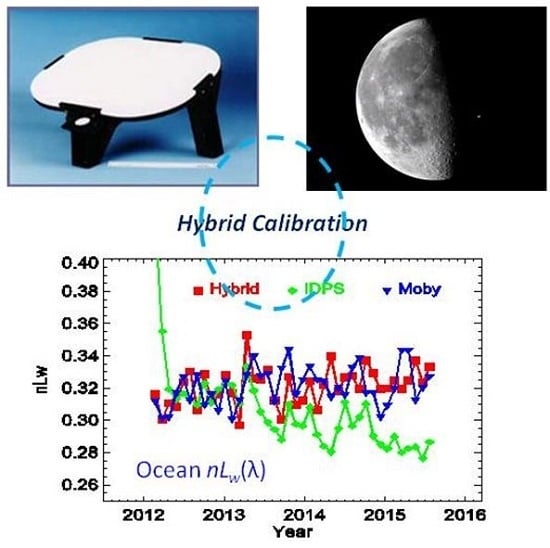
3.3. Hybrid Approach
4. Ocean Color EDR Improvements
5. Summary
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Cao, C.; Deluccia, F.; Xiong, X.; Wolfe, R.; Weng, F. Early on-orbit performance of the Visible Infrared Imaging Radiometer Suite (VIIRS) onboard the Suomi National Polar-orbiting Partnership (S-NPP) satellite. IEEE Trans. Geosci. Remote Sens. 2014, 52, 1142–1156. [Google Scholar] [CrossRef]
- Xiong, X.; Butler, J.; Chiang, K.; Efremova, B.; Fulbright, J.; Lei, N.; McIntire, J.; Oudrari, H.; Sun, J.; Wang, Z.; et al. VIIRS on-orbit calibration methodology and performance. J. Geophys. Res. Atmos. 2014, 119, 5065–5078. [Google Scholar] [CrossRef]
- Lei, N.; Wang, Z.; Fulbright, J.; Lee, S.; McIntire, J.; Chiang, K.; Xiong, X. Initial on-orbit radiometric calibration of the Suomi NPP VIIRS reflective solar bands. Proc. SPIE 2012, 8510. [Google Scholar] [CrossRef]
- Cardema, J.C.; Rausch, K.; Lei, N.; Moyer, D.I.; DeLuccia, F. Operational calibration of VIIRS reflective solar band sensor data records. Proc. SPIE 2012, 8510, 851019. [Google Scholar]
- Sun, J.; Wang, M. On-orbit calibration of the Visible Infrared Imaging Radiometer Suite reflective solar bands and its challenges using a solar diffuser. Appl. Opt. 2015, 54, 7210–7223. [Google Scholar] [CrossRef] [PubMed]
- Hass, E.; Moyer, D.; DeLuccia, F.; Rausch, K.; Fulbright, J. VIIRS solar diffuser bidirectional reflectance distribution function (BRDF) degradation factor operational trending and update. Proc. SPIE 2012, 8510, 851016. [Google Scholar]
- Fulbright, J.; Lei, N.K.; Chiang, K.; Xiong, X. Characterization and performance of the Suomi-NPP VIIRS solar diffuser stability monitor. Proc. SPIE 2012, 8510, 851015. [Google Scholar]
- Sun, J.; Wang, M. Visible infrared image radiometer suite solar diffuser calibration and its challenges using solar diffuser stability monitor. Appl. Opt. 2014, 36, 8571–8584. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Xiong, X. Solar and lunar observation planning for Earth-observing sensor. Proc. SPIE 2011, 8176, 817610. [Google Scholar]
- Sun, J.; Xiong, X.; Butler, J. NPP VIIRS on-orbit calibration and characterization using the Moon. Proc. SPIE 2012, 8510, 85101I. [Google Scholar]
- Xiong, X.; Sun, J.; Fulbright, J.; Z. Wang, Z.; Butler, J. Lunar Calibration and Performance for S-NPP VIIRS Reflective Solar Bands. IEEE Trans. Geosci. Remote Sens. 2016. [Google Scholar] [CrossRef]
- Eplee, R.E., Jr.; Turpie, K.R.; Meister, G.; Patt, F.S.; Franz, B.A.; Bailey, S.W. On-orbit calibration of the Suomi National Polar-Orbiting Partnership Visible Infrared Imaging Radiometer Suite for ocean color applications. Appl. Opt. 2015, 54, 1984–2006. [Google Scholar] [CrossRef] [PubMed]
- Baker, N. Joint Polar Satellite System (JPSS) VIIRS Radiometric Calibration Algorithm Theoretical Basis Document (ATBD); Goddard Space Flight Center: Greenbelt, MA, USA, 2013. [Google Scholar]
- Sun, J.; Wang, M. Radiometric Calibration of the Visible Infrared Imaging Radiometer Suite Reflective Solar Bands with Robust Characterizations and Hybrid Calibration Coefficients. Appl. Opt. 2015, 54, 9331–9342. [Google Scholar] [CrossRef] [PubMed]
- McIntire, J.; Moyer, D.; Efremova, B.; Oudrari, H.; Xiong, X. On-Orbit Characterization of S-NPP VIIRS Transmission Functions. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2354–2365. [Google Scholar] [CrossRef]
- Sun, J.; Wang, M. On-orbit characterization of the VIIRS solar diffuser and solar diffuser screen. Appl. Opt. 2015, 54, 236–252. [Google Scholar] [CrossRef] [PubMed]
- Kieffer, H.H. Photometric Stability of the Lunar Surface. Icarus 1997, 130, 323–327. [Google Scholar] [CrossRef]
- Kieffer, H.H.; Stone, T.C. The Spectral Irradiance of the Moon. Astronom. J. 2005, 129, 2887–2901. [Google Scholar] [CrossRef]
- Sun, J.; Wang, M. VIIRS Reflective Solar Bands On-Orbit Calibration and Performance: A Three-Year Update. Proc. SPIE 2014, 9264, 92640L. [Google Scholar]
- Gordon, H.R.; Wang, M. Retrieval of water-leaving radiance and aerosol optical thickness over the oceans with SeaWiFS: A Preliminary Algorithm. Appl. Opt. 1994, 33, 443–452. [Google Scholar] [CrossRef] [PubMed]
- Wang, M. Remote sensing of the ocean contributions from ultraviolet to near-infrared using the shortwave infrared bands: Simulations. Appl. Opt. 2007, 46, 1535–1547. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Shi, W. The NIR-SWIR combined atmospheric correction approach for MODIS ocean color data processing. Opt. Express 2007, 15, 15722–15733. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Tang, J.; Shi, W. MODIS-derived ocean color products along the China east coastal region. Geophys. Res. Lett. 2007, 34, L06611. [Google Scholar] [CrossRef]
- Wang, M.; Shi, W.; Tang, J. Water property monitoring and assessment for China’s inland Lake Taihu from MODIS-Aqua measurements. Remote Sens. Environ. 2011, 115, 841–845. [Google Scholar] [CrossRef]
- Wang, M.; Liu, X.; Tan, L.; Jiang, L.; Son, S.; Shi, W.; Rausch, K.; Voss, K. Impact of VIIRS SDR performance on ocean color products. J. Geophys. Res. Atmos. 2013, 118, 10347–10360. [Google Scholar] [CrossRef]
- Wang, M.; Liu, X.; Jiang, L.; Son, S.; Sun, J.; Shi, W.; Tan, L.; Naik, P.; Mikelsons, K.; Wang, X.; Lance, V. Evaluation of VIIRS ocean color products. Proc. SPIE 2014, 9261, 92610E. [Google Scholar]
- Xiong, X.; Sun, J.; Barnes, W.; Salomonson, V.; Esposito, J.; Erives, H.; Guenther, B. Multiyear on-orbit calibration and performance of Terra MODIS reflective solar bands. IEEE Trans. Geosci. Remote Sens. 2007, 45, 879–889. [Google Scholar] [CrossRef]
- Xiong, X.; Sun, J.; Xie, X.; Barnes, W.L.; Salomonson, V.V. On-orbit calibration and performance of Aqua MODIS reflective solar bands. IEEE Trans. Geosci. Remote Sens. 2010, 48, 535–545. [Google Scholar] [CrossRef]
- Oudrari, H.; McIntire, J.; Xiong, X.; Butler, J.; Lee, S.; Lei, N.; Schwarting, T.; Sun, J. Prelaunch radiometric characterization and calibration of THE S-NPP VIIRS sensor. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2195–2210. [Google Scholar] [CrossRef]
- Sun, J.; Wang, M.; Tan, L.; Jiang, L. An Efficient Approach for VIIRS RDR to SDR Data Processing. IEEE. Trans. Geosci. Remote Sens. Lett. 2014, 11, 2037–2041. [Google Scholar]
- Sun, J.; Xiong, X.; Angal, A.; Chen, H.; Wu, A.; Geng, X. Time dependent response versus scan angle for MODIS reflective solar bands. IEEE Trans. Geosci. Remote Sens. 2014, 52, 3159–3174. [Google Scholar] [CrossRef]
- Lessel, K.; McClain, S. Low uncertainty measurements of bidirectional reflectance factor on the NPOESS/VIIRS solar diffuser. Proc. SPIE 2007, 6677, 66771O. [Google Scholar]
- JPSS. Joint Polar Satellite System (JPSS) VIIRS Reflective Solar Bands—Performance Verification Report (PVR); NASA Goddard Space Flight Center: Greenbelt, MD, USA, 2011. [Google Scholar]
- Lei, N.; Xiong, X. Determination of the SNPP VIIRS solar diffuser BRDF degradation factor over wavelengths longer than 1 µm. Proc. SPIE 2015, 9607, 96071W. [Google Scholar]
- Xiong, X.; Angal, A.; Fulbright, J.; Lei, N.; Mu, Q.; Wang, Z.; Wu, A. Calibration improvements for MODIS and VIIRS SWIR spectral bands. Proc. SPIE 2015, 9607, 96071Z. [Google Scholar]
- Lei, N.; Guenther, B.; Wang, Z.; Xiong, X. Modeling SNPP VIIRS reflective solar bands optical throughput degradation and its impacts on the relative spectral response. Proc. SPIE 2013, 8866, 88661H. [Google Scholar]
- De Luccia, F.; Moyer, D.; Johnson, E.; Rausch, K.; Lei, N.; Chiang, K.; Xiong, X.; Fulbright, J.; Haas, E.; Iona, G. Discovery and characterization of on-orbit degradation of the Visible Infrared Imaging Radiometer Suite (VIIRS) Rotating Telescope Assembly (RTA). Proc. SPIE 2012, 8510, 85101A. [Google Scholar]
- Barrie, J.D.; Fugua, P.D.; Meshishnek, M.J.; Ciofalo, M.R.; Chu, C.T.; Chaney, J.A.; Moision, R.M.; Graziani, L. Root cause determination of on-orbit degradation of the VIIRS rotating telescope assembly. Proc. SPIE 2012, 8510, 8510B. [Google Scholar]
- Iona, G.; Butler, J.; Guenther, B.; Graziani, L.; Johnson, E.; Kenedy, B.; Kent, C.; Lambeck, R.; Waluschka, E.; Xiong, X. VIIRS on-orbit optical anomaly—Investigation, analysis, root cause determination and lessons learned. Proc. SPIE 2014, 8510, 85101C. [Google Scholar]
- Sun, J. Sigma Space Corporation: Lanham, MD, USA, Unpublished; 2010.
- Stone, T.C.; Kieffer, H.H. Assessment of Uncertainty in ROLO Lunar Irradiance for On-orbit Calibration. Proc. SPIE 2004, 5542, 300–310. [Google Scholar]
- Sun, J.; Xiong, X.; Barnes, W.L.; Guenther, B. MODIS Reflective Solar Bands On-Orbit Lunar Calibration. IEEE Trans. Geosci. Remote Sens. 2007, 43, 2383–2393. [Google Scholar] [CrossRef]
- Barnes, R.A.; Eplee, R.E., Jr.; Patt, F.S.; McClain, C.R. Changes in the radiometric stability of SeaWiFS determined from lunar and solar measurements. Appl. Opt. 1999, 38, 4649–4664. [Google Scholar] [CrossRef] [PubMed]
- Wang, M. A sensitivity study of SeaWiFS atmospheric correction algorithm: Effects of Spectral Band Variations. Remote Sens. Environ. 1999, 67, 348–359. [Google Scholar] [CrossRef]
- Wang, M.; Franz, B.A. Comparing the ocean color measurements between MOS and SeaWiFS: A Vicarious Intercalibration Approach for MOS. IEEE Trans. Geosci. Remote Sens. 2000, 38, 184–197. [Google Scholar] [CrossRef]
- Wang, M.; Isaacman, A.; Franz, A.B.; McClain, C.R. Ocean color optical property data derived from the Japanese Ocean Color and Temperature Scanner and the French Polarization and Directionality of the Earth’s Reflectances: A Comparison Study. Appl. Opt. 2002, 41, 974–990. [Google Scholar] [CrossRef] [PubMed]
- Clark, D.; Gordon, H.; Voss, K.; Broenkow, W.; Trees, C. Validation of atmospheric correction over the oceans. J. Geophys. Res. 1997, 102, 17209–17217. [Google Scholar] [CrossRef]
- Clark, D.; Yarbrough, M.; Feinholz, M.; Flora, S.; Broenkow, W.; Kim, Y.S.; Johnson, B.C.; Brown, S.W.; Yuen, M.; Mueller, J.W. MOBY, A Radiometric Buoy for Performance Monitoring and Vicarious Calibration of Satellite Ocean Color Sensors: Measurement and Data Analysis Protocols. In Ocean. Optics Protocols for Satellite Ocean Color Sensor Validation; Mueller, J., Fargion, G., McClain, C., Eds.; National Aeronautics and Space Administration Goddard Space Flight Center: Greenbelt, MD, USA, 2003; pp. 3–34. [Google Scholar]

















| SDSM | VIIRS RSB | ||||
|---|---|---|---|---|---|
| Detector | CW (nm) | Band | CW (nm) | BW(nm) | Gain |
| D1 | 412 | M1 | 410 | 20 | DG |
| D2 | 450 | M2 | 443 | 18 | DG |
| D3 | 488 | M3 | 486 | 20 | DG |
| D4 | 555 | M4 | 551 | 20 | DG |
| NA | NA | I1 | 640 | 80 | SG |
| D5 | 672 | M5 | 671 | 20 | DG |
| D6 | 746 | M6 | 745 | 15 | SG |
| D7 | 865 | M7 | 862 | 39 | DG |
| D7 | 865 | I2 | 862 | 39 | SG |
| D8 | 935 | NA | NA | NA | NA |
| NA | NA | M8 | 1238 | 20 | SG |
| NA | NA | M9 | 1378 | 15 | SG |
| NA | NA | M10 | 1610 | 60 | SG |
| NA | NA | I3 | 1610 | 60 | SG |
| NA | NA | M11 | 2250 | 50 | SG |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, J.; Wang, M. VIIRS Reflective Solar Bands Calibration Progress and Its Impact on Ocean Color Products. Remote Sens. 2016, 8, 194. https://doi.org/10.3390/rs8030194
Sun J, Wang M. VIIRS Reflective Solar Bands Calibration Progress and Its Impact on Ocean Color Products. Remote Sensing. 2016; 8(3):194. https://doi.org/10.3390/rs8030194
Chicago/Turabian StyleSun, Junqiang, and Menghua Wang. 2016. "VIIRS Reflective Solar Bands Calibration Progress and Its Impact on Ocean Color Products" Remote Sensing 8, no. 3: 194. https://doi.org/10.3390/rs8030194
APA StyleSun, J., & Wang, M. (2016). VIIRS Reflective Solar Bands Calibration Progress and Its Impact on Ocean Color Products. Remote Sensing, 8(3), 194. https://doi.org/10.3390/rs8030194