Next Article in Journal
A Concise Review of Multicomponent Reactions Using Novel Heterogeneous Catalysts under Microwave Irradiation
Next Article in Special Issue
Recent Mechanistic Understanding of Fischer-Tropsch Synthesis on Fe-Carbide
Previous Article in Journal
Light-Assisted Catalysis in Water and Indoor Air Cleaning: Challenges and Perspectives
Previous Article in Special Issue
Conversion of CO2 Hydrogenation to Methanol over K/Ni Promoted MoS2/MgO Catalyst
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Catalysts
Volume 13
Issue 7
10.3390/catal13071033
catalysts-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

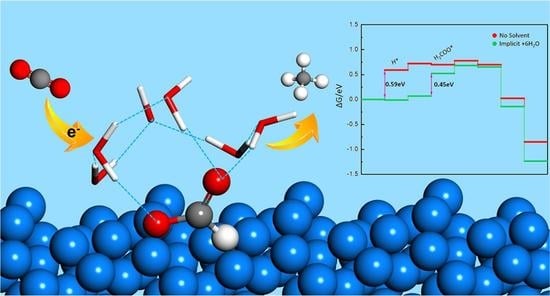
Effect of Explicit Water Molecules on the Electrochemical Hydrogenation of CO2 on Sn(112)

by
Jia Wang
1,†,
Chaonan Cui
2,†,
Xinli Zhu
1,
Hua Wang
1,* and
Qingfeng Ge
3,*
1
Collaborative Innovation Centre of Chemical Science and Engineering, School of Chemical Engineering and Technology, Tianjin University, Tianjin 300072, China
2
Beijing National Laboratory for Molecular Sciences (BNLMS), State Key Laboratory for Structural Chemistry of Unstable and Stable Species, Institute of Chemistry, Chinese Academy of Sciences, Beijing 100190, China
3
Department of Chemistry and Biochemistry, Southern Illinois University, Carbondale, IL 62901, USA
*
Authors to whom correspondence should be addressed.
†
These authors contributed equally to this work.
Catalysts 2023, 13(7), 1033; https://doi.org/10.3390/catal13071033
Submission received: 31 May 2023 / Revised: 18 June 2023 / Accepted: 19 June 2023 / Published: 23 June 2023
(This article belongs to the Special Issue Catalysis for Selective Hydrogenation of CO and CO2)
Browse Figures
Versions Notes

Abstract

:
Water is typically treated as an implicit solvent in modeling electrochemical reactions in an aqueous environment. Such treatment may not be adequate, as a series of concerted or sequential proton-electron transfer steps that explicitly involve water molecules are likely to play important roles in a reaction, such as the electrochemical hydrogenation of CO2. Herein, we use the electrochemical hydrogenation of CO2 on the Sn(112) surface as a model, and employ the density functional theory (DFT) method to examine the effect of up to 12 explicit water molecules on the stability of the hydrogenation intermediates. Our results show that six water molecules are needed to account for the local interaction between an intermediate and the water solvent. Furthermore, the hydrogen bonding interaction between the explicit water molecules and intermediates causes a significant stabilization to the O-containing intermediates, such as the HCOO* and CHO* + OH* species. The inclusion of explicit water molecules also altered the prediction of the potential-limiting step from the formation of H* atoms without the explicit water molecules to the formation of H2COO* in the presence of water molecules and increased selectivity towards methane. This work provides useful insights into the electrocatalytic hydrogenation of CO2, emphasizing the importance of including explicit water molecules to account for the hydrogen bonding interaction between solvent water molecules and the reaction intermediates.

Graphical Abstract

1. Introduction

Electrochemical processes have the versatility of transforming chemical energy into electricity or producing valuable chemicals using electricity [1,2,3], and play important roles in consumer products and clean and renewable energy applications, such as battery, fuel cells, and CO2 conversion and utilization [4,5]. In particular, the electrochemical reduction of CO2 can be interfaced with the renewable electricity from wind or solar power and help to reduce the overall CO2 emission and contribute positively to the “Net Zero” goal [6,7,8].
There have been many studies on the mechanism of CO2 reduction on different electrode materials, especially the metal and metal oxide supported electrodes, to pursue an efficient conversion of CO2 [8,9,10,11,12,13,14,15,16,17,18,19,20]. Most electrochemical reactions are carried out in an aqueous environment, so it is necessary to understand the basic chemical processes of CO2 electrochemical hydrogenation, including the solvation effect and solvent molecules participating in the chemical transformation. In fact, the solvent effect has been demonstrated for reactions involving the metal catalysts [21,22,23,24]. For example, Thomas et al. studied the solvent structure surrounding the carbon dioxide reduction intermediate on Cu(211) and found that solvation can stabilize the adsorbate and promote the hydrogenation of CO2 [25]. Moreover, the water molecules have been shown to not only facilitate the reaction by stabilizing surface adsorbates, but also they directly participate in the reaction, in processes such as electrochemical methanol oxidation [26], oxygen reduction [27,28], and water activation [29,30,31]. In those studies, two to several layers of explicit water molecules were included in the model simulating the solvent environment.
Density functional theory (DFT) calculations, combined with the implicit or explicit solvents, have been used to describe the solvation effect [25,32,33,34,35,36,37,38]. Many studies used the implicit solvent model in the study of electrochemical CO2 reduction [20,39,40,41]. Satish et al. studied the effect of implicit solvent on the adsorption energy of common adsorbates on the Pt(111) surface, and showed that the adsorption energy of those adsorbates could be changed due to the solvation effect [42]. However, the implicit solvent model does not directly consider the possible hydrogen-bonding formation between adsorbates and solvent molecules and the proton transfer facilitated by the solvent molecules [43]. Therefore, it is imperative to include explicit water molecules surrounding the adsorbates to account for such effects.
The explicit solvent models, including a single to a few water molecules, have been adopted. Federico et al. showed that three water molecules stabilized the adsorption of *OH and *OOH by −0.59 eV and −0.47 eV, respectively [44]. Zhao et al. showed a change of relative stability of reaction intermediates by including six water molecules. Those authors showed that the hydrogen-bonding interaction between water molecules and adsorbates increased the adsorption energy of the COOH* intermediate but reduced the adsorption energy of HCOO* [45]. Meng et al. concluded that hydrogen-bonding interactions between the water molecules and the intermediate, in an environment with 30 H2O molecules, reduced the overpotential for both methane and ethene formation [46]. Valter et al. studied the effect of implicit solvent effect and explicit solvation by water molecules on the intermediates of a methanol-electrooxidation reaction and concluded that six water molecules were needed to achieve a convergent result [47]. Clearly, including explicit water molecules is necessary to properly account for its contribution to the electrochemical hydrogenation of CO2. On the other hand, increasing the number of water molecules will not only increase the cost of calculations but also the complexity of structures. It is important to establish the minimum number of explicit water molecules for the electrochemical hydrogenation of CO2.
Herein, we use the electrochemical hydrogenation of CO2 on Sn(112), the stepped surface which is considered active for C–O bond breaking, as a model to study the effect of explicit water molecules based on the mechanism proposed in our previous work [48]. We use a hybrid solvent model, i.e., explicit solvent with up to 12 explicit water molecules in combination with the implicit water solvent. The effect of implicit and explicit solvent models has been studied separately and their effect has been quantified. Our results show that explicit water molecules enhance the stability of the intermediate and reduce the free energy barrier of CO2 electrochemical hydrogenation. The presence of explicit water molecules also causes a change in the potential limiting step and improves the selectivity towards methane.

2. Results and Discussion

Based on our previous study, the key intermediate for electrochemical hydrogenation of CO2 on Sn(112) is formate (HCOO*), which is a result of CO2 reacting with H from a proton-coupled electron transfer [48]. Further reduction of HCOO* may generate the H2COO* or CHO* + OH* intermediates, which can then be further reduced to methane or carbon monoxide. Herein, we focus on the solvent effect on the steps leading to H2COO* and CHO + OH* formation.

2.1. Implicit Solvent Effect

We first calculated the energies of intermediates with only the implicit solvent model and compared them with the results under the vacuum condition. For the clean surface and H*, the implicit solvent model exhibits little effect. The implicit solvent stabilizes H2COO* by 0.09 eV. A significant stabilization due to implicit solvent was observed for HCOO* (0.22 eV) and CHO* + OH* (0.25 eV) (See Figure S2). These results indicate that including implicit solvent stabilizes the hydroxyl and other O-containing intermediates by less than 0.25 eV but causes little change to the energy of the clean surface and the hydrogen adatom. This observation is consistent with the previous studies [49,50,51]. However, the extent of the stabilization towards O-containing intermediates (<0.25 eV) is much weaker than some of the previous studies, which reported a stabilization up to 0.5 eV for OH* and 0.25 eV for R-OH* groups. Furthermore, the implicit solvent model is not able to capture the ubiquitous hydrogen bonding interaction that existed in an aqueous solution. Explicit water molecules are needed to allow the hydrogen bonding interaction between an intermediate and the solvent. Therefore, we study the effect of the explicit water molecules in the next section.

2.2. Explicit Solvent Effect

2.2.1. Interaction between Adsorbates and Explicit Water Molecules

The effect of explicit solvent has been studied by including 1–12 water molecules explicitly in the calculations. Figure 1 shows the interaction energies between adsorbates and water clusters calculated using Equation (6). For H* and H2COO* intermediates, the interaction energies, −0.20 eV and −0.80 eV, respectively, do not change with the number of water molecules. Bader charge analysis shows that the hydrogen adatom carriers a negative charge of −0.32 |e|, whereas the hydrogen atom of the water molecule carries a positive charge of +0.58 |e| (Table 1 and Figure 1) [52,53]. Therefore, there will be a strong electrostatic interaction between the H atom of a solvent water molecule and H* at a distance of 1.97 Å. Adding additional water molecules will not enhance the stability of H* further. Similarly, the H atom of the first water molecule is attracted to the oxygen atom (labeled O2 in Table 1) of H2COO*, forming a hydrogen bond. The O-H distance is 1.64 Å, corresponding to a much stronger interaction (−0.80 eV). The other oxygen atom (O1) of H2COO* binds the tin atoms of the surface and is not available to bind the solvent water molecules. Additionally, a tetrahedral structure of H2COO* exposes two hydrogen atoms to the solvent and sterically prevents additional water molecules approaching the oxygen atoms. Therefore, additional water molecules will not enhance the interaction between H2COO* and solvent molecules.
For the HCOO* and CHO* + OH* intermediates, the interaction energy between adsorbates and water molecules increases as the number of water molecules is increased. Since HCOO* lies nearly flat on the surface, both oxygen atoms of HCOO* (O1, O2) can interact with the surface and solvent water molecules. The first water molecule has an interaction energy of −0.70 eV. Both oxygen atoms in HCOO* are nearly −1.00 |e| charged. The O-H distance with one water molecules is 1.90 Å. The O-H distances between the O atoms of HCOO* and surrounding water molecules with different number of water molecules are labelled in the corresponding structures in Table S2. It can be seen that the number of hydrogen bonds increases as the number of the H2O molecules increases, enhancing the stability of the system. As shown in Figure 2, when four to seven water molecules are added, the structure of HCOO* is reversed: both O atoms are pulled away from the surface and further exposed to water molecules for hydrogen bonding, resulting in greater stabilization of the adsorption structure. This is consistent with the literature report that the number of hydrogen bonds will affect the stability of the intermediate [46,47]. However, after eight water molecules are added, the contribution of direct hydrogen bond formation diminishes as the solvation shell is complete.
For the CHO* + OH* intermediate, O1 of CHO* and O2 of OH* can interact with the solvent water molecules, with the first water molecule forming two hydrogen bonds with both O1 and O2. Adding more water molecules will result in more hydrogen bonds and eventually form a chain of hydrogen bonds. The interaction energy between CHO* + OH* and explicit water molecules fluctuates around −1.8 eV with six and more water molecules in the system. The results indicate that the adsorbates become saturated by five to six water molecules.
As mentioned, the added water molecules prefer to form hydrogen bond with the adsorbate, resulting in the stabilized intermediate state. As shown in the optimized structures with water molecules, a chain or ring of hydrogen bonds can be formed when three to four water molecules were included. The tetramer ring is the smallest ring formed through hydrogen bonds in this study (Figure 3a). The pentamer and hexamer rings can also be formed when more water molecules were added (Figure 3b–e, Table S2). Moreover, the hexamer ring is the largest as the additional water molecules were found to scatter and will coalesce into a new tetrameric, pentameric and hexameric ring when sufficient number of water molecules are present. Both CHO* and OH* species expose oxygen atoms for hydrogen bonding with the H atoms of H2O and can participate in ring formation. Figure 3f presents a pentamer ring formed from the CHO* + OH* intermediate with three H2O. Significant stabilization of CHO* + OH* by the water molecules can be observed. Fluctuation of interaction energy decreases after three water molecules, as the O atoms of the intermediate are all hydrogen bonded. These results are consistent with the previous studies [34,36,37].

2.2.2. Explicit Solvent Effect for the System

After assessing the interaction between adsorbates and solvating water molecules (ΔEads/H2O), we also examined ΔEsurf/H2O and ΔEH−B and found ΔEads/H2O approached saturation with four water molecules (Figure S3). We noted that the contribution from ΔEsurf/H2O and ΔEH−B was smaller than ΔEads/H2O, indicating that the direct interaction between adsorbates and solvating water molecules was the key factor for intermediate stabilization. To determine the number of water molecules needed to saturate the interaction with the adsorbate, we calculated the averaged explicit solvent energy per water (ΔEsys/n) including all three contributions (Figure 4a). Clearly, the first few explicit water molecules result in a significant stabilization, and the extent depends on the nature of the intermediates. Stabilization of CHO* + OH* is the strongest with one water molecule (−1.10 eV). For the HCOO* and H2COO* intermediates, the stabilization per water oscillates within 0.10 eV when increasing the number of water molecules. The results indicate that the contribution from the localized interaction of most adsorbates with the explicit solvating water molecules approaches saturation at six. The final value of ΔEsys/n is stable at −0.48 eV. By including the ZPE and entropy corrections, we determined the average free energy change per water (ΔGsys/n) was at temperatures of 298.15 K (Figure S4). Notably, the average free energy follows the same tendency as the average energy change and approaches a constant value after four water molecules.
The contribution of water molecules to the reaction has been characterized by the explicit solvent assistant reaction energy ( Δ E a s s n ). As shown in Figure 4b, all intermediates are stabilized and the stability increases as the number of explicit water molecules is increased. There are variations among the intermediates in their dependence on the number of water molecules up to four. Beyond this number, the solvent-assisted reaction energy scales linearly with the number of water molecules, as shown in Figure 4b. The results indicate that the stability of every intermediate will increase as the number of explicit water molecules increases, and the magnitude scales linearly with the number of the water molecules (0.50 eV). This indicates that the contribution to the stability is likely to originate from the hydrogen bonding interaction between the water molecules. Consequently, a minimum of four explicit water molecules is needed to capture the major contribution of the local interactions between specific intermediates and the solvating water molecules.

2.3. Combined Effect of Implicit and Explicit Solvents

The combined effect of explicit water molecules and implicit water solvent was then evaluated by varying the number of water molecules from 1 to 12. As shown in Figure 5, implicit solvent stabilizes the adsorbed intermediates and its effect increases with the number of the explicit water molecules increasing. After six water molecules were added, the energies become relatively constant. These results indicate that six explicit water molecules are needed to capture the local interactions between the reaction intermediates and the solvating molecules when the implicit solvent is included. The overall trend is consistent with that of explicit water molecules, indicating additional stabilization of implicit solvent to the explicit water molecules, although the exact numbers of water molecules are different. The energy difference induced by implicit solvent model between each intermediate with the same number of explicit water molecules remains at approximately −0.2 eV. Consequently, the presence of implicit solvent is not expected to drastically change the relative stability between the reactant and product states along a reaction pathway. Therefore, the reaction mechanism predicted without including the solvent effect should still be valid when the solvent effect is only considered implicitly.

2.4. Solvent Effect on the Potential Limiting Step and Limiting Potential

By considering both implicit and explicit solvent effects, we calculated the reaction free energies along the pathway of electrochemical hydrogenation of CO2 on Sn(112) under four different conditions, including (M1) without any solvent correction, (M2) the effect implicit solvent, (M3) adding six explicit water molecules and (M4) combining the six explicit water molecules and implicit solvent. As shown in Figure S5, M1 and M2 follow the same mechanism with HCOO* and CHO* + OH* being stabilized by 0.20 eV in M2. In contrast, the stabilization caused by six explicit water molecules in M3 alters the potential limiting step. This clearly demonstrates that the explicit solvating water molecules play important roles in the electrochemical reactions and are needed to simulate the reaction appropriately. In Figure 6, we compare the results of including six explicit water molecules together with the implicit solvent, with those of no solvent effect, i.e., M4 vs. M1. As we reported in our previous study, the reduction of CO2 on Sn(112) may follow two different pathways after HCOO* formation. One pathway goes through H2COO* → H2COHO* → CH2O* → CH3O* → CH4, while the other pathway follows CHO* + OH* → CHO* + H2O → CHOH* → CH* → CH2* → CH3* → CH4 [48]. The present results show that including the solvent effect reduces the reaction energies. There are significant stabilizations towards the HCOO* and CHO* + OH* intermediates from the explicit water molecules and implicit solvent. Other intermediates, such as CHOH* and O*, are also greatly stabilized. On the other hand, the effect of the solvent is largely negligible for the intermediates not interacting with water, due to either no water-exposing oxygen atom or containing no oxygen atom at all, including H2COO*, CHO*, CH* and H (<0.10 eV).
The overall solvent effect for CHO* + OH* intermediate is consistent with the corrections used in other works (i.e., 0.50 eV for OH* and 0.10 eV for CHO* groups) [49,50,51]. For hydrogen adsorption, the implicit solvent effect is negligible (only 0.01 eV), but an explicit water molecule could provide a significant stabilization of 0.60 eV. As a result, the first step for the electrochemical hydrogenation of CO2 can be promoted significantly. The strong stabilization of the H* intermediate by the explicit water cluster can be attributed to the strong electrostatic interaction, as shown by the Bader charges on H* and proton of the water molecules (Table 1). Not only does the explicit water molecules stabilize the H* intermediate, but this H*-H+ interaction also allows a delocalized proton transfer through a network of hydrogen bonds, thereby promoting the hydrogenation of carbon dioxide. Several previous studies reported an enhancement of proton diffusion and proton transfer phenomenon at the liquid/solid interface [38,54,55,56].
Without considering the solvent effect, the potential limiting step of the H2COO* pathway was found to be the formation of H* and that of the CHO* + OH* pathway, which formed CHO* + OH*. In the presence of the explicit water molecules and implicit solvent, the H* intermediates are greatly stabilized and its formation is no longer potential limiting. The potential limiting step was shifted to the formation of H2COO* and the limiting potential was reduced from 0.59 eV to 0.45 eV. On the other hand, the formation of the CHO* + OH* intermediates from HCOO* became more endergonic, indicating the CHO* + OH* pathway will unlikely contribute to the hydrogenation of CO2. In summary, including explicit water molecules is necessary to appropriately model electrochemical CO2 hydrogenation in an aqueous solution and six water molecules can capture the local solvent environment surrounding an adsorbed intermediate.

3. Methods

3.1. Density Functional Theory Calculations

All DFT calculations in this work were performed using the Vienna ab initio Simulation Package (VASP) with the Perdew–Burke–Ernzerhof (PBE) exchange–correlation functional [57,58]. We used the projector-augmented wave (PAW) potential and set the cutoff energy of the plane wave basis set to 500 eV. On the basis of the mechanism established in our previous work [48], up to 12 explicit water molecules were placed next to the adsorbates to quantify the effect of explicit solvent molecules. To minimize the intuitive bias, a molecular dynamic (MD), run up to 0.5 ps, was performed to sample the initial water configurations for optimization. In all calculations, the atoms in the bottom two layers of Sn(112) were fixed, whereas those in the top two layers, together with the adsorbates and water molecules, were allowed to relax.
The implicit solvation model was implemented in VASPsol [59,60] and a dielectric constant of ε = 80 for water [43,59] was used in the present study. The effect of implicit solvent (ΔEim) was defined as:
∆ E i m = E i m − E e l e c
where Eelec is the electronic energy of the optimized structure without solvent and Eim is the single point energy obtained with VASPsol for the same optimized structure.

3.2. Reference Models

The explicit solvent contribution can be partitioned into (1) the interaction between water molecules and the adsorbate (ΔEads/H2O); (2) the interaction between water molecules and Sn(112) (ΔEsurf/H2O); and (3) the hydrogen bonding (ΔEH−B) between water molecules within the solvent clusters [61]. To separate the interactions, we defined the “reference models” schematically, as shown in Figure 7.
As shown in Figure 7, models A, B and C allow us to calculate the energies of the clean surface, the adsorbed intermediate on the surface and the intermediate with explicit water molecules on the surface, respectively. Model D is the surface with the water molecules fixed in their optimized positions in the presence of adsorbate but with the adsorbate being deleted. Model E is the water cluster in the same position without the surface and adsorbate. Together with the energies of isolated water, carbon dioxide and hydrogen molecules, we can determine the formation energy of the adsorbed intermediate without the explicit water molecule (ΔEads) and the energy change, due to the presence of explicit water molecules. This treatment will allow us to quantify the solvation energy due to explicit water molecules (ΔEsys/H2O):
∆ E a d s = B − A − x F ( C O 2 , H 2 )
∆ E s y s / H 2 O = C − B − n F ( H 2 O )
where n is the number of explicit water molecules, xF is the energy of the reference molecules. The averaged explicit solvation energy per water molecule was used to determine the contribution of a water molecule to the solvation as the number of water molecules is increased.
Both adsorbate formation energy (ΔEads) and explicit solvation energy (ΔEsys/H2O) can influence the reaction energy of a reaction step. ΔEads + ΔEsys/H2O will be used to characterize the explicit solvent effect and referred to as explicit solvent assisted reaction energy ( Δ E a s s n ).
The interaction between a specific water cluster and the surface (ΔEsurf/H2O) and the hydrogen bonding energy within the cluster (ΔEH−B) can be obtained based on the following equations:
∆ E s u r f / H 2 O = D − E − A
∆ E H − B = E − n F ( H 2 O )
In order to determine the interaction between the adsorbate and water molecules, we excluded the interaction between the water molecules and the surface and the hydrogen bonding energy between the water molecules within the cluster. These were achieved by calculating the energy of the frozen configuration of water molecules and the surface without the adsorbate. By combining Equations (3)–(5), we derived ΔEads/H2O as:
∆ E a d s / H 2 O = ∆ E s y s / H 2 O − ∆ E s u r f / H 2 O − ∆ E H − B = A + C − B − D
In this study, all these interactions will be investigated. We will focus on the interaction between adsorbates and water clusters shown in Equation (6) as it may have a significant stabilization effect on the system. Additional information on the interaction between water molecules and the surface, and the hydrogen bonding energy among the water molecules in a cluster, can be seen in Supporting Information.
The free energy of each intermediate in the solvent environment was calculated based on the energy of the DFT-optimized structure with solvating water molecules and implicit solvent, Zero Point Energy (ZPE) and entropy (TS) corrections. The ZPE and TS corrections of adsorbed species were determined from the calculated harmonic frequencies based on the finite difference method implemented in VASP [62]. The ZPE and entropy (TS) corrections for gas-phase species were taken from the previous work of Nørskov et al. [51]. The averaged ZPE and entropy corrections per water at 298.15 K are approximately 0.65 eV and 0.17 eV, respectively, similar to the previous report [63]. Details are provided in Supporting Information.

4. Conclusions

We have examined the effect of implicit solvent and explicit water molecules on the electrochemical hydrogenation of CO2 on Sn(112). Our results show that the implicit solvent stabilizes the reaction intermediate by less than 0.25 eV. In contrast, including water molecules explicitly changes the adsorption energy of the intermediates differently. Explicit water molecules exhibit a limited effect on H2COO*, CHO*, CH*. Other O-containing groups, such as HCOO* and CHO* + OH*, are stabilized significantly by forming hydrogen bonds with the water molecules. Both implicit solvent and explicit water molecules are important to account for the effect of solvent environment on the reaction free energy, thereby affecting the potential of an elementary redox step. The presence of the explicit water molecules reduces the reaction free energy of the elementary step, changes the potential limiting step from H* formation to HCOO* hydrogenation to H2COO*, making the H2COO* pathway the dominant route for CH4 formation. Our results also show that six water molecules can capture the direct interaction between the adsorbed intermediate with the solvating water molecules.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/catal13071033/s1. Figure S1. The calculated Zero Point Energy and entropy of the water clusters as a function of the number of water molecules. Figure S2. Free energy diagram for CO2 reduction on Sn(112) with and without implicit solvent, no explicit water considered. Figure S3. The interaction between water cluster and surface (a), and the hydrogen bonding energy inside water cluster (b) with 1 to 12 water molecules. As one water cannot form hydrogen bond, no hydrogen bonding energy is shown for n = 1. Figure S4. The calculated average energy per water molecule of explicit solvent for different intermediates as a function of the number of the explicit water molecules in the system. Figure S5. Comparison of the reaction mechanisms for electrochemical hydrogenation of CO2 on Sn(112) with different solvent conditions. The red line shows the mechanism with no solvent stabilizations. The green line shows the mechanism employing the implicit solvent model. The blue line shows the mechanism with six explicit water molecules forming the solvation shell. Table S1. Bader charges of hydrogen and oxygen atoms for the intermediate with up to 12 water molecules. The labels shown in the figures specify the atoms and the charges are in in unit of |e|. Table S2. Top view of the optimized intermediate configurations with one to seven water molecules. Every structure is shown in two unit-cells [63,64].

Author Contributions

J.W. and C.C. performed the calculations and drafted the manuscript; X.Z. helped to collect and analyze the data; H.W. and Q.G. revised the manuscript. All authors have read and agreed to the published version of the manuscript.

Funding

We acknowledge the financial support from the National Natural Science Foundation of China (Nos. 21873067 and 21576204) and the Fundamental Research Funds for the Central Universities.

Data Availability Statement

No additional data availability; all the data were included in the manuscript.

Acknowledgments

The High-Performance Computing Center of Tianjin University is acknowledged for providing services to computing resources.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Dattila, F.; Seemakurthi, R.R.; Zhou, Y.; López, N. Modeling Operando Electrochemical CO2 Reduction. Chem. Rev. 2022, 122, 11085–11130. [Google Scholar] [CrossRef]
  2. Wang, F.; Li, Y.; Xia, X.; Cai, W.; Chen, Q.; Chen, M. Metal–CO2 Electrochemistry: From CO2 Recycling to Energy Storage. Adv. Energy Mater. 2021, 11, 2100667. [Google Scholar] [CrossRef]
  3. Yang, X.; Zhuang, Y.; Zhu, J.; Le, J.; Cheng, J. Recent progress on multiscale modeling of electrochemistry. WIREs Comput. Mol. Sci. 2022, 12, e1559. [Google Scholar] [CrossRef]
  4. Sajid, A.; Pervaiz, E.; Ali, H.; Noor, T.; Baig, M.M. A perspective on development of fuel cell materials: Electrodes and electrolyte. Int. J. Energy Res. 2022, 46, 6953–6988. [Google Scholar] [CrossRef]
  5. Zhong, W.; Huang, W.; Ruan, S.; Zhang, Q.; Wang, Y.; Xie, S. Electrocatalytic Reduction of CO2 Coupled with Organic Conversion to Selectively Synthesize High-Value Chemicals. Chem. A Eur. J. 2022, 29, e202203228. [Google Scholar] [CrossRef]
  6. Al-Tamreh, S.A.; Ibrahim, M.H.; El-Naas, M.H.; Vaes, J.; Pant, D.; Benamor, A.; Amhamed, A. Electroreduction of Carbon Dioxide into Formate: A Comprehensive Review. ChemElectroChem 2021, 8, 3207–3220. [Google Scholar] [CrossRef]
  7. Xiao, C.; Zhang, J. Architectural Design for Enhanced C2 Product Selectivity in Electrochemical CO2 Reduction Using Cu-Based Catalysts: A Review. ACS Nano 2021, 15, 7975–8000. [Google Scholar] [CrossRef]
  8. Figueiredo, M.C.; Ledezma-Yanez, I.; Koper, M.T.M. In Situ Spectroscopic Study of CO2 Electroreduction at Copper Electrodes in Acetonitrile. ACS Catal. 2016, 6, 2382–2392. [Google Scholar] [CrossRef]
  9. Landaeta, E.; Kadosh, N.I.; Schultz, Z.D. Mechanistic Study of Plasmon-Assisted In Situ Photoelectrochemical CO2 Reduction to Acetate with a Ag/Cu2O Nanodendrite Electrode. ACS Catal. 2023, 13, 1638–1648. [Google Scholar] [CrossRef]
  10. Ibn Shamsah, S.M. Electrochemical Performance of Cupric Oxide Loaded Carbon Nanotubes as Electrode Material for CO2 Reduction. J. New Mater. Electrochem. Syst. 2021, 24, 9–13. [Google Scholar] [CrossRef]
  11. Li, M.; Li, W.; Song, W.; Wang, C.; Yao, Y.; Wu, C.; Luo, W.; Zou, Z. Do Cu Substrates Participate in Bi Electrocatalytic CO2 Reduction? ChemNanoMat 2021, 7, 128–133. [Google Scholar] [CrossRef]
  12. Silva, B.C.E.; Irikura, K.; Galvao Frem, R.C.; Boldrin Zanoni, M.V. Effect of Cu (BDC-NH2) MOF deposited on Cu/Cu2O electrode and its better performance in photoelectrocatalytic reduction of CO2. J. Electroanal. Chem. 2021, 880, 114856. [Google Scholar] [CrossRef]
  13. Chen, Y.; Wrubel, J.A.; Vise, A.E.; Intia, F.; Harshberger, S.; Klein, E.; Smith, W.A.; Ma, Z.; Deutsch, T.G.; Neyerlin, K.C. The effect of catholyte and catalyst layer binders on CO2 electroreduction selectivity. Chem. Catal. 2022, 2, 400–421. [Google Scholar] [CrossRef]
  14. Ao, C.; Feng, B.; Qian, S.; Wang, L.; Zhao, W.; Zhai, Y.; Zhang, L. Theoretical study of transition metals supported on g-C3N4 as electrochemical catalysts for CO2 reduction to CH3OH and CH4. J. CO2 Util. 2020, 36, 116–123. [Google Scholar] [CrossRef]
  15. Shi, N.; Yin, X.; Gao, W.; Wang, J.; Zhang, S.; Fan, Y.; Wang, M. Competition between electrocatalytic CO2 reduction and H+ reduction by Cu(II), Co(II) complexes containing redox-active ligand. Inorg. Chim. Acta 2021, 526, 120548. [Google Scholar] [CrossRef]
  16. Zhu, L.; Lin, Y.; Liu, K.; Cortes, E.; Li, H.; Hu, J.; Yamaguchi, A.; Liu, X.; Miyauchi, M.; Fu, J.; et al. Tuning the intermediate reaction barriers by a CuPd catalyst to improve the selectivity of CO2 electroreduction to C-2 products. Chin. J. Catal. 2021, 42, 1500–1508. [Google Scholar] [CrossRef]
  17. Zhang, X.G.; Zhao, Y.; Chen, S.; Xing, S.M.; Dong, J.C.; Li, J.F. Electrolyte effect for carbon dioxide reduction reaction on copper electrode interface: A DFT prediction. J. Chem. Phys. 2023, 158, 094704. [Google Scholar] [CrossRef]
  18. Zhai, L.; Cui, C.; Zhao, Y.; Zhu, X.; Han, J.; Wang, H.; Ge, Q. Titania-Modified Silver Electrocatalyst for Selective CO2 Reduction to CH3OH and CH4 from DFT Study. J. Phys. Chem. C 2017, 121, 16275–16282. [Google Scholar] [CrossRef]
  19. Sun, L.; Han, J.; Ge, Q.; Zhu, X.; Wang, H. Understanding the role of Cu+/Cu0 sites at Cu2O based catalysts in ethanol production from CO2 electroreduction -A DFT study. RSC Adv. 2022, 12, 19394–19401. [Google Scholar] [CrossRef]
  20. Masood, Z.; Ge, Q. Electrochemical reduction of CO2 at the earth-abundant transition metal-oxides/copper interfaces. Catal. Today 2023, 409, 53–62. [Google Scholar] [CrossRef]
  21. Varghese, J.J.; Mushrif, S.H. Origins of complex solvent effects on chemical reactivity and computational tools to investigate them: A review. React. Chem. Eng. 2019, 4, 165–206. [Google Scholar] [CrossRef]
  22. Du, Y.; An, W. Effects of Uniaxial Lattice Strain and Explicit Water Solvation on CO2 Electroreduction over a Cu Electrode: A Density Functional Theory Perspective. J. Phys. Chem. C 2021, 125, 9138–9149. [Google Scholar] [CrossRef]
  23. Sathishkumar, N.; Wu, S.; Chen, H. Mechanistic insights into chemical reduction of CO2 by reverse water-gas shift reaction on Ru(0001) surface: The water promotion effect. Appl. Surf. Sci. 2022, 581, 152354. [Google Scholar] [CrossRef]
  24. Wang, Y.X.; Zheng, M.; Wang, X.; Zhou, X. Electrocatalytic Reduction of CO2 to C-1 Compounds by Zn-Based Monatomic Alloys: A DFT Calculation. Catalysts 2022, 12, 1617. [Google Scholar] [CrossRef]
  25. Ludwig, T.; Gauthier, J.A.; Brown, K.S.; Ringe, S.; Norskov, J.K.; Chan, K. Solvent-Adsorbate Interactions and Adsorbate-Specific Solvent Structure in Carbon Dioxide Reduction on a Stepped Cu Surface. J. Phys. Chem. C 2019, 123, 5999–6009. [Google Scholar] [CrossRef] [Green Version]
  26. Garcia Ratés, M.; García Muelas, R.; López, N. Solvation Effects on Methanol Decomposition on Pd(111), Pt(111), and Ru(0001). J. Phys. Chem. C 2017, 121, 13803–13809. [Google Scholar] [CrossRef] [Green Version]
  27. Li, Y.; Liu, Z. Modeling the effect of an anion on the free energy surfaces along the reaction pathways of oxygen reduction on Pt(111). Chem. Phys. Lett. 2019, 736, 136813. [Google Scholar] [CrossRef]
  28. Briquet, L.G.V.; Sarwar, M.; Mugo, J.; Jones, G.; Calle-Vallejo, F. A New Type of Scaling Relations to Assess the Accuracy of Computational Predictions of Catalytic Activities Applied to the Oxygen Evolution Reaction. ChemCatChem 2017, 9, 1261–1268. [Google Scholar] [CrossRef]
  29. Sakong, S.; Groß, A. The Importance of the Electrochemical Environment in the Electro-Oxidation of Methanol on Pt(111). ACS Catal. 2016, 6, 5575–5586. [Google Scholar] [CrossRef]
  30. Rossmeisl, J.; Nørskov, J.K.; Taylor, C.D.; Janik, M.J.; Neurock, M. Calculated Phase Diagrams for the Electrochemical Oxidation and Reduction of Water over Pt(111). J. Phys. Chem. B 2006, 110, 21833–21839. [Google Scholar] [CrossRef]
  31. Filhol, J.S.; Neurock, M. Elucidation of the Electrochemical Activation of Water over Pd by First Principles. Angew. Chem. Int. Ed. 2006, 45, 402–406. [Google Scholar] [CrossRef]
  32. Bu, Y.; Cui, T.; Zhao, M.; Zheng, W.; Gao, W.; Jiang, Q. Evolution of Water Structures on Stepped Platinum Surfaces. J. Phys. Chem. C 2018, 122, 604–611. [Google Scholar] [CrossRef]
  33. Mu, R.; Zhao, Z.; Dohnálek, Z.; Gong, J. Structural motifs of water on metal oxide surfaces. Chem. Soc. Rev. 2017, 46, 1785–1806. [Google Scholar] [CrossRef]
  34. Chen, J.; Schusteritsch, G.; Pickard, C.J.; Salzmann, C.G.; Michaelides, A. Two Dimensional Ice from First Principles: Structures and Phase Transitions. Phys. Rev. Lett. 2016, 116, 025501. [Google Scholar] [CrossRef] [Green Version]
  35. Björneholm, O.; Hansen, M.H.; Hodgson, A.; Liu, L.M.; Limmer, D.T.; Michaelides, A.; Pedevilla, P.; Rossmeisl, J.; Shen, H.; Tocci, G.; et al. Water at Interfaces. Chem. Rev. 2016, 116, 7698–7726. [Google Scholar] [CrossRef]
  36. Carrasco, J.; Hodgson, A.; Michaelides, A. A molecular perspective of water at metal interfaces. Nat. Mater. 2012, 11, 667–674. [Google Scholar] [CrossRef] [Green Version]
  37. Kolb, M.J.; Wermink, J.; Calle Vallejo, F.; Juurlink, L.B.F.; Koper, M.T.M. Initial stages of water solvation of stepped platinum surfaces. Phys. Chem. Chem. Phys. 2016, 18, 3416–3422. [Google Scholar] [CrossRef] [Green Version]
  38. Farnesi Camellone, M.; Negreiros Ribeiro, F.; Szabova, L.; Tateyama, Y.; Fabris, S. Catalytic Proton Dynamics at the Water/Solid Interface of Ceria-Supported Pt Clusters. J. Am. Chem. Soc. 2016, 138, 11560–11567. [Google Scholar] [CrossRef]
  39. Heenen, H.H.; Gauthier, J.A.; Kristoffersen, H.H.; Ludwig, T.; Chan, K. Solvation at metal/water interfaces: An ab initio molecular dynamics benchmark of common computational approaches. J. Chem. Phys. 2020, 152, 144703. [Google Scholar] [CrossRef] [Green Version]
  40. Ringe, S.; Hörmann, N.G.; Oberhofer, H.; Reuter, K. Implicit Solvation Methods for Catalysis at Electrified Interfaces. Chem. Rev. 2022, 122, 10777–10820. [Google Scholar] [CrossRef]
  41. Bramley, G.A.; Nguyen, M.T.; Glezakou, V.A.; Rousseau, R.; Skylaris, C.K. Understanding Adsorption of Organics on Pt(111) in the Aqueous Phase: Insights from DFT Based Implicit Solvent and Statistical Thermodynamics Models. J. Chem. Theory Comput. 2022, 18, 1849–1861. [Google Scholar] [CrossRef]
  42. Iyemperumal, S.K.; Deskins, N.A. Evaluating Solvent Effects at the Aqueous/Pt(111) Interface. ChemPhysChem 2017, 18, 2171–2190. [Google Scholar] [CrossRef]
  43. Petrosyan, S.A.; Rigos, A.A.; Arias, T.A. Joint density-functional theory: Ab initio study of Cr2O3 surface chemistry in solution. J. Phys. Chem. B 2005, 109, 15436–15444. [Google Scholar] [CrossRef]
  44. Calle Vallejo, F.; de Morais, R.F.; Illas, F.; Loffreda, D.; Sautet, P. Affordable Estimation of Solvation Contributions to the Adsorption Energies of Oxygenates on Metal Nanoparticles. J. Phys. Chem. C 2019, 123, 5578–5582. [Google Scholar] [CrossRef] [Green Version]
  45. Zhao, C.X.; Bu, Y.F.; Gao, W.; Jiang, Q. CO2 Reduction Mechanism on the Pb(111) Surface: Effect of Solvent and Cations. J. Phys. Chem. C 2017, 121, 19767–19773. [Google Scholar] [CrossRef]
  46. Meng, Y.; Xu, Z.; Shen, Z.; Xia, Q.; Cao, Y.; Wang, Y.; Li, X. Understanding the water molecule effect in metal-free B-based electrocatalysts for electrochemical CO2 reduction. J. Mater. Chem. A 2022, 10, 6508–6522. [Google Scholar] [CrossRef]
  47. Valter, M.; Wickman, B.; Hellman, A. Solvent Effects for Methanol Electrooxidation on Gold. J. Phys. Chem. C 2021, 125, 1355–1360. [Google Scholar] [CrossRef]
  48. Cui, C.; Wang, H.; Zhu, X.; Han, J.; Ge, Q. A DFT study of CO2 electrochemical reduction on Pb(211) and Sn(112). Sci. China Chem. 2015, 58, 607–613. [Google Scholar] [CrossRef]
  49. Rossmeisl, J.; Greeley, J.; Karlberg, G.S. Electrocatalysis and Catalyst Screening from Density Functional Theory Calculations. In Fuel Cell Catalysis; John Wiley & Sons: Hoboken, NJ, USA, 2009; Chapter 3; pp. 57–92. [Google Scholar] [CrossRef]
  50. Peterson, A.A.; Abild-Pedersen, F.; Studt, F.; Rossmeisl, J.; Nørskov, J.K. How copper catalyzes the electroreduction of carbon dioxide into hydrocarbon fuels. Energy Environ. Sci. 2010, 3, 1311–1315. [Google Scholar] [CrossRef]
  51. Hansen, H.A.; Montoya, J.H.; Zhang, Y.-J.; Shi, C.; Peterson, A.A.; Nørskov, J.K. Electroreduction of Methanediol on Copper. Catal. Lett. 2013, 143, 631–635. [Google Scholar] [CrossRef]
  52. Bader, R.F.W. Atoms in Molecules: A Quantum Theory; Clarendon Press: London, UK, 1990. [Google Scholar]
  53. Henkelman, G.; Arnaldsson, A.; Jónsson, H. A fast and robust algorithm for Bader decomposition of charge density. Comput. Mater. Sci. 2006, 36, 354–360. [Google Scholar] [CrossRef]
  54. Zhao, X.; Wang, J.; Lian, L.; Zhang, G.; An, P.; Zeng, K.; He, H.; Yuan, T.; Huang, J.; Wang, L.; et al. Oxygen Vacancy-Reinforced Water-Assisted Proton Hopping for Enhanced Catalytic Hydrogenation. ACS Catal. 2023, 13, 2326–2334. [Google Scholar] [CrossRef]
  55. Zhao, Y.; Zhu, X.; Wang, H.; Han, J.; Mei, D.; Ge, Q. Aqueous Phase Aldol Condensation of Formaldehyde and Acetone on Anatase TiO2(101) Surface: A Theoretical Investigation. ChemCatChem 2020, 12, 1220–1229. [Google Scholar] [CrossRef]
  56. Tayyebi, E.; Hussain, J.; Skúlason, E. Why do RuO2 electrodes catalyze electrochemical CO2 reduction to methanol rather than methane or perhaps neither of those? Chem. Sci. 2020, 11, 9542–9553. [Google Scholar] [CrossRef]
  57. Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef] [PubMed]
  58. Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  59. Mathew, K.; Sundararaman, R.; Letchworth Weaver, K.; Arias, T.A.; Hennig, R.G. Implicit solvation model for density-functional study of nanocrystal surfaces and reaction pathways. J. Chem. Phys. 2014, 140, 084106. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  60. Mathew, K.; Kolluru, V.S.C.; Mula, S.; Steinmann, S.N.; Hennig, R.G. Implicit self-consistent electrolyte model in plane-wave density-functional theory. J. Chem. Phys. 2019, 151, 234101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  61. Li, X.Z.; Walker, B.; Michaelides, A. Quantum nature of the hydrogen bond. Proc. Natl. Acad. Sci. USA 2011, 108, 6369–6373. [Google Scholar] [CrossRef] [Green Version]
  62. Wang, Y.X.; Wang, G.C. A Systematic Theoretical Study of Water Gas Shift Reaction on Cu(111) and Cu(110): Potassium Effect. ACS Catal. 2019, 9, 2261–2274. [Google Scholar] [CrossRef]
  63. Kolb, M.J.; Farber, R.G.; Derouin, J.; Badan, C.; Calle-Vallejo, F.; Juurlink, L.B.F.; Killelea, D.R.; Koper, M.T.M. Double-Stranded Water on Stepped Platinum Surfaces. Phys. Rev. Lett. 2016, 116, 136101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  64. Psofogiannakis, G.; St-Amant, A.; Ternan, M. Methane oxidation mechanism on Pt(111): A cluster model DFT study. J. Phys. Chem. B 2006, 110, 24593–24605. [Google Scholar] [CrossRef] [PubMed]
Catalysts 13 01033 g001 550
Figure 1. The interaction energy between adsorbates and explicit water solvent as a function of the number of water molecules. Top figure shows the optimized structures and O-H or H-H bond distance formed with one water molecule. The Sn, C, H and O atoms are shown as blue, grey, white and red balls.
Figure 1. The interaction energy between adsorbates and explicit water solvent as a function of the number of water molecules. Top figure shows the optimized structures and O-H or H-H bond distance formed with one water molecule. The Sn, C, H and O atoms are shown as blue, grey, white and red balls.
Catalysts 13 01033 g001
Catalysts 13 01033 g002 550
Figure 2. The structures of HCOO* with (a) 3H2O, (b) 7H2O, (c) 8H2O and (d) 9H2O.
Figure 2. The structures of HCOO* with (a) 3H2O, (b) 7H2O, (c) 8H2O and (d) 9H2O.
Catalysts 13 01033 g002
Catalysts 13 01033 g003 550
Figure 3. The (a) tetramer, (b,f) pentamer and (c–e) hexamer rings formed on the surface with 4H2O, 5H2O, CHO* + OH with 3H2O and clean surface with 6H2O, 7H2O, and 8H2O.
Figure 3. The (a) tetramer, (b,f) pentamer and (c–e) hexamer rings formed on the surface with 4H2O, 5H2O, CHO* + OH with 3H2O and clean surface with 6H2O, 7H2O, and 8H2O.
Catalysts 13 01033 g003
Catalysts 13 01033 g004 550
Figure 4. Averaged explicit solvation energy per water (a) and solvent assistant reaction energies (b) for different intermediates as a function of the number of explicit water molecules (n starts from 1 for (a) and 0 for (b), and the linear regression equation for each intermediate starting from 4H2O are shown in (b)).
Figure 4. Averaged explicit solvation energy per water (a) and solvent assistant reaction energies (b) for different intermediates as a function of the number of explicit water molecules (n starts from 1 for (a) and 0 for (b), and the linear regression equation for each intermediate starting from 4H2O are shown in (b)).
Catalysts 13 01033 g004
Catalysts 13 01033 g005 550
Figure 5. The effect of implicit solvent on different intermediate with 1~12 explicit water molecules.
Figure 5. The effect of implicit solvent on different intermediate with 1~12 explicit water molecules.
Catalysts 13 01033 g005
Catalysts 13 01033 g006 550
Figure 6. Comparison of electrochemical hydrogenation of CO2 on Sn(112) with and without solvent effect. The red line shows the mechanism with no solvent stabilizations. The green line shows the mechanism including six explicit water molecules and implicit solvent. The pink stars and arrows represent the intermediates have relative stronger solvent effect. The blue triangles indicate the species less influenced by the solvent effect.
Figure 6. Comparison of electrochemical hydrogenation of CO2 on Sn(112) with and without solvent effect. The red line shows the mechanism with no solvent stabilizations. The green line shows the mechanism including six explicit water molecules and implicit solvent. The pink stars and arrows represent the intermediates have relative stronger solvent effect. The blue triangles indicate the species less influenced by the solvent effect.
Catalysts 13 01033 g006
Catalysts 13 01033 g007 550
Figure 7. Reference models to calculate the energies used in Equations (2)–(6). The models shown in the figure are the representative structures of clean surface (A), intermediate adsorbed on the surface (B) and intermediate adsorbed on the surface with a cluster of water molecules (C), the cluster of water molecules fixed in their positions optimized with the adsorbate but without the adsorbate on the surface (D), and the cluster of water molecules without adsorbate and surface (E). Isolated gas molecules—water, carbon dioxide, hydrogen—were also calculated (F). The energies of the reference models were calculated without implicit solvent. Sn: blue; C: gray; O: red; H: white.
Figure 7. Reference models to calculate the energies used in Equations (2)–(6). The models shown in the figure are the representative structures of clean surface (A), intermediate adsorbed on the surface (B) and intermediate adsorbed on the surface with a cluster of water molecules (C), the cluster of water molecules fixed in their positions optimized with the adsorbate but without the adsorbate on the surface (D), and the cluster of water molecules without adsorbate and surface (E). Isolated gas molecules—water, carbon dioxide, hydrogen—were also calculated (F). The energies of the reference models were calculated without implicit solvent. Sn: blue; C: gray; O: red; H: white.
Catalysts 13 01033 g007
Table
Table 1. Bader charges (|e|) of hydrogen and oxygen atoms in different intermediate. The labels shown in the figures specify the atoms.
Table 1. Bader charges (|e|) of hydrogen and oxygen atoms in different intermediate. The labels shown in the figures specify the atoms.
SpeciesCatalysts 13 01033 i001
H1−0.32+0.10+0.06+0.13
H2--+0.02+0.59
O1-−1.17−1.09−1.08
O2-−1.17−1.12−1.19
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Wang, J.; Cui, C.; Zhu, X.; Wang, H.; Ge, Q. Effect of Explicit Water Molecules on the Electrochemical Hydrogenation of CO2 on Sn(112). Catalysts 2023, 13, 1033. https://doi.org/10.3390/catal13071033

AMA Style

Wang J, Cui C, Zhu X, Wang H, Ge Q. Effect of Explicit Water Molecules on the Electrochemical Hydrogenation of CO2 on Sn(112). Catalysts. 2023; 13(7):1033. https://doi.org/10.3390/catal13071033

Chicago/Turabian Style

Wang, Jia, Chaonan Cui, Xinli Zhu, Hua Wang, and Qingfeng Ge. 2023. "Effect of Explicit Water Molecules on the Electrochemical Hydrogenation of CO2 on Sn(112)" Catalysts 13, no. 7: 1033. https://doi.org/10.3390/catal13071033

APA Style

Wang, J., Cui, C., Zhu, X., Wang, H., & Ge, Q. (2023). Effect of Explicit Water Molecules on the Electrochemical Hydrogenation of CO2 on Sn(112). Catalysts, 13(7), 1033. https://doi.org/10.3390/catal13071033

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop