Calculation of the Electrical Conductivity of Polymer Nanocomposites Assuming the Interphase Layer Surrounding Carbon Nanotubes
Abstract
:1. Introduction
2. Theoretical Analysis
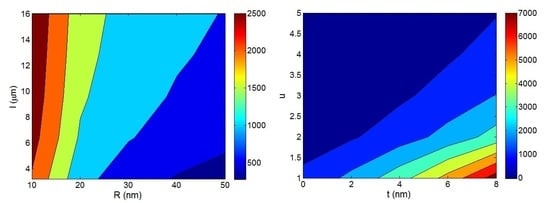
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zare, Y.; Rhee, K.Y. Prediction of loss factor (tan δ) for polymer nanocomposites as a function of yield tress, relaxation time and the width of transition region between Newtonian and power-law behaviors. J. Mech. Behav. Biomed. Mater. 2019, 96, 136–143. [Google Scholar] [CrossRef]
- Mittal, G.; Rhee, K.Y. Chemical vapor deposition-based grafting of CNTs onto basalt fabric and their reinforcement in epoxy-based composites. Compos. Sci. Technol. 2018, 165, 84–94. [Google Scholar] [CrossRef]
- Mittal, G.; Nešović, K.; Rhee, K.Y.; Mišković-Stanković, V. Investigation of corrosion behaviour of carbon nanotubes coated basalt fabric as a reinforcement material. Compos. Part B Eng. 2019, 178, 107493. [Google Scholar] [CrossRef]
- Tang, Z.; Jia, S.; Shi, X.; Li, B.; Zhou, C. Coaxial Printing of Silicone Elastomer Composite Fibers for Stretchable and Wearable Piezoresistive Sensors. Polymers 2019, 11, 666. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, S.; Wu, G.; Chen, X.; Zhang, X.; Yu, J.; Liu, M.; Zhang, Y.; Wang, P. Degradation Behavior In Vitro of Carbon Nanotubes (CNTs)/Poly (lactic acid)(PLA) Composite Suture. Polymers 2019, 11, 1015. [Google Scholar] [CrossRef] [Green Version]
- Otaegi, I.; Aranburu, N.; Iturrondobeitia, M.; Ibarretxe, J.; Guerrica-Echevarría, G. The Effect of the Preparation Method and the Dispersion and Aspect Ratio of CNTs on the Mechanical and Electrical Properties of Bio-Based Polyamide-4, 10/CNT Nanocomposites. Polymers 2019, 11, 2059. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.-F.; Wang, W.-N.; Lin, C.-H.; Lee, K.-J.; Hu, C.-C.; Lai, J.-Y. Facile Fabrication of Durable Superhydrophobic Films from Carbon Nanotube/Main-Chain Type Polybenzoxazine Composites. Polymers 2019, 11, 1183. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wu, G.; Gu, Y.; Hou, X.; Li, R.; Ke, H.; Xiao, X. Hybrid Nanocomposites of Cellulose/Carbon-Nanotubes/Polyurethane with Rapidly Water Sensitive Shape Memory Effect and Strain Sensing Performance. Polymers 2019, 11, 1586. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Cao, C.; Chen, X.; Ren, S.; Chen, Y.; Yu, D.; Chen, X. Orientation and Dispersion Evolution of Carbon Nanotubes in Ultra High Molecular Weight Polyethylene Composites under Extensional-Shear Coupled Flow: A Dissipative Particle Dynamics Study. Polymers 2019, 11, 154. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Keshtkar, M.; Mehdipour, N.; Eslami, H. Thermal Conductivity of Polyamide-6, 6/Carbon Nanotube Composites: Effects of Tube Diameter and Polymer Linkage between Tubes. Polymers 2019, 11, 1465. [Google Scholar] [CrossRef] [Green Version]
- Yue, Y.; Wang, X.; Wu, Q.; Han, J.; Jiang, J. Assembly of Polyacrylamide-Sodium Alginate-Based Organic-Inorganic Hydrogel with Mechanical and Adsorption Properties. Polymers 2019, 11, 1239. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, X.; Wang, H.; Liu, B. Carbon Nanotube-Based Organic Thermoelectric Materials for Energy Harvesting. Polymers 2018, 10, 1196. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zagho, M.; AlMaadeed, M.; Majeed, K. Thermal properties of TiO2NP/CNT/LDPE hybrid nanocomposite films. Polymers 2018, 10, 1270. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kalkhoran, A.H.Z.; Naghib, S.M.; Vahidi, O.; Rahmanian, M. Synthesis and characterization of graphene-grafted gelatin nanocomposite hydrogels as emerging drug delivery systems. Biomed. Phys. Eng. Express 2018, 4, 055017. [Google Scholar] [CrossRef]
- Naghib, S.M. Two dimensional functionalized methacrylated graphene oxide nanosheets as simple and inexpensive electrodes for biosensing applications. Micro Nano Lett. 2019, 14, 462–465. [Google Scholar] [CrossRef]
- Askari, E.; Naghib, S.M.; Seyfoori, A.; Maleki, A.; Rahmanian, M. Ultrasonic-Assisted Synthesis and in Vitro Biological Assessments of a Novel Herceptin-Stabilized Graphene Using Three Dimensional Cell Spheroid. Ultrason. Sonochem. 2019, 58, 104615. [Google Scholar] [CrossRef]
- Zare, Y.; Rhee, K.Y. Modeling of viscosity and complex modulus for poly (lactic acid)/poly (ethylene oxide)/carbon nanotubes nanocomposites assuming yield stress and network breaking time. Compos. Part B Eng. 2019, 156, 100–107. [Google Scholar] [CrossRef]
- Zare, Y.; Rhee, K.Y. Following the morphological and thermal properties of PLA/PEO blends containing carbon nanotubes (CNTs) during hydrolytic degradation. Compos. Part B Eng. 2019, 175, 107132. [Google Scholar] [CrossRef]
- Salahandish, R.; Ghaffarinejad, A.; Naghib, S.M.; Majidzadeh-A, K.; Sanati-Nezhad, A. A novel graphene-grafted gold nanoparticles composite for highly sensitive electrochemical biosensing. IEEE Sens. J. 2018, 18, 2513–2519. [Google Scholar] [CrossRef]
- Naghib, S.M.; Parnian, E.; Keshvari, H.; Omidinia, E.; Eshghan-Malek, M. Synthesis, characterization and electrochemical evaluation of polyvinylalchol/graphene oxide/silver nanocomposites for glucose biosensing application. Int. J. Electrochem. Sci. 2018, 13, 1013–1026. [Google Scholar] [CrossRef]
- Rostami, A.; Vahdati, M.; Nazockdast, H. Unraveling the localization behavior of MWCNTs in binary polymer blends using thermodynamics and viscoelastic approaches. Polym. Compos. 2018, 39, 2356–2367. [Google Scholar] [CrossRef]
- Rostami, A.; Eskandari, F.; Masoomi, M.; Nowrouzi, M. Evolution of Microstructure and Physical Properties of PMMA/MWCNTs Nanocomposites upon the Addition of Organoclay. J. OilGas Petrochem. Technol. 2019, 6, 28–38. [Google Scholar]
- Kim, S.; Zare, Y.; Garmabi, H.; Rhee, K.Y. Variations of tunneling properties in poly (lactic acid)(PLA)/poly (ethylene oxide)(PEO)/carbon nanotubes (CNT) nanocomposites during hydrolytic degradation. Sens. Actuators A Phys. 2018, 274, 28–36. [Google Scholar] [CrossRef]
- Zare, Y.; Park, S.P.; Rhee, K.Y. Analysis of complex viscosity and shear thinning behavior in poly (lactic acid)/poly (ethylene oxide)/carbon nanotubes biosensor based on Carreau–Yasuda model. Results Phys. 2019, 13, 102245. [Google Scholar] [CrossRef]
- Naghib, S.M. Fabrication of Nafion/Silver Nanoparticles/Reduced Graphene Nanosheets/Glucose Oxidase Nanobiocomposite for Electrochemical Glucose Biosensing. Anal. Bioanal. Electrochem. 2016, 8, 453–465. [Google Scholar]
- Zare, Y.; Rhee, K.Y.; Park, S.J. Simple model for hydrolytic degradation of poly (lactic acid)/poly (ethylene oxide)/carbon nanotubes nanobiosensor in neutral phosphate-buffered saline solution. J. Biomed. Mater. Res. Part. A 2019, 107, 2706–2717. [Google Scholar] [CrossRef]
- Mamaghani, K.R.; Naghib, S.M.; Zahedi, A.; Kalkhoran, A.H.Z.; Rahmanian, M. Fast synthesis of methacrylated graphene oxide: A graphene-functionalised nanostructure. Micro Nano Lett. 2018, 13, 195–197. [Google Scholar] [CrossRef]
- Martins, J.N.; Bassani, T.S.; Barra, G.M.; Oliveira, R.V. Electrical and rheological percolation in poly (vinylidene fluoride)/multi-walled carbon nanotube nanocomposites. Polym. Int. 2011, 60, 430–435. [Google Scholar] [CrossRef]
- Maiti, S.; Shrivastava, N.K.; Khatua, B. Reduction of percolation threshold through double percolation in melt-blended polycarbonate/acrylonitrile butadiene styrene/multiwall carbon nanotubes elastomer nanocomposites. Polym. Compos. 2013, 34, 570–579. [Google Scholar] [CrossRef]
- Clingerman, M.L.; King, J.A.; Schulz, K.H.; Meyers, J.D. Evaluation of electrical conductivity models for conductive polymer composites. J. Appl. Polym. Sci. 2002, 83, 1341–1356. [Google Scholar] [CrossRef]
- Zare, Y.; Rhee, K.Y. Evaluation of the Tensile Strength in Carbon Nanotube-Reinforced Nanocomposites Using the Expanded Takayanagi Model. JOM 2019, 71, 3980–3988. [Google Scholar] [CrossRef]
- Esbati, A.; Irani, S. Effect of functionalized process and CNTs aggregation on fracture mechanism and mechanical properties of polymer nanocomposite. Mech. Mater. 2018, 118, 106–119. [Google Scholar] [CrossRef]
- Combessis, A.; Bayon, L.; Flandin, L. Effect of filler auto-assembly on percolation transition in carbon nanotube/polymer composites. Appl. Phys. Lett. 2013, 102, 011907. [Google Scholar] [CrossRef]
- Chang, L.; Friedrich, K.; Ye, L.; Toro, P. Evaluation and visualization of the percolating networks in multi-wall carbon nanotube/epoxy composites. J. Mater. Sci. 2009, 44, 4003–4012. [Google Scholar] [CrossRef]
- Kara, S.; Arda, E.; Dolastir, F.; Pekcan, Ö. Electrical and optical percolations of polystyrene latex–multiwalled carbon nanotube composites. J. Colloid Interface Sci. 2010, 344, 395–401. [Google Scholar] [CrossRef]
- Ma, H.; Gao, X.-L. A three-dimensional Monte Carlo model for electrically conductive polymer matrix composites filled with curved fibers. Polymer 2008, 49, 4230–4238. [Google Scholar] [CrossRef]
- Zare, Y.; Rhim, S.; Garmabi, H.; Rhee, K.Y. A simple model for constant storage modulus of poly (lactic acid)/poly (ethylene oxide)/carbon nanotubes nanocomposites at low frequencies assuming the properties of interphase regions and networks. J. Mech. Behav. Biomed. Mater. 2018, 80, 164–170. [Google Scholar] [CrossRef]
- Zare, Y.; Rhee, K.Y.; Park, S.-J. A modeling methodology to investigate the effect of interfacial adhesion on the yield strength of MMT reinforced nanocomposites. J. Ind. Eng. Chem. 2019, 69, 331–337. [Google Scholar] [CrossRef]
- Zare, Y.; Rhee, K.Y. Tensile strength prediction of carbon nanotube reinforced composites by expansion of cross-orthogonal skeleton structure. Compos. Part B Eng. 2019, 161, 601–607. [Google Scholar] [CrossRef]
- Zare, Y.; Rhee, K.Y. Effects of interphase regions and filler networks on the viscosity of PLA/PEO/carbon nanotubes biosensor. Polym. Compos. 2019, 40, 4135–4141. [Google Scholar] [CrossRef]
- Mortazavi, B.; Bardon, J.; Ahzi, S. Interphase effect on the elastic and thermal conductivity response of polymer nanocomposite materials: 3D finite element study. Comput. Mater. Sci. 2013, 69, 100–106. [Google Scholar] [CrossRef]
- Montazeri, A.; Naghdabadi, R. Investigation of the interphase effects on the mechanical behavior of carbon nanotube polymer composites by multiscale modeling. J. Appl. Polym. Sci. 2010, 117, 361–367. [Google Scholar] [CrossRef]
- Celzard, A.; McRae, E.; Deleuze, C.; Dufort, M.; Furdin, G.; Marêché, J. Critical concentration in percolating systems containing a high-aspect-ratio filler. Phys. Rev. B 1996, 53, 6209. [Google Scholar] [CrossRef] [PubMed]
- Qiao, R.; Brinson, L.C. Simulation of interphase percolation and gradients in polymer nanocomposites. Compos. Sci. Technol. 2009, 69, 491–499. [Google Scholar] [CrossRef]
- Lu, P.; Leong, Y.; Pallathadka, P.; He, C. Effective moduli of nanoparticle reinforced composites considering interphase effect by extended double-inclusion model–Theory and explicit expressions. Int. J. Eng. Sci. 2013, 73, 33–55. [Google Scholar] [CrossRef]
- Shin, H.; Yang, S.; Choi, J.; Chang, S.; Cho, M. Effect of interphase percolation on mechanical behavior of nanoparticle-reinforced polymer nanocomposite with filler agglomeration: A multiscale approach. Chem. Phys. Lett. 2015, 635, 80–85. [Google Scholar] [CrossRef]
- Razavi, R.; Zare, Y.; Rhee, K.Y. The roles of interphase and filler dimensions in the properties of tunneling spaces between CNT in polymer nanocomposites. Polym. Compos. 2019, 40, 801–810. [Google Scholar] [CrossRef]
- Baxter, S.C.; Robinson, C.T. Pseudo-percolation: Critical volume fractions and mechanical percolation in polymer nanocomposites. Compos. Sci. Technol. 2011, 71, 1273–1279. [Google Scholar] [CrossRef]
- Du, F.; Scogna, R.C.; Zhou, W.; Brand, S.; Fischer, J.E.; Winey, K.I. Nanotube networks in polymer nanocomposites: Rheology and electrical conductivity. Macromolecules 2004, 37, 9048–9055. [Google Scholar] [CrossRef]
- Takeda, T.; Shindo, Y.; Kuronuma, Y.; Narita, F. Modeling and characterization of the electrical conductivity of carbon nanotube-based polymer composites. Polymer 2011, 52, 3852–3856. [Google Scholar] [CrossRef]
- Deng, F.; Zheng, Q.-S. An analytical model of effective electrical conductivity of carbon nanotube composites. Appl. Phys. Lett. 2008, 92, 071902. [Google Scholar] [CrossRef]
- Zare, Y.; Rhee, K.Y.; Park, S.-J. A developed equation for electrical conductivity of polymer carbon nanotubes (CNT) nanocomposites based on Halpin-Tsai model. Results Phys. 2019, 14, 102406. [Google Scholar] [CrossRef]
- Zare, Y.; Rhee, K.Y.; Park, S.-J. Modeling the roles of carbon nanotubes and interphase dimensions in the conductivity of nanocomposites. Results Phys. 2019, 15, 102562. [Google Scholar] [CrossRef]
- Zare, Y.; Rhee, K.Y. A multistep methodology for effective conductivity of carbon nanotubes reinforced nanocomposites. J. Alloy. Compd. 2019, 793, 1–8. [Google Scholar] [CrossRef]
- Kim, Y.J.; Shin, T.S.; Do Choi, H.; Kwon, J.H.; Chung, Y.-C.; Yoon, H.G. Electrical conductivity of chemically modified multiwalled carbon nanotube/epoxy composites. Carbon 2005, 43, 23–30. [Google Scholar] [CrossRef]
- Zare, Y.; Rhee, K.Y. The effective conductivity of polymer carbon nanotubes (CNT) nanocomposites. J. Phys. Chem. Solids 2019, 131, 15–21. [Google Scholar] [CrossRef]
- Zare, Y.; Rhee, K.Y. A Simulation Work for the Influences of Aggregation/Agglomeration of Clay Layers on the Tensile Properties of Nanocomposites. JOM 2019, 71, 3989–3995. [Google Scholar] [CrossRef]
- Lisunova, M.; Mamunya, Y.P.; Lebovka, N.; Melezhyk, A. Percolation behaviour of ultrahigh molecular weight polyethylene/multi-walled carbon nanotubes composites. Eur. Polym. J. 2007, 43, 949–958. [Google Scholar] [CrossRef]
- Sevostianov, I.; Kachanov, M. Effect of interphase layers on the overall elastic and conductive properties of matrix composites. Applications to nanosize inclusion. Int. J. Solids Struct. 2007, 44, 1304–1315. [Google Scholar] [CrossRef] [Green Version]
- Joshi, P.; Upadhyay, S. Effect of interphase on elastic behavior of multiwalled carbon nanotube reinforced composite. Comput. Mater. Sci. 2014, 87, 267–273. [Google Scholar] [CrossRef]
- Zare, Y.; Rhee, K.Y. A multistep methodology for calculation of the tensile modulus in polymer/carbon nanotube nanocomposites above the percolation threshold based on the modified rule of mixtures. RSC Adv. 2018, 8, 30986–30993. [Google Scholar] [CrossRef] [Green Version]
- Arenhart, R.; Barra, G.; Fernandes, C. Simulation of percolation threshold and electrical conductivity in composites filled with conductive particles: Effect of polydisperse particle size distribution. Polym. Compos. 2016, 37, 61–69. [Google Scholar] [CrossRef]
- Berhan, L.; Sastry, A. Modeling percolation in high-aspect-ratio fiber systems. I. Soft-core versus hard-core models. Phys. Rev. E 2007, 75, 041120. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Celzard, A.; Furdin, G.; Mareche, J.; McRae, E. Non-linear current-voltage characteristics in anisotropic epoxy resin-graphite flake composites. J. Mater. Sci. 1997, 32, 1849–1853. [Google Scholar] [CrossRef]
- Paredes-Madrid, L.; Palacio, C.; Matute, A.; Parra Vargas, C. Underlying physics of conductive polymer composites and force sensing resistors (FSRs) under static loading conditions. Sensors 2017, 17, 2108. [Google Scholar] [CrossRef] [Green Version]
- Koke, S.; Grebing, C.; Frei, H.; Anderson, A.; Assion, A.; Steinmeyer, G. Direct frequency comb synthesis with arbitrary offset and shot-noise-limited phase noise. Nat. Photonics 2010, 4, 462. [Google Scholar] [CrossRef]
- Chen, S.; Sarafbidabad, M.; Zare, Y.; Rhee, K.Y. Estimation of the tensile modulus of polymer carbon nanotube nanocomposites containing filler networks and interphase regions by development of the Kolarik model. RSC Adv. 2018, 8, 23825–23834. [Google Scholar] [CrossRef] [Green Version]






© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zare, Y.; Rhee, K.Y. Calculation of the Electrical Conductivity of Polymer Nanocomposites Assuming the Interphase Layer Surrounding Carbon Nanotubes. Polymers 2020, 12, 404. https://doi.org/10.3390/polym12020404
Zare Y, Rhee KY. Calculation of the Electrical Conductivity of Polymer Nanocomposites Assuming the Interphase Layer Surrounding Carbon Nanotubes. Polymers. 2020; 12(2):404. https://doi.org/10.3390/polym12020404
Chicago/Turabian StyleZare, Yasser, and Kyong Yop Rhee. 2020. "Calculation of the Electrical Conductivity of Polymer Nanocomposites Assuming the Interphase Layer Surrounding Carbon Nanotubes" Polymers 12, no. 2: 404. https://doi.org/10.3390/polym12020404
APA StyleZare, Y., & Rhee, K. Y. (2020). Calculation of the Electrical Conductivity of Polymer Nanocomposites Assuming the Interphase Layer Surrounding Carbon Nanotubes. Polymers, 12(2), 404. https://doi.org/10.3390/polym12020404