Analysis of the Connecting Effectiveness of the Interphase Zone on the Tensile Properties of Carbon Nanotubes (CNT) Reinforced Nanocomposite
Abstract
:1. Introduction
2. Equations and Developed Models
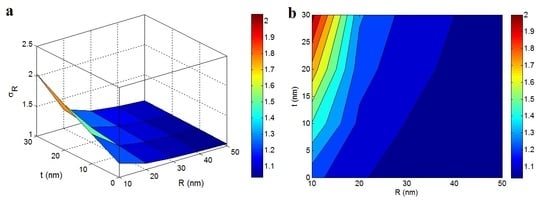
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zare, Y.; Rhee, K.Y. Prediction of loss factor (tan δ) for polymer nanocomposites as a function of yield tress, relaxation time and the width of transition region between Newtonian and power-law behaviors. J. Mech. Behav. Biomed. Mater. 2019, 96, 136–143. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Wu, G.; Chen, X.; Zhang, X.; Yu, J.; Liu, M.; Zhang, Y.; Wang, P. Degradation Behavior In Vitro of Carbon Nanotubes (CNTs)/Poly (lactic acid)(PLA) Composite Suture. Polymers 2019, 11, 1015. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Otaegi, I.; Aranburu, N.; Iturrondobeitia, M.; Ibarretxe, J.; Guerrica-Echevarría, G. The Effect of the Preparation Method and the Dispersion and Aspect Ratio of CNTs on the Mechanical and Electrical Properties of Bio-Based Polyamide-4, 10/CNT Nanocomposites. Polymers 2019, 11, 2059. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zagho, M.; AlMaadeed, M.; Majeed, K. Thermal properties of TiO2NP/CNT/LDPE hybrid nanocomposite films. Polymers 2018, 10, 1270. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Wang, H.; Liu, B. Carbon Nanotube-Based Organic Thermoelectric Materials for Energy Harvesting. Polymers 2018, 10, 1196. [Google Scholar] [CrossRef] [Green Version]
- Eltayeb, N.E.; Khan, A. Design and Preparation of a New and Novel Nanocomposite with CNTs and Its Sensor Applications. J. Mater. Res. Technol. 2019, 8, 2238–2246. [Google Scholar] [CrossRef]
- Rao, Y.A.; Ramji, K.; Rao, P.S.; Srikanth, I. Effect of A-MWCNTs and ETBN toughener on impact, compression and damping properties of carbon fiber reinforced epoxy composites. J. Mater. Res. Technol. 2019, 8, 896–903. [Google Scholar] [CrossRef]
- Wang, C.-F.; Wang, W.-N.; Lin, C.-H.; Lee, K.-J.; Hu, C.-C.; Lai, J.-Y. Facile Fabrication of Durable Superhydrophobic Films from Carbon Nanotube/Main-Chain Type Polybenzoxazine Composites. Polymers 2019, 11, 1183. [Google Scholar] [CrossRef] [Green Version]
- Wu, G.; Gu, Y.; Hou, X.; Li, R.; Ke, H.; Xiao, X. Hybrid Nanocomposites of Cellulose/Carbon-Nanotubes/Polyurethane with Rapidly Water Sensitive Shape Memory Effect and Strain Sensing Performance. Polymers 2019, 11, 1586. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Cao, C.; Chen, X.; Ren, S.; Chen, Y.; Yu, D.; Chen, X. Orientation and Dispersion Evolution of Carbon Nanotubes in Ultra High Molecular Weight Polyethylene Composites under Extensional-Shear Coupled Flow: A Dissipative Particle Dynamics Study. Polymers 2019, 11, 154. [Google Scholar] [CrossRef] [Green Version]
- Keshtkar, M.; Mehdipour, N.; Eslami, H. Thermal Conductivity of Polyamide-6, 6/Carbon Nanotube Composites: Effects of Tube Diameter and Polymer Linkage between Tubes. Polymers 2019, 11, 1465. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zare, Y.; Rhee, K.Y. Following the morphological and thermal properties of PLA/PEO blends containing carbon nanotubes (CNTs) during hydrolytic degradation. Compos. Part B Eng. 2019, 175, 107132. [Google Scholar] [CrossRef]
- Zare, Y.; Rhee, K.Y. Effects of interphase regions and filler networks on the viscosity of PLA/PEO/carbon nanotubes biosensor. Polym. Compos. 2019, 40, 4135–4141. [Google Scholar] [CrossRef]
- Zare, Y.; Rhee, K.Y.; Park, S.J. Simple model for hydrolytic degradation of poly (lactic acid)/poly (ethylene oxide)/carbon nanotubes nanobiosensor in neutral phosphate-buffered saline solution. J. Biomed. Mater. Res. Part A 2019, 107, 2706–2717. [Google Scholar] [CrossRef] [PubMed]
- Rostami, A.; Moosavi, M.I. High-performance thermoplastic polyurethane nanocomposites induced by hybrid application of functionalized graphene and carbon nanotubes. J. Appl. Polym. Sci. 2019, 137, 48520. [Google Scholar] [CrossRef]
- Rostami, A.; Vahdati, M.; Alimoradi, Y.; Karimi, M.; Nazockdast, H. Rheology provides insight into flow induced nano-structural breakdown and its recovery effect on crystallization of single and hybrid carbon nanofiller filled poly (lactic acid). Polymer 2018, 134, 143–154. [Google Scholar] [CrossRef]
- Rostami, A.; Vahdati, M.; Nazockdast, H. Unraveling the localization behavior of MWCNTs in binary polymer blends using thermodynamics and viscoelastic approaches. Polym. Compos. 2018, 39, 2356–2367. [Google Scholar] [CrossRef]
- Hassanzadeh-Aghdam, M.K.; Mahmoodi, M.J.; Ansari, R. Creep performance of CNT polymer nanocomposites-An emphasis on viscoelastic interphase and CNT agglomeration. Compos. Part B Eng. 2019, 168, 274–281. [Google Scholar] [CrossRef]
- Hassanzadeh-Aghdam, M.; Ansari, R.; Mahmoodi, M.; Darvizeh, A. Effect of nanoparticle aggregation on the creep behavior of polymer nanocomposites. Compos. Sci. Technol. 2018, 162, 93–100. [Google Scholar] [CrossRef]
- Zare, Y.; Rhee, K.Y. A Simulation Work for the Influences of Aggregation/Agglomeration of Clay Layers on the Tensile Properties of Nanocomposites. JOM 2019, 71, 3989–3995. [Google Scholar] [CrossRef]
- Abdolmaleki, A.; Mallakpour, S.; Borandeh, S. Amino acid-functionalized multi-walled carbon nanotubes for improving compatibility with chiral poly (amide-ester-imide) containing l-phenylalanine and l-tyrosine linkages. Appl. Surf. Sci. 2013, 287, 117–123. [Google Scholar] [CrossRef]
- Orgilés-Calpena, E.; Arán-Aís, F.; Torró-Palau, A.M.; Orgilés-Barceló, C. Chemical functionalization and dispersion of carbon nanofibers in waterborne polyurethane adhesives. J. Adhes. 2013, 89, 174–191. [Google Scholar]
- Zare, Y.; Rhee, K.Y. Calculation of the Electrical Conductivity of Polymer Nanocomposites Assuming the Interphase Layer Surrounding Carbon Nanotubes. Polymers 2020, 12, 404. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zare, Y.; Rhee, K.Y.; Park, S.-J. A developed equation for electrical conductivity of polymer carbon nanotubes (CNT) nanocomposites based on Halpin-Tsai model. Results Phys. 2019, 14, 102406. [Google Scholar] [CrossRef]
- Zare, Y.; Rhee, K.Y. The effective conductivity of polymer carbon nanotubes (CNT) nanocomposites. J. Phys. Chem. Solids 2019, 131, 15–21. [Google Scholar] [CrossRef]
- Zare, Y.; Garmabi, H.; Rhee, K.Y. Prediction of complex modulus in phase-separated poly (lactic acid)/poly (ethylene oxide)/carbon nanotubes nanocomposites. Polym. Test. 2018, 66, 189–194. [Google Scholar] [CrossRef]
- Zare, Y.; Rhee, K.Y. A multistep methodology for calculation of the tensile modulus in polymer/carbon nanotube nanocomposites above the percolation threshold based on the modified rule of mixtures. RSC Adv. 2018, 8, 30986–30993. [Google Scholar] [CrossRef] [Green Version]
- Zare, Y.; Rhee, K.Y. Tensile modulus prediction of carbon nanotubes-reinforced nanocomposites by a combined model for dispersion and networking of nanoparticles. J. Mater. Res. Technol. 2020, 9, 22–32. [Google Scholar] [CrossRef]
- Favier, V.; Chanzy, H.; Cavaille, J. Polymer nanocomposites reinforced by cellulose whiskers. Macromolecules 1995, 28, 6365–6367. [Google Scholar] [CrossRef]
- Zare, Y.; Rhee, K.Y. Study on the Effects of the Interphase Region on the Network Properties in Polymer Carbon Nanotube Nanocomposites. Polymers 2020, 12, 182. [Google Scholar] [CrossRef] [Green Version]
- Zare, Y.; Rhee, K.Y.; Park, S.-J. Modeling the roles of carbon nanotubes and interphase dimensions in the conductivity of nanocomposites. Results Phys. 2019, 15, 102562. [Google Scholar] [CrossRef]
- Sisakht Mohsen, R.; Saied, N.K.; Ali, Z.; Hosein, E.M.; Hasan, P. Theoretical and experimental determination of tensile properties of nanosized and micron-sized CaCO3/PA66 composites. Polym. Compos. 2009, 30, 274–280. [Google Scholar] [CrossRef]
- Fornes, T.; Paul, D. Modeling properties of nylon 6/clay nanocomposites using composite theories. Polymer 2003, 44, 4993–5013. [Google Scholar] [CrossRef]
- Peng, W.; Rhim, S.; Zare, Y.; Rhee, K.Y. Effect of “Z” factor for strength of interphase layers on the tensile strength of polymer nanocomposites. Polym. Compos. 2019, 40, 1117–1222. [Google Scholar] [CrossRef]
- Chen, S.; Sarafbidabad, M.; Zare, Y.; Rhee, K.Y. Estimation of the tensile modulus of polymer carbon nanotube nanocomposites containing filler networks and interphase regions by development of the Kolarik model. RSC Adv. 2018, 8, 23825–23834. [Google Scholar] [CrossRef] [Green Version]
- Zare, Y.; Rhee, K.Y. Tensile modulus of polymer/CNT nanocomposites containing networked and dispersed nanoparticles. AIChE J. 2018, 64, 220–225. [Google Scholar] [CrossRef]
- Baxter, S.C.; Robinson, C.T. Pseudo-percolation: Critical volume fractions and mechanical percolation in polymer nanocomposites. Compos. Sci. Technol. 2011, 71, 1273–1279. [Google Scholar] [CrossRef]
- Celzard, A.; McRae, E.; Deleuze, C.; Dufort, M.; Furdin, G.; Marêché, J. Critical concentration in percolating systems containing a high-aspect-ratio filler. Phys. Rev. B 1996, 53, 6209. [Google Scholar] [CrossRef]
- Zare, Y.; Rhee, K.Y. A multistep methodology for effective conductivity of carbon nanotubes reinforced nanocomposites. J. Alloys Compd. 2019, 793, 1–8. [Google Scholar] [CrossRef]
- Loos, M.; Manas-Zloczower, I. Micromechanical models for carbon nanotube and cellulose nanowhisker reinforced composites. Polym. Eng. Sci. 2013, 53, 882–887. [Google Scholar] [CrossRef]
- Chatterjee, A.P. A model for the elastic moduli of three-dimensional fiber networks and nanocomposites. J. Appl. Phys. 2006, 100, 054302. [Google Scholar] [CrossRef]
- Ouali, N.; Cavaillé, J.; Perez, J. Elastic, viscoelastic and plastic behavior of multiphase polymer blends. Plast. Rubber Compos. Process. Appl. (UK) 1991, 16, 55–60. [Google Scholar]
- Pukanszky, B. Influence of interface interaction on the ultimate tensile properties of polymer composites. Composites 1990, 21, 255–262. [Google Scholar] [CrossRef]
- Lazzeri, A.; Phuong, V.T. Dependence of the Pukánszky’s interaction parameter B on the interface shear strength (IFSS) of nanofiller-and short fiber-reinforced polymer composites. Compos. Sci. Technol. 2014, 93, 106–113. [Google Scholar] [CrossRef]
- Szazdi, L.; Pozsgay, A.; Pukanszky, B. Factors and processes influencing the reinforcing effect of layered silicates in polymer nanocomposites. Eur. Polym. J. 2007, 43, 345–359. [Google Scholar] [CrossRef]
- Callister, W.D.; Rethwisch, D.G. Materials Science and Engineering: An Introduction; Wiley: New York, NY, USA, 2007. [Google Scholar]
- Durmus, A.; Kaşgöz, A.; Macosko, C.W. Mechanical Properties of Linear Low-density Polyethylene (LLDPE)/clay Nanocomposites: Estimation of Aspect Ratio and İnterfacial Strength by Composite Models. J. Macromol. Sci. Part B Phys. 2008, 47, 608–619. [Google Scholar] [CrossRef]
- Zare, Y.; Daraei, A.; Vatani, M.; Aghasafari, P. An analysis of interfacial adhesion in nanocomposites from recycled polymers. Comput. Mater. Sci. 2014, 81, 612–616. [Google Scholar] [CrossRef]
- Crosby, A.J.; Lee, J.Y. Polymer nanocomposites: The “nano” effect on mechanical properties. Polym. Rev. 2007, 47, 217–229. [Google Scholar] [CrossRef]
- Li, D.; Kaner, R.B. How nucleation affects the aggregation of nanoparticles. J. Mater. Chem. 2007, 17, 2279–2282. [Google Scholar] [CrossRef]
- Zhou, Z.; Sarafbidabad, M.; Zare, Y.; Rhee, K.Y. Prediction of storage modulus in solid-like poly (lactic acid)/poly (ethylene oxide)/carbon nanotubes nanocomposites assuming the contributions of nanoparticles and interphase regions in the networks. J. Mech. Behav. Biomed. Mater. 2018, 86, 368–374. [Google Scholar] [CrossRef]
- Zare, Y.; Rhim, S.; Garmabi, H.; Rhee, K.Y. A simple model for constant storage modulus of poly (lactic acid)/poly (ethylene oxide)/carbon nanotubes nanocomposites at low frequencies assuming the properties of interphase regions and networks. J. Mech. Behav. Biomed. Mater. 2018, 80, 164–170. [Google Scholar] [CrossRef] [PubMed]
- Frankland, S.; Caglar, A.; Brenner, D.; Griebel, M. Molecular simulation of the influence of chemical cross-links on the shear strength of carbon nanotube−polymer interfaces. J. Phys. Chem. B 2002, 106, 3046–3048. [Google Scholar] [CrossRef]
- Isitman, N.A.; Aykol, M.; Kaynak, C. Nanoclay assisted strengthening of the fiber/matrix interface in functionally filled polyamide 6 composites. Compos. Struct. 2010, 92, 2181–2186. [Google Scholar] [CrossRef]
- Jamalzadeh, N.; Heidary, S.; Zare, Y.; Rhee, K.Y. A multistep methodology based on developed Takayanagi, Paul and Ouali models for tensile modulus of polymer/carbon nanotubes nanocomposites above percolation threshold assuming the contribution of interphase regions. Polym. Test. 2018, 69, 1–8. [Google Scholar] [CrossRef]
- Zou, W.; Du, Z.-J.; Liu, Y.-X.; Yang, X.; Li, H.-Q.; Zhang, C. Functionalization of MWNTs using polyacryloyl chloride and the properties of CNT–epoxy matrix nanocomposites. Compos. Sci. Technol. 2008, 68, 3259–3264. [Google Scholar] [CrossRef]








© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zare, Y.; Rhee, K.Y. Analysis of the Connecting Effectiveness of the Interphase Zone on the Tensile Properties of Carbon Nanotubes (CNT) Reinforced Nanocomposite. Polymers 2020, 12, 896. https://doi.org/10.3390/polym12040896
Zare Y, Rhee KY. Analysis of the Connecting Effectiveness of the Interphase Zone on the Tensile Properties of Carbon Nanotubes (CNT) Reinforced Nanocomposite. Polymers. 2020; 12(4):896. https://doi.org/10.3390/polym12040896
Chicago/Turabian StyleZare, Yasser, and Kyong Yop Rhee. 2020. "Analysis of the Connecting Effectiveness of the Interphase Zone on the Tensile Properties of Carbon Nanotubes (CNT) Reinforced Nanocomposite" Polymers 12, no. 4: 896. https://doi.org/10.3390/polym12040896
APA StyleZare, Y., & Rhee, K. Y. (2020). Analysis of the Connecting Effectiveness of the Interphase Zone on the Tensile Properties of Carbon Nanotubes (CNT) Reinforced Nanocomposite. Polymers, 12(4), 896. https://doi.org/10.3390/polym12040896