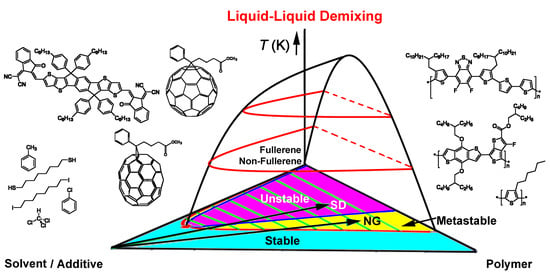
Phase Diagrams of Ternary π-Conjugated Polymer Solutions for Organic Photovoltaics
Abstract
:1. Introduction
2. Experimental Methods
3. Theoretical Methods
4. Results and Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Flory, P.J. Thermodynamics of High Polymer Solutions. J. Chem. Phys. 1942, 10, 51–61. [Google Scholar] [CrossRef]
- Huggins, M.L. Some Properties of Solutions of Long-chain Compounds. J. Phys. Chem. 1942, 46, 151–158. [Google Scholar] [CrossRef]
- Flory, P.J. Principles of Polymer Chemistry; Cornell University Press: Ithaca, NY, USA, 1953. [Google Scholar]
- Scott, R.A. The Thermodynamics of High Polymer Solutions. V. Phase Equilibria in the Ternary System: Polymer 1—Polymer 2—Solvent. J. Chem. Phys. 1949, 17, 279–284. [Google Scholar] [CrossRef]
- Tompa, H. Phase relationships in polymer solutions. Trans. Faraday Soc. 1949, 45, 1142–1152. [Google Scholar] [CrossRef]
- Tompa, H. Polymer Solutions; Academic Press: Cambridge, MA, USA, 1956. [Google Scholar]
- Loeb, S.; Sourirajan, S. Sea Water Demineralization by Means of an Osmotic Membrane. Adv. Chem. Ser. 1963, 38, 117–132. [Google Scholar] [CrossRef]
- Wienk, I.M.; Boom, R.M.; Beerlage, M.A.M.; Bulte, A.M.W.; Smolders, C.A.; Strathmann, H. Recent advances in the formation of phase inversion membranes made from amorphous or semi-crystalline polymers. J. Membr. Sci. 1996, 113, 361–371. [Google Scholar] [CrossRef] [Green Version]
- Guillen, G.R.; Pan, Y.; Li, M.; Hoek, M.V. Preparation and Characterization of Membranes Formed by Nonsolvent Induced Phase Separation: A Review. Ind. Eng. Chem. Res. 2011, 50, 3798–3817. [Google Scholar] [CrossRef]
- Altena, F.W.; Smolders, C.A. Calculation of liquid-liquid phase separation in a ternary system of a polymer in a mixture of a solvent and a nonsolvent. Macromolecules 1982, 15, 1491–1497. [Google Scholar] [CrossRef] [Green Version]
- Yilmaz, L.; McHugh, A.J. Analysis of nonsolvent–solvent–polymer phase diagrams and their relevance to membrane formation modeling. J. Appl. Polym. Sci. 1986, 31, 997–1018. [Google Scholar] [CrossRef]
- Qian, C.; Mumby, S.J.; Eichinger, B.E. Phase diagrams of binary polymer solutions and blends. Macromolecules 1991, 24, 1655–1661. [Google Scholar] [CrossRef]
- Hu, Y.; Ying, X.; Wu, D.T.; Prausnitz, J.M. Continuous thermodynamics for polydisperse polymer solutions. Fluid Phase Equilibria 1995, 104, 229–252. [Google Scholar] [CrossRef]
- Flory, P.J. Fifteenth Spiers Memorial Lecture. Thermodynamics of polymer solutions. Discuss. Faraday Soc. 1970, 49, 7–29. [Google Scholar] [CrossRef]
- Hsu, C.C.; Prausnitz, J.M. Thermodynamics of Polymer Compatibility in Ternary Systems. Macromolecules 1974, 7, 320–324. [Google Scholar] [CrossRef]
- Bates, F.S. Polymer-Polymer Phase Behavior. Science 1991, 251, 898–905. [Google Scholar] [CrossRef] [Green Version]
- Hellebust, S.; Nilsson, S.; Blokhus, A.M. Phase Behavior of Anionic Polyelectrolyte Mixtures in Aqueous Solution. Effects of Molecular Weights, Polymer Charge Density, and Ionic Strength of Solution. Macromolecules 2003, 36, 5372–5382. [Google Scholar] [CrossRef]
- Kim, J.Y. Order–Disorder Phase Equilibria of Regioregular Poly(3-hexylthiophene-2,5-diyl) Solution. Macromolecules 2018, 51, 9026–9034. [Google Scholar] [CrossRef]
- Kim, J.Y. Phase Diagrams of Binary Low Bandgap Conjugated Polymer Solutions and Blends. Macromolecules 2019, 52, 4317–4328. [Google Scholar] [CrossRef]
- Shirakawa, H.; Louis, E.J.; MacDiarmid, A.G.; Chiang, C.K.; Heeger, A.J. Synthesis of electrically conducting organic polymers: Halogen derivatives of polyacetylene, (CH) x. J. Chem. Soc. Chem. Commun. 1977, 578–580. [Google Scholar] [CrossRef]
- Chiang, C.K.; Fincher, C.R., Jr.; Park, Y.W.; Heeger, A.J.; Shirakawa, H.; Louis, E.J.; Gau, S.C.; MacDiarmid, A.G. Electrical Conductivity in Doped Polyacetylene. Phys. Rev. Lett. 1977, 39, 1098–1101. [Google Scholar] [CrossRef]
- Heeger, A.J. Semiconducting and Metallic Polymers: The Fourth Generation of Polymeric Materials (Nobel Lecture). Angew. Chem. Int. Ed. 2001, 40, 2591–2611. [Google Scholar] [CrossRef]
- Sariciftci, N.S.; Smilowitz, L.; Heeger, A.J.; Wudl, F. Photoinduced Electron Transfer from a Conducting Polymer to Buckminsterfullerene. Science 1992, 258, 1474–1476. [Google Scholar] [CrossRef] [PubMed]
- Halls, J.J.M.; Walsh, C.A.; Greenham, N.C.; Marseglia, E.A.; Friend, R.H.; Moratti, S.C.; Holmes, A.B. Efficient photodiodes from interpenetrating polymer networks. Nature 1995, 376, 498–500. [Google Scholar] [CrossRef]
- Yu, G.; Gao, J.; Hummelen, J.C.; Wudl, F.; Heeger, A.J. Polymer Photovoltaic Cells: Enhanced Efficiencies via a Network of Internal Donor-Acceptor Heterojunctions. Science 1995, 270, 1789–1791. [Google Scholar] [CrossRef] [Green Version]
- Mikhnenko, O.V.; Blom, P.W.M.; Nguyen, T.-Q. Exciton diffusion in organic semiconductors. Energy Environ. Sci. 2015, 8, 1867–1888. [Google Scholar] [CrossRef]
- Tamai, Y.; Ohkita, H.; Benten, H.; Ito, S. Exciton Diffusion in Conjugated Polymers: From Fundamental Understanding to Improvement in Photovoltaic Conversion Efficiency. J. Phys. Chem. Lett. 2015, 6, 3417–3428. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Firdaus, Y.; Le Corre, V.M.; Karuthedath, S.; Liu, W.; Markina, A.; Huang, W.; Chattopadhyay, S.; Nahid, M.M.; Nugraha, M.I.; Lin, Y.; et al. Long-range exciton diffusion in molecular non-fullerene acceptors. Nat. Commun. 2020, 11, 5220. [Google Scholar] [CrossRef] [PubMed]
- Vogelsang, J.; Adachi, T.; Brazard, J.; Vanden Bout, D.A.; Barbara, P.F. Self-assembly of highly ordered conjugated polymer aggregates with long-range energy transfer. Nat. Mater. 2011, 10, 942–946. [Google Scholar] [CrossRef]
- Jin, X.-H.; Price, M.B.; Finnegan, J.R.; Boott, C.E.; Richter, J.M.; Rao, A.; Menke, S.M.; Friend, R.H.; Whittell, G.R.; Manners, I. Long-range exciton transport in conjugated polymer nanofibers prepared by seeded growth. Science 2018, 360, 897–900. [Google Scholar] [CrossRef] [Green Version]
- Hoppe, H.; Sariciftci, N.S. Morphology of polymer/fullerene bulk heterojunction solar cells. J. Mater. Chem. 2006, 16, 45–61. [Google Scholar] [CrossRef]
- Moule, A.J.; Meerholtz, K. Morphology Control in Solution-Processed Bulk-Heterojunction Solar Cell Mixtures. Adv. Funct. Mater. 2009, 19, 3028–3036. [Google Scholar] [CrossRef]
- Richter, L.J.; Delongchamp, D.M.; Amassian, A. Morphology Development in Solution-Processed Functional Organic Blend Films: An In Situ Viewpoint. Chem. Rev. 2017, 117, 6332–6366. [Google Scholar] [CrossRef]
- Nilsson, S.; Bernasik, A.; Budkowski, A.; Moons, E. Morphology and Phase Segregation of Spin-Casted Films of Polyfluorene/PCBM Blends. Macromolecules 2007, 40, 8291–8301. [Google Scholar] [CrossRef]
- Kim, J.Y.; Frisbie, C.D. Correlation of Phase Behavior and Charge Transport in Conjugated Polymer/Fullerene Blends. J. Phys. Chem. C 2008, 112, 17726–17736. [Google Scholar] [CrossRef]
- Müller, C.; Ferenczi, T.A.M.; Campoy-Quiles, M.; Frost, J.M.; Bradley, D.D.C.; Smith, P.; Stingelin-Stutzmann, N.; Nelson, J. Binary Organic Photovoltaic Blends: A Simple Rationale for Optimum Compositions. Adv. Mater. 2008, 20, 3510–3515. [Google Scholar] [CrossRef]
- Zhao, J.; Swinnen, Z.; Van Assche, G.; Manca, J.; Vanderzande, D.; Van Mele, B. Phase Diagram of P3HT/PCBM Blends and Its Implication for the Stability of Morphology. J. Phys. Chem. B 2009, 113, 1587–1591. [Google Scholar] [CrossRef]
- Ballantyne, A.M.; Ferenczi, T.A.; Campoy-Quiles, M.; Clarke, T.M.; Maurano, A.; Wong, K.H.; Zhang, W.; Stingelin-Stutzmann, N.; Kim, J.-S.; Bradley, D.D.; et al. Understanding the Influence of Morphology on Poly(3-hexylselenothiophene):PCBM Solar Cells. Macromolecules 2010, 43, 1169–1174. [Google Scholar] [CrossRef]
- Kozub, D.R.; Vakhshouri, K.; Orme, L.M.; Wang, C.; Hexemer, A.; Gomez, E.D. Polymer Crystallization of Partially Miscible Polythiophene/Fullerene Mixtures Controls Morphology. Macromolecules 2011, 44, 5722–5726. [Google Scholar] [CrossRef]
- Nicolet, C.; Deribew, D.; Renaud, C.; Fleury, G.; Brochon, C.; Cloutet, E.; Vignau, L.; Wantz, G.; Cramail, H.; Geoghegan, M.; et al. Optimization of the Bulk Heterojunction Composition for Enhanced Photovoltaic Properties: Correlation between the Molecular Weight of the Semiconducting Polymer and Device Performance. J. Phys. Chem. B 2011, 115, 12717–12727. [Google Scholar] [CrossRef] [PubMed]
- Müller, C.; Bergqvist, J.; Vandewal, K.; Tvingstedt, K.; Anselmo, A.S.; Magnusson, R.; Alonso, M.I.; Moons, E.; Arwin, H.; Campoy-Quiles, M.; et al. Phase behaviour of liquid-crystalline polymer/fullerene organic photovoltaic blends: Thermal stability and miscibility. J. Mater. Chem. 2011, 21, 10676–10684. [Google Scholar] [CrossRef]
- Miller, N.C.; Gysel, R.; Miller, C.E.; Verploegen, E.; Beiley, Z.; Heeney, M.; McCulloch, I.; Bao, Z.; Toney, M.F.; McGehee, M.D. The phase behavior of a polymer-fullerene bulk heterojunction system that contains bimolecular crystals. J. Polym. Sci. B Polym. Phys. 2011, 49, 499–503. [Google Scholar] [CrossRef]
- Li, N.; Machui, F.; Waller, D.; Koppe, M.; Brabec, C.J. Determination of phase diagrams of binary and ternary organic semiconductor blends for organic photovoltaic devices. Sol. Energy Mater. Sol. Cells 2011, 95, 3465–3471. [Google Scholar] [CrossRef]
- Li, N.; Perea, J.D.; Kassar, T.; Richter, M.; Heumueller, T.; Matt, G.J.; Hou, Y.; Güldal, N.S.; Chen, H.; Chen, S.; et al. Abnormal strong burn-in degradation of highly efficient polymer solar cells caused by spinodal donor-acceptor demixing. Nat. Commun. 2017, 8, 14541. [Google Scholar] [CrossRef] [Green Version]
- Ghasemi, M.; Hu, H.; Peng, Z.; Rech, J.J.; Angunawela, I.; Carpenter, J.H.; Stuard, S.J.; Wadsworth, A.; McCulloch, I.; You, W.; et al. Delineation of Thermodynamic and Kinetic Factors that Control Stability in Non-fullerene Organic Solar Cells. Joule 2019, 3, 1–21. [Google Scholar] [CrossRef]
- Kouijzer, S.; Michels, J.J.; Van den Berg, M.; Gevaerts, V.S.; Turbiez, M.; Wienk, M.M.; Janssen, R.A.J. Predicting Morphologies of Solution Processed Polymer:Fullerene Blends. J. Am. Chem. Soc. 2013, 135, 12057–12067. [Google Scholar] [CrossRef] [PubMed]
- Shao, M.; Keum, J.K.; Kumar, R.; Chen, J.; Browning, J.F.; Das, S.; Chen, W.; Hou, J.; Do, C.; Littrell, K.C.; et al. Understanding How Processing Additives Tune the Nanoscale Morphology of High Efficiency Organic Photovoltaic Blends: From Casting Solution to Spun-Cast Thin Film. Adv. Funct. Mater. 2014, 24, 6647–6657. [Google Scholar] [CrossRef]
- Michels, J.; Moons, E. Simulation of Surface-Directed Phase Separation in a Solution-Processed Polymer/PCBM Blend. Macromolecules 2013, 46, 8693–8701. [Google Scholar] [CrossRef]
- Schaefer, C.; Michels, J.J.; Van Der Schoot, P. Structuring of Thin-Film Polymer Mixtures upon Solvent Evaporation. Macromolecules 2016, 49, 6858–6870. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.-H.; Gadisa, A.; Schaefer, C.; Yao, H.; Gautam, B.R.; Balar, N.; Ghasemi, M.; Constantinou, I.; So, F.; O’Connor, B.T.; et al. Strong polymer molecular weight-dependent material interactions: Impact on the formation of the polymer/fullerene bulk heterojunction morphology. J. Mater. Chem. A 2017, 5, 13176–13188. [Google Scholar] [CrossRef]
- Bokel, F.A.; Engmann, S.; Herzing, A.A.; Collins, B.A.; Ro, H.W.; DeLongchamp, D.M.; Richter, L.J.; Schaible, E.; Hexemer, A. In Situ X-ray Scattering Studies of the Influence of an Additive on the Formation of a Low-Bandgap Bulk Heterojunction. Chem. Mater. 2017, 29, 2283–2293. [Google Scholar] [CrossRef]
- Negi, V.; Wodo, O.; Van Franeker, J.J.; Janssen, R.A.J.; Bobbert, P.A. Simulating Phase Separation during Spin Coating of a Polymer–Fullerene Blend: A Joint Computational and Experimental Investigation. ACS Appl. Energy Mater. 2018, 1, 725–735. [Google Scholar] [CrossRef] [Green Version]
- Xin, J.; Meng, X.; Xu, X.; Zhu, Q.; Naveed, B.; Ma, W. Cold Crystallization Temperature Correlated Phase Separation, Performance, and Stability of Polymer Solar Cells. Matter 2019, 1, 1–15. [Google Scholar] [CrossRef]
- Cahn, J.W. Phase Separation by Spinodal Decomposition in Isotropic Systems. J. Chem. Phys. 1965, 42, 93–99. [Google Scholar] [CrossRef]
- Favvas, E.P.; Mitropoulos, A.C. What is spinodal decomposition? J. Eng. Sci. Technol. Rev. 2008, 1, 25–37. [Google Scholar] [CrossRef]
- Van de Witte, P.; Dijkstra, P.J.; Van den Berg, J.W.A.; Feijen, J. Phase separation processes in polymer solutions in relation to membrane formation. J. Membr. Sci. 1996, 117, 1–31. [Google Scholar] [CrossRef] [Green Version]
- Vaynzof, Y.; Kabra, D.; Zhao, L.; Chua, L.L.; Steiner, U.; Friend, R.H. Surface-Directed Spinodal Decompositionin Poly[3 -hexylthiophene] and C61-Butyric Acid Methyl Ester Blends. ACS Nano 2011, 5, 329–336. [Google Scholar] [CrossRef]
- McNeill, C.R.; Greenham, N.C. Conjugated-Polymer Blends for Optoelectronics. Adv. Mater. 2009, 21, 3840–3850. [Google Scholar] [CrossRef]
- Campoy-Quiles, M.; Ferenczi, T.; Agostinelli, T.; Etchegoin, P.G.; Kim, Y.; Anthopoulos, T.D.; Stavrinou, P.N.; Bradley, D.D.C.; Nelson, J. Morphology evolution via self-organization and lateral and vertical diffusion in polymer:fullerene solar cell blends. Nat. Mater. 2008, 7, 158–164. [Google Scholar] [CrossRef]
- Natta, G.; Corradini, P. Conformation of linear chains and their mode of packing in the crystal state. J. Polym. Sci. 1959, 39, 29–46. [Google Scholar] [CrossRef]
- Kim, J.Y.; Cho, H.; Noh, S.; Lee, Y.; Nam, Y.M.; Lee, C.; Jo, W.H. Charge transport in amorphous low bandgap conjugated polymer/fullerene films. J. Appl. Phys. 2012, 111, 043710. [Google Scholar] [CrossRef]
- Lin, Y.; Wang, J.; Zhang, Z.-G.; Bai, H.; Li, Y.; Zhu, D.; Zhan, X. An Electron Acceptor Challenging Fullerenes for Efficient Polymer Solar Cells. Adv. Mater. 2015, 27, 1170–1174. [Google Scholar] [CrossRef]
- He, Z.; Zhong, C.; Su, S.; Xu, M.; Wu, H.; Cao, Y. Enhanced power-conversion efficiency in polymer solar cells using an inverted device structure. Nat. Photon. 2012, 6, 591–595. [Google Scholar] [CrossRef]
- Collins, B.A.; Li, Z.; Tumbleston, J.R.; Gann, E.; McNeill, C.R.; Ade, H. Absolute Measurement of Domain Composition and Nanoscale Size Distribution Explains Performance in PTB7:PC71BM Solar Cells. Adv. Energy Mater. 2013, 3, 65–74. [Google Scholar] [CrossRef]
- Reid, D.R.; Jackson, N.E.; Bourque, A.J.; Snyder, C.R.; Jones, R.L.; De Pablo, J.J. Aggregation and Solubility of a Model Conjugated Donor–Acceptor Polymer. J. Phys. Chem. Lett. 2018, 9, 4802–4807. [Google Scholar] [CrossRef]
- Liu, Y.; Zhao, J.; Li, Z.; Mu, C.; Ma, W.; Hu, H.; Jiang, K.; Lin, H.; Ade, H.; Yan, H. Aggregation and morphology control enables multiple cases of high-efficiency polymer solar cells. Nat. Commun. 2014, 5, 5293. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hiemenz, P.C.; Lodge, T.P. Polymer Chemistry, 2nd ed.; CRC Press Taylor & Francis Group: Boca Raton, FL, USA, 2007. [Google Scholar]
- Li, D.; Neumann, A.W. A reformulation of the equation of state for interfacial tensions. J. Colloid Interface Sci. 1990, 137, 304–307. [Google Scholar] [CrossRef]
- Li, D.; Neumann, A.W. Contact angles on hydrophobic solid surfaces and their interpretation. J. Colloid Interface Sci. 1992, 148, 190–200. [Google Scholar] [CrossRef]
- Perea, J.D.; Langner, S.; Salvador, M.; Sanchez-Lengeling, B.; Li, N.; Zhang, C.; Jarvas, G.; Kontos, J.; Dallos, A.; Aspuru-Guzik, A.; et al. Introducing a New Potential Figure of Merit for Evaluating Microstructure Stability in Photovoltaic Polymer-Fullerene Blends. J. Phys. Chem. C 2017, 121, 18153–18161. [Google Scholar] [CrossRef]
- Belmares, M.; Blanco, M.; Goddard, W.A., III; Ross, R.B.; Caldwell, G.; Chou, S.-H.; Pham, J.; Olofson, P.M.; Thomas, C. Hildebrand and Hansen Solubility Parameters from Molecular Dynamics with Applications to Electronic Nose Polymer Sensors. J. Comput. Chem. 2004, 25, 1814–1826. [Google Scholar] [CrossRef] [Green Version]
- Dereje, M.M.; Ji, D.; Kang, S.-H.; Yang, C.; Noh, Y.-Y. Effect of pre-aggregation in conjugated polymer solution on performance of diketopyrrolopyrrole-based organic field-effect transistors. Dyes Pigm. 2017, 145, 270–276. [Google Scholar] [CrossRef]
- Yao, K.; Xu, Y.-X.; Wang, X.; Li, F.; Yuan, J. The critical role of additives in binary halogen-free solvent systems for the general processing of highly efficient organic solar cells. RSC Adv. 2015, 5, 93689–93696. [Google Scholar] [CrossRef]
- Salim, T.; Wong, L.H.; Bräuer, B.; Kukreja, R.; Foo, Y.L.; Bao, Z.; Lam, Y.M. Solvent additives and their effects on blend morphologies of bulk heterojunctions. J. Mater. Chem. 2011, 21, 242–250. [Google Scholar] [CrossRef]
- Lee, J.K.; Ma, W.L.; Brabec, C.J.; Yuen, J.; Moon, J.S.; Kim, J.Y.; Lee, K.; Bazan, G.C.; Heeger, A.J. Processing Additives for Improved Efficiency from Bulk Heterojunction Solar Cells. J. Am. Chem. Soc. 2008, 130, 3619–3623. [Google Scholar] [CrossRef] [PubMed]
- Peet, J.; Cho, N.S.; Lee, S.K.; Bazan, G.C. Transition from Solution to the Solid State in Polymer Solar Cells Cast from Mixed Solvents. Macromolecules 2008, 41, 8655–8659. [Google Scholar] [CrossRef]
- Liao, H.-H.; Ho, C.-C.; Chang, C.-Y.; Jao, M.-H.; Darling, S.B.; Su, W.-F. Additives for morphology control in high-efficiency organic solar cells. Mater. Today 2013, 16, 326–336. [Google Scholar] [CrossRef]








| Materials | (cal/cm3)1/2 | MPa1/2 | MW (g/mol) | (cm3/mol) | (g/cm3) | Chemical Structure | Ref |
|---|---|---|---|---|---|---|---|
| P3HT | 8.7 | 17.83 | 22,000 | 20,000 | 1.1 | (C10H14S)n | [18,19] |
| PTB7 | 8.8 | 18.03 | 80,000 | 68,376 | 1.17 | (C41H53FO4S4)n | [65] |
| PffBT4T-2OD | 9.4 | 19.26 | 50,000 | 41,322 | 1.21 | (C62H88F2N2S5)n | [44,70] |
| PC61BM | 11.3 | 23.15 | 910 | 607 | 1.5 | C72H14O2 | [18,19] |
| PC71BM | 11.2 | 22.95 | 1031 | 687 | 1.5 | C82H14O2 | [18,19] |
| ITIC | 11.8 | 24.18 | 1428 | 1152 | 1.24 | C94H82N4O2S4 | [53] |
| Solvent | (cal/cm3)1/2 | MPa1/2 | MW (g/cm3) | (cm3/mol) | (g/cm3) | bp (°C) | Chemical Structure | Ref |
|---|---|---|---|---|---|---|---|---|
| CB | 9.5 | 19.47 | 112.56 | 101.41 | 1.11 | 132 | C6H5Cl | [71] |
| CF | 9.2 | 18.85 | 119.38 | 80.12 | 1.49 | 61 | CHCl3 | [72] |
| TOL | 8.9 | 18.24 | 92.14 | 105.91 | 0.87 | 111 | C7H8 | [71] |
| DIO | 9.2 | 18.85 | 336.02 | 186.68 | 1.8 | 168 | C8H16I2 | [73] |
| ODT | 9.1 | 18.65 | 178.36 | 183.92 | 0.97 | 269 | C8H18S2 | [74] |
| Ternary System | Flory-Huggins Interaction Parameter * | Molar Volume Ratio * | |||
|---|---|---|---|---|---|
| CB/P3HT/PC61BM | 32.7 K/T + 0.34 | 165.4 K/T + 0.34 | 345.0 K/T + 0.34 | 0.005071 | 0.167068 |
| CF/P3HT/PC61BM | 10.1 K/T + 0.34 | 177.8 K/T + 0.34 | 272.6 K/T + 0.34 | 0.004006 | 0.131993 |
| TOL/P3HT/PC61BM | 2.1 K/T + 0.34 | 307.0 K/T + 0.34 | 360.3 K/T + 0.34 | 0.005296 | 0.174481 |
| DIO/P3HT/PC61BM | 23.5 K/T + 0.34 | 414.3 K/T + 0.34 | 635.1 K/T + 0.34 | 0.009344 | 0.307858 |
| ODT/P3HT/PC61BM | 14.8 K/T + 0.34 | 448.0 K/T + 0.34 | 625.7 K/T + 0.34 | 0.009196 | 0.302998 |
| CB/P3HT/PC71BM | 32.7 K/T + 0.34 | 147.5 K/T + 0.34 | 319.0 K/T + 0.34 | 0.005071 | 0.147613 |
| CB/P3HT/ITIC | 32.7 K/T + 0.34 | 270.0 K/T + 0.34 | 490.5 K/T + 0.34 | 0.005071 | 0.071015 |
| CB/PTB7/ITIC | 25.0 K/T + 0.34 | 270.0 K/T + 0.34 | 459.3 K/T + 0.34 | 0.001483 | 0.088029 |
| CB/PffBT4T-2OD/ITIC | 0.5 K/T + 0.34 | 270.0 K/T + 0.34 | 294.0 K/T + 0.34 | 0.002448 | 0.088030 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, J.Y. Phase Diagrams of Ternary π-Conjugated Polymer Solutions for Organic Photovoltaics. Polymers 2021, 13, 983. https://doi.org/10.3390/polym13060983
Kim JY. Phase Diagrams of Ternary π-Conjugated Polymer Solutions for Organic Photovoltaics. Polymers. 2021; 13(6):983. https://doi.org/10.3390/polym13060983
Chicago/Turabian StyleKim, Jung Yong. 2021. "Phase Diagrams of Ternary π-Conjugated Polymer Solutions for Organic Photovoltaics" Polymers 13, no. 6: 983. https://doi.org/10.3390/polym13060983
APA StyleKim, J. Y. (2021). Phase Diagrams of Ternary π-Conjugated Polymer Solutions for Organic Photovoltaics. Polymers, 13(6), 983. https://doi.org/10.3390/polym13060983