The Structure, Morphology, and Complex Permittivity of Epoxy Nanodielectrics with In Situ Synthesized Surface-Functionalized SiO2
Abstract
:1. Introduction
2. Materials and Methods
3. Results
3.1. Dispersion and Morphology of the In Situ Synthesized Nanoparticles
3.2. Structure of the Inorganic Components
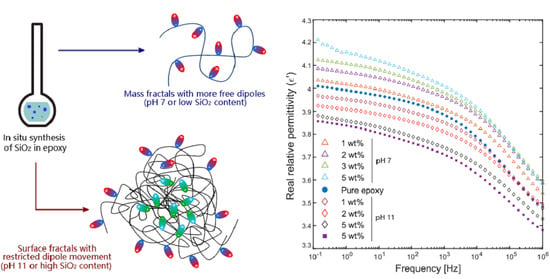
3.3. Complex Permittivity of the Nanocomposites
4. Discussion
4.1. The Effect of the SCA on the State of Dispersion
4.2. The Structure of the In Situ Synthesized SiO2
4.3. The Effect of the SiO2 on the Complex Permittivity at Room Temperature
4.4. The High Temperature Complex Permittivity
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Adnan, M.M.; Tveten, E.G.; Glaum, J.; Ese, M.-H.G.; Hvidsten, S.; Glomm, W.; Einarsrud, M.-A. Epoxy-Based Nanocomposites for High-Voltage Insulation: A Review. Adv. Electron. Mater. 2019, 5, 1800505. [Google Scholar] [CrossRef]
- Nelson, J.K.; Nelson, J.K. Dielectric Polymer Nanocomposites; Springer: New York, NY, USA, 2010; ISBN 978-1-4419-1590-0. [Google Scholar]
- Plesa, I.; Notingher, P.V.; Schlögl, S.; Sumereder, C.; Muhr, M. Properties of Polymer Composites Used in High-Voltage Applications. Polymers 2016, 8, 173. [Google Scholar] [CrossRef]
- Lewis, T.J. Interfaces are the Dominant Feature of Dielectrics at the Nanometric Level. IEEE Trans. Dielectr. Electr. Insul. 2004, 11, 739–753. [Google Scholar] [CrossRef]
- Calebrese, C.; Hui, L.; Schadler, L.S.; Nelson, J.K. A Review on the Importance of Nanocomposite Processing to Enhance Electrical Insulation. IEEE Trans. Dielectr. Electr. Insul. 2011, 18, 938–945. [Google Scholar] [CrossRef]
- Adnan, M.M.; Dalod, A.R.M.; Balci, M.H.; Glaum, J.; Einarsrud, M.-A. In situ synthesis of hybrid inorganic-polymer nanocomposites. Polymers 2018, 10, 1129. [Google Scholar] [CrossRef] [Green Version]
- Gao, F. Advances in Polymer Nanocomposites: Types and Applications; Woodhead Publishing Limited: Cambridge, UK, 2012; ISBN 9781845699406. [Google Scholar]
- Heid, T.; Fréchette, M.; David, E. Epoxy/BN micro- and submicro-composites: Dielectric and thermal properties of enhanced materials for high voltage insulation systems. IEEE Trans. Dielectr. Electr. Insul. 2015, 22, 1176–1185. [Google Scholar] [CrossRef]
- Nelson, J.K.; Fothergill, J.C. Internal charge behaviour of nanocomposites. Nanotechnology 2004, 15, 586–595. [Google Scholar] [CrossRef] [Green Version]
- Kochetov, R.; Andritsch, T.; Morshuis, P.H.F.; Smit, J.J. Anomalous Behaviour of the Dielectric Spectroscopy Response of Nanocomposites. IEEE Trans. Dielectr. Electr. Insul. 2012, 19, 107–117. [Google Scholar] [CrossRef]
- Virtanen, S.; Krentz, T.; Nelson, J.K.; Schadler, L.; Bell, M.; Benicewicz, B.; Hillborg, H.; Zhao, S. Dielectric Breakdown Strength of Epoxy Bimodal-polymer-Brush-Grafted Core Functionalized Silica Nanocomposites. IEEE Trans. Dielectr. Electr. Insul. 2014, 21, 563–570. [Google Scholar] [CrossRef]
- Bell, M.; Krentz, T.; Nelson, J.K.; Schadler, L.; Wu, K.; Breneman, C.; Zhao, S.; Hillborg, H.; Benicewicz, B. Investigation of dielectric breakdown in silica-epoxy nanocomposites using designed interfaces. J. Colloid Interface Sci. 2017, 495, 130–139. [Google Scholar] [CrossRef] [PubMed]
- Yeung, C.; Vaughan, A.S. On the Effect of Nanoparticle Surface Chemistry on the Electrical Characteristics of Epoxy-Based Nanocomposites. Polymers 2016, 8, 126. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sanchez, C.; Ribot, F. Design of Hybrid Organic-Inorganic Materials Synthesized Via Sol-Gel Chemistry. New J. Chem. 1994, 18, 1007–1047. [Google Scholar] [CrossRef]
- Brinker, C.J.; Scherer, G.W. Sol-Gel Science: The Physics and Chemistry of Sol–Gel Processing; Academic Press, Inc.: Cambridge, MA, USA, 1990; ISBN 9780080571034. [Google Scholar]
- Judeinstein, P.; Sanchez, C. Hybrid organic–inorganic materials: A land of multidisciplinarity. J. Mater. Chem. 1996, 6, 511–525. [Google Scholar] [CrossRef]
- Matějka, L.; Dušek, K.; Pleštil, J.; Kříž, J.; Lednický, F. Formation and structure of the epoxy-silica hybrids. Polymer 1999, 40, 171–181. [Google Scholar] [CrossRef]
- Matějka, L.; Pleštil, J.; Dušek, K. Structure evolution in epoxy–silica hybrids: Sol–gel process. J. Non-Cryst. Solids 1998, 226, 114–121. [Google Scholar] [CrossRef]
- Nazir, T.; Afzal, A.; Siddiqi, H.M.; Ahmad, Z.; Dumon, M. Thermally and mechanically superior hybrid epoxy-silica polymer films via sol-gel method. Prog. Org. Coat. 2010, 69, 100–106. [Google Scholar] [CrossRef]
- Afzal, A.; Siddiqi, H.M.; Saeed, S.; Ahmad, Z. Exploring resin viscosity effects in solventless processing of nano-SiO2/epoxy polymer hybrids. RSC Adv. 2013, 3, 3885–3892. [Google Scholar] [CrossRef]
- Donato, R.K.; Matějka, L.; Schrekker, H.S.; Pletil, J.; Jigounov, A.; Brus, J.; Slouf, M. The multifunctional role of ionic liquids in the formation of epoxy-silica nanocomposites. J. Mater. Chem. 2011, 21, 13801–13810. [Google Scholar] [CrossRef]
- Donato, R.K.; Donato, K.Z.; Schrekker, H.S.; Matějka, L. Tunable reinforcement of epoxy-silica nanocomposites with ionic liquids. J. Mater. Chem. 2012, 22, 9939–9948. [Google Scholar] [CrossRef] [Green Version]
- Khare, H.S.; Burris, D.L. A quantitative method for measuring nanocomposite dispersion. Polymer 2010, 51, 719–729. [Google Scholar] [CrossRef]
- Adnan, M.M.; Tveten, E.G.; Miranti, R.; Hvidsten, S.; Ese, M.-H.G.; Glaum, J.; Einarsrud, M.-A. In situ synthesis of epoxy nanocomposites with hierarchical surface-modified SiO2 clusters. J. Sol-Gel Sci. Technol. 2020, 95, 783–794. [Google Scholar] [CrossRef] [Green Version]
- Beaucage, G. Approximations Leading to a Unified Exponential/Power-Law Approach to Small-Angle Scattering. J. Appl. Crystallogr. 1995, 28, 717–728. [Google Scholar] [CrossRef]
- Dalod, A.; Grendal, O.; Blichfeld, A.; Furtula, V.; Pérez, J.; Henriksen, L.; Grande, T.; Einarsrud, M.-A. Structure and Optical Properties of Titania-PDMS Hybrid Nanocomposites Prepared by In Situ Non-Aqueous Synthesis. Nanomaterials 2017, 7, 460. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Beaucage, G. Small-angle scattering from polymeric mass fractals of arbitrary mass-fractal dimension. J. Appl. Crystallogr. 1996, 29, 134–146. [Google Scholar] [CrossRef] [Green Version]
- Cherny, A.Y.; Anitas, E.M.; Osipov, V.A.; Kuklin, A.I. Scattering from surface fractals in terms of composing mass fractals. J. Appl. Cryst 2017, 50, 919–931. [Google Scholar] [CrossRef] [Green Version]
- Rubio, F.; Rubio, J.; Oteo, J.L. A FT-IR Study of the Hydrolysis of Tetraethylorthosilicate (TEOS). Spectrosc. Lett. 1998, 31, 199–219. [Google Scholar] [CrossRef]
- Hoebbel, D.; Nacken, M.; Schmidt, H. On the Existence and Hydrolytic Stability of Titanosiloxane Bonds in the System: Glycidoxypropyltrimethoxysilane-Water-Titaniumtetraethoxide. J. Sol-Gel Sci. Technol. 1998, 13, 37–43. [Google Scholar] [CrossRef]
- Piscitelli, F.; Buonocore, G.G.; Lavorgna, M.; Verdolotti, L.; Pricl, S.; Gentile, G.; Mascia, L. Peculiarities in the structure—Properties relationship of epoxy-silica hybrids with highly organic siloxane domains. Polymer 2015, 63, 222–229. [Google Scholar] [CrossRef] [Green Version]
- Piscitelli, F.; Lavorgna, M.; Buonocore, G.G.; Verdolotti, L.; Galy, J.; Mascia, L. Plasticizing and reinforcing features of siloxane domains in amine-cured epoxy/silica hybrids. Macromol. Mater. Eng. 2013, 298, 896–909. [Google Scholar] [CrossRef]
- Lysenkov, E.A.; Leonova, N.G.; Zhiltsova, S.V. Effect of the Silicon-Containing Phase on the Hierarchy of the Structure of Epoxy–Silica Nanocomposites. Theor. Exp. Chem. 2019, 55, 250–257. [Google Scholar] [CrossRef]
- Ponyrko, S.; Kobera, L.; Brus, J.; Matějka, L. Epoxy-silica hybrids by nonaqueous sol-gel process. Polymer 2013, 54, 6271–6282. [Google Scholar] [CrossRef]
- Perchacz, M.; Beneš, H.; Zhigunov, A.; Serkis, M.; Pavlova, E. Differently-catalyzed silica-based precursors as functional additives for the epoxy-based hybrid materials. Polymer 2016, 99, 434–446. [Google Scholar] [CrossRef]
- Alhabill, F.N.; Ayoob, R.; Andritsch, T.; Vaughan, A.S. Influence of filler/matrix interactions on resin/hardener stoichiometry, molecular dynamics, and particle dispersion of silicon nitride/epoxy nanocomposites. J. Mater. Sci. 2018, 53, 4144–4158. [Google Scholar] [CrossRef] [Green Version]
- Pochan, J.M.; Gruber, R.J.; Pochan, D.F. Dielectric relaxation phenomena in a series of polyhydroxyether copolymers of bisphenol-A—endcapped polyethylene glycol with epichlorohydrin. J. Polym. Sci. Polym. Phys. Ed. 1981, 19, 143–149. [Google Scholar] [CrossRef]
- Vassilikou-Dova, A.; Kalogeras, I.M. Dielectric Analysis (DEA). In Thermal Analysis of Polymers: Fundamentals and Applications; Menczel, J.D., Prime, R.B., Eds.; Wiley & Sons: Hoboken, NJ, USA, 2009; pp. 497–613. ISBN 9780471769170. [Google Scholar]
- Fuqiang, T.; Lin, Z.; Junliang, Z.; Xiao, P. Space charge and dielectric behavior of epoxy composite with SiO2-Al2O3 nano-micro fillers at varied temperatures. Compos. Part B Eng. 2017, 114, 93–100. [Google Scholar] [CrossRef]
- García-Sánchez, M.F.; M’Peko, J.C.; Ruiz-Salvador, A.R.; Rodríguez-Gattorno, G.; Echevarría, Y.; Fernández-Gutierrez, F.; Delgado, A. An elementary picture of dielectric spectroscopy in solids: Physical basis. J. Chem. Educ. 2003, 80, 1062–1073. [Google Scholar] [CrossRef]
- Jonscher, A.K. Dielectric relaxation in solids. J. Phys. D Appl. Phys. 1999, 32, 57–70. [Google Scholar] [CrossRef]
- Gao, Y.; Liang, X.; Dissado, L.A.; Dodd, S.J.; Chalashkanov, N.M. Dielectric response of filled high temperature vulcanized silicone rubber. IEEE Trans. Dielectr. Electr. Insul. 2016, 23, 3683–3695. [Google Scholar] [CrossRef] [Green Version]
- Fuqiang, T.; Yoshimichi, O. Electric Modulus Powerful Tool for Analyzing Dielectric Behavior. IEEE Trans. Dielectr. Electr. Insul. 2014, 21, 929–931. [Google Scholar] [CrossRef]
- Yang, G.; Cui, J.; Ohki, Y.; Wang, D.; Li, Y.; Tao, K. Dielectric and relaxation properties of composites of epoxy resin and hyperbranched-polyester-treated nanosilica. RSC Adv. 2018, 8, 30669–30677. [Google Scholar] [CrossRef] [Green Version]
















| Filler Content | pH | SCA:DGEBA Mass Ratio | SCA |
|---|---|---|---|
| 1–5 wt% | 2 1 | 1:10 | APTES |
| 1, 2, 3, and 5 wt% | 7 | ||
| 1,2 and 5 wt% | 11 | ||
| 5 wt% | 11 | 1:30 | |
| 2, 3, 4, and 5 wt% | 2 | 1:10 | GPTMS |
| Sample | Structural Level | D | Rg (nm) | d (nm) | |
|---|---|---|---|---|---|
| pH | Filler Content (wt.%) | ||||
| 7 | 1 1 | 1 | 1.3 | - | - |
| 2 | 1 | 1.5 | 3.3 ± 0.1 | 8.5 | |
| 2 | 2.2 | 11.6 ± 0.9 | 30.0 | ||
| 3 | 1 | 1.6 | 4.1 ± 0.4 | 10.6 | |
| 2 | 2.4 | 12.1 ± 1.0 | 31.2 | ||
| 5 | 1 | 1.9 | 3.3 ± 0.1 | 8.5 | |
| 2 | 3.1 | 13.3 ± 1.7 | 34.3 | ||
| 11 | 1 1 | 1 | 1.5 | - | - |
| 2 1 | 1 | 2 | - | - | |
| 5 | 1 | 1.9 | 3.3 ± 0.1 | 8.5 | |
| 2 | 3.3 | 14.7 ± 1.8 | 38.0 | ||
| 5 1,2 | 1 | 1.2 | - | - | |
| 2 | 3.5 | - | - | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adnan, M.M.; Nylund, I.-E.; Jaworski, A.; Hvidsten, S.; Ese, M.-H.G.; Glaum, J.; Einarsrud, M.-A. The Structure, Morphology, and Complex Permittivity of Epoxy Nanodielectrics with In Situ Synthesized Surface-Functionalized SiO2. Polymers 2021, 13, 1469. https://doi.org/10.3390/polym13091469
Adnan MM, Nylund I-E, Jaworski A, Hvidsten S, Ese M-HG, Glaum J, Einarsrud M-A. The Structure, Morphology, and Complex Permittivity of Epoxy Nanodielectrics with In Situ Synthesized Surface-Functionalized SiO2. Polymers. 2021; 13(9):1469. https://doi.org/10.3390/polym13091469
Chicago/Turabian StyleAdnan, Mohammed Mostafa, Inger-Emma Nylund, Aleksander Jaworski, Sverre Hvidsten, Marit-Helen Glomm Ese, Julia Glaum, and Mari-Ann Einarsrud. 2021. "The Structure, Morphology, and Complex Permittivity of Epoxy Nanodielectrics with In Situ Synthesized Surface-Functionalized SiO2" Polymers 13, no. 9: 1469. https://doi.org/10.3390/polym13091469
APA StyleAdnan, M. M., Nylund, I. -E., Jaworski, A., Hvidsten, S., Ese, M. -H. G., Glaum, J., & Einarsrud, M. -A. (2021). The Structure, Morphology, and Complex Permittivity of Epoxy Nanodielectrics with In Situ Synthesized Surface-Functionalized SiO2. Polymers, 13(9), 1469. https://doi.org/10.3390/polym13091469