Land Surface Temperature Retrieval Using High-Resolution Vertical Profiles Simulated by WRF Model †
Abstract
:1. Introduction
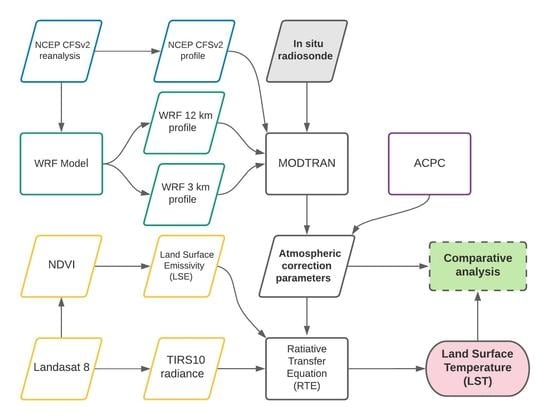
2. Materials and Methods
2.1. Study Area and In Situ Radiosonde Data
2.2. Landsat 8 Satellite Data and Case Days
2.3. Reanalysis Data
2.4. WRF Model Configuration
2.5. Land Surface Emissivity Estimation
2.6. Atmospheric Correction and LST Retrieval
2.6.1. Atmospheric Parameters Calculation with MODTRAN and ACPC
2.6.2. Radiative Transfer Equation (RTE)-Based LST Retrieval Method
- SBPA local radiosonde;
- NCEP CFSv2 reanalysis;
- WRF G12;
- WRF G03;
- ACPC.
2.7. Metrics for Performance Evaluation
3. Results and Discussion
3.1. Evaluation of Atmospheric Parameters
3.1.1. Overall Results
3.1.2. Analysis by Meteorological Conditions
3.2. Application to RTE-Based LST Retrieval
4. Conclusions
- Our main conclusion is that there is no special need to increase the horizontal resolution of reanalysis profiles aiming at general RTE-based LST retrieval. We recommend the use of NCEP CFSv2 profiles for these applications.
- The results reinforce the validity and feasibility of ACPC, which is free of charge.
- Even though the overall statistical metrics for WRF profiles were inferior, their results were satisfactory for the estimation of both atmospheric parameters and LST values.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cao, B.; Liu, Q.; Du, Y.; Roujean, J.L.; Gastellu-Etchegorry, J.P.; Trigo, I.F.; Zhan, W.; Yu, Y.; Cheng, J.; Jacob, F.; et al. A Review of Earth Surface Thermal Radiation Directionality Observing and Modeling: Historical Development, Current Status and Perspectives. Remote Sens. Environ. 2019, 232, 111304. [Google Scholar] [CrossRef]
- WMO. The Global Observing System for Climate: Implementation Needs; World Meteorological Organization (WMO): Geneva, Switzerland, 2016; Volume 200. [Google Scholar]
- Anderson, M.C.; Norman, J.M.; Kustas, W.P.; Houborg, R.; Starks, P.J.; Agam, N. A Thermal-Based Remote Sensing Technique for Routine Mapping of Land-Surface Carbon, Water and Energy Fluxes from Field to Regional Scales. Remote Sens. Environ. 2008, 112, 4227–4241. [Google Scholar] [CrossRef]
- Tardy, B.; Rivalland, V.; Huc, M.; Hagolle, O.; Marcq, S.; Boulet, G. A Software Tool for Atmospheric Correction and Surface Temperature Estimation of Landsat Infrared Thermal Data. Remote Sens. 2016, 8, 696. [Google Scholar] [CrossRef] [Green Version]
- Wu, P.; Yin, Z.; Zeng, C.; Duan, S.-B.; Gottsche, F.-M.; Li, X.; Ma, X.; Yang, H.; Shen, H. Spatially Continuous and High-Resolution Land Surface Temperature Product Generation: A Review of Reconstruction and Spatiotemporal Fusion Techniques. IEEE Geosci. Remote Sens. Mag. 2021, 9, 112–137. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Del Frate, F.; Drusch, M.; Jiménez-Muñoz, J.C.; Manunta, P.; Regan, A. Review of Thermal Infrared Applications and Requirements for Future High-Resolution Sensors. IEEE Trans. Geosci. Remote Sens. 2016, 54, 2963–2972. [Google Scholar] [CrossRef]
- Montaner-Fernández, D.; Morales-Salinas, L.; Rodriguez, J.S.; Cárdenas-Jirón, L.; Huete, A.; Fuentes-Jaque, G.; Pérez-Martínez, W.; Cabezas, J. Spatio-Temporal Variation of the Urban Heat Island in Santiago, Chile during Summers 2005–2017. Remote Sens. 2020, 12, 3345. [Google Scholar] [CrossRef]
- Candy, B.; Saunders, R.W.; Ghent, D.; Bulgin, C.E. The Impact of Satellite-Derived Land Surface Temperatures on Numerical Weather Prediction Analyses and Forecasts. J. Geophys. Res. Atmos. 2017, 122, 9783–9802. [Google Scholar] [CrossRef] [Green Version]
- Hu, X.; Ren, H.; Tansey, K.; Zheng, Y.; Ghent, D.; Liu, X.; Yan, L. Agricultural Drought Monitoring Using European Space Agency Sentinel 3A Land Surface Temperature and Normalized Difference Vegetation Index Imageries. Agric. For. Meteorol. 2019, 279, 107707. [Google Scholar] [CrossRef]
- Jiménez-Muñoz, J.C.; Mattar, C.; Sobrino, J.A.; Malhi, Y. Digital Thermal Monitoring of the Amazon Forest: An Intercomparison of Satellite and Reanalysis Products. Int. J. Digit. Earth 2016, 9, 477–498. [Google Scholar] [CrossRef]
- Magarreiro, C.; Gouveia, C.; Barroso, C.; Trigo, I. Modelling of Wine Production Using Land Surface Temperature and FAPAR—The Case of the Douro Wine Region. Remote Sens. 2019, 11, 604. [Google Scholar] [CrossRef] [Green Version]
- Pavlidou, E.; van der Meijde, M.; van der Werff, H.; Hecker, C. Time Series Analysis of Land Surface Temperatures in 20 Earthquake Casesworldwide. Remote Sens. 2019, 11, 61. [Google Scholar] [CrossRef] [Green Version]
- Gemitzi, A.; Dalampakis, P.; Falalakis, G. International Journal of Applied Earth Observations and Geoinformation Detecting Geothermal Anomalies Using Landsat 8 Thermal Infrared Remotely Sensed Data. Int. J. Appl. Earth Obs. Geoinf. 2021, 96, 102283. [Google Scholar] [CrossRef]
- da Rocha, N.S.; Käfer, P.S.; Skokovic, D.; Veeck, G.; Diaz, L.R.; Kaiser, E.A.; Carvalho, C.M.; Cruz, R.C.; Sobrino, J.A.; Roberti, D.R.; et al. The Influence of Land Surface Temperature in Evapotranspiration Estimated by the S-SEBI Model. Atmosphere 2020, 11, 1059. [Google Scholar] [CrossRef]
- Anderson, M.C.; Yang, Y.; Xue, J.; Knipper, K.R.; Yang, Y.; Gao, F.; Hain, C.R.; Kustas, W.P.; Cawse-Nicholson, K.; Hulley, G.; et al. Interoperability of ECOSTRESS and Landsat for Mapping Evapotranspiration Time Series at Sub-Field Scales. Remote Sens. Environ. 2021, 252, 112189. [Google Scholar] [CrossRef]
- Maffei, C.; Alfieri, S.M.; Menenti, M. Relating Spatiotemporal Patterns of Forest Fires Burned Area and Duration to Diurnal Land Surface Temperature Anomalies. Remote Sens. 2018, 10, 1777. [Google Scholar] [CrossRef] [Green Version]
- Singh, N.; Chatterjee, R.S.; Kumar, D.; Panigrahi, D.C.; Mujawdiya, R. Retrieval of Precise Land Surface Temperature from ASTER Night-Time Thermal Infrared Data by Split Window Algorithm for Improved Coal Fire Detection in Jharia Coalfield, India. Geocarto Int. 2020, 1–18. [Google Scholar] [CrossRef]
- Anderson, M.C.; Allen, R.G.; Morse, A.; Kustas, W.P. Use of Landsat Thermal Imagery in Monitoring Evapotranspiration and Managing Water Resources. Remote Sens. Environ. 2012, 122, 50–65. [Google Scholar] [CrossRef]
- Tavares, M.H.; Cunha, A.H.F.; Motta-Marques, D.; Ruhoff, A.L.; Fragoso, C.R.; Munar, A.M.; Bonnet, M.P. Derivation of Consistent, Continuous Daily River Temperature Data Series by Combining Remote Sensing and Water Temperature Models. Remote Sens. Environ. 2020, 241, 111721. [Google Scholar] [CrossRef]
- Meng, X.; Cheng, J. Evaluating Eight Global Reanalysis Products for Atmospheric Correction of Thermal Infrared Sensor—Application to Landsat 8 TIRS10 Data. Remote Sens. 2018, 10, 474. [Google Scholar] [CrossRef] [Green Version]
- Rosas, J.; Houborg, R.; McCabe, M.F. Sensitivity of Landsat 8 Surface Temperature Estimates to Atmospheric Profile Data: A Study Using MODTRAN in Dryland Irrigated Systems. Remote Sens. 2017, 9, 988. [Google Scholar] [CrossRef] [Green Version]
- Cristóbal, J.; Jiménez-Muñoz, J.; Prakash, A.; Mattar, C.; Skoković, D.; Sobrino, J. An Improved Single-Channel Method to Retrieve Land Surface Temperature from the Landsat-8 Thermal Band. Remote Sens. 2018, 10, 431. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.-L.; Tang, B.-H.; Wu, H.; Ren, H.; Yan, G.; Wan, Z.; Trigo, I.F.; Sobrino, J.A. Satellite-Derived Land Surface Temperature: Current Status and Perspectives. Remote Sens. Environ. 2013, 131, 14–37. [Google Scholar] [CrossRef] [Green Version]
- Jiménez-Muñoz, J.C.; Sobrino, J.A.; Mattar, C.; Franch, B. Atmospheric Correction of Optical Imagery from MODIS and Reanalysis Atmospheric Products. Remote Sens. Environ. 2010, 114, 2195–2210. [Google Scholar] [CrossRef]
- Tang, H.; Li, Z.-L. Quantitative Remote Sensing in Thermal Infrared; Springer Remote Sensing/Photogrammetry; Springer: Berlin/Heidelberg, Germany, 2014; ISBN 978-3-642-42026-9. [Google Scholar]
- Galve, J.M.; Sánchez, J.M.; Coll, C.; Villodre, J. A New Single-Band Pixel-by-Pixel Atmospheric Correction Method to Improve the Accuracy in Remote Sensing Estimates of LST. Application to Landsat 7-ETM+. Remote Sens. 2018, 10, 826. [Google Scholar] [CrossRef] [Green Version]
- Barsi, J.A.; Schott, J.R.; Palluconi, F.D.; Hook, S.J. Validation of a Web-Based Atmospheric Correction Tool for Single Thermal Band Instruments. In Proceedings of the Earth Observing Systems X, San Diego, CA, USA, 18 August 2005; Volume 5882, p. 58820E. [Google Scholar]
- Price, J.C. Estimating Surface Temperatures from Satellite Thermal Infrared Data—A Simple Formulation for the Atmospheric Effect. Remote Sens. Environ. 1983, 13, 353–361. [Google Scholar] [CrossRef]
- Barsi, J.A.; Barker, J.L.; Schott, J.R. An Atmospheric Correction Parameter Calculator for a Single Thermal Band Earth-Sensing Instrument. In Proceedings of the IGARSS 2003 IEEE International Geoscience and Remote Sensing Symposium, Toulouse, France, 21–25 July 2003; Volume 5, pp. 3014–3016. [Google Scholar]
- Sobrino, J.A.; Jiménez-Muñoz, J.C.; Paolini, L. Land Surface Temperature Retrieval from LANDSAT TM 5. Remote Sens. Environ. 2004, 90, 434–440. [Google Scholar] [CrossRef]
- Sekertekin, A. Validation of Physical Radiative Transfer Equation-Based Land Surface Temperature Using Landsat 8 Satellite Imagery and SURFRAD in-Situ Measurements. J. Atmos. Sol.-Terr. Phys. 2019, 196, 105161. [Google Scholar] [CrossRef]
- Coll, C.; Caselles, V.; Valor, E.; Niclòs, R. Comparison between Different Sources of Atmospheric Profiles for Land Surface Temperature Retrieval from Single Channel Thermal Infrared Data. Remote Sens. Environ. 2012, 117, 199–210. [Google Scholar] [CrossRef]
- Pérez-Planells, L.; García-Santos, V.; Caselles, V. Comparing Different Profiles to Characterize the Atmosphere for Three MODIS TIR Bands. Atmos. Res. 2015, 161–162, 108–115. [Google Scholar] [CrossRef] [Green Version]
- Mira, M.; Olioso, A.; Rivalland, V.; Courault, D.; Marloie, O.; Guillevic, P. Quantifying Uncertainties in Land Surface Temperature Due to Atmospheric Correction: Application to Landsat-7 Data over a Mediterranean Agricultural Region. In Proceedings of the 2014 IEEE Geoscience and Remote Sensing Symposium, IEEE, Quebec City, QC, Canada, 13–18 July 2014; pp. 2375–2378. [Google Scholar]
- Coll, C.; Caselles, V.; Galve, J.M.; Valor, E.; Niclòs, R.; Sánchez, J.M.; Rivas, R. Ground Measurements for the Validation of Land Surface Temperatures Derived from AATSR and MODIS Data. Remote Sens. Environ. 2005, 97, 288–300. [Google Scholar] [CrossRef]
- Mattar, C.; Durán-Alarcón, C.; Jiménez-Muñoz, J.C.; Santamaría-Artigas, A.; Olivera-Guerra, L.; Sobrino, J.A. Global Atmospheric Profiles from Reanalysis Information (GAPRI): A New Database for Earth Surface Temperature Retrieval. Int. J. Remote Sens. 2015, 36, 5045–5060. [Google Scholar] [CrossRef]
- Duan, S.-B.; Li, Z.-L.; Wang, C.; Zhang, S.; Tang, B.-H.; Leng, P.; Gao, M.-F. Land-Surface Temperature Retrieval from Landsat 8 Single-Channel Thermal Infrared Data in Combination with NCEP Reanalysis Data and ASTER GED Product. Int. J. Remote Sens. 2018, 40, 1763–1778. [Google Scholar] [CrossRef]
- Vanhellemont, Q. Automated Water Surface Temperature Retrieval from Landsat 8/TIRS. Remote Sens. Environ. 2020, 237, 111518. [Google Scholar] [CrossRef]
- Malakar, N.K.; Hulley, G.C.; Hook, S.J.; Laraby, K.; Cook, M.; Schott, J.R. An Operational Land Surface Temperature Product for Landsat Thermal Data: Methodology and Validation. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5717–5735. [Google Scholar] [CrossRef]
- Yang, J.; Duan, S.B.; Zhang, X.; Wu, P.; Huang, C.; Leng, P.; Gao, M. Evaluation of Seven Atmospheric Profiles from Reanalysis and Satellite-Derived Products: Implication for Single-Channel Land Surface Temperature Retrieval. Remote Sens. 2020, 12, 791. [Google Scholar] [CrossRef] [Green Version]
- Alghamdi, A.S. Evaluation of Four Reanalysis Datasets against Radiosonde over Southwest Asia. Atmosphere 2020, 11, 402. [Google Scholar] [CrossRef] [Green Version]
- Berk, A.; Conforti, P.; Kennett, R.; Perkins, T.; Hawes, F.; van den Bosch, J. MODTRAN6: A Major Upgrade of the MODTRAN Radiative Transfer Code. In Proceedings of the Workshop on Hyperspectral Image and Signal Processing, Evolution in Remote Sensing, Lausanne, Switzerland, 13 June 2014; Volume 2014, p. 90880H. [Google Scholar]
- Kalnay, E.; Kanamitsu, M.; Kistler, R.; Collins, W.; Deaven, D.; Gandin, L.; Iredell, M.; Saha, S.; White, G.; Woollen, J.; et al. The NCEP/NCAR 40-Year Reanalysis Project. Bull. Am. Meteorol. Soc. 1996, 77, 437–471. [Google Scholar] [CrossRef] [Green Version]
- National Centers for Environmental Prediction National Weather Service NOAA. U.S. Department of Commerce NCEP FNL Operational Model Global Tropospheric Analyses, Continuing from July 1999; National Centers for Environmental Prediction National Weather Service NOAA: College Park, MD, USA, 2000. [CrossRef]
- Borbas, E.; Menzel, P. MODIS Atmosphere L2 Atmosphere Profile Product; NASA MODIS Adaptive Processing System; Goddard Space Flight Center: Greenbelt, MD, USA, 2017.
- Skokovic, D.; Sobrino, J.A.; Jimenez-Munoz, J.C. Vicarious Calibration of the Landsat 7 Thermal Infrared Band and LST Algorithm Validation of the ETM+ Instrument Using Three Global Atmospheric Profiles. IEEE Trans. Geosci. Remote Sens. 2017, 55, 1804–1811. [Google Scholar] [CrossRef]
- Li, H.; Liu, Q.; Du, Y.; Jiang, J.; Wang, H. Evaluation of the NCEP and MODIS Atmospheric Products for Single Channel Land Surface Temperature Retrieval with Ground Measurements: A Case Study of HJ-1B IRS Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 1399–1408. [Google Scholar] [CrossRef]
- Aumann, H.H.; Chahine, M.T.; Gautier, C.; Goldberg, M.D.; Kalnay, E.; McMillin, L.M.; Revercomb, H.; Rosenkranz, P.W.; Smith, W.L.; Staelin, D.H.; et al. AIRS/AMSU/HSB on the Aqua Mission: Design, Science Objectives, Data Products, and Processing Systems. IEEE Trans. Geosci. Remote Sens. 2003, 41, 253–264. [Google Scholar] [CrossRef] [Green Version]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim Reanalysis: Configuration and Performance of the Data Assimilation System. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Rienecker, M.M.; Suarez, M.J.; Gelaro, R.; Todling, R.; Bacmeister, J.; Liu, E.; Bosilovich, M.G.; Schubert, S.D.; Takacs, L.; Kim, G.K.; et al. MERRA: NASA’s Modern-Era Retrospective Analysis for Research and Applications. J. Clim. 2011, 24, 3624–3648. [Google Scholar] [CrossRef]
- Kanamitsu, M.; Ebisuzaki, W.; Woollen, J.; Yang, S.K.; Hnilo, J.J.; Fiorino, M.; Potter, G.L. NCEP-DOE AMIP-II Reanalysis (R-2). Bull. Am. Meteorol. Soc. 2002, 83, 1631–1644. [Google Scholar] [CrossRef]
- Kobayashi, S.; Ota, Y.; Harada, Y.; Ebita, A.; Moriya, M.; Onoda, H.; Onogi, K.; Kamahori, H.; Kobayashi, C.; Endo, H.; et al. The JRA-55 Reanalysis: General Specifications and Basic Characteristics. J. Meteorol. Soc. Japan. Ser. II 2015, 93, 5–48. [Google Scholar] [CrossRef] [Green Version]
- Chen, B.; Liu, Z. Global Water Vapor Variability and Trend from the Latest 36 Year (1979 to 2014) Data of ECMWF and NCEP Reanalyses, Radiosonde, GPS, and Microwave Satellite. J. Geophys. Res. Atmos. 2016, 121, 11442–11462. [Google Scholar] [CrossRef]
- Chen, G.; Iwasaki, T.; Qin, H.; Sha, W. Evaluation of the Warm-Season Diurnal Variability over East Asia in Recent Reanalyses JRA-55, ERA-Interim, NCEP CFSR, and NASA MERRA. J. Clim. 2014, 27, 5517–5537. [Google Scholar] [CrossRef]
- Tonooka, H. An Atmospheric Correction Algorithm for Thermal Infrared Multispectral Data over Land-a Water-Vapor Scaling Method. IEEE Trans. Geosci. Remote Sens. 2001, 39, 682–692. [Google Scholar] [CrossRef]
- Wee, T.K.; Kuo, Y.H.; Lee, D.K.; Liu, Z.; Wang, W.; Chen, S.Y. Two Overlooked Biases of the Advanced Research Wrf (Arw) Model in Geopotential Height and Temperature. Mon. Weather Rev. 2012, 140, 3907–3918. [Google Scholar] [CrossRef]
- Hassanli, H.; Rahimzadegan, M. Investigating Extracted Total Precipitable Water Vapor from Weather Research and Forecasting (WRF) Model and MODIS Measurements. J. Atmos. Sol. -Terr. Phys. 2019, 193, 105060. [Google Scholar] [CrossRef]
- Lee, H.; Won, J.S.; Park, W. An Atmospheric Correction Using High Resolution Numericalweather Prediction Models for Satellite-Borne Single-Channel Mid-Wavelength and Thermal Infrared Imaging Sensors. Remote Sens. 2020, 12, 853. [Google Scholar] [CrossRef] [Green Version]
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Zhiquan, L.; Berner, J.; Wang, W.; Powers, J.G.; Duda, M.G.; Barker, D.M.; et al. A Description of the Advanced Research WRF Model Version 4; National Center for Atmospheric Research: Boulder, CO, USA, 2019. [Google Scholar]
- Powers, J.G.; Klemp, J.B.; Skamarock, W.C.; Davis, C.A.; Dudhia, J.; Gill, D.O.; Coen, J.L.; Gochis, D.J.; Ahmadov, R.; Peckham, S.E.; et al. The Weather Research and Forecasting Model: Overview, System Efforts, and Future Directions. Bull. Am. Meteorol. Soc. 2017, 98, 1717–1737. [Google Scholar] [CrossRef]
- Onwukwe, C.; Jackson, P.L. Meteorological Downscaling with Wrf Model, Version 4.0, and Comparative Evaluation of Planetary Boundary Layer Schemes over a Complex Coastal Airshed. J. Appl. Meteorol. Climatol. 2020, 59, 1295–1319. [Google Scholar] [CrossRef]
- Kioutsioukis, I.; de Meij, A.; Jakobs, H.; Katragkou, E.; Vinuesa, J.; Kazantzidis, A. High Resolution WRF Ensemble Forecasting for Irrigation: Multi-Variable Evaluation. Atmos. Res. 2016, 167, 156–174. [Google Scholar] [CrossRef]
- Moya-Álvarez, A.S.; Estevan, R.; Kumar, S.; Flores Rojas, J.L.; Ticse, J.J.; Martínez-Castro, D.; Silva, Y. Influence of PBL Parameterization Schemes in WRF_ARW Model on Short-Range Precipitation’s Forecasts in the Complex Orography of Peruvian Central Andes. Atmos. Res. 2020, 233, 104708. [Google Scholar] [CrossRef]
- Fekih, A.; Mohamed, A. Evaluation of the WRF Model on Simulating the Vertical Structure and Diurnal Cycle of the Atmospheric Boundary Layer over Bordj Badji Mokhtar (Southwestern Algeria). J. King Saud Univ.-Sci. 2019, 31, 602–611. [Google Scholar] [CrossRef]
- Mylonas, M.P.; Douvis, K.C.; Polychroni, I.D.; Politi, N.; Nastos, P.T. Analysis of a Mediterranean Tropical-Like Cyclone. Sensitivity to WRF Parameterizations and Horizontal Resolution. Atmosphere 2019, 10, 425. [Google Scholar] [CrossRef] [Green Version]
- Tyagi, B.; Magliulo, V.; Finardi, S.; Gasbarra, D.; Carlucci, P.; Toscano, P.; Zaldei, A.; Riccio, A.; Calori, G.; D’Allura, A.; et al. Performance Analysis of Planetary Boundary Layer Parameterization Schemes in WRF Modeling Set up over Southern Italy. Atmosphere 2018, 9, 272. [Google Scholar] [CrossRef] [Green Version]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 Global Reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2046. [Google Scholar] [CrossRef]
- Saha, S.; Moorthi, S.; Wu, X.; Wang, J.; Nadiga, S.; Tripp, P.; Behringer, D.; Hou, Y.-T.; Chuang, H.; Iredell, M.; et al. The NCEP Climate Forecast System Version 2. J. Clin. 2014, 27, 2185–2208. [Google Scholar] [CrossRef]
- Vanhellemont, Q. Combined Land Surface Emissivity and Temperature Estimation from Landsat 8 OLI and TIRS. ISPRS J. Photogramm. Remote Sens. 2020, 166, 390–402. [Google Scholar] [CrossRef]
- Porto Alegre City Hall. Neighborhood Law No. 12.112/16; Porto Alegre Official Gazette: Porto Alegre, Brazil, 2016; p. 37. [Google Scholar]
- Alvares, C.A.; Stape, J.L.; Sentelhas, P.C.; De Moraes Gonçalves, J.L.; Sparovek, G. Köppen’s Climate Classification Map for Brazil. Meteorol. Z. 2013, 22, 711–728. [Google Scholar] [CrossRef]
- Matzenauer, R.; Radin, B.; Almeida, I.R. de Atlas Climático Do Rio Grande Do Sul; CemetRS: Porto Alegre, Brazil, 2011.
- Roy, D.P.; Wulder, M.A.; Loveland, T.R.; C.E., W.; Allen, R.G.; Anderson, M.C.; Helder, D.; Irons, J.R.; Johnson, D.M.; Kennedy, R.; et al. Landsat-8: Science and Product Vision for Terrestrial Global Change Research. Remote Sens. Environ. 2014, 145, 154–172. [Google Scholar] [CrossRef] [Green Version]
- Sekertekin, A.; Bonafoni, S. Land Surface Temperature Retrieval from Landsat 5, 7, and 8 over Rural Areas: Assessment of Different Retrieval Algorithms and Emissivity Models and Toolbox Implementation. Remote Sens. 2020, 12, 294. [Google Scholar] [CrossRef] [Green Version]
- Wang, W.; Bruyere, C.; Michael, D.; Duhia, J.; Dave, G.; Kavulich, M.; Werner, K.; Chen, M.; Hui-Chuan, L.; Michalakes, J.; et al. Advanced Research WRF (ARW) Version 4 Modeling System User´s Guide; National Center for Atmospheric Research: Boulder, CO, USA, 2019; Volume 456. [Google Scholar]
- Xie, B.; Fung, J.C.H.; Chan, A.; Lau, A. Evaluation of Nonlocal and Local Planetary Boundary Layer Schemes in the WRF Model. J. Geophys. Res. Atmos. 2012, 117. [Google Scholar] [CrossRef]
- Stensrud, D.J. Parameterization Schemes; Cambridge University Press: Cambridge, UK, 2007; Volume 9780521865, ISBN 9780511812590. [Google Scholar]
- García-Díez, M.; Fernández, J.; Fita, L.; Yagüe, C. Seasonal Dependence of WRF Model Biases and Sensitivity to PBL Schemes over Europe. Q. J. R. Meteorol. Soc. 2013, 139, 501–514. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.-H.; Sun, W.-Y. A One-Dimensional Time Dependent Cloud Model. J. Meteorol. Soc. Japan Ser. II 2002, 80, 99–118. [Google Scholar] [CrossRef] [Green Version]
- Hong, S.-Y.; Noh, Y.; Dudhia, J. A New Vertical Diffusion Package with an Explicit Treatment of Entrainment Processes. Mon. Weather Rev. 2006, 134, 2318–2341. [Google Scholar] [CrossRef] [Green Version]
- Janjić, Z.I. The Step-Mountain Eta Coordinate Model: Further Developments of the Convection, Viscous Sublayer, and Turbulence Closure Schemes. Mon. Weather Rev. 1994, 122, 927–945. [Google Scholar] [CrossRef] [Green Version]
- Dudhia, J. Numerical Study of Convection Observed during the Winter Monsoon Experiment Using a Mesoscale Two-Dimensional Model. J. Atmos. Sci. 1989, 46, 3077–3107. [Google Scholar] [CrossRef]
- Mlawer, E.J.; Taubman, S.J.; Brown, P.D.; Iacono, M.J.; Clough, S.A. Radiative Transfer for Inhomogeneous Atmospheres: RRTM, a Validated Correlated-k Model for the Longwave. J. Geophys. Res. Atmos. 1997, 102, 16663–16682. [Google Scholar] [CrossRef] [Green Version]
- Tewari, M.; Chen, F.; Wang, W.; Dudhia, J.; LeMone, M.A.; Mitchell, K.; Ek, M.; Gayno, G.; Wegiel, J.; Cuenca, R.H. Implementation and Verification of the Unified Noah Land Surface Model in the WRF Model. Bull. Am. Meteorol. Soc. 2004, 2165–2170. [Google Scholar] [CrossRef]
- Jiménez, P.A.; Dudhia, J.; González-Rouco, J.F.; Navarro, J.; Montávez, J.P.; García-Bustamante, E. A Revised Scheme for the WRF Surface Layer Formulation. Mon. Weather Rev. 2012, 140, 898–918. [Google Scholar] [CrossRef] [Green Version]
- Diaz, L.R.; Santos, D.C.; Käfer, P.S.; Iglesias, M.L.; da Rocha, N.S.; da Costa, S.T.L.; Kaiser, E.A.; Rolim, S.B.A. Reanalysis Profile Downscaling with WRF Model and Sensitivity to PBL Parameterization Schemes over a Subtropical Station. J. Atmos. Sol.-Terr. Phys. 2021, 222, 105724. [Google Scholar] [CrossRef]
- Santos, D.C.; Nascimento, E.D.L. Numerical Simulations of the South American Low Level Jet in Two Episodes of MCSs: Sensitivity to PBL and Convective Parameterization Schemes. Adv. Meteorol. 2016, 2016. [Google Scholar] [CrossRef] [Green Version]
- Diaz, L.R.; Santos, D.C.; Käfer, P.S.; da Rocha, N.S.; da Costa, S.T.L.; Kaiser, E.A.; Rolim, S.B.A. Atmospheric Correction of Thermal Infrared Landsat Images Using High-Resolution Vertical Profiles Simulated by WRF Model. Environ. Sci. Proc. 2021, 8, 27. [Google Scholar] [CrossRef]
- Sobrino, J.; Raissouni, N.; Li, Z.-L. A Comparative Study of Land Surface Emissivity Retrieval from NOAA Data. Remote Sens. Environ. 2001, 75, 256–266. [Google Scholar] [CrossRef]
- Li, Z.L.; Wu, H.; Wang, N.; Qiu, S.; Sobrino, J.A.; Wan, Z.; Tang, B.H.; Yan, G. Land Surface Emissivity Retrieval from Satellite Data. Int. J. Remote Sens. 2013, 34, 3084–3127. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Jimenez-Munoz, J.C.; Soria, G.; Romaguera, M.; Guanter, L.; Moreno, J.; Plaza, A.; Martinez, P. Land Surface Emissivity Retrieval from Different VNIR and TIR Sensors. IEEE Trans. Geosci. Remote Sens. 2008, 46, 316–327. [Google Scholar] [CrossRef]
- Van de Griend, A.A.; Owe, M. On the Relationship between Thermal Emissivity and the Normalized Difference Vegetation Index for Natural Surfaces. Int. J. Remote Sens. 1993, 14, 1119–1131. [Google Scholar] [CrossRef]
- Yu, X.; Guo, X.; Wu, Z. Land Surface Temperature Retrieval from Landsat 8 TIRS—Comparison between Radiative Transfer Equation-Based Method, Split Window Algorithm and Single Channel Method. Remote Sens. 2014, 6, 9829–9852. [Google Scholar] [CrossRef] [Green Version]
- Li, S.; Jiang, G.-M. Land Surface Temperature Retrieval from Landsat-8 Data With the Generalized Split-Window Algorithm. IEEE Access 2018, 6, 18149–18162. [Google Scholar] [CrossRef]
- Valor, E.; Caselles, V. Mapping Land Surface Emissivity from NDVI: Application to European, African, and South American Areas. Remote Sens. Environ. 1996, 57, 167–184. [Google Scholar] [CrossRef]
- Käfer, P.S.P.S.; Rolim, S.B.A.; Iglesias, M.L.; da Rocha, N.S.; Diaz, L.R. Land Surface Temperature Retrieval by LANDSAT 8 Thermal Band: Applications of Laboratory and Field Measurements. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 2332–2341. [Google Scholar] [CrossRef]
- Sekertekin, A.; Bonafoni, S. Sensitivity Analysis and Validation of Daytime and Nighttime Land Surface Temperature Retrievals from Landsat 8 Using Different Algorithms and Emissivity Models. Remote Sens. 2020, 12, 2776. [Google Scholar] [CrossRef]
- Oltra-Carrió, R.; Sobrino, J.A.; Franch, B.; Nerry, F. Land Surface Emissivity Retrieval from Airborne Sensor over Urban Areas. Remote Sens. Environ. 2012, 123, 298–305. [Google Scholar] [CrossRef]
- Harod, R.; Eswar, R.; Bhattacharya, B.K. Effect of Surface Emissivity and Retrieval Algorithms on the Accuracy of Land Surface Temperature Retrieved from Landsat Data. Remote Sens. Lett. 2021, 12, 983–993. [Google Scholar] [CrossRef]
- Ihlen, V.; Zanter, K. Landsat 8 (L8) Data Users Handbook; USGS: Sioux Falls, SD, USA, 2019; Volume 5.
- Jiménez-Muñoz, J.C.; Cristobal, J.; Sobrino, J.A.J.A.; Sòria, G.; Ninyerola, M.; Pons, X.; Jimenez-Munoz, J.C.; Cristobal, J.; Sobrino, J.A.J.A.; Soria, G.; et al. Revision of the Single-Channel Algorithm for Land Surface Temperature Retrieval from Landsat Thermal-Infrared Data. IEEE Trans. Geosci. Remote Sens. 2009, 47, 339–349. [Google Scholar] [CrossRef]
- Carlson, T.N.; Ripley, D.A. On the Relation between NDVI, Fractional Vegetation Cover, and Leaf Area Index. Remote Sens. Environ. 1997, 62, 241–252. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Raissouni, N. Toward Remote Sensing Methods for Land Cover Dynamic Monitoring: Application to Morocco. Int. J. Remote Sens. 2000, 21, 353–366. [Google Scholar] [CrossRef]
- Berk, A.; Anderson, G.P.; Acharya, P.K.; Hoke, M.L.; Chetwynd, J.H.; Bernstein, L.S.; Shettle, E.P.; Matthew, M.W.; Adler-Golden, S.M. MODTRAN4 Version 3 Revision 1 USER’S MANUA.; Air Force Research Laboratory: Hanscom AFB, MA, USA, 2003. [Google Scholar]
- Atmospheric Correction Parameter Calculator. Mid-Latitude Summer Standard Profile. Available online: https://atmcorr.gsfc.nasa.gov/RSD/mid_lat_summer_stdatm_RH_units.rsd (accessed on 16 December 2020).
- Atmospheric Correction Parameter Calculator. Mid-Latitude Winter Standard Profile. Available online: https://atmcorr.gsfc.nasa.gov/RSD/mid_lat_winter_stdatm_units.rsd (accessed on 16 December 2020).
- Chai, T.; Draxler, R.R. Root Mean Square Error (RMSE) or Mean Absolute Error (MAE)?–Arguments against Avoiding RMSE in the Literature. Geosci. Model Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef] [Green Version]
- Willmott, C.J.; Matsuura, K. Advantages of the Mean Absolute Error (MAE) over the Root Mean Square Error (RMSE) in Assessing Average Model Performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef]
- Taylor, K.E. Summarizing Multiple Aspects of Model Performance in a Single Diagram. J. Geophys. Res. Atmos. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- Pérez-Jordán, G.; Castro-Almazán, J.A.; Muñoz-Tuñón, C.; Codina, B.; Vernin, J. Forecasting the Precipitable Water Vapour Content: Validation for Astronomical Observatories Using Radiosoundings. Mon. Not. R. Astron. Soc. 2015, 452, 1992–2003. [Google Scholar] [CrossRef]
- Lin, C.; Chen, D.; Yang, K.; Ou, T. Impact of Model Resolution on Simulating the Water Vapor Transport through the Central Himalayas: Implication for Models’ Wet Bias over the Tibetan Plateau. Clim. Dyn. 2018, 51, 3195–3207. [Google Scholar] [CrossRef] [Green Version]
- Mohan, M.; Sati, A.P. WRF Model Performance Analysis for a Suite of Simulation Design. Atmos. Res. 2016, 169, 280–291. [Google Scholar] [CrossRef]
- Tavares, M.H.; Cunha, A.H.F.; Motta-Marques, D.; Ruhoff, A.L.; Cavalcanti, J.R.; Fragoso, C.R.; Bravo, J.M.; Munar, A.M.; Fan, F.M.; Rodrigues, L.H.R. Comparison of Methods to Estimate Lake-Surface-Water Temperature Using Landsat 7 ETM+ and MODIS Imagery: Case Study of a Large Shallow Subtropical Lake in Southern Brazil. Water 2019, 11, 168. [Google Scholar] [CrossRef] [Green Version]
- Coll, C.; Galve, J.M.; Sanchez, J.M.; Caselles, V. Validation of Landsat-7/ETM+ Thermal-Band Calibration and Atmospheric Correction with Ground-Based Measurements. IEEE Trans. Geosci. Remote Sens. 2010, 48, 547–555. [Google Scholar] [CrossRef]
- García-Santos, V.; Cuxart, J.; Martínez-Villagrasa, D.; Jiménez, M.A.; Simó, G. Comparison of Three Methods for Estimating Land Surface Temperature from Landsat 8-TIRS Sensor Data. Remote Sens. 2018, 10, 1450. [Google Scholar] [CrossRef] [Green Version]
- Windahl, E.; de Beurs, K. An Intercomparison of Landsat Land Surface Temperature Retrieval Methods under Variable Atmospheric Conditions Using in Situ Skin Temperature. Int. J. Appl. Earth Obs. Geoinf. 2016, 51, 11–27. [Google Scholar] [CrossRef] [Green Version]
- Käfer, P.S.; Rolim, S.B.A.; Diaz, L.R.; da Rocha, N.S.; Iglesias, M.L.; Rex, F.E. Comparative analysis of split-window and single-channel algorithms for land surface temperature retrieval of a pseudo-invariant target. Bull. Geod. Sci. 2020, 26. [Google Scholar] [CrossRef]
- Wang, D.; Liu, Y.; Yu, T.; Zhang, Y.; Liu, Q.; Chen, X.; Zhan, Y. A Method of Using WRF-Simulated Surface Temperature to Estimate Daily Evapotranspiration. J. Appl. Meteorol. Climatol. 2020, 59, 901–914. [Google Scholar] [CrossRef] [Green Version]
- Wang, D.; Yu, T.; Liu, Y.; Gu, X.; Mi, X.; Shi, S.; Ma, M.; Chen, X.; Zhang, Y.; Liu, Q.; et al. Estimating Daily Actual Evapotranspiration at a Landsat-like Scale Utilizing Simulated and Remote Sensing Surface Temperature. Remote Sens. 2021, 13, 225. [Google Scholar] [CrossRef]









| Scene ID | Acquisition Date | Case Day | Season | Air T [°C] | PWV [g/cm2] |
|---|---|---|---|---|---|
| LC82210812013322LGN01 | 18 November 2013 | 1 | spring | 23 | 1.57 |
| LC82210812013338LGN01 | 4 December 2013 | 2 | spring | 21 | 2.43 |
| LC82210812014037LGN01 | 6 February 2014 | 3 | summer | 31 | 4.10 |
| LC82210812014293LGN01 | 20 October 2014 | 4 | spring | 19.8 | 1.18 |
| LC82210812014341LGN01 | 7 December 2014 | 5 | spring | 26.6 | 1.99 |
| LC82210812015024LGN01 | 24 January 2015 | 6 | summer | 24.4 | 2.66 |
| LC82210812015056LGN01 | 25 February 2015 | 7 | summer | 24.6 | 3.26 |
| LC82210812015312LGN01 | 8 November 2015 | 8 | spring | 24.4 | 2.79 |
| LC82210812016075LGN01 | 15 March 2016 | 9 | summer | 22.8 | 2.23 |
| LC82210812016235LGN02 | 22 August 2016 | 10 | winter | 9.4 | 0.91 |
| LC82210812016347LGN01 | 12 December 2016 | 11 | summer | 23.4 | 3.27 |
| LC82210812017093LGN01 | 3 April 2017 | 12 | autumn | 22 | 3.31 |
| LC82210812017173LGN00 | 22 June 2017 | 13 | winter | 10.6 | 1.85 |
| LC82210812017205LGN00 | 24 July 2017 | 14 | winter | 13.4 | 1.93 |
| LC82210812017237LGN00 | 25 August 2017 | 15 | winter | 22.2 | 2.82 |
| LC82210812017317LGN00 | 13 November 2017 | 16 | spring | 20 | 1.83 |
| LC82210812017349LGN00 | 15 December 2017 | 17 | spring | 25.2 | 3.17 |
| LC82210812018048LGN00 | 17 February 2018 | 18 | summer | 23.4 | 2.36 |
| LC82210812018112LGN00 | 22 April 2018 | 19 | autumn | 19 | 3.26 |
| LC82210812018160LGN00 | 9 June 2018 | 20 | autumn | 6.6 | 0.84 |
| LC82210812018240LGN00 | 28 August 2018 | 21 | winter | 9.4 | 0.60 |
| LC82210812018272LGN00 | 29 September 2018 | 22 | spring | 23 | 3.60 |
| LC82210812018320LGN00 | 16 November 2018 | 23 | spring | 23.6 | 1.74 |
| LC82210812019083LGN00 | 24 March 2019 | 24 | autumn | 25.8 | 2.53 |
| LC82210812019099LGN00 | 9 April 2019 | 25 | autumn | 19.6 | 1.72 |
| LC82210812019227LGN00 | 15 August 2019 | 26 | winter | 10.8 | 1.08 |
| LC82210812019323LGN00 | 19 November 2019 | 27 | spring | 24.8 | 2.33 |
| WRF Model Configuration | |
|---|---|
| Version | 4.1.2 |
| Dynamical solver | ARW |
| Boundary conditions | NCEP CFSv2 |
| Map projection | Lambert |
| Grid size | Domain 1: (119 × 116) × 33 Domain 2: (169 × 165) × 33 |
| Horizontal resolution | Domain 1: 12 km Domain 2: 3 km |
| Nesting | One-way |
| Time step | 72 s |
| Static geographical data | USGS |
| Cloud Microphysics | Purdue Lin |
| Planetary Boundary Layer (PBL) | Yonsei University (YSU) |
| Cumulus | Betts–Miller–Janjic (BMJ) 1 |
| Shortwave Radiation | Dudhia |
| Longwave Radiation | Rapid Radiative Transfer Model (RRTM) |
| Land Surface Model (LSM) | Unified NOAH |
| Surface-layer | Revised MM5 |
| CFSv2 | WRF G12 | WRF G03 | ACPC | ||
|---|---|---|---|---|---|
| Transmittance | R | 0.96 | 0.93 | 0.93 | 0.97 |
| bias | 0.01 | 0.00 | 0.00 | 0.01 | |
| MAE | 0.02 | 0.03 | 0.03 | 0.02 | |
| RMSE | 0.03 | 0.04 | 0.04 | 0.03 | |
| Upwelling | R | 0.97 | 0.94 | 0.94 | 0.98 |
| bias | −0.12 | −0.04 | −0.02 | −0.06 | |
| MAE | 0.21 | 0.24 | 0.24 | 0.16 | |
| RMSE | 0.27 | 0.33 | 0.34 | 0.20 | |
| Downwelling | R | 0.97 | 0.95 | 0.95 | 0.98 |
| bias | −0.15 | −0.05 | −0.03 | 0.08 | |
| MAE | 0.28 | 0.30 | 0.30 | 0.21 | |
| RMSE | 0.35 | 0.42 | 0.43 | 0.27 |
| CFSv2 | WRF G12 | WRF G03 | ACPC | ||
|---|---|---|---|---|---|
| LST [K] | R | 0.99 | 0.99 | 0.99 | 0.99 |
| bias | 0.23 | 0.32 | 0.36 | −0.38 | |
| MAE | 0.54 | 0.79 | 0.81 | 0.56 | |
| RMSE | 0.55 | 0.79 | 0.82 | 0.56 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Diaz, L.R.; Santos, D.C.; Käfer, P.S.; Rocha, N.S.d.; Costa, S.T.L.d.; Kaiser, E.A.; Rolim, S.B.A. Land Surface Temperature Retrieval Using High-Resolution Vertical Profiles Simulated by WRF Model. Atmosphere 2021, 12, 1436. https://doi.org/10.3390/atmos12111436
Diaz LR, Santos DC, Käfer PS, Rocha NSd, Costa STLd, Kaiser EA, Rolim SBA. Land Surface Temperature Retrieval Using High-Resolution Vertical Profiles Simulated by WRF Model. Atmosphere. 2021; 12(11):1436. https://doi.org/10.3390/atmos12111436
Chicago/Turabian StyleDiaz, Lucas Ribeiro, Daniel Caetano Santos, Pâmela Suélen Käfer, Nájila Souza da Rocha, Savannah Tâmara Lemos da Costa, Eduardo Andre Kaiser, and Silvia Beatriz Alves Rolim. 2021. "Land Surface Temperature Retrieval Using High-Resolution Vertical Profiles Simulated by WRF Model" Atmosphere 12, no. 11: 1436. https://doi.org/10.3390/atmos12111436
APA StyleDiaz, L. R., Santos, D. C., Käfer, P. S., Rocha, N. S. d., Costa, S. T. L. d., Kaiser, E. A., & Rolim, S. B. A. (2021). Land Surface Temperature Retrieval Using High-Resolution Vertical Profiles Simulated by WRF Model. Atmosphere, 12(11), 1436. https://doi.org/10.3390/atmos12111436