Non-Dimensional Groups, Film Thickness Equations and Correction Factors for Elastohydrodynamic Lubrication: A Review
Abstract
:1. Introduction
2. Non-Dimensional Groups
3. Film Thickness Equations
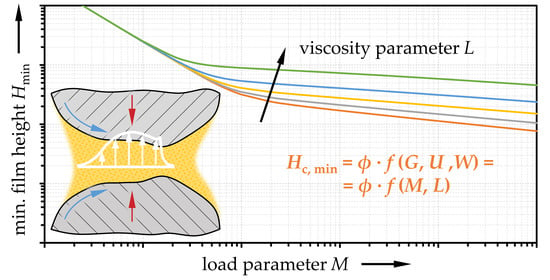
3.1. Line-Contacts (2D)
3.2. Point- and Elliptical Contacts (3D)
4. Correction Factors
4.1. Fluid Compressibility
4.2. Thermal Effects
4.3. Non-Newtonian Fluid Behavior
4.4. Starvation
4.5. Surface Roughness and Asperity Contact
5. Applicability, Limitations and Future Directions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| aH | small Hertzian half-axis |
| A | normalized amplitude |
| bH | large Hertzian half-axis |
| Ei | Young’s modulus |
| E’ | reduced Young’s modulus |
| F | normal load |
| gi | Greenwood parameter |
| G | material parameter |
| G | effective liquid shear modulus |
| h | lubricant gap |
| hc | central lubricant gap |
| hliq | lubricant layer height |
| hmin | minimum lubricant gap |
| hn | film thickness derived from Newtonian calculation |
| H | fluid film parameter |
| H00 | asymptote parameter |
| Hc | central fluid film parameter |
| Hmin | minimum fluid film parameter |
| k | ellipticity parameter |
| l | line-contact length |
| L | viscosity parameter |
| m | inlet meniscus |
| m* | fully flooded-starved boundary |
| M | load parameter |
| n | Slotte exponent |
| n | Carreau exponent |
| Na | Nahme-Griffith number |
| p | pressure |
| pH | Hertzian pressure |
| PE | elasticity parameter |
| Pα | pressure-viscosity parameter |
| Q | thermal stress parameter |
| r | asymptote exponent |
| Ri | Radius |
| s | asymptote exponent |
| SRR | slide-to-roll ratio |
| t | asymptote exponent |
| T0 | reference temperature |
| Ts | Slotte constant |
| ui | velocity |
| um | hydrodynamic effective velocity |
| U | velocity parameter |
| V | dimensionless hardness number |
| W | load parameter |
| αp | pressure-viscosity coefficient |
| β | viscosity-temperature coefficient |
| γ | Peklenik factor |
| shear rate | |
| η | viscosity |
| η0 | base viscosity |
| η∞ | second Newtonian viscosity |
| θm | fractional film content |
| κ | ellipticity parameter |
| λ | thermal conductivity |
| λτ | limiting stress-pressure coefficient |
| λΓ | relaxation time |
| Λ | fluid film parameter |
| νi | Poisson’s ratio |
| ρ | density |
| ρ0 | base density |
| σ | quadratic mean surface roughness |
| τ | shear stress |
| τl | limiting shear stress |
| τu | unbound shear stress |
| ϕi | correction factor |
| Γ | Weissenberg number |
References
- Van Leeuwen, H.H.; Schouten, M.J.W. Die Elastohydrodynamik: Geschichte und Neuentwicklungen; VDI Verlag: Düsseldorf, Germany, 1995. [Google Scholar]
- Hertz, H. Über die Berührung fester elastischer Körper. J. Für Die Reine und Angew. Math. 1882, 1882, 156–171. [Google Scholar]
- Czichos, H.; Habig, K.-H. Tribologie-Handbuchb. Tribometrie, Tribomaterialien, Tribotechnik; Springer Fachmedien Wiesbaden: Wiesbaden, Germany, 2015; ISBN 978-3-8348-2236-9. [Google Scholar]
- Gohar, R. Elastohydrodynamics; Horwood, E., Ed.; Halsted Press: Chichester, NY, USA, 1988; ISBN 9780853128205. [Google Scholar]
- Hartinger, M.; Dumont, M.-L.; Ioannides, S.; Gosman, D.; Spikes, H. CFD Modeling of a Thermal and Shear-Thinning Elastohydrodynamic Line Contact. J. Tribol. 2008, 130, 41503–4150316. [Google Scholar] [CrossRef]
- Reynolds, O. On the Theory of Lubrication and Its Application to Mr. Beauchamp Tower’s Experiments, Including an Experimental Determination of the Viscosity of Olive Oil. Philos. Trans. R. Soc. Lond. 1886, 177, 157–234. [Google Scholar]
- Venner, C.H.; Lubrecht, A.A. Multigrid techniques: A fast and efficient method for the numerical simulation of elastohydrodynamically lubricated point contact problems. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2000, 214, 43–62. [Google Scholar] [CrossRef]
- Venner, C.H.; Lubrecht, A.A. Multilevel Methods in Lubrication; Elsevier: Amsterdam, The Netherlands, 2000; ISBN 0-444-50503-2. [Google Scholar]
- Habchi, W.; Demirci, I.; Eyheramendy, D.; Morales-Espejel, G.; Vergne, P. A finite element approach of thin film lubrication in circular EHD contacts. Tribol. Int. 2007, 40, 1466–1473. [Google Scholar] [CrossRef]
- Habchi, W. Finite Element Modeling of Elastohydrodynamic Lubrication Problems; John Wiley & Sons Incorporated: Newark, NJ, USA, 2018; ISBN 978-1119225126. [Google Scholar]
- Dowson, D.; Higginson, G.R. A numerical solution to the elasto-hydrodynamic problem. J. Mech. Eng. Sci. 1959, 1, 6–15. [Google Scholar] [CrossRef]
- Dowson, D.; Song, E.S.; Taylor, C.M. Non-Dimensional Groups in Elastohydrodynamic Lubrication. In Thin Films in Tribology, Proceedings of the 19th Leeds-Lyon Symposium on Tribology, Leeds, UK, 8–11 September 1993; Elsevier: Amsterdam, The Netherlands, 1993; pp. 237–242. ISBN 9780444897893. [Google Scholar]
- Dowson, D.; Higginson, G.R. The Effect of Material Properties on the Lubrication of Elastic Rollers. J. Mech. Eng. Sci. 1960, 2, 188–194. [Google Scholar] [CrossRef]
- Dowson, D.; Higginson, G.R.; Whitaker, A.V. Elasto-hydrodynamic lubrication: A survey of isothermal solutions. J. Mech. Eng. Sci. 1962, 4, 121–126. [Google Scholar] [CrossRef]
- Wiśniewski, M. Elastohydrodynamische Schmierung. Grundlagen und Anwendungen; Expert-Verlag: Renningen-Malmsheim, Germany, 2000; ISBN 9783816917458. [Google Scholar]
- Moes, H. Discussion on Paper D1 by D. Dowson. Proc. Inst. Mech. Eng. 1966, 180, 244–245. [Google Scholar]
- Moes, H. Communications. In Proceedings of the Symposium on Elastohydrodynamic Lubrication, London, UK, 21–23 September 1965; pp. 244–245. [Google Scholar]
- Greenwood, J.A. Presentation of Elastohydrodynamic Film-Thickness Results. J. Mech. Eng. Sci. 1969, 11, 128–132. [Google Scholar] [CrossRef]
- Johnson, K.L. Regimes of elastohydrodynamic lubrication. J. Mech. Eng. Sci. 1970, 12, 9–16. [Google Scholar] [CrossRef]
- Habchi, W.; Bair, S.; Vergne, P. On friction regimes in quantitative elastohydrodynamics. Tribol. Int. 2013, 58, 107–117. [Google Scholar] [CrossRef]
- Bird, R.B.; Armstrong, R.C.; Hassager, O. Dynamics of Polymeric Liquids, 2nd ed.; Wiley: New York, NY, USA, 1996; ISBN 978-0-471-80245-7. [Google Scholar]
- Bair, S. Shear thinning correction for rolling/sliding elastohydrodynamic film thickness. Proc. IMechE 2005, 219, 69–74. [Google Scholar] [CrossRef]
- Winter, H.H. Viscous Dissipation in Shear Flows of Molten Polymers. In Advances in Heat Transfer; Elsevier: Amsterdam, The Netherlands, 1977; Volume 13, pp. 205–267. ISBN 9780120200139. [Google Scholar]
- Greenwood, J.A. Elastohydrodynamic Lubrication. Lubricants 2020, 8, 51. [Google Scholar] [CrossRef]
- Dowson, D. Elastohydrodynamics. Proc. Inst. Mech. Eng. 1968, 182, 151–157. [Google Scholar]
- Jacobson, B.O.; Hamrock, B.J. Non-Newtonian Fluid Model Incorporated Into Elastohydrodynamic Lubrication of Rectangular Contacts. J. Tribol. 1984, 106, 275. [Google Scholar] [CrossRef] [Green Version]
- Dowson, D.; Toyoda, S. A central film thickness formula for elastohydrodynamic line contacts. In Proceedings of the 5th Leeds-Lyon Symposium on Tribology, Leeds, UK, September 1978; pp. 60–65. [Google Scholar]
- Myers, T.G.; Hall, R.W.; Savage, M.D.; Gaskell, P.H. The transition region of elastohydrodynamic lubrication. Proc. R. Soc. Lond. A 1991, 432, 467–479. [Google Scholar] [CrossRef]
- Lubrecht, A.A. The Numerical Solution of the Elastohydrodynamically Lubricated Line- and Point Contact Problem, Using Multigrid Techniques. Ph.D. Thesis, University of Twente, Enschede, The Netherlands, 1987. [Google Scholar]
- Venner, C.H. Multilevel Solution of the EHL Line and Point Contact Problems. Ph.D. Thesis, University of Twente, Enschede, The Netherlands, 1991. [Google Scholar]
- Moes, H. Optimum Similarity Analysis with applications to Elastohydrodynamic Lubrication. Wear 1992, 159, 57–66. [Google Scholar] [CrossRef] [Green Version]
- Moes, H. Lubrication and Beyond–University of Twente Lecture Notes Code 115531; University of Twente: Enschede, The Netherlands, 2000. [Google Scholar]
- Evans, H.P.; Snidle, R.W. The Isothermal Elastohydrodynamic Lubrication of Spheres. J. Lubr. Technol. 1981, 103, 547–557. [Google Scholar] [CrossRef]
- Hamrock, B.J.; Dowson, D. Isothermal Elastohydrodynamic Lubrication of Point Contacts. Part III - Fully Flooded Results. J. Lubr. Technol. 1977, 99, 264–279. [Google Scholar] [CrossRef]
- Chittenden, R.J.; Dowson, D.; Dunn, J.F.; Taylor, C.M. A theoretical analysis of the isothermal elastohydrodynamic lubrication of concentrated contacts. I. Direction of lubricant entrainment coincident with the major axis of the Hertzian contact ellipse. Proc. R. Soc. Lond. A 1985, 397, 245–269. [Google Scholar] [CrossRef]
- Nijenbanning, G.; Venner, C.H.; Moes, H. Film thickness in elastohydrodynamically lubricated elliptic contacts. Wear 1994, 176, 217–229. [Google Scholar] [CrossRef] [Green Version]
- Chaomleffel, J.-P.; Dalmaz, G.; Vergne, P. Experimental results and analytical film thickness predictions in EHD rolling point contacts. Tribol. Int. 2007, 40, 1543–1552. [Google Scholar] [CrossRef]
- Sperka, P.; Krupka, I.; Hartl, M. Analytical Formula for the Ratio of Central to Minimum Film Thickness in a Circular EHL Contact. Lubricants 2018, 6, 80. [Google Scholar] [CrossRef] [Green Version]
- Dyson, A.; Naylor, H.; Wilson, A.R. Paper 10: The Measurement of Oil-Film Thickness in Elastohydrodynamic Contacts. Proc. Inst. Mech. Eng. Conf. Proc. 1965, 180, 119–134. [Google Scholar] [CrossRef]
- Dowson, D.; Higginson, G.R. Elasto-Hydrodynamic Lubrication, SI ed.; Pergamon Press: Oxford, UK, 1977; ISBN 0080213022. [Google Scholar]
- Vergne, P.; Bair, S. Classical EHL Versus Quantitative EHL: A Perspective Part I—Real Viscosity-Pressure Dependence and the Viscosity-Pressure Coefficient for Predicting Film Thickness. Tribol. Lett. 2014, 54, 1–12. [Google Scholar] [CrossRef]
- Venner, C.H.; Bos, J. Effects of lubricant compressibility on the film thickness in EHL line and circular contacts. Wear 1994, 173, 151–165. [Google Scholar] [CrossRef] [Green Version]
- Habchi, W.; Bair, S. Quantitative Compressibility Effects in Thermal Elastohydrodynamic Circular Contacts. J. Tribol. Trans. ASME 2013, 135, 6. [Google Scholar] [CrossRef]
- Canzi, A.; Venner, C.H.; Lubrecht, A.A. Film thickness prediction in elastohydrodynamically lubricated elliptical contacts. Proc. IMechE 2010, 224, 917–923. [Google Scholar] [CrossRef]
- Cheng, H.S. Isothermal Elastohydrodynamic Theory for the Full Range of Pressure-Viscosity Coefficient. J. Lubr. Technol. 1972, 94, 35–43. [Google Scholar] [CrossRef] [Green Version]
- Greenwood, J.A.; Kauzlarich, J.J. Inlet Shear Heating in Elastohydrodynamic Lubrication. J. Lubr. Technol. 1973, 95, 417–423. [Google Scholar] [CrossRef]
- Herschel, W.H. The Change in Viscosity of Oils with the Temperature. J. Ind. Eng. Chem. 1922, 14, 715–722. [Google Scholar] [CrossRef]
- Crook, A.W. The lubrication of rollers III. A theoretical discussion of friction and the temperatures in the oil film. Philos. Trans. R. Soc. Lond. A 1961, 254, 237–258. [Google Scholar] [CrossRef]
- Crook, A.W. The lubrication of rollers II. Film thickness with relation to viscosity and speed. Philos. Trans. R. Soc. Lond. A 1961, 254, 223–236. [Google Scholar] [CrossRef]
- Murch, L.E.; Wilson, W.R.D. A Thermal Elastohydrodynamic Inlet Zone Analysis. J. Lubr. Technol. 1975, 97, 212. [Google Scholar] [CrossRef]
- Jackson, A. A Simple Method for Determining Thermal EHL Correction Factors for Rolling Element Bearings and Gears. ASLE Trans. 1981, 24, 159–163. [Google Scholar] [CrossRef]
- Wilson, W.R.D.; Sheu, S. Effect of Inlet Shear Heating Due to Sliding on Elastohydrodynamic Film Thickness. J. Lubr. Technol. 1983, 105, 187–188. [Google Scholar] [CrossRef]
- Pandey, R.K.; Ghosh, M.K. Thermal effects on film thickness and traction in rolling/sliding EHL line contacts—An accurate inlet zone analysis. Wear 1996, 192, 118–127. [Google Scholar] [CrossRef]
- Gupta, P.K.; Cheng, H.S.; Zhu, D.; Forster, N.H.; Schrand, J.B. Viscoelastic Effects in MIL-L-7808-Type Lubricant, Part I: Analytical Formulation. Tribol. Trans. 1992, 35, 269–274. [Google Scholar] [CrossRef]
- Wang, S.; Cusano, C.; Conry, T.F. Thermal Analysis of Elastohydrodynamic Lubrication of Line Contacts Using the Ree-Eyring Fluid Model. J. Tribol. Trans. ASME 1991, 113, 232–242. [Google Scholar] [CrossRef] [Green Version]
- Ståhl, J.; Jacobson, B.O. A non-Newtonian model based on limiting shear stress and slip planes—Parametric studies. Tribol. Int. 2003, 36, 801–806. [Google Scholar] [CrossRef]
- Carreau, P.J. Rheological Equations from Molecular Network Theories. Trans. Soc. Rheol. 1972, 16, 99–127. [Google Scholar] [CrossRef]
- Jang, J.Y.; Khonsari, M.M.; Bair, S. Correction Factor Formula to Predict the Central and Minimum Film Thickness for Shear-Thinning Fluids in EHL. J. Tribol. Trans. ASME 2008, 130, 235. [Google Scholar] [CrossRef]
- Kumar, P.; Khonsari, M.M. EHL Circular Contact Film Thickness Correction Factor for Shear-Thinning Fluids. J. Tribol. Trans. ASME 2008, 130, 3271. [Google Scholar] [CrossRef]
- Habchi, W.; Bair, S.; Qureshi, F.; Covitch, M. A Film Thickness Correction Formula for Double-Newtonian Shear-Thinning in Rolling EHL Circular Contacts. Tribol. Lett. 2013, 50, 59–66. [Google Scholar] [CrossRef]
- Hamrock, B.J.; Schmid, S.R.; Jacobson, B.O. Fundamentals of Fluid Film Lubrication; Dekker: New York, NY, USA, 2004; ISBN 0-8247-5371-2. [Google Scholar]
- Hamrock, B.J.; Dowson, D. Isothermal Elastohydrodynamic Lubrication of Point Contacts: Part IV—Starvation Results. J. Lubr. Technol. 1977, 99, 15. [Google Scholar] [CrossRef]
- Wedeven, L.D.; Evans, D.; Cameron, A. Optical Analysis of Ball Bearing Starvation. J. Lubr. Technol. 1971, 93, 349–361. [Google Scholar] [CrossRef] [Green Version]
- Wiśniewski, M. Einfluß eines begrenzten Ölangebotes auf die elastohydrodynamische Schmierung von Zahnrädern. Tribol. Schmierungstech. 1983, 30, 270–277. [Google Scholar]
- Rosenkranz, A.; Szurdak, A.; Gachot, C.; Hirt, G.; Mücklich, F. Friction reduction under mixed and full film EHL induced by hot micro-coined surface patterns. Tribol. Int. 2016, 95, 290–297. [Google Scholar] [CrossRef]
- Marian, M.; Grützmacher, P.; Rosenkranz, A.; Tremmel, S.; Mücklich, F.; Wartzack, S. Designing surface textures for EHL point-contacts—Transient 3D simulations, meta-modeling and experimental validation. Tribol. Int. 2019, 137, 152–163. [Google Scholar] [CrossRef]
- Marian, M.; Tremmel, S.; Wartzack, S. Microtextured surfaces in higher loaded rolling-sliding EHL line-contacts. Tribol. Int. 2018, 127, 420–432. [Google Scholar] [CrossRef]
- Simon, V. Influence of machine tool setting parameters on EHD lubrication in hypoid gears. Mech. Mach. Theory 2009, 44, 923–937. [Google Scholar] [CrossRef]
- Simon, V.V. Improved mixed elastohydrodynamic lubrication of hypoid gears by the optimization of manufacture parameters. Wear 2019, 438–439. [Google Scholar] [CrossRef]
- Choo, J.W.; Olver, A.V.; Spikes, H.A. The influence of transverse roughness in thin film, mixed elastohydrodynamic lubrication. Tribol. Int. 2007, 40, 220–232. [Google Scholar] [CrossRef]
- Venner, C.H.; Lubrecht, A.A. Numerical Simulation of a Transverse Ridge in a Circular EHL Contact under Rolling/Sliding. J. Tribol. 1994, 116, 751. [Google Scholar] [CrossRef]
- Choo, J.W.; Olver, A.V.; Spikes, H.A.; Dumont, M.-L.; Ioannides, E. The Influence of Longitudinal Roughness in Thin-Film, Mixed Elastohydrodynamic Lubrication. Tribol. Trans. 2006, 49, 248–259. [Google Scholar] [CrossRef]
- Ehret, P.; Dowson, D.; Taylor, C.M. Waviness Orientation in EHL Point Contact. In The Third Body Concept Interpretation of Tribological Phenomena; Elsevier: Amsterdam, The Netherlands, 1996; pp. 235–244. ISBN 9780444825025. [Google Scholar]
- Redlich, A.C.; Bartel, D.; Schorr, H.; Deters, L. A Deterministic EHL Model for Point Contacts in Mixed Lubrication Regime. In Thinning Films and Tribological Interfaces, Proceedings of the 26th Leeds-Lyon Symposium on Tribology, Leeds, UK, 14–17 September 1999; Elsevier: Amsterdam, The Netherlands, 2000; pp. 85–93. ISBN 9780444505316. [Google Scholar]
- Choo, J.W.; Glovnea, R.P.; Olver, A.V.; Spikes, H.A. The Effects of Three-Dimensional Model Surface Roughness Features on Lubricant Film Thickness in EHL Contacts. J. Tribol. 2003, 125, 533. [Google Scholar] [CrossRef]
- Venner, C.H.; Napel, W.E. ten. Surface Roughness Effects in an EHL Line Contact. J. Tribol. Trans. ASME 1992, 114, 616–622. [Google Scholar] [CrossRef]
- Bartel, D. Simulation von Tribosystemen. Grundlagen und Anwendungen, 1st ed.; Vieweg + Teubner: Wiesbaden, Germany, 2010; ISBN 978-3-8348-1241-4. [Google Scholar]
- Zhu, D.; Cheng, H.S. Effect of Surface Roughness on the Point Contact EHL. J. Tribol. Trans. ASME 1988, 110, 32–37. [Google Scholar] [CrossRef]
- Patir, N.; Cheng, H.S. An Average Flow Model for Determining Effects of Three-Dimensional Roughness on Partial Hydrodynamic Lubrication. J. Lubr. Technol. 1978, 100, 12–17. [Google Scholar] [CrossRef]
- Johnson, K.L.; Greenwood, J.A.; Poon, S.Y. A simple theory of asperity contact in elastohydro-dynamic lubrication. Wear 1972, 19, 91–108. [Google Scholar] [CrossRef]
- Greenwood, J.A.; Tripp, J.H. The Contact of Two Nominally Flat Rough Surfaces. Proc. Inst. Mech. Eng. 1970, 185, 625–633. [Google Scholar] [CrossRef]
- Patir, N.; Cheng, H.S. Application of Average Flow Model to Lubrication between Rough Sliding Surfaces. J. Lubr. Technol. 1979, 101, 220–229. [Google Scholar] [CrossRef]
- Peklenik, J. Grundlagen zur korrelationstheorie technischer Oberflächen. Ind. Anz. 1965, 87, 456–462. [Google Scholar]
- Kumar, P.; Jain, S.C.; Ray, S. Study of surface roughness effects in elastohydrodynamic lubrication of rolling line contacts using a deterministic model. Tribol. Int. 2001, 34, 713–722. [Google Scholar] [CrossRef]
- Masjedi, M.; Khonsari, M.M. On the effect of surface roughness in point-contact EHL: Formulas for film thickness and asperity load. Tribol. Int. 2015, 82, 228–244. [Google Scholar] [CrossRef]
- Wheeler, J.-D.; Vergne, P.; Fillot, N.; Philippon, D. On the relevance of analytical film thickness EHD equations for isothermal point contacts: Qualitative or quantitative predictions? Friction 2016, 4, 369–379. [Google Scholar] [CrossRef] [Green Version]
- Eyring, H. Viscosity, Plasticity, and Diffusion as Examples of Absolute Reaction Rates. J. Chem. Phys. 1936, 4, 283. [Google Scholar] [CrossRef]
- Lee, R.-T.; Hamrock, B.J. A Circular Non-Newtonian Fluid Model: Part I—Used in Elastohydrodynamic Lubrication. J. Tribol. Trans. ASME 1990, 112, 486–495. [Google Scholar] [CrossRef]
- Wang, J.; Venner, C.H.; Lubrecht, A.A. Central film thickness prediction for line contacts under pure impact. Tribol. Int. 2013, 66, 203–207. [Google Scholar] [CrossRef]
- Venner, C.H.; Wang, J.; Lubrecht, A.A. Central film thickness in EHL point contacts under pure impact revisited. Tribol. Int. 2016, 100, 1–6. [Google Scholar] [CrossRef]
- Holmberg, K.; Andersson, P.; Erdemir, A. Global energy consumption due to friction in passenger cars. Tribol. Int. 2012, 47, 221–234. [Google Scholar] [CrossRef]
- Björling, M.; Habchi, W.; Bair, S.; Larsson, R.; Marklund, P. Friction Reduction in Elastohydrodynamic Contacts by Thin-Layer Thermal Insulation. Tribol. Lett. 2014, 53, 477–486. [Google Scholar] [CrossRef] [Green Version]
- Vakis, A.I.; Yastrebov, V.A.; Scheibert, J.; Nicola, L.; Dini, D.; Minfray, C.; Almqvist, A.; Paggi, M.; Lee, S.; Limbert, G.; et al. Modeling and simulation in tribology across scales: An overview. Tribol. Int. 2018, 125, 169–199. [Google Scholar] [CrossRef]
- Otero, J.E.; Ochoa, E.D.L.G.; Tanarro, E.C.; Morgado, P.L.; Lantada, A.D.; Munoz-Guijosa, J.M.; Sanz, J.L.M. Artificial neural network approach to predict the lubricated friction coefficient. Lubr. Sci. 2014, 26, 141–162. [Google Scholar] [CrossRef]






| Parameter | Typical Range |
|---|---|
| G | 1500–6000 |
| U | 10−13–10−8 |
| W | 10−6–10−3 |
| Hc | 1.5 × 10−5–25 × 10−5 |
| Hmin | 10−5–2 × 10−4 |
| Line-Contact | Point-Contact | Elliptical Contact | ||
|---|---|---|---|---|
| minimum film thickness | Dowson and Higginson [14], Moes [16], Dowson [25], Jacobson and Hamrock [26], Johnson [19], Myers et al. [28], Moes [31] | Evans and Snidle [33], Hamrock and Dowson [34], Chittenden et al. [35], | Hamrock and Dowson [34], Chittenden et al. [35] | |
| central film thickness | Dowson and Toyoda [27], Moes [32] | Evans and Snidle [33], Hamrock and Dowson [34], Chittenden et al. [35], Moes [32], Nijenbanning et al. [36] | Hamrock and Dowson [34], Chittenden et al. [35], Nijenbanning et al. [36] | |
| correction factor for | fluid compressibility | Canzi et al. [44] | Canzi et al. [44] | Canzi et al. [44] |
| thermal effects | Greenwood and Kauzlarich [46], Murch and Wilson [50], Jackson [51], Wilson and Sheu [52], Pandey and Gosh [53] | |||
| non-Newtonian fluid behavior | Bair [22], Jang et al. [58] | Kumar et al. [59], Habchi et al. [60] | ||
| starvation | Hamrock and Dowson [62] Wisniewski [64] | |||
| surface roughness and asperity contact | Kumar et al. [84] | Zhu and Cheng [78], Masjedi and Khonsari [85] | Masjedi and Khonsari [85] |
| Numerical EHL Simulation | Analytically Solvable Proximity Equation | Machine Learning Algorithm | |
|---|---|---|---|
| software resources | High | very low | low |
| calculation time | minutes to hours | few minutes | few seconds |
| accuracy | very high | medium to good | good |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marian, M.; Bartz, M.; Wartzack, S.; Rosenkranz, A. Non-Dimensional Groups, Film Thickness Equations and Correction Factors for Elastohydrodynamic Lubrication: A Review. Lubricants 2020, 8, 95. https://doi.org/10.3390/lubricants8100095
Marian M, Bartz M, Wartzack S, Rosenkranz A. Non-Dimensional Groups, Film Thickness Equations and Correction Factors for Elastohydrodynamic Lubrication: A Review. Lubricants. 2020; 8(10):95. https://doi.org/10.3390/lubricants8100095
Chicago/Turabian StyleMarian, Max, Marcel Bartz, Sandro Wartzack, and Andreas Rosenkranz. 2020. "Non-Dimensional Groups, Film Thickness Equations and Correction Factors for Elastohydrodynamic Lubrication: A Review" Lubricants 8, no. 10: 95. https://doi.org/10.3390/lubricants8100095
APA StyleMarian, M., Bartz, M., Wartzack, S., & Rosenkranz, A. (2020). Non-Dimensional Groups, Film Thickness Equations and Correction Factors for Elastohydrodynamic Lubrication: A Review. Lubricants, 8(10), 95. https://doi.org/10.3390/lubricants8100095